蓄意施放化学战剂CWA(chemical warfare agent)或生物战剂BWA(biological warfare agent)毒剂对建筑人居环境健康、安全提出了挑战[1-3].随着建筑集中式空调系统污染与卫生问题日益突出,管内微生物及颗粒污染控制受到重视,但与生化预警的技术策略不同[4-5]. Chen等[6-8]运用多目标函数优化法对建筑多区网络模型中的传感器优化布置进行了分析,但并未考虑建筑风系统中可能发生的突发污染.文献[9-10]深入分析了空调风系统在生化扩散应对策略方面存在的争议性问题,比如,到底应该关闭空调系统、全新风运行还是加压送风,以及如何确定系统响应机制等.中国公共建筑面积超过50亿平方米,5亿平方米以上设有集中式空调风系统(以集中处理的空气为介质,通过风管道输送到建筑内各区域,再经过回风形成一个空气循环回路),集中空调风系统内污染扩散速度快,一般几分钟内即可将污染物输送至整个建筑,极易被利用作为挥发性CWA等毒剂的传播通道,其潜在危险性已引起关注[11-13].
本文以空调风系统最低污染物输出量为优化目标函数, 基于遗传算法实现了空调风系统内传感器的优化布置.在优化过程中,首先将空调风系统划分为若干节点,每一个节点均是一个可能的污染源释放位置及传感器布置位置,污染物在节点处的释放概率假设与该节点处的风量相关,即以某节点风量/所有节点的总风量作为污染物在某节点的释放概率,得到污染源在风系统内的概率分布后,以传感器的布置位置为具体优化参数,运用遗传算法在风系统内所有节点进行全局寻优,最后得到风系统最低污染物输出量所对应的传感器优化布置方案.
1 优化模型的建立 1.1 优化目标函数对于空调风系统传感器布置优化,需解决的核心问题是在突发污染预警中,构建基于系统最低输出量的优化目标函数,即污染物在风系统内任意位置投放后,通过该目标函数优化后的传感器布置方案可以保证当传感器监测到污染物时经由风系统内各风口进入室内的污染物量最小.
风系统最低输出量Jrel是在传感器报警后,确定经由风系统末端进入到建筑空间的污染物量,用于判断每次生化袭击对建筑的危害程度.首先需要确定第k释放位置的风系统总污染物输出量Ek(假设风系统内所需布置的传感器的数目已知),Ek定义为
| $ {\mathit{E}_\mathit{k}}{\rm{ = }}\sum\limits_{\mathit{m} = 1}^\mathit{S} {\sum\limits_{\mathit{t} = 0}^{{\mathit{t}_{{\rm{det - }}\mathit{k}}}} {{\rm{Exp}}\left( {\mathit{m}{\rm{, }}\mathit{t}} \right)} } {\rm{, }} $ | (1) |
式中:Exp(m, t)为第m风口在时间t时的污染物输出量,S为风口数量,tdet-k为假设在k位置投放污染物时距离污染源最近的传感器监测到污染物的时间,该时间可根据式(2)进行计算,这里假设所用传感器均为理想传感器,即不存在监测误差且监测浓度阈值趋于0(当传感器监测断面的浓度大于0时,传感器即发出报警).
| $ {\mathit{t}_{{\rm{det - }}\mathit{k}}}{\rm{ = }}{\mathit{\mu }_{{\rm{near}}}}{\rm{ - 3}}{\mathit{\sigma }_{{\rm{near}}}}{\rm{, }} $ | (2) |
式中:μnear为距离污染源最近的传感器节点达到峰值浓度的时间;σnear为距离污染源最近的传感器节点时间的总体方差,其详细推导参考文献[15].
Exp(m, t)可根据式(3)~(6)进行计算.
| $ {\rm{Exp}}\left( {\mathit{m}{\rm{, }}\mathit{t}} \right){\rm{ = }}\int_{\mathit{\mu - }{\rm{3}}{\mathit{\sigma }_{\mathit{m - }{\rm{1}}}}}^{\mathit{\mu }{\rm{ + 3}}{\mathit{\sigma }_{\mathit{m - }{\rm{1}}}}} {{\mathit{C}_{{\rm{1}}\mathit{m}}}{\rm{\cdot}}{\mathit{Q}_\mathit{m}}{\rm{d}}\mathit{t}} {\rm{, }} $ | (3) |
| $ \begin{array}{l} {\mathit{C}_{{\rm{1}}\mathit{m}}}{\rm{ = }}\frac{{{\mathit{C}_{{\rm{2}}\mathit{m - }{\rm{1}}}}{\mathit{u}_{\mathit{m - }{\rm{1}}}}}}{{\sqrt {{\rm{4 \mathit{ π} }}{\mathit{\varepsilon }_\mathit{x}}{\rm{(}}{\mathit{t}_\mathit{m}}{\rm{ - }}{\mathit{t}_{\mathit{m - }{\rm{1}}}}{\rm{)}}} }}{\rm{\cdot}}\\ \;\;\;\;\;\;\;\;{\rm{exp - }}\left[{\frac{{{{{\rm{(}}{\mathit{x}_\mathit{m}}{\rm{-}}{\mathit{x}_{\mathit{m-}{\rm{1}}}}{\rm{-}}{\mathit{u}_{\mathit{m - }{\rm{1}}}}{\rm{(}}{\mathit{t}_\mathit{m}}{\rm{ - }}{\mathit{t}_{\mathit{m - }{\rm{1}}}}{\rm{))}}}^{\rm{2}}}}}{{{\rm{4}}{\mathit{\varepsilon }_\mathit{x}}{\rm{(}}{\mathit{t}_\mathit{m}}{\rm{ - }}{\mathit{t}_{\mathit{m - }{\rm{1}}}}{\rm{)}}}}} \right]{\rm{ = }}\\ \;\;\;\;\;\;\;\;\;\;\frac{{{{\rm{C}}_{{\rm{2}}\mathit{m} - {\rm{1}}}}}}{{\sqrt {{\rm{2 \mathit{ π}} }}{\mathit{\sigma }_{\mathit{m - }{\rm{1}}}} }} \cdot {\rm{exp}}\left[{{\rm{-}}\frac{{{{\left( {{\mathit{t}_\mathit{m}}{\rm{-}}{\mathit{t}_{\mathit{m-}{\rm{1}}}}{\rm{ - }}\frac{{{\mathit{x}_\mathit{m}}{\rm{ - }}{\mathit{x}_{\mathit{m - }{\rm{1}}}}}}{{{\mathit{u}_{\mathit{m - }{\rm{1}}}}}}} \right)}^{\rm{2}}}}}{{{\rm{2}}\mathit{\sigma }_{\mathit{m}{\rm{ - 1}}}^2}}} \right]{\rm{.}} \end{array} $ | (4) |
| $ \mathit{\mu }{\rm{ = }}{\mathit{t}_{\mathit{pm}}}{\rm{ = }}{\mathit{t}_{\mathit{pm}{\rm{ - 1}}}}{\rm{ + }}\frac{{{\mathit{x}_\mathit{m}}{\rm{ - }}{\mathit{x}_{\mathit{m - }{\rm{1}}}}}}{{{\mathit{u}_{\mathit{m - }{\rm{1}}}}}}{\rm{, }} $ | (5) |
| $ {\mathit{\sigma }_{\mathit{m}{\rm{ - 1}}}}{\rm{ = }}\sqrt {{\rm{2}}{\mathit{\varepsilon }_\mathit{x}}\left( {{\mathit{t}_\mathit{m}}{\rm{ - }}{\mathit{t}_{\mathit{m}{\rm{ - 1}}}}} \right){\rm{/}}\mathit{u}_{\mathit{m}{\rm{ - 1}}}^2} {\rm{.}} $ | (6) |
式中:tpm为m节点位置处的污染物浓度峰值时间(即该节点达到污染物浓度峰值时的系统时间);σm-1与σnear的定义相似,均为时间方差,表示污染物浓度在风口处的持续时间;C1m为风口m处污染物浓度;Qm为风口m处的风量,可用风量测试设备实际测得或通过风系统水力计算得到;C2m-1为风口m上游m-1节点位置处的污染物浓度;tm为m节点位置处的系统时间;um为风口m之前管段的平均风速;xm为风口m至污染源的距离;εx为湍流扩散系数.各参数的理论推导及相关实验验证详见文献[14-15].
对于所有可能的N个释放位置,风系统污染物总输出量Jrel定义为
| $ {\mathit{J}_{{\rm{rel}}}}{\rm{ = }}\sum\limits_{\mathit{k} = 1}^\mathit{N} {{\mathit{P}_\mathit{k}}{\rm{ \times }}{\mathit{E}_\mathit{k}}} {\rm{, }} $ | (7) |
式中Pk为在k节点位置处污染物的投放概率,从形式上看,Jrel实质上是一个风系统污染物概率输出量.
假设袭击者对风系统的构造及运行规律有一定的了解,那么他在风量越大的节点投放污染物的概率也越高,定义一个基于风系统风量分布的污染物投放概率函数:
| $ {\mathit{P}_\mathit{k}}{\rm{ = }}\frac{{{\mathit{Q}_\mathit{k}}}}{{\sum\limits_{\mathit{k} = 1}^\mathit{N} {{\mathit{Q}_\mathit{k}}} }}{\rm{, }} $ | (8) |
式中Qk为风系统第k个节点处的风量,N为风系统内节点总数.
1.2 优化变量与约束条件在空调风系统传感器优化布置过程中,首先需将风系统划分为若干节点,节点划分依据主要是参考前人在水污染领域及室内空气品质领域的研究.首先在水污染领域,为了对污染监测站的位置进行优化,设置节点进行分析是常用方法[16, 18];其次在室内空气品质领域,污染物多区模型建立的实质就是节点分析法,将各房间当作节点考虑并添加适当的边界条件,从而得到简化后的模型[8, 10].由此可知节点的设置是对所求问题的适当简化,否则系统内所有点都将作为待计算或待优化参数,优化过程中将会产生巨量的计算负荷.本文假设每一个节点均是一个可能的袭击者投放污染物的位置及传感器布置位置,以传感器的布置位置X为具体优化参数,将该参数作为优化变量,给出X的约束范围:
| $ \mathit{X} \in {\rm{(}}{\mathit{X}_{{\rm{node1}}}}{\rm{, }}{\mathit{X}_{{\rm{node2}}}}{\rm{, }} \cdots {\rm{, }}{\mathit{X}_{{\rm{node, max}}}}{\rm{), }} $ | (9) |
式中(Xnode1, Xnode2, …, Xnode, max)分别为风系统中各节点所对应的位置.上述位置均预先存储在遗传算法所需调用的数据库中.
1.3 基于遗传算法的传感器优化布置方法遗传算法(GA)模拟自然界的生物演化过程,利用复制、交叉、变异等操作,使优胜者繁殖, 劣败者淘汰,一代代的重复同样的操作最终找到最优解或接近最优解,对高度非线性优化问题更显示出较强的适应性[16-18].基于遗传算法的诸多优点,本文将这一算法应用于求解传感器优化目标函数,即遗传算法的适应度函数,其数学表达式如下:
| $ \mathit{g}\left( \mathit{a} \right){\rm{ = min(}}{\mathit{J}_{{\rm{rel}}}}{\rm{)}}{\rm{.}} $ | (10) |
传感器优化实现流程如图 1所示,其具体算法步骤描述如下:

|
图 1 传感器优化实现过程 Figure 1 Process of optimal sensor layout |
1) 初始化种群.在给定的参数范围内随机均匀地产生用二进制编码方式表示的初始种群,种群数量为N,这里的种群即为传感器可能的布置位置.
2) 计算适应度.计算对于所有可能的N个污染物投放位置,采用某传感器布置方案下的风系统经由风口输出到建筑内污染物的量Jrel.
3) 交叉.将步骤1)中筛选出的N个种群个体进行杂交.杂交算法采用如下公式:
| $ \left\{ \begin{array}{l} \mathit{X'}{\rm{ = }}\mathit{rX}{\rm{ + }}\left( {{\rm{1 - }}\mathit{r}} \right)\mathit{Y}{\rm{, }}\\ \mathit{Y'}{\rm{ = }}\mathit{rY}{\rm{ + }}\left( {{\rm{1 - }}\mathit{r}} \right)\mathit{X}{\rm{.}} \end{array} \right. $ | (11) |
式中:X与Y分别为父代个体,X′与Y′分别为新产生的子代个体,r为[0, 1]上的均匀实数.
4) 变异.对步骤3)中的N个个体按一定的变异率进行变异,变异操作为随机对个体的某位二进制编码进行改变,并重复步骤2).
5) 对步骤2)中计算所得到的适应度按由大到小的顺序排序,挑选出适应度小的个体.
6) 比较判断新一代个体是否满足终止条件.结果满足则停止,否则转至步骤2)继续进行迭代计算.
2 传感器优化布置结果及分析 2.1 采用不同数目传感器的优化结果对比针对如图 2所示的风系统,通过前期计算已知该系统总风量及各管段风量,完成了管网的一维动力学模型构建,风系统各主要参数见表 1.
|
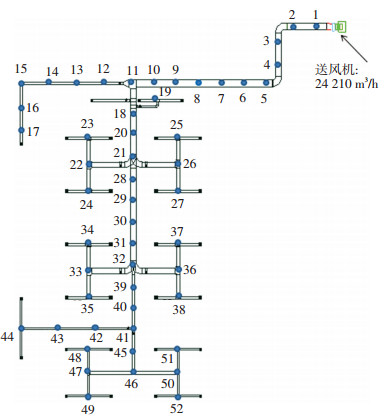
圆点表示所设节点,数字代表节点编号 图 2 设置节点后的风系统示意 Figure 2 Air duct system |
| 表 1 风系统主要参数 Table 1 Parameters of ventilation system |
通过前述算法可以模拟传感器位于系统内任意节点时,源位置处投放的污染物经由风系统传播至最近传感器节点的时刻,同时可计算该时刻下,通过风系统末端输出到整个建筑内污染物的量.
假设袭击者于风系统中的某节点处投放100 mg的污染物,则共有52个节点可供袭击者投放污染物,根据式(8)计算的k节点位置处污染物的投放概率Pk见表 2,其中节点1~11位于主风管,且该管段不含送风口,故节点风量最大,均等于总送风量24 210 m3/h,基于风量分布的污染物投放概率也最大,在这些节点投放污染物对整个风系统所负责的区域危害最大且是等效的.风系统末端节点(如节点48~49等)的风量最小,基于风量分布计算的污染物投放概率也最小,在这些节点投放污染物对整个风系统所负责的区域危害最小.
| 表 2 k节点位置处的污染物投放概率Pk Table 2 Probability Pk for the kth injection node to occur |
由式(9)已知待优化传感器布置位置的约束范围为X∈(Xnode1, Xnode2, …, Xnode52).由于对该风系统而言,所需布置的传感器数目是未知的,故首先考虑传感器数目对风系统最低输出量的影响.假设传感器数目Ns的变化范围为1≤Ns≤5, Ns∈int,遗传算法基本参数设置见表 3.
| 表 3 遗传算法基本参数设置 Table 3 Parameters of GA method |
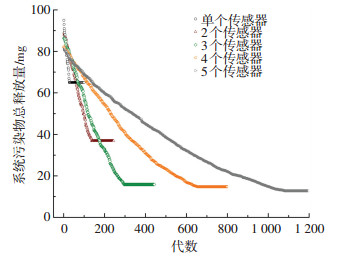
根据上述优化已知条件及待优化参数约束范围,按照遗传算法的计算步骤,计算出采用不同数目传感器的系统污染物总输出量(适应度函数)随遗传子代数的变化规律,见图 3.可以看出,风系统内所设传感器数目越多,系统污染物总输出量越小,但遗传算法收敛所需子代数越多,从而导致计算所需的负荷越大,时间也越长.
|
图 3 系统污染物总输出量随遗传代数的变化 Figure 3 Curves of the total contaminant exposure with the genetic generations |
表 4为采用不同数目传感器条件下的风系统传感器优化布置结果.可以看出,当风系统中只设置单个传感器时,由于只有52种可能的传感器布置方案,遗传算法收敛很快,但按概率投放至风系统内的100 mg污染物中有65.0 mg在首个传感器监测到污染物(或污染源位于传感器所在位置之后,传感器无法监测到该污染物)时已通过风口进入到室内,对室内人员造成杀伤,可见风系统内仅设置单个传感器并不能有效应对可能的突发污染事件.当风系统内采用2个传感器时,经优化布置后的传感器位于节点11和41,这两个节点上的传感器能够有效覆盖风系统的主管段,系统污染物的最低输出量降至36.8 mg.随着风系统内传感器数目的增多,系统污染物最低输出量降低的幅度越来越小,但遗传算法收敛所需子代数却大幅上升.当风系统中的传感器数目超过3个时,每增加一个传感器,风系统污染物最低输出量占污染物总量的比仅降低2.0%左右,考虑到单个传感器成本较高,该风系统宜采用的传感器数目为3个.
| 表 4 采用不同数目传感器的风系统传感器优化布置结果 Table 4 Comparison among optimal sensor layouts in ventilation system using different number of sensors |
根据上述分析可知,对于如图 2所示的风系统,在其中设置3个传感器进行优化既可以得到较低的系统污染物总输出量,也可兼顾监控系统成本,本节对比了该风系统在安装3个传感器时经优化与未经优化的传感器布置方案.由于3个传感器共有C523=22 100种布置方案,故仅将遗传算法优化后的传感器布置方案(见表 4)与遗传算法初始随机生成的20种方案进行对比,结果如图 4所示,其中方案1~20均为未经优化的传感器布置方案,方案21为经优化后的传感器布置方案.由图 4可以看出,遗传算法初始随机生成的20种方案的系统污染物总输出量维持在一个较高的水平,说明即使在风系统中设置3个传感器,随机地决定各传感器的布置位置并不能在突发污染发生时快速而有效地监测到污染物,大部分污染物仍会经由风系统末端进入室内;而经遗传算法优化后的传感器布置方案将系统污染物总输出量降至15 mg,仅为袭击者初始投放总量的15%,同时比未经优化方案的系统污染物总输出量平均降低59.3%.说明优化后的传感器布置方案能够在突发污染发生时对室内人员提供较大程度的保护,满足当首个传感器监测到污染物浓度数据时,污染物对该风系统所负责的建筑局域影响最小,此时,将浓度数据反馈回安控中心,利用一定的方法反演出污染源位置并采取相应的应急措施,对为室内人员争取足够的逃生时间,形成空气传播突发污染的预警技术具有重要的实际应用价值.

|
图 4 经优化与未经优化的传感器布置方案对比 Figure 4 Comparison between optimal sensor layout and un-optimized sensor layouts |
风系统内部节点划分主要参考地下水及输配水系统中节点划分的原则[18-19],首先系统流量发生变化的位置需要设置节点,包括系统中的三通/四通等;其次,由于生化袭击具有随机性,理论上风系统中的每个位置都可能成为污染物的投放位置,因此,对于长直管段也需要将其进一步划分为若干节点,这样划分风系统既能保证传感器的布置优化是一个全局寻优过程,又能避免将系统内的所有点都作为待计算或待优化参数产生巨量计算负荷.
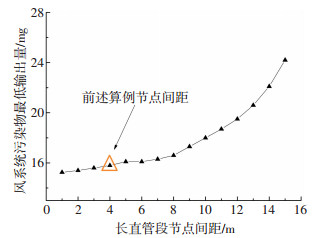
对于风系统内设置3个传感器的系统,长直管段上节点间距的选取对风系统污染物最低输出量的影响见图 5.图中每个点均是该节点划分条件下经遗传算法优化后的传感器布置方案所对应的风系统污染物最低输出量.可以看出,在三通/四通位置处的节点已设置的条件下,风系统污染物最低输出量随长直管段节点间距的减小而减小,但该优化目标函数值对间距的大小并不敏感,当长直管段节点间距小于10 m时,通过末端风口进入房间的污染物量变化较小.这是因为当长直管段节点间距在一定范围内增大时,系统所包含的节点总数降低,也就意味着可能发生突发污染的节点数减少.根据式(8),风系统内某节点的风量Qk并不会改变,可能发生突发污染的节点总数N降低,则某节点污染物投放概率Pk增大,仍然满足
|
图 5 节点间距对优化目标函数值的影响 Figure 5 Impact of nodes' distance on the optimized objective function value |
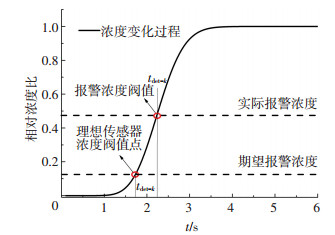
前述算例中的传感器均为理想传感器,即假设不存在监测误差且报警浓度阈值趋于0,而在实际应用中,传感器都会有监测误差范围和报警浓度阈值,所以,需要讨论传感器可靠性对优化结果的影响.根据式(1),传感器监测误差并不影响传感器报警时的风系统污染物最低输出量,当传感器监测到风系统中有污染物浓度时就会报警并向建筑安控中心反馈实时浓度,传感器监测误差实际只影响反馈实时浓度的准确性而与传感器优化布置结果无关.报警浓度阈值会影响式(1)中的tdet-k,由于tdet-k为假设在k位置投放污染物时距离污染源最近的传感器监测到污染物的时间,而该时间所对应的浓度正是传感器的报警浓度阈值,所以在浓度上升曲线上,报警浓度阈值提高所对应的tdet-k增大,如图 6所示.根据式(1),风系统污染物最低输出量也会随之增大.
|
图 6 报警浓度阈值对tdet-k的影响 Figure 6 Impact of alarm concentration threshold on the tdet-k |
1) 通过对比算例中采用不同数量传感器的优化布置结果,表明针对某一特定风系统,所设传感器数量越多,得到的风系统污染物最低输出量越小.但当风系统中的传感器数目超过3个时,每增加一个传感器,系统污染物最低输出量占污染物总量的比仅降低2.0%左右,考虑到单个传感器成本较高,该风系统宜采用的传感器数目为3个.
2) 对比了算例中风系统采用3个传感器时,经优化与未经优化的传感器布置方案.结果表明,经遗传算法优化后的传感器布置方案将系统污染物总输出量降至15 mg,仅为袭击者投放总量的15%,同时比未经优化方案的系统污染物总输出量平均降低59.3%.
3) 风系统污染物最低输出量传感器在三通/四通位置处节点已设置的条件下,风系统污染物最低输出量对长直管段节点间距的大小并不敏感,当长直管段节点间距小于10 m时,通过末端风口进入房间的污染物量变化较小.传感器监测误差增大并不影响传感器的优化布置结果和目标函数值的大小,而风系统污染物最低输出量随传感器报警浓度阈值的升高而上升.
| [1] |
蔡浩, 龙惟定, 程宝义. 空气传播的生化袭击与建筑环境安全(3):生化毒剂的剂量反应关系[J].
暖通空调, 2006, 36(8): 42-46.
CAI Hao, LONG Weiding, CHENG Baoyi. Airborne biochemical attacks and building environment security (3):Relationship between dose of CBW agents and human responses[J]. Journal Heating Ventilating and Airconditioning, 2006, 36(8): 42-46. |
| [2] |
吴春晓. 化学战剂的发展与防护[D]. 甘肃: 兰州大学, 2007.
WU Chunxiao. The progress and defence of chemical warfare agents[D]. Gansu: Lanzhou University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10730-2007114212.htm |
| [3] |
蔡浩, 龙惟定, 谭洪卫, 等. 空气传播的生化袭击与建筑环境安全(2):典型生化袭击场景的分析与评价[J].
暖通空调, 2005, 35(2): 52-56.
CAI Hao, LONG Weiding, TAN Hongwei, et al. Airborne biochemical attacks and building environment security (2): Analysis and evaluation of typical scenes of chemical and biological attacks[J]. Journal Heating Ventilating and Airconditioning, 2005, 35(2): 52-56. |
| [4] |
WILLIAM W N. Particle deposition from turbulent flow: Review of published research and its applicability to ventilation ducts in commercial buildings[R]. California: Lawrence Berkeley National Laboratory, 2003.
|
| [5] |
蔡嘉一, 林石碇, 江士豪, 等. 高铁地下站区发生化学攻击时之空调系统因应策略[J].
隧道建设, 2011, 31(1): 425-428.
CAI Jiayi, LIN Shiding, JIANG Shihao, et al. A response strategy of HVAC system for a chemical attack on high speed train subway station[J]. Tunnel Construction, 2011, 31(1): 425-428. |
| [6] |
CHEN Y L, WEN J. Comparison of sensor systems designed using multizone, zonal, and CFD data for protection of indoor environments[J].
Building and Environment, 2010, 45: 1061-1071.
DOI: 10.1016/j.buildenv.2009.10.015 |
| [7] |
CHEN Y L, WEN J. The selection of the most appropriate airflow model for designing indoor air sensor systems[J].
Building and Environment, 2012, 50: 34-43.
DOI: 10.1016/j.buildenv.2011.10.007 |
| [8] |
CHEN Y L, WEN J. Sensor system design for building indoor air protection[J].
Building and Environment, 2008, 43: 1278-1285.
DOI: 10.1016/j.buildenv.2007.03.011 |
| [9] |
瓦迪斯瓦夫·扬·科瓦尔斯基. 免疫建筑综合技术[M]. 蔡浩, 王晋生, 译. 北京: 中国建筑工业出版社, 2006.
KOWALSKI W J. Synthesis technique of immune building[M]. CAI Hao, WANG Jinsheng, translate. Beijing: China Building Industry Press, 2006. |
| [10] |
彭小勇. 大空间建筑突发事件毒气扩散和控制方法的研究[D]. 湖南: 国防科学技术大学, 2007.
PENG Xiaoyong. Research of the poison gas diffusion and controlling methods on emergent events in large space buildings[D]. Hunan: National University of Defense Technology, 2007. http://cdmd.cnki.com.cn/article/cdmd-90002-2008098737.htm |
| [11] |
WANG H, HARRISON K. Bayesian update method for contaminant source characterization in water distribution systems[J].
Water Resources Planning and Management, 2013, 139(1): 13-22.
DOI: 10.1061/(ASCE)WR.1943-5452.0000221 |
| [12] |
ZHANG T, CHEN Q, LIN C. Optimal sensor placement for airborne contaminant detection in an aircraft cabin[J].
HVAC & R Research, 2007, 13(5): 683-696.
|
| [13] |
CHEN C, CHEN Q. Predicting transient particle transport in enclosed environments with the combined computational fluid dynamics and Markov Chain method[J].
Indoor Air, 2014, 24: 81-92.
DOI: 10.1111/ina.2014.24.issue-1 |
| [14] |
曾令杰. 公共建筑风系统突发污染一维反问题研究[D]. 上海: 同济大学, 2016.
ZENG Lingjie. Research on one-dimensional inverse problem of sudden contamination through ventilation system in public buildings[D]. Shanghai: Tongji University, 2016. |
| [15] |
GAO Jun, ZENG Lingjie, WU Li, et al. Solution for sudden contamination transport through air duct system: Under a puff release[J].
Building and Environment, 2016, 100: 19-27.
DOI: 10.1016/j.buildenv.2016.01.024 |
| [16] |
董深, 吕谋, 盛泽斌, 等. 基于遗传算法的供水管网反问题漏失定位[J].
哈尔滨工业大学学报, 2013, 45(2): 106-110.
DONG Shen, LV Mou, SHENG Zebin, et al. Inverse transient leakage location of water supply network based on genetic algorithm[J]. Journal of Harbin Institute of Technology, 2013, 45(2): 106-110. DOI: 10.11918/j.issn.0367-6234.2013.02.019 |
| [17] |
赵麒, 谭羽非, 王琛. 基于火积耗散原理的热网加热器优化设计与分析[J].
哈尔滨工业大学学报, 2016, 48(8): 136-140.
ZHAO Qi, TANG Yufei, WANG Chen. Optimization design of thermal-system heater based on entransy dissipation theory[J]. Journal of Harbin Institute of Technology, 2016, 48(8): 136-140. DOI: 10.11918/j.issn.0367-6234.2016.08.023 |
| [18] |
PREIS A, OSTFELD A. Multi-objective contaminant sensor network design for water distribution systems[J].
Journal of Water Resources Planning and Management, 2008, 134: 366-377.
DOI: 10.1061/(ASCE)0733-9496(2008)134:4(366) |
| [19] |
BITHIN D, DIBAKAR C, ANIRBAN D. Identification of unknown groundwater pollution sources using classical optimization with linked simulation[J].
Journal of Hydro-environment Research, 2011, 5: 25-36.
|
 2018, Vol. 50
2018, Vol. 50


