2. 现代城市交通技术江苏高校协同创新中心(东南大学),南京 210096;
3. 南昌航空大学 土木建筑学院,南昌 330063
2. Jiangsu Province Collaborative Innovation Center of Modern Urban Traffic Technologies (Southeast University), Nanjing 210096, China;
3. School of Civil Engineering and Architecture, Nanchang Hangkong University, Nanchang 330063, China
公交换乘是指客流以实现出行为目的,在相邻或相同站点间以较短时间进行转移并变更公交线路的过程,换乘量体现了这种转移的强度[1-2].一个设置合理的城市公交换乘系统可以减少居民出行时间、提高公交系统效率、促进城市交通可持续发展[3].因此,准确获取和识别换乘特征数据具有较强的理论意义与实践应用价值.近年来,公交GPS与IC卡的普及为获取公交换乘数据提供了新的途经,且GPS和IC卡系统数据量大,信息真实可靠,可全面反应公交乘客出行特征,许多学者亦基于此来分析居民公交换乘行为[4-5];文献[6]通过分析公交定位数据获得乘客换乘时间,用以判断乘客的两次乘车是否为换乘行为;文献[7]通过融合公交IC卡和AVL数据,比较换乘前下车时间、换乘上车时间与换乘线路的车辆到站时间来进行换乘识别.
基于公交GPS和IC卡数据进行公交换乘识别是目前较为常用的算法,具有识别准确率高等优点,但算法复杂,对于公交线网庞大的城市来说工作量大,难以推广应用.换乘问题属于模式分类问题,目前应用比较广泛的模式分类算法包括BP神经网络、极限学习机、支持向量机等.其中,支持向量机(support vector machine,SVM)在非线性问题中不仅泛化能力强于BP网络,而且能避免神经网络训练结果不稳定的固有缺陷[8];而极限学习机随机化隐含层的做法,虽然运算速度较快,但易产生过拟合的现象;正因SVM在解决小样本、非线性及高维模式识别中的特有优势,也逐渐被运用于交通领域[9-12].本文将换乘行为分为同站换乘、异站换乘、不换乘3种类别,利用多分类支持向量机(multi-class SVM)的智能学习能力进行换乘识别.虽然multi-class SVM可在小样本情况下完成大量数据分析和预测工作,但公交换乘样本不易获取;而通过融合公交GPS和IC卡数据的方法完成少量公交出行数据的识别,可为multi-class SVM提供训练样本,然后结合SVM训练模型和公交GPS及IC卡记录的换乘数据推广至大规模城市公交换乘识别应用.
1 支持向量机 1.1 二分类支持向量机(binary-class SVM)支持向量机是文献[13]提出的建立在统计学习理论基础上发展起来的机器学习理论,基于VC维理论和结构化风险最小理论,以置信范围最小化作为优化目标,以训练误差作为约束条件,选择相应的判别函数,在预测精度和学习能力之间寻求平衡,具有较好的推广性,在解决小样本、非线性、高维模式识别等问题中具有较大优势.
二分类支持向量机的原理:假设对于给定空间R的训练样本{xi, yi},i = 1, 2, 3, …, l,l为训练样本量,xi∈R,yi∈{-1, 1},构建SVM分类机,定义最优线性超平面使其分类间隔最大,并把寻找最优线性超平面转化为求解二次规划问题,进而基于Mercer定理,通过将低维空间的非线性问题映射到高维空间H,在高维特征空间中采用线性方法进行分类. SVM的求解最后转化为一个二次凸规划问题,存在唯一全局最优解.
对于线性可分问题,SVM构造超平面:
| $ \left( {w \cdot x} \right) + b = 0. $ | (1) |
其中w为高维空间H中的向量,b为空间R中的常数.
寻找最优超平面,同时满足yi[(w·x)+b]≥1,i=1, 2, 3, …, l,且分类间隔
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{w \in H, b \in R, {\xi _i} \in R} \frac{1}{2}\left\| w \right\| + c\sum\nolimits_{i = 1}^l {{\xi _i}, } }\\ {{\rm{s}}{\rm{.t}}{\rm{.}}{y_i}\left[ {\left( {w \cdot x} \right) + b} \right] \ge 1 - {\xi _i}, i = 1, 2, \ldots , l;}\\ {{\xi _i} \ge 0, i = 1, 2, \ldots , l.} \end{array} $ | (2) |
其中‖w‖表示向量w的范数;C>0为常数,称为误差惩罚参数,由它来控制对错分样本惩罚的程度;ξi是在处理训练样本线性不可分时引入的非负松弛变量.
引入Lagrange函数,得到优化的对偶形式,则该问题转化为求解下列不等式约束下的二次函数极值问题:
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{{\alpha _i} \in R} \sum\nolimits_{i = 1}^l {{\alpha _i} - \frac{1}{2}\sum\nolimits_{i, j = 1}^l {{\alpha _i}{\alpha _j}{y_i}{y_j}\left( {\varphi \left( {{x_i}} \right)\cdot\varphi \left( {{y_i}} \right)} \right), } } }\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\sum\nolimits_{i = 1}^l {{\alpha _i}{y_i} = 0, } }\\ {0 \le {\alpha _i} \le C, i = 1, 2, \ldots , l.} \end{array} $ | (3) |
其中αi, αj ≥0为Lagrange系数;φ(xi)·φ(yi)为高维空间H中的内积.
将低维空间向量映射到高维空间过程时,高维度空间的内积运算会造成算法复杂度的增加,采用核函数来代替内积能大大简化算法.将输入量xi通过映射Φ: Rn→ H映射到高维特征空间,并引入核函数K(xi, yi),此时优化的目标函数变为
| $ Q{\left( \alpha \right)_{\max }}\sum\nolimits_{i = 1}^l {{\alpha _i} - \frac{1}{2}\sum\nolimits_{i, j = 1}^l {{\alpha _i}{\alpha _j}{y_i}{y_j}K\left( {{x_i}, {y_i}} \right).} } $ | (4) |
SVM算法最初是为二类分类问题设计的,当处理多类分类问题时,就需要构造合适的多类分类机.目前,构造SVM多类分类机的方法主要有两类[14-15]:一类是直接法,通过修改目标函数从而求解一个大的二次规划问题,同时将多个类别分开,这种方法思想上简单,但计算复杂度高,训练时间长;另一类是间接法,通过组合多个二分类机来实现多分类机的构造,包括一类对余类法、一类对一类法、决策二叉树法、决策导向无环图法和纠错输出编码法等.实际应用表明第二类方法更适合于应用[16].
其中,一类对一类法中的每个分类机只涉及两类训练样本,训练时间大幅度缩短,此外,每个分类机的训练样本是平衡的,训练精度较高,在针对类别较少的分类问题时整体性能优于其他方法.因此,本文采用一类对一类法进行公交换乘识别,若需识别k种类别,该方法需要在这k类训练样本中构造所有可能的二类分类机,各类别两两组合后共构造k(k-1)/2个分类机,从而对多分类问题进行简化.本文将公交换乘识别类别分为同站换乘、异站换乘、无换乘3种类别,分类类别数k=3,因此构造的分类机个数为k(k-1)/2=3.若训练区分类别m和类别n样本之间的分类机,即为求解以下问题:
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{{w^{mn}}, {b^{mn}}, \xi _i^{mn}} \frac{1}{2}\left\| {{w^{mn}} \ge + C\sum\nolimits_{i = 1}^3 {\xi _i^{mn}} } \right., }\\ {{\rm{s}}{\rm{.t}}{\rm{.}}{y_i}[({w^{mn}}\cdot x) + {b^{mn}}] \ge 1 - \xi _i^{mn}, m, n = 1, 2, 3;}\\ {\xi _i^{mn} \ge 0, m, n = 1, 2, 3.} \end{array} $ | (5) |
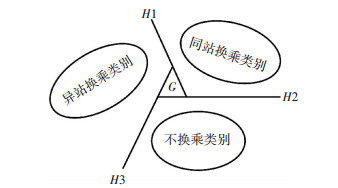
在一类对一类法具体实现时,需要采用投票法进行类别识别,分类示意图如图 1所示.
|
图 1 应用于换乘识别的多分类支持向量机 Figure 1 Multi-class SVM for public transit transfer recognition |
对于任意公交换乘数据样本x,共需用3个分类机进行分类,分别为同站换乘类别和异站换乘类别分类机、同站换乘类别和无换乘类别分类机、异站换乘类别和无换乘类别分类机.在第一个分类机分类时,若x属于同站换乘类别时,则在该类别的票数上加1,反之在异站换乘类别的票数上加1,直到所有分类机分类完成,得票最多的类别则为输入样本所属的类别.当投票结果为1:1:1时,为不可识别区域,采取随机分类的方法完成识别工作(不可识别区域较少,为图 1中的区域G,因此对分类精度影响不大).
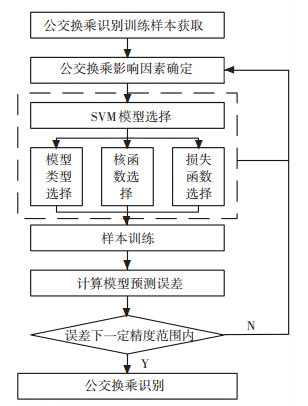
2 基于multi-class SVM的公交换乘识别公交换乘识别方法基本思路:首先准备换乘的基础数据,并将基于公交GPS和IC卡方法[4-7]获得的换乘识别结果作为multi-class SVM的训练样本,其次选择合适的SVM模型和训练样本量,当确定最优参数组合时,即完成训练,最后将训练好的SVM模型推广应用于城市公交换乘识别,具体步骤如下,流程图如图 2所示.
|
图 2 公交换乘识别流程图 Figure 2 Flow chart of public transit transfer recognition |
步骤1 训练样本获取.通过GPS和公交IC卡数据获取SVM的训练样本,并对公交换乘识别的影响因素进行筛选.乘客在相邻两次公交出行之间是否发生换乘,受换乘便捷程度影响,还与乘客个人属性相关.本文选择候车时间、换乘时间(前次下车与后次上车的时间间隔)、公交出行总时间、换乘距离(前次下车与后次上车站点距离)、持卡人类型(1代表少年、2代表成年、3代表老年)作为换乘识别影响因素;分别用1、2、3表示同站换乘、异站换乘、不换乘.
步骤2 SVM模型选择及参数标定.模型选择包括模型类型选择、核函数选择及损失函数选择[17-18].关于模型类型选择,本文的换乘识别结果涉及3种类别,因此选取multi-class SVM模型.核函数包含线性核函数、多项式核函数、RBF核函数、Sigmoid核函数等,其中,RBF核函数能够逼近任意非线性函数,学习收敛速度快、泛化能力好,相较于其他核函数应用更加广泛,因此本文选取RBF核函数.损失函数包含ε不敏感损失函数、二次损失函数、Huber损失函数等,ε不敏感损失函数对于小样本训练集来说具有很大的计算优势,能确保全局最小解的存在,一般采用ε不敏感损失函数.完成SVM模型选择后,需结合实际情况对模型中函数参数进行标定.
步骤3 最优训练样本量获取.将步骤1得到的样本分为两部分,一部分用来进行训练与检验,一部分用来进行实际换乘识别.将第一部分样本根据乘客换乘情况,形成关于公交换乘与其影响因素之间的训练集:T={(x1, y1), (x2, y2), …, (xn, yn)},其中,xi∈x∈Rn,yi∈y∈{1, -1},n为样本量,采用SVM模型基于该训练集进行多组样本的训练,研究训练样本量与预测精度之间的关系,获取最优样本量. (本文提出的公交换乘识别算法,可以为公交前期规划、运营管理等阶段服务,在公交前期规划阶段,对精度要求不高,可直接采用较少样本进行预测;反之,在公交运营管理等阶段,对精度要求较高,需采用该方法得到精度最高的最优样本量.)
步骤4 误差控制.训练样本量大小将影响模型的训练和分类结果,SVM模型及模型参数标定对预测精度也有直接影响.本文采用多组样本进行训练,以期获取最优训练样本量与最优模型参数组合,从而完成multi-class SVM模型的训练.若训练结果不满足预设精度要求,应返回步骤1或步骤2,重新考虑公交换乘识别的影响因素或重新进行SVM模型选择.
步骤5 公交换乘识别.基于步骤4完成的multi-class SVM训练模型、公交GPS和IC卡系统提供的换乘数据,可完成公交出行换乘识别工作.
3 换乘识别算法应用结合佛山市中心城区换乘识别案例详细说明如何应用multi-class SVM进行城市级的大规模公交换乘识别.
3.1 换乘数据与换乘样本获取对佛山市中心城区2013年3月18日至3月22日5个工作日的市民全部公交出行数据进行换乘识别,获取公交运营数据.市民使用IC卡付费的出行人数占总人数70%以上,故IC卡数据可客观反应全市人口的公交出行特征. IC卡的刷卡形式为仅上车刷卡,下车不刷卡;公交车GPS设备的上传频率为5 s,公交GPS与IC卡数据的传输时间存在6 s的偏移,需进行校对.
本文采用公交GPS和IC卡系统获取这5 d的全部出行数据,基于数据融合技术完成对所有持卡人每天的公交出行信息采集,通过处理无效和缺省数据,获得换乘识别基础数据.基于公交GPS和IC卡的方法识别换乘行为较为准确,对于小规模数据具有一定效果.因此,本文采用该方法对少量公交换乘数据进行识别,获得了329条换乘识别数据,以作为multi-class SVM的训练样本,部分数据见表 1.其中,在持卡人类型这一列,1代表学生卡,2代表普通卡,3代表老年卡;在换乘类别这一列中,1代表同站换乘,2代表异站换乘,3代表无换乘.
| 表 1 基于GPS和公交IC卡的换乘样本 Table 1 Public transit transfer samples based on GPS and intelligent card |
将基于公交GPS和IC卡方法识别的329条数据作为multi-class SVM的训练和检验样本,换乘识别样本数据的自变量包括候车时间、换乘时间、出行总时间、换乘距离、持卡人类型,因变量为换乘类型.接下来,本文将具体介绍如何选取合适的训练样本量,如何对RBF核函数的参数组合进行标定,从而训练出最优SVM分类模型以对佛山市公交出行数据进行换乘识别.
3.2.1 训练样本量选取SVM主要针对小样本训练,样本过多易产生“过拟合”现象.针对不同训练样本数量,文献[19]采用UCI数据集作了模拟实验,结果显示数据量为200时训练出来的SVM模型最好,优于更大数据量训练出来的SVM模型.因此,本文共获取了329组GPS与IC卡数据作为训练样本和测试样本,用以选取最佳训练样本量.在这329个样本中取训练样本量为20、40、60、80、100、120、140、160和180的9组数据,分别对样本进行训练分类,获取每组样本的分类预测精度、同站换乘精度、异站换乘精度以及不换乘精度.分类识别精度为
| $ \eta = \frac{{{N_{\rm{s}}} + {N_{\rm{d}}} + {N_0}}}{N}. $ | (6) |
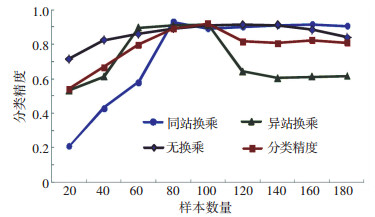
其中:η为分类识别精度,Ns为正确识别同站换乘的样本数,Nd为正确识别异站换乘的样本数,N0为正确识别不换乘的样本数,N为训练样本量.样本分类精度与样本数量的关系如图 3所示.
|
图 3 分类精度与样本数量的关系图 Figure 3 Relationship of classification accuracy and sample size |
研究发现:当样本量为100时,训练模型的分类识别精度最高,为93.90%,当样本量超过100时,分类识别精度有所下降.其中,同站换乘和无换乘的识别精度基本保持不变,异站换乘精度的降幅较大,可以认为总体分类预测精度的下降是由于异站换乘识别准确性下降带来的.异站换乘识别结果受到包括换乘距离、步行时间、换乘等待时间等多种因素的制约,而随着训练样本数据量增大,会导致数据偏斜,从而使学习得到的分类机产生误差.以此同时,可以发现模型分类预测精度的变化趋势是从低至高再缓慢降低并趋于平缓,同站换乘、异站换乘以及不换乘精度的变化趋势与之相似.上述样本训练结果恰好证实了SVM在小样本训练限制下的应用优势,亦说明了SVM较好的泛化能力.
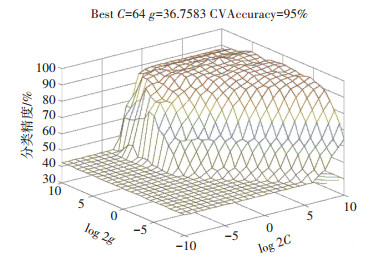
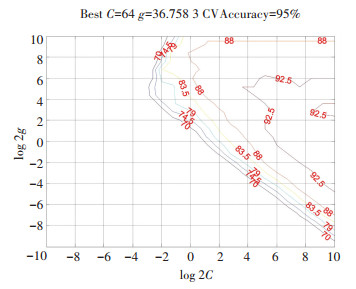
3.2.2 SVM模型选择本文选取较为常用的RBF核函数,并对核函数中Gamma函数的参数g和损失函数的参数C值进行研究.目前对于参数C和g的选取尚无通用方法,本文在给定参数C和g范围的基础上,通过网格搜索法(grid-search)进行寻优.网格搜索法是将准备搜索参数的空间划分为网格,遍历网格中的每一个点来寻找最优参数.为获取更准确的参数组合,本文扩大了C和g的搜索范围,将C和g的取值区间均设为[0, 1 024].由于参数搜索范围较大,grid-search算法不可避免地会造成计算时间过长等问题.为此,本文引入粒子优化算法(particle swarm optimization,PSO),与grid-search算法结合使用,从而避免grid-search算法时间长和PSO算法易陷入局部寻优等问题.运用MATLAB获取最优参数组合,当C=64,g=36.758 3时,训练模型的精度可达到95%左右.采用grid-search_PSO方法进行参数选择过程如图 4、5所示.其中,图 4的Accuracy代表分类精度,Best C和g代表分类精度最佳情况下的参数组合.
|
图 4 grid-search_PSO参数选择(3D图) Figure 4 Parameter selection by using the grid-search_PSO method (3D) |
|
图 5 grid-search_PSO参数选择(等高线图) Figure 5 Parameter selection by using the grid-search_PSO method (contour map) |
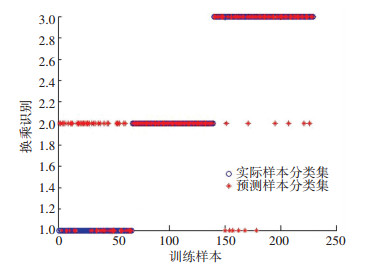
为进一步验证模型参数的适用性,将余下229条数据作为样本测试集,运用模型进行分类识别,其识别精度可达到90.4%,样本检验集换乘识别结果如图 6所示.
|
图 6 样本检验集换乘识别结果 Figure 6 Publictransit transfer identification results of test samples |
确定最佳训练样本量和最优核函数后,即完成了对multi-class SVM模型的训练,实现了SVM探索学习公交换乘内在规律的过程.然后,依照该模型对佛山市中心城区这五天全部公交换乘数据进行识别.
3.2.4 换乘识别结果扩算与分析通过预测结果可推测持卡出行乘客比例:首先,应对换乘数据进行处理,得到按照IC卡号和刷卡时间依次排序的分类识别数组.其次,由于IC卡持卡用户较多,可大致反应居民换乘规律,故根据持卡乘客的比例进行相应扩算以求出真实的公交换乘数据.假设公交运营总收入STotal,公交数卡收费总额为SIC,公交刷卡优惠为α,可推算出持卡出行乘客占总出行量的比例为
| $ \eta '=\frac{{{S_{{\rm{IC}}}}}}{{{S_{{\rm{IC}}}} + \left( {1 - \alpha } \right)\left( {{S_{{\rm{Total}}}} - {S_{{\rm{IC}}}}} \right)}}. $ | (7) |
完成对佛山市中心城区2013年3月18日至22日全部公交换乘数据的识别后,对换乘结果进行扩算.佛山公交公司提供的年票务收入为34 045万元,其中IC卡收入26 964万元,换乘折扣为0.2,根据式(7)可推算公交持卡比例约为67.9%. 5个工作日的换乘识别结果见表 2,数据显示5 d平均公交换乘量为20 479人次,平均公交换乘率为1.35%,其中同站换乘平均占65.72%.以3月18日为例,得到该工作日在高峰与平峰时期同站换乘、异站换乘的结果见表 3.可以看出,同站换乘日均总量达16 263人次,占换乘比例79.41%,异站换乘日均总量达4 216人次,占换乘比例20.59%.
| 表 2 佛山中心城公交换乘识别结果 Table 2 Transfer recognition results in Foshan Central City |
| 表 3 3月18日不同时段公交换乘比例 Table 3 Transfer percentage of different periods in Foshan Central City (March 18th, 2013) |
1) 提出一种适用于较大规模公交线网的城市公交换乘识别方法,该方法采用multi-class SVM模型并结合公交GPS和IC卡数据对公交换乘数据进行样本训练和换乘识别.主要步骤包括:换乘数据采集、训练样本获取、multi-class SVM最佳训练样本量选取、核函数最优参数组合标定等.
2) 本质上来说,目前较为流行的公交GPS和IC卡方法也可以进行换乘识别,但所需数据准备工作过于复杂,算法也较为繁琐,对于大规模应用存在一定的局限性.但该方法具有换乘识别精准的优点,可用于少量换乘数据识别以作为multi-class SVM的训练样本,并最终推广至大规模应用阶段.
3) multi-class SVM的训练与预测结果表明:运用多分类支持向量机进行公交换乘识别较传统方法更加简洁,适合推广于大规模应用中;支持向量机可以很好学习居民公交换乘出行的内在规律.通过佛山市中心城区公交换乘识别案例,说明该方法可以计算出包括换乘总量、换乘率在内的相关换乘出行数据,可为公交规划、运营以及管理提供一定的数据支撑,具有深远的工程应用价值.
| [1] |
王小娟. 西安市轨道交通与常规公交换乘站点分析与评价研究[D]. 北京: 北京交通大学, 2015. WANG Xiaojuan. The evaluation study and analysis of urban rail transit and bus transfer site in Xi'an[D]. Beijing: Beijing Jiaotong University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10004-1015611547.htm |
| [2] |
简志伟, 冯军锋. 基于GIS的城市公交换乘模型与实现[J]. 城市勘测, 2014(3): 42-47. JIAN Zhiwei, FENG Junfeng. GIS-bsaed city public transit model and its implementation[J]. Urban Geotechnical Investigation and Surveying, 2014(3): 42-47. DOI:10.3969/j.issn.1672-8262.2014.03.013 |
| [3] |
周亿迎, 毛保华. 采用可变时间参数的公交换乘识别方法[J]. 物流技术, 2013, 32(4): 106-152. ZHOU Yiying, MAO Baohua. Study on identification of bus interchange based on variable time parameters[J]. Logistics Technology, 2013, 32(4): 106-152. DOI:10.3969/j.issn.1005-152X.2013.04.035 |
| [4] |
HOFMANN M, WILSON P S, WHITE P. Automated identification of linked trips at trip level using electronic fare collection data[C]//Transportation Research Board 88th Annual Meeting. Washington DC: Transportation Research Board, 2009: 750-760.
|
| [5] |
王若琳, 赵娅丽, 谭永凯. 基于IC卡数据的公共交通换乘识别方法[J]. 城市轨道交通研究, 2014, 17(2): 76-85. WANG Ruolin, ZHAO Yali, TAN Yongkai. Recognition method of transit transfer based on intelligent card data[J]. Urban Mass Transit, 2014, 17(2): 76-85. |
| [6] |
张孜, 邹亮, 朱玲湘. 基于公交IC卡的公交换乘数据获取方法研究[J]. 交通信息与安全, 2011, 29(164): 21-24. ZHANG Zi, ZOU Liang, ZHU Lingxiang. Method to collect public transportation transfer data based on IC card[J]. Journal of Transportation Information and Safety, 2011, 29(164): 21-24. DOI:10.3963/j.ISSN1674-4861.2011.06.005 |
| [7] |
李海波, 陈学武. 基于公交IC卡和AVL数据的换乘行为识别方法[J]. 交通运输系统工程与信息, 2013, 13(6): 73-79. LI Haibo, CHEN Xuewu. A method to identify public transit transfers based on IC and AVL data[J]. Journal of Transportation Systems Engineering and Information Technology, 2013, 13(6): 73-79. DOI:10.3969/j.issn.1009-6744.2013.06.012 |
| [8] |
VAPNIK V N. The nature of statistical learning theory[M]. New York: Springer-Verlag, 1995.
|
| [9] |
SUN Jie, SUN Jian. Real-time crash prediction on urban expressways: identification of key variables and a hybrid support vector machine model[J]. Transportation Science and Technology, 2016, 10(5): 331-337. |
| [10] |
ZHONG Shiquan, HU Juanjuan, KE Shuiping, et al. A hybrid model based on support vector machine for bus travel-time prediction[J]. Transportation Science and Technology, 2015, 27(4): 291-300. |
| [11] |
XIAO Jianli, GAO Xiang, KONG Qingjie, et al. More robust and better: a multiple kernel support vector machine ensemble approach for traffic incident detection[J]. Journal of advanced transportation, 2014, 48(7): 858-875. DOI:10.1002/atr.v48.7 |
| [12] |
WONG P, WONG H, VONG C, et al. Online wavelet least-squares support vector machine fuzzy predictive control for engine lambda regulation[J]. International Journal of Engine Research, 2016, 17(8): 866-885. DOI:10.1177/1468087415623909 |
| [13] |
ZHANG Ning, ZHANG Yunlong, WANG Xuemei. Forecasting of short-term urban rail transit passenger flow with support vector machine hybrid online model[C]//The 2012 Annual Meeting of the Transportation Research Record. Washington DC: Transportation Research Board, 2012.
|
| [14] |
杨珮鑫, 张沛超. 基于多分类支持向量机的分布式发电系统并网保护[J]. 电力系统自动化, 2015, 39(22): 110-151. YANG Peixin, ZHANG Peichao. Distributed generation system interconnection protection based on multi-class SVM[J]. Automation of Electric Power Systems, 2015, 39(22): 110-151. DOI:10.7500/AEPS20150421006 |
| [15] |
LI Daoliang, YANG Wenzhu, WANG Sile. Classification of foreign fibers in cotton lint using machine vision and multi-class support vector machine[J]. Computers and Electronics in Agriculture, 2010, 74(2): 274-279. DOI:10.1016/j.compag.2010.09.002 |
| [16] |
LI Chunna, HUANG Yunfeng, WU Hejie, et al. Multiple recursive projection twin support vector machine for multi-class classification[J]. International Journal of Machine Learning and Cybernetics, 2016, 7(5): 729-740. DOI:10.1007/s13042-014-0289-2 |
| [17] |
苏高利, 邓芳萍. 关于支持向量回归机的模型选择[J]. 科技通报, 2006, 22(2): 154-158. SU Gaoli, DENG Fangping. Introduction to model selection of SVM regression[J]. Bulletin of Science and Technology, 2006, 22(2): 154-158. DOI:10.3969/j.issn.1001-7119.2006.02.004 |
| [18] |
GANAPATHIRAJU A, HAMAKER J, PICONE J. Applications of support vector machines to speech recognition[J]. IEEE Trans Signal Process, 2004, 52(8): 121-167. DOI:10.1109/TSP.2004.831018 |
| [19] |
罗瑜. 支持向量机在机器学习中的应用研究[D]. 成都: 西南交通大学, 2007. DOI: 10.7666/d.y1237452. LUO Yu. Researches on application of Support Vector Machine in machine learning[D]. Chengdu: Southwest Jiaotong University, 2007. DOI: 10.7666/d.y1237452. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1237452 |
 2018, Vol. 50
2018, Vol. 50


