2. 中国民航大学 航空地面特种设备基地,天津 300300;
3. 中国民用航空局第二研究所,成都 610041
2. Ground Support Equipment Research Base, Civil Aviation University of China, Tianjin 300300, China;
3. The Second Research Institute of CAAC, Chengdu 610041, China
飞机滑出过程的拥堵排队现象是导致离港成本居高不下的原因之一,同时也造成了大量的废气排放,据统计,机场进离港地面运行过程占整个航行时间的10%~30%,并且有5%~10%的航空燃油在此期间消耗[1].飞机离港滑出过程是指飞机撤轮档从离开停机位开始到飞机起飞之间的过程,其中分别包括推出与滑行两个过程[2].由飞机引擎驱动,过长的飞机滑行等待队列会引起不必要的燃油消耗以及废气排放,然而如果减少滑行排队又会降低机场跑道运行效率,因此,合理的控制飞机推出频率是均衡燃油成本和跑道运行效率的有效手段.
针对飞机滑行过程研究,文献[3]提出了一种混合排队模型并对不同的离港滑行过程作对比.文献[4]等分析了滑出过程中的各种影响因子并预测了飞机的滑行时间,以合理安排推出时间.文献[5-6]用Dijkstra算法对滑行路径进行动态规划优化,并建立一种非线性反馈系统来精确评估离港滑行时间以合理安排航班的推出时刻.文献[7]用整数规划模型和滑行节点优化模型对离港过程进行研究以减少滑行过程中的停车次数.文献[8-9]同样用整数规划的方法对大规模进离港流下的滑行路径、速度以及地面等待管制过程进行优化.文献[10]通过在协同决策机制下进行推出时隙分配来优化离港过程.文献[11]提出了一种推出时隙交易机制,使得航空公司可以自主交易推出时隙并验证了其可行性.文献[12]等基于弹性滑行容量机制对飞机的有效推出时隙进行了研究,结果证明算法有效降低了离港延误.文献[13-14]针对离港滑行计划和滑行路径问题建立多商品流网络模型,分别用分枝定界法和拉格朗日分解法来规划滑行路径.文献[15-16]提出了一种基于离散差分进化的飞机推出控制策略,建立了飞机地面运行成本及乘客停机位等待时间的双目标优化模型,通过离散差分进化算法来分配推出时隙.文献[17]提出了队长阈值控制概念(N控制),其表述为:如果滑行道上离港飞机排队数达到一个阈值,将拒绝其他飞机的推出申请,直到排队数低于此阈值,这种方法又叫做推出频率控制策略,其核心是寻找最优滑行道排队阈值.文献[18]开发了一种N控制策略支持工具.文献[19]侧重研究不同的停机位等待时间对于N控制策略的影响,对N控制策略进行了拓展.在机场实际操作层面,当前国内大多数机场根据航班时刻表采用先到先服务的飞机推出策略;文献[20]开发的离港调度软件(departure manager)在欧洲主要枢纽机场投入使用来进行推出控制;文献[21-22]以成本为目标对传统N控制策略进行动态优化,并于波士顿机场开展了应用研究.
N控制方法是一种有效的推出控制策略,但是其本身具有一些缺点,比如一旦队长阈值确定,推出率便被决定,只要未达到队长阈值,即使在滑行道排队长度很大的情况下,依然可以依概率1推出.针对这一缺点,本文提出一种基于惩罚机制的离港推出控制方法,使得推出频率不仅仅由队长阈值控制,而且会根据当前排队长度实时调整的一种动态控制方法,通过将飞机的滑行等待时间转化为停机位等待时间,以降低滑行燃油消耗和保证跑道利用率为目标,来减少机场场面拥堵,并与传统控制策略进行比较,验证策略的有效性.
1 飞机离港推出控制策略 1.1 飞机离港过程的描述与基本假设机场的离港系统由登机口(停机位)系统、滑行道系统及跑道系统3个部分组成:飞机在登机口进行旅客登机、配餐等程序,收到推出指令便进行推出;经推出后进入滑行道系统;待收到最终起飞指令便可以起飞.相邻飞机起飞的间隔不小于最低尾流间隔标准.离港系统结构如图 1所示.

|
图 1 离港系统结构图 Figure 1 Structure chart of departure process |
离港飞机处于不同的系统,成本也不同,比如飞机处于停机位等待推出指令时,会产生机组成员成本(crew cost),而且此时如果延迟推出会造成停机位占用及跑道利用率的降低(utilization lost);而飞机处于滑行系统时,又要承担滑行燃油消耗成本(fuel-burn cost).
当前所研究的传统N控制策略为:如果离港队列达到一个阈值Nctrl,则拒绝新的推出请求并使其在停机位等待,直到队长小于Nctrl方可进行推出.为了使模型具有一般性,在不影响模型适用性的基础上,对模型作如下假设:1)不考虑天气因素的影响;2)推出过程由牵引车完成,不产生油耗,在此忽略推出所消耗的时间;3)为方便各推出策略效果的对比,采用先到先服务原则以及固定的滑行服务时间,即不考虑不同机型的起飞尾流间隔影响.
1.2 推出频率控制策略控制策略的思想是在保证跑道利用率的前提下,将飞机在滑行道上的排队等待时间转化为停机位等待时间,以减少燃油消耗.在推出过程中,当一个推出请求被拒绝时,被拒绝飞机将停留在停机位等待下次申请.与传统N控制策略P1不同的是,本文所提出策略的输入率根据当前队长实时变化,因此,除传统N控制策略之外,本文提出了3种推出控制策略P2、P3和P4,4种输入率分别如下.
| $ {\rm{P}}1:\lambda ' = \left\{ \begin{array}{l} \lambda , n < N;\\ 0, n < N. \end{array} \right. $ |
| $ {\rm{P}}2:\lambda ' = \left\{ \begin{array}{l} \lambda \left( {1 - \frac{n}{N}} \right), n < N;\\ 0, \;\;\;\;\;\;\;\;n < N. \end{array} \right. $ |
| $ {\rm{P}}3:\lambda ' = \left\{ \begin{array}{l} \lambda {{\rm{e}}^{\frac{n}{N}}}\left( {1 - \frac{n}{N}} \right), n < N;\\ 0\;\;\;\;\;\;\;, n \ge N. \end{array} \right. $ |
| $ {\rm{P}}4:\lambda ' = \left\{ \begin{array}{l} \lambda , n < 0.3N;\\ \frac{{10\lambda }}{7}\left( {1 - \frac{n}{N}} \right), 0.3K \le n < N;\\ 0, \;\;\;\;\;\;\;\;n \ge N. \end{array} \right. $ |
其中:λ′为实际推出率;λ为请求推出率;N为当前滑行道排队长度;N为滑行道队长阈值.
4种推出策略中,P1策略的特点是在滑行道排队飞机数量未达到队长阈值N时,同意所有推出请求,而滑行道排队飞机数一旦达到队长阈值N,则拒绝所有请求;P2策略的特点是推出概率随着滑行道排队长度的增加呈线性下降趋势;P3则是非线性指数函数控制策略,这种策略的特点是队长较短时,推出拒绝率缓慢增加,但随着排队长度达到一定值,推出拒绝率迅速增加;P4为分段线性控制策略,表示当前队长n < 0.3N时,同意所有推出请求,当前队长n≥0.3N时,推出概率线性降低.4种推出策略的特征曲线如图 2所示(此处假设滑行道排队阈值为20).

|
图 2 推出策略特征曲线 Figure 2 Characteristic curves of each pushback strategy |
由图 2可以直观看到P3、P4策略的控制强度是介于P1和P2策略之间的.然而,减少滑行道等待飞机数量意味着在停机位等待的飞机增加,将导致停机位资源的占用及跑道利用率的降低.因此,本文提出一种惩罚策略,对占用停机位的飞机给予一个惩罚,也可视作滑行道利用率降低带来的损失.
2 基于惩罚的推出控制模型 2.1 目标函数飞机离港一般遵循先到先服务原则,其离港过程可抽象为一个单服务台排队系统[4]. P1为传统N控制策略,这里不作赘述,在此重点分析P2策略,其服务率为μ,推出率为
| $ \lambda ' = \left\{ \begin{array}{l} \lambda \left( {1 - \frac{n}{N}} \right), n < N;\\ 0\;\;\;\;\;\;\;\;, n \ge N. \end{array} \right. $ |
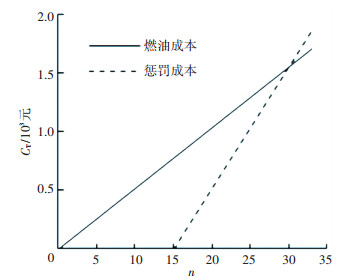
飞机推出总成本CT由两部分组成:1)进入队列滑行所消耗的燃油成本;2)推出请求被拒绝时飞机停留在停机位.停机位占用和跑道利用率降低将产生惩罚费用,惩罚费用越高,表示跑道利用率越低,反之则越高.根据中国民航局准点率报告对准点/晚点的定义:对于机场来说,如果一个航班在计划起飞时间后30 min内完成起飞(机轮离地),即认为该航班准点放行;反之即为晚点[23].在此选取线性函数为惩罚项,令燃油成本和惩罚成本在停机位停留时间为30 min处相等,当停机位等待时间小于30 min时,惩罚成本将小于同等时长下燃油消耗成本,一旦停机位等待时间超过30 min,惩罚成本将因为延误而迅速增加,并超过同等时长下燃油消耗成本.起始惩罚时间可以根据机场实际运行情况进行选择,这里设定为15 min,即停机位停留时间小于15 min时,不进行惩罚,一旦停机位停留时间超过15 min,惩罚开始.燃油成本和惩罚成本曲线见图 3.
|
图 3 燃油成本及惩罚成本曲线 Figure 3 Relationships of fuel-burn and gate-hold costs versus time |
图 3中,燃油成本曲线斜率根据数据采集日期油价计算得到,令燃油成本曲线和惩罚成本曲线在停机位等待时间为30 min处相交,惩罚成本曲线斜率为惩罚系数.
目标为总成本最低,记为
| $ \begin{array}{*{20}{c}} {\min {C_{\rm{T}}} = \sum\limits_{i = 1}^M {\left( {c \cdot E\left[ {{W_i}} \right] + \beta \left\{ {E\left[ {{G_i}} \right]\left| {\left( {{G_i} > 15} \right) - 15} \right.} \right\}} \right)} , }\\ {{\rm{s}}.\;{\rm{t}}.\;0 \le n \le N.} \end{array} $ | (1) |
式中:i为第i架申请推出飞机;M为飞机申请推出总数;c为平均滑行燃油成本,元/min;W为滑行时间,min;β为惩罚系数;G为停机位等待时间,min.
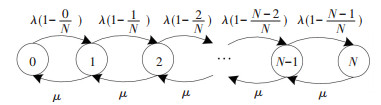
2.2 模型分析P2策略模型为具有有限容量和可变输入率的等待制排队过程.策略所描绘离港过程具有两个状态:停机位滞留状态及推出后滑行道排队状态.经拟合优度检验,原始推出申请时间服从泊松分布,其马尔科夫状态转移如图 4所示.
|
图 4 状态转移图 Figure 4 State transition process |
根据状态转移方程
| $ \lambda \left( {1 - \frac{0}{N}} \right){\pi _0} = \mu {\pi _1}, $ | (2) |
| $ \begin{array}{*{20}{c}} {\left[ {\lambda \left( {1 - \frac{n}{N}} \right) + \mu } \right]{\pi _n} = \lambda \left( {1 - \frac{{n - 1}}{N}} \right){\pi _{n - 1}} + \mu {\pi _{n + 1}}, }\\ {n = 1, 2, \cdots , N - 1, } \end{array} $ | (3) |
| $ \lambda \left( {1 - \frac{{N - 1}}{N}} \right){\pi _{N - 1}} = \mu {\pi _N}. $ | (4) |
由正则方程
| $ {\pi _0} = {\left\{ {1 + \sum\limits_{n = 1}^N {\left[ {{{\left( {\frac{\lambda }{\mu }} \right)}^n}\prod\limits_{l = 0}^{n - 1} {\left( {1 - \frac{l}{N}} \right)} } \right]} } \right\}^{ - 1}}, $ | (5) |
求解方程(2)~(4),得到队列长度的一般表达式
| $ {\pi _n} = {\left( {\frac{\lambda }{\mu }} \right)^n}\prod\limits_{l = 0}^{n - 1} {\left( {1 - \frac{l}{N}} \right){\pi _0}} , \;\;\;\;n = 1, 2, \cdots , N, $ | (6) |
滑行道排队长度f的期望的表达式为
| $ E\left[ f \right] = \sum\limits_{n = 1}^N {n{\pi _n}} = \sum\limits_{n = 1}^N {n{{\left( {\frac{\lambda }{\mu }} \right)}^n}\prod\limits_{l = 0}^{n - 1} {\left( {1 - \frac{l}{N}} \right){\pi _0}} } , $ | (7) |
推出频率λ′的期望为
| $ E\left[ {\lambda '} \right] = \sum\limits_{n = 0}^{N - 1} {\lambda {\pi _n}} = \lambda \sum\limits_{n = 0}^{N - 1} {n{{\left( {\frac{\lambda }{\mu }} \right)}^n}\prod\limits_{l = 0}^n {\left( {1 - \frac{l}{N}} \right){\pi _0}} } . $ | (8) |
由Little公式,通过式(7)、(8)可得到滑行道等待时间期望为
| $ E\left[ W \right] = \frac{{E\left[ f \right]}}{{E\left[ {\lambda '} \right]}} = \frac{{\sum\limits_{n = 1}^N {n{{\left( {\frac{\lambda }{\mu }} \right)}^n}\prod\limits_{l = 0}^{n - 1} {\left( {1 - \frac{l}{N}} \right){\pi _0}} } }}{{\lambda \sum\limits_{n = 0}^{N - 1} {n{{\left( {\frac{\lambda }{\mu }} \right)}^n}\prod\limits_{l = 0}^n {\left( {1 - \frac{l}{N}} \right){\pi _0}} } }}. $ | (9) |
由于惩罚项成本与停机位等待时间相关联,停机位等待时间同样需要计算.排队系统的输入率为1-n/N,则停机位等待概率为n/N,因此当前队长为n(n≠N)时,记τ为平均滑行时间,停机位等待时间G期望为
| $ E\left[ {G\left| {n = l} \right.} \right] = \left[ {\sum\limits_{m = 1}^\infty {m \cdot \tau \cdot {{\left( {\frac{l}{N}} \right)}^m}} } \right]\left( {\frac{{N - l}}{N}} \right) = \tau \left( {\frac{l}{{N - l}}} \right), $ | (10) |
当前队长为N时,有
| $ E\left[ {G\left| {n = N} \right.} \right] = \tau + E\left[ G \right], $ | (11) |
则对所有n,停机位等待时间G期望为
| $ \begin{array}{*{20}{c}} {E\left[ G \right] = \sum\limits_{l = 1}^{N - 1} {E\left[ {G\left| {n = l} \right.} \right] \cdot {\pi _l}} + E\left[ {G\left| {n = N} \right.} \right] \cdot {\pi _N} = }\\ {\frac{{\sum\limits_{l = 1}^{N - 1} {\tau \cdot \left( {\frac{l}{{N - l}}} \right) \cdot {\pi _l}} + \tau \cdot {\pi _N}}}{{1 - {\pi _N}}}.} \end{array} $ | (12) |
针对推出过程模型的求解,本文提出了一种基于连续时间马尔科夫链的迭代优化算法,首先利用拟合优度检验检测推出申请数据集的分布,其次利用迭代循环搜索在不同的滑行道排队长度阈值的情况下的最低成本.算法分为两层循环:外循环和内循环.其中内循环遍历所有推出申请序列,结合之前参数计算结果,在滑行道排队阈值为N的条件下进行总成本计算;外循环则为滑行道排队阈值N的循环,N的取值为[1,30][19].算法流程见图 5.

|
图 5 基于连续时间马尔科夫链的迭代优化算法流程图 Figure 5 Flowchart of optimization algorithm based on continuous time Markov chain |
图 5中,R为生成的随机数集合, 且Ri∈(0, 1),用来模拟策略推出概率,例如当N=10,n=4时,新申请推出飞机的推出概率为1-n/N=0.6,此时进行判断,若随机数Ri < 0.6,即为“准许推出”,反之为“拒绝推出”.其他参数同前所述,当飞机i申请推出,如果滑行道队长N达到设定阈值,则拒绝推出进行停机位等待,反之进行概率判断,若不满足判断条件,则拒绝推出,停留在停机位等待下一次申请.直到两次判断条件同时满足被推出进入滑行道.此期间,停机位停留时间G和滑行道的滑行时间W分别由式(5)、(9)给出.然后进行第i+1架飞机的推出过程.当所有飞机推出完毕,计算式(12)得到目标函数CT.更新滑行道排队阈值N以完成下一个循环直到上限.最终输出最优成本CT*及其对应的队长阈值N*、登机口停留时间G*和滑行道滑行时间W*.
3 实例分析为验证提出的推出控制模型的有效性,本文以首都机场实际运行数据为基础,对提出的P2策略进行仿真.北京首都机场(PEK)结构为3条平行跑道,其中18L/36R为主起飞跑道,36L/18R为主降落跑道,01/19跑道为起降混合跑道,3条跑道为平行跑道,相互影响较小,且18L/36R跑道受到的降落航班干扰较小.因此,本文选择其离港数据作为实例分析.仿真采用MATLAB2012a软件,数据取自2013年11月13日6:00—22:00时在18L/36R跑道起飞的航班推出申请信息数据集,对推出数据集的χ2分布检验证明在95%的置信区间内数据集符合泊松分布.推出申请航班总数M=498架.滑行油耗参数取自数据采集日期油价c=51.8元/min,惩罚因子由图 3得β=103.6.当不使用任何推出策略时,飞机序列的仿真滑行道排队长度和离港滑行时间如图 6所示.

|
图 6 无控制推出过程的滑行道排队长度和滑行时间 Figure 6 Queuing length and taxi-out time without pushback control strategy |
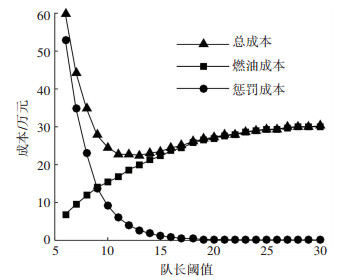
此时没有任何的惩罚成本,总成本即为燃油消耗成本,计算得CT=Σc·Wi=354 505.6元.平均滑行道排队长度和平均滑行时间分别为7.5和13.7 min.图 7为P2策略全天总成本、燃油成本及惩罚成本仿真结果.
|
图 7 总成本、燃油成本和惩罚成本随队长阈值变化曲线 Figure 7 Effect of taxiway queue limit on total cost, fuel burn cost and penalty cost |
由图 7曲线可以看出,滑行道队长阈值N较小时,大量的航班由于推出申请被拒绝而在停机位等待,此时燃油成本较低而惩罚成本为影响总成本的主要因素;随着队长阈值N的增加,当队长阈值N超过20时,总成本因交通量限制趋于平稳;总成本在滑行道队长阈值N=13时达到最低,即最优结果,此时总成本N=238 736.9元.值得一提的是,当队长阈值N=9时,燃油成本和惩罚成本达到平衡,此时虽然总成本非最优,但是其燃油成本却低于最优结果,更加有利于能源节约和减少污染排放.
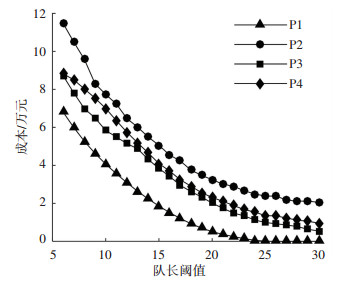
本文将同一天数据分别对前述包括传统N控制策略在内的4种推出控制策略以及无控制策略的情形进行仿真,得到在不同滑行排队阈值N下各策略的平均滑行时间、平均停机位停留时间和总成本分别如图 8~10所示.

|
图 8 推出策略在不同队长阈值下平均滑行时间 Figure 8 Mean taxi-out time of each pushback strategy with various taxiway queue limit |
|
图 9 推出策略在不同队长阈值下平均停机位停留时间 Figure 9 Mean gate-hold time of each pushback strategy with various taxiway queue limit |
|
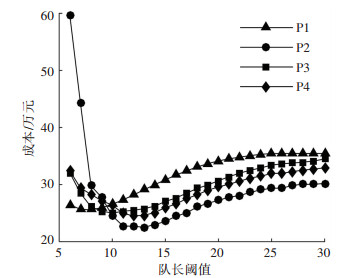
图 10 推出策略在不同队长阈值下总成本 Figure 10 Total cost of each pushback strategy with various taxiway queue limit |
由图 8、9可见,平均滑行时间W和平均停机位停留时间G随着队长阈值的增加,呈现负相关趋势,P2策略的平均停机位停留时间最大,由此也可看出P2策略的控制强度最大,传统N控制策略P1的控制强度最弱,P3与P4策略的控制强度介于P1与P2之间.
由图 10可见,4种控制策略随着滑行道队长阈值N的增加,均呈现先减后增趋势,其中,P2策略在队长阈值N=13时达到最优.
当传统N控制策略的队长阈值足够大时(N≥25),模型演化为无控制策略的情形.其详细对比结果见表 1.
| 表 1 推出控制策略最优结果对比 Table 1 Comparison of optimal results for various pushback control strategy |
表 1中,VF为燃油消耗量,Fn为停机位停留飞机数,RT为燃油节省量,PF为燃油节省百分比,RW为总滑行时间减少量,RFPF为平均每架飞机燃油节省量。在无控制时CT=354 505.6元,VF=122 502.9 kg,W=13.7 min.由表 1可知,传统N控制推出策略的最优队长阈值为8,总成本为268 084.4元,比无控制时总成本减少24.38%,燃油成本节省38.59%,总滑行时间比无控制时减少2 622 min/d,平均每架飞机滑行燃油减少量为94.9 kg,其停机位停留飞机数为193架;而P2、P3和P4策略均优于传统N控制策略,尤其是P2策略,其最优队长阈值为13,总成本为238 736.9元,比无控制时总成本减少32.66%,燃油成本节省44.04%,总滑行时间减少2 995 min/d,平均每架飞机滑行燃油减少量为108.3 kg,停机位停留飞机数为381架,控制强度最高,更具经济性和环保性.
4 结论1) 提出了一种推出频率随当前滑行道排队长度实时变化的基于惩罚的推出控制策略,其推出控制强度更高,可以有效将飞机滑行等待时间转化为停机位停留时间,以减少燃油消耗.
2) 合理的队长阈值选择可以有效降低滑行成本,阈值的选择需兼顾成本及跑道运行效率两方面.
3) 针对提出的推出频率控制模型,设计了一种基于连续时间马尔科夫链的迭代优化算法,首都机场数据结果分析表明:实施P2控制策略后,总滑行时间减少2 995 min/d,滑行成本降低44.04%.推出频率随当前滑行道排队长度实时变化的控制策略更具合理性与灵活性,比传统N控制策略在资源节约方面更具优势.
| [1] |
KHADILKAR H, BALAKRISHNAN H. Estimation of aircraft taxi fuel burn using flight data recorder archives[J]. Transportation Research Part D: Transport and Environment, 2012, 17(7): 532-537. DOI:10.1016/j.trd.2012.06.005 |
| [2] |
SIMAIAKIS I, BALAKRISHNAN H. A queuing model of the airport departure process[J]. Transportation Science, 2015, 50(1): 94-109. |
| [3] |
PUJET N, DELCAIRE B, FERON E. Input-output modeling and control of the departure process of congested airports[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit. Portland: American Institute of Aeronautics & Astronautics, 1999.
|
| [4] |
IDRIS H, CLARKE J P, BHUVA R, et al. Queuing model for taxi-out time estimation[J]. Air Traffic Control Quarterly, 2002, 10(1): 1-22. DOI:10.2514/atcq.10.1.1 |
| [5] |
CHENG V H L. Airport surface operation collaborative automation concept[C]//Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit. Austin: American Institute of Aeronautics & Astronautics, 2003.
|
| [6] |
CHENG V H L, SHARMA V, FOYLE D C. A study of aircraft taxi performance for enhancing airport surface traffic control[J]. IEEE Transactions on Intelligent Transportation Systems, 2001, 2(2): 39-54. DOI:10.1109/6979.928715 |
| [7] |
LEE H, SIMAIAKIS I, BALAKRISHNAN H. A comparison of aircraft trajectory-based and aggregate queue-based control of airport taxi processes[C]//Proceedings of the IEEE/AIAA 29th Digital Avionics System Conference. Salt Lake City: the Institute of Electrical and Electronics Engineers, 2010.
|
| [8] |
BERTSIMAS D, LULLI G, ODONI A. An integer optimization approach to large-scale air traffic flow management[J]. Operations Research, 2011, 59(1): 211-227. DOI:10.1287/opre.1100.0899 |
| [9] |
ROLING P, VISSER H. Optimal airport surface traffic planning using mixed integer linear programming[J]. International Journal of Aerospace Engineering, 2008, 2008(1): 1-11. |
| [10] |
高强, 严俊, 朱金福. CDM机制下航空公司时隙分配优化决策[J]. 交通运输系统工程与信息, 2011, 11(5): 94-98. GAO Qiang, YAN Jun, ZHU Jinfu. Airlines' optimization decision of slot allocation in CDM[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(5): 94-98. |
| [11] |
VOSSEN T, BALL M. Slot trading opportunities in collaborative ground delay programs[J]. Transportation Science, 2006, 40(1): 29-43. DOI:10.1287/trsc.1050.0121 |
| [12] |
张亚平, 刘丽华, 郝斯琪, 等. 基于弹性滑行容量的飞机有效推出时隙研究[J]. 武汉理工大学学报, 2016, 40(6): 937-942. ZHANG Yaping, LIU Lihua, HAO Siqi, et al. Aircraft effective pushback slot based on elastic taxiing capacity[J]. Journal of Wuhan University of Technology, 2016, 40(6): 937-942. |
| [13] |
MARÍN Á G. Airport management: taxi planning[J]. Annals of Operations Research, 2006, 143(1): 191-202. DOI:10.1007/s10479-006-7381-2 |
| [14] |
MARÍN Á G. Airport taxi planning: Lagrangian decomposition[J]. Journal of Advanced transportation, 2013, 47(4): 461-474. DOI:10.1002/atr.v47.4 |
| [15] |
刘丽华, 张亚平, 邢志伟, 等. 基于离散差分进化的飞机推出决策优化[J]. 交通运输系统工程与信息, 2016, 16(6): 196-203. LIU Lihua, ZHANG Yaping, XING Zhiwei, et al. Optimization of aircraft pushback decision based on discrete differential evolution[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(6): 196-203. |
| [16] |
LIU Lihua, ZHANG Yaping, LIU Lan, et al. Congestion pricing for aircraft pushback slot allocation[J]. Plos One, 2017, 12(1): 1-15. |
| [17] |
FERON E R, HANSMAN R J, ODONI A R, et al. The departure planner: a conceptual discussion[R]. Cambridge: Massachusetts Institute of Technology, 1997.
|
| [18] |
SANDBERG M, SIMAIAKIS I, BALAKRISHNAN H. A decision support tool for the pushback rate control of airportdepartures[J]. IEEE Transactions on Human-Machine Systems, 2014, 44(3): 416-421. DOI:10.1109/THMS.2014.2305906 |
| [19] |
MARTINEZ H F, BALAKRISHNAN H. Analysis of potential implementations of pushback rate control at LaGuardia airport[C]//Proceedings of the Transportation Research Board 94th Annual Meeting. Washington DC: Transportation Research Board Meeting, 2015.
|
| [20] |
BÖHME D. Tactical departure management with the Eurocontrol/DLR DMAN[C]//Proceedings of 6th USA/Europe Air Traffic Manage. Baltimore: Rts1 Demo Day Im Gate-to-gate Projekt, 2005.
|
| [21] |
SIMAIAKIS I, SANDBERG M, BALAKRISHNAN H. Dynamic control of airport departures: algorithm development and fieldevaluation[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(1): 285-295. DOI:10.1109/TITS.2013.2278484 |
| [22] |
SIMAIAKIS I, KHADIKAR H, BALAKRISHNAN H, et al. De-monstration of reduced airport congestion through pushback rate control[J]. Transportation Research Part A: Policy and Practice, 2014, 66: 251-267. DOI:10.1016/j.tra.2014.05.014 |
| [23] |
中国民航局. 2015年飞常准年度准点率报告[R/OL]. (2015-11-14)[2016-11-17]. http://cdn.feeyo.com/vedio/2016/zhdl2015.pdf. Civil Aviation Administration of China. Chinese mainland fight punctuality rate[R/OL]. (2015-11-14)[2016-11-17]. http://cdn.feeyo.com/vedio/2016/zhdl2015.pdf. |
 2018, Vol. 50
2018, Vol. 50


