2. 深圳高速工程顾问有限公司,广东 深圳518094;
3. 深圳市市政设计研究院有限公司,广东 深圳518029
2. Shenzhen Highway Engineering Consulting Company, Shenzhen 518094, Guangdong, China;
3. Shenzhen Municipal Design & Research Institute Co., Ltd., Shenzhen 518029, Guangdong, China
当前公路桥梁车桥耦合振动研究主要集中于确定车载下桥梁结构的动力行为分析方面,这与日常运营状态随机车流作用下桥梁的动力响应存在较大的差异,而国内外对随机车流作用下桥梁动力行为的研究还相对较少[1-2].开展随机交通荷载下桥梁结构的动力行为分析研究,可为既有桥梁的性能评定和预测、健康监测及基于车桥振动的结构损伤评定等提供必要的理论基础和方法支撑,具有重要意义,相关研究正吸引越来越多的关注[3-8].
文献[4]采用分离法建立车桥振动分析模型,依托单主梁和梁格法桥梁分析模型,提出了随机车流与桥梁耦合振动分析的框架并编制了相关程序,指出计算代价主要受子步迭代次数和收敛条件影响;文献[5]基于该方法开展了随机车流下双曲拱桥的车桥振动响应分析.文献[6-7]基于车桥耦合振动的整体分析模型,针对大跨度索体系桥梁提出将随机车流的动力作用等效为移动荷载列的方法,实现了随机车流与桥梁耦合振动分析的简化;文献[8]利用多类车辆单独过桥形成随机车辆等效荷载库,然后用等效荷载形式进行随机车流下桥梁动力行为分析,达到降低计算代价的目的,但其分析精度也受到了较大的影响.
综上分析,当前随机车流与桥梁耦合振动分析的方法主要包含分离迭代法和整体分析法两种,其中分离迭代法在每个时间步均需迭代,迭代次数的不确定性和收敛条件的合理选择对计算成本影响明显;而采用车桥整体分析与随机交通流简化为等效移动荷载列结合的方法,其计算成本的降低常以分析精度为代价,对于大跨度桥梁该法尚可接受,而对于常规桥梁则会造成较大误差.研究提出一种可实现更好的平衡计算成本和分析精度关系的随机车流与桥梁耦合振动分析方法十分必要.
为此,本文提出一种车桥系统运动方程维度时变的随机车流与桥梁耦合振动分析方法,保持了整体法直接求解、无需时间步内迭代的优点,通过对车桥系统运动方程的运动方程维度时变化的处理,有效降低了计算代价.结果表明所提出的方法能够以较经济的计算代价实现满足工程精度要求的随机车流与桥梁动力相互作用分析.所提出的数值方法适用于随机车流作用下各类桥梁的动力行为分析,能够应用于既有桥梁的疲劳损伤评估和预测、基于监测系统的桥梁损伤预后和基于车桥振动的结构损伤评定等相关研究,可为上述研究所需的随机交通流与桥梁动力相互作用的合理预测提供有效的分析方法.
1 随机车流模拟方法既有的相关研究表明,公路上通行的实际交通流是一个随机过程,在道路观测断面上任一时刻出现的车辆类型、车重、车辆间距都服从一定的随机分布[9].通过对实测过桥交通量和动态称重数据的统计分析,并结合相关随机车流参数研究的结果,可将随机车辆模拟的特征参数确定为车型、车重和车辆间距3类[9].其中车型一般服从均匀分布,车重和轴重服从极值Ⅰ型分布,一般运营状态的时间间隔和车间距服从对数正态分布,密集运营状态下的时间间隔和车间距服从伽马分布[9-10].
针对具体桥例,首先对随机车流进行观测和调查统计,然后利用K-S检验法对车辆特征参数进行随机分布的优度拟合,用极大似然法进行车辆荷载各随机变量的参数估计,可确定随机车辆荷载各特征参数符合的随机分布类型及参数.最后以年平均日交通量作为模拟样本容量,根据MATLAB程序自身包含的多种随机函数,编制随机车流的Monte-Carlo模拟程序,实现随机车流样本的模拟生成,具体模拟步骤和过程详见文献[11],不再赘述.后继将结合算例进一步说明随机车流模型的参数选取、交通调查数据等问题.
2 车桥耦合振动分析原理现有的车桥耦合系统运动方程建立方法可分为整体式和分离式两类.整体式所建立的车桥系统总体运动方程优点是求解过程不需要迭代,但方程维度高,占用内存大;而分离子系统独立建模的方法,虽能降低单个方程规模,但需要进行分离迭代,计算代价仍较大[3].
本文采用整体法,通过车辆与桥梁接触点的作用力和位移的协调关系,建立车辆、桥梁耦合系统的整体运动方程,可表达为
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_{\rm{v}}}}&{\bf{0}}\\ {\bf{0}}&{{\mathit{\boldsymbol{M}}_{\rm{B}}}} \end{array}} \right]\left\{ \begin{array}{l} {{\mathit{\boldsymbol{\ddot X}}}_{\rm{v}}}\\ {{\mathit{\boldsymbol{\ddot q}}}_{\rm{B}}} \end{array} \right\} + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_{\rm{v}}}}&{{\mathit{\boldsymbol{C}}_{{\rm{vB}}}}}\\ {{\mathit{\boldsymbol{C}}_{{\rm{Bv}}}}}&{{\mathit{\boldsymbol{C}}_{\rm{B}}} + \mathit{\boldsymbol{C}}_{\rm{B}}^{\rm{v}}} \end{array}} \right]\left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot X}}}_{\rm{v}}}\\ {{\mathit{\boldsymbol{\dot q}}}_{\rm{B}}} \end{array} \right\} + }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_{\rm{v}}}}&{{\mathit{\boldsymbol{K}}_{{\rm{vB}}}}}\\ {{\mathit{\boldsymbol{K}}_{{\rm{Bv}}}}}&{{\mathit{\boldsymbol{K}}_{\rm{B}}} + \mathit{\boldsymbol{K}}_{\rm{B}}^{\rm{v}}} \end{array}} \right]\left\{ \begin{array}{l} {\mathit{\boldsymbol{X}}_{\rm{v}}}\\ {\mathit{\boldsymbol{q}}_{\rm{B}}} \end{array} \right\} = \left\{ \begin{array}{l} \mathit{\boldsymbol{F}}_{\rm{v}}^{\rm{r}}\\ \mathit{\boldsymbol{F}}_{\rm{B}}^{{\rm{rG}}} \end{array} \right\}.} \end{array} $ | (1) |
式中:M, C, K分别为质量、阻尼和刚度矩阵;下标“B”和“v”分别代表桥梁和车辆;Xv和qB分别为车辆和桥梁位移响应向量;在刚度和阻尼中的上标“v”表示车辆的贡献项;下标“Bv”和“vB”表示车桥耦合项;上标“r”和“G”表示由于桥面不平度和车辆自重产生的作用力.
本文采用模态综合方法,在模态坐标下建立分析对象桥梁的运动方程.首先利用通用有限元软件建立桥梁的空间分析模型,然后进行模态分析并提取结构的振型和频率等模态信息,用于计算车桥动力响应.基于上述原理,本文采用MATLAB开发了专门的车桥耦合振动分析程序.
现以三轴整车为例,对车辆计算模型进行简要介绍,如图 1所示.该模型包含16个自由度,Zvr、θvr、φvr、Yvr分别为车体竖向沉浮、绕Y轴的转动、绕X轴的侧滚和横向摆动自由度;ZsLi、ZsRi分别为悬架X轴左侧、右侧刚体竖向沉浮自由度;YsLi、YsRi分别为悬架X轴左侧、右侧刚体横向摆动自由度;下标vr表示车体;s表示悬架;L、R分别表示X轴左侧、右侧刚体.上述车桥耦合振动方程中质量、刚度、阻尼和荷载向量,车辆运动方程及详细参数可详见文献[12],此不赘述.

|
图 1 车辆模型 Figure 1 Vehicle model |
常规的整体法车桥振动分析模型,车辆过桥计算过程中,运动方程的维度保持不变,仅在每个时间步对式(1)中的车桥耦联阻尼CvB, CBv和刚度项KvB, KBv进行更新.如直接应用于随机车流-桥梁耦合振动计算,必然导致庞大的计算成本.为此,本文下面提出一种考虑随机车流过桥过程中,车桥耦合运动方程维度实时更新变化的车桥耦合振动分析方法.
3 随机车流与桥梁耦合振动整体分析算法 3.1 分析流程与关键步骤处理方法随机车流过桥时,每一时刻桥上车辆及车轴数都在发生变化,通过对车桥系统运动方程维度的实时更新,实现方程维度时变的随机车流与桥梁振动分析.该方法的分析框架如图 2所示.结合该框架,将该分析方法的具体流程总结如下:1)基于交通调查开展随机交通流的数值模拟. 2)基于模态分析或实测得到的桥梁模态参数,得到方程(1)中的[MB]Nb×Nb, [KB]Nb×Nb, [CB]Nb×Nb(其中Nb为参与计算振型阶数). 3)胞元数组表达车型矩阵.重车车型分为整车和挂车两类,按轴数又分为5种,车辆计算模型见文献[13];分别建立2×5的胞元数组{Mvt}、{Kvt}和{Cvt},其中各元素对应各车型质量、刚度和阻尼矩阵. 4)建立车桥响应存储矩阵[Uv]Nv×nt和[Ub]Nb×nt. nt为随机车流过桥需要的总时间步数,Nv为全部车辆自由度总数. 5)随机车队相对桥梁运行状态判定. a)首先对车队序列进行车轴编号,起始时刻t0各轴横、纵坐标的标量矩阵为{xz}1×n和[yz]1×2n,n为车道数,x表示纵坐标,y表示横坐标,z表示车轴;b)车队开始运行后计算各时刻车轴的新坐标,依次判断各轴是否处于桥面范围;将当前时刻处于桥面上的车轴编号存储为变量{VZB}1×n(每个元素为当前时刻某车道桥面上的车轴编号向量);c)最后,据{VZB}1×n可确定当前时刻桥面上的车型序列{VTB}1×n,各元素为某车道上的车型序列向量(桥上车轴、车型向量维度为时变的,且只要某车型任意车轴在桥则认为该车在桥上). 6)任意时刻车辆运动方程的构建.质量、刚度和阻尼矩阵分别为[Mv]nvi×nvi、[Kv]nvi×nvi、[Cv]nvi×nvi,nvi为第i时间步开始时刻桥上车辆自由度总数. 7)车桥耦合项和荷载项计算.对当前时刻桥上各车型的每一车轴进行循环,由车轴坐标插值确定对应车轮位置的不平度和各阶振型分量,进而计算得到车桥耦合项矩阵KBv和CBv,及荷载项Fvr和FBrG. 8)维度时变的车桥耦合振动方程求解.按步骤1~7组成的任意时刻车桥耦合运动方程,采用Newmark-β法求解,其上一时间步各车辆响应值由[Uv]中对应车辆位置提取,当前步车辆响应获得后存储到[Uv];重复以上步骤直到随机车队全部过桥.

|
图 2 随机车流与桥梁耦合振动分析流程图 Figure 2 Analysis frame for coupled vibration of random traffic flow and bridges |
以两车道随机车流通过某跨径为20 m的简支梁桥为例,说明本文随机车流与桥梁耦合振动的算法的实现过程和关键步骤.为分解说明关键步骤,采用了一个简单的2列共5辆车的随机车队排列情况,如图 2所示.根据此车队排列,则程序中车型数组和区分整车挂车的数组可设定为
| $ \left\{ {V_Z^{\rm{p}}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} 2&4&3 \end{array}} \right]}\\ {\left[ {\begin{array}{*{20}{c}} 2&3 \end{array}} \right]} \end{array}} \right\};\;\left\{ {{V_{\rm{T}}}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} 1&2&1 \end{array}} \right]}\\ {\left[ {\begin{array}{*{20}{c}} 1&1 \end{array}} \right]} \end{array}} \right\}. $ |
其中{VZp}数组元素表示车队中各车辆相对位置和车辆轴数;{VT}数组中“1”表示整车,“2”表示挂车.
车辆间距实际由随机车流模拟结果确定,为说明问题,假设各车间距均为1 m,定义上桥侧桥头为纵坐标原点,车辆行驶方向为正,各车道首车的前轴坐标为小于0的任意值,在此对车道1、2分别取-1、-5 m.根据各车型轴距参数可得到随机车队各轴的纵坐标数组表示为
| $ {x_z} = \left\{ \begin{array}{l} \left[ \begin{array}{l} - {\rm{1, }} - {\rm{4}}{\rm{.75, }} - {\rm{5}}{\rm{.75, }} - {\rm{9}}{\rm{.5, }} - {\rm{18}}{\rm{.1, }}\\ - {\rm{19}}{\rm{.4, }} - {\rm{20}}{\rm{.4, }} - {\rm{25}}{\rm{.2, }} - {\rm{26}}{\rm{.55}} \end{array} \right]\\ \left[ { - {\rm{5, }} - {\rm{8}}{\rm{.75, }} - {\rm{9}}{\rm{.75, }} - {\rm{14}}{\rm{.55, }} - {\rm{15}}{\rm{.9}}} \right] \end{array} \right\}. $ |
设随机车流过桥车速为50 km/h,时程分析的步长为0.01 s,总时间步数为ns,则单位时间步内车队前进距离为0.14 m,可计算得到任意时刻车队内各车各轴的坐标.现以随机车流过桥的以下几个典型时刻来对本文维度时变的随机车流与桥梁振动分析的算法进行说明.
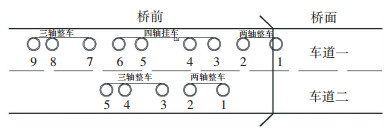
1) 时刻1.首车上桥(见图 3),当ns=8时,车道1上的1号车轴坐标为0.12 m,表明该轴已上桥.此时桥上车轴编号数组{VZB}和桥上车型数组{VTB}分别为
| $ \left\{ {V_{\rm{Z}}^{\rm{B}}} \right\} = \left\{ {\left[ 1 \right]} \right\};\;\;\left\{ {V_{\rm{T}}^{\rm{B}}} \right\} = \left\{ {\left[ 2 \right]} \right\}. $ |
|
图 3 随机车流过桥状况1 Figure 3 Case 1 for random traffic flow passing bridges |
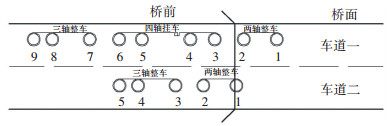
2) 时刻2.车道2首车上桥(车流与桥相对位置如图 4所示):当ns=36时,车道2首车上桥.此时桥上车轴编号数组{VZB}的维度及其元素的维度均发生改变,桥上车型数组维度也随之改变,具体为
| $ \left\{ {qsz} \right\} = \left\{ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} 1&2 \end{array}} \right]}\\ {\left[ 1 \right]} \end{array}} \right\};\;\;\left\{ {ncx} \right\} = \left\{ \begin{array}{l} \left[ 2 \right]\\ \left[ 2 \right] \end{array} \right\}. $ |
|
图 4 随机车流过桥状况2 Figure 4 Case 2 for random traffic flow passing bridges |
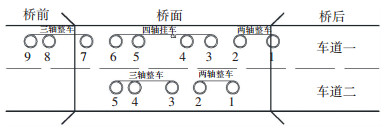
3) 时刻3.车道1的1号车轴下桥(如图 5所示):ns=151时,车道1的1号车轴下桥,2号车轴仍在桥面上.此时桥上车轴编号数组{qsz}的元素较前一时刻发生改变,而桥上车型数组{ncx}较前一时刻没有变化,具体为
| $ \begin{array}{*{20}{c}} {\left\{ {V_{\rm{Z}}^{\rm{B}}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} 2&3&4&5&6&7 \end{array}} \right]}\\ {\left[ {\begin{array}{*{20}{c}} 1&2&3&4&5 \end{array}} \right]} \end{array}} \right\};}\\ {\left\{ {V_{\rm{T}}^{\rm{B}}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} 2&4&3 \end{array}} \right]}\\ {\left[ {\begin{array}{*{20}{c}} 2&3 \end{array}} \right]} \end{array}} \right\}.} \end{array} $ |
|
图 5 随机车流过桥状况3 Figure 5 Case 3 for random traffic flow passing bridges |
通过以上3个典型时刻的分析,说明了车辆及车轴处于上、下桥等状态在程序中的实现方法.
3.2.3 维度时变的随机车桥耦合振动方程组建过程在完成了各时刻桥上车轴编号数组和桥上车型数组确定方法后,下面开始组建车桥耦合振动方程中的车辆相关项矩阵(Mv, Kv, Cv)和车桥耦合项矩阵(Kvb, Cvb)),进而完成车桥耦合振动方程的组建工作.现以前述“时刻3”情况为例,以车辆刚度矩阵Kv为代表说明车辆相关矩阵的组建方法.
| $ \begin{array}{l} {\mathit{\boldsymbol{K}}_{\rm{v}}} = \\ \left[ {\begin{array}{*{20}{c}} {{{\left[ {\mathit{\boldsymbol{K}}_2^{\rm{Z}}} \right]}_{12 \times 12}}}&{}&{}&{}&{}\\ {}&{{{\left[ {\mathit{\boldsymbol{K}}_4^{\rm{G}}} \right]}_{23 \times 23}}}&{}&{}&{}\\ {}&{}&{{{\left[ {\mathit{\boldsymbol{K}}_3^{\rm{Z}}} \right]}_{12 \times 12}}}&{}&{}\\ {}&{}&{}&{{{\left[ {\mathit{\boldsymbol{K}}_2^{\rm{Z}}} \right]}_{12 \times 12}}}&{}\\ {}&{}&{}&{}&{{{\left[ {\mathit{\boldsymbol{K}}_3^{\rm{Z}}} \right]}_{16 \times 16}}} \end{array}} \right] \end{array} $ |
其中KiZ为i轴整车的刚度矩阵,KiG为i轴挂车的刚度矩阵,阻尼和质量矩阵的组建方法与此类似.
车桥耦合项矩阵的组建方法:确定桥上各车轴车轮坐标(xi, yi)后,振型差值得到各轮位置的桥梁振型和振型偏导向量值,按照已推导得到的耦合项公式[12],对桥上各轴编号数组中各元素进行依次计算,得到各轴自由度对应的车桥耦合项刚度和阻尼矩阵元素值.需要注意组成耦合项矩阵过程中要将车辆自由度从单车矩阵中位置转换为车队中的位置.如前述时刻3车道1的第3号轴左轮的竖向自由度在四轴挂车运动方程中处于第8行,而在车桥耦合矩阵中应放置在第20行.
车辆和桥梁荷载项表达式详见文献[12],将以上各项组合后形成车桥耦合振动方程,采用New-mark-β法求解,每个时间步方程求解后将车辆响应向量存储至[Uv],下一时间步开始前更新车桥振动方程维度后开始该步的求解.
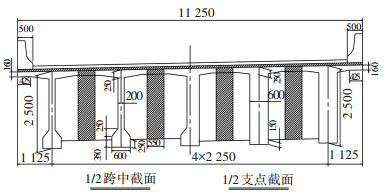
4 工程实例分析 4.1 桥梁概况及有限元模型以G307国道河北省境内一座跨径为3×40 m的预应力混凝土简支转连续T梁桥为例.桥面宽度为11.25 m(双向分离式桥梁的一幅),单向两车道,荷载等级为公路-Ⅰ级.预制及现浇混凝土均采用C50;普通钢筋采用R235和HRB335钢筋,钢筋直径小于12 mm采用R235钢筋;预应力钢筋采用抗拉强度标准值fpk =1 860 MPa(跨中和支点截面如图 6所示.)
|
图 6 桥梁跨中和支点主梁截面(mm) Figure 6 Typical section in the mid and end of the bridge(mm) |
依据该桥设计资料,采用ANSYS建立了桥梁的精细化分析模型,如图 7所示,其中主梁、横隔梁采用SOLID65实体单元模拟,钢筋及预应力采用LINK8杆单元模拟,桥面铺装采用Shell63板单元模拟,总计400 824个单元.该有限元模型模态分析所得数据将用于后继的车桥耦合振动分析.

|
图 7 桥梁计算模型 Figure 7 Analysis model of bridges |
通过对G307国道河北段井陉西收费站为期两周的车辆调查,过站车辆总数为175 712辆,车型客货比为3:7,过桥载重货车交通量为122 998辆.各类货车车型占比信息汇总见表 1[10].依据交通调查数据并结合全国公路车辆荷载分类研究结果,将该桥过桥车辆的重型车型分为7类,各类车型参数见文献[10].由于小客车自重较小,荷载效应与重车相比较低,参考同类研究在分析中对其进行了忽略处理,但考虑了其对车辆间距的影响.
| 表 1 车型占比情况 Table 1 Ratio of different vehicles |
基于实际交通观测数据,利用K-S检验法对车辆特征参数进行随机分布优度拟和,用极大似然法进行车辆荷载各随机变量的参数估计,确定随机车辆荷载各特征参数符合的随机分布类型及参数如表 2所示.
| 表 2 随机车流特征参数服从的概率分布 Table 2 The probability distribution of characteristic parameters for random traffic flow |
采用Monte-Carlo方法进行随机车流荷载模拟.下面基于自编的随机车流模拟程序,选取重车样本容量300为例,模拟得到各车型分布和密集运行状态下车辆间距分布如图 8所示.

|
图 8 随机车流模型 Figure 8 Model of random traffic flow |
为分析本文提出车桥振动算法的适用性和计算效率,现针对算例分别采用以下3种方法进行计算:本文算法(算法1);方程维度恒定的车桥振动整体分析方法(算法2);车桥分离迭代方法(算法3).车桥分析工况基本参数:车速恒定为50 km/h,时间步长取为0.01 s,随机车流车辆数为300,随机车队总长度为2 521 m.算法3分离迭代法中,以车轮与桥面相互作用力误差10 N作为收敛条件.
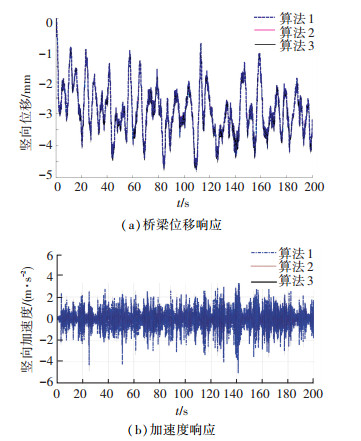
以桥梁中跨右侧边梁跨中竖向位移和加速度响应为例,将3种算法的计算结果进行比较(见图 9),发现算法1和算法2得到的结果基本相同,与算法3的差别也十分微小,最大相对误差小于3.5%.表明所提出的算法与常用方法的结果吻合良好,具有较好的适用性.
|
图 9 随机车载下桥梁跨中动力响应比较 Figure 9 Comparison of dynamic response for the bridge in midspan under random traffic flow |
通过对3种算法计算过程信息的汇总和对比,可发现各算法的计算效率情况,见表 3,其中na为单个时间步内平均迭代次数. 3种算法总计算时间步数均为7 488.算法1由于采用了方程维度时变处理方法,使车桥振动方程的单步求解维度明显降低,从而较传统整体分析算法2有了大幅的提高,总用时仅为算法3的14.8%;同算法3相比,两者计算效率差别不大,既有研究[3]表明算法3的计算效率受到步内迭代次数、收敛误差取值的影响明显,且存在步内迭代不收敛的风险.分析表明,本文所提出的算法具有较高的计算效率,可用于随机车流下各类桥梁的车桥振动分析及考虑风荷载、地震荷载多场动力分析.
| 表 3 计算效率比较分析 Table 3 Comparison of computational efficiency |
1) 针对随机车流过桥动力行为数值分析问题,提出了一种基于车桥整体运动方程维度时变的随机车桥振动计算方法.该法保持了整体法计算稳定、无需子步迭代的优势,通过方程维度的动态时变化处理,有效提高计算效率,拓展了车桥振动整体分析方法的适用范围.
2) 详细阐述了所提方法的分析框架和关键步骤,并依托算例给出了具体的实现方法和处理策略,可为相关随机车流与桥梁振动分析算法和程序的编制提供参考.
3) 依托工程实例对所提算法与常用方法的计算效率进行比较分析,结果表明该算法较方程维度恒定的整体算法计算效率提高达近10倍,与分离迭代方法相比差异不明显.该方法不存在分离迭代法经常遇到的迭代次数不确定和不易收敛导致的计算时间预估难度大和耗时增长问题,具有很好的应用价值.
| [1] |
FENG D M, SUN H, FENG M Q. Simultaneous identification of bridge structural parameters and vehicle loads[J]. Computers and Structures, 2015, 157: 76-88. DOI:10.1016/j.compstruc.2015.05.017 |
| [2] |
LOMBAERT G, JOEL P C. Random vibration analysis of dynamic vehiclek-bridge interaction due to road unevenness[J]. Journal of Engineering Mechanics, 2012, 138: 816-825. DOI:10.1061/(ASCE)EM.1943-7889.0000386 |
| [3] |
夏禾, 张楠, 郭薇薇, 等. 车桥耦合振动工程[M]. 北京: 科学出版社, 2014. XIA He, ZHANG Nan, GUO Weiwei, et al. Coupling vibrations of train-bridge system[M]. Beijing: Science Press, 2014. |
| [4] |
韩万水, 马麟, 汪炳, 等. 随机车流-桥梁系统耦合振动精细化分析与动态可视化[J]. 中国公路学报, 2013, 26(4): 78-87. HAN Wanshui, MA Lin, WANG Bing, et al. Refinement analysis and dynamic visualization of traffic-bridge coupling vibration system[J]. China Journal of Highway and Transport, 2013, 26(4): 78-87. |
| [4] |
王达, 刘杨, 黄平明. 随机车流作用下双曲拱桥车桥耦合振动研究[J]. 中国公路学报, 2009, 22(6): 67-72. WANG Da, LIU Yang, HUANG Pingmin. Research on vehicle-bridge coupled vibration for two-way curved arch bridge under random traffic flow[J]. China Journal of Highway and Transport, 2009, 22(6): 67-72. http://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200906009.htm |
| [5] |
殷新锋, 邓露. 随机车流作用下桥梁冲击系数分析[J]. 湖南大学学报(自然科学版), 2015, 42(9): 68-75. YIN Xinfeng, DENG Lu. Impact factor analysis of bridges under random traffic loads[J]. Journal of Hunan University (Natural Sciences), 2015, 42(9): 68-75. |
| [6] |
CHEN S R, WU J. Modeling stochastic live load for long-span bridge based on microscopic traffic flow simulation[J]. Computers and Structures, 2011, 89: 813-824. DOI:10.1016/j.compstruc.2010.12.017 |
| [7] |
李扬海, 鲍卫刚, 郭修武, 等. 公路桥梁结构可靠度与概率极限状态设计[M]. 北京: 人民交通出版社, 1997. LI Yanghai, BAO Weigang, GUO Xiuwu, et al. Structural reliability for highway bridges and probability based limit state design[M]. Beijing: China Communications Press, 1997. |
| [8] |
CHEN S R, WU J. Dynamic performance simulation of long-span bridge under combined loads of stochastic traffic and wind[J]. Journal of Bridge Engineering, 2010, 15(3): 219-230. DOI:10.1061/(ASCE)BE.1943-5592.0000078 |
| [9] |
张喜刚. 公路桥梁汽车荷载标准研究[M]. 北京: 人民交通出版社, 2014: 220-241. ZHANG Xigang. Study on vehicle load standard of Highway Bridge[M]. Beijing: China Communications Press, 2014: 220-241. |
| [10] |
李岩, 吕大刚, 盛洪飞. 考虑随机车载-风载联合作用的斜拉桥拉索疲劳可靠性分析[J]. 中国公路学报, 2012, 25(2): 60-66. LI YAN, LU Dagang, SHENG Hongfei. Fatigure reliability analysis on cable of cable-stayed bridge under random vehicle load and wind load[J]. China Journal of Highway and Transport, 2012, 25(2): 60-66. |
| [11] |
LI Y, CAI C S, LIU Y, Chen Y J, LIU J F. Dynamic analysis of a large span specially shaped hybrid girder bridge with concrete-filled steel tube arches[J]. Engineering Structures, 2016, 106: 243-260. DOI:10.1016/j.engstruct.2015.10.026 |
| [12] |
刘佳锋. 车载下既有损伤公路混凝土简支梁桥动力响应分析[D]. 哈尔滨: 哈尔滨工业大学, 2014. LIU Jiafeng. Dynamic response analysis of highway concrete simply supported beam bridges with damage under moving vehicles[D]. Harbin: Harbin Institute of Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10213-1014084598.htm |
 2018, Vol. 50
2018, Vol. 50


