崩塌落石作为地震次生灾害严重威胁灾区生命线工程正常运营[1-2],造成不可估量的损失.如2008年汶川地震中,位于灾区生命通道国道213线的彻底关大桥遭岷江左岸崩塌落石撞击倒塌,经过恢复重建,2009年岷江右岸发生崩塌,落石再次击中彻底关新桥墩柱,造成8号墩墩柱断裂两跨落梁[2-3].然而,目前针对桥梁结构落石冲击的研究仍然很少,桥梁管理者对此类事故重视程度仍然不足.
现有研究在钢筋混凝土柱侧向冲击行为和落石冲击荷载研究两个方面独立开展,而对桥梁墩柱落石冲击行为的研究很少.钢筋混凝土柱侧向冲击行为研究方面,文献[4]考虑钢筋与混凝土粘结滑移,采用非线性有限元方法分析了刚性球对钢筋混凝土柱的冲击效应.文献[5]提出一种基于竖向剩余承载力的钢筋混凝土柱撞击损伤评估方法,定义了钢筋混凝土柱撞击损伤级划分标准.文献[6]的钢筋混凝土柱落锤冲击实验表明较高冲击能量下钢筋混凝土柱主导失效模式为局部冲剪破坏.文献[7]的冲击荷载试验表明,冲击荷载下钢筋混凝土构件的有效弯曲型动力响应滞后于直剪破坏.文献[8]假定落石冲击荷载为半波正弦型脉冲,研究不同冲击荷载持续时间、荷载峰值、冲击位置、冲击角度对钢筋混凝土柱冲击响应行为的影响.落石冲击力表达式方面,文献[9]以Hertz接触理论为基础,建立了大块石对桥梁结构的冲击作用模型,推导了大块石冲击力表达式.文献[10-11]采用修正系数方法描述大块石冲击过程摩擦、结构损伤等因素对冲击力的影响,但该方法最大不足在于修正系数通过主观确定,缺乏理论依据.中国路基规范公式,日本道路公团公式和瑞士规范公式均给出了冲击力等效静力值与落石尺寸和撞击速度关系式[12],但这些公式均为基于特定实验条件的经验表达式,各公式计算值存在显著差异,难以准确评价墩柱抗落石冲击性能.总体来看,现有研究主要关注试验荷载下钢筋混凝土柱的动态响应行为和基于经验公式的落石冲击力表达式研究,而对桥梁墩柱落石冲击行为及其损伤评价的研究仍然不足.
本文在数值模拟方法可靠性验证基础上,建立一种基于等效静力分析的RC柱式桥墩落石撞击损伤状态分析方法.以墩柱受剪破坏建立极限状态方程,撞击荷载等效静力为作用效应,截面动载抗剪能力为结构抗力,以剪力破坏参数定义截面损伤状态.以彻底关大桥事故失效墩柱为例,分析了墩柱失效模式和撞击荷载特征,讨论了落石冲击能量、混凝土强度、墩柱截面面积、箍筋配筋率、墩柱长细比对墩柱落石冲击损伤状态的影响,分析结果为落石威胁区桥梁结构安全评估和墩柱落石冲击设计提供参考.
1 墩柱落石冲击分析方法 1.1 墩柱失效模式结构或构件外荷载作用下是否满足某一确定的功能要求可以表示为
| $ Z = g\left( {R, S} \right) = R - S. $ | (1) |
式中S为荷载效应和R为结构抗力.
钢筋混凝土墩柱侧向冲击下典型失效模式包括整体破坏和局部破坏[4-5].墩柱发生整体破坏表现为墩柱发破坏前整体变形显著发展,冲击能量由墩柱整体变形吸收,弯曲失效为主导失效模式.低速冲击局部破坏表现为局部混凝土压碎,以及撞击位置局部和临近边界区域的剪切失效.整体型失效一般发生在冲击体局部刚度较小,撞击力时程存在缓长的上升段情形,局部破坏发生在短时高峰值的强冲击场景.彻底关大桥事故数值模拟研究[3, 8]表明,墩柱落石撞击下主导破坏模式为撞击点以下位置的直剪破坏.文献[13]调研了车辆撞击下墩柱失效模式,认为截面剪力早于弯矩超出截面能力是墩柱失效的主要原因,而落石冲击荷载持时更短.本文以剪切破坏建立墩柱落石撞击极限状态方程,参照文献[14]关于混凝土构件受剪性能的划分标准定义墩柱损伤阶段,并通过非线性有限元分析进一步验证.
1.2 落石冲击荷载落石与墩柱的界面接触力为作用效应.中国现有公路和铁路桥梁设计规范中均建议落石冲击力应根据经验取值,但均未给出冲击力建议值或确定方法.而基于落石与缓冲垫层冲击试验回归的落石冲击荷载表达式难以用于落石对墩柱冲击荷载预测.落石与墩柱撞击过程隶属冲击动力学范畴,撞击过程伴随剧烈的能量释放、传递和转化以及材料在较高应变率下的大变形.非线性有限元方法能够有效的考虑撞击过程中复杂的非线性特征进而获得精确的撞击力时间过程.对于接触问题,泛函可以表示为
| $ \mathit{\Pi = }{\mathit{\Pi }_{\rm{u}}} + {\mathit{\Pi }_{{\rm{CP}}}}. $ | (2) |
式中Πu为接触问题中不包括接触边界约束条件的总位能,ΠCP为引入接触定解条件的附加泛函.
根据泛函变分驻值条件δΠ=δΠu+δΠCP=0,可得到接触问题求解方程.用罚函数法引入接触定解条件时,界面接触力虚功表示为
| $ \begin{array}{l} {}^{t + \Delta t}{W_{\rm{c}}} = - \delta {\mathit{\Pi }_{{\rm{CP}}}} = \int_{t + \Delta t} {\left[ { - {a_{\rm{N}}}\left( {u_{\rm{N}}^{\rm{A}} - u_{\rm{N}}^{\rm{B}}{ + ^t}\overline {{g_{\rm{N}}}} } \right) + } \right.} \\ \;\;\;\;\;\;\;\;\;\;{\left. {{a_1}\left( {u_1^{\rm{A}} - u_1^{\rm{B}}} \right)2 + {a_2}{{\left( {u_2^{\rm{A}} - u_2^{\rm{B}}} \right)}^2}} \right]^{t + \Delta t}}{\rm{d}}S, \end{array} $ | (3) |
| $ {}^{t + \Delta t}F_{\rm{N}}^{\rm{A}} = { - ^{t + \Delta t}}F_{\rm{N}}^{\rm{B}} = - {\alpha _{\rm{N}}}\left( {u_{\rm{N}}^{\rm{A}} - u_{\rm{N}}^{\rm{B}}{ + ^t}\overline {{g_{\rm{N}}}} } \right). $ | (4) |
式中:t+ΔtWc为时步t+Δt内界面接触力虚功;δ表示对物理量进行变分运算;αN, α1, α2为罚参数;uNA, uNB分别为从、主接触点法向位移分量;
在合理的罚参数取值下,数值方法能够在保证一定计算效率的显式积分时间步长下求得界面接触力精确解.相比于理论推导和试验方法,合理参数取值下数值方法能够更有效的模拟撞击接触过程,且更方便的获取大量撞击力时程样本的统计规律.因此,本文采用非线性有限元方法获得的撞击力时程,在此基础上考虑等峰值和等冲量原则建立半波正弦型简化撞击荷载模型.
1.3 墩柱抗力模型考虑材料强度率相关性的截面动态抗剪能力为抗力.墩柱抗剪能力主要由截面混凝土、抗剪钢筋与轴向压力提供,本文参照文献[15]将墩柱抗剪能力表示为
| $ {V_{\rm{D}}} = {V_{\rm{C}}} + {V_{\rm{S}}} + {V_{\rm{P}}}. $ | (5) |
其中
| $ {V_{\rm{C}}} = k\sqrt {{f_{\rm{c}}}} {A_{\rm{e}}}, $ | (6) |
| $ {V_{\rm{S}}} = \frac{{\rm{ \mathit{ π} }}}{2}\frac{{{A_{{\rm{sh}}}}{f_{{\rm{yh}}}}D'}}{S}\cot \theta , $ | (7) |
| $ {V_{\rm{P}}} = P\tan \alpha . $ | (8) |
式(5)~(8)中参数含义和详细计算方法见文献[15-16].
Priestley抗剪能力表达式适用于静态过程以及应变率较低的准静态过程.钢筋混凝土构件在快速加载下极限抗剪能力存在一定提高,提高幅度与混凝土的抗压或抗拉强度的提高幅度一致[3-5].混凝土材料的应变率效应通过混凝土强度增大系数(动载强度/静载强度)表示.本文混凝土强度增大系数采用K & C模型,该模型为CEB模型基础改进而来[17],混凝土动载抗压强度增大系数表示为
| $ {C_{{\rm{DIF}}}} = \frac{{{f_{{\rm{cd}}}}}}{{{f_{{\rm{cs}}}}}} = \left\{ \begin{array}{l} {\left( {\frac{{{{\dot \varepsilon }_{\rm{d}}}}}{{{{\dot \varepsilon }_{{\rm{cs}}}}}}} \right)^{1.206\alpha }}, {{\dot \varepsilon }_{\rm{d}}} \le 30{{\rm{s}}^{ - 1}};\\ \gamma {\left( {_{\rm{d}}^{\dot \varepsilon }} \right)^{\frac{1}{3}}}, {{\dot \varepsilon }_{\rm{d}}} > 30{{\rm{s}}^{ - 1}}. \end{array} \right. $ | (9) |
| $ \alpha = {\left( {5 + \frac{3}{4}{f_{{\rm{cs}}}}} \right)^{ - 1}}, \lg \gamma = 6.156a - 0.49. $ |
式中:fcd为应变率为
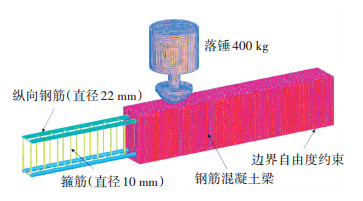
建立文献[18]中RC梁冲击实验有限元模型,通过实验结果对比验证数值模拟方法有效性. 图 1给出RC梁落锤试验装置,图 2为落锤冲击有限元模型,试验中S2222型试验梁梁长1.7 m,受拉区和受压区各配置两根直径22 mm纵向钢筋,箍筋直径10 mm,间距为75 mm.混凝土抗压强度42 MPa,骨料最大粒径10 mm.落锤总质量400 kg,采用R90锤头,梁体两端通过螺栓锚杆约束,落锤落高分别为0.3、0.6、1.2、2.4 m.

|
图 1 冲击实验装置(mm) Figure 1 The impact experiment equipment(mm) |
|
图 2 钢筋混凝土梁数值模型 Figure 2 The numerical model of the RC beam |
基于罚函数的面面接触算法用于模拟落锤与钢筋混凝土梁的接触撞击过程,通过对称引入罚因子处理每个时间步落锤节点与钢筋混凝土梁节点组穿透量得到接触界面力合力时程.由于落锤与钢筋混凝土梁接触持时短暂,未考虑钢筋与混凝土粘结滑移作用,耦合钢筋节点与临近混凝土节点自由度.混凝土连续面盖帽模型(CSCM)[19]用以模拟混凝土材料低速冲击下的损伤和破坏行为,模型参数取值参照文献[9],连续面盖帽模型塑性面表示为
| $ f\left( {{J_1}, {{J'}_2}, {{J'}_3}, k} \right) = {{J'}_2} - {R^2}F_{\rm{f}}^2{F_{\rm{c}}}, $ | (10) |
| $ {F_{\rm{f}}}\left( {{J_1}} \right) = \alpha - \lambda {\exp ^{ - \beta {J_1}}} + \theta {J_1}, $ | (11) |
| $ {F_{\rm{c}}}\left( {{J_1}, k} \right) = 1 - \frac{{\left[ {{J_1} - L\left( k \right)} \right]\left[ {\left| {{J_1} - L\left( k \right)} \right| + {J_1} - L\left( k \right)} \right]}}{{2{{\left[ {X\left( k \right) - L\left( k \right)} \right]}^2}}}. $ | (12) |
式中:Ff(J1)为剪切失效面;Fc(J1, k)为硬化盖帽面函数;J1, J2′, J3′分别为应力第一不变量、偏应力第二、第三不变量;k为盖帽硬化参数,R为Rubin折减函数,α, β, λ, θ为混凝土回归参数,X(k), L(k)为算子函数.
忽略接触过程锤头变形,采用刚性体模型加速计算.纵向钢筋与箍筋采用双线性随动强化模型,纵筋屈服强度为418 MPa,抗剪钢筋屈服强度为295 MPa.考虑动载作用下钢筋屈服强度强化效应,钢筋动载屈服强度参照Cowper-Symonds公式[20]表示为
| $ {\sigma _{\rm{y}}} = {\sigma _{\rm{0}}}{\left[ {1 + \frac{{\dot \varepsilon }}{c}} \right]^{\frac{1}{p}}}. $ | (13) |
式中:σ0为钢筋静力屈服强度;c, p为应变率表达式参数;
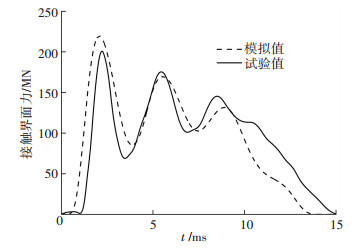
图 3为2.4m落高工况梁体破坏与数值模拟损伤图对比,梁体损伤区域基本一致,为锤头与梁体接触局部损伤区和梁体底部的锥形破坏区. S2222梁0.3 m落高接触界面力时程数值模拟与实验结果对比在图 4中给出,数值模拟冲击力时程与试验结果吻合较好,由于数值模拟中落锤刚性体假设、材料变形的零热耗散假设以及边界条件理想化,这些假设使得计算忽略了冲击体变形能和构件变形热能,进而导致构件以更大的变形消耗冲击动能.总体来看,本文数值模拟方法和模型参数取值能够满足钢筋混凝土结构低速冲击分析精度要求.
|
图 3 梁体冲击损伤扩展(2.4 m落高) Figure 3 Extension of dynamic damage in RC beam (falling height: 2.4 m) |

|
图 4 冲击力时程数值模拟与试验结果对比 Figure 4 Comparison of simulation and tests results on time history curves of falling force (falling height: 0.3 m) |
以彻底关大桥落石冲击倒塌事故墩柱开展算例分析.按照文献[8]给出的彻底关大桥墩柱几何尺寸,考虑冲击过程桩基和土层相互作用影响,建立彻底关大桥墩柱落石冲击有限元模型.混凝土强度30 MPa,纵向钢筋采用为直径28 mmHRB335钢筋,箍筋为直径10 mmR235钢筋,箍筋间距20 cm.
纵筋采用梁单元BEAM161模拟,箍筋采用杆单元LINK160模拟,混凝土结构、土层和球体落石采用实体单元SOLID164模拟.连续面盖帽模型*MAT_159用于模拟墩柱混凝土低速冲击下力学行为,混凝土轴心抗压强度为30 MPa.纵筋和箍筋材料模型使用弹塑性随动强化模型*MAT_3,纵筋屈服强度335 MPa,箍筋屈服强度235 MPa,钢筋动屈服强度率相关特征通过式(10)描述.土壤材料模型采用*MAT_MOHR_COULOMB,如图 5所示,模型参数按文献[8, 21]推荐值在表 1中给出.分析中未考虑钢筋与混凝土粘结滑移,钢筋节点与混凝土单元节点通过约束自由度方式耦合[19-20],土层边界通过非反射边界消除非真实应力震荡[21].

|
图 5 RC双柱墩有限元模型 Figure 5 The FE model of the RC substructure |
| 表 1 土层材料模型参数 Table 1 Material parameters for soil layers |
分析了冲击动能范围35~470.4 kJ的9个不同强度的撞击工况,落石质量分别为697、1 361、2 352 kg,每个质量等级落石撞击速度分别取为10、15、20 m/s.工程设计中需要采用一定简化方法对冲击动态过程等效为静力荷载作用,普遍采用的方法为全局平均等效静力和峰值等效静力[22].峰值等效静力以冲击动态过程接触界面力峰值作为等效静力荷载.全局平均法等效静力为对撞击力时程进行时域内平均,等效静力表示为
| $ {P_t} = \frac{1}{t}\int_0^t {P\left( t \right){\rm{d}}t} . $ | (14) |
式中P(t)为接触界面力时程,t为冲击荷载持续时间.
图 6给出9个撞击工况的界面接触力时程曲线,落石撞击荷载为由升压段和衰减段组成的同向荷载[4-5],撞击力峰值和撞击持时与撞击强度正相关.考虑撞击荷载波形特征以半波正弦型曲线简化冲击荷载,以等峰值与等冲量为原则确定简化半波正弦荷载参数,简化冲击荷载模型表示为
| $ F\left( t \right) = {F_{\max }}\sin \left( {\frac{{{\rm{ \mathit{ π} }}t}}{{{t_1}}}} \right), $ |
| $ \int_0^{{t_1}} {F\left( t \right){\rm{d}}t} = \int_0^{{t_2}} {P\left( t \right){\rm{d}}t} , $ |
| $ {t_1} = \frac{{\rm{ \mathit{ π} }}}{2}\frac{{\int_0^{{t_2}} {P\left( t \right){\rm{d}}t} }}{{{F_{\max }}}}. $ |

|
图 6 撞击力时程样本与简化冲击荷载对比 Figure 6 Comparison of the force-time history samples and the simplified impact load model |
式中:F(t)为等效冲击力时程;Fmax为接触界面力峰值;t1为等效冲击力持时;t2为数值模拟接触界面力持时.
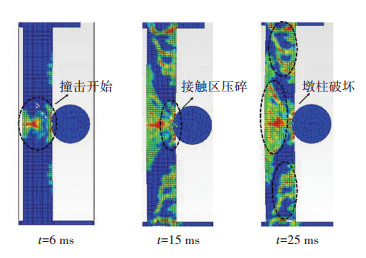
图 7给出墩柱落石撞击失效过程损伤发展,墩柱损伤区域包括整体弯曲变形损伤区和局部受剪破坏损伤区,计算冲击能量范围内最终导致墩柱失效倒塌的原因为柱顶盖梁位置和柱底位置的剪切失效,此时墩柱整体弯曲变形尚未完全发展.
|
图 7 墩柱损伤发展过程 Figure 7 Failure process of the RC columns subjected to rockfall impact |
考虑两种方式落石冲击等效静力荷载生成方式,以强度破坏准则定义墩柱受剪损伤状态,参考文献[14]定义钢筋混凝土柱落石冲击损伤等级为轻微损伤(D1),中等损伤(D2),严重损伤(D3),倒塌(D4).对应各个损伤阶段,剪力破坏参数分别为0.3、0.5、0.8、1.0,表 2为不同落石撞击场景截面损伤状态.
| 表 2 不同强度落石撞击墩柱损伤状态 Table 2 Damage states of RC columns subjected to rockfall impact |
图 8给出撞击等效静力与落石质量关系.峰值等效静力与落石质量正相关,其增加速度随墩柱损伤程度增加而逐渐降低.全局平均等效静力[22]在墩柱损伤程度较低时与落石质量正相关,在墩柱发生一定程度损伤后随落石质量增加而降低,原因是墩柱塑性变形使得撞击力时程衰减段持时显著增加.可见全局平均由于过度描述落石撞击荷载衰减段而使计算值偏低,而峰值等效静力更适用于落石撞击荷载等效静力简化.

|
图 8 等效静力与落石质量关系 Figure 8 Relationship between the equivalent static load and the rockfall mass |
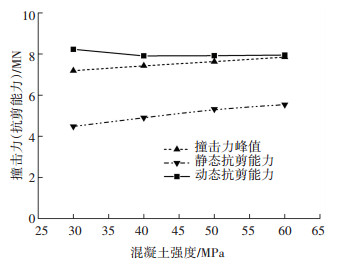
图 9给出153.1 kJ动能撞击场景撞击力峰值、截面抗剪能力随混凝土抗压强度变化规律.混凝土抗压强度30、40、50、60 MPa对应撞击力峰值分别为7.19、7.43、7.63、7.85 MN.对应截面静载抗剪能力分别为4.48、4.90、5.22、5.54 MN,以升压段平均应变速度计算截面动态抗剪能力分别为8.23、7.97、7.92、7.95 MN.混凝土强度提高引起撞击力峰值增大和墩柱静载抗剪强度提高,然而相同应变速率下低强度等级混凝土动屈服强度率相关性更显著[4].按峰值等效静力计算,随混凝土强度等级增大,截面剪力破坏参数分别为0.87、0.93、0.96、0.99.因此,混凝土动载强度增大系数随混凝土强度等级提高而减小,特定冲击条件下混凝土强度等级提高对墩柱抗冲击能力提高有限.
|
图 9 撞击力-抗剪能力与混凝土抗压强度关系 Figure 9 Relationship between impact load-shear capacity and the concrete strength |
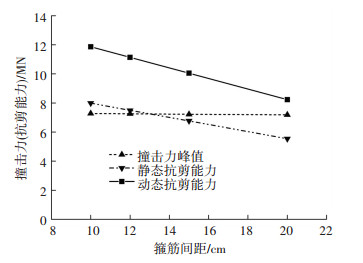
改变箍筋间距讨论箍筋配筋率对截面落石撞击损伤的影响,图 10给出153.1 kJ动能撞击场景撞击力峰值、截面抗剪能力与箍筋间距关系.由图 10箍筋间距10、12、15、20 cm对应撞击力峰值分别为7.28、7.26、7.22、7.19 MN,由于箍筋间距增大造成局部冲击刚度减小对冲击力峰值影响不显著.按冲击荷载升压段应变率计算截面动态抗剪能力分别为11.87、11.14、10.05、8.23 MN,截面剪力破坏参数随箍筋间距增大而增大,分别为0.61、0.65、0.72、0.87.因此,加密箍筋能够在不显著影响冲击力峰值条件下提高截面抗剪能力,从而显著降低截面损伤程度.
|
图 10 撞击力-抗剪能力与箍筋间距关系 Figure 10 Relationship between impact load-shear capacity with the stirrup space |
图 11给出153.1 kJ动能撞击,截面面积增加10%、20%、30%后,撞击力、截面抗剪能力变化规律.截面增加前后撞击力峰值分别为7.19、7.65、7.95、8.29 MN.对应动载截面抗剪能力分别为8.23、9.09、9.95、10.81 MN.峰值等效静力下截面剪力破坏参数分别为0.87、0.84、0.80、0.77.因此,由于截面面积增大,冲击力峰值随之增大,截面动态抗剪能力增大,虽然整体来看截面损伤程度随截面面积增大而降低,但降低程度有限.

|
图 11 撞击力-抗剪能力与截面面积关系 Figure 11 Relationship between impact load-shear capacity with the sectional area |
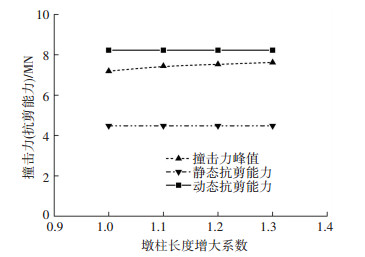
改变柱长讨论墩柱长细比对截面落石冲击损伤的影响,图 12为153.1 kJ撞击场景撞击力峰值、截面抗剪能力与墩柱长度关系.墩柱长度增加接触界面力峰值呈增加趋势,这与文献[23]的钢筋混凝土模型柱刚性小车撞击试验结论一致.原始模型与柱长增加10%、20%、30%对应的接触界面力峰值分别为7.19、7.44、7.53、7.62 MN,增大比例分别为3.5%、4.7%、6.0%.按照本文方法计算截面损伤参数分别为0.87、0.90、0.91、0.93.
|
图 12 撞击力-抗剪能力与柱长关系 Figure 12 Relationship between impact load-shear capacity with column length |
1) 在数值模拟可靠性验证基础上,建立了一种基于峰值等效静力的钢筋混凝土柱式桥墩落石撞击损伤状态分析方法.
2) 全局平均等效静力方法应用于落石撞击荷载静力简化存在缺陷,在高冲击强度场景下衰减段长持时使得全局平均静力偏低.
3) 在本文分析条件下,箍筋加密能够有效降低墩柱落石撞击损伤和控制撞击点挠度,截面面积增加一定程度上降低截面冲击损伤,特定冲击条件下混凝土强度等级提高对墩柱抗冲击能力提高有限.
| [1] |
裴来政, 刘应辉, 庄建琦. 汶川地震震后都汶公路的恢复与重建[J]. 四川大学学报(自然科学版), 2010, 42(增刊1): 140-146. PEI Laizheng, LIU Yinghui, ZHUANG Jianqi. Restoration and reconstruction of Du-Wen Highway after the Wenchuan Earthquake[J]. Journal of Sichuan University (Engineering Science Edition), 2010, 42(Sup1): 140-146. |
| [2] |
叶欣, 熊文, 张娟秀. 滚石-桥墩防撞物刚性碰撞精细化分析及设计方法[J]. 哈尔滨工业大学学报, 2015, 47(2): 117-122. YE Xin, XIONG Wen, ZHANG Juanxiu. Collision simulation and rigid design between rolling stone and anti-collision structure for bridge piers[J]. Journal of Harbin Institute of Technology, 2015, 47(2): 117-122. DOI:10.11918/j.issn.0367-6234.2015.02.021 |
| [3] |
何思明, 庄卫林, 张雄, 等. 都汶公路彻底关大桥桥墩抗滚石冲击防护研究[J]. 岩土力学与工程学报, 2013, 32(增刊2): 3421-3427. HE Siming, ZHUANG Weilin, ZHANG Xiong, et al. Reaserch on rockfall impact prevention of Chediguan Bridge pier, Duwen Road[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(Sup2): 3421-3427. |
| [4] |
程小卫, 李易, 陆新征, 等. 撞击荷载下钢筋混凝土柱动力响应的数值研究[J]. 工程力学, 2015, 32(2): 53-63. CHENG Xiaowei, LI Yi, LU Xinzheng, et al. Numerical investigation on dynamic response of reinforced concrete columns subjected to impact loading[J]. Engineering Mechanics, 2015, 32(2): 53-63. DOI:10.6052/j.issn.1000-4750.2014.03.0229 |
| [5] |
田力, 朱聪. 碰撞冲击荷载作用下钢筋混凝土柱的损伤评估及防护技术[J]. 工程力学, 2013, 30(9): 144-150. TIAN Li, ZHU Cong. Damage evaluation and protection technique of RC columns under impulsive load[J]. Engineering Mechanics, 2013, 30(9): 144-150. DOI:10.6052/j.issn.1000-4750.2012.05.0341.j.issn.1000-4750.2012.05.0341 |
| [6] |
THILAKARATHNA H M I, THAMBIRATNAM D P, DHANASEKAR M, et al. Numerical simulation of axially loaded concrete co-lumns under transverse impact and vulnerability assessment[J]. International Journal of Impact Engineering, 2010, 37(11): 1100-1112. DOI:10.1016/j.ijimpeng.2010.06.003 |
| [7] |
KRAUTHAMMER T, SHAHRIAR S, SHANAA H M. Response of reinforced concrete element severe impulsive loads[J]. Journal of Structure Engineering, 1990, 116(4): 1061-1079. DOI:10.1061/(ASCE)0733-9445(1990)116:4(1061) |
| [8] |
LU Y E, ZHANG L M. Analysis of failure of a bridge foundation under rock impact[J]. Acta Geotechnica, 2012, 7(1): 57-68. DOI:10.1007/s11440-011-0156-1 |
| [9] |
陈剑, 王全才, 陈颖骐, 等. 基于Hertz理论的泥石流大块石冲击力修正计算[J]. 哈尔滨工业大学学报, 2017, 49(2): 124-129. CHEN Jian, WANG Quancai, CHEN Yingqi, et al. Amending calculation on impact force of boulders in debris flow based on Hertz theory[J]. Journal of Harbin Institute of Technology, 2017, 49(2): 124-129. DOI:10.11918/j.issn.0367-6234.2017.02.020 |
| [10] |
THORNTON C. Coefficient of restitution for collinear collisions of elastic-perfectly plastic spheres[J]. Journal of Applied Mechanics, 1997, 64(2): 383-386. DOI:10.1115/1.2787319 |
| [11] |
MIZUYAMA T. Computational method and some considerations on impulsive force of debris flow acting on Sabo dams[J]. Erosion Control, 1979, 11(2): 40-43. |
| [12] |
周晓宇, 马如进, 陈艾荣. 钢筋混凝土柱式墩落石冲击抗剪性能可靠性分析[J]. 振动与冲击, 2017, 36(7): 262-270. ZHOU Xiaoyu, MA Rujin, CHEN Airong. Anti-shear reliability analysis for a reinforced concrete column subjected to rockfall impact[J]. Journal of Vibration and Shock, 2017, 36(7): 262-270. DOI:10.13465/j.cnki.jvs.2017.07.039 |
| [13] |
BUTH C E, WILLIAMS W F, BRACKIN M S, et al. Analysis of large truck collisions with bridge piers[R]. Texas: Texas Transportation Institute, 2010.
|
| [14] |
WATABA M, FUKUZAWA R, CHIBA O, et al. Study on load-deflection characteristics of heavily reinforced concrete shear walls[C]//The 10th International Conference on Structure Mechanics. [S. l. ]: AASMiRT, 1989.
|
| [15] |
PRIESTLEY M J N, VERMA R, XIAO Y. Seismic shear strength of reinforced concrete columns[J]. Journal of structural enginee-ring, 1994, 120(8): 2310-2329. DOI:10.1061/(ASCE)0733-9445(1994)120:8(2310) |
| [16] |
雷帅, 朱尔玉, 刘驰昊. 国内外钢筋混凝土桥墩地震作用下抗剪计算方法对比[J]. 北京交通大学学报, 2014, 38(1): 94-98. LEI Shuai, ZHU Eryu, LIU Chihao. Contrast and analysis of shea-ring resistance calculation of reinforced concrete pier under geological process at home and abroad[J]. Journal of Beijing Jiaotong University, 2014, 38(1): 94-98. DOI:10.11860/j.issn.1673-0291.2014.01.017 |
| [17] |
MALVAR L J, ROSS C A. Review of strain rate effects for concrete in tension[J]. Materials Journal, 1998, 95(6): 735-739. |
| [18] |
FUJIKAKE K, LI Bing, SOEUM S. Impact response of reinforced concrete beam and its analytical evaluation[J]. Journal of Structural Engineering, 2009, 135(8): 938-950. DOI:10.1061/(ASCE)ST.1943-541X.0000039 |
| [19] |
HALLQUIST J O. LS-DYNA keyword user's manual[M]. California: Livermore Software Technology Corporation, 2007: 1430-1432.
|
| [20] |
COWPER G R, SYMONDS P S. Strain-hardening and strain-rate effects in the impact loading of cantilever beams[R]. Providence, RI, United States: Report to Brown University, 1957.
|
| [21] |
FAN W, YUAN W C. Numerical simulation and analytical modeling of pile-supported structures subject to ship collisions including soil-structure intersection[J]. Ocean Engineering, 2014, 91(8): 11-27. DOI:10.1016/j.oceaneng.2014.08.011 |
| [22] |
崔鹏, 夏禾, 夏超逸, 等. 汽车撞击桥墩瞬态撞击力的等效静力计算[J]. 振动与冲击, 2014, 33(4): 48-53. CUI Peng, XIA He, XIA Chaoyi, et al. Equivalent static force calculation methods for transient impact force of a vehicle in collision with piers[J]. Journal of Vibration and Shock, 2014, 33(4): 48-53. DOI:10.13465/j.cnki.jvs.2014.01.010 |
| [23] |
朱亚迪, 卢文良. 小车墩柱撞击力模型试验研究[J]. 振动与冲击, 2013, 32(21): 182-185. ZHU Yadi, LU Wenliang. Model tests for collision force between a vehicle and piers[J]. Journal of Vibration and Shock, 2013, 32(21): 182-185. DOI:10.13465/j.cnki.jvs.2013.21.0 |
 2018, Vol. 50
2018, Vol. 50


