2. 山东省交通规划设计院, 济南 250031;
3. 先进土木工程材料教育部重点试验室(同济大学), 上海 201804;
4. 上海罗洋新材料科技有限公司, 上海 200092
2. Shandong Provincial Communications Planning and Design Institute, Jinan 250031, China;
3. Key Laboratory of Advanced Civil Engineering Materials(Tongji University), Ministry of Education, Shanghai 201804, China;
4. Shanghai Royang Innovative Material Technologies Co., Ltd., Shanghai 200092, China
高应变强化型超高性能混凝土(ultra-high performance concrete,后简称UHPC)具有高强度、塑性变形能力[1],也具有相比较低应变强化和应变软化UHPC来说更强的裂缝控制能力[2].
目前国内外对UHPC材料制备和基本力学性能(抗压性能[3-4]、抗拉性能[5-6]等)已经有较多的研究,对UHPC梁的弯曲性能和承载能力计算方法也有一定的研究[7-9].各国研究者对UHPC纤维增强增韧理论的研究[10-12]分为两种,第一种是以混合法则为依据的复合力学理论,另一种是以断裂力学为基础的纤维间距理论,根据纤维对裂缝的约束作用来计算纤维的增强和增韧作用.尽管这些理论在推导时都存在一定的假设和前提,但在实际工程中仍然对纤维参数、纤维与基体的粘结力等参数设计选择时提供理论依据,具有重要的理论意义.但目前来说,各国针对应变强化UHPC的文献研究屈指可数,对配筋应变强化UHPC梁的内部破坏机理,UHPC抗拉强度对截面抗力的贡献度更是缺少相关研究,没有明确说明抗弯承载力计算时考虑抗拉贡献的原因.
本文采用上海罗洋新材料科技有限公司提供的常温养护高应变强化型UHPC材料,将5根T形配筋超高性能混凝土梁弯曲性能试验成果,作为分析其弯曲破坏机理的研究资料,根据试验结果分析钢筋与UHPC协同工作性及钢筋和UHPC对抗弯承载力的贡献度,揭示抗弯承载力计算中考虑UHPC抗拉贡献的原因,为应变强化型UHPC的结构应用奠定理论基础.
1 试验概况 1.1 UHPC材料制备试验材料采用的应变强化UHPC是基于最紧密堆积原理由计算机精确设计,可将宏观缺陷降到最低,形成高度致密的无机质基体.在常温养护条件下,具备超高强、应变强化、高耐久性、优异施工性能等特征.UHPC基体配合比中,水泥、硅灰、磨细石英粉、细集料、水、高效减水剂质量比为1:0.3:0.3:1.34:0.2:0.005,扩展度为720 mm,如图 1所示.钢纤维的抗拉强度为2 500 MPa,弹性模量为200 GPa,长度为13 mm,直径为200 mm,长径比为65,密度为7 850 kg/m3.

|
图 1 扩展度测试 Figure 1 The test of scalability for UHPC |
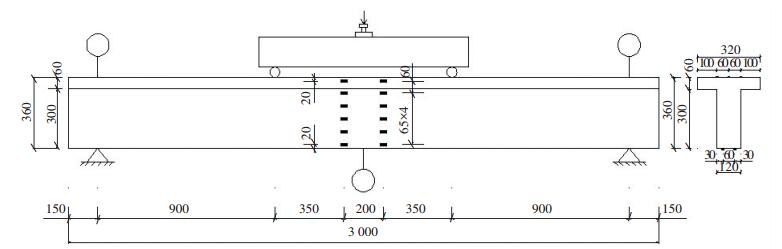
UHPC试验梁的腹板宽为120 mm,高为300 mm,翼缘板宽和高分别为320、60 mm,试验梁的长度为3 000 mm,为防止两端的锚固破坏,加载时两边各预留150 mm,计算跨度为2 700 mm.两侧支座处采用增大截面处理,两端各250 mm范围内为矩形截面,250~350 mm范围内截面渐变. T形试验梁的跨中截面、构造见图 2.试验梁的变化参数为钢筋配筋率和种类,配筋基本参数见表 1.
|
图 2 T形配筋UHPC梁跨中截面和构造图(mm) Figure 2 Midspan cross section and structure diagram of reinforced UHPC T beam (mm) |
| 表 1 T形梁配筋情况表 Table 1 Reinforcement situation of T-shape beam |
为防止加载过程中弯剪段发生剪切破坏,箍筋采用Φ10HPB300钢筋,两侧矩形截面区箍筋间距为50mm,弯剪段箍筋间距为100mm,跨中纯弯段无箍筋无架立钢筋.
1.3 测试内容在浇筑试验梁时,浇筑养护完成2组(6个)100 mm×100 mm×100 mm的立方体试块,按照标准养护条件(温度20 ℃±2 ℃,湿度≥95%)养护28 d后进行立方体抗压强度试验.立方体抗压强度试验值见表 2.
| 表 2 UHPC立方体抗压强度 Table 2 Cube compressive strength of UHPC |
在立方体抗压强度试验过程中(特别是即将达到极限荷载前),可以听到钢纤维从基体中脱离开来的噼啪声,当立方体试块被压碎时,由于钢纤维的搭接作用,试块仍保持整体.根据试验确定的UHPC立方体抗压强度标准值为(试验均值-1.645倍的标准差)[13].参考文献[14],轴拉试件为狗骨头形,测试段尺寸为50 mm×100 mm×500 mm,轴拉试件见图 3.三分点纯弯试验加载现场照片见图 4.

|
图 3 轴拉试件 Figure 3 Specimens for axial tensile test |

|
图 4 现场加载照片 Figure 4 Loading test on site |
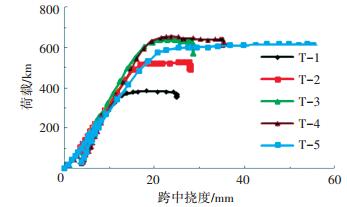
试验梁的荷载-跨中挠度曲线见图 5.从曲线可知配筋T梁的整个受力破坏过程大致可分为3个阶段:1)弹性阶段.试验加载初期,跨中纯弯段区域弯矩较小,UHPC配筋梁受力形态与均匀弹性体基本一致,荷载-挠度曲线呈直线. 2)裂缝发展阶段. UHPC初裂后,原来由该部分承担的拉力转移到钢纤维和受拉纵向钢筋上去,裂缝沿着梁高向上发展,受拉区进入塑性阶段的部分逐渐增多,荷载-挠度曲线斜率逐渐减小. 3)持荷至破坏阶段.纵向受拉钢筋逐渐屈服,受压区也逐渐开始进入弹性阶段的后期,跨中纯弯段裂缝沿梁高迅速发展且宽度增大,截面到达其极限荷载,荷载-挠度曲线斜率逐渐趋于0,当荷载-挠度曲线斜率为负时,试验梁跨中严重下挠,试验梁出现明显的主裂缝(1~3条).
|
图 5 荷载-跨中挠度曲线 Figure 5 Curves between load and midspan deflection |
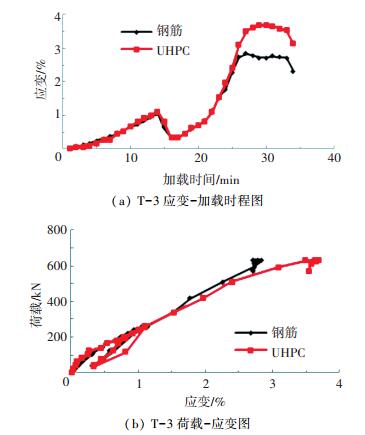
对于配筋高应变强化UHPC试验梁来说,由于UHPC在拉应力作用下表现出应变强化的特性,且强化的极限应变超过了普通钢筋的屈服应变约0.002,UHPC开裂意味着此时钢筋已经屈服,钢筋与应变强化UHPC可以长时间保持共同受力,协同应变工作.当UHPC轴拉应变达到0.002时,其裂缝宽度仅为0.02 mm,具有极强的裂缝控制能力,能够控制在高应变情况下裂缝宽度[2]. T-3试验梁钢筋与UHPC协同变形结果见图 6.从图 6可知:试验梁在荷载控制阶段及位移控制的初始阶段,UHPC的应变比钢筋应变稍微大一点(与试验梁浇筑中钢筋位置稍微错动有关).当加载到510 kN时,钢筋应变为0.002 26,而梁体侧面UHPC应变为0.002 4,到下一加载节点590 kN时,钢筋的应变为0.002 73,而UHPC的应变为0.003 1,两者差距增大.此时钢筋处于屈服状态,UHPC应变继续发展,处于正常工作状态,峰值应变是0.003 6,最终应变基本稳定在0.003 5左右,此后裂缝迅速发展,试验梁破坏.其余4根T形梁的变化规律与T-3基本相同. 图 6(a)中曲线存在“下折上起”的原因是:加载由力控制转向位移控制,存在一个卸荷过程.综上分析可知:在钢筋达到屈服应变之前,钢筋与UHPC粘结可靠,保持应变一致性而共同受力;钢筋屈服后,UHPC应变继续发展,最终UHPC与钢筋分离,裂缝迅速发展,试验梁宣告破坏.
|
图 6 钢筋与UHPC协同应变 Figure 6 Relationship curves between UHPC and reinforcement |
为进一步分析破坏过程中钢筋和UHPC应变的变化,通过对底面UHPC应变片和钢筋的对比,分阶段考虑钢筋与UHPC抗拉性能的参与度和对截面抗弯承载力的贡献度.
通过对钢筋和UHPC应变数据定量取均值的处理方法,以UHPC应变为0.000 8、0.002 5,以及整个过程为阶段展现T-1试验梁底面应变(裂缝)发展动态.分阶段应变动态结果见图 7.

|
图 7 T-1试验梁钢筋与底部UHPC应变对比 Figure 7 Strain comparison of rebar and the bottom of UHPC on T-1 beam |
由图 7(a)可知:在应变为0.22×10-3时,附近UHPC和钢筋荷载-应变曲线有明显的偏折,说明在应变较小阶段,该处UHPC出现了微裂缝,大小约为0.2×10-3,而钢筋应力激增,也出现了小部分应变突增;从图 7(b)中可以发现,两者的应变均基本沿着线性发展,底面UHPC的应变发展较钢筋应变发展更为迅速,说明在该阶段,底部裂缝逐渐增多;从全过程应变对比可知:在应变为0.002 2~0.002 5(钢筋屈服)之后,UHPC应变会迅速发展,说明此时底面裂缝开展加快,逐步反应到梁体侧面,沿着截面向上发展,贯穿大部分横截面. 图 7(c)可以看出,UHPC极限拉应变为0.003左右,小于其轴拉应变测试强度0.004 2,原因为国内市场混凝土拉应变计量程普遍只有0.002 5~0.003,实验时UHPC应变超过该值时应变计读数不准确,同时大体积试件内部缺陷较多,未达到轴拉应变已无法加荷.
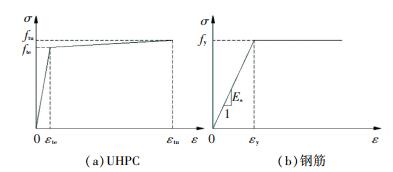
根据上述分析,结合UHPC和钢筋的理想受拉应力-应变关系(见图 8),将整个加载过程分解为UHPC应变为0~0.000 25,0.000 25~0.002,0.002~0.003 5, 0.003 5以后4个阶段,每个阶段中钢筋和UHPC抗拉性能对截面抗力贡献度分析如下.
|
图 8 理想受拉应力-应变关系 Figure 8 Ideal tensile stress-strain relationship curves |
1) 0~0.000 25阶段. UHPC和钢筋均处于弹性段,两者协同应变工作.设此时受拉区高度为h1,受拉钢筋到受拉边缘的距离为a0,受拉区UHPC和钢筋对中性轴取矩,提供的截面抗力计算公式为
| $ {M_{\rm{c}}} = \frac{1}{3}bh_1^2{E_{\rm{c}}}{\varepsilon _{\rm{c}}}, $ | (1) |
| $ {M_{\rm{s}}} = {A_{\rm{s}}}{E_{\rm{s}}}{\varepsilon _{\rm{s}}}\left( {{h_1}-{a_0}} \right). $ | (2) |
式中: Mc为受拉区UHPC承担的弯矩; Ms为钢筋承担的弯矩; b为T形截面腹板宽; h1为中性轴距底边高度; Ec为UHPC弹性模量; εc为受拉区底缘UHPC的应变; As为受拉钢筋面积; Es为钢筋弹性模量; εs为钢筋的应变; a0为钢筋距底边高度.
2) 0.000 25~0.002阶段.在此阶段钢筋处于弹性上升段,而UHPC处于平台段,此时UHPC应力值保持不变.设此时受拉区高度为h2,受拉区UHPC和钢筋对中性轴取矩,提供的截面抗力计算公式为
| $ {M_{\rm{c}}} = \frac{1}{2}bh_2^2{f_{{\rm{te}}}}, $ | (3) |
| $ {M_{\rm{s}}} = {A_{\rm{s}}}{E_{\rm{s}}}{\varepsilon _{\rm{s}}}\left( {{h_2}-{a_0}} \right). $ | (4) |
式中h2为中性轴距底边高度,fte为UHPC的弹性抗拉强度,其余参数说明见式(1).
3) 0.002~0.003 5阶段.在此阶段纵向钢筋屈服,UHPC处于平台段,构件已达到了承载能力极限状态.设此时受拉区高度为h3,受拉区UHPC和钢筋对中性轴取矩,提供的截面抗力计算公式为
| $ {M_{\rm{c}}} = \frac{1}{2}bh_3^2{f_{{\rm{te}}}}, $ | (5) |
| $ {M_{\rm{s}}} = {A_{\rm{s}}}{f_{\rm{y}}}\left( {{h_3}-{a_0}} \right). $ | (6) |
式中:h3为中性轴距底边高度; fy为钢筋的屈服强度; 其余参数说明见式(1).
4) 0.003 5之后阶段.在此阶段钢筋处平台段,UHPC处于下降段,此时UHPC退出工作.设此时受拉区高度为h4,钢筋对中性轴取矩,提供的截面抗力计算公式为
| $ {M_{\rm{s}}} = {A_{\rm{s}}}{f_{\rm{y}}}\left( {{h_4}-{a_0}} \right). $ | (7) |
为分析UHPC抗拉性能对截面抗力的贡献度,对应4个阶段节点的受拉区高度根据初始状态、阶段状态和极限状态,分别根据压区混凝土应变计读数推算取为0.5 h,0.6 h,0.7 h,0.75 h;相应的a0均按照实际情况取值,T-1和T-4试验梁的计算结果见表 3.
| 表 3 T-1和T-4试验梁各阶段钢筋和UHPC抗拉贡献度对比 Table 3 Tensile contribution comparison of rebar and UHPC in each state for T-1 and T-4 beams |
表 3中数据只是针对钢筋和UHPC受拉区对中性轴取矩的计算结果. T-1试验梁(配筋率为1.77%)在第1阶段中,UHPC的抗拉贡献是钢筋的2.79倍,在第2阶段和第3阶段分别可占钢筋的0.60和0.69倍;T-4试验梁(配筋率为4.40%)在第1阶段中,UHPC的抗拉贡献是钢筋的1.12倍,在第2阶段和第3阶段分别为钢筋的0.24和0.28倍.第4阶段,由于UHPC完全退出工作,此时抗力仅由钢筋提供,试验梁荷载值呈现下降阶段,截面总抗力减小.截面极限抗弯承载力的计算以第3阶段结束时为基准.
由上表分析可知:普通钢筋混凝土梁受拉抗力主要由钢筋提供,而UHPC抗拉强度提供的抗力与钢筋提供的相比占据重要比例(在配筋率1.77%时可达到0.69),因此在UHPC截面极限抗弯承载力计算时,应充分考虑UHPC的抗拉贡献.
3 结论1) T形配筋UHPC简支梁的破坏模态分为3阶段——弹性阶段、裂缝发展阶段和持荷破坏阶段,5根T形配筋试验梁均以受拉区主裂缝开展(受压区未压碎)宣告破坏.
2) 钢筋在达到屈服应变之前与UHPC粘结可靠,保持应变一致性而共同受力;在钢筋屈服后,UHPC的应变可以继续发展,最终UHPC与钢筋分离,裂缝迅速发展,试验梁宣告破坏.钢筋与UHPC的应变发展和分离是试验梁开裂及最终破坏的原因.
3) 分析截面受拉抗力时,UHPC抗拉强度提供的抗力与钢筋提供的相比占据重要比例(低配筋率时更大).因此在进行截面承载力计算时,应充分考虑UHPC抗拉强度的作用,保证承载能力计算方法的准确性.
| [1] |
MCS-EPFL. Ultra-high performance fibre reinforced cement-based composites (UHPFRC): construction material, dimensioning and application[S]. Switzerland: Switzerland Swiss Federal Institute of Technology, 2016.
|
| [2] |
王俊颜, 耿莉萍, 郭君渊, 等. UHPC的轴拉性能与裂缝宽度控制能力研究[J]. 哈尔滨工业大学学报, 2017, 49(12): 1-5. WANG Junyan, GENG Liping, GUO Junyuan, et al. Experimental study on crack width control ability of ultra-high performance concrete[J]. Journal ofHarbin Institute of Technology, 2017, 49(12): 1-5. DOI:10.11918/j.issn.0367-6234.201708027 |
| [3] |
FEHLING E, LEUTBECHER T, BUNJE K. Design relevant properties of hardened ultra high performance concrete[C]// Proceedings of the International Symposium on Ultra High Performance Concrete. Kassel: University of Kassel, 2004: 327-338.
|
| [4] |
杨剑, 方志. 超高性能混凝土单轴受压应力-应变关系研究[J]. 混凝土, 2008(7): 11-15. YANG Jian, FANG Zhi. Research on stress-strain relation of ultra high performance concrete[J]. Concrete, 2008(7): 11-15. |
| [5] |
WILLE K, EL-TAWIL S. Properties of strain hardening ultra high performance fiber reinforced concrete (UHP-FRC) under direct tensile loading[J]. Cement & Concrete Composites, 2014, 48(2): 53-66. |
| [6] |
张哲, 邵旭东, 李文光, 等. 超高性能混凝土轴拉性能试验[J]. 中国公路学报, 2015, 28(8): 50-58. ZHANG Zhe, SHAO Xudong, LI Wenguang, et al. Axial tensile behavior test of ultra high performance concrete[J]. China Journal of Highway and Transport, 2015, 28(8): 50-58. |
| [7] |
YOO D Y, BANTHIA N, KIM S W, et al. Response of ultra high performance fiber-reinforced concrete beams with continuous steel reinforcement subjected to low-velocity impact loading[J]. Composite Structures, 2015, 126: 233-245. DOI:10.1016/j.compstruct.2015.02.058 |
| [8] |
孙小凯, 刁波, 叶英华. 钢筋超高性能纤维混凝土梁抗弯性能研究[J]. 工业建筑, 2012, 42(11): 16-21. SUN Xiaokai, DIAO Bo, YE Yinghua. Flexural behavior experiments of ultra-high performance concrete beams reinforced with steel bar and hybrid-fiber[J]. Industrial Construction, 2012, 42(11): 16-21. |
| [9] |
徐海宾, 邓宗才. 预应力超高性能钢纤维混凝土梁受弯性能试验研究[J]. 建筑结构学报, 2014, 35(12): 58-64. XU Haibin, DENG Zongcai. Experimental research on flexural behavior of prestressed ultra-high performance steel fiber concrete beams[J]. Journal of Building Structures, 2014, 35(12): 58-64. |
| [10] |
BAYARD O, PLE O. Fracture mechanics of reactive powder concrete: material modeling and experimental investigations[J]. Engineering Fracture Mechanics, 2003, 70(7/8): 839-851. |
| [11] |
GRAYBEAL B A. Compressive behavior of ultra high performance fiber reinforced concrete[J]. ACI Materials Journal, 2007, 104(2): 146-152. |
| [12] |
高旭明. 钢纤维对超高性能混凝土性能影响的研究[D]. 长沙: 湖南大学, 2013. GAO Xuming. Research on the effects of steel fiber on high perfor-mance concrete performance[D]. Changsha: Hunan University, 2013. |
| [13] |
全国混凝土标准化技术委员会. 活性粉末混凝土: GB/T 31387—2015[S]. 北京: 中国标准出版社, 2015. National Standardization Technical Committee for Concrete. Reactive powder concrete: GB/T31387—2015[S]. Beijing: China Stan-dard Press, 2015. |
| [14] |
LAMPROPOULOS A P, PASCHALIS S A, TSIOULOU O T, et al. Strengthening of reinforced concrete beams using ultra high perfor-mance fibre reinforced concrete (UHPFRC)[J]. Engineering Structures, 2016, 106: 370-384. DOI:10.1016/j.engstruct.2015.10.042 |
 2018, Vol. 50
2018, Vol. 50



 18
18