信号交叉口发生交通拥堵的根本原因是到达的交通流量大于交叉口通行能力.而交叉口通行能力除了与信号配时方案有关外,还与各股流向的机动车可以利用的车道数密切相关.以一个进口方向为例,在过饱情况下如果给直行车分配较多的车道,那么左转车将严重拥堵;如果给左转车分配较多车道,那么直行车将严重拥堵.为了缓解过饱和交叉口的拥堵,交通工程领域的学者提出了多种管理方法,比如禁止左转[1-3]、综合待行区[4-5]、钩形转弯[6-10]等,并在不同的交通场景下进行应用. 2012年以来济南市、邯郸市在市区多个交叉口实施了一种借对向车道左转的特殊设计方法,不仅可以增大交叉口左转车通行能力,还可以避免左转车绕行或者停车次数的增加.
近年来,一些学者对借对向车道左转(以下简称“借道左转”)这种交叉口设计方法进行了理论分析.比如文献[11]以在邯郸市采集的实际数据为基础,建立了左转机动车通行能力校正方法以及估计模型,并将该方法与综合待行区方法进行对比.文献[12]在驾驶模拟器中分析对比了64名驾驶员对借道左转的适应能力,并分析了交通标志、交通标线以及交通状态的影响.文献[13]选择闯红灯、交通事故数、车道选择正确率等作为评价指标,从交通安全的角度对这种类型交叉口的左转交通流进行分析.
综合来看,目前在“借道左转”方面的理论研究还比较少,对于信号控制影响下的车辆排队、消散情况考虑不够全面;而在工程方面各地交通管理部门依靠经验设计信号配时方案,缺乏理论依据,限制了交叉口控制效益的提升.因此,本文以“借道左转”交叉口为研究对象,以车均延误最小为目标建立交叉口信号配时方案的优化方法,这对于提高交叉口交通流运行效率、缓解交通拥堵具有重要意义.
1 交通流运行特征分析图 1给出了一个十字交叉口机动车借道左转情况下的渠化方案. N0、N1等代表车道编号.以南进口为例,渠化区内有2条左转车道、1条直行车道、1条直右共用车道.与传统交叉口相比,图 1所示交叉口在每个进口方向通过占用对向的出口车道增设了1条左转进口车道.其中车道N0、N4、N8、N12均为借用对向出口车道而增设.
|
图 1 借对向车道左转交叉口车道设计方案 Figure 1 Design scheme of approaching lanes at the intersection with contraflow left-turn lane |
图 1所示交叉口的相位相序如图 2所示.该交叉口一共包括6个信号相位,其中4个主信号相位(M1、M2、M3、M4)、2个预信号相位(P1、P2).其中M代表主信号(Main signal),P代表预信号(pre-signal),M1、M2、M3和M4分别控制主信号的南北左转、南北直行、东西左转、东西直行交通流;P1、P2分别控制预信号的南北左转、东西左转交通流.为了避免南进口车道N0内的左转车与对向的直行车或者东进口的左转车发生冲突,在南进口黄实线开口位置处设置一组预信号.当允许左转车驶入车道N0时,预信号显示绿灯;否则显示红灯,此时左转车只能使用车道N1.

|
图 2 借道左转交叉口信号相位相序 Figure 2 Phasing scheme of the intersection with contraflow left-turn lane |
当南北直行相位M2或者东西左转相位M3显示绿灯期间,南北进口的预信号相位P1需要显示红灯;不过此时东西进口的预信号相位P2可以显示绿灯,即东西方向的左转车驶入车道N4、N12.当东西直行相位M4或者南北左转相位M1显示绿灯期间,南北方向的预信号P1可以显示绿灯,即南北方向的左转车驶入车道N0、N8;此时东西方向的预信号P2需要显示红灯.
关于主、预信号之间的绿灯启亮/结束时刻之差,有两点需要说明:1)为了避免主信号相位M1、M3绿灯结束后有左转车滞留在车道N0、N4、N8、N12内,预信号相位P1、P2的绿灯需要较相位M1、M3提前η1秒结束;η1与左转车道停车线至预信号的距离、车辆平均运行速度有关. 2)相位M4的绿灯启亮η2秒后,相位P1的绿灯才能启亮;同理,相位M2的绿灯启亮η2后,相位P2的绿灯才能启亮.以相位M4和P1为例,在M4绿灯启亮时刻,东西左转机动车刚驶离交叉口、尚未到达南北进口黄实线开口处;如果此时P1也启亮绿灯,南北进口的左转车驶入车道N0、N8,将与东西左转驶来的机动车发生冲突;因此,相位P1的绿灯需要延迟η2秒启亮,η2与左转车从车道N4、N12的停车线至南北进口黄实线开口处的行驶距离、车辆平均运行速度有关.
通过上面的分析可以看出,通过相位相序设计可以避免借道左转车与其他交通流的冲突.当左转车流量较大时,可以借用对向出口更多的车道供左转车使用.在本文中仅研究借用对向出口1条车道的情况.
2 信号控制方案优化方法以图 1所示的“借道左转”交叉口为例,给出其信号控制方案以及车道N0、N4、N8、N12长度的优化方法.
2.1 交叉口参数描述实施“借道左转”交叉口的主信号周期时长为C,车道N0的长度(从黄实线开口处至停车线)为LN0,能够容纳QN0max辆机动车排队;主信号相位Mi的绿灯时间用gmi表示,绿灯间隔时间用Imi表示,红灯时间用Rmi表示,其中i=1, 2, 3, 4;预信号相位Pi的绿灯时间用gpi表示,绿灯间隔时间用Ipi表示,红灯时间用Rpi表示,其中i=1, 2.则
| $ C = \sum\limits_{i = 1}^4 {\left( {{g^{mi}} + {I^{mi}}} \right)} , $ |
| $ {g^{p1}} = {g^{m4}} + {I^{m4}} - {\eta _2} + {g^{m1}} - {\eta _1}, $ |
| $ {g^{p2}} = {g^{m2}} + {I^{m2}} - {\eta _2} + {g^{m3}} - {\eta _1}. $ |
式中:η1为预信号相位P1、P2的绿灯较相位M1、M3的绿灯提前结束时间;η2为预信号相位P1、P2的绿灯较相位M4、M2的绿灯延迟启亮时间.
相位Mi的最大、最小绿灯时间分别用gmaxmi、gminmi表示;相位Pi的最大、最小绿灯时间分别用gmaxpi、gminpi表示.设一个周期内主信号相位Mi的绿灯启亮时刻为tgmi,绿灯结束时刻为
| $ {g^{mi}} = \vec t_g^{mi} - t_g^{mi}, $ |
| $ {g^{pi}} = \vec t_g^{pi} - t_g^{pi}. $ |
图 1中直行与直右车道的流量用q表示,如qN2、qN3分别代表车道N2、N3的到达流量.东、西、南、北4个进口的左转到达流量用qle、qlw、qls、qln表示.以南进口为例,左转车将驶入车道N0、N1,所以qls代表车道N0、N1的到达左转车流量之和.
2.2 交叉口各相位车均延误计算本文选择以车均延误最小为目标优化主信号相位周期时长C、各个相位的绿灯时间gmi、gpi以及借对向车道的左转车道长度LN0、LN4、LN8、LN12.主信号直行相位Mi(i=2, 4)的机动车运行与传统交叉口相同,可以采用美国道路通行能力手册(HCM2000)中的公式计算车均延误,即
| $ \begin{array}{l} {\varphi _{mi}} = \frac{{0.5C{{\left( {1 - {\lambda _{mi}}} \right)}^2}}}{{1 - \left[ {\min \left( {1,{x_{mi}}} \right){\lambda _{mi}}} \right]}} + 900T\left[ {\left( {{x_{mi}} - 1} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\sqrt {{{\left( {{x_{mi}} - 1} \right)}^2} + \frac{{8 \times 0.5 \times {x_{mi}}}}{{Ca{p_{mi}}T}}} } \right],\;\;i = 2,4. \end{array} $ | (1) |
式中:φmi为主信号直行相位Mi关键车道的车均延误;λmi为相位Mi绿信比;xmi为相位Mi关键车道的饱和度;Capmi为相位Mi关键车道的通行能力,等于车道饱和流率乘以绿信比;T为分析时段长度,默认值0.25 h.
主信号直行相位Mi关键车道的车总延误Φmi为
| $ {\mathit{\Phi }_{mi}} = {\varphi _{mi}} \times C \times {q_{mi}},i = 2,4. $ |
式中qmi为主信号直行相位Mi关键车道的到达流量,pcu/s.以相位M2为例,qm2等于车道N2、N3、N10、N11到达流量中的最大值.
而对于主信号左转相位M1、M3以及预信号相位P1、P2,它们的交通流运行受预信号以及左转车道N0、N4、N8、N12的影响,与传统交叉口存在明显差异,无法采用式(1)计算,所以需要单独分析.
仍以图 1所示交叉口南进口为例分析左转车的运动过程.车道N0的长度为LN0,能够容纳QN0max辆机动车排队.在预信号P1显示红灯期间,到达南进口的左转车首先在车道N1排队.在预信号P1的绿灯启亮时刻(即时刻tgp1),如果车道N1的累积排队左转车辆数QN1(tgp1)≤QN0max,则这QN1(tgp1)辆左转车将继续在车道N1排队,无法换道至N0;后续到达的左转车将驶入车道N0排队,直至车道N0的排队车辆数也达到QN1(tgp1);之后到达的左转车将分别选择驶入车道N0、N1,使得车道N0、N1的排队长度维持相等.当满足下列两个条件之一时左转车将不再驶入车道N0:1)车道N0的排队车辆数已经达到QN0max.此时车道N0已经排满,后续车辆无法驶入. 2)主信号M1绿灯启亮后车道N1的排队已经消散.后续到达的左转车如果选择车道N0,将进行一次变道;所以可以直接选择车道N1驶离交叉口,无需变道或者减速停车.
在时刻tgp1,如果车道N1的累积排队左转车辆数QN1(tgp1)>QN0max,则从QN0max+1至第QN1(tgp1)辆机动车将换道至车道N0,所以车道N1的排队车辆数将暂时减少,后续到达的左转车也驶入车道N0,使得车道N0、N1的排队长度维持相等.当满足条件1或者2时,左转车将不再驶入车道N0,而是选择车道N1.所以通过对比tgp1时刻QN1(tgp1)与QN0max的关系,可以将南进口左转机动车的运行分为两种情况分析,进而分别计算左转车的延误.
2.2.1 QN1(tgp1)≤QN0max时的运行情况在交通流均匀到达的情况下,如果满足QN1(tgp1)≤QN0max,则
| $ \left( {{g^{m2}} + {I^{m2}} + {g^{m3}} + {I^{m3}} + {\eta _2}} \right) \times q_l^{\rm{s}} \le Q_{N0}^{\max }. $ |
式中:gm2+Im2+gm3+Im3+η2为本周期相位M1红灯开始时刻至tgpi时刻的已显示红灯时间.
根据上式可以得到
| $ q_l^{\rm{s}} \le Q_{N0}^{\max }/\left( {{g^{m2}} + {I^{m2}} + {g^{m3}} + {I^{m3}} + {\eta _2}} \right). $ |
车道N0的排队车辆数是否达到QN1(tgp1)以及车道N1的排队完全消散时刻,对两条车道的机动车延误具有重要影响.下面分4种情况进行分析,其中从情况1至情况4左转流量逐渐增大.
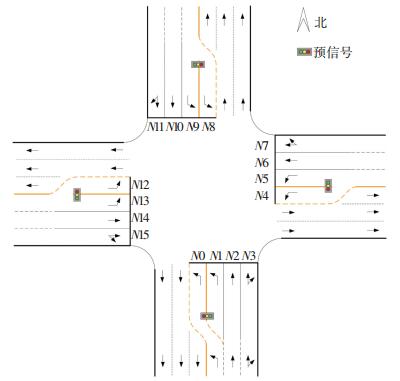
情况1 预信号相位P1绿灯结束前车道N1的排队已完全消散,且车道N0的排队车辆数未达到QN1(tgp1).此时两条左转车道的车辆到达与驶离图式如图 3所示.在图 3中横坐标代表时刻,纵坐标代表累积到达车辆数. 图 3(a)中蓝线代表车道N1的累积排队长度变化,Sls为南进口左转车道的饱和流率;图 3(b)中红线代表车道N0的累积排队长度变化.
|
图 3 情况1中车道N0与N1累积排队变化图式 Figure 3 Cumulative queue change patterns of lane N0 and N1(Case 1) |
以主信号M1的红灯启亮时刻(即主信号M2的绿灯启亮时刻tgm2)作为0时刻点,此时预信号P1也在显示红灯,左转车无法驶入车道N0,所以均匀到达的左转车在车道N1排队.在tgp1时刻车道N1的累积到达车辆数达到QN1(tgp1).在P1相位绿灯启亮后,后续到达的左转车将驶入车道N0,并在图 3(b)中的K点时刻开始在车道N0排队.其中K点与tgp1的时刻之差为左转车从黄线开口处行驶至车道N0停车线所需的行程时间.所以从tgp1时刻开始车道N1的排队长度将不再增加.主信号M1的绿灯在tgm1时刻启亮后,车道N0、N1的开始消散.由于车道N0的排队长度小于等于车道N1的排队长度,所以车道N0的排队完全消散时刻将早于车道N1的排队完全消散时刻.在图 3中,车道N1的排队在F点完全消散,车道N0的排队在G点完全消散.之后到达的左转车将驶入车道N1,不再驶入车道N0;在相位M1绿灯结束之前,这些左转车可以直接通过交叉口.
经过上述分析可知,车道N1的左转车辆累积延误为图 3(a)中多边形OAFE的面积,其中O为坐标原点;车道N0的左转车辆累积延误为图 3(b)中多边形KGU的面积.
多边形OAFE的面积θOAFE为
| $ \begin{array}{l} {\theta _{OAFE}} = \frac{1}{2}\left( {OE + AF} \right) \times FD = \frac{1}{2}\left[ {t_g^{m1} - t_g^{m2} + t_g^{m1} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {t_g^{p1} + {Q_{N1}}\left( {t_g^{p1}} \right)/S_l^{\rm{s}}} \right] \times {Q_{N1}}\left( {t_g^{p1}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{2}\left[ {2t_g^{m1} - t_g^{m2} - t_g^{p1} + {Q_{N1}}\left( {t_g^{p1}} \right)/S_l^{\rm{s}}} \right]. \end{array} $ |
多边形KGU的面积θKGU为
| $ \begin{array}{l} {\theta _{KGU}} = \frac{{KU \times GG'}}{2} = \frac{1}{2}\left( {t_g^{m1} - t_g^{p1} - \frac{{{L_{N0}}}}{{{V_{N0}}}}} \right) \times \\ \frac{{\left( {t_g^{m1} - t_g^{p1} - \frac{{{L_{N0}}}}{{{V_{N0}}}}} \right) + q_l^{\rm{s}} \times \left( {t_g^{m1} - t_g^{p1} - \frac{{{L_{N0}}}}{{{V_{N0}}}}} \right)/\left( {S_l^{\rm{s}} - q_l^{\rm{s}}} \right)}}{{S_l^{\rm{s}}}} \times \\ q_l^{\rm{s}} = \frac{{q_l^{\rm{s}}\left( {t_g^{m1} - t_g^{p1} - {L_{N0}}/{V_{N0}}} \right)^2}}{{2\left( {S_l^{\rm{s}} - q_l^{\rm{s}}} \right)}}. \end{array} $ |
式中:VN0为车辆在车道N0上的行驶速度,m/s;Φm1sl为交叉口南进口左转相位每周期的车总延误,Φm1sl=θOAFE+θKGU.
情况2 预信号相位P1绿灯结束前车道N1的排队未完全消散,且车道N0的排队车辆数未达到QN1(tgp1).此时两条左转车道的车辆到达与驶离图式如图 4所示.车道N1的排队消散时间大于

|
图 4 情况2中车道N0与N1累积排队变化图式 Figure 4 Cumulative queue change patterns of lane N0 and N1(Case 2) |
在情况2,车道N1的左转车辆累积延误为图 4(a)中多边形OAFWUB的面积,车道N0的左转车辆累积延误为图 4(b)中多边形EGU的面积.
多边形OAFWUB的面积θOAFWUB为
| $ \begin{array}{l} {\theta _{OAFWUB}} = \frac{1}{2}{Q_{N1}}\left( {t_g^{p1}} \right)\left( {2t_g^{m1} - t_g^{m2} - t_g^{p1}} \right) + \\ \frac{{\left( {\vec t_g^{p1} - t_g^{m1}} \right)}}{2}\left[ {2{Q_{N1}}\left( {t_g^{p1}} \right) - S_l^{\rm{s}}\left( {\vec t_g^{p1} - t_g^{m1}} \right)} \right] + \\ \frac{{{{\left[ {{Q_{N1}}\left( {t_g^{p1}} \right) - S_l^{\rm{s}}\left( {\vec t_g^{p1} - t_g^{m1}} \right)} \right]}^2}}}{{2\left( {S_l^{\rm{s}} - q_l^{\rm{s}}} \right)}}. \end{array} $ |
多边形EGU的面积θEGU为
| $ {\theta _{EGU}} = \frac{1}{2}EU \times GG' = \frac{{q_l^{\rm{s}}{{\left( {t_g^{m1} - t_g^{p1} - {L_{N0}}/{V_{N0}}} \right)}^2}}}{{2\left( {S_l^{\rm{s}} - q_l^{\rm{s}}} \right)}}. $ |
交叉口南进口左转相位每周期的车总延误Φm1sl=θOAFWUB+θEGU.
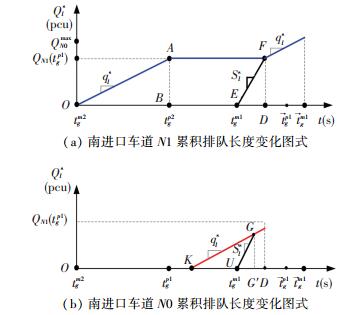
情况3 预信号相位P1绿灯结束前车道N1的排队已完全消散,且车道N0的排队车辆数达到QN1(tgp1).当车道N0的排队车辆数达到QN1(tgp1)后,再驶来的左转车将分别选择车道N0和N1,在一定时间段内这两条车道的车辆到达率均维持在0.5qls.这是与情况1、2的主要区别.从图 5可以看出在Z点车道N0的排队车辆数达到QN1(tgp1),而在F点车道N1排队才完全消散.所以从Z点所对应时刻至F点所对应时刻,车道N0和N1的车辆到达率均为0.5qls.在车道N1的排队完全消散后,左转车辆将只选择车道N1,所以该车道的车辆到达率升为qls.
|
图 5 情况3中车道N0与N1累积排队变化图式 Figure 5 Cumulative queue change patterns of lane N0 and N1(Case 3) |
在情况3,车道N1的左转车辆累积延误为图 5(a)中多边形OAWFE的面积,车道N0的左转车辆累积延误为图 5(b)中多边形KZGU的面积.
多边形OAWFE的面积θOAWFE为
| $ \begin{array}{l} {\theta _{OAWFE}} = \frac{1}{2}{Q_{N1}}\left( {t_g^{p1}} \right)\left( {2t_g^{m1} - t_g^{m2} - t_g^{p1}} \right) + \\ \;\;\;\;\frac{1}{2}\left[ {\frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{q_l^{\rm{s}}}} - t_g^{m1} + t_g^{p1} + \frac{{{L_{N0}}}}{{{V_{N0}}}}} \right]\left[ {2{Q_{N1}}\left( {t_g^{p1}} \right) - } \right.\\ \;\;\;\;\left. {S_l^{\rm{s}}\left( {\frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{q_l^{\rm{s}}}} - t_g^{m1} + t_g^{p1} + \frac{{{L_{N0}}}}{{{V_{N0}}}}} \right)} \right] + \\ \;\;\;\;\frac{{{Q_{N1}}\left( {t_g^{p1}} \right) - S_l^{\rm{s}}\left( {\frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{q_l^{\rm{s}}}} - t_g^{m1} + t_g^{p1} + \frac{{{L_{N0}}}}{{{V_{N0}}}}} \right)}}{2} \times \\ \;\;\;\;\frac{{\left[ {{Q_{N1}}\left( {t_g^{p1}} \right) - S_l^{\rm{s}}\left( {\frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{S_l^{\rm{s}}}} - t_g^{m1} + t_g^{p1} + \frac{{{L_{N0}}}}{{{V_{N0}}}}} \right)} \right]}}{{S_l^{\rm{s}} - 0.5q_l^{\rm{s}}}}. \end{array} $ |
多边形KZGU的面积θKZGU为
| $ \begin{array}{l} {\theta _{KZGU}} = \frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{2}\left( {3t_g^{m1} - 2t_g^{p1} + \frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{S_l^{\rm{s}}}} - \frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{q_l^{\rm{s}}}}} \right) + \\ \;\;\;\left( {2t_g^{m1} + \frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{S_l^{\rm{s}}}} - \frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{q_l^{\rm{s}}}} - t_g^{p1} + \frac{{{L_{N0}}}}{{{V_{N0}}}}} \right) \times \\ \;\;\;\frac{{\left[ {{Q_{N1}}\left( {t_g^{p1}} \right) - S_l^{\rm{s}}\left( {\frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{S_l^{\rm{s}}}} - t_g^{m1} + t_g^{p1} + \frac{{{L_{N0}}}}{{{V_{N0}}}}} \right)} \right]}}{{2\left( {S_l^{\rm{s}} - 0.5q_l^{\rm{s}}} \right)}}. \end{array} $ |
交叉口南进口左转相位每周期的车总延误Φm1sl=θOAWFE+θKZGU.
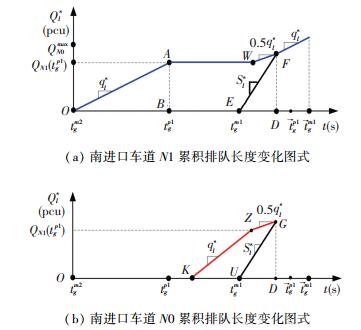
情况4 预信号相位P1绿灯结束前车道N1的排队未完全消散,且车道N0的排队车辆数达到QN1(tgp1).从图 6可以看出,从A点至W点车道N1的排队长度不再增加,在F点排队完全消散.在Z点车道N0的排队车辆数达到QN1(tgp1),在G点排队完全消散.在情况4,车道N1的左转车辆累积延误为图 6(a)中多边形OAWFE的面积,车道N0的左转车辆累积延误为图 6(b)中多边形KZGU的面积.需要注意的是:图 6(a)中从W点至H点,车辆平均到达率为0.5qls;从H点至F点,车辆平均到达率为qls.这是情况4与情况3的主要区别.
|
图 6 情况4中车道N0与N1累积排队变化图式 Figure 6 Cumulative queue change patterns of lane N0 and N1 (Case 4) |
多边形OAWFE的面积θOAWFE为
| $ \begin{array}{l} {\theta _{OAWFE}} = \frac{1}{2}{Q_{N1}}\left( {t_g^{p1}} \right)\left( {2t_g^{m1} - t_g^{m2} - t_g^{p1}} \right) + \frac{1}{2}\left[ {\frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{q_l^{\rm{s}}}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {t_g^{m1} + t_g^{p1} + \frac{{{L_{N0}}}}{{{V_{N0}}}}} \right]\left[ {2{Q_{N1}}\left( {t_g^{p1}} \right) - S_l^{\rm{s}}\left( {\frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{q_l^{\rm{s}}}} - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {t_g^{m1} + t_g^{p1} + \frac{{{L_{N0}}}}{{{V_{N0}}}}} \right)} \right] + \frac{{\vec t_g^{p1} - t_g^{p1} - \frac{{{L_{N0}}}}{{{V_{N0}}}}}}{2} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\left[ {2{Q_{N1}}\left( {t_g^{p1}} \right) + {\alpha _1} - S_l^{\rm{s}}\left( {\frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{q_l^{\rm{s}}}} + \frac{{{L_{N0}}}}{{{V_{N0}}}} + } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {2t_g^{m1} - t_g^{p1} - \vec t_g^{p1}} \right) + \frac{{{Q_{N1}}\left( {t_g^{p1}} \right) + {\alpha _1}}}{2} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{{Q_{N1}}\left( {t_g^{p1}} \right) + {\alpha _1} - S_l^{\rm{s}}\left( {\vec t_g^{p1} - t_g^{m1}} \right)}}{{S_l^{\rm{s}} - q_l^{\rm{s}}}}. \end{array} $ |
式中
| $ {\alpha _1} = 0.5q_l^{\rm{s}}\left( {\vec t_g^{p1} - t_g^{p1} - \frac{{{L_{N0}}}}{{{V_{N0}}}} - \vec t_g^{p1} + \frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{q_l^{\rm{s}}}} + t_g^{p1} \cdot } \right. $ |
多边形KZGU的面积θKZGU为
| $ \begin{array}{l} {\theta _{KZGU}} = \frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{2}\left( {2t_g^{m1} - t_g^{p1} + \frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{S_l^{\rm{s}}}} - \frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{q_l^{\rm{s}}}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {\frac{{{L_{N0}}}}{{{V_{N0}}}}} \right) + \frac{1}{2}\left( {t_g^{m1} - t_g^{p1} + \frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{S_l^{\rm{s}}}} - \frac{{{Q_{N1}}\left( {t_g^{p1}} \right)}}{{q_l^{\rm{s}}}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {\frac{{{L_{N0}}}}{{{V_{N0}}}}} \right) \times \left[ {S_l^{\rm{s}}\left( {\vec t_g^{p1} - t_g^{m1}} \right) - {Q_{N1}}\left( {t_g^{p1}} \right)} \right]. \end{array} $ |
交叉口南进口左转相位每周期的车总延误Φm1sl=θOAWFE+θKZGU.
在实际计算南进口左转相位的车总延误时,如何辨识南进口属于哪种情况也非常关键.情况1~4除了需要满足QN1(tgp1)≤QN0max外,还需要分别满足:
| $ \begin{array}{l} {Q_{N1}}\left( {t_g^{p1}} \right)/S_l^{\rm{s}} \le \left( {\vec t_g^{p1} - t_g^{m1}} \right)且\left[ {{Q_{N1}}\left( {t_g^{p1}} \right)/S_l^{\rm{s}} + t_g^{m1} - } \right.\\ \;\;\left. {\left( {t_g^{p1} + {L_{V0}}/{N_{V0}}} \right)} \right] \le {Q_{N1}}\left( {t_g^{p1}} \right); \end{array} $ |
| $ \begin{array}{l} {Q_{N1}}\left( {t_g^{p1}} \right)/S_l^{\rm{s}} > \left( {\vec t_g^{p1} - t_g^{m1}} \right)且\left[ {{Q_{N1}}\left( {t_g^{p1}} \right)/S_l^{\rm{s}} + t_g^{m1} - } \right.\\ \;\;\left. {\left( {t_g^{p1} + {L_{V0}}/{N_{V0}}} \right)} \right] \le {Q_{N1}}\left( {t_g^{p1}} \right); \end{array} $ |
| $ \begin{array}{l} {Q_{N1}}\left( {t_g^{p1}} \right)/S_l^{\rm{s}} \le \left( {\vec t_g^{p1} - t_g^{m1}} \right)且\left[ {{Q_{N1}}\left( {t_g^{p1}} \right)/S_l^{\rm{s}} + t_g^{m1} - } \right.\\ \;\;\left. {\left( {t_g^{p1} + {L_{V0}}/{N_{V0}}} \right)} \right] > {Q_{N1}}\left( {t_g^{p1}} \right); \end{array} $ |
| $ \begin{array}{l} {Q_{N1}}\left( {t_g^{p1}} \right)/S_l^{\rm{s}} > \left( {\vec t_g^{p1} - t_g^{m1}} \right)且\left[ {{Q_{N1}}\left( {t_g^{p1}} \right)/S_l^{\rm{s}} + t_g^{m1} - } \right.\\ \;\;\left. {\left( {t_g^{p1} + {L_{V0}}/{N_{V0}}} \right)} \right] > {Q_{N1}}\left( {t_g^{p1}} \right); \end{array} $ |
如果满足QN1(tgp1)>QN0max,则存在
| $ \left( {{g^{m2}} + {I^{m2}} + {g^{m3}} + {I^{m3}} + {\eta _2}} \right) \times q_l^{\rm{s}} > Q_{N0}^{\max }, $ |
| $ q_l^{\rm{s}} > Q_{N0}^{\max }/\left( {{g^{m2}} + {I^{m2}} + {g^{m3}} + {I^{m3}} + {\eta _2}} \right). $ |
根据相位M1绿灯启亮时刻,车道N0排队是否达到QN0max以及相位P1绿灯结束时刻车道N1的排队是否完全消散,也可以将左转车辆的运行分为4种情况,编号为情况5~8.
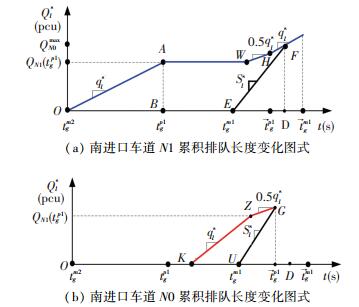
情况5 相位M1绿灯启亮前车道N0排队车辆数已经达到QN0max,且相位P1绿灯结束前车道N1排队已经完全消散.如图 7所示,在时刻tgp1车道N1的到达车辆数QN1(tgp1)大于等于QN0max,所以当相位P1的绿灯启亮后,部分排队车辆将转向车道N0,而且后续新到达的左转车也将选择车道N0.从K点开始车道N0的累积排队车辆数逐渐增加,当达到QN0max后左转车将选择车道N1.
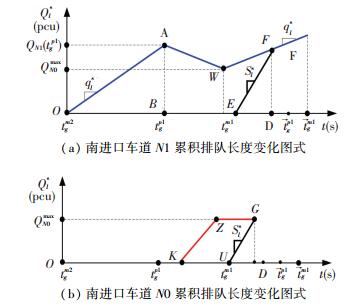
|
图 7 情况5中车道N0与N1累积排队变化图式 Figure 7 Cumulative queue change patterns of lane N0 and N1(Case 5) |
在情况5,车道N1的左转车辆累积延误为图 7(a)中多边形OAWFE的面积,车道N0的左转车辆累积延误为图 7(b)中梯形KZGU的面积.
多边形OAWFE的面积θOAWFE为
| $ \begin{array}{l} {\theta _{OAWFE}} = \frac{1}{2}{Q_{N1}}\left( {t_g^{p1}} \right)\left( {t_g^{p1} - t_g^{m2}} \right) + \frac{1}{2}\left[ {{Q_{N1}}\left( {t_g^{p1}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {Q_{N0}^{\max }} \right] \times \left[ {{Q_{N1}}\left( {t_g^{p1}} \right) - Q_{N0}^{\max }} \right]/S_l^{\rm{s}} + \frac{1}{2}\left( {Q_{N0}^{\max } + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{\alpha _2}} \right) \times \left( {t_g^{p1} - t_g^{m2} - \frac{{{Q_{N1}}\left( {t_g^{p1}} \right) - Q_{N0}^{\max }}}{{S_l^{\rm{s}}}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{\alpha _2} \times \frac{{Q_{N0}^{\max } + S_l^{\rm{s}}\left( {{\alpha _2} - Q_{N0}^{\max }} \right)/q_l^{\rm{s}}}}{{S_l^{\rm{s}} - q_l^{\rm{s}}}}. \end{array} $ |
式中
多边形KZGU的面积为
| $ \begin{array}{l} {\theta _{KZGU}} = \frac{{Q_{N0}^{\max }}}{2}\left[ {2t_g^{m1} - 2t_g^{p1} - \frac{{2{L_{N0}}}}{{{V_{N0}}}} - \frac{{{Q_{N1}}\left( {t_g^{p1}} \right) - Q_{N0}^{\max }}}{{S_l^{\rm{s}}}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\frac{{2Q_{N0}^{\max } - {Q_{N1}}\left( {t_g^{p1}} \right)}}{{q_l^{\rm{s}}}} + \frac{{Q_{N0}^{\max } + S_l^{\rm{s}}\left( {{\alpha _2} - Q_{N0}^{\max }} \right)/q_l^{\rm{s}}}}{{S_l^{\rm{s}} - q_l^{\rm{s}}}} - \\ \;\;\;\;\;\;\;\;\;\;\;\left. {\left( {{\alpha _2} - Q_{N0}^{\max }} \right)/q_l^{\rm{s}}} \right]. \end{array} $ |
交叉口南进口左转相位每周期的车总延误Φm1sl=θOAWFE+θKZGU.
情况6 相位M1绿灯启亮前车道N0排队车辆数尚未达到QN0max,且相位P1绿灯结束前车道N1排队已经完全消散. 图 8中多边形OAWHFE的面积为
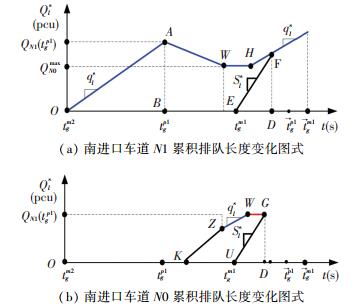
|
图 8 情况6中车道N0与N1累积排队变化图式 Figure 8 Cumulative queue change patterns of lane N0 and N1 (Case 6) |
| $ \begin{array}{l} {\theta _{OAWHFE}} = \frac{1}{2}{Q_{N1}}\left( {t_g^{p1}} \right)\left( {t_g^{p1} - t_g^{m2}} \right) + \frac{1}{2}\left[ {{Q_{N1}}\left( {t_g^{p1}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {Q_{N0}^{\max }} \right] \times \left[ {{Q_{N1}}\left( {t_g^{p1}} \right) - Q_{N0}^{\max }} \right]/S_l^{\rm{s}} + \frac{1}{2}Q_{N0}^{\max } \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {t_g^{m1} - t_g^{p1} - \frac{{{L_{N0}}}}{{{V_{N0}}}} - \left( {{Q_{N1}}\left( {t_g^{p1}} \right) - Q_{N0}^{\max }} \right)/S_l^{\rm{s}}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{2Q_{N0}^{\max } - S_l^{\rm{s}}\left[ {2Q_{N0}^{\max } - {Q_{N1}}\left( {t_g^{p1}} \right)} \right]/q_l^{\rm{s}}}}{2} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{2Q_{N0}^{\max } - {Q_{N1}}\left( {t_g^{p1}} \right)}}{{q_l^{\rm{s}}}} + \frac{1}{{2\left( {S_l^{\rm{s}} - q_l^{\rm{s}}} \right)}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left[ {Q_{N0}^{\max } - \frac{{S_l^{\rm{s}}\left( {2Q_{N0}^{\max } - {Q_{NQ}}\left( {t_g^{p1}} \right)} \right)}}{{q_l^{\rm{s}}}}} \right]^2}. \end{array} $ |
多边形KZWGU的面积θKZWGU为
| $ \begin{array}{l} {\theta _{KZWGU}} = \left( {t_g^{m1} - t_g^{p1} - \frac{{{L_{N0}}}}{{{V_{N0}}}}} \right) \times \frac{{{Q_{N1}}\left( {t_g^{p1}} \right) - Q_{N0}^{\max }}}{{S_l^{\rm{s}}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}\left[ {\left( {t_g^{m1} - t_g^{p1} - \frac{{{L_{N0}}}}{{{V_{N0}}}}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{{Q_{N0}^{\max }q_l^{\rm{s}} - S_l^{\rm{s}}\left( {2Q_{N0}^{\max } - {Q_{N1}}\left( {t_g^{p1}} \right)} \right)}}{{q_l^{\rm{s}}\left( {S_l^{\rm{s}} - q_l^{\rm{s}}} \right)}}} \right] \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left( {2Q_{N0}^{\max } - {Q_{N1}}\left( {t_g^{p1}} \right)} \right). \end{array} $ |
交叉口南进口左转相位每周期的车总延误Φm1sl等于θOAWHFE与θKZWGU之和.
情况7 相位M1绿灯启亮前车道N0排队车辆数已经达到QN0max,且相位P1绿灯结束前车道N1排队尚未完全消散.情况7与情况5的区别在于前者车道N1的排队完全消散发生在相位P1绿灯结束后,而后者发生在相位P1绿灯结束前.对比图 7与图 9可以发现,两条车道的车辆到达与驶离图式相似,车总延误的计算方法也基本相同,在此不再赘述. 图 9中交叉口南进口左转相位每周期的车总延误Φm1sl=θOAWFE+θKZGU.
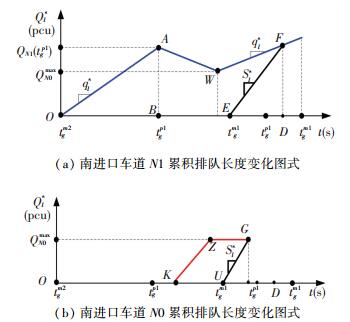
|
图 9 情况7中车道N0与N1累积排队变化图式 Figure 9 Cumulative queue change patterns of lane N0 and N1 (Case 7) |
情况8 相位M1绿灯启亮前车道N0排队车辆数尚未达到QN0max,且相位P1绿灯结束前车道N1排队尚未完全消散.
情况8与情况6的区别在于前者车道N1的排队完全消散发生在相位P1绿灯结束后,而后者发生在相位P1绿灯结束前.对比图 8与图 10可以发现,两条车道的车辆到达与驶离图式相似,车总延误的计算方法也基本相同,在此不再赘述. 图 10中交叉口南进口左转相位每周期的车总延误Φm1sl=θOAWHFE+θKZWGU.情况5~8除了需满足QN1(tgp1)>QN0max外,还需分别满足:
| $ \begin{array}{l} Q_{N0}^{\max }/S_l^{\rm{s}} \le t_g^{m1} - \left( {t_g^{p1} + {L_{V0}}/{N_{V0}}} \right)且\;Q_{N0}^{\max } + q_l^{\rm{s}}\left( {\vec t_g^{p1} - } \right.\\ \;\;\;\left. {t_g^{p1} - {L_{V0}}/{N_{V0}} - Q_{N0}^{\max }/S_l^{\rm{s}}} \right) \le S_l^{\rm{s}}\left( {\vec t_g^{p1} - t_g^{m1}} \right); \end{array} $ |
| $ \begin{array}{l} Q_{N0}^{\max }/S_l^{\rm{s}} > t_g^{m1} - \left( {t_g^{p1} + {L_{V0}}/{N_{V0}}} \right)且\;Q_{N0}^{\max } + q_l^{\rm{s}}\left( {\vec t_g^{p1} - } \right.\\ \;\;\;\left. {t_g^{p1} - {L_{V0}}/{N_{V0}} - Q_{N0}^{\max }/S_l^{\rm{s}}} \right) \le S_l^{\rm{s}}\left( {\vec t_g^{p1} - t_g^{m1}} \right); \end{array} $ |
| $ \begin{array}{l} Q_{N0}^{\max }/S_l^{\rm{s}} \le t_g^{m1} - \left( {t_g^{p1} + {L_{V0}}/{N_{V0}}} \right)且\;Q_{N0}^{\max } + q_l^{\rm{s}}\left( {\vec t_g^{p1} - } \right.\\ \;\;\;\left. {t_g^{p1} - {L_{V0}}/{N_{V0}} - Q_{N0}^{\max }/S_l^{\rm{s}}} \right) > S_l^{\rm{s}}\left( {\vec t_g^{p1} - t_g^{m1}} \right); \end{array} $ |
| $ \begin{array}{l} Q_{N0}^{\max }/S_l^{\rm{s}} > t_g^{m1} - \left( {t_g^{p1} + {L_{V0}}/{N_{V0}}} \right)且\;Q_{N0}^{\max } + q_l^{\rm{s}}\left( {\vec t_g^{p1} - } \right.\\ \;\;\;\left. {t_g^{p1} - {L_{V0}}/{N_{V0}} - Q_{N0}^{\max }/S_l^{\rm{s}}} \right) > S_l^{\rm{s}}\left( {\vec t_g^{p1} - t_g^{m1}} \right). \end{array} $ |

|
图 10 情况八中车道N0与N1累积排队变化图式 Figure 10 Cumulative queue change patterns of lane N0 and N1 (Case 8) |
本文以各个相位关键车道的车均延误最小为目标优化信号配时方案.东、西、北3个进口左转机动车延误的计算方法与南进口相同,不再赘述.具体优化目标函数为
| $ \min\mathit{\Phi } = \frac{{{\mathit{\Phi }_{m2}} + {\mathit{\Phi }_{m4}} + \max \left( {\mathit{\Phi }_{m1}^{{\rm{sl}}},\mathit{\Phi }_{m1}^{{\rm{nl}}}} \right) + \max \left( {\mathit{\Phi }_{m1}^{{\rm{el}}},\mathit{\Phi }_{m3}^{{\rm{wl}}}} \right)}}{{\left[ {{q_{m2}} + {q_{mi4}} + \max \left( {q_l^{\rm{s}},q_l^{\rm{n}}} \right) + \max \left( {q_l^{\rm{e}},q_l^{\rm{w}}} \right)} \right] \times C}}. $ | (2) |
式中max(Φm1sl, Φm1nl)为将南、北进口左转机动车每周期总延误中的最大者作为相位1的每周期车总延误;max(Φm3el, Φm3wl)为将东、西进口左转机动车每周期总延误中的最大者作为相位3的每周期车总延误.
式(2)等号右侧分母代表每周期交叉口各关键车道到达的车辆数之和.之所以采用车均延误指标而非车总延误指标,是因为在优化求解过程中周期时长会发生变化,进而影响每周期到达的车辆数;而车总延误模型不仅与配时方案有关,也与到达的车辆数有关;采用车总延误指标无法客观描述信号配时方案与交通流运行效率之间的关系.式(2)中的优化变量包括主信号相位周期时长C、各个相位的绿灯时间gmi、gpi以及借对向车道的左转车道长度LN0、LN4、LN8、LN12.其中约束条件为
| $ \left\{ \begin{array}{l} g_{\min }^{mi} \le {g^{mi}} \le g_{\max }^{mi};\\ {C_{\min }} \le C \le {C_{\max }};\\ L_{Nj}^{\min } \le {L_{Nj}} \le L_{Nj}^{\max },j = 0,4,8,12. \end{array} \right. $ | (3) |
式中Cmin、Cmax分别为交叉口的最小周期、最大周期;LNjmin、分别为借对向车道的左转车道最小长度、最大长度.由式(2)、(3)组成的优化模型一共包括11个优化变量,很难采用穷举法、整数规划法或者基于梯度的算法进行求解.而遗传算法只需要计算目标函数(适应度函数),无需计算梯度,适用于求解类似的优化问题.因此本文选择采用遗传算法进行求解.由于篇幅的限制,对遗传算法不再介绍,有兴趣的读者可以查阅相关文献.
3 算例分析 3.1 交叉口数据输入以图 1所示交叉口为例验证第2节所建立的优化方法,该交叉口采用图 2所示的相位方案,绿灯间隔时间设置为3 s. Cmin、Cmax分别设置为90、160 s;gminmi、gmaxmi分别设置为15、50s;LNjmin、LNjmax分别设置为15、150 m. η1=LNj/VNj;η2=LNj/VNj+5. VNj(j=0, 4, 8, 12)取值为10 m/s.左转、直行车道的饱和流率分别取0.417、0.5 pcu/s.
为了评价不同负荷下的交叉口交通流运行情况,设计两种流量输入方案.在每种方案下,各个进口的左转、直行、右转流量均相等.在方案一下,每个进口的左转、直行、右转流量分别为0.076、0.208、0.028 pcu/s;在方案二下,每个进口的左转、直行、右转流量分别为0.097、0.236、0.042 pcu/s.
将本文所建立的交叉口信号控制方案(简称“优化方案”)与传统的交叉口信号控制方案(简称“传统方案”)进行对比,分析不同流量方案下二者的车均延误变化情况.在传统方案下,交叉口执行四相位控制,最小、最大周期分别为90、160 s;最小、最大绿灯时间分别为15、50 s;每个进口方向有1条左转车道、1条直行车道、1条直右车道;采用式(1)计算传统方案下的车均延误,并以车均延误最小为目标优化其配时方案.
3.2 仿真结果分析首先在MATLAB中编程计算两种流量输入情况下优化方案、传统方案的信号配时参数.利用遗传算法进行求解,终止进化代数200,交叉概率0.8,变异概率设置为0.05.具体见表 1.由于各个进口的流量输入相同,所以gp1=gp2、LN0=LN4=LN8=LN12.
| 表 1 不同流量下交叉口优化信号配时参数 Table 1 Optimal signal timing parameters of the intersection under different traffic volumes |
从表 1、2可以看出,优化方案下的交叉口周期时长小于传统方案下的交叉口周期时长.在流量方案Ⅱ下,传统方案的周期时长为160 s,此时传统交叉口处于高负荷状态;而优化方案的周期时长为142 s,尚处于非饱和状态.这是因为在优化方案下采用借对向出口车道左转,每个进口增加了1条左转车道,使得左转车的通行能力增加,所需要的绿灯时间减少,进而使得交叉口整体周期时长减小.
| 表 2 不同流量下交叉口传统信号配时参数 Table 2 Traditional signal timing parameters of the intersection under different traffic volumes |
而在表 3中,优化方案下的左转车、直行车以及交叉口整体车均延误都小于传统方案.在高负荷状态下交叉口车均延误可以下降23.8%.这首先是因为优化方案下左转车通行能力增加,降低了左转车延误;其次,由于左转相位的绿灯时间减少,导致直行相位的红灯时间减少,进而降低了直行相位的车均延误.例如在表 3中的流量方案一下,优化方案的gm1为15 s,仅仅达到最小绿灯时间;而表4中传统方案的gm1达到了21 s.在流量方案Ⅱ下也出现了相同的规律.在表 3中LNj分别等于21、56 m.由于在排队状态下车头间距为7 m,所以它们分别能够容纳3辆和8辆左转车.即使在高负荷状态下,LNj的取值也并不大.这主要是因为在预信号显示红灯期间,左转车只能选择在原有左转车道排队(如南进口车道N1);如果LNj取值过大,则在车道N1距离停车线小于等于LNj的排队车辆将无法在预信号显示绿灯期间转至车道N0.而且当车道N1的排队完全消散后,左转车仍只能选择车道N1,所以LNj取值稍小可以提高车道N0的利用率.
| 表 3 不同控制方案下交通流车均延误 Table 3 Average vehicle delays under different control plans |
1) 借对向出口车道左转是一种有效提高交叉口通行能力、缓解交通拥堵的措施.借对向出口车道左转交叉口的交通流运行与传统交叉口存在显著差异,进而导致信号配时方案优化方法、评价指标计算方面的不同.
2) 考虑不同的左转车流量以及排队释放所需的绿灯时间,建立了8种图式下的车均延误计算方法,这是本文建模的核心.最后以车均延误最小为目标对信号控制方案进行优化.
3) 所建立的信号控制方案优化方法可以在不同的交通负荷条件下减少交叉口车均延误;在高负荷状态下可以减少23.8%.为了提高借对向左转车道的利用率,该车道长度不宜过大.
| [1] |
徐良杰, 王炜. 信号交叉口左转非机动车影响分析[J]. 中国公路学报, 2006, 19(1): 89-92. XU Liangjie, WANG Wei. Analysis of influence of left-turn non-motors in signalized intersection[J]. China Journal of Highway and Transport, 2006, 19(1): 89-92. |
| [2] |
蒋贤才, 汪贝, 曾永松. 不良天气和路面环境对交通信号配时方案的影响[J]. 公路交通科技, 2014, 31(7): 135-142. JIANG Xiancai, WANG Bei, ZENG Yongsong. Influence of incle-ment weather and poor road condition on traffic signal timing scheme[J]. Journal of Highway and Transportation Research and Development, 2014, 31(7): 135-142. |
| [3] |
王殿海, 郭伟伟, 宋现敏, 等. 交通控制中展宽段设计与信号配时的优化[J]. 控制理论与应用, 2010, 27(12): 1598-1604. WANG Dianhai, GUO Weiwei, SONG Xianmin, et al. The optimization of stretching segment and signal timing in traffic control[J]. Control Theory and Applications, 2010, 27(12): 1598-1604. |
| [4] |
HE H, GULER S I, MENENDEZ M. Adaptive control algorithm to provide bus priority with a pre-signal[J]. Transportation Research Part C: Emerging Technologies, 2016, 64: 28-44. DOI:10.1016/j.trc.2016.01.009 |
| [5] |
BIE Y, LIU Z, WANG Y. A real-time traffic control method for the intersection with pre-signals under the phase swap sorting strategy[J]. PLoS One, 2017, 12(5): e0177637. DOI:10.1371/journal.pone.0177637 |
| [6] |
HOUNSELL N B, YAP Y H. Hook turns as a solution to the right-turning traffic problem[J]. Transportation Science, 2013, 49(1): 1-12. |
| [7] |
BIE Y, LIU Z, LU L. Optimization of coordinated signal settings for hook-turn intersections[J]. Journal of Advanced Transportation, 2016, 50(2): 197-213. DOI:10.1002/atr.v50.2 |
| [8] |
LIU Z, BIE Y. Comparison of hook-turn scheme with U-turn scheme based on actuated traffic control algorithm[J]. Transportmetrica A: Transport Science, 2015, 11(6): 484-501. DOI:10.1080/23249935.2015.1018855 |
| [9] |
成卫, 别一鸣, 刘志远. 基于机动车延误的Hook-turn交叉口信号控制方案优化方法[J]. 中国公路学报, 2015, 28(3): 94-101. CHENG Wei, BIE Yiming, LIU Zhiyuan. Signal control scheme optimization method for intersection with Hook-turn based on motor vehicle delay[J]. China Journal of Highway and Transport, 2015, 28(3): 94-101. |
| [10] |
CURRIE G, REYNOLDS J. Managing trams and traffic at intersections with Hook turns[J]. Transportation Research Record: Journal of the Transportation Research Board, 2011, 2219: 10-19. DOI:10.3141/2219-02 |
| [11] |
WU J, LIU P, TIAN Z Z, et al. Operational analysis of the contraflow left-turn lane design at signalized intersections in China[J]. Transportation Research Part C: Emerging Technologies, 2016, 69: 228-241. DOI:10.1016/j.trc.2016.06.011 |
| [12] |
ZHAO J, YUN M, ZHANG H M, et al. Driving simulator evaluation of drivers' response to intersections with dynamic use of exit-lanes for left-turn[J]. Accident Analysis & Prevention, 2015, 81: 107-119. |
| [13] |
ZHAO J, LIU Y. Safety evaluation of intersections with dynamic use of exit-lanes for left-turn using field data[J]. Accident Analysis & Prevention, 2017, 102: 31-40. |
 2018, Vol. 50
2018, Vol. 50


