2. 西南交通大学 土木工程学院,成都 610031
2. Civil Engineering School, Southwest Jiaotong University, Chengdu 610031, China
自2000年美国太平洋地震研究中心提出“性能化地震工程”理论框架后,基于性能的抗震设计方法已逐渐成为结构抗震评估的重要途径[1],其中结构地震易损性分析是当前抗震分析领域研究的热点之一[2].随着各国学者深入开展桥梁结构地震易损性分析研究,地震易损性分析已经深入到桥梁抗震分析的各个领域中[3-4].
地震易损性分析方法一般包括:经验法[5]、试验分析法[6]、理论分析法[7].近年来,由于很多地区缺乏实桥震害资料,桥梁理论易损性分析得到了各国学者更加广泛而深入地研究,文献[8]基于极大似然估计法对汶川地区典型公路简支梁桥开展了易损性评估.文献[9]基于云图法对某公路高墩连续刚构桥开展了易损性分析,并结合公路桥梁抗震设计细则提出了一种新的桥梁地震易损性分析方法.文献[10]对加拿大魁北克地区一座3跨连续梁桥进行了加固修复设计,基于云图法建立加固前、后桥梁各构件的地震易损性曲线.文献[11]针对美国中东部典型高速公路简支梁桥,基于云图法对该桥进行了易损性分析,研究了纵桥向倾角、墩高等参数对桥梁易损性的影响.文献[12]针对伊朗90年代建成的32 m简支梁桥,建立了该桥的概率地震需求模型,并研究了近、远场地震作用下桥梁的抗震性能.上述研究主要基于云图法[13](cloud method, CM)或者极大似然法[14](maximum likelihood estimation, MLE)来建立桥梁地震易损性曲线,采用这两种方法时往往需要根据实际工程经验假设易损性函数为对数正态累计分布函数,而后通过样本计算易损性函数未知参数.但文献[15-16]研究表明:桥梁各构件的易损性曲线并非全部满足对数正态分布假设,大多数桥梁构件只是近似服从上述假设,部分桥梁构件并不服从上述假设,此时,若依然采用该分布假设来建立易损性曲线,则分析结果必将与实际情况不相符.
因此,为得到更加真实可靠的桥梁结构地震易损性曲线,本文基于非参数估计法中的核密度估计法[17](kernel density estimation, KDE),在不假设结构易损性函数分布形式的基础上,建立了一种核密度估计的桥梁易损性分析方法(下文简称KDE法).以某典型铁路4跨高墩刚构-连续梁桥为研究对象,运用KDE法建立了该桥各关键部位的易损性曲线,而后采用蒙特卡罗法(Monte Carlo simulation method, MCS)验证了本文方法的正确性和适应性,在此基础上,对比研究本文方法与常用方法计算结果的优缺点及差异性.
1 核密度估计的桥梁地震易损性分析方法 1.1 核密度估计的易损性计算理论地震易损性是指在某特定强度地震作用下,结构损伤破坏程度超过特定损伤状态的发生概率[15],则桥梁构件地震易损概率计算公式为
| $ {P_{\rm{f}}}\left( {IM, C} \right) = P{\left[{D \ge C|IM} \right]^{\left[8 \right]}}. $ | (1) |
式中:D为桥梁构件地震响应的需求值;C为桥梁构件抵抗地震作用的能力值;IM为地震动强度值;Pf(IM, C)为在强度为的IM地震作用下,桥梁构件出现特定损伤破坏状态的概率.
将桥梁构件抗震能力的条件概率密度函数fD|IM代入式(1).则易损概率计算公式可变为
| $ \begin{array}{l} {P_{\rm{f}}}\left( {a, C} \right) = P\left[{D \ge C|IM = a} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int_C^{ + \infty } {{f_D}\left( {c|IM = a} \right){\rm{d}}c} . \end{array} $ | (2) |
根据概率统计分析理论[17]可得桥梁构件抗震能力的概率密度函数计算公式为
| $ {f_D}\left( {c|IM = a} \right) = \frac{{{f_{D, IM}}\left( {c, a} \right)}}{{{f_{IM}}\left( a \right)}}. $ | (3) |
式中fD, IM(·)为抗震能力和地震动强度的联合概率密度分布函数,fIM(·)为IM的边缘分布函数,其他符号同上.如果已知fD, IM(·)和fIM(·),则利用式(2)便可计算桥梁构件的损伤概率,从而建立桥梁地震易损性曲线.
为建立桥梁构件易损性曲线,本文将基于N组{(IMi, Di), i=1, …, N }地震强度与结构时程分析最大响应数据,引入核密度估计法[18],推导桥梁结构联合概率密度函数与边缘分布函数的计算公式.
先讨论单参数随机变量X的情况,假设X变量有n个样本点{x1, …, xn}.由核密度估计的定义[19]可知,概率密度分布函数的核密度估计可表达为
| $ {\hat f_h}\left( x \right) = \frac{1}{{nh}}\sum\limits_{i = 1}^n {K\left( {\frac{{x-{x_i}}}{h}} \right).} $ | (4) |
式中h为带宽参数,K(·)为核函数,目前常用核函数有均匀核函数、高斯核函数等,具体函数形式见文献[20].
文献[21]研究表明,当计算样本点充足时,无论选择何种函数类型,均不影响评估结果的精度.因此本文采用高斯核函数作为核函数,即
| $ {\hat f_h}\left( x \right) = \frac{1}{{nh}}\sum\limits_{i = 1}^n {\varphi \left( {\frac{{x-{x_i}}}{h}} \right)} . $ | (5) |
文献[21]研究表明,式(5)中最优带宽参数h*≈1.059σ·n-0.2,σ为X的标准差,研究表明h的取值将直接影响到评估结果的正确性[20].利用式(5)便可评估强度为IM的地震边缘分布函数,即通过n组{IMi, i=1, …, n}地震动强度估计出
| $ {\hat f_{IM}}\left( a \right) = \frac{1}{{n{h_{IM}}}}\sum\limits_{i = 1}^n \varphi \left( {\frac{{a-I{M_i}}}{{{h_{IM}}}}} \right). $ | (6) |
下面讨论多元随机变量X∈Rd的情况,d代表维数,若已知n元变量X={x1, …, xn},各xi(i=1, 2…, n)变量之间相互独立,且各xi变量中有m个样本点,则核密度估计为
| $ {\hat f_X}\left( x \right) = \frac{1}{{n{{\left| \mathit{\boldsymbol{H}} \right|}^{\frac{1}{2}}}}}\sum\limits_{i = 1}^n {K\left( {{\mathit{\boldsymbol{H}}^{-\frac{1}{2}}}\left( {\mathit{\boldsymbol{x}}-{\mathit{\boldsymbol{x}}_i}} \right)} \right)} . $ | (7) |
式中H为带宽矩阵,属于对称正定矩阵,|H|为对H矩阵求行列式.常用二元参数化带宽矩阵包括:完整型、对称型、混合型,具体形式详见文献[22].将多元参数变量的标准正态核函数代入式(7),则核密度估计求解式为
| $ {\hat f_X}\left( x \right) = \frac{1}{{n{{\left| \mathit{\boldsymbol{H}} \right|}^{\frac{1}{2}}}}}\sum\limits_{i = 1}^n {\frac{1}{{{{\left( {2\pi } \right)}^{\frac{d}{2}}}}}} \times {{\rm{e}}^{\left[{-\frac{1}{2}{{\left( {\mathit{\boldsymbol{x}}-{\mathit{\boldsymbol{x}}_i}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{H}}^{-1}}\left( {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_i}} \right)} \right]}}. $ | (8) |
对于多元参数变量,当各变量之间相关性未知时,通常采用完全型带宽矩阵进行核密度估计,而完全型带宽矩阵可采用平滑交叉估计法[20, 23]计算得到.而后对桥梁开展n组地震作用下的时程分析,提取结构最大动力响应及地震动强度值{(IMi, Di),i=1, …, n},利用式(8)便可计算桥梁构件联合概率密度函数
| $ {\hat f_{D, IM}}\left( {c, a} \right) = \frac{1}{{2\pi n{{\left| \mathit{\boldsymbol{H}} \right|}^{\frac{1}{2}}}}}\sum\limits_{i = 1}^n {{{\rm{e}}^{\left[{-\frac{1}{2}{{\left( {\begin{array}{*{20}{c}} {c-{D_i}}\\ {a-I{M_i}} \end{array}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{H}}^{ - 1}}\left( {\begin{array}{*{20}{c}} {c - {D_i}}\\ {a - I{M_i}} \end{array}} \right)} \right]}}} . $ | (9) |
将式(6)、(9)代入式(3),计算桥梁构件抗震能力的概率密度函数fD(c|IM=a),然后积分求解式(2),最终获得桥梁构件地震易损概率
| $ \begin{array}{l} {P_f}\left( {a, C} \right) = P\left[{D \ge C|IM = a} \right] = \int_C^{ + \infty } {{f_D}\left( {c|IM = a} \right){\rm{d}}c} = \\ \frac{{{h_{IM}}}}{{2\pi {{\left| \mathit{\boldsymbol{H}} \right|}^{\frac{1}{2}}}}}\frac{{\int\limits_C^{ + \infty } {\sum\limits_{i = 1}^n {{{\rm{e}}^{\left[{-\frac{1}{2}{{\left( {\begin{array}{*{20}{c}} {c-{D_i}}\\ {a-I{M_i}} \end{array}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{H}}^{ - 1}}\left( {\begin{array}{*{20}{c}} {c - {D_i}}\\ {a - I{M_i}} \end{array}} \right)} \right]{\rm{d}}c}}} } }}{{\sum\limits_{i = 1}^n {\varphi \left( {\frac{{a -I{M_i}}}{{{h_{IM}}}}} \right)} }}. \end{array} $ | (10) |
采用式(10)便可算出桥梁构件的损伤概率,从而建立桥梁易损性曲线,式中最优带宽参数h和带宽矩阵H的确定是实现本文算法的关键问题,因此在运用式(10)前,先参考文献[21]的方法确定最优带宽参数,然后选择多组带宽矩阵进行试算,建立对应的易损性曲线,通过与MCS法计算结果进行比较,确定适用于算例桥的带宽矩阵形式.
1.2 本文方法的计算流程本文所提方法的基本流程如图 1所示.具体分析步骤如下:1)研究桥梁结构关键参数的不确定性,明确各关键参数的分布特征,运用拉丁超立方体抽样法[24]对参数进行抽样,生产桥梁结构参数样本,从而形成桥梁分析样本库;2)研究地震动输入的随机性,建立地震样本库;3)随机配对桥梁样本与地震样本,形成地震动-桥梁分析样本库,并开展时程分析,提取结构最大动力响应数据;4)确定构件损伤指标及其量化方法;5)利用时程分析结果,计算最优带宽参数h,比选合理的带宽矩阵H,并基于平滑交叉验证估计法求解H;6)利用核密度估计的桥梁易损性分析方法求解桥梁构件易损性曲线.
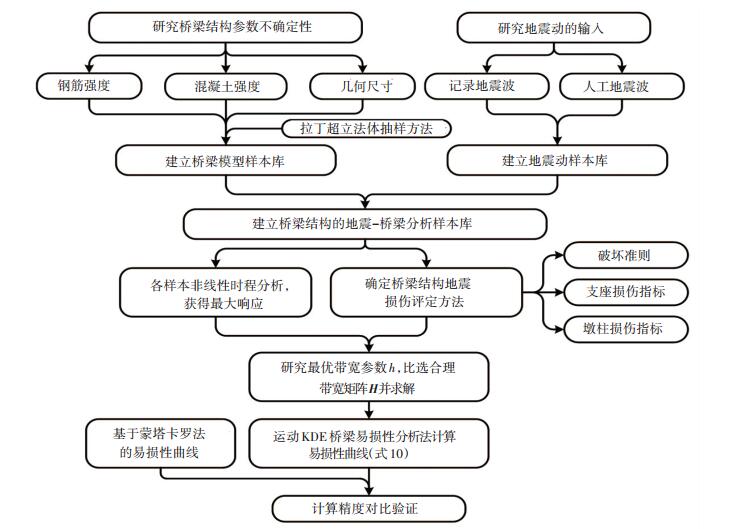
|
图 1 核密度估计的桥梁易损性分析流程 Figure 1 Schematic flow chart of fragility analysis by using the KDE method |
本文以某典型铁路4跨高墩刚构-连续梁桥为研究对象,该桥跨径布置为68 m+2×120 m+68 m+3×32 m+24 m,上部结构为变截面连续箱梁,采用C55混凝土;各桥墩为空心矩形截面,1#~4#墩高度分别为40.95、93.0、93.0、61 m;采用ZK活载形式;0#承台支座、1#墩支座、4#边墩支座均采用纵向活动球型钢支座,支座型号分别是TJGZ-LX-Q9000-ZX-e150-0.1g、TJGZ-LX-Q55000-ZX-e100-0.1g、TJGZ-LX-Q9000-ZX-e100-0.1g,支座纵向水平承载力为竖向承载力的5%,支座横向水平承载力为竖向承载力的15%,全桥布置图见图 2.
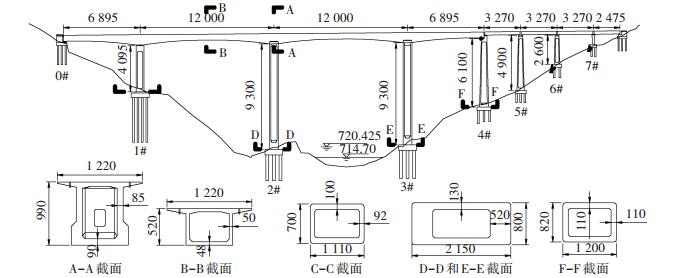
|
图 2 全桥布置示意图(cm) Figure 2 General situation of the bridge structure (cm) |
采用OpenSees软件建立全桥有限元模型,上部结构采用梁单元进行模拟,考虑自重、二期恒载及列车荷载,列车荷载按文献[25]第7.1.4条规定:顺桥向不计算列车引起的地震力,横桥向抗震分析时计入50%列车质量参与地震作用,列车活载竖向力按列车竖向静荷载的100%参与静力计算;桥墩采用纤维单元模拟,赋予桥墩钢筋、混凝土材料的本构模型,混凝土材料采用Kent-Park本构模型[26],普通混凝土材料本构模型依据文献[27]进行取值,约束混凝土本构模型采用Mander模型[28]计算得到,钢筋的本构关系由Giuffré-Menegotto-Pinto模型[29]确定;支座用双线性弹簧单元模拟[6],桥台采用OpenSees内置的零长度单元赋予材料特性来模拟,桥台的有效刚度及被动土压力则根据文献[30]进行求解;采用6个弹簧单元等效模拟桥梁桩基础,依据文献[31]附录D可求解各桥墩桩基础等效刚度,详见表 1,此外还采用了OpenSees程序中Impact Material材料来模拟碰撞效应,碰撞单元参数计算方法见文献[32].根据上述模拟方法,运用OpenSees软件建立全桥计算模型,如图 3所示.
| 表 1 各墩底土弹簧刚度表 Table 1 Spring stiffness of soil at the bottom of each pier |
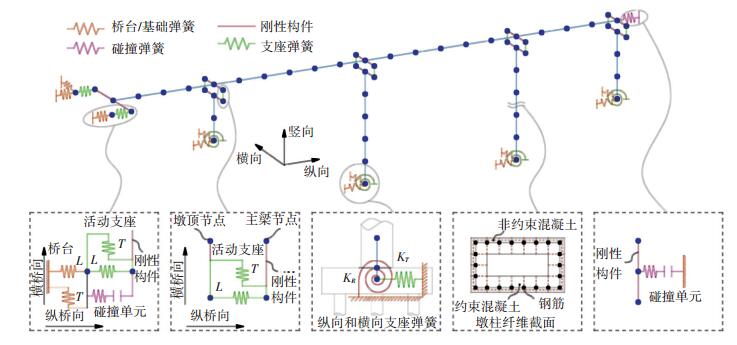
|
图 3 桥梁有限元模型示意图 Figure 3 Finite element model of the bridge structure |
鉴于本文算例桥位于四川地区,时程分析所用地震动应尽可能采用该地区实测地震动,这样才能保证计算结果与实际工程相吻合,故本文选用2008年汶川实测地震动来进行算例桥的地震易损性分析.在综合考虑地震动强度和实测数据完整性基础上,从四川省内40个观测台站中选出了100条地震动,图 4给出了各地震动的加速度反应谱及其均值谱.对100条地震动进行调幅,得到10个峰值加速度PGA(peak ground acceleration)等级,从0.1g至1.0g,调幅步长为0.1g,生成1 000组地震分析样本.
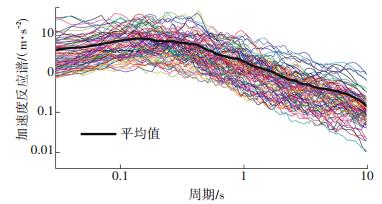
|
图 4 反应频谱特性图(ξ=0.05) Figure 4 Characteristics curves of response spectrum (ξ=0.05) |
由于桥梁结构在建造过程中常受到各类因素(如原料、施工工艺、外界干扰等)影响,使得材料特性、构件力学行为、荷载效应存在随机性,上述因素将影响桥梁结构自身的抗震性能,因此在开展易损性分析时,需要考虑上述因素的不确定性.文献[33-34]针对桥梁结构抗震特点,研究了影响桥梁抗震性能的关键参数,包括混凝土强度、混凝土密度、钢筋屈服应力、钢筋硬化比、二期恒载、支座摩擦系数等.因此本文模型分析时考虑上述6种关键参数,各参数具体取值见文献[6, 13],针对各关键参数,采用拉丁超立方体抽样法[35]对这些参数进行抽样,生成桥梁模型参数样本,从而形成桥梁分析样本库.鉴于计算规模和所选用的抽样方法,本文采用1 000次试验,生成1 000个桥梁模型样本.
2.4 桥梁结构损伤指标本文研究对象为高墩大跨刚构-连续梁桥,其墩身高度较大,且各桥墩的高差非常明显(最大高差达到50.05 m).为了建立这种高墩大跨非规则桥梁的易损性曲线,需要明确桥梁各易损部位的损伤指标.而文献[6, 9]针对高墩大跨连续刚构桥的特点,详细研究了这类桥型高墩和支座构件合理损伤指标的选取及指标的计算方法,因此本文在参考上述文献研究成果的基础上,选取截面曲率作为桥墩损伤指标,以支座相对位移作为球型钢支座的损伤指标,具体损伤指标计算方法见文献[6, 9].由于篇幅有限,表 2仅给出了桥墩和支座构件顺桥向损伤指标计算结果.
| 表 2 桥梁构件顺桥向损伤指标 Table 2 Values of damage indexes of bridge member in longitudinal direction |
以往桥梁震害资料[36]表明:对于大跨度连续刚构桥,刚构墩(墩底、墩顶区域)和支座是这类桥型震害最为严重的构件,边墩的震害相对较小,震害主要集中在墩底.文献[4, 6]对大跨刚构-连续梁桥易损性部位进行了研究,分析结果与实际桥梁震害情况一致,因此在开展地震易损性分析时,本文参考文献[4, 6]研究成果,将重点研究2#、3#墩顶和墩底截面,1#、4#墩底截面,0#台支座,1#、4#墩支座这些危险部位的易损性情况.
将2.2节生成的地震动样本与2.3节生成的模型桥样本进行随机配对,形成地震动-桥梁分析样本库,而后对样本库进行时程分析,获得各构件的最大动力响应,而后结合2.4节确定的损伤指标,运用本文提出的核密度估计的桥梁地震易损性分析方法,便可生成桥梁构件的地震易损性曲线.本文建立了桥梁纵向、横向地震易损性曲线,分析中选取Sa(即桥梁结构一阶纵向、一阶横向自振周期对应的谱加速度值)作为地震动的强度指标.
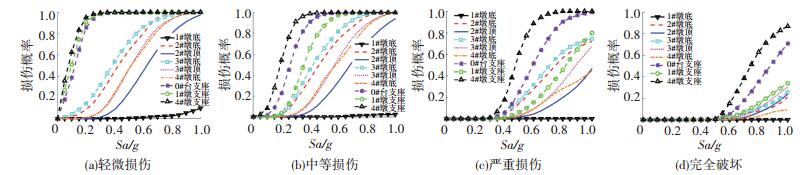
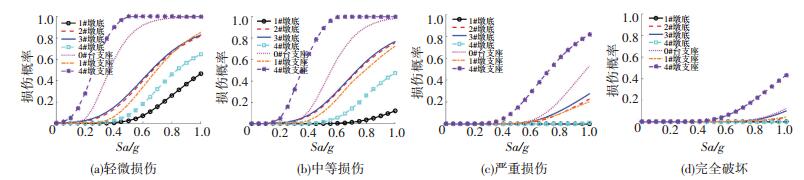
图 5、6分别给出了各危险部位纵、横向易损性曲线,由图分析可知,各部位易损性曲线有类似的形状,损伤概率均随着Sa的增加而增大.在地震作用下,4#墩支座最易损,其次是0#承台支座,1#墩底截面最不容易出现地震损伤.运用这些生成的易损性曲线,可评估各易损部位在不同强度地震动作用下的损伤破坏概率,进一步指导桥梁结构抗震优化设计、设计桥梁加固维修方案、评估桥梁加固优先顺序、评估震后桥梁经济损失等.
|
图 5 各危险部位纵桥向地震易损性曲线 Figure 5 Seismic fragility curves of different components in longitudinal direction |
|
图 6 各危险部位横桥向地震易损性曲线 Figure 6 Seismic fragility curves of different components in transverse direction |
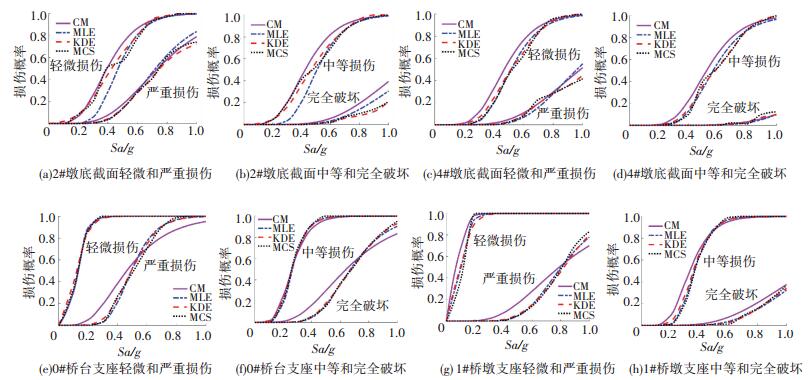
为验证本文方法的正确性及适应性,拟比较分析本文算法与常用易损性分析方法的优缺点,将4种易损性分析方法(CM法、MLE法,简称参数估计法;KDE法、MCS法,简称非参数法)所得结果绘于同一图中.由于每种分析方法都会生成4条曲线(对应4种破坏状态),共计16条,若所有曲线放在一幅图中将很难辨别,故将轻微和严重损伤状态、中等和完全破坏状态所对应的曲线分别绘于两幅图中,如图 7所示.
|
图 7 4种分析方法得到的各构件纵向易损性曲线 Figure 7 Comparison of seismic fragility curves based on four methods |
为验证本文所提方法的正确性,拟采用基于MCS的易损性分析方法与KDE法的计算结果进行对比验证. MCS法是通过概率的基本定义来计算桥梁构件地震损伤破坏概率,其计算结果是统计的实际概率值,与MCS法计算结果越接近的曲线越准确[8, 15],因此本文将MCS法作为参考依据来验证KDE法.由于篇幅有限,图 7仅列举出了部分桥梁易损构件的对比分析结果.由图 7分析可知,在4种损伤状态下,KDE法和MCS法建立的曲线总体吻合良好.尽管KDE法和MCS法的核心算法截然不同,但两种易损性曲线变化规律较为一致,两种方法计算的损伤概率值相差较小,这充分表明本文所提KDE法是正确的.由图 7(a)分析发现,对于2#墩底截面在轻微损伤状态下,MCS法建立的易损曲线不连续,曲线存在明显的折角.而出现折角的主要原因是:分析所采用地震动样本中,谱加速度Sa在0.4g~0.6g范围内的样本数量偏少,导致易损性曲线不光滑,需适当增加地震动样本来提升MCS法的计算精度,因此本文又补充计算了100条地震波的时程响应数据,重新运用MCS法建立了新的易损性曲线(如图 8所示),并将原先的易损性曲线同时绘制于图 8中,在桥梁模型中运算100条和200条地震时程分析的总耗时分别为55.2、118.4 h.由图 8分析可知,采用MCS法按200条地震波计算出的易损性曲线,其光滑程度、计算精度均显著提高,但地震分析计算耗时却成倍增加;对比分析KDE法(按100条地震波计算)与MCS法(按200条地震波计算)所建立的易损性曲线可知:两种曲线的变化规律一致,相同Sa条件下两种方法所得损伤概率偏差很小,上述分析表明本文所提KDE法的计算效率高于MCS法.

|
图 8 精度对比分析图 Figure 8 Accuracy comparison between different method |
综上所述:MCS法与KDE法建立的桥梁构件地震易损性曲线变化趋势一致,两种方法计算的易损概率相差较小,因MCS法是通过概率的基本定义计算的地震损伤破坏概率,其计算结果是统计的实际概率值,故本文提出的KDE法是正确的.此外KDE分析法在地震动分析样本不明显增加的前提下,可以获得精度更高且连续光滑的地震易损性曲线,这间接说明本文提出的KDE法具有较高的计算精度及良好的计算效率.
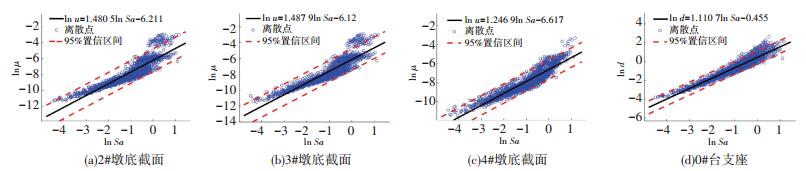
3.2 各种方法对比分析为了选取适用于铁路高墩大跨度桥梁易损性分析的计算方法,下文将对比分析4种桥梁易损性计算方法的优缺点,分析比较不同方法的计算精度及差异性.在对比分析前需要进行补充说明:目前国内外文献[3, 9, 12, 15, 32]在采用CM法建立易损性曲线时,其桥梁结构的概率地震需求模型一般采用线性回归函数,但文献[16]研究表明,在对数空间内,一些桥梁构件的地震响应与地震强度的需求模型并不满足线性关系,需要选取非线性拟合方式来建立更合适的桥梁需求模型,提高计算精度.为此,本文采用两种回归拟合方式建立需求模型(即常用的线性回归以及二次抛物线回归),先确定适用于算例桥梁的需求模型后再建立易损性曲线. 图 9、10给出了桥梁部分易损构件的概率地震需求模型,对比分析表明,二次抛物线回归所得需求模型拟合精度较高,故采用此模型建立易损性曲线.
|
图 9 部分构件概率地震需求线性回归模型 Figure 9 Linear regression models of the probabilistic seismic demand for some components |

|
图 10 部分构件概率地震需求二次抛物线回归模型 Figure 10 Quadratic parabolic regression models of the probabilistic seismic demand for some components |
由图 7(a)、7(b)分析可知,对于2#墩底截面,在4种损伤状态下,基于MCS法和KDE法建立的地震易损性曲线较为吻合.下面以MCS法作为参考依据对CM法和MLE法进行分析.针对MLE法的计算结果,在轻微、中等损伤状态下,当Sa < 0.5g时MLE法建立的易损性曲线与MCS法结果存在较大差异,当Sa>0.5g时MLE法与MCS法计算结果基本吻合;在严重、完全损伤状态下,MLE法建立的易损性曲线与MCS法结果非常接近;针对CM法的计算结果,在轻微、中等损伤状态下,当Sa < 0.4g时CM法与MCS法计算结果较为一致,当Sa>0.4g时CM法高估了2#墩底截面发生地震损伤破坏的概率,这与MLE法结果正好相反,在严重损伤状态下,CM法与MCS结果一致,在完全破坏状态下,CM法高估了2#墩底截面发生地震损伤破坏的概率,与其他3种方法计算结果差异较大.
由图 7(c)、7(d)分析可知,对于4#墩底截面,在轻微、中等损伤状态下,两种非参数法与MEL法建立的易损性曲线基本吻合.严重、完全破坏状态下,当Sa较小时,两种非参数法与MLE法计算结果一致,当Sa较大时,MLE法高估了4#墩底截面的地震损伤破坏概率.而CM法与其他3种方法计算结果存在一定的差异.由图 7(e)、7(f)分析可知,0#承台支座在4种损伤状态下,MLE法建立的易损性曲线与KDE法、MCS法计算结果几乎重合. CM法在轻微、中等损伤状态下,与其他3种分析法计算结果一致,而在严重损伤、完全破坏条件下,CM法与其他3种方法的结果存在明显不同,这表明CM法计算结果不稳定.由图 7(g)、7(h)分析可知,1#墩顶支座易损性曲线与0#承台支座的易损性曲线变化规律相近,这里不再详细分析.
与两种非参数法相比,CM法、MLE法计算结果与其存在一定偏差,主要原因如下:1)CM法和MLE法均假设构件地震易损性函数是对数正态分布函数,但文献[16]研究表明,大部分桥梁构件只是近似服从该假设,一些桥梁构件并不服从该假设;2)评估结构易损性函数相关参数的具体算法会影响计算精度[3, 8, 15],如CM法采用二次抛物线方程来反映结构响应与地震动强度指标的关系,由图 9、10分析可知,桥梁构件回归模型的对数标准差,随着Sa的增大而不断增加,但CM法却假设易损函数的对数标准差为常数,这使得当Sa较小时,对数标准差被高估了,Sa较大时被低估了,从而导致求解的损伤概率与实际不相符.
综上所述,以MCS法求解的易损性曲线作为参考依据,KDE法的计算精度最好,其次是MLE法,上述两种方法计算精度明显高于CM法.而在运用MCS法求解易损性曲线时,常会遇到计算样本不足导致易损性曲线不连续、不光滑的情况,为此只有增加分析样本数量,才能提高MCS法的计算精度,但增加样本会使计算耗时成倍递增,有点得不偿失.而本文提出的KDE法克服了上述3种方法的缺点,在分析样本数量不明显增加的前提下,可获得精度较高、连续光滑的地震易损性曲线,故本文提出的KDE法具有较高的计算精度及良好的计算效率.因此建议采用本文方法开展桥梁结构地震易损性分析.
4 结论1) 建立了核密度估计的桥梁易损性分析方法,并详细推导了桥梁结构地震损伤概率计算理论.对比分析本文方法与蒙特卡罗法的计算结果表明:本文方法计算结果正确,在满足计算精度前提下显著提高了计算效率,具有较好的适应性.
2) 对比分析KDE法与常用方法(CM法、MLE法、MCS法)的计算结果表明:KDE法克服了常用方法的缺点,有效地提高了计算精度,具有较好的适应性,建议采用KED法开展铁路高墩大跨桥梁地震易损性分析.
3) CM法、MLE法对比分析表明:两种分析法计算结果的可靠性与桥梁结构形式、概率地震需求模型的类型、易损性曲线特征参数评估方法等因素紧密相关. MLE法计算精度高于CM法.
| [1] |
MACKIE K, STOJADINOVIC B. Fragilitybasis for california highway overpass bridge seismic decision making[R]. Berkeley: University of California, 2005.
|
| [2] |
沈国煜, 袁万城, 庞于涛. 基于Nataf变换的桥梁结构地震易损性分析[J]. 工程力学, 2014, 31(6): 92-100. SHEN Guoyu, YUAN Wancheng, PANG Yutao. Bridge seismic fragility analysis based on nataf transformation[J]. Engineering Mechanics, 2014, 31(6): 92-100. |
| [3] |
HWANG H, LIU J B, Chiu Y. Seismic fragility analysis of highway bridges[R]. Tennessee: University of Memphi, 2001.
|
| [4] |
董俊. 铁路高墩大跨刚构-连续组合体系桥梁近场地震易损性分析研究[D]. 成都: 西南交通大学, 2016. DONG Jun. Fragility analysis of railway long span rigid frame-continuous combination system bridge with high pier subjected to near-fault ground motion[D]. Chengdu: Southwest Jiaotong University, 2016. |
| [5] |
DUKES J. DESROCHES R, PADGETT J E. Sensitivitystudy of design parameters used to develop bridge specific fragility curves[C]//15th World Conference of Earthquake Engineering. Lisbon: [s. n. ], 2012: 34-39.
|
| [6] |
董俊, 单德山, 张二华, 等. 非规则连续刚构桥地震易损性分析[J]. 西南交通大学学报, 2015, 50(5): 845-851. DONG Jun, SHAN Deshan, ZHANG Erhua, et al. Seismic fragility of irregular continuous rigid frame bridge[J]. Journal of Southwest Jiaotong University, 2015, 50(5): 845-851. |
| [7] |
ROSSETTO T, ELNASHAI A A. Newanalytical procedure for the derivation of displacement-based vulnerability curves for populations of RC structures[J]. Engineering Structures, 2005, 27(5): 397-409. |
| [8] |
陈力波. 汶川地区公路桥梁地震易损性分析研究[D]. 成都: 西南交通大学, 2012. CHEN Libo. Seismic vulnerability analysis for highway bridges in wenchuan region[D]. Chendu: Southwest Jiaotong University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10613-1014251544.htm |
| [9] |
肖明洋. 高墩混凝土连续刚构桥地震易损性分析[D]. 成都: 西南交通大学, 2013. XIAO Mingyang. Seismic vulnerability analysis for concrete continuous rigid bridge with high piers[D]. Chendu: Southwest Jiaotong University, 2013. |
| [10] |
SIQUEIRA G H, TAVARES D H, PAULTRE P. Seismicfragility of a highway bridge in quebec retrofitted with natural rubber isolators[J]. Ibracon Structures and Materials Journal, 2014, 7(4): 534-547. |
| [11] |
NOORI H Z, AMIRI G G, NEKOOEI M, et al. Seismic fragility assessment of skewed MSSS-I girder concrete bridges with unequal height columns[J]. Journal of Earthquake and Tsunami, 2015, 10(1): 1-16. |
| [12] |
MOSLEH A, RAZZAGHI M S, JARA J, et al. Seismic fragility analysis of typical pre-1990 bridges due to near-and far-field ground motions[J]. International Journal of Advanced Structural Engineering, 2016, 8(1): 1-9. DOI:10.1007/s40091-016-0108-y |
| [13] |
董俊, 单德山, 张二华, 等. 非规则桥梁近、远场地震易损性对比分析[J]. 哈尔滨工业大学学报, 2016, 48(3): 159-165. DONG Jun, SHAN Deshan, ZHANG Erhua, et al. Near and far-field seismic fragility comparative analysis of irregular bridge[J]. Jouranal of Harbin Institute of Technology, 2016, 48(3): 159-165. DOI:10.11918/j.issn.0367-6234.2016.03.027 |
| [14] |
SEYEDI D M, GEHL P, DOUGLAS J, et al. Development of seismic fragility surfaces for reinforced concrete buildings by means of nonlinear time-history analysis[J]. Earthquake Engineering & Structural Dynamics, 2010, 39(1): 91-108. |
| [15] |
NIELSON B G. Analytical fragility curves for highway bridges in moderate seismic zones[D]. Atlanta: GA Georgia Institute of Technology, 2005.
|
| [16] |
袁万城, 袁新哲, 庞于涛, 等. 非线性参数拟合的桥梁概率地震需求模型研究[J]. 哈尔滨工程大学学报, 2015, 36(9): 1212-1216. YUAN Wancheng, YUAN Xinzhe, PANG Yutao, et al. A probabilistic seismic demand model by nonlinear parameter fitting method[J]. Journal of Harbin Engineering University, 2015, 36(9): 1212-1216. |
| [17] |
DEGROOT M H, SCHERVISH M J. Probability and statistics[M]. Englewood Cliff: Pearson Higher Isai Education, 2010.
|
| [18] |
PARZEN E. On estimation of a probability density function and mode[J]. Annuals of Mathematical Statistics, 1962, 33(3): 1065-1076. DOI:10.1214/aoms/1177704472 |
| [19] |
CACOULLOS T. Estimation of amultivariate density[J]. Annuals of Mathematical Statistics, 1966, 18(2): 179-189. |
| [20] |
DUONG T. Bandwidth selectors for multivariate kernel density estimation[J]. Bulletin of the Australian Mathematical Societ, 2005, 71(2): 351-352. DOI:10.1017/S0004972700038314 |
| [21] |
WAND M, JONES M. C. Kernels moothing[M]. London: Chapman & Hall, 1995: 1-212.
|
| [22] |
WAND M P, JONES M C. Comparison of smoothing parameterizations in bivariate kernel density estimation[J]. Journal of the American Statistical Association, 1993, 88(422): 520-528. DOI:10.1080/01621459.1993.10476303 |
| [23] |
DUONG T, HAZELTON M L. Cross-validation bandwidth matrices for multivariate kernel density estimation[J]. Scandinavian Journal of Statistics, 2005, 32(3): 485-506. DOI:10.1111/sjos.2005.32.issue-3 |
| [24] |
SWIDZINSKI J F, CHANG K. Nonlinearstatistical modeling and yield estimation technique for use in Monte Carlo simulations[J]. Microwave Theory & Techniques IEEE Transactions on, 2000, 48(12): 2316-2324. |
| [25] |
铁路工程抗震设计规范: GB20111—2006[S]. 北京: 中国计划出版社, 2006. Code for seismic design of railway engineering: GB20111—2006[S]. Beijing: China Planning Press, 2006. |
| [26] |
KENT D C, PARK R. Flexural members with confined concrete[J]. Journal of The Structural Division, 1971, 97(7): 1969-1990. |
| [27] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010. Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2010. |
| [28] |
MANDER J B, PRIESTLEY M J, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804-1826. DOI:10.1061/(ASCE)0733-9445(1988)114:8(1804) |
| [29] |
MENEGOTTO M, PINTO P. Methodof analysis for cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending[J]. IABSE Proceedings Lisbon, 1973, 15-22. |
| [30] |
California Department of Transportation. Caltrans seismic design criteria Version1. 6[S]. Sacramenton: California Department of Transportation, 2010.
|
| [31] |
铁路桥涵地基和基础设计规范: TB 10002. 5—2005[S]. 北京: 中国铁道出版社, 2005. Code for design on subsoil and foundation of railway bridge and culvert: TB 10002. 5—2005[S]. Beijing: China Railway Press, 2005. |
| [32] |
吴文朋. 考虑不确定性的钢筋混凝土桥梁地震易损性研究[D]. 长沙: 湖南大学, 2016. WU Wenpeng. Seismic fragility of reinforced concrete bridges with consideration of various sources of uncertainty[D]. Changsha: Hunan University, 2016. |
| [33] |
TAVARES D H, PADGETT J E, PAULTRE P. Fragility curves of typical as-built highway bridges in eastern Canada[J]. Engineering Structures, 2012, 40(7): 107-118. |
| [34] |
MEHDIZADEH M. Uncertaintytreatment in performance based seismic assessment of typical bridge classes in United States[D]. Florida: University of Central Florida, 2014.
|
| [35] |
SWIDZINSKI J F, CHANG K. Nonlinear statistical modeling and yield estimation technique for use in Monte Carlo Simulations[J]. IEEE Transactions on Microwave Theory and Techniques, 2000, 48(12): 2316-2324. DOI:10.1109/22.898980 |
| [36] |
李乔, 赵世春. 汶川大地震工程震害分析[M]. 成都: 西南交通大学出版社, 2008.
|
 2018, Vol. 50
2018, Vol. 50


