近年来碳纤维增强复合材料(carbon fiber reinforced polymer,CFRP)被广泛的应用于混凝土结构加固中,外贴CFRP通过环氧树脂与混凝土表面粘结,其能否有效提高加固后结构的承载力,取决于CFRP与混凝土界面能否有效传递应力.大量的实践发现,加固后构件的破坏往往都是源于CFRP-混凝土界面层的破坏.
目前,国内外学者针对CFRP-混凝土界面粘结性能及剥离机理进行了大量研究.文献[1-2]等指出线性上升然后线性下降的粘结-滑移曲线可能与实际情况最为接近;文献[3]通过一系列双面剪切试验,指出界面的粘结滑移关系可用三角形模型表示;文献[4-5]等基于30个面内剪切试验,通过FRP应变分布给出了界面的粘结-滑移本构关系;文献[6]基于29个面内剪切试验给出了双曲线形式的界面粘结-滑移本构关系,文献[7]基于精细单元有限元模型分析,提出了简化的双线性粘结滑移本构关系.
从材料组成来看,CFRP-混凝土界面由粘结胶和被胶液渗透的混凝土表层组成,混凝土材料在荷载持续作用下会发生徐变,而粘结胶材料在已有的大量试验中均表现出了与应力和时间相关的黏弹性特征[8],因此,CFRP-混凝土界面在持续荷载作用下的力学性能必然会发生改变,但目前的相关文献中鲜少见到有关持续荷载对CFRP-混凝土界面性能影响的研究,文献[9]基于预应力CFRP加固梁试验建立了界面的黏弹性本构关系,分析了胶层蠕变对外贴预应力CFRP应力分布的影响;文献[10]研究了胶层蠕变对CFRP加固梁应变分布的影响;文献[11]通过18组双面剪切试验分析了持续荷载对外贴CFRP应变分布的影响;文献[12]通过对两个双剪试件长达1 000 d的测试,基于有效模量的概念推导了界面应力随时间的变化规律.值得注意的是在文献[9, 11]的试验中均出现了试件在持续荷载作用下发生破坏的现象,但他们对于持续荷载下界面的破坏机理均未进行深入研究,已有的界面长期性能研究也大都针对外贴CFRP应变以及界面应力随时间的变化,因此本文进行了4个荷载水平下,包含不同加载时间的27组双剪试验,以分析荷载水平及持载时间对界面粘结性能的影响.
1 试验 1.1 试验材料本试验外贴CFRP采用东丽UT70-30型碳纤维布,粘结胶采用Araldite XH180环氧树脂,混凝土强度等级为C30,养护28 d后进行粘贴CFRP等工作.CFRP抗拉强度、弹性模量、伸长率、厚度分别为3 920 MPa、2.37×105 MPa、1.71%、0.167 mm.粘结胶抗拉强度、弹性模量、伸长率分别为47 MPa、2 859 MPa、1.90%.混凝土抗压、抗拉强度、弹性模量分别为40.8 MPa、3.9 MPa、2.77×104 MPa,加载龄期为40 d.
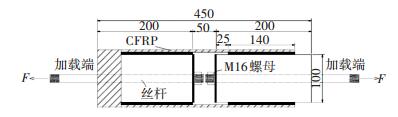
1.2 试件设计和试验方案本文采用的试验形式为面内双剪试验,试件由两个100 mm×100 mm×200 mm的混凝土棱柱体构成,在棱柱体相对的两个侧面粘贴一层宽度为50 mm的碳纤维布,如图 1所示,左半部分为锚固区,为防止其破坏,采用满贴的同时在端部用50 mm宽碳纤维布进行缠绕粘贴,右半部分测量区粘结长度为140 mm,加载端预留25 mm非粘结段以避免端部混凝土撕裂对界面剥离行为的影响.
|
图 1 试件设计(mm) Figure 1 Design of specimens (mm) |
试验共计27组双剪试件,其中3组用于静力破坏以确定界面的极限剥离荷载Pu,其余24组试件按照0.3Pu、0.5Pu、0.7Pu、0.9Pu进行持续荷载试验,试件具体分组见表 1,各试件在达到规定的加载时间后卸载,随后进行破坏试验以确定极限剥离荷载.应变片按图 2所示沿粘贴长度进行布置.
| 表 1 双剪试件分组 Table 1 Arrangement of specimens |

|
图 2 应变片布置图(mm) Figure 2 Layout of strain gage (mm) |
用于确定极限荷载的3组试件破坏模式一致,如图 3所示,均为发生在混凝土层的界面剥离破坏,剥离后的CFRP上粘有一层2~5 mm厚的混凝土,说明CFRP与混凝土粘结质量较好, 3组试件的极限剥离荷载Pu分别为25.4、26.2、24.1 kN.

|
图 3 界面剥离破坏 Figure 3 Delaminating damage of interface |
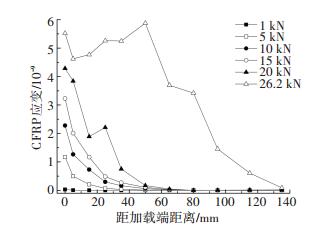
图 4给出了不同荷载作用下应变沿CFRP的分布情况.由图 4可知,在加载初期,靠近加载端附近的CFRP应变有明显增长,随着距离增加,CFRP应变迅速减小,当荷载在一定范围内(对本试验为20 kN左右),随着荷载的增加,有效粘结长度范围内应变不断增大,在此区域以外,应变几乎保持不变,直至接近极限荷载时,伴随着界面剥离向自由端发展,此部分CFRP才开始承受荷载.
|
图 4 各级荷载下CFRP应变分布 Figure 4 Strain distribution of CFRP under different load |
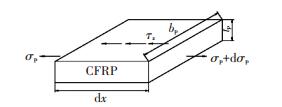
对外贴CFRP取一微段,受力情况如图 5所示.
|
图 5 外贴CFRP力学机理 Figure 5 Mechanical mechanism of CFRP |
图中σp为外贴CFRP中轴向拉应力,dx为微段长度,bp和tp为CFRP宽度和厚度,τx为界面剪应力,根据平衡条件可得
| $ {\sigma _{\rm{p}}}{b_{\rm{p}}}{t_{\rm{p}}} + {\tau _x}{b_{\rm{p}}}{d_x} = \left( {{\sigma _{\rm{p}}} + {\rm{d}}{\sigma _{\rm{p}}}} \right){b_{\rm{p}}}{t_{\rm{p}}}, $ | (1) |
| $ {\sigma _{\rm{p}}} = {E_{\rm{p}}}{\varepsilon _{\rm{p}}}, $ | (2) |
| $ {\tau _x} = {E_{\rm{p}}}{t_{\rm{p}}}\frac{{{\rm{d}}{\varepsilon _{\rm{p}}}}}{{{\rm{d}}x}}. $ | (3) |
式中εp为CFRP应变,当应变片布置足够密集时,可近似认为该点的剪应力与相邻两个应变片之间的平均剪应力相等,所以式(3)可改写为差分形式, 即
| $ {\tau _x} = {E_{\rm{p}}}{t_{\rm{p}}}\frac{{{\varepsilon _i} - {\varepsilon _{i - 1}}}}{{\Delta {x_i}}}. $ | (4) |
式中:Ep为CFRP弹性模量,Δxi为应变片之间距离,εi为第i个应变片的应变值.第i个应变片位置处的滑移量si可以通过对CFRP应变从自由端开始按下式的积分得出
| $ s = \int {{\varepsilon _{\rm{p}}}{\rm{d}}x} . $ | (5) |
改写成差分形式为
| $ {s_i} = \frac{{\left( {{\varepsilon _0}\Delta {x_0} + {\varepsilon _i}\Delta {x_i}} \right)}}{2} + \sum\limits_{j = 1}^{i - 1} {{\varepsilon _j}\Delta {x_j}} . $ | (6) |
式中:ε0为CFRP自由端应变值,按照式(4)和式(6)对试验结果进行处理,得到的界面粘结滑移结果如图 6所示.由于CFRP-混凝土界面剥离属于脆性破坏,一般来说只有靠近加载端的高应力区域能够得到完整的粘结滑移曲线,且由于混凝土材料的非均匀性,所得到的峰值粘结剪应力τmax以及界面的滑移量s会有一定差异,为了能够较好的对比各组试件结果,图 6中数据均经过标准化处理.

|
图 6 粘结滑移曲线 Figure 6 Bond-slip curve of specimens |
从图 6可以看出,CFRP-混凝土界面的粘结-滑移关系曲线可以分为如下4个阶段:1)上升段,在此阶段界面整体呈线弹性,界面刚度较大,剪应力随滑移迅速增加;2)软化段,当界面剪应力达到τcr时,界面开裂并出现局部滑移,界面刚度下降,对应上节中裂缝发展阶段的起点;3)下降段,剪应力达到峰值τmax后,界面开始剥离并随着滑移的继续增加,剥离逐渐向自由端延伸,已剥离的区域剪应力随着滑移的增加而减小;4)当滑移增大到极限滑移量su时,界面完全剥离,此时的界面上的荷载全部由混凝土骨料之间的摩擦和机械咬合作用承担. 图 6试验结果中的上升段数据都很接近,但在下降段和破坏阶段呈现出一定差异,这是由于界面材料的不均匀性造成的.
根据上节试验结果,界面的剥离破坏一般发生在紧邻胶层的混凝土层中,通过增强系数α考虑粘结胶对混凝土抗拉强度的增强作用,根据试验结果,峰值粘结应力τmax可以写为
| $ {\tau _{\max }} = \alpha {\beta _{\rm{w}}}{f_{\rm{t}}} = 2.595{\beta _{\rm{w}}}{f_{\rm{t}}}. $ | (7) |
式中:ft为混凝土抗拉强度,βw为外贴CFRP和混凝土构件宽度比影响系数,βw表达式采用文献[13]研究成果,
Popovics模型[14]是根据试验提出用来描述混凝土应力应变关系的模型,该模型的曲线形状与界面的粘结滑移曲线具有相似的特征,因此采用此模型对本文试验结果进行拟合,结果见式(8)及图 6所示,R2=0.919.
| $ \frac{\tau }{{{\tau _{\max }}}} = \frac{s}{{{s_0}}}\frac{{3.2959}}{{2.2959 + {{\left( {\frac{s}{{{s_0}}}} \right)}^{3.2959}}}}. $ | (8) |
文献[6-7, 15]等基于双曲线形式给出过界面的粘结滑移本构模型,通过对本试验曲线的上升段和下降段分别进行回归,得到的双曲线模型为
| $ \left\{ \begin{array}{l} \frac{\tau }{{{\tau _{\max }}}} = {\left( {\frac{s}{{{s_0}}}} \right)^{0.77135}},\;\;\;\;\;s \le {s_0};\\ \frac{\tau }{{{\tau _{\max }}}} = {{\rm{e}}^{ - 0.56288\left( {\frac{s}{{{s_0}}} - 1} \right)}},\;\;\;\;s > {s_0}. \end{array} \right. $ | (9) |
R2=0.897,同样将拟合结果绘制于图 6中,对比两种模型,可以发现上升段相差不大,下降段双曲线模型预测的界面刚度略大于Popovics模型,曲线的下降趋势更为平缓,但是在s=s0时,双曲线模型在此位置形成一个尖角,无法模拟出塑性软化段,与试验结果存在一定误差,综合来看,Popovics模型对界面的粘结滑移关系模拟结果更优.
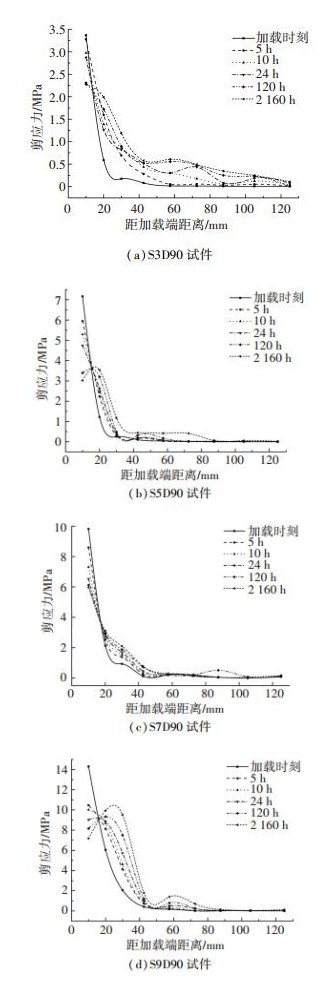
3 持续荷载对界面粘结性能的影响 3.1 界面剪应力根据第2节中获得的极限剥离荷载,取均值为25.2 kN,按照表 1中对应的荷载水平和持载时间对各试件进行加载,界面的剪应力变化如图 7所示.
|
图 7 界面剪应力变化 Figure 7 Changes of interfacial shear stress |
由图 7可知,随着荷载持续时间的增加,靠近加载端的第一个测点处界面剪应力逐渐减小,其余测点处剪应力逐渐增大,增大幅度沿粘贴长度逐渐减小,剪应力的改变在前期发展较快,随后变化速率逐渐降低.对于本试验0.3Pu、0.5Pu、0.7Pu和0.9Pu情况下,第一个测点处在加载2 160 h后剪应力分别降低了1.10、3.14、3.85、7.12 MPa,说明界面的蠕变可以有效地降低剪应力峰值,减缓界面的应力集中现象,使剪应力沿粘结长度分布更加均匀.
3.2 界面粘结-滑移本构关系表 1中各试件分别在达到规定加载时间后进行静力破坏试验,所得各试件在持载90 d后的界面粘结-滑移曲线如图 8所示,图中10 mm-A/B表示测试点位于A/B面(A、B面分别为双剪试件粘贴CFRP的两个测试面)距加载端距离为10 mm的测点结果.

|
图 8 界面粘结滑移关系变化 Figure 8 Changes of interfacial bond-slip curve |
由图 8可知,对于S3D90,各测点的粘结滑移曲线形状较为接近;对于S5D90,靠近加载端测点的粘结-滑移曲线与其他测点相比峰值应力τmax有所降低,界面的初始刚度也有所下降,这一现象在S7D90和S9D90中更为明显,且粘结滑移曲线下降段发展更为迅速,界面破坏的延性与其他测点相比有所下降,粘结滑移曲线更接近于双线性结构,除加载端第一个测点外,其他测点之间的粘结滑移曲线并无明显差异.表 2给出了各组试件距加载端10 mm处测点的τmax及s0试验结果,从表中数据可以看出,当荷载水平较低时(0.3Pu),随着荷载持续时间的增加,峰值剪应力τmax没有明显改变,而当荷载水平较高时(≥0.5Pu),随着荷载持续时间的增加,τmax逐渐减小,且荷载水平越高,对应的τmax越小,对s0来说,随着荷载水平和持载时间的增长,s0没有明显变化,但与未经持续荷载作用的试件相比,s0有所减小.这些试验结果说明:在外荷载超过一定荷载水平后,荷载的持续作用会对CFRP-混凝土界面造成一定损伤,使得界面的峰值应力τmax及其所对应的界面滑移s0有所减小,τmax和s0的减小程度与外荷载大小和持续时间相关,损伤界面的粘结滑移关系曲线与未损伤的相比下降段更短,界面延性降低,曲线形状更接近于双线性,但界面的损伤局限于局部范围内,产生这一现象的原因主要是界面剪应力沿粘结长度减小较快,而较小的剪应力并不会引起峰值应力τmax的降低.从本试验结果来看损伤范围大致处于从加载端开始的15 mm之内.
| 表 2 峰值剪应力及对应滑移 Table 2 Peak shear stress and corresponding slip |
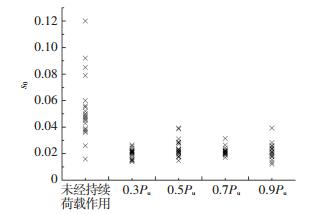
与未经持续荷载作用的试件相比,经持续荷载作用后,所有测点的界面滑移量s0均有所降低,两种情况下s0的对比如图 9所示.
|
图 9 峰值剪应力对应滑移对比 Figure 9 Comparison between slip corresponding and peak shear stress |
由图 9可知,s0的减小量与荷载大小和持续时间无明显相关,s0可以表示为峰值应力与界面刚度之比
| $ {s_0} = {\tau _{\max }}/\beta {K_i}. $ | (10) |
式中β为与界面刚度相关的系数,可根据试验结果回归求出,Ki为界面刚度,由于界面是由混凝土和胶层共同组成,因此Ki应为胶层剪切刚度和混凝土层剪切刚度串联而成,可以表示为Ki=KaKc/(Ka+Kc),其中Ka为胶层剪切刚度,Kc为混凝土层剪切刚度,分别写为Ka=Ga/ta,Kc=Gc/tc,ta、tc分别为胶层厚度和混凝土层参与剪切变形的厚度,ta根据试验测量结果取为0.53 mm,根据试件破坏结果,界面剥离后CFRP上粘贴的混凝土层厚度约为2~5 mm,并参考文献[16]的有限元分析结果,tc取值为5 mm,根据试验结果拟合可得
| $ {s_0} = \left\{ \begin{array}{l} {\tau _{\max }}/0.1431{K_i},\;\;\;\;短期荷载作用;\\ {\tau _{\max }}/0.3277{K_i},\;\;\;\;持续荷载作用. \end{array} \right. $ | (11) |
对于0.5Pu及其以上荷载情况,可将损伤部位的应力峰值写为与荷载水平和持载时间相关的函数,首先根据试验结果以持载时间作为变量对界面峰值应力进行回归分析,如图 10所示.

|
图 10 剪应力峰值与时间回归分析 Figure 10 Regression analysis between peak shear stress and time |
由图 10可知,应力峰值与时间的关系在不同荷载水平下均可以写为相同的函数形式,因此将回归方程中的两个系数分别作为荷载水平的函数并进行回归分析,结果如图 11所示.

|
图 11 应力峰值与荷载水平回归分析 Figure 11 Regression analysis between peak shear stress and load level |
由图 11可知,持续荷载下靠近加载端的局部界面应力峰值可写为
| $ \left\{ \begin{array}{l} {{\tau '}_{\max }}\left( {\bar p,t} \right) = {A_1}\left( {\bar p} \right){t^{{A_2}\left( {\bar p} \right)}}{\tau _{\max }},\\ {A_1}\left( {\bar p} \right) = 1.353\;28 - 0.550\;25\bar p + 0.346\;88{{\bar p}^2},\\ {A_2}\left( {\bar p} \right) = 0.206\;05 - 0.661\;55\bar p + 0.366\;87{{\bar p}^2}. \end{array} \right. $ | (12) |
式中p=P/Pu,P为施加在试件上的恒定荷载,Pu为界面的极限剥离荷载,τmax按照式(7)进行计算.综上所述,CFRP-混凝土界面的粘结滑移本构关系可以概括如下.
1) 对于短期荷载作用情况下,采用基于Popovics的模型对界面粘结滑移关系为
| $ \left\{ \begin{array}{l} \frac{\tau }{{{\tau _{\max }}}} = \frac{s}{{{s_0}}}\frac{{3.2959}}{{2.2959 + {{\left( {\frac{s}{{{s_0}}}} \right)}^{3.2959}}}},\\ {\tau _{\max }} = 2.5959{\beta _{\rm{w}}}{f_{\rm{t}}},\\ {s_0} = {\tau _{\max }}/0.1431{K_i},\\ {K_i} = {K_{\rm{a}}}{K_{\rm{c}}}/\left( {{K_{\rm{a}}} + {K_{\rm{c}}}} \right). \end{array} \right. $ | (13) |
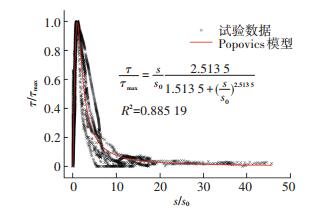
2) 在持续荷载作用下,考虑材料蠕变影响后,界面的粘结滑移本构关系,当p < 0.5时,界面的粘结滑移关系仍可采用基于Popovics模型的表达形式,参数n根据试验结果拟合为2.513 5,拟合结果见图 12所示.
|
图 12 本构模型与试验数据对比 Figure 12 Comparison between constitutive model and test data |
| $ \left\{ \begin{array}{l} \frac{\tau }{{{\tau _{\max }}}} = \frac{s}{{{s_0}}}\frac{{2.5135}}{{1.5135 + {{\left( {\frac{s}{{{s_0}}}} \right)}^{2.5135}}}},\\ {s_0} = {\tau _{\max }}/0.3277{K_i}. \end{array} \right. $ | (14) |
式中τmax及Ki按照式(13)计算.
当p≥0.5时,距离加载端一定距离以外的位置处,界面的粘结滑移模型仍采用式(14)进行模拟,但对于距离加载端15 mm以内时,界面的粘结滑移模型以双线性形式给出,即
| $ \left\{ \begin{array}{l} \frac{\tau }{{{{\tau '}_{\max }}}} = \frac{s}{{{s_0}}},\;\;\;\;\;\;s \le {s_0};\\ \frac{\tau }{{{{\tau '}_{\max }}}} = \frac{{{s_{\rm{u}}} - s}}{{{s_{\rm{u}}} - {s_0}}},\;\;\;\;{s_0} < s \le {s_{\rm{u}}};\\ \tau = 0,\;\;\;\;\;{s_{\rm{u}}} < s. \end{array} \right. $ | (15) |
式中:τ′max按照式(12)进行计算,s0按式(14)计算,su为根据试验结果拟合为su=0.174-2.117s0.
3.3 界面剥离荷载各试件经持续荷载作用后,界面的极限剥离荷载Pu及破坏过程中首次出现界面剥离时的荷载Pdb见表 3所示.
| 表 3 CFRP-混凝土界面剥离承载力 Table 3 Debonding strength of CFRP-concrete interface |
根据试验结果,持续荷载作用并未对界面的极限剥离荷载产生明显影响,产生这一现象的原因主要为外荷载小于0.5Pu时,界面的峰值剪应力并未随时间改变,对于更高的荷载水平,持续荷载作用仅造成靠近加载端局部界面的τmax及s0降低,但对于整个界面来说,粘贴长度大于有效粘结长度,因此局部界面由于荷载持续作用产生的损伤并不会对界面最终的剥离承载力造成影响.但表中数据显示持续荷载作用会使界面首次出现剥离的荷载Pdb有所降低,且Pdb的降低与界面剪应力峰值的降低规律相同,对于0.3Pu荷载持续作用下,Pdb未发生明显改变,而对于0.5Pu、0.7Pu、0.9Pu持续作用90 d后,Pdb分别降低了42%、54%、66%.
4 结论1) 持续荷载作用下,界面的剪应力峰值随时间逐渐减小,且减小幅度随外荷载水平的增加而增大.
2) 经持续荷载作用后,靠近加载端15 mm范围内的τmax有所降低,降低程度与荷载水平和荷载持续时间相关,在此范围外,与未经持续荷载作用的试件相比,τmax并无明显变化.与τmax对应的界面滑移s0在荷载持续作用后降低了约50%,且s0的降低与荷载水平和荷载持续时间无明显相关.
3) 在保证粘结长度大于有效粘结长度的情况下,持续荷载造成的局部界面损伤并不会引起界面极限剥离荷载的降低,仅会对界面首次出现剥离的荷载Pdb产生影响,对于0.5Pu、0.7Pu、0.9Pu持续作用2 160 h后,Pdb分别降低了42%、54%、66%.
| [1] |
YUAN H. WU Zhishen. Interfacial fracture theory in structures strengthened with composite of continuous fiber[C]// Proceedings of Symposium of China and Japan. Tokyo: Science and Technology of 21st Century, 1999: 142-155.
|
| [2] |
TALJSTEN B. Strengthening of existing concrete structures with epoxy bonded plates of steel or fiber reinforced plastics[D]. Sweden: Lulea University of Technology, 2012.
|
| [3] |
NEUBAUER U, ROSTASY F S. Bond failure of concrete fiber reinforced polymer plates at inclined cracks-experiments and fracture mechanics model[J]. Special publication, 1999, 188: 369-382. |
| [4] |
NAKABA K, TOSHIYUKI K, TOMOKI F, et al. Bond behavior between fiber-reinforced polymer laminates and concrete[J]. ACI Structural Journal, 2011, 98(3): 359-367. |
| [5] |
SAVIOA M, FARRACUTI B, MAZZOTTI C. Non-linear bond-slip law for FRP-concrete interface[C]// Proc 6th International Symposium on FRP Reinforcement for Concrete Structures. Singapore: World Scientific Publications, 2003: 163-172.
|
| [6] |
DAI J G, UEDA T. Local bond stress slip relations for FRP sheets-concrete interfaces[C]// Proc 6th International Symposium on FRP Reinforcement for Concrete Structures. Singapore: World Scientific Publications, 2003: 143-152.
|
| [7] |
陆新征. FRP-混凝土界面行为研究[D]. 北京: 清华大学, 2004. LU Xinzheng. Studies on FRP-Concrete Interface[D]. Beijing: Tsinghua University, 2004. |
| [8] |
COSTA I, BARROS J. Creep of structural adhesives: an overview[C]// CICE 6th International Conference on FRP Composites in Civil Engineering. Roma: International Institute for FRP in Construction, 2012: 1-8.
|
| [9] |
WU Z S, DIAB H. Constitutive model for time-dependent behavior of FRP-concrete interface[J]. Journal of Composite for Construction(ASCE), 2007, 11(5): 477-486. DOI:10.1061/(ASCE)1090-0268(2007)11:5(477) |
| [10] |
FERRIER E, MICHEL L, JURKIEWIEZ B, et al. Creep behavior of adhesives used for external FRP strengthening of RC structures[J]. Construction and Building Materials, 2014, 25: 461-467. |
| [11] |
PANIA M, KYOUNG-KYU C, MAHMOUD M, et al. Experimental and analytical investigations of creep of epoxy adhesive at the concrete-FRP interfaces[J]. International Journal of Adhesion & Adhesives, 2009, 29: 56-66. |
| [12] |
MAZZOTTI C, SAVOIA M. Sustained properties of bond between concrete and FRP[C]// Proceedings of the International Symposium on Bond Behaviour of FRP in Structures. Roma: International Institute for FRP in Construction, 2005, 531-538.
|
| [13] |
CHEN J F, TENG J G. Shear capacity of FRP-strengthened RC beams: FRP debonding[J]. Construction and Building Materials, 2003, 17(1): 27-41. DOI:10.1016/S0950-0618(02)00091-0 |
| [14] |
POPOVICS S. A numerical approach to the complete stress-strain curve of concrete[J]. Cement and Concrete Research, 1973, 3(5): 583-599. DOI:10.1016/0008-8846(73)90096-3 |
| [15] |
MONTI M, RENZELLI M, LUCIANI P. FRP adhesion in uncracked and cracked concrete zones[C]// Proc 6th International Symposium on FRP Reinforcement for Concrete Structures. Singapore: World Scientific Publications, 2013: 183-192.
|
| [16] |
陆新征, 谭壮, 叶列平, 等. FRP布-混凝土界面粘结性能的有限元分析[J]. 工程力学, 2004, 21(6): 45-50. LU Xinzheng, TAN Zhuang, YE Lieping, et al. Finite element analysis of debonding at the interface between FRP and concrete[J]. Engineering Mechanics, 2004, 21(6): 45-50. |
 2018, Vol. 50
2018, Vol. 50



