2. 长沙理工大学 能源与动力工程学院,长沙 410076
2. School of Energy and Power Engineering, Changsha University of Science and Technology, Changsha 410076, China
牵引变压器是现代电力机车中重要的电气设备之一,如果不能及时发现并处理变压器绕组故障,会影响列车正常运行,严重时将造成设备损坏、列车停运.文献[1-6]表明,长期以来FRA(频率响应分析)在检测变压器绕组故障方面已经得到了广泛的应用.各类FRA方法固然使变压器故障诊断更加准确可靠,但也存在诸多不足之处.如当前FRA技术依然需要依赖专业的FRA发生和检测设备,被测变压器需要终止运行,离线完成检测.且由于变压器性能各异,业内缺乏统一的FRA特性分析标准.除了FRA方法外,还有文献[7-12]等提出外加信号注入装置,获得响应信号分析变压器绕组故障,此类方法主要适用于电力变压器,对于跟随机车移动的牵引变压器有一定局限性.也有研究[13-15]提出了一些绕组故障的在线诊断方法.文献[16-17]提到交流机车主变压器故障主要出现在绕组中,且由于交流电力机车特殊的工作条件(机械振动多、接触网电压变动大、容易受大气过电压和操作过电压等影响),加上变压器主体卧式安装不易拆卸,发展一种受非线性因素影响小、可靠性高,外加检测设备少的机车主变压器绕组故障在线诊断方法十分必要.因此,本文提出一种基于分布参数模型的非侵入式交流电力机车主变压器绕组故障在线诊断方法.该方法不需要外加其他频率的信号和特殊检测设备,不受交流机车工作环境和非线性因素的影响,可以快速简便地识别绕组故障类型.
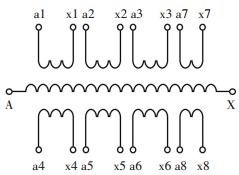
1 ΔV-i1关系理论分析本文的研究对象是机车主变压器,除主变压器外,机车牵引变压器还包括了平波电抗器,功率因数补偿电抗器,高压电流互感器等其他器件.交流电力机车主变压器多采用饼式线圈交错排列, 以满足机车线路对变压器提出的阻抗电压要求. 图 1为某型号交流机车主变压器结构图.
|
图 1 交流电力机车主变压器结构图 Figure 1 Structure diagram of main transformer of AC electric locomotive |
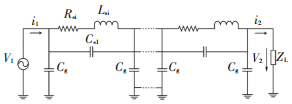
可以看出主变压器为单相多绕组的分裂式变压器,每个牵引绕组都有它对应的高压绕组部分,它们之间是非耦合的,故可以分拆任何一部分看作一个单相的双绕组变压器进行研究.交流机车主变压器的绕组线圈多采用饼式结构,每一饼线圈都可以等效为一个由RLC组成的π型电路.本文以某型电力机车为研究对象, 将机车主变压器等效为图 2所示的π型级联分布参数电路模型,相比传统的集总参数模型可以更好地模拟变压器内部状态.
|
图 2 主变压器牵引绕组等效电路原理图 Figure 2 The equivalent circuit of traction transformer |
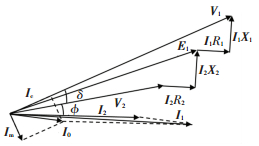
图 2中,V1为牵引电网输入电压,V2为输出电压. i1为输入电流,i2为输出电流,Csi为等效串联电容,Cg为等效对地电容. Zsi为单个π型电路的短路阻抗(其中Lsi为等效串联电感,Rsi为等效串联电阻). 图 3为电路相量图.其中R1、X1为一次侧阻抗,R2、X2为二次侧阻抗,δ为输入电压和输出电压之间的相位偏移;
|
图 3 主变压器牵引绕组等效电路相量图 Figure 3 The space vector diagram of traction transformer equivalent circuit |
令
| $ {V_1}\left( t \right) = {V_{{\rm{m1}}}}\sin \left( {\omega t + \delta } \right), $ | (1) |
| $ {V_2}\left( t \right) = {V_{{\rm{m2}}}}\sin \left( {\omega t} \right), $ | (2) |
| $ x = {i_1}\left( t \right) = {I_{{\rm{m1}}}}\sin \left( {\omega t - \varphi } \right). $ | (3) |
其中:ω为电压角频率,Vm1、Vm2分别为输入电压峰值和输出电压峰值.
理想地认为Vm1= Vm2 = Vm,故得到
| $ y = \Delta V = {V_1} - {V_2} = {V_{\rm{m}}}\left[ {\sin \left( {\omega t + \delta } \right) - \sin \left( {\omega t} \right)} \right]. $ | (4) |
其中ΔV为输入输出电压相量差.
根据三角函数和差化积公式sin a-sin b=
| $ y = \Delta V = 2{V_{\rm{m}}}\cos \frac{{2\omega t + \delta }}{2}\sin \frac{\delta }{2}. $ | (5) |
由式(3)、(5)可得
| $ \omega t = {\sin ^{ - 1}}\left( {\frac{x}{{{I_{{\rm{m1}}}}}}} \right) + \varphi . $ | (6) |
| $ \omega t = {\cos ^{ - 1}}\left( {\frac{y}{{2{V_{\rm{m}}}\sin \frac{\delta }{2}}}} \right) - \frac{\delta }{2}. $ | (7) |
联立式(6)、(7)得
| $ \varphi + \frac{\delta }{2} = {\cos ^{ - 1}}\left( {\frac{y}{{2{V_{\rm{m}}}\sin \frac{\delta }{2}}}} \right) - {\sin ^{ - 1}}\left( {\frac{x}{{{I_{{\rm{m1}}}}}}} \right). $ | (8) |
对式(8)求正弦,并且利用三角变换公式化简得到
| $ \begin{array}{*{20}{c}} {\sin \left( {\varphi + \frac{\delta }{2}} \right) = \sqrt {\frac{{{{\left( {2{V_{\rm{m}}}\sin \frac{\delta }{2}} \right)}^2} - {y^2}}}{{2{V_{\rm{m}}}\sin \frac{\delta }{2}}}} \cdot \sqrt {\frac{{I_{{\rm{m1}}}^2 - {x^2}}}{{{I_{{\rm{m1}}}}}}} - }\\ {\frac{{yx}}{{2{I_{{\rm{m1}}}}{V_{\rm{m}}}\sin \frac{\delta }{2}}}.} \end{array} $ | (9) |
对式(9)进行化简, 得
| $ \begin{array}{l} {\left( {2{V_{\rm{m}}}\sin \frac{\delta }{2}} \right)^2}{x^2} + I_{{\rm{m1}}}^2{y^2} + {\left( {2{V_{\rm{m}}}\sin \frac{\delta }{2}} \right)^2}{\sin ^2}\left( {\varphi + \frac{\delta }{2}} \right) + \\ \;\;\;4{I_{m1}}{V_{\rm{m}}}\sin \frac{\delta }{2}\sin \left( {\varphi + \frac{\delta }{2}} \right)xy + \\ \;\;\left\{ {2{V_{\rm{m}}}{I_{m1}}\sin \frac{\delta }{2} \cdot \sin \left( {\varphi + \frac{\delta }{2}} \right)} \right\} - \\ \;\;{\left( {2{V_{\rm{m}}}\sin \frac{\delta }{2}} \right)^2} = 0. \end{array} $ | (10) |
椭圆的一般方程式为
| $ A{x^2} + Bxy + C{y^2} + Dx + Ey + F = 0. $ | (11) |
将式(10)代入式(11)中, 可得
| $ A = {\left( {2{V_{\rm{m}}}\sin \frac{\delta }{2}} \right)^2}, $ | (12) |
| $ B = 4{I_{m1}}{V_{\rm{m}}}\sin \frac{\delta }{2}\sin \left( {\varphi + \frac{\delta }{2}} \right), $ | (13) |
| $ D = E = 0, $ | (14) |
| $ C = I_{{\rm{m1}}}^2. $ | (15) |
将式(12)~(15)代入到椭圆的数学判据B2-4AC < 0,可得
| $ - 16I_{{\rm{m1}}}^2V_{\rm{m}}^2{\sin ^2}\frac{\delta }{2} \cdot {\cos ^2}\left( {\varphi + \frac{\delta }{2}} \right) < 0. $ | (16) |
因此,ΔV-i1是一个中心点位于直角坐标系原点的斜椭圆轨迹.变压器绕组故障如匝间短路、盘间短路、径向位移、轴向位移等均会影响变压器参数的变化,表现在ΔV-i1轨迹上就是倾角θ和椭圆离心率e、椭圆相对面积S以及椭圆的长短轴a, b等参数的变化.本文提出的在线故障诊断方法就是利用这些椭圆参数的变化来完成的.
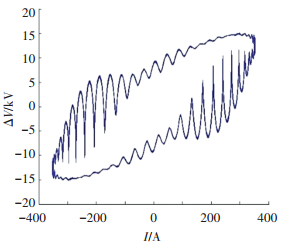
2 交流机车主要非线性条件影响分析 2.1 牵引供电网高次谐波的影响以及消除策略当前电气化铁路的牵引供电网是由接触网、馈电线、钢轨,回流线等组成的牵引供电系统.机车与牵引网耦合时会在供电系统中产生谐波,引起谐振,产生过电压,进而引起椭圆畸变,影响诊断方法的灵敏度.由于交流电力机车运行时,牵引变压器的主要负载为感性负载(牵引变流器、电机),故本文以感性负载情况为主进行谐波分析.在模型中注入文献[18]得出的牵引网馈出母线电压在谐波谐振时刻的谐波源,实验结果如图 4所示,高次谐波的存在导致了ΔV-i1轨迹的严重畸变,降低了绕组故障在线诊断方法准确性和可靠性.
|
图 4 高次谐波对感性负载的影响 Figure 4 The effect of high order harmonic on inductive load |
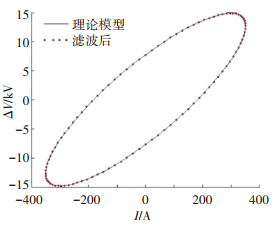
为了使高次谐波对方法的影响达到最小,本文利用双线性变换法对采样信号ΔV和i1同时进行滤波处理.文献[19]指出双线性变换法优点在于能够克服多值映射的关系,消除频率的混叠.在进行滤波之前,首先需要进行预畸,以减小滤波所产生的畸变对本方法造成的影响.此后,分别对采样信号ΔV和i1进行滤波.由于ΔV和i1的滤波器设计完全相同,采样信号ΔV和i1经过滤波后产生的相位差也相同,因此,由于滤波造成的相移不会对椭圆轨迹产生影响.从图 5可以看出,经过滤波处理,牵引电网高次谐波引起椭圆轨迹畸变已经消除,在线故障诊断方法的可靠性得到了提高.
|
图 5 数字滤波效果 Figure 5 The effect of digital filter |
假设阻抗幅值保持不变则保证了电流幅值不变,文献[20]指出在交流传动系统中,主变压器的牵引绕组以四象限变流器作为负载,属于感性负载,负载功率因数通常滞后电流的相位滞后于电压,此时0° <

|
图 6 同一负载类型下功率因数影响 Figure 6 Influence of power factor under the same load type |
国标规定的铁路电网电压为27.5 kV,当供电网电压过高时,铁芯磁密将大大增加,导致励磁电流加大,从而烧坏变压器.文献[21]指出,相比于电力变压器,交流机车牵引变压器的铁芯磁密很小,一般不超过1.6 T.较小的磁密使铁芯有很大的线性工作区间,大大减少了铁芯饱和现象出现.而在交流电力机车启动时,即使由于牵引变压器外加电压出现突变,引起的铁芯饱和也只是一个暂态过程,仅会造成个别周期的椭圆轨迹的畸变,故分布参数变压器模型完全可以忽略铁芯影响进行故障诊断.文献[22-24]也表明,变压器分布参数模型可以忽略铁芯饱和的影响.
3 诊断方法与诊断结果 3.1 诊断方法交流电力机车主变压器绕组形变故障类型主要有盘间短路、轴向位移、匝间短路、机械应力形变、泄露故障、径向位移以及局部放电等等.研究文献[25-26]表明变压器绕组的故障变化可以表现为分布参数模型的单个或多个参数的值的变化.例如,当发生匝间短路时,变压器的等效电感会发生不同程度的减小;当变压器发生盘间短路时,不同程度的短路对应不同数量的RLC电路短接;而变压器绕组的径向位移则可以导致串联电容值得大幅度上升等.
在机车运行时,牵引供电网提供的工频交流电经过受电弓传到交流电力机车上.在主变压器被测绕组对应端子上测量输入电压V1,以及输入电流i1, 在输出端测量输出电压V2,采集运行过程中的一个完整周期的数据,进行滤波处理,得到的数据构成直角标系下的椭圆轨迹,通过分析轨迹特征参数,可以确定故障类型和故障程度.
3.2 诊断实验本文实验主要包含以下内容:1)在额定工作条件下,验证变压器正常状态下的ΔV-i1轨迹为直角坐标系下的椭圆. 2)设置牵引变压器典型绕组故障,得到各故障状态下的ΔV-i1轨迹并完成诊断分析.
由于本实验室不具备等同牵引供电网27.5 kV的单相交流电,考虑实验成本和可操作性,采用dSPACE实验平台搭建机车主电路模型进行验证. 图 7为电力牵引系统故障诊断实验室环境一览. dSPACE主要由DS1007主处理器板,DS2002高精度A/D采样板和DS4004高速I/O板组成,具有强大的运算处理能力,可以满足包括变压器分布参数模型及其负载(变流器、电机)组成的复杂模型的运算要求,提供了一个综合实验和测试环境.

|
1—dSPACE运算处理单元; 2—传感器箱; 3—高精度A/D采样器; 4—高速I/O板; 5—AC/DC/AC变换器; 6—控制器; 7—负载; 8—计算机处理终端 图 7 电力牵引系统故障诊断实验室环境图 Figure 7 Fault diagnosis of electric traction system laboratory environment |
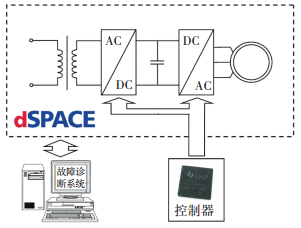
通过MATLAB/Simulink搭建变压器和负载模型,由dSPACE提供的专用实时接口库建立适用于dSPACE系统的在线仿真模型,模型中变压器负载各参数均按实际参数给定,利用硬件电路通过高速I/O板实现对dSPACE模型中负载的控制.采用dSPACE提供的Control Desk软件可以在计算机终端完成实时的信号监测与采集、参数修改以及结果显示等. 图 8为机车主变压器故障诊断示意图.
|
图 8 机车主变压器故障诊断示意图 Figure 8 Diagram for on-line fault diagnosis of winding |
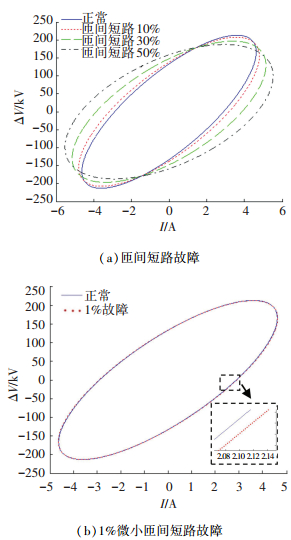
文献[26]指出当主变压器绕组发生匝间短路故障时,剩下的绕组仍然具有变压器功能,只是相当于在原来的绕组中减少了部分匝数. 图 9(a)显示了当机车主变压器发生10%、30%、50%的匝间短路故障.随着短路百分比的增大,椭圆越来越鼓,面积也越来越大. 图 9(b)为1%的微小线圈短路轨迹与健康轨迹的对比图,可以看出本方法适用于细微的匝间短路故障.
|
图 9 不同程度的匝间短路故障 Figure 9 Inter-turn short circuit fault |
除了定性的轨迹分析,还可以通过计算得到不同程度的故障参数. 表 1为计算得到的不同程度匝间短路故障时的ΔV-i1椭圆相关参数的变化情况.可以看出,随着匝间短路程度的加深,椭圆长轴与直角坐标系水平轴形成的夹角θ基本不变.从匝间短路10%~50%,椭圆长轴明显变短,短轴变长,且椭圆轨迹的离心率变小,椭圆形状随着故障程度加深越来越鼓.而椭圆的面积随着故障程度的加深而变大.
| 表 1 不同程度匝间短路故障椭圆参数变化 Table 1 The variation of ellipse parameters in different degree of inter-turn short circuit fault |
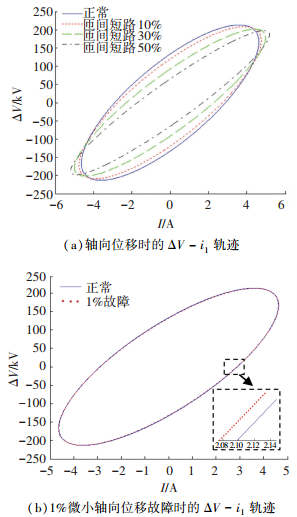
文献[27]提到轴向位移主要是由高低压绕组之间因短路电流引起的磁不平衡产生的.由于位移造成的变压器内部电磁场的变化,也会导致高低压绕组等效阻抗的变化. 图 10(a)为主变压器绕组发生10%、30%、50%的轴向位移时的ΔV-i1轨迹,从图中可以看出,当绕组发生轴向位移时呈“梭形”,其离心率不断增大,说明椭圆越来越扁.此外,椭圆长轴和短轴不断减小,椭圆面积S明显减小.椭圆轨迹与之前的局部放电故障时的ΔV-i1轨迹有明显的区别.即使是微小的形变故障,也与正常的椭圆轨迹有所不同,如图 10(b)所示.
|
图 10 不同程度轴向位移故障 Figure 10 The axial displacement fault in different degree |
表 2所示为计算得到的轴向位移故障椭圆参数变化情况.轴向位移从10%变化到50%,可以看出椭圆倾角θ发生了明显的顺时针偏转,变化幅度比同程度局部放电时要大.椭圆长轴a则随着故障程度加深而稍有变短,短轴b明显变短,长、短轴参数均小于正常变压器的椭圆短轴参数.椭圆面积S随着故障程度的加深越来越小.即使发生1%的轴向位移,也可以被清楚地识别.因为在所有变化参数中,椭圆面积变化最为显著,故可将椭圆面积作为轴向位移故障的主要参考变量,用于估计故障程度.
| 表 2 不同程度轴向位移故障椭圆参数变化 Table 2 The variation of the ellipse parameters in different degree of axial displacement |
盘间短路可看作更为严重的匝间短路,因此相比于匝间短路,应该引起ΔV-i1轨迹更明显的变化.如图 11所示,随着短路盘数的增加,ΔV-i1轨迹越来越扁,椭圆面积S也越来越小,并且长轴呈现顺时针方向的偏转.相关的参数数值变化见表 3.随着故障程度的加深, 椭圆轨迹倾角θ大幅度偏转, 其长轴a有轻微减小,短轴则越来越短,在盘间短路故障中,椭圆倾角θ变化最为明显,可作为主要参考变量.

|
图 11 盘间短路故障 Figure 11 Disc short-circuit fault |
| 表 3 不同程度盘间短路故障时椭圆参数变化 Table 3 The variation of the ellipse parameters in different degree of disc short-circuit |
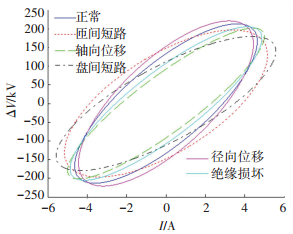
除上述故障之外,本文提出的方法也可用于径向位移、绕组强制屈曲、绕组盘对地泄漏故障等常见机车主变压器内部故障的在线诊断. 图 12为感性负载情况下,机车主变压器发生同一程度的各类故障时对应的ΔV-i1轨迹.从图中可以看出,同一程度的不同故障对变压器1轨迹造成的影响明显不同,从而可以清楚地判断出相应的故障类型.
|
图 12 不同类型绕组故障类型对比图 Figure 12 Comparison of different winding faults on elliptical track |
1) 提出了一种基于分布参数模型的非侵入式交流机车主变压器绕组故障在线诊断方法.
2) 非侵入式机车主变压器绕组故障在线诊断方法既可以定性地从图形上分析变压器的工作状态以及是否存在绕组形变故障以外,也可以利用椭圆轨迹的倾角、离心率、长短轴以及椭圆相对面积等参数估计故障程度.该方法消除了牵引供电网高次谐波对方法造成的影响,同时也不受铁芯状况和负载功率因数的影响.
3) 通过dSPACE实验平台对这一在线绕组故障诊断方法进行了验证.结果表明所提出的在线诊断方法对机车主变压绕组匝间短路故障、轴向位移故障以及盘间短路、径向位移、绝缘损耗等多种绕组故障有很好的诊断效果.
4) 当输入输出电压在正常情况下发生变化时,轨迹的大小会发生变化,轨迹的部分参数可能会受到影响,如轨迹的面积大小会增大(或减小),长短轴会以相同的比例增大(或减小),而其他参数如倾角仍然保持不变.这些参数的变化趋势与目前在试验中已发现的故障类型的参数变化趋势均不相同,因此不会影响诊断结果.
| [1] |
ABEYWICKRAMA N, SERDYUK Y V, GUBANSKI S M. High-frequency modeling of power transformers for use in frequency response analysis (FRA)[J]. IEEE Transactions on Power Delivery, 2008, 23(4): 2042-2049. DOI:10.1109/TPWRD.2008.917896 |
| [2] |
ZHANG Haijun, WANG Shuhong, YUAN Dongsheng, et al. Dou-bleladder circuit model of transformer winding for frequency response analysis considering frequency-dependent losses[J]. IEEE Transactions on Magnetics, 2015, 51(11): 1-4. DOI:10.1109/TMAG.2015.2442831 |
| [3] |
YOUSOF M F M, EKANAYAKE C, SAHA T K. Study of transfor-mer winding deformation by frequency response analysis[C]//IEEE Power and Energy Society General Meeting(PES). Vancouver: IEEE, 2013: 1-5. DOI: 10.1109/PESMG.2013.6672525.
|
| [4] |
PHAM D A K, PHAM T M T, BORSI H, et al. A new method for purposes of failure diagnostics and FRA interpretation applicable to power transformers[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2013, 20(6): 2026-2034. DOI:10.1109/TDEI.2013.6678850 |
| [5] |
ARISPE J C G, MOMBELLO E E. Detection of failures within transformers by FRA using multiresolution decomposition[J]. IEEE Transactions on Power Delivery, 2014, 29(3): 1127-1137. DOI:10.1109/TPWRD.2014.2306674 |
| [6] |
ALJOHANI O, ABU-SIADA A. Application of FRA polar plot technique to diagnose internal faults in power transformers[C]//2014 IEEE PES General Meeting: Conference & Exposition. Maryland: IEEE, 2014: 1-5. DOI: 10.1109/PESGM.2014.6939160.
|
| [7] |
郭俊, 汲胜昌, 沈琪, 等. 盲源分离技术在振动法检测变压器故障中的应用[J]. 电工技术学报, 2012, 27(10): 68-78. GUO Jun, JI Shengchang, SHEN Qi, et al. Blind source separation technology for the detection of transformer fault based on vibration method[J]. Transactions of China Electrotechnical Society, 2012, 27(10): 68-78. |
| [8] |
李剑, 夏珩轶, 杜林, 等. 变压器绕组轻微变形ns级脉冲响应分析法[J]. 高电压技术, 2012, 38(1): 35-42. LI Jian, XIA Hengyi, DU Lin, et al. Nanosecond impulse response analysis on transformers winding slight deformation[J]. High Voltage Engineering, 2012, 38(1): 35-42. |
| [9] |
RAJAMANI P, CHAKRAVORTI S. Identification of simultaneously occurring dynamic disc-to-disc insulation failures in transformer winding under impulse excitation[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2012, 19(2): 443-453. DOI:10.1109/TDEI.2012.6180237 |
| [10] |
姚陈果, 赵仲勇, 李成祥, 等. 基于暂态过电压特性的电力变压器绕组变形故障在线检测[J]. 高电压技术, 2015, 41(3): 873-880. YAO Chenguo, ZHAO Zhongyong, LI Chengxiang, et al. Online detecting winding deformation of power transformer based on transient overvoltage[J]. High Voltage Engineering, 2015, 41(3): 873-880. |
| [11] |
邓祥力, 谢海远, 熊小伏, 等. 基于支持向量机和有限元分析的变压器绕组变形分类方法[J]. 中国电机工程学报, 2015, 35(22): 5778-5786. DENG Xiangli, XIE Haiyuan, XIONG Xiaofu, et al. Classification method of transformer winding deformation based on SVM and finite element analysis[J]. Proceedings of the CSEE, 2015, 35(22): 5778-5786. DOI:10.13334/j.0258-8013.pcsee.2015.22.012 |
| [12] |
MORTAZAVIAN S, SHABESTARY M M, MOHAMED A R I, et al. Experimental studies on monitoring and metering of radial deformations on transformer HV winding using image processing and UWB transceivers[J]. IEEE Transactions on Industrial Informatics, 2015, 11(6): 1334-1345. DOI:10.1109/TⅡ.2015.2479582 |
| [13] |
ABU-SIADA A, ISLAM S. A novel online technique to detect power transformer winding faults[J]. IEEE Transactions on Power Delivery, 2012, 27(2): 849-857. DOI:10.1109/TPWRD.2011.2180932 |
| [14] |
ASADI N, KELK H M. Modeling, analysis, and detection of internal winding faults in power transformers[J]. IEEE Transactions on Power Delivery, 2015, 30(6): 2419-2426. DOI:10.1109/TPWRD.2015.2431972 |
| [15] |
朱佼佼, 陈特放, 付强, 等. 一种新的交流机车主变压器绕组状态在线监测方法[J]. 中国电机工程学报, 2016, 36(8): 2280-2288. ZHU Jiaojiao, CHEN Tefang, FU Qiang, et al. A new online status monitoring method for the windings of AC locomotive main transfor-mer[J]. Proceedings of the CSEE, 2016, 36(8): 2280-2288. |
| [16] |
付强, 陈特放, 朱佼佼. 采用自组织RBF网络算法的变压器故障诊断[J]. 高电压技术, 2012, 38(6): 1368-1375. FU Qiang, CHEN Tefang, ZHU Jiaojiao. Transformer fault diagnosis using self-adaptive RBF neural network algorithm[J]. High Voltage Engineering, 2012, 38(6): 1368-1375. |
| [17] |
ZHU Jiaojiao, CHEN Tefang, FU Qiang. The research and application of wnn in the fault diagnosis technology of electric locomotive main transformer[C]//The 7th IET International Conference on Power Electronics Machines and Drives. Manchester: IET, 2014. DOI: 10.1049/cp.2014.0257.
|
| [18] |
王硕禾, 蔡清亮, 许继勇, 等. 基于模态分析的牵引供电系统谐波谐振过电压研究[J]. 铁道学报, 2013, 35(7): 32-41. WANG Shuohe, CAI Qingliang, XU Jiyong, et al. Haimonic resonance over-voltage of traction power supply system based on modal analysis[J]. Journal of the China Railway Society, 2013, 35(7): 32-41. |
| [19] |
程佩青. 数字信号处理教程[M]. 北京: 清华大学出版社, 2000: 245-322. CHENG Peiqing. Digital signal processing tutorial[M]. Beijing: Tsinghua University press, 2000: 245-322. |
| [20] |
马录宝, 姜悦礼, 张金平. 交流传动机车牵引变压器设计时应考虑的几个问题[J]. 变压器, 2000, 37(5): 22-25. MA Lubao, JIANG Yueli, ZHANG Jinping. Questions on traction transformer design of AC driving locomotive[J]. Tansformer, 2000, 37(5): 22-25. |
| [21] |
王慧芳, 何奔腾. 电气化铁路负荷最大电流突变量的估算方法[J]. 电力系统自动化, 2008, 32(9): 79-82. WANG Huifang, HE Benteng. Calculation method of maximal current mutation in electrical railway load[J]. Automation of Electric Power Systems, 2008, 32(9): 79-82. |
| [22] |
DICK E P, ERVEN C C. Transformer diagnostic testing by frequuency response analysis[J]. IEEE Transactions on Power Apparatus and Systems, 1978, PAS-97(6): 2144-2153. DOI:10.1109/TPAS.1978.354718 |
| [23] |
MIKI A, HOSOYA T, OKUYAMA K. A calculation method for impulse voltage distribution and transferred voltage in transformer windings[J]. IEEE Transactions on Power Apparatus and Systems, 1978, PAS-97(3): 930-939. DOI:10.1109/TPAS.1978.354566 |
| [24] |
焦在滨, 马涛, 屈亚军, 等. 基于励磁电感参数识别的快速变压器保护[J]. 中国电机工程学报, 2014, 34(10): 1658-1666. JIAO Zaibin, MA Tao, QU Yajun, et al. A novel excitation induc-tance-based power transformer protection scheme[J]. Proceedings of the CSEE, 2014, 34(10): 1658-1666. |
| [25] |
ISLAM S M. Detection of shorted turns and winding movements in large power transformers using frequency response analysis[C]//Power Engineering Society Winter Meeting. Singapore: IEEE, 2000: 2233-2238. DOI: 10.1109/PESW.2000.847703.
|
| [26] |
谭喜堂, 吕佩佩, 朱琴跃, 等. 单相双绕组变压器匝间短路故障诊断[J]. 电气自动化, 2015, 37(1): 73-74. TAN Xitang, LYU Peipei, ZHU Qinyue, et al. Diagnosis of inter-turn short circuit fault in single-phase two winding transformers[J]. Electrical automation, 2015, 37(1): 73-74. |
| [27] |
RAHIMPOUR E, CHRISTIAN J, FESER K, et al. Transfer function method to diagnose axial displacement and radial deformation of transformer windings[J]. IEEE Transactions on Power Delivery, 2003, 18(2): 493-505. DOI:10.1109/TPWRD.2003.809692 |
 2018, Vol. 50
2018, Vol. 50


