随着各类危险化学品的社会需求量持续增加，越来越多的危险品运输车辆在路网内行驶，形成流动的危险源，危及社会公共安全.在城市非爆炸品类的危险品事故中，由运输原因造成的事故数量占32%^[1]，对危险品运输路径优化是降低运输风险的重要途径之一^[2].对危险品运输风险评价是实施路径优化的前提，诸多学者对此进行了研究并建立数学模型^[3].其中传统风险模型以路段事故发生概率与潜在受影响人数的乘积作为路段风险值，该模型满足经典风险理论和“运输风险评价定理”，应用最为广泛^[4].

在危险品运输网络中，不同路径上的行程时间和运输风险存在差异，即使在同一路径上并采用相同车辆在不同时段经由运输，由于交通流量和路段附近人数的变化，车辆行驶时间和运输风险都会改变，使运输时间和运输风险具有时间依赖特征.在实际运输过程中，各路段上的行程时间并不能准确预测，通常设为服从具有某种随机分布特征的变量；同理，各路段附近的人口密度也可采用符合某种随机分布特征的函数表示^[5].因此，危险品是在具有随机时间依赖(stochastic time dependent, STD)特征的路网内运输，分析路径的STD特征，对降低运输风险和减少运输时间有重要现实意义.

危险品运输商在选择路径时需要综合考虑运输时间、运输费用以及运输风险大小，危险品的运输路径优化问题可归约为多准则优化问题，需结合路网的STD特征进行研究.文献[3]首次对STD路网中的路径优化问题进行了研究；文献[6-7]分别对时间依赖路网中危险品运输路径优化问题作了研究；文献[8]将危险品运输风险定义为具有时间依赖特征的模糊随机变量，建立了优化模型并提出求解算法；文献[9]对STD路网中的危险品运输问题提出一种逼近预期路径长度的启发式方法，并由^[10]扩展到多准则路径优化问题；文献[11]对STD条件下危险品最短路问题进行了研究；文献[12]研究了时间依赖路网中危险品运输路径的双准则优化问题.既有研究通常将路径随机属性的数学期望作为选择标准，而较少地考虑随机属性的方差对决策者的影响.计算随机属性的方差，可反映计算结果与期望值的偏离程度，以满足不同类型决策者的选择需求.针对STD路网内的危险品运输路径优化问题，计算各优化准则对应的随机属性的方差，可对各随机属性的稳定性和运输路径的可靠性进行分析.

在危险品运输过程中设置到达时间窗约束，既可满足企业的无库存生产需求，也可避免因重复装卸或再次存储带来的额外风险.文献[13]对静态路网中有时间窗约束的危险品运输路径优化问题进行了研究；文献[14]研究了STD路网中的危险品运输路径选择问题，建立有时间窗约束的多目标模型；文献[15]考虑时变条件对危险品运输事故率的影响，建立有运输时间约束的路径决策模型.既有研究中所建立的模型以到达时间窗或运输时间作为约束条件，但未界定运输网络的STD属性，也未分析到达时间窗的改变对运输路径的影响.

本文将研究STD路网内的危险品运输路径多准则优化问题，在分析路径STD特征的基础上，考虑到达时间窗约束，分别以运输时间、运输风险的期望值和标准差为优化准则建立数学模型.设计两阶段多维标号修正算法，计算在不同时刻出发并以给定置信水平满足时间窗约束的非支配路径集合，为运输商在不同准则下的路径选择提供决策支持.

1 问题描述与分析

危险品在无向路网G=(N, A, I)内运输，N为节点集合，i和j为G中节点，i∈N, j∈N且i≠j；A为路段集合，(i, j)∈A为G中路段，l_ij为(i, j)的长度，ρ_{ij, jk}为(i, j)和(j, k)的行程时间相关系数；I={I₁, …, I_k}为分段连续的时间段集合；Γ(i)为i在G中的邻接节点集合；o∈N为起点，d∈N为终点，且o≠d；p_od^t_o为t_o时刻从o出发到d的路径，t_o∈I；c_ij^t_o为t_o时刻从o出发在(i, j)上的行程时间，t_i为到达i的时刻；x_ij^t_o为决策变量，当(i, j)∈p_od^t_o时取值为1，否则为0；x为多个x_ij^t_o组成的向量.

1.1 行程时间分析

在实际交通网络中，影响人们日常出行时间变化的主要因素是道路拥挤或交通管制等，这些因素导致各路段上的行程时间呈周期性变化，可采用正态分布、对数正态分布或移位正态分布等函数来描述变化特征^[16].考虑各路段行程时间分布曲线的非对称性，以及观察错误或样本缺乏而导致的估计分布不合理，可采用截断对数正态分布来描述路段行程时间.通过设置截断边界使概率密度曲线与实际分布曲线的贴近度更高，并可排除对数正态分布中右长尾产生的不合理值^[17].采用截断对数正态分布模型描述分段连续时间区间内的路段行程时间，可保证行程时间的连续性，使运输网络满足先进先出(first in first out, FIFO)性质^[18].

当路段行程时间服从截断对数正态分布时，(i, j)上的行程时间c_ij的概率密度函数为

$ f\left( {{c_{ij}};{\mu _{ij}},{\sigma _{ij}},{a_{ij}},{b_{ij}}} \right) = \frac{{ - {{\left( {{\eta _{ij}}} \right)}^2}}}{{2{\sigma _{ij}}\sqrt {2{\rm{ \mathsf{ π} }}} {c_{ij}}\left( {\mathit{\Phi }\left( {{\alpha _{ij}}} \right) - \mathit{\Phi }\left( {{\beta _{ij}}} \right)} \right)}}. $

(1)

式中：μ_ij和σ_ij分别为ln(c_ij)的位置参数和尺度参数；a_ij为(i, j)上自由流时的行程时间，b_ij为(i, j)上最大行程时间，通常设b_ij=5a_ij^[19]；α_ij、β_ij和η_ij为临时变量，${\alpha _{ij}} = {\rm{ln}}\left( {\frac{{{a_{ij}}}}{{{\mu _{ij}}}}} \right){\sigma _{ij}}^{-1}$，${\beta _{ij}} = {\rm{ln}}\left( {\frac{{{b_{ij}}}}{{{\mu _{ij}}}}} \right){\sigma _{ij}}^{-1}$，${\eta _{ij}} = {\rm{ln}}\left( {\frac{{{c_{ij}}}}{{{\mu _{ij}}}}} \right){\sigma _{ij}}^{-1}$；Φ(·)为标准正态累积分布函数.

当c_ij服从标准对数正态分布时，c_ij的期望值E[c_ij]和方差V[c_ij]为

$ E\left[ {{c_{ij}}} \right] = {\mu _{ij}} + \exp \left( {0.5\sigma _{ij}^2} \right), $

(2)

$ V\left[ {{c_{ij}}} \right] = \mu _{ij}^2 + \exp \left( {\sigma _{ij}^2} \right)\left[ {\exp \left( {\sigma _{ij}^2} \right) - 1} \right]. $

(3)

在设定c_ij的左右截断边界后，即a_ij≤c_ij≤b_ij，对c_ij修正后的期望值m_ij和标准差v_ij分别为

$ {m_{ij}} = E\left[ {{c_{ij}}} \right]\frac{{\mathit{\Phi }\left( {{\beta _{ij}} - {\sigma _{ij}}} \right) - \mathit{\Phi }\left( {{\alpha _{ij}} - {\sigma _{ij}}} \right)}}{{\mathit{\Phi }\left( {{\beta _{ij}}} \right) - \mathit{\Phi }\left( {{\alpha _{ij}}} \right)}}, $

(4)

$ \begin{array}{*{20}{c}} {v_{ij}^2 = {{\left( {E\left[ {{c_{ij}}} \right]} \right)}^2}\left\{ \begin{array}{l} \frac{{\mathit{\Phi }\left( {{\beta _{ij}} - 2{\sigma _{ij}}} \right) - \mathit{\Phi }\left( {{\alpha _{ij}} - 2{\sigma _{ij}}} \right)}}{{\mathit{\Phi }\left( {{\beta _{ij}}} \right) - \mathit{\Phi }\left( {{\alpha _{ij}}} \right)}} - \\ {\left[ {\frac{{\mathit{\Phi }\left( {{\beta _{ij}} - {\sigma _{ij}}} \right) - \mathit{\Phi }\left( {{\alpha _{ij}} - {\sigma _{ij}}} \right)}}{{\mathit{\Phi }\left( {{\beta _{ij}}} \right) - \mathit{\Phi }\left( {{\alpha _{ij}}} \right)}}} \right]^2} \end{array} \right\} + }\\ {V\left[ {{c_{ij}}} \right]\frac{{\mathit{\Phi }\left( {{\beta _{ij}} - 2{\sigma _{ij}}} \right) - \mathit{\Phi }\left( {{\alpha _{ij}} - 2{\sigma _{ij}}} \right)}}{{\mathit{\Phi }\left( {{\beta _{ij}}} \right) - \mathit{\Phi }\left( {{\alpha _{ij}}} \right)}}.} \end{array} $

(5)

1.2 运输风险分析

采用传统风险评价模型计算各路段上的风险值，设(i, j)上可能发生事故的概率为r_ij，潜在受影响人数为P_ij，则(i, j)上的风险值z_ij为

$ {z_{ij}} = {r_{ij}}{P_{ij}}. $

(6)

若不考虑道路等级差异，r_ij的取值可借鉴文献[20]中的取值方法，用(i, j)的长度数值乘以10^-6来近似表示(i, j)上的事故发生概率.在实际运输环境中，r_ij的值与车辆通过(i, j)的时间段有关，通常认为在夜间或交通高峰时段，r_ij的取值较大^[7].

在实际运输网络中，由于各路段附近的用地类型、公共服务设施等存在差异，致使人口密度分布不同.对于同一路段，不同时段的人口变化情况具有一定的规律性^[21].将P_ij的变化分布曲线按照峰谷分布划分，采用移位对数正态分布函数分段拟合，可得P_ij的估计数据，其计算表达式为

$ {P_{ij}} = {\gamma _{ij}} + \exp \left( {{\omega _{ij}} + {\chi _{ij}}{\delta _{ij}}} \right). $

(7)

式中：γ_ij为P_ij的最小取值(不变人口数量)；ω_ij为P_ij中波动人数取自然对数后的期望值；δ_ij为P_ij中波动人数取自然对数后的标准差；χ_ij为服从标准正态分布的随机变量.

由式(6)、(7)可计算z_ij的期望值ε_ij和方差ψ_ij分别为

$ {\varepsilon _{ij}} = E\left[ {{z_{ij}}} \right] = {\gamma _{ij}}{r_{ij}} + \exp \left( {{\omega _{ij}} + 0.5{\delta _{ij}}^2} \right){r_{ij}}, $

(8)

$ {\psi _{ij}} = V\left[ {{z_{ij}}} \right] = \exp \left( {2{\omega _{ij}} + {\delta _{ij}}^2} \right)\left( {\exp \left( {{\delta _{ij}}^2} \right) - 1} \right){r_{ij}}^2. $

(9)

2 模型建立与分析

在STD路网内运输危险品时，还需考虑运输网络的其他性质，给出如下假设：1)运输网络为无向图结构，各路段均满足FIFO性质；2)运输车辆选择最短路径行驶，不存在绕行或途中停靠现象；3)在不同的时间段内，各路段附近人口密度服从独立的随机分布.

基于问题描述和条件假设，p_od^t_o上的行程时间T(p_od^t_o)和累积运输风险Z(p_od^t_o)分别为

$ T\left( {p_{od}^{{t_o}}} \right) = \sum\limits_{\left( {i,j} \right) \in A} {\eta _{ij}^{{t_o}}x_{ij}^{{t_o}}} , $

(10)

$ Z\left( {p_{od}^{{t_o}}} \right) = \sum\limits_{\left( {i,j} \right) \in A} {\zeta _{ij}^{{t_o}}x_{ij}^{{t_o}}} . $

(11)

式中：η_ij^t_o和ζ_ij^t_o分别为p_od^t_o中(i, j)上行程时间和运输风险，η_ij^t_o和ζ_ij^t_o为随机变量.

T(p_od^t_o)的期望值f_e(x)和标准差f_v(x)、Z(p_od^t_o)的期望值g_e(x)和标准差g_v(x)分别为

$ {f_{\rm{e}}}\left( \mathit{\boldsymbol{x}} \right) = E\left[ {T\left( {p_{od}^{{t_o}}} \right)} \right] = \sum\limits_{\left( {i,j} \right) \in A} {\iota _{ij}^{{t_o}}x_{ij}^{{t_o}}} , $

(12)

$ \begin{array}{l} {f_{\rm{v}}}\left( \mathit{\boldsymbol{x}} \right) = \sqrt {V\left[ {T\left( {p_{od}^{{t_o}}} \right)} \right]} = \\ \;\;\;\;\;\;\;\;\;\sqrt {\sum\limits_{\left( {i,j} \right) \in A} {\nu _{ij}^{{t_o}}{}^2x_{ij}^{{t_o}}} + \sum\limits_{\left( {i,j} \right) \in A,\left( {j,k} \right) \in A} {\nu _{ij}^{{t_o}}x_{ij}^{{t_o}}\nu _{jk}^{{t_o}}x_{jk}^{{t_o}}{\rho _{ij,jk}}} } , \end{array} $

(13)

$ {g_{\rm{e}}}\left( \mathit{\boldsymbol{x}} \right) = E\left[ {Z\left( {p_{od}^{{t_o}}} \right)} \right] = \sum\limits_{\left( {i,j} \right) \in A} {\zeta _{ij}^{{t_o}}x_{ij}^{{t_o}}} , $

(14)

$ {g_{\rm{v}}}\left( \mathit{\boldsymbol{x}} \right) = \sqrt {V\left[ {Z\left( {p_{od}^{{t_o}}} \right)} \right]} = \sqrt {\sum\limits_{\left( {i,j} \right) \in A} {\vartheta _{ij}^{{t_o}}x_{ij}^{{t_o}}} } . $

(15)

式中：ι_ij^t_o、ν_ij^t_o、ζ_ij^t_o和ϑ_ij^t_o分别为p_od^t_o中(i, j)上m_ij、v_ij、ε_ij和ψ_ij的对应值.

给定到达时间窗为[T_e, T_l]，建立STD路网内有时间窗约束的多准则路径优化模型为

$ F\left( x \right) = \left( {\min {f_{\rm{e}}}\left( \mathit{\boldsymbol{x}} \right),\min {f_{\rm{v}}}\left( \mathit{\boldsymbol{x}} \right),\min {g_{\rm{e}}}\left( \mathit{\boldsymbol{x}} \right),\min {g_{\rm{v}}}\left( \mathit{\boldsymbol{x}} \right)} \right), $

(16)

$ {\rm{s}}.{\rm{t}}.\sum\limits_{\left( {i,j} \right) \in A} {x_{ij}^{{t_o}}} - \sum\limits_{\left( {j,k} \right) \in A} {x_{jk}^{{t_o}}} = \left\{ \begin{array}{l} \;\;1,j = o;\\ \;\;0,j \ne o\mathit{\& j} \ne \mathit{d};\\ - 1,j = d. \end{array} \right. $

(17)

$ {t_o} + T\left( {p_{od}^{{t_o}}} \right) \in \left[ {{T_e},{T_l}} \right]. $

(18)

$ x_{ij}^{{t_o}} \in \left\{ {0,1} \right\}. $

(19)

式(16)为不同优化准则的目标函数值构成的决策向量；式(17)为路径的无环约束；式(18)为到达时间窗约束；式(19)为决策变量取值空间.

2.1 路网的STD特征分析

危险品在有时间窗约束的STD路网内运输，选择不同的出发时间，既会影响车辆行程时间，也会使运输风险发生变化.因此，计算不同出发时刻对应的行程时间是运输路径优化的必要条件，首先给出STD路网的相关命题.

命题1 在STD的FIFO路网中，若p_od^t_o为最短路径，则p_od^t_o中任意i(i≠o, i≠d)对应的子路径p_oi^t_o也为最短路径.

证明 假设p_od^t_o为最短路径，在t_o时刻从o出发到达i的时间为t_i，到达d的时间为t_d.若p_oi^t_o非最短路径，则存在p_oi^t_o'(p_oi^t_o'≠p_oi^t_o)，到达i的时间为t_i^*，有t_i^* < t_i.则在t_i^*从i出发，到达d的时间为t_d^*.根据路网性质有t_i^*+T(p_id^t_d*)=t_d^* < t_i+T(p_id^t_i)=t_d，与p_od^t_o为最短路径矛盾.

命题2 在STD的FIFO路网中，对于任意节点i和j之间的最短路径p_ij^t_i，到达时间t_j是关于出发时间t_i的非减函数.

证明 任意节点i到j的行程时间关系式为t_j=t_i+T(p_ij^t_i)，T(p_ij^t_i)为最短行程时间.对于任意出发时刻t_i^′，当t_i^′>t_i时，有t_j^′=t_i^′+T(p_ij^t_i′).因为路网满足FIFO性质，所以有t_j^′≤t_j，可得t_j是关于t_i的非减函数.

因为路径行程时间具有随机性，设置准时到达置信水平$φ$(0≤$φ$≤1)来满足时间窗约束，表达式为

$ \mathit{Pr}\left( {{T_e} \le {t_o} + T\left( {p_{od}^{{t_o}}} \right) \le {T_l}} \right) \le \varphi . $

(20)

对于给定的$φ$，至少存在一个时刻T_$φ$，使Pr(T_e≤T_$φ$≤T_l)=$φ$.在[T_e, T_l]内，T_$φ$取值并不唯一.

命题3 当T_$φ$给定时(T_$φ$∈[T_e, T_l])，至少存在一个出发时间t_o和相应最短时间T(p_od^t_o)，使T_$φ$=t_o+T(p_od^t_o)；反之则不一定成立.

证明 由路网性质和命题2可知，对于任意出发时刻t_o，因为T(p_od^t_o)非负，且t_o+T(p_od^t_o)是关于t_o非减的.当t_o↑T_$φ$时，对于[T_e, T_l]内的给定值T_$φ$，总存在t_o使T_$φ$=t_o+T(p_od^t_o)成立.相反，对于给定的任意t_o及其对应的最短行程时间T(p_od^t_o)，结合假设条件(2)可知，t_o+T(p_od^t_o)的值不一定在[T_e, T_l]之内.

$φ$值给定后，可利用累积分布函数计算路径行程时间的近似值^[22]. $φ$和T_$φ$的关系式为

$ \mathit{\Phi }\left( {\frac{{\left( {{T_\varphi } - {t_o}} \right) - {f_{\rm{e}}}\left( \mathit{\boldsymbol{x}} \right)}}{{\sqrt {{f_{\rm{v}}}\left( \mathit{\boldsymbol{x}} \right)} }}} \right) = \varphi . $

(21)

利用累积分布函数的逆函数Φ^－1(·)，计算出发时间t_o的表达式为

$ {t_o} = {T_\varphi } - {\mathit{\Phi }^{ - 1}}\left( \varphi \right){f_{\rm{v}}}\left( \mathit{\boldsymbol{x}} \right) - {f_{\rm{e}}}\left( \mathit{\boldsymbol{x}} \right). $

(22)

因此，在t_o时刻出发并以置信水平$φ$准时到达的路径行程时间T(p_od^t_o)为

$ T\left( {p_{od}^{{t_o}}} \right) = {T_\varphi } - {t_o} = {\mathit{\Phi }^{ - 1}}\left( \varphi \right){f_{\rm{v}}}\left( \mathit{\boldsymbol{x}} \right) - {f_{\rm{e}}}\left( \mathit{\boldsymbol{x}} \right). $

(23)

同理，在t_o时刻出发，从i到j的行程时间为

$ c_{ij}^{{t_o}} = T\left( {p_{oj}^{{t_o}}} \right) - T\left( {p_{oi}^{{t_o}}} \right). $

(24)

2.2 模型特征分析

对运输路径进行多准则优化，需确定路径间的优劣关系，可根据不同优化准则的目标值采用支配关系比较进行确定^[23].

通过路径间的支配关系比较，可在计算过程中决定路径的取舍.当路网规模较大或优化准则数量较多时，完全列出非支配路径并不可取.本文设计准则权重和阈值支配方法，既体现运输商对优化准则的偏好，也可避免对非支配路径的完全枚举.假设各优化准则以取小为优，准则m对应目标函数为h_m(·)，各准则占优权重的计算过程如下.

步骤1 根据运输商的路径选择偏好，为每个准则m设定权重π_m，$\sum\limits_{m = 1}^M {{\pi _m} = 1} $，M为优化准则总数.

步骤2 设p_x和p_y为待比较路径，w(p_x)和w(p_y)分别为p_x和p_y的占优权重，初始值为0.

步骤3 对于任意准则m，若h_m(p_x) < h_m(p_y)，则w(p_x)=w(p_x)+π_m；若h_m(p_x)=h_m(p_y)，令w(p_x)=w(p_x)+π_m，w(p_y)=w(p_y)+π_m；否则w(p_y)=w(p_y)+π_m.

得到w(p_x)和w(p_y)的值后，设置支配阈值Δ，判定p_x和p_y的支配关系.若w(p_x)－w(p_y)≥Δ，则称p_x支配p_y；若w(p_y)－w(p_x)≥Δ，则称p_y支配p_x；若|w(p_x)－w(p_y)| < Δ，称p_y与p_x相互支配.

设计准则权重和阈值支配方法，可实现求解质量和求解效率的有效均衡.

3 求解算法设计

由命题1和命题2可知，静态网络中的Bellman最优原理同样适用于STD的FIFO网络.在FIFO网络中，可利用静态网络中的最短路径算法来求解动态网络的最短路径^[24].本文设计两阶段多维标号修正算法对模型求解，首先根据各路段的随机行程时间、时间窗[T_e, T_l]和准时到达置信水平$φ$来计算出发时间；然后生成关于行程时间和运输风险的非支配路径集合.

命题4 在STD的FIFO路网中，若给定[T_e, T_l]和$φ$，则一定存在从o出发的最迟时刻ħ_o，满足Pr(ħ_o+T(p_od^ħ_o)≤T_l)≥$φ$，且当$\forall $t_o>ħ_o时，Pr(t_o+T(p_od^t_o)＞T_l)>$φ$不成立.

证明 假设ħ_o不存在，即对于$\forall $t_o∈I，有Pr(t_o+T(p_od^t_o)≤T_l)≥$φ$恒成立.则对于任意$φ$，若Pr(t_o+T(p_od^t_o)＞T_l)=1，则Pr(t_o+T(p_od^t_o)≤T_l)≥$φ$恒成立.所以，假设成立的充分条件是在任意t_o，有t_o+T(p_od^t_o)≤T_l.由命题2可知，t_o+T(p_od^t_o)是关于t_o的非减函数，且T(p_od^t_o)>0(o≠d).因此，当t_o↑T_l时，一定存在最迟出发时间ħ_o使ħ_o+T(p_od^ħ_o)=T_l，当t_o>ħ_o时，t_o+T(p_od^t_o)>T_l，与假设矛盾.

根据命题4，ħ_o的计算步骤如下.

步骤1 网络初始化，给定[T_e, T_l]和$φ$，设置出发时间区间[λ_o, ħ_o](λ_o < < ħ_o)和终止判断值${\bar \omega }$，初始化标号队列为空.

步骤2 令出发时间κ=0.5(λ_o+ħ_o)，将起点o从队尾插入队列，并令t_o=κ；路网中其他节点i标号为t_i=∞(i∈N\{o}).

步骤3 从队头取节点i，并从队列中删除i.根据式(21)、(22)计算j∈Γ(i)的到达时间t_j，与j的原标号t_j^′比较，若t_j≤t_j^′，更新j的标号为t_j；若j已入过队列中，则将j从队头插入，否则从队尾插入.

步骤4 若队列为空且t_d≠∞，根据到达时间t_d判断t_o是否为最迟的出发时间：1)若t_d≤T_l且ħ_o－λ_o>${\bar \omega }$，说明存在大于κ的最迟出发时间，令λ_o=κ，转步骤2；2)若t_d≤T_l且ħ_o－λ_o≤${\bar \omega }$，可认为κ为最迟出发时间，搜索终止，输出κ；3)若t_d>T_l且ħ_o－λ_o≤${\bar \omega }$，搜索终止，输出ħ_o；4)若t_d>T_l，说明κ大于最迟出发时间，令ħ_o=κ，转步骤2.若出发时间t_o小于ħ_o，可能存在多条有效路径p_od^t_o，能在T_l前到达d.同理，t_o应有一个下界λ_o，若要满足到达时间窗约束，t_o不能早于λ_o.

命题5 在STD的FIFO路网中，给定[T_e, T_l]和$φ$，若p_od^t_o为最短路径，则一定有最早出发时间λ_o，满足Pr(λ_o+T(p_od^λ_o)≥T_e)≥$φ$，且t_o < λ_o时，Pr(λ_o+T(p_od^λ_o)≥T_e)≥$φ$不成立.

证明 证明过程与命题4类似，不再赘述.

当t_o < λ_o时，满足Pr(t_o+T(p_od^t_o)≥T_e)≥$φ$的路径可能存在多条，但这些路径只是可行路径，一定不是最短路径.

推论1 在具有STD属性的FIFO路网中，若存在最短路径p_od^t_o，则对于给定的[T_e, T_l]和$φ$，一定存在对应的出发时间窗[λ_o, ħ_o].

得到ħ_o后，令t_o=ħ_o，设置调整步长λ，使t_o=t_o－λ，可计算不同出发时刻对应的路径，并计算各路径运输风险的期望值和标准差，构成多准则决策空间，以满足运输商的路径选择需求.

在多维标号修正算法中，$φ$_eⁱ、$φ$_vⁱ、γ_eⁱ和γ_vⁱ分别用来记录当前路径中从o到任意i的f_e(x)、f_v(x)、g_e(x)和g_v(x)的临时标号，$\ell$(i)为当前路径中i的前驱节点编号，∂(i)标识i是否被访问.路径生成步骤为6步.

步骤1 网络初始化，起点o的标号为($φ$_e^o=0, $φ$_v^o=0, γ_e^o=0, γ_v^o=0, t_o=0, $\ell$(o)=－1)，将o插入队列，∂(o)=1；其他i(i∈N\{o})标号为($φ$_eⁱ=0, $φ$_vⁱ=0, γ_eⁱ=0, γ_vⁱ=0, t_i=∞, $\ell$(i)=－1)，∂(i)=0.

步骤2 根据[T_e, T_l]计算ħ_o，设置各准则权重π_m和支配阈值Δ，初始化节点队列和路径链表为空.

步骤3 从队列中取头节点i，并从队列中删除.取节点j∈Γ(i)，扩展当前路径p_oi^t_o，生成路径p_oj^t_o.由式(12)~(15), (21)、(22)计算节点j的多维标号，令$\ell$(j)=i，∂(j)=1，将j存入路径链表.

步骤4 根据π_m和Δ，将p_oj^t_o与路径链表中以j为终点的所有p_oj^t_o′进行比较，分3种情况：1)若p_oj^t_o支配p_oj^t_o′，则从队列、链表中删除p_oj^t_o′及其子路径，并将p_oj^t_o存入链表和队列；若节点j已在队列中，将j从队头插入，否则将j从队尾插入；2)若p_oj^t_o被p_oj^t_o′支配，则删除p_oj^t_o；3)若p_oj^t_o与p_oj^t_o′相互支配，将p_oj^t_o存入链表；若j已入过队列，将j从队头插入，否则插入队尾.

步骤5 如果队列非空，转步骤3；否则检查链表中节点d对应的各p_od^t_o的属性值，删除t_d不在[T_e, T_l]内的路径，剩余路径构成非支配路径集合.

步骤6 调整t_o的取值，执行步骤1~5，直至无可行路径生成，得到满足[T_e, T_l]约束的路径集合.

4 实验及结果分析

某市部分区域的危险品运输网络结构及路段长度l_ij见图 1，并设危险品运输事故发生后波及范围的半径为1.0 km.

各路段可双向通行，在同一时段内不同方向上的行程时间和路段附近受影响人数相同.按照实际交通流量获取各路段在整个时间区间内行程时间的变化曲线，根据峰谷分布将时间区间I分为6段, 分别定义为I₁= (00:00, 05:30]，I₂= (05:30, 10:30]，I₃= (10:30, 14:30]，I₄= (14:30, 17:00]，I₅= (17:00, 21:30]，I₆= (21:30, 24:00].基于各路段上的行程时间变化曲线，对不同时段内的行程时间数据整理，利用截断对数正态分布函数和最小二乘法进行数据拟合，得到各时段内c_ij的相关参数值见表 1.

考虑I₁和I₆处于夜间时段，I₂和I₅为交通流量高峰时段，将这4个时段的r_ij修正为r_ij^′=r_ij(1.0+rand(0.28, 0.51))^[25].

利用手机网络数据动态感知技术来获取各路段附近可能受影响人数，得到给定区域内分人口数量在整个时间区间内的变化曲线.利用最小二乘法对各时段内人口数据变化曲线进行移位对数正态分布拟合，计算出P_ij的估计参数值见表 2.

危险品运输时间区间是连续的，根据不同的时间窗来计算t_o时，若t_o < 00:00，则令t_o=t_o+24:00.以节点1为起点，节点13为终点，设f_e(x)和f_v(x)的权重分别为π₁=0.4和π₂=0.15，g_e(x)和g_v(x)的权重分别为π₃=0.35和π₄=0.1，支配阈值Δ=0.4；ρ_{ij, jk}取值为(-0.2, 0.2)内均匀分布的随机数；调整步长λ=30 min.设置不同场景s₁和s₂，在s₁中设置[T_e, T_l]=16:00, 18:00，s₂中[T_e, T_l]=[21:00, 22:00]，准时到达置信水平均为τ=0.95.

首先计算各场景中的出发时间窗，设λ_o=00:00，ħ_o=T_L，搜索终止判断值${\tilde \omega }$=0.01，可计算出s₁和s₂中的出发时间窗分别为[λ_o, ħ_o]=[12:46, 14:41]和[λ_o, ħ_o]=[16:49, 17:50].当t_o分别取λ_o和ħ_o时，得到不同t_o对应的最短路径及其属性值见表 3.

由表 3可知，运输车辆在不同时刻出发，对应的路径及其属性值不同.在同一场景内，路径间的随机属性值变化较小，不同场景间的对应属性值变化较大，因为两种场景的到达时间窗不同，决定了出发时间的可选范围不同.在s₂中，危险品的运输需经过交通晚高峰时段，其行程时间、运输风险的期望值和标准差均高于s₁中路径的对应值.因此危险品运输商应尽量避免车辆经由交通高峰时段，以减少运输风险并缩短行程时间.

得到出发时间窗口后，可根据λ来计算不同t_o对应的非支配路径，生成运输路径集合.以s₁为例，生成不同t_o对应的非支配路径及各条路径的属性值见表 4.

由表 4可知，在出发时间窗内对t_o取不同值时，存在多条满足[T_e, T_l]约束的非支配路径，由多个t_o和p_od^t_o组成决策矩阵，使运输商根据优化准则进行有偏好的路径选择.

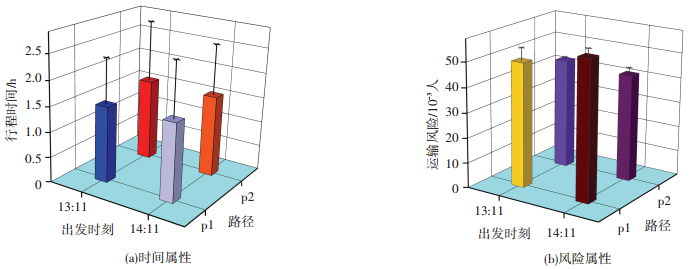
为直观表示不同优化准则下运输路径属性差异，取t_o=13:11时的路径p₁(1, 4, 9, 12, 13)和p₂(1, 4, 5, 8, 12, 13)，以及t_o^′=14:11时的路径p₁^′(1, 4, 5, 6, 10, 13)和p₂^′(1, 2, 6, 10, 13)进行数据对比分析，得到各路径的属性值如图 2所示.

在图 2(a)中，p₂与p₂^′相比较，两者的f_e(x)的值相差甚小，但p₂的f_v(x)值变化较大.对保守型运输商来说，p₂^′的行程时间更为可靠.

由图 2(b)可知，如果运输商以风险值最小为优化准则，p₁明显优于p₁^′，p₁上的运输风险在最坏情况下也低于p₁^′上的风险.若在p₂与p₂^′中进行选择，两者的g_e(x)值近似相等，但p₂的g_v(x)值较小，说明p₂上风险值的稳定性更好.

在给定[T_e, T_l]后，τ值的改变会影响不同类型(保守型、中间型和冒险型)运输商的出发时间选择.以s₁为例，令τ分别取值0.95、0.5和0.2，计算ħ_o和对应的路径属性值，计算结果见表 5.

由表 5可知，保守型运输商的出发时间较早，路径行程时间的标准差较小，表明其可靠性性较好，能以较大的置信度准时到达；而冒险型运输商的出发时间较晚，路径行程时间的标准差较大，说明行程时间的可靠性较差，准时到达的可信度较低.计算结果符合实际运输过程中不同类型运输商对出发时间的选择方式.

考虑运输商的路径选择偏好，改变π_m和Δ的取值，分6种场景来分析参数变化对运输路径的影响，所有场景中令τ=0.95，t_o=14:30.在场景1和场景2中，假设运输商追求f_e(x)和f_v(x)取值最小，给出各π_m的值为(0.45, 0.30, 0.15, 0.10)，Δ分别为0.5和0.1时，得到2种场景下的非支配路径集合及路径属性值见表 6.

同理，采用相同的计算方式，分别计算以下4种场景下的非支配运输路径.在场景3和4中假设运输商追求g_e(x)和g_v(x)最小，各π_m取值为(0.15, 0.10, 0.45, 0.30)，Δ分别为0.5和0.1；在场景5和6中假设运输商无选择偏好，各π_m取值为(0.25, 0.25, 0.25, 0.25)，Δ分别为0.5和0.1.

由6种场景下的计算结果可知，改变π_m和Δ的取值，可生成不同的非支配路径.当Δ值相同时，π_m的取值越平均，各准则之间的占优关系越不明显，产生的非支配路径数量较多.当π_m取值不变时，Δ值越小，路径间的支配关系越明确，但是计算过程中被删除的可行路径数量增多，导致最终的非支配路径数量减少，求解效率提高.因此，调整π_m和Δ的取值，可为不同偏好的运输商提供路径选择决策支持，并实现求解质量和求解效率的有效均衡.

5 结论

1) 根据危险品运输网络的动态特征，对运输路径的行程时间和运输风险的STD属性进行了分析，建立了基于到达时间窗约束和准时到达置信水平的多准则路径优化模型.

2) 根据STD路网的FIFO性质，设计了两阶段多维标号修正算法对模型求解.首先根据各路段的随机属性值、准时到达置信水平和给定的到达时间窗，利用可信性理论求解出发时间区间，并设定调整步长得到多个出发时刻；然后设计准则权重和阈值支配方法，计算不同出发时刻对应的非支配路径集合，并实现求解质量和求解效率的均衡.

3) 文中假设危险品运输网络为非可等待的FIFO网络，具有一定的局限性.在具有STD属性的FIFO网络或非FIFO网络中设置可等待节点，是下一步要研究的内容.