受限水域是指相对于宽水域而言,可航水域宽度变窄、船舶操纵受到限制的航行水域,如:近岸、港湾、入海口和内河航道以及对在航船舶的航行路线相对限制比较严格的水域等.目前,国内外对船舶自动避碰的研究主要集中在宽水域内,对于受限水域的船舶自动避碰研究还不够深入,没有较为成熟的研究结果可以实际应用于船舶的自动避碰乃至于自动航行中.船舶碰撞危险度是表示船舶在其航行过程中发生碰撞危险(risk of collision)的可能性大小及相应碰撞程度的重要参数.因此建立船舶碰撞危险度量化模型,结合在航船舶操纵性能,进而可以作出科学、有效的避碰决策,对解决船舶避碰问题,提高船舶的航行安全具有重要的科学价值和现实意义.
目前对于碰撞危险度主要以船舶会遇最近距离DCPA(distance of closest point of approach)和两船会遇最近时间TCPA(time to closest point of approach)作为量化衡准,对于受限水域而言,由于航行环境的复杂,当前的位置和速度不能够完全体现船舶碰撞危险,还需要对来船的未来运动位置和运动速度进行预判,仅用DCPA和TCPA作为碰撞危险度量化衡准,难以充分反映真实的碰撞危险.本文将静态碍航物的碰撞危险、动态目标的碰撞危险以及当前的环境等因素进行综合考虑与评价,同时将势场理论、船舶避碰领域理论以及船舶动界理论相结合,建立了考虑浅底、岸壁、风和流等多因素的受限水域中船舶碰撞危险度量化模型,为船舶自动避碰研究奠定基础和提供基本依据.
1 受限水域中船舶避碰操纵运动数学模型Abkowitz的整体模型将船、桨、舵看成一个整体系统,整个水动力按照泰勒级数展开,各项水动力导数系数物理意义不明确,与MMG分离建模中物理意义明确的水动力导数系数区别较大[1].为继续沿用静水中的船舶操纵模型,借鉴MMG分离模型的思路,研究其在外界环境综合作用影响下的操纵运动,作出以下假设:1)不考虑几何流场影响,浅底影响和岸壁影响以修正方式进行;2)忽略船舶横摇、纵摇和垂荡运动及其影响;3)外力可线性叠加并相互不影响,不考虑非线性因素作用.
在此基础上,着重考虑船舶操纵运动在受限水域中受风、流作用和浅底、岸壁的影响.
1.1 浅底的影响浅底的影响是在深水中的船舶操纵数学模型基础上,通过系列船模的变水深约束试验来对各个水动力导数进行修正来体现[2],即
| $ {D_{{\rm{SHW}}}} = f\left( {d/H} \right){D_{{\rm{dep}}}}. $ | (1) |
式中:DSHW为浅水中的各项水动力导数,Ddep为深水中的各项水动力导数,d为船舶平均吃水,H为浅水区水深.
借鉴MMG分离模型思想的修正方式,对浅底的影响以修正水动力导数系数的方式进行.因整体模型中各个水动力系数是经泰勒级数展开而来的,因此在修正时,借鉴式(1)对各个水动力导数系数进行船模试验修正,得到
| $ \left\{ \begin{array}{l} m\dot u = \sum {{f_P}\left( {d/H} \right) \cdot {X_p} \cdot {p^n}} ,\\ m\left( {\dot v + {u_1}r} \right) = \sum {{f_P}\left( {d/H} \right) \cdot {Y_p} \cdot {p^n}} ,\\ {I_z}\dot r = \sum {{f_P}\left( {d/H} \right) \cdot {N_p} \cdot {p^n}} . \end{array} \right. $ | (2) |
式中:m为船舶质量,d和H分别为船舶平均吃水和浅水区水深,P为船舶的各个运动参数,即u、v、r、
航行于受限水域的船舶由于受到航道岸壁边界的限制以及与其相邻的船舶的影响,船体周围的流场发生变化以至于对船舶的水动力产生干扰,这些干扰将对船舶的操纵运动产生影响[3].
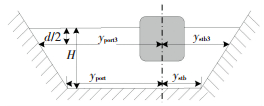
对于受限水域中岸壁效应的计算,主要是通过理论计算或者通过船舶试验经验公式计算岸壁吸力和岸推力矩.采用澳大利亚海运学院通过水池试验(见图 1)提出的计算公式[2]为
| $ \begin{array}{l} {Y_S} = 0.001 \times \left( {0.5\rho {V^2}{L^2}} \right)\left\{ {{a_5}{y_{B3}}\left| {{y_{B3}}} \right|Fn + } \right.\\ \;\;\;\;\;\;\;{a_7}{y_{B3}}\left[ {d/\left( {H - d} \right)} \right] + {a_9}{y_{B3}}Fn\left[ {d/\left( {H - d} \right)} \right] + \\ \;\;\;\;\;\;\;\left. {{a_{13}}{y_{B3}}{{\left[ {d/\left( {H - d} \right)} \right]}^2}} \right\} + \delta Y, \end{array} $ | (3) |
| $ \begin{array}{l} {N_S} = 0.001 \times \left( {0.5\rho {V^2}{L^3}} \right)\left\{ {{b_8}{y_{B3}}\left| {{y_{B3}}} \right|\left[ {d/\left( {H - d} \right)} \right] + } \right.\\ \;\;\;\;\;\;\;{b_{13}}{y_{B3}}{\left[ {d/\left( {H - d} \right)} \right]^2} + {b_{14}}{y_{B3}}\left| {{y_{B3}}} \right|{\left[ {d/\left( {H - d} \right)} \right]^2} + \\ \;\;\;\;\;\;\;\left. {{b_{16}}{y_{B3}}F{n^2}{{\left[ {d/\left( {H - d} \right)} \right]}^2}} \right\} + \delta N, \end{array} $ | (4) |
| $ \begin{array}{l} {\rm{ \mathsf{ δ} }}Y = 0.001 \times \left( {0.5\rho {V^2}{L^2}} \right)\left\{ {0.11{y_B}{C_T}\left[ {d/\left( {H - d} \right)} \right] + } \right.\\ \;\;\;\;\;\;\;\left. {0.0006{y_B}C_T^2{{\left[ {d/\left( {H - d} \right)} \right]}^2}} \right\}, \end{array} $ | (5) |
| $ \begin{array}{l} {\rm{ \mathsf{ δ} }}N = 0.001 \times \left( {0.5\rho {V^2}{L^3}} \right)\left\{ {0.0009{y_B}C_T^2\left[ {d/\left( {H - d} \right)} \right] - } \right.\\ \;\;\;\;\;\;\;\left. {0.004\;4{y_B}\left| {{y_B}} \right|C_T^2\left[ {d/\left( {H - d} \right)} \right]} \right\}. \end{array} $ | (6) |
|
图 1 航道岸壁边界示意图 Figure 1 Schematic diagram of sailing channel boundary |
式中:
| $ {y_B} = B\left( {1/{y_{{\rm{port}}}} + 1/{y_{{\rm{stb}}}}} \right)/2, $ |
| $ {y_{B3}} = B\left( {1/{y_{{\rm{port3}}}} + 1/{y_{{\rm{stb3}}}}} \right)/2, $ |
| $ {a_5} = - 59.3 + 34.7{C_b}\left( {B/d} \right), $ |
| $ {a_7} = 1.87 + 0.328{C_b}\left( {B/d} \right), $ |
| $ {a_9} = - 0.896 - 3.22{C_b}\left( {B/d} \right), $ |
| $ {a_{13}} = 0.0145 - 0.234{C_b}\left( {B/d} \right), $ |
| $ {b_8} = - 1.1 + 0.389{C_b}\left( {B/d} \right), $ |
| $ {b_{13}} = - 0.159 + 0.0191{C_b}\left( {B/d} \right), $ |
| $ {b_{14}} = 0.0379 - 0.0413{C_b}\left( {B/d} \right), $ |
| $ {b_{16}} = - 4.21 - 1.69{C_b}\left( {B/d} \right). $ |
其中:V为船舶航行速度,d、H分别为船舶平均吃水和航行区浅水水深,Fn为傅汝德系数,yport、ystb分别为船舶中心在航道水底处离左、右岸壁的距离,yport3、ystb3分别为船舶中心在吃水一半处离左、右岸壁的距离,CT为船舶推力系数.
受限水域中岸壁对船舶操纵的影响主要采用对船舶操纵运动方程修正的形式进行.由于岸壁效应可体现为额外作用在船体上的岸壁吸力和岸推力矩,因此在进行岸壁效应修正时,可把岸壁吸力和岸推力矩视为外加作用力和力矩.根据前文假定,外力可直接线性叠加到船舶操纵方程的等式右边,如式(3)、(4),以此对岸壁吸力和岸推力矩效应进行修正.
1.3 风、流的作用在计算风和流的作用力时,关键需要得到来自不同角度的风压力系数和流作用力系数[1].对于这些系数的计算,通常是按照经验公式估算,计算比较复杂.本文把船舶系统作为一个整体来考虑,以定常均匀风和定常均匀流来计算风载荷和流载荷对船舶运动的影响,并且假设其风压力和流作用力恒定不变.依据常规定义的风和流方向,即风来流去[4].故而风舷角α为正向的风载荷对船舶向前航行产生推力,而流向角β为正向的流载荷对船舶向前航行产生阻力.假设风压力和流作用力为定常作用力,且船舶均匀受力,风载荷和流载荷的作用中心为船舶中心,即风载荷和流载荷的作用力矩暂时忽略不计.
1.4 综合外界环境的操纵运动船舶航行于受限水域中,浅水效应和风、流外界环境的干扰往往不是单独出现的,而是经常同时出现,多种影响相互叠加,并且多样化,使得对船舶避碰操纵运动的影响更加复杂.为更加真实地模拟船舶的避碰操作,需要综合考虑船舶航行中所受到的浅水效应和风、流的干扰影响,对船舶避碰操纵运动方程进行综合修正,对船舶避碰操纵进行模拟.
2 用于船舶避碰的船舶领域模型 2.1 航道间静态碍航物领域模型1) 对于航道上的静态碍航物,如桥墩、礁石等,其领域应是一个围绕在其周围的包围圈.根据文献[5]的规定,航行中船舶应尽量以向右回转的方式避开碍航物,与以本船为中心保持的Goodwin领域模型[6]相反,在本船驾驶员眼中的碍航物领域的左边安全距离应比右边的稍大些.为了建立统一的连续平滑曲线方程,可在圆形模型的基础上对其进行偏移修正,以蛋圆曲线建立航道静态碍航物的领域模型.其曲线方程为
| $ \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{{\left( {ny + a} \right)}^2}}} = 1. $ | (7) |
式中:x方向为船行方向,y方向为船右舷方向,a为圆形曲线半径,n为偏移修正系数(且-1﹤n﹤0).
对于该领域尺度的大小,本文参考藤井模型,式(8)中a的取值为0.8L+r(L为本船船长,r为该碍航物的平均半径).再根据Goodwin理论,取其模型左右舷处的领域尺寸比,进而换算到蛋圆曲线模型中,可以确定模型左边最大尺寸为0.875L+ r,右边最大尺寸为0.725L+r.故此,可以推算出偏移修正系数n=-0.093 75.
因此,静态碍航物的领域模型方程可以定为
| $ \frac{{{x^2}}}{{{{\left( {0.8L + r} \right)}^2}}} + \frac{{{y^2}}}{{{{\left( { - 0.093\;75y + 0.8L + r} \right)}^2}}} = 1. $ | (8) |
式中L为本船船长,r为该碍航物的平均半径.
2) 当目标船航速为零时,可参照静态碍航物领域模型,假定船舶动态领域模型为对称的椭圆形状,同时考虑到船间效应等的影响及不同的会遇形式,可对短轴增加0.5BS的富裕度.因此其模型方程(其中x为目标船船头方向,y为目标船右舷方向)为
| $ \frac{{{x^2}}}{{{{\left( {0.8L + 0.5{L_{\rm{S}}}} \right)}^2}}} + \frac{{{y^2}}}{{{{\left( {0.8L + {B_{\rm{S}}}} \right)}^2}}} = 1. $ | (9) |
式中:L为本船船长,LS、BS分别为目标船船长、船宽.
2.2 航道边界的领域模型航道边界,如岸壁、定线制航道边界等,其领域应为与边界线大致平行的隔离带.所谓航迹带宽度是指船舶在受限水域中保持航向稳定所需要的水域宽度.受限水域中的船舶航迹带是伴随在本船两侧的一个“安全领域”,本文定义的领域是针对碍航物周围的,因此可以把船舶航迹带宽度的一半分别挪移至航道边界两侧,就形成了航道边界的领域,只要船舶不“侵入”该领域就不会发生碰撞危险.此外,根据文献[5]规定:“沿狭水道或航道行驶的船舶,只要安全可行,应尽量靠近其右舷的该水道或航道的外缘行驶. ”在航道左侧边界的领域尺寸应比航道右侧边界的领域尺寸大一些,可添加一个修正值t,即航道左侧边界领域尺寸为(A/2)+t,右侧边界领域尺寸为(A/2)-t.从文献[7]可以知道,船舶航迹带宽度A的大小与船舶的操纵性能、操船者的工作技能和心理、航行环境等因素有关.当其挪移至航道边界后,其大小就必须考虑到岸壁效应的影响.从文献[8]的仿真结果看,船舶受岸壁效应的影响范围与文献[9]中所述的船舶航迹带宽度的推荐值相差不大.考虑到船舶在受限水域中的操纵性能受影响,考虑中等风速和流速的综合影响,采用操纵性能较差的船舶,其航迹带宽度的推荐值为2B+0.5B+B,考虑到浅底和岸壁坡度的影响,加上富裕度0.5B,因此取A=4B.另外,修正值t仍参照Goodwin理论,取其模型左右舷处的领域尺寸比,可换算得到t=0.387B.得到航道边界的领域模型,航道左侧边界为尺寸2.387B的带状领域,航道右侧边界为尺寸1.613B的带状领域.
2.3 船舶动态领域模型动界理论模型是由英国学者Davis等提出,该模型可以把未来船舶会遇情况考虑进船舶碰撞危险的预判评估中,以便及时确定采取避让行动的时机.但Davis的动界模型是固定尺寸的区域,不能随本船或者目标船的速度变化,因而不能充分体现航速对碰撞危险的影响.
船舶动态领域是本船驾驶员人为地在目标船周围建立的领域,只要在未来时段内不“侵入”这个领域,就不会发生碰撞.以动界理论模型为原型,同时考虑船舶航速的影响,建立船舶动态领域模型.
运动的船舶由动界理论对上述蛋圆曲线形状偏移修正,其方程为
| $ \frac{{{x^2}}}{{{{\left( {mx + 0.8L + 0.5{L_{\rm{S}}}} \right)}^2}}} + \frac{{{y^2}}}{{{{\left( {0.8L + {B_{\rm{S}}}} \right)}^2}}} = 1. $ | (10) |
式中m为偏移修正系数.
本文借鉴文献[10]中给定的船舶动界领域尺寸计算公式(11),获得目标船动态领域模型尺寸大小的具体数据,动界尺寸大小为其领域大小加上相对运动距离再取一定富裕度,即
| $ A = {V_{\rm{R}}} \cdot \left( {T + \frac{{k \cdot N \cdot {S_{{\rm{DCPA}}}}}}{{{V_{\rm{R}}}}}} \right). $ | (11) |
式中:A为不同方位的动界尺寸,SDCPA为两船间的安全会遇距离,VR为来船的相对速度,T为本船满舵旋回转向90°所需时间.
本文设定由本船独立承担避让责任,为建立统一的船舶动态领域模型,可假定这个富裕度为0.25VST(其中VS为目标船航速).进而可计算目标船动态领域模型在其航行方向上的尺寸为0.25VS·T+0.8L+0.5LS,可得式(10)中的偏移修正系数为
| $ m = \frac{{1.25{V_{\rm{S}}}T}}{{1.25{V_{\rm{S}}}T + 0.8L + 0.5{L_{\rm{S}}}}}. $ | (12) |
因此,可得到统一的船舶动态领域模型方程为
| $ \begin{array}{l} \frac{{{x^2}}}{{{{\left( {\frac{{1.25{V_{\rm{S}}}T}}{{1.25{V_{\rm{S}}}T + 0.8L + 0.5{L_{\rm{S}}}}}x + 0.8L + 0.5{L_{\rm{S}}}} \right)}^2}}} + \\ \frac{{{y^2}}}{{{{\left( {0.8L + {B_{\rm{S}}}} \right)}^2}}} = 1. \end{array} $ | (13) |
式中VS为目标船航速,T为本船满舵旋回转向90°所需要的时间.
3 船舶碰撞危险度量化模型 3.1 势场法量化船舶碰撞危险度船舶与碍航物越接近,发生碰撞危险的可能性越大,即碰撞危险度越大;处于碍航物安全距离之外时,碰撞危险度为零.这与势场法中的斥力势场相似,当越靠近于势场中心,势场强度剧增;而处于势场影响范围之外时,势场强度为零[11].因此,可假设在碍航物的领域范围内存在一个斥力势场,其势场强度相当于船舶的碰撞危险度.当靠近领域中心时,势场强度急剧增大;处于领域范围之外时,势场强度为零.故此,可以运用这种方法在已建立的船舶领域模型中量化船舶碰撞危险度.为使船舶碰撞危险度更加明确,本文将其划分为多个等级,以变量ϕ(表示船舶碰撞危险度)作为衡量划分依据,并作出如下等级对应规定以作参考,见表 1.
| 表 1 船舶碰撞危险度等级对应表 Table 1 Ship collision risk grade and the value |
在表 1中,规定当本船位于船舶领域以内ϕ>1,领域以外ϕ < 1.考虑到船舶领域边界的模糊性[12],本文取领域以内的碰撞危险度ϕ=1~1.2(其中1.2是假定的参考值)的一般危险情况作为船舶领域的模糊边界,以便更贴近于航海实际.
3.2 静态碍航物的船舶碰撞危险度量化模型按照与领域中心距离的平方作为比例量化碰撞危险度的原理,可以根据其领域模型方程(式(5))设定其在随船运动坐标系下的船舶危险度量化模型方程,模型方程为
| $ \frac{1}{\phi } = \frac{{{{\left( {x - {x_0}} \right)}^2}}}{{{{\left( {0.8L + r} \right)}^2}}} + \frac{{{{\left( {y - {y_0}} \right)}^2}}}{{{{\left[ { - 0.093\;75\left( {y - {y_0}} \right) + 0.8L + r} \right]}^2}}}. $ | (14) |
式中:ϕ为在随船运动坐标系下(x,y)处的船舶碰撞危险度,(x0,y0)为航道居间碍航物中心在随船运动坐标系下的位置,r为该碍航物的平均半径.
3.3 目标船的船舶碰撞危险度量化模型按照与领域中心距离的平方作为比例评估碰撞危险度的原理,可以根据其领域模型方程式(8)换算到本船随船运动坐标系,并设定其船舶危险度量化模型方程,模型方程为
| $ \begin{array}{l} \frac{1}{\phi } = \frac{{{{\left[ {\left( {x - {x_0}} \right)\cos \gamma + \left( {y - {y_0}} \right)\sin \gamma } \right]}^2}}}{{{{\left\{ {\frac{{1.25{V_{\rm{S}}}T}}{{1.25{V_{\rm{S}}}T + 0.8L + 0.5{L_{\rm{S}}}}}\left[ {\left( {x - {x_0}} \right)\cos \gamma + \left( {y - {y_0}} \right)\sin \gamma } \right] + 0.8L + 0.5{L_{\rm{S}}}} \right\}}^2}}} + \\ \;\;\;\;\;\;\;\frac{{{{\left[ {\left( {y - {y_0}} \right)\cos \gamma - \left( {x - {x_0}} \right)\sin \gamma } \right]}^2}}}{{{{\left( {0.8L + {B_{\rm{S}}}} \right)}^2}}}. \end{array} $ | (15) |
式中:γ为目标船与本船的首向交角,VS为目标船航速,T为本船满舵旋回转向90°所需要的时间,每间隔时间步长T后需重新计算下一位置上的船舶碰撞危险度.
3.4 航道边界的船舶碰撞危险度量化模型本文建立的航道边界的领域模型是大致平行于航道边界线的线型模型.按照比例量化碰撞危险度的原理,可以设定其在随船运动坐标系下的船舶危险度量化模型方程,模型方程为
| $ \frac{1}{\phi } = \left\{ \begin{array}{l} \frac{{{{\left( {x - {x_0}} \right)}^2}}}{{{{\left( {2.387B} \right)}^2}}} + \frac{{{{\left( {y - {y_0}} \right)}^2}}}{{{{\left( {2.387B} \right)}^2}}},\;y < 0;\\ \frac{{{{\left( {x - {x_0}} \right)}^2}}}{{{{\left( {1.613B} \right)}^2}}} + \frac{{{{\left( {y - {y_0}} \right)}^2}}}{{{{\left( {1.613B} \right)}^2}}},\;y > 0. \end{array} \right. $ | (16) |
在实际航海过程中,假设各个碍航物的船舶碰撞危险度都是单一独立的,忽略其相互间的影响.因此,船舶航行于某一位置的船舶碰撞危险度即为各个碍航物在该位置的船舶碰撞危险度的叠加.考虑综合环境影响的船舶碰撞危险度量化模型为
| $ \phi = \sum {{\phi _i}} . $ | (17) |
式中:ϕi为该位置处第i个碍航物的船舶碰撞危险度,若ϕi < 1,则取ϕi=0.
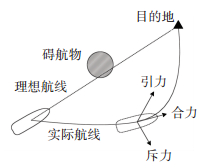
4 基于改进势场法的船舶自动避碰模型 4.1 人工势场法基本原理人工势场法的基本原理是:在运动物体的运动空间范围内构建一个虚拟势场,由目的地为中心的引力场和障碍物为中心的斥力场合成,其中引力场产生引力指引运动物体向目的地靠近,而障碍物则对运动物体产生排斥力排斥其靠近,在这两种力的联合作用下控制运动物体的运动方向.在本文的船舶避碰研究中,将本船航行的目的地作为低势能引力场的中心点,将航道水域中静态碍航物和动态目标船作为高势能斥力场中心,由其合势场的势场梯度负方向引导船舶避开静态碍航物和目标船而沿着安全的路径向航行目的地行驶,如图 2所示.
|
图 2 人工势场法在船舶避碰的应用 Figure 2 Application of artificial potential field method in collision avoidance of ships |
船舶航行于受限水域中,在某一位置处的总势能为引力势场和斥力势场的叠加, 即
| $ {U_{{\rm{total}}}} = {U_{{\rm{att}}}} + \sum {U_{{\rm{rep}}}^i} . $ |
式中:Utotal为总势能,Uatt为目的地的引力势场势能,Urepi为受限水域中静态碍航物和动态目标船的斥力势场势能.
在这个合势场中,引导船舶航行方向的作用力为总势能的负梯度方向
| $ {F_{{\rm{total}}}} = - \nabla {U_{{\rm{total}}}} = - \nabla {U_{{\rm{att}}}} - \sum {\nabla U_{{\rm{rep}}}^i} . $ |
参考传统势场模型在运动规划方面的应用,及船舶在受限水域中的操纵运动习惯,总结传统势场模型在船舶自动避碰应用中的局限性有以下几个:1)目标不可达问题.当在航行目的地不远处有碍航物,船舶向目的地航行且离目的地距离比较近时,随着与目的地的接近,目的地引力势场逐渐减弱,但同时在不远处的碍航物斥力势场急剧增强.如图 2所示,当斥力大于引力时,将使船舶向远离目的地的方向行驶.从而导致船舶在目的地附近反复靠近和远离相互交替在水域中前后震荡,以至于达不到目的地.再者,对于在航船舶来说,采取倒车避碰并不符合常规船舶避碰操纵习惯. 2)局部极小值问题.在船舶航道水域虚拟势场中的某一位置,碍航物对船舶的斥力与航行目的地对船舶的引力刚好抵消,使得船舶所受到的势场合力为零.船舶陷入这一局部陷阱区域,前后震荡然后停止在这个极小值点,不能再继续移动. 3)动态环境下的不适应问题.传统势场模型只考虑船舶与碍航物,船舶与目的地的距离,而没有考虑它们之间的运动趋势.船舶对动态碍航物未来时刻的运动位置始料不及,可能会出现“刹不住车”避碰不及,即便能够成功避碰,避让路线也会非常复杂,与船舶的避碰操纵习惯不符.
4.3 改进势场法的船舶运动规划人工势场法是采用单纯的目的地引力和碍航物斥力矢量合成的方法来规划运动物体的运动路径,其局限性从根本上都是由于引力和斥力的矢量合力的不同结果产生的.为解决这些局限性,从根源上出发,需要对人工势场法中单纯矢量合成方法进行改进.从实际的航海习惯来看,操船者不希望为了避让碍航物而使船舶回转过大的角度,甚至停车倒航.因此,可限制寻求船舶新航向的范围,如图 3所示,在船舶原有航向的±α角度(α < 90°)范围内计算搜索合适的“斥力势场场强”,并以此作为船舶下一步的航行方向.

|
图 3 限制搜索船舶新航向的范围 Figure 3 Scope of searching for new course of ship |
船舶的理想航线是能够一直朝着航行目的地的方向直航而行,故而航行目的地对船舶的指引作用应始终贯彻在整个航行过程中.因此在计算搜索船舶新航向时,可将航行目的地的引力势场的引力方向作为搜索的优先指引方向,致使每次搜索得到新航向都尽量靠近于航行目的地的方向.
本文改进后的势场法可以总结为:用受限水域中综合环境的船舶碰撞危险度“分布场”代替碍航物的斥力势场,以航行目的地引力势场的引力方向作为指引方向,在船舶原有航行方向的一定角度范围内计算搜索与引力方向偏离最小角度且船舶碰撞危险度满足安全航行要求的方向,将其看作合势场中合力的方向,船舶在任意时刻都将沿着势场合力指引的方向航行.运用本文改进势场法进行航行路线规划时,需要注意以下几个细节问题.
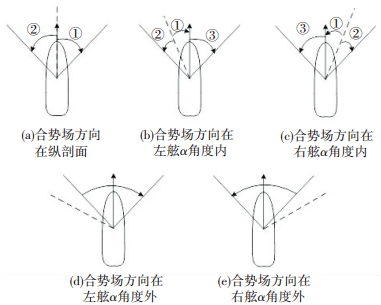
1) 搜索安全航向的搜索顺序.船舶航行于受限水域中,最优选择航线为指向航行目的地方向的航线.因而在搜索安全新航向时,与该方向偏离角度小的航向应优先于偏离角度大的航向.另外,根据文献[5]规定,在航船舶应尽量向右回转避让碍航物,故而在航向搜索时向右回转的方向应优先于向左回转的方向.综合考虑这些因素,船舶搜索安全航向设定的顺序是:根据航行目的地的方向(即引力势场引力的方向)与船舶原航行方向的夹角不同,分为如图 4(其中虚线为引力方向)所示的5种情况,针对不同情况,在船舶原航向的±α角度范围内,按照图中所标的夹角区间顺序以及箭头所指的方向进行搜索.在这个搜索的过程中,只要找到满足条件的位置即可停止搜索.
|
图 4 船舶搜索安全新航向的搜索顺序 Figure 4 Order of ship′s searching for safety course |
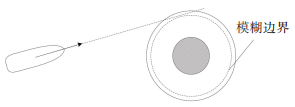
2) 搜索安全新航向的判定指标.在受限水域船舶碰撞危险度评估模型中,规定危险度
|
图 5 领域的模糊边界示意图 Figure 5 Fuzzy boundary diagram of the domain |
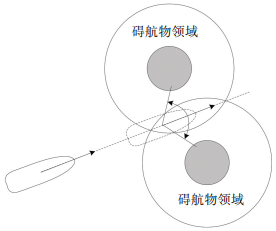
3) 预防陷入“低危陷阱”.本文建立的船舶碰撞危险度评估模型是计算某一位置处在未来t时刻的碰撞危险度,虽其具有预判性,但只是针对于该位置在未来t时刻内有效.若某一位置通过搜索满足条件后,船舶航行t时间至此位置后,在进行新一轮搜索新航向时,可能会因搜索范围的局限搜索不到满足要求的航向,如图 6所示,可将这种情况称为“低危陷阱”.为使船舶在陷入“低危陷阱”之前增强“警惕性”,本文规定在船舶航行至前一次搜索的位置之前,就提前进入下一次搜索.即每次搜索时间步长多于每次搜索完的航行时间步长.若搜索时间步长为t,本文取航行时间步长为(2/3)t.因而船舶通过搜索t时刻的船舶碰撞危险度得到船舶t时间内的安全航线之后,但按照这航线航行(2/3)t之后就提前进入下一轮航向搜索.这样就可以给船舶在陷入“低危陷阱”之前保留一定的反应时间,以重新搜索合适的航线.
|
图 6 船舶搜索新航向的“低危陷阱” Figure 6 ″Low risk trap″ searching for new course |
4) 搜索时间步长t和搜索范围α的取值.本文的搜索船舶航行路线是指搜索计算船舶未来航行t时间之后到达某一位置处时该位置的船舶碰撞危险度,这个时间步长t就是搜索时间步长.搜索时间步长若取值过大则容易“越过”高危点,若取值过小则会增加计算量.目标船动态领域模型所使用的运动时间步长T为本船满舵旋回转90°所需要的时间,船舶碰撞危险度评估模型中也是针对于时间T建立的,因此暂以时间T作为搜索时间步长t.船舶在35°舵角下回转90°所需要的时间为150 s,故取t=150 s.由于搜索的目标位置范围是船舶航行t时间之后所能到达的位置范围之内,所以搜索范围α的取值应基于船舶的操纵性能而定.
5) 搜索不到满足要求的航向问题.若在±α角度范围内搜索不到满足要求的航向,则说明船舶无法在保持原有航速的情况下进行避碰.属于高危情况,需要船舶减速或者倒航进行避碰,或者由本船和目标船进行协调避碰,这将是非常复杂的问题,暂不考虑这种情况.
5 模型仿真应用与验证长江水域是我国的交通要道,其航道复杂繁忙,船舶发生碰撞的几率较大,航行安全深受威胁.为进一步验证本文提出的船舶避碰模型的有效性,选取长江水域太阳洲的一段水域进行避碰航行仿真验证,如图 7所示.

|
图 7 太阳洲水域航道 Figure 7 Channel of Sunland waters |
仿真初始条件:船舶初始坐标为(0 m,0 m)航向角-30°,航行目的地坐标为(120 m,0 m),航道边界宽度为30 m,目标船S1在(10 m,5 m)以VS1=0.5 V的速度沿-30°方向行驶,目标船S2在(95 m,24 m)以VS2=0.5 V的速度沿-180°方向行驶.假设船舶在航行过程中同时受到固定坐标系下-180°的定常均匀风载荷(Va/V0=2,其中V0为船速)的作用.在整个避碰过程中,本船与目标船在不同时刻的相对位置如图 8所示.
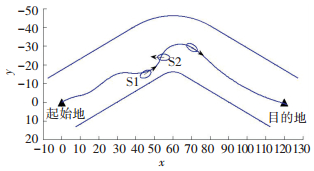
|
图 8 航道中船舶自动避碰航行路径 Figure 8 Ship automatic collision avoidance navigation path in channel |
根据各个时间段的船舶碰撞危险度评估模型,经过13次搜索,每次在航行坐标点上搜索得到的船舶的航向偏角(与原航向的偏角)见表 2.
| 表 2 避碰过程中航行坐标和航向漂角 Table 2 Navigation coordinates and heading drift in the process of collision avoidance |
由复杂环境影响下本船与目标船的避碰航行路径可以看出,本船能够成功追越目标船S1,提前偏转角度绕过交叉相遇的目标船S2,并且和岸壁保持在一定距离之外.故从整个船舶避碰航行过程中,本船能够有效地绕开目标船,避免发生碰撞.
6 结论1) 建立了考虑浅底、岸壁、风和流等多因素联合影响的受限水域中的本船和目标船的船舶动态领域模型和船舶碰撞危险度量化模型,通过仿真实时给出未来t时间段内的航行路线规划,并给出了相应参数取值方法.
2) 基于改进势场法建立了船舶自动避碰模型,解决了传统势场模型在船舶自动避碰应用中目标不可达、局部陷阱、动态环境下的不适应等几个局限性问题,为开发船舶自动驾驶系统提供了帮助.
3) 通过模型和实例仿真验证,在复杂环境下本文建立的自动航行避碰模型能够在受限水域中有效避开静态、动态碍航物,在合理的操舵范围内完成避碰自动航行,具有一定的实用意义.由于船舶在复杂环境中的自动航行避碰过程是一个非常复杂的问题,建立的自动避碰危险度量化模型还存在不足之处,在后续工作中有待进一步研究和完善.
| [1] |
张秀凤. 规则波中船舶运动六自由度数学模型[J]. 交通运输工程学报, 2007, 7(3): 40-43. ZHANG Xiufeng. Ship motion mathematical model with six degrees of freedom in regular wave[J]. Journal of Traffic and Transportation Engineering, 2007, 7(3): 40-43. |
| [2] |
乐美龙. 船舶操纵性预报与港航操纵运动仿真[M]. 上海: 上海交通大学出版社, 2004: 78-81. LE Meilong. Ship maneuvering forecast and shipping maneuvering motion simulation[M]. Shanghai: Shanghai Jiaotong University Press, 2004: 78-81. |
| [3] |
洪碧光. 船舶操纵[M]. 大连: 大连海事大学出版社, 2008: 100-104. HONG Biguang. Ship maneuvering[M]. Dalian: Dalian Maritime University Press, 2008: 100-104. |
| [4] |
张晓兔, 刘祖源. 三峡通航船队的操纵计算与仿真[J]. 武汉交通科技大学学报, 2000, 24(2): 212-214. ZHANG Xiaotu, LIU Zuyuan. Maneuvering calculation and simulation of fleet passing through the three corges[J]. Wuhan University of Science and Technology, 2000, 24(2): 212-214. |
| [5] |
海司航保部. 1972年国际海上避碰规则[M]. 人民交通出版社, 1981.
|
| [6] |
周伟. 宽水域船舶智能避碰决策算法验证及优化[D]. 厦门: 集美大学, 2011. ZHOU Wei. The verification and optimization of algorithm for vessel intelligent collision avoidance decision-making[D]. Xiamen: Jimei University, 2011. |
| [7] |
杨神化. 基于Multi-agent的船舶避碰决策支持系统[D]. 上海: 上海海事大学, 2008. YANG Shenhua. Based on multi-agent of ship collision avoidance support system[D]. Shanghai: Shanghai Maritime University, 2008. |
| [8] |
HARRIS C J, HONG X, WILSON P A. An intelligent guidance and control system for ship obstacle avoidance[J]. Journal of Systems and Control Engineering, 1999, 213: 311-320. DOI:10.1243/0959651991540179 |
| [9] |
SMIERZCHALSKI R, MCHALEWICZ Z. Modeling of ship trajectory in collision situations by an evolutionary algorithm[J]. IEEE Trans on Evolutionary, 2000, 4(3): 227-241. DOI:10.1109/4235.873234 |
| [10] |
ZENG X M. Evolution of the safe path for ship navigation[J]. Applied Artificial Intelligence, 2003, 17(2): 87-104. DOI:10.1080/08839510390183345 |
| [11] |
SU Chenmin, CHANG Kiyin, CHENG Chenyung. Fuzzy decision on optimal collision avoidance measures for ships in vessel traffic service[J]. Journal of Marine Science and Technology, 2012, 20(1): 38-48. |
| [12] |
AHMAD C, INARA T, LEE B, et al. An intelligent real-time multi-vessel collision risk assessment system from VTS view point based on fuzzy inference system[J]. Expert Systems with Application, 2013, 40(4): 1220-1230. DOI:10.1016/j.eswa.2012.08.016 |
| [13] |
赵劲松, 王逢辰. 船舶避碰学原理[M]. 大连: 大连海事大学出版社, 1999: 93-97. ZHAO Jinsong, WANG Fengchen. Ship collision avoidance principles[M]. Dalian: Dalian Maritime University Press, 1999: 93-97. |
 2018, Vol. 50
2018, Vol. 50


