捷联惯性导航系统由于自主性、连续性等诸多优点,作为一种核心导航系统被广泛应用于导航领域[1-4].然而,被各种误差源激励的振荡误差严重降低了惯导系统导航精度,所以,阻尼导航算法常被用于阻尼惯导系统振荡误差,以提高捷联惯导系统导航精度[5-8].
传统的阻尼算法以经典控制理论为基础,在相应振荡回路中添加阻尼网络来实现振荡误差的抑制.但是,由于惯导系统平衡条件被阻尼网络破坏,使得状态切换过程中存在明显的超调误差,且振荡误差收敛时间较长,一般为1~2个振荡周期[9-11].文献[12]提出了一种基于模糊卡尔曼的内阻尼算法,可有效抑制惯导系统振荡误差,提高捷联惯导系统导航精度.文献[13]在具有外速常值误差的假设下,利用卡尔曼滤波的反馈校正技术,实现了惯导水平阻尼,抑制了状态切换过程中超调误差的产生.文献[14]提出了一种基于卡尔曼滤波的阻尼导航算法,该方法以外速变化为外部输入,不仅可以有效抑制超调误差的产生并缩短误差收敛所用时间,而且屏蔽了常值外速误差对系统的影响.以速度误差为观测量的组合导航算法,也可用于抑制捷联惯导系统振荡误差,但是,计程仪测速设备存在常值测速误差[13],该外速常值误差影响组合导航精度,严重时导致系统发散.
为了进一步提高捷联惯导系统外阻尼导航精度,本文提出了一种基于双滤波器的外阻尼导航算法.首先,以速度误差为观测量,利用组合导航算法对外部参考速度进行平滑,并得到相应的误差状态估计.然后,利用平滑后的高精度外部参考速度,以速度变化量作为外部参考输入进行滤波,并得到相应的状态估计,然后对两个滤波器的估计结果进行信息融合,以得到精度更高的估计结果.该方法利用了以速度误差为观测量的组合导航算法的短时导航精度及速度平滑作用,使得外阻尼导航算法的导航精度进一步提高.
1 基于卡尔曼滤波的阻尼导航算法捷联惯性导航系统的误差状态方程[15]为
| $ \mathit{\boldsymbol{\dot X}} = \mathit{\boldsymbol{FX}} + \mathit{\boldsymbol{W}}. $ | (1) |
式中:W为系统噪声向量,W~N(0, Q),Q为系统过程噪声向量的方差矩阵;X为状态向量;X=[δvE, δvN, δL, δλ,
Cbn为载体系到地理系的转换矩阵;τf为加速度计误差自相关时间常数;τg为陀螺仪误差自相关时间常数;vE、vN分别为东向速度和北向速度;L为纬度;ωie为地球自转角速度;R为地球半径;fE、fN、fU分别为比力在地理坐标系上东、北、天向的投影.则
| $ \mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{D}}_{2 \times 3}^1}&{{{\bf{0}}_{2 \times 1}}}&{\mathit{\boldsymbol{D}}_{2 \times 3}^2}&{\mathit{\boldsymbol{D}}_{2 \times 3}^3}&{{{\bf{0}}_{2 \times 3}}}\\ {\mathit{\boldsymbol{D}}_{2 \times 3}^4}&{{{\bf{0}}_{2 \times 1}}}&{{{\bf{0}}_{2 \times 3}}}&{{{\bf{0}}_{2 \times 3}}}&{{{\bf{0}}_{2 \times 3}}}\\ {\mathit{\boldsymbol{D}}_{3 \times 3}^5}&{{{\bf{0}}_{3 \times 1}}}&{\mathit{\boldsymbol{D}}_{3 \times 3}^6}&{{{\bf{0}}_{3 \times 3}}}&{\mathit{\boldsymbol{D}}_{3 \times 3}^7}\\ {{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 1}}}&{{{\bf{0}}_{3 \times 3}}}&{\mathit{\boldsymbol{D}}_{3 \times 3}^8}&{{{\bf{0}}_{3 \times 3}}}\\ {{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 1}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{\mathit{\boldsymbol{D}}_{3 \times 3}^9} \end{array}} \right]. $ |
| $ \mathit{\boldsymbol{D}}_{2 \times 3}^1 = \left[ {\begin{array}{*{20}{c}} {\frac{{{v_{\rm{N}}}}}{R}\tan L}&{2{\omega _{ie}}\sin L + \frac{{{v_{\rm{E}}}}}{R}\tan L}&{2{v_{\rm{N}}}{\omega _{ie}}\cos L + \frac{{{v_{\rm{E}}}{v_{\rm{N}}}}}{R}{{\sec }^2}L}\\ { - 2{\omega _{ie}}\sin L - \frac{{{v_{\rm{E}}}}}{R}\tan L}&0&{ - 2{v_{\rm{E}}}{\omega _{ie}}\cos L - \frac{{v_{\rm{E}}^2}}{R}{{\sec }^2}L} \end{array}} \right]; $ |
| $ \mathit{\boldsymbol{D}}_{2 \times 3}^2 = \left[ {\begin{array}{*{20}{c}} 0&{ - {f_{\rm{U}}}}&{{f_{\rm{N}}}}\\ {{f_{\rm{U}}}}&0&{ - {f_{\rm{E}}}} \end{array}} \right]; $ |
| $ \mathit{\boldsymbol{D}}_{2 \times 3}^3 = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0 \end{array}} \right]\mathit{\boldsymbol{C}}_b^n; $ |
| $ \mathit{\boldsymbol{D}}_{2 \times 3}^4 = \left[ {\begin{array}{*{20}{c}} 0&{\frac{1}{R}}&0\\ {\frac{{\sec L}}{R}}&0&{\frac{{{v_{\rm{E}}}}}{R}\sec L\tan L} \end{array}} \right]; $ |
| $ \mathit{\boldsymbol{D}}_{3 \times 3}^5 = \left[ {\begin{array}{*{20}{c}} 0&{ - \frac{1}{R}}&0\\ {\frac{1}{R}}&0&{ - {\omega _{ie}}\sin L}\\ {\frac{{\tan L}}{R}}&0&{{\omega _{ie}}\cos L + \frac{{{v_{\rm{E}}}}}{R}{{\sec }^2}L} \end{array}} \right]; $ |
| $ \begin{array}{l} \mathit{\boldsymbol{D}}_{3 \times 3}^6 = \\ \left[ {\begin{array}{*{20}{c}} 0&{{\omega _{ie}}\sin L + \frac{{{v_{\rm{E}}}}}{R}\tan L}&{ - {\omega _{ie}}\cos L - \frac{{{v_{\rm{E}}}}}{R}}\\ { - {\omega _{ie}}\sin L - \frac{{{v_{\rm{E}}}}}{R}\tan L}&0&{ - \frac{{{v_{\rm{N}}}}}{R}}\\ {{\omega _{ie}}\cos L + \frac{{{v_{\rm{E}}}}}{R}}&{\frac{{{v_{\rm{N}}}}}{R}}&0 \end{array}} \right]; \end{array} $ |
| $ \mathit{\boldsymbol{D}}_{3 \times 3}^7 = \mathit{\boldsymbol{C}}_b^n; $ |
| $ \mathit{\boldsymbol{D}}_{3 \times 3}^8 = \left[ {\begin{array}{*{20}{c}} { - \frac{1}{{\tau _{\rm{f}}^1}}}&0&0\\ 0&{ - \frac{1}{{\tau _{\rm{f}}^2}}}&0\\ 0&0&{ - \frac{1}{{\tau _{\rm{f}}^3}}} \end{array}} \right]; $ |
| $ \mathit{\boldsymbol{D}}_{3 \times 3}^9 = \left[ {\begin{array}{*{20}{c}} { - \frac{1}{{\tau _{\rm{g}}^1}}}&0&0\\ 0&{ - \frac{1}{{\tau _{\rm{g}}^2}}}&0\\ 0&0&{ - \frac{1}{{\tau _{\rm{g}}^3}}} \end{array}} \right]. $ |
观测方程表述为
| $ \mathit{\boldsymbol{Z}} = \mathit{\boldsymbol{HX}} + \delta \mathit{\boldsymbol{Z}}. $ | (2) |
式中
| $ \mathit{\boldsymbol{H}} = \frac{1}{T}\int\limits_{{t_1}}^{{t_2}} {\mathit{\boldsymbol{\tilde H}}{\rm{d}}t} , $ |
| $ \begin{array}{l} \mathit{\boldsymbol{\tilde H}} = \\ \left[ {\begin{array}{*{20}{c}} {\frac{{{v_{\rm{N}}}}}{R}\tan L}&{2{\omega _{ie}}\sin L + \frac{{{v_{\rm{E}}}}}{R}\tan L}&{2{v_{\rm{N}}}{\omega _{ie}}\cos L + \frac{{{v_{\rm{E}}}{v_{\rm{N}}}}}{R}{{\sec }^2}L}&0&0&{ - {f_{\rm{U}}}}&{{f_{\rm{N}}}}&{{C_{11}}}&{{C_{12}}}&{{C_{13}}}&0&0\\ { - 2{\omega _{ie}}\sin L - \frac{{{v_{\rm{E}}}}}{R}\tan L}&0&{ - \left( {2{v_{\rm{E}}}{\omega _{ie}}\cos L + \frac{{v_{\rm{E}}^2}}{R}{{\sec }^2}L} \right)}&0&{{f_{\rm{U}}}}&0&{ - {f_{\rm{E}}}}&{{C_{21}}}&{{C_{22}}}&{{C_{23}}}&0&0 \end{array}} \right]. \end{array} $ |
式中Cij为Cbn的第i行第j列元素,δZ为量测误差.
式(2)中的观测量Z根据下式求取,即
| $ \mathit{\boldsymbol{Z}} = \frac{1}{T}\int\limits_{{t_1}}^{{t_2}} {\left( {\mathit{\boldsymbol{BC}}_b^c{\mathit{\boldsymbol{f}}^b} - {\mathit{\boldsymbol{A}}^c}} \right){\rm{d}}t} - \frac{1}{T}\left[ \begin{array}{l} v_{\rm{E}}^{{t_2}} - v_{\rm{E}}^{{t_1}}\\ v_{\rm{N}}^{{t_2}} - v_{\rm{N}}^{{t_1}} \end{array} \right]. $ |
其中:
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0 \end{array}} \right]; $ |
| $ {\mathit{\boldsymbol{A}}^c} = \left[ {\begin{array}{*{20}{c}} { - \left( {{\omega _{ie}}\sin {L^c} + \frac{{v_{\rm{E}}^c}}{R}\tan {L^c}} \right)v_{\rm{N}}^c}\\ {\left( {2{\omega _{ie}}\sin {L^c} + \frac{{v_{\rm{E}}^c}}{R}\tan {L^c}} \right)v_{\rm{N}}^c} \end{array}} \right]; $ |
Cbc为惯导计算姿态矩阵;fb为载体系三轴加速度计测量值;Lc为惯导计算纬度;vEc、vNc分别为惯导计算东向速度和北向速度;vEt1、vEt2分别为外参考速度在t1和t2时刻的东向速度;vNt1、vNt2分别为外参考速度在t1、t2时刻的北向速度.
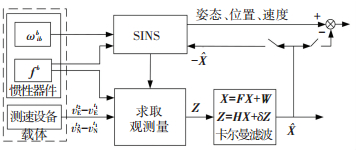
时间差T为积分时间,T=t2-t1,当T < 1 s时,会将放大后的外部参考速度误差引入到滤波器中,从而降低滤波器估计精度,所以应取T≥1 s.适当增大积分时间T有助于提高观测量精度,从而提高滤波器的估计精度.惯性导航系统误差具有低频特性,在短时间内可认为其误差为常值,基于卡尔曼滤波的外阻尼算法正是基于此特性设计的,因此积分时间也不能过大,一般T≤15 s为宜.基于卡尔曼滤波的外阻尼原理图[14]如图 1所示.
|
图 1 基于卡尔曼滤波的外阻尼原理图 Figure 1 Principle diagram of damping SINS based on Kalman filter |
由图 1可知,基于卡尔曼滤波的外阻尼算法,以速度的变化作为外部参考输入,屏蔽了常值测速误差对整个系统的干扰.
2 基于双滤波器的改进外阻尼导航算法以速度误差为观测量的组合导航算法的系统状态方程如式(1)所示,其观测模型为
| $ {\mathit{\boldsymbol{Z}}_1} = {\mathit{\boldsymbol{H}}_1}\mathit{\boldsymbol{X}} + \delta {\mathit{\boldsymbol{Z}}_1}. $ | (3) |
式中:H1=[I2×2 02×11],Z1为惯导东向速度、北向速度分别与外参考东向速度、北向速度的差值所构成的速度误差矢量.
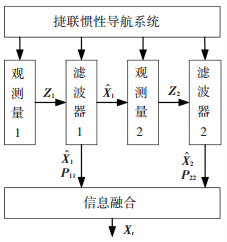
以速度误差作为观测量虽然会将常值测速误差引入到系统当中,导致系统发散[16].但是,相比图 1所示的方法,该方法可以使误差快速收敛,尤其是对于地球振荡误差而言,其误差收敛速度提升更为明显.因此,为了进一步提高系统精度及误差收敛速度,充分利用两种滤波器的优点,设计如图 2所示的串行结构进行信息融合,其中,滤波器1和滤波器2的校正机制均为输出校正,滤波器1和滤波器2的系统状态方程模型均如式(1)所示,滤波器1的观测模型如式(3)所示,滤波器2的观测模型如式(2)所示.
|
图 2 基于双滤波器的外阻尼导航算法 Figure 2 Principle diagram of external damping SINS based on double-filters |
如图 2所示,滤波器1采用式(3)所示观测量进行卡尔曼滤波估计,然后利用滤波器1得到的估计,补偿捷联惯导系统速度误差,得到平滑后的外部参考速度值.捷联惯导系统输出的东向速度和北向速度分别为vINSE和vINSN,滤波器1估计得到的东向速度误差和北向速度误差分别为
| $ \mathit{\boldsymbol{\tilde v = }}{\left[ {\begin{array}{*{20}{c}} {v_{{\rm{INS}}}^{\rm{E}} - \hat v_{\rm{1}}^{\rm{E}}}&{v_{{\rm{INS}}}^{\rm{N}} - \hat v_{\rm{1}}^{\rm{N}}} \end{array}} \right]^{\rm{T}}}. $ | (4) |
速度
在滤波过程中,原始外速参考设备输出速度经平滑后,其误差中的高频噪声被有效滤除,剩余误差中主要含有低频误差,且剩余误差较小,滤波器2以速度差值作为外部参考输入,对低频误差不敏感,工程上可将滤波器2的外部参考输入误差视为高斯白噪声,以构造滤波器2的观测模型.
利用速度
设两个局部滤波器的状态估计分别为
| $ {{\mathit{\boldsymbol{\hat X}}}_{\rm{r}}} = {\mathit{\boldsymbol{A}}_1}{{\mathit{\boldsymbol{\hat X}}}_1}\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{A}}_2}{{\mathit{\boldsymbol{\hat X}}}_2}. $ | (5) |
式中:A1和A2为待定的加权对角阵,且满足A1+A2=I.
由于估计误差协方差矩阵的对角阵表征了相应状态的估计精度,因此,需求得待定加权对角阵,使得全局估计
| $ {\mathit{\boldsymbol{P}}_{\rm{r}}} = {\rm{diag}}\left( {E\left\{ {\left( {\mathit{\boldsymbol{X}} - {{\mathit{\boldsymbol{\hat X}}}_{\rm{r}}}} \right){{\left( {\mathit{\boldsymbol{X}} - {{\mathit{\boldsymbol{\hat X}}}_{\rm{r}}}} \right)}^{\rm{T}}}} \right\}} \right). $ | (6) |
经过推导[15],并利用方差上界技术[16]简化后,得到信息融合后的全局估计
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{P}}_{\rm{g}}} = {\left( {{\rm{diag}}{{\left( {{\mathit{\boldsymbol{P}}_{11}}} \right)}^{ - 1}} + {\rm{diag}}{{\left( {{\mathit{\boldsymbol{P}}_{22}}} \right)}^{ - 1}}} \right)^{ - 1}},\\ {{\mathit{\boldsymbol{\hat X}}}_{\rm{g}}} = {\mathit{\boldsymbol{P}}_{\rm{g}}}\left( {{\rm{diag}}{{\left( {{\mathit{\boldsymbol{P}}_{11}}} \right)}^{ - 1}}{{\hat X}_1} + {\rm{diag}}{{\left( {{\mathit{\boldsymbol{P}}_{22}}} \right)}^{ - 1}}{{\mathit{\boldsymbol{\hat X}}}_2}} \right). \end{array} \right. $ | (7) |
当外部参考速度存在常值误差时,必然导致滤波器1得到的估计结果随时间发散,而由于卡尔曼滤波是一种无偏估计,所以,随着时间的增加,滤波器1的估计误差协方差矩阵的可信度将降低,因此,需要引入加权系数β对P11进行加权处理,以降低常值速度误差对整个系统的影响.
| $ {{\mathit{\boldsymbol{P'}}}_{11}} = \beta {\mathit{\boldsymbol{P}}_{11}}, $ | (8) |
且
| $ \left\{ \begin{array}{l} \beta = \mathit{\boldsymbol{I}} + \gamma \mathit{\boldsymbol{\bar X}}{{\mathit{\boldsymbol{\bar X}}}^{\rm{T}}}\mathit{\boldsymbol{P}}_{11}^{ - 1},\\ \gamma = \frac{1}{{1 + {{\rm{e}}^{ - a\left( {t - {t_0} - {t_m}} \right)}}}}. \end{array} \right. $ | (9) |
式中:
由式(9)可知,X为两个滤波器估计状态间的差值的平均值,当存在外速常值误差时,滤波器1的状态估计精度降低,且估计误差随时间发散,而滤波器2采用速度变化作为外部输入,其估计精度不受常值速度误差影响,所以,XXT在一定程度上反映了滤波器1估计状态的发散程度,其值越大,表明发散越严重,滤波器1的估计值可信度越低.然而,滤波初期,滤波时间较短,滤波器1发散并不严重,其短时精度相对较高,而滤波器2的各误差状态处于收敛状态,尤其是地球振荡误差收敛时间最长,因此,滤波初期,XXT的可信度较低. γ随时间由0到1连续变化,利用γ对XXT进行加权,降低滤波初期XXT对信息融合的影响,以获得较高的初期估计精度.引入加权系数β后,式(7)变为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{P}}_{\rm{g}}} = {\left( {{\rm{diag}}{{\left( {\beta {\mathit{\boldsymbol{P}}_{11}}} \right)}^{ - 1}} + {\rm{diag}}{{\left( {\beta {\mathit{\boldsymbol{P}}_{22}}} \right)}^{ - 1}}} \right)^{ - 1}},\\ {{\mathit{\boldsymbol{\hat X}}}_{\rm{g}}} = {\mathit{\boldsymbol{P}}_{\rm{g}}}\left( {{\rm{diag}}{{\left( {\beta {\mathit{\boldsymbol{P}}_{11}}} \right)}^{ - 1}}{{\mathit{\boldsymbol{\hat X}}}_1} + {\rm{diag}}{{\left( {{\mathit{\boldsymbol{P}}_{22}}} \right)}^{ - 1}}{{\mathit{\boldsymbol{\hat X}}}_2}} \right). \end{array} \right. $ | (10) |
由式(10)可知,随着时间的增加,β逐渐增加,使得
由式(9)可知,加权修正因子的作用是在滤波初期对XXT进行加权处理,以降低滤波器2的处于收敛状态的各误差对信息融合精度的影响,当加权修正因子由0过渡到1后,对XXT的信任程度到达最大,此时信息融合精度主要由XXT的值进行调节. XXT的值越大,则说明滤波器1误差发散的越为严重,加权系数β的值也随之增大,从而降低了
陀螺仪常值漂移为0.005 °/h,加速度计零偏为5×10-5g.
惯导系统初始纬度误差为2″,初始经度误差为2″,初始东向速误差为0.1 m/s,初始北向速度误差为0.1 m/s,初始纵摇角误差为0.7′,初始横摇角误差为0.7′,初始航向角误差为7.7′.
外部参考速度模型为
| $ {\mathit{\boldsymbol{v}}_{\rm{r}}} = \left[ {\begin{array}{*{20}{c}} {v_{\rm{r}}^{\rm{E}}}\\ {v_{\rm{r}}^{\rm{N}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{C_{\rm{E}}}}\\ {{C_{\rm{N}}}} \end{array}} \right] + \delta {\mathit{\boldsymbol{v}}_{\rm{r}}}. $ | (11) |
式中:vrE为东向参考速度真值,vrN为北向参考速度真值;CE为东向常值误差,CN为北向常值误差;δvr为白噪声误差向量.
载体在0~1 000 s间处于静止状态,1 000 s后载体开始作加速运动,加速运动持续100 s,之后载体处于匀速运动状态,东向速度恒定在10 m/s,北向速度恒定在8 m/s,直到仿真结束.
滤波器1的驱动噪声矩阵Q1和量测噪声矩阵R1分别为
| $ \begin{array}{l} {\mathit{\boldsymbol{Q}}_1} = 2{\rm{diag}}\left( {\left[ {{{\left( {{{10}^{ - 4}}g} \right)}^2},{{\left( {{{10}^{ - 4}}g} \right)}^2},0,0,{{\left( {{{0.01}^ \circ }/h} \right)}^2},} \right.} \right.\\ \;\;\;\;\;\;\;{\left( {{{0.01}^ \circ }/h} \right)^2},{\left( {{{0.01}^ \circ }/h} \right)^2}{\left( {{{10}^{ - 5}}g} \right)^2},{\left( {{{10}^{ - 5}}g} \right)^2},\\ \;\;\;\;\;\;\;{\left( {{{10}^{ - 5}}g} \right)^2},{\left( {{{0.001}^ \circ }/h} \right)^2},{\left( {{{0.001}^ \circ }/h} \right)^2},\\ \;\;\;\;\;\;\;\left. {{{\left. {{{\left( {{{0.001}^ \circ }/h} \right)}^2}} \right]}^{\rm{T}}}} \right), \end{array} $ |
| $ {\mathit{\boldsymbol{R}}_1} = {\rm{diag}}\left( {{{\left[ {{{\left( {0.05\;{\rm{m}}/{\rm{s}}} \right)}^2},{{\left( {0.05\;{\rm{m}}/{\rm{s}}} \right)}^2}} \right]}^{\rm{T}}}} \right). $ |
滤波器2的驱动噪声矩阵Q2和量测噪声矩阵R2分别为
| $ \begin{array}{l} {\mathit{\boldsymbol{Q}}_2} = 2{\rm{diag}}\left( {\left[ {{{\left( {{{10}^{ - 4}}g} \right)}^2},{{\left( {{{10}^{ - 4}}g} \right)}^2},0,0,{{\left( {{{0.01}^ \circ }/{\rm{h}}} \right)}^2},} \right.} \right.\\ \;\;\;\;\;\;\;{\left( {{{0.01}^ \circ }/{\rm{h}}} \right)^2},{\left( {{{0.01}^ \circ }/{\rm{h}}} \right)^2}{\left( {{{10}^{ - 5}}g} \right)^2},{\left( {{{10}^{ - 5}}g} \right)^2},\\ \;\;\;\;\;\;\;{\left( {{{10}^{ - 5}}g} \right)^2},{\left( {{{0.001}^ \circ }/{\rm{h}}} \right)^2},{\left( {{{0.001}^ \circ }/{\rm{h}}} \right)^2},\\ \;\;\;\;\;\;\;\left. {{{\left. {{{\left( {{{0.001}^ \circ }/{\rm{h}}} \right)}^2}} \right]}^{\rm{T}}}} \right), \end{array} $ |
| $ {\mathit{\boldsymbol{R}}_2} = {\rm{diag}}\left( {{{\left[ {{{\left( {0.001\;{\rm{m}}/{\rm{s}}} \right)}^2},{{\left( {0.001\;{\rm{m}}/{\rm{s}}} \right)}^2}} \right]}^{\rm{T}}}} \right). $ |
其中diag(·)表示矢量·的对角阵.加权修正因子γ相关参数选取:a=0.000 5,t0=2.5×3 600 s,tm=4×3 600 s.滤波器2的积分时间T=5 s,外部参考速度常值误差CE=CN=-0.3 m/s.
3.2 仿真结果及分析
|
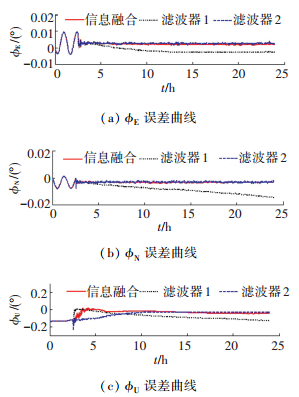
图 3 姿态误差角仿真曲线 Figure 3 Simulation curves of attitude angle errors |
|
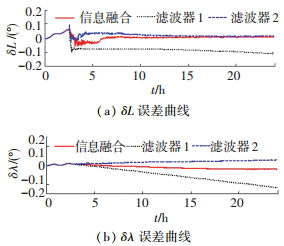
图 4 位置误差仿真曲线 Figure 4 Simulation curves of position errors |
|
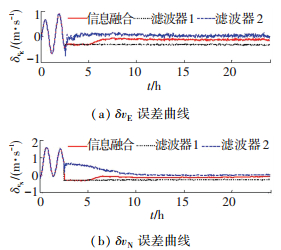
图 5 速度误差仿真曲线 Figure 5 Simulation curves of velocity errors |
由图 3~5可知,滤波器1的位置误差和姿态误差随着时间的增加而不断发散,其长期精度较差,但是在滤波初期,由于滤波时间较短,滤波器发散并不严重,其滤波精度依然满足导航需求.滤波器1在滤波开始后迅速完成了误差收敛,尤其是地球振荡误差的收敛速度明显优于滤波器2.滤波器2采用速度变化作为外部参考输入,其各项误差不会因外速常值误差而发散,所以滤波器2的长期精度高,但是,其地球振荡误差在约12 h后才完成有效收敛,收敛速度明显慢于滤波器1.经过信息融合后,系统误差结合了两种滤波器的优点.当滤波时间较短时,滤波器1的估计误差状态在融合状态中占有较大比重,此时,融合后误差状态迅速收敛到较小的误差范围内;随着滤波时间的增加,滤波器1的估计误差在融合状态中的比重逐渐减小,滤波器2的误差状态在融合状态中的比重逐渐增加,从而使得系统的长期精度得到有效保证.对于速度误差而言,信息融合后的误差状态精度也有显著提高,外参考速度常值误差得到有效补偿.
为了进一步验证信息融合算法的有效性,在其它仿真条件不变的前提下,进行了不同外速常值误差条件下的算法仿真,共5组对比仿真,外速常值误差分别取-0.1、-0.2、-0.3、-0.4、-0.5 m/s,得到的仿真结果见表 1和表 2.
| 表 1 信息融合算法在不同外速常值误差条件下的各稳态误差值 Table 1 Steady-state error values of information fusion algorithm under different external velocity constant errors |
| 表 2 滤波器1在不同外速常值误差条件下的各稳态误差值 Table 2 Steady-state error values of Filter 1 under different external velocity constant errors |
由表 2可知,随着外速常值误差的增加,滤波器1的各稳态误差的绝对值逐渐变大,有明显的发散趋势,这说明滤波器1对外速常值误差极为敏感,增加外速常值误差会严重降低滤波器1的估计精度.由表 1可知,在外速常值误差增加的过程中,信息融合后的各稳态误差值也有变化,但是没有明显的发散趋势.且对比表 1和表 2的结果可知,随着外速常值误差的增加,信息融合后的各稳态误差值始终保持在较小的范围内,明显优于滤波器1.所以,信息融合算法可以抑制外速常值误差造成的系统发散,有效提高系统导航精度.
综上所述,相较于滤波器2而言,经过信息融合后的导航误差的地球振荡误差收敛速度明显加快,其短期精度得到显著提高;相较于滤波器1而言,经过信息融合后,其稳态导航精度得到显著提高.基于双滤波器的外阻尼导航算法结合了两种滤波方法的优点,当存在外速常值误差时,有效地提高了捷联惯导系统的整体导航精度.
4 结论1) 以速度误差为观测量的组合导航系统受常值外速度误差影响严重,而基于卡尔曼滤波的外阻尼导航算法误差收敛速度相对较慢,为了抑制捷联惯导系统振荡误差,提出了一种基于双滤波器的外阻尼导航算法.
2) 该算法设计了串行的双滤波器算法,利用滤波器1对外部参考速度的平滑作用,获得相应状态估计值.而后,利用平滑后的高精度外部参考速度,以其变化值作为滤波器2的输入进行滤波,获得相应状态估计值,然后以信息融合手段进行双滤波器信息融合,以得到精度更高的估计结果.
3) 仿真结果表明:所提出的基于双滤波器的外阻尼导航算法充分结合两种滤波器的优点,降低了外速常值误差对系统精度的影响,有效缩短误差收敛时间,提高了外阻尼导航算法导航精度.
| [1] |
GAO Wei, ZHANG Ya, WANG Jianguo. Research on initial alignment self-calibration of rotary strapdown inertial navigation system[J]. Sensors, 2015, 15(2): 3154-3171. DOI:10.3390/s150203154 |
| [2] |
高伟, 叶攀, 石惠文, 等. 捷联惯导系统极区动基座对准[J]. 系统工程与电子技术, 2015, 37(3): 627-632. GAO Wei, YE Pan, SHI Huiwen, et al. Polar moving base alignment for strapdown inertial navigation system[J]. Systems Engineering and Electronics, 2015, 37(3): 627-632. DOI:10.3969/j.issn.1001-506X.2015.03.24 |
| [3] |
WANG Liduan, JIN Wenrui, ZHAN Xingqun, et al. Performance improvement and study of the space-oriented strapdown inertial navigation system[J]. Measurement Science and Technology, 2011, 22(11): 115201. DOI:10.1088/0957-0233/22/11/115201 |
| [4] |
AKEILA E, SALCIC Z, SWAIN A. Reducing low-cost INS error accumulation in distance estimation using self-resetting[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(1): 177-184. DOI:10.1109/TIM.2013.2273595 |
| [5] |
高钟毓. 惯性导航系统技术[M]. 北京: 清华大学出版社, 2012: 401-426. GAO Zhongyu. Inertial navigation system technology[M]. Beijing: Tsinghua University Press, 2012: 401-426. |
| [6] |
李魁, 张京娟, 刘芳. 长航时惯导系统的模糊控制内阻尼算法[J]. 哈尔滨工程大学学报, 2012, 33(4): 485-488. LI Kui, ZHANG Jingjuan, LIU Fang. A fuzzy control inertial damping algorithm in a long-endurance inertial navigation system[J]. Journal of Harbin Engineering University, 2012, 33(4): 485-488. DOI:10.3969/j.issn.1006-7043.201104041 |
| [7] |
程建华, 时俊宇, 荣文婷, 等. 多阻尼系数的全阻尼惯导系统的设计与实现[J]. 哈尔滨工程大学学报, 2011, 32(6): 786-791. CHENG Jianhua, SHI Junyu, RONG Wenting, et al. Research and realization of an azimuth damping inertial navigation system based on multi-damping coefficient[J]. Journal of Harbin Engineering University, 2011, 32(6): 786-791. DOI:10.3969/j.issn.1006-7043.2011.06.016 |
| [8] |
李倩, 孙枫, 奔粤阳, 等. 横坐标系捷联惯导系统极区导航及阻尼设计[J]. 系统工程与电子技术, 2014, 36(12): 2496-2503. LI Qian, SUN Feng, BEN Yueyang, et al. Transversal strapdown INS and damping design in polar region[J]. Systems Engineering and Electronics, 2014, 36(12): 2496-2503. DOI:10.3969/j.issn.1001-506X.2014.12.26 |
| [9] |
何虔恩, 高钟毓, 吴秋平. 基于未补偿偏置滤波器的惯导动态初始对准[J]. 中国惯性技术学报, 2015, 23(2): 184-188. HE Qian'en, GAO Zhongyu, WU Qiuping. Initial alignment based on uncompensated bias filter for inertial navigation systems under dynamic conditions[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 184-188. DOI:10.13695/j.cnki.12-1222/o3.2015.02.009 |
| [10] |
黄德鸣, 程禄. 惯性导航系统[M]. 北京: 国防工业出版社, 1986: 107-135. HUANG Deming, CHENG Lu. Inertial navigation system[M]. Beijing: National Defense Industry Press, 1986: 107-135. |
| [11] |
覃方君, 李安, 许江宁, 等. 阻尼参数连续可调的惯导水平内阻尼方法[J]. 中国惯性技术学报, 2011, 19(3): 290-301. TAN Fangjun, LI An, XU Jiangning, et al. Horizontal inner damping method with continuously adjustable parameter for inertial navigation system[J]. Journal of Chinese Inertial Technology, 2011, 19(3): 290-301. DOI:10.13695/j.cnki.12-1222/o3.2011.03.012 |
| [12] |
DU Yaling, LIU Jianye, LIU Ruihua, et al. The fuzzy Kalman filtering of damp attitude algorithm[J]. Journal of Astronaut, 2007, 28(2): 305-309. |
| [13] |
刘飞, 刘超, 翁海娜, 等. 基于Kalman滤波技术的捷联惯导系统水平阻尼算法[J]. 中国惯性技术学报, 2013, 21(3): 285-288. LIU Fei, LIU Chao, WENG Haina, et al. Level damping algorithm of SINS based on Kalman filtering[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 285-288. DOI:10.13695/j.cnki.12-1222/o3.2013.03.024 |
| [14] |
ZHAO Lin, LI Jiushun, CHENG Jianhua, et al. Damping strapdown inertial navigation system based on a Kalman filter[J]. Measurement Science and Technology, 2016, 27(11): 115102. DOI:10.1088/0957-0233/27/11/115102 |
| [15] |
秦永元, 张洪越, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 2007: 193-194. QIN Yongyuan, ZHANG Hongyue, WANG Shuhua. Principle of Kalman filtering and integrated navigation[M]. Xi'an: Northwestern Polytechnical University Press, 2007: 193-194. |
| [16] |
杨宏韬. 基于多源数据融合的光电跟踪系统精度提高方法的研究[D]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2016. YANG Hongtao. Research on the method of improving accuracy of photoelectric tracking system based on multi-source data fusion[D]. Changchun: University of Chinese Academy of Sciences (Changchun Institute of Optics, Fine Mechanics and Physics), 2016. |
 2018, Vol. 50
2018, Vol. 50


