近年来,深空探测、空间碎片清除和在轨服务等项目逐渐得到了较大的重视与关注.面对这些复杂多样的任务,航天器姿态跟踪控制性能将起到至关重要的作用.除特殊的任务要求以外,复杂的空间环境、航天器姿态动力学的耦合与高度非线性、大型太阳帆板等挠性结构存在的振动影响以及严格的性能指标约束均对控制系统设计提出巨大的挑战,因此研究可靠性高、性能优良的姿态跟踪控制方法具有一定的理论价值与工程意义.
面对空间环境以及姿态动力学特性带来的不确定因素,自适应控制能够通过实时调整自身参数以适应干扰等不确定性的影响,适用于挠性航天器姿态跟踪控制系统中.并且可以与其他控制方法相结合应用,进一步提升处理系统不确定性的能力.文献[1-2]应用直接自适应控制方法设计了挠性航天器姿态控制器,使姿态跟踪参考模型输出,该方法不依赖于航天器惯量以及挠性振动模态信息,具有较强的鲁棒性.针对敏捷卫星的三轴姿态控制与挠性振动抑制问题,文献[3]采用了自适应鲁棒控制方法应对参数不确定性与干扰影响,设计中适当减少待估计系统参数的数量,以便于进行实时在线控制.基于滑模控制的方法,文献[4]提出了一种航天器姿态跟踪控制器,并对控制参数进行自适应估计,有效降低了模型不确定性对系统性能产生的影响.文献[5]在存在模型参数不确定性和外界干扰的情况下采用自适应滑模控制实现了挠性航天器姿态跟踪控制任务.文献[6]将一种基于自适应方法的积分滑模控制策略应用于挠性航天器容错控制中,所构造的自适应滑模控制器可以补偿外界干扰和未知时变故障,增加了系统的可靠性.神经网络具有较强的自学习和非线性函数映射能力,因此可用来逼近外界干扰和模型不确定性信息,并通过自适应调整权值信息,实现对不确定系统的自适应控制[7].考虑执行机构饱和与部分失效故障等问题,文献[8]研究了一种挠性航天器姿态跟踪控制策略,引入单层神经网络处理模型不确定性,并设计自适应律估计故障的上界.为完成挠性航天器高精度高稳定度的姿态控制需求,文献[9]采用RBF神经网络估计并补偿非线性耦合、未知干扰和挠性等不确定性的影响.文献[10]基于多层神经网络设计了航天器自适应被动容错控制器,并提出了一种新型学习算法,增强了神经网络的逼近能力.
在执行某些特定任务时,要求航天器姿态能够快速且准确的跟踪目标.例如,对某区域或星体快速定向并拍照.此时则需要姿态控制系统具有期望的动态过程和高稳态精度.通常情况下所采用的方法是事先规划姿态运动轨迹再设计控制器进行跟踪[11],或利用全局滑模控制的思想使误差轨迹按期望情况运行[12].上述方法虽然可以预先给定姿态的期望性能,然而最终的姿态跟踪效果取决于控制器的能力或控制增益的大小.2008年希腊学者Bechlioulis等[13]提出了一种预设性能(prescribed performance)控制方法.该方法通过引入性能函数与误差变换,使收敛速度、超调以及跟踪误差获得预先设定的性能,一定程度上放宽了对控制参数选取的要求.近年来,预设性能方法在一些领域中得到了广泛的应用,如挠性关节机器人系统[14]、伺服系统[15]、挠性吸气式高超声速飞行器系统[16]和随机系统[17]等.
本文针对挠性航天器的姿态跟踪控制问题,提出一种基于预设性能方法的自适应神经网络控制器.采用RBF神经网络逼近未知干扰和挠性振荡等形成的模型不确定性,并自适应估计逼近误差的上界,避免需要对其已知的限制条件.采用预设性能方法,结合误差变换,使系统的姿态跟踪误差具有期望的动态过程以及稳态响应,并给出完整的自适应控制器.仿真结果表明,采用所提出的方法可以抑制干扰和挠性振动产生的影响,同时获得预先设定的期望姿态跟踪性能.
1 挠性航天器姿态的数学模型考虑航天器安装有两块挠性太阳能帆板,则挠性航天器姿态动力学方程可表示为如下形式[18]:
| $ \mathit{\boldsymbol{J\dot \omega }} + {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }} + \sum\nolimits_l {\left( {{\mathit{\boldsymbol{F}}_{{\rm{s}}l}}{{\mathit{\boldsymbol{\ddot \eta }}}_l} + {\mathit{\boldsymbol{\omega }}^ \times }{\mathit{\boldsymbol{F}}_{{\rm{s}}l}}{{\mathit{\boldsymbol{\dot \eta }}}_l}} \right)} = \mathit{\boldsymbol{u}} + \mathit{\boldsymbol{d}}, $ | (1) |
| $ {{\mathit{\boldsymbol{\ddot \eta }}}_l} + 2{\mathit{\boldsymbol{\xi }}_l}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_l}{{\mathit{\boldsymbol{\dot \eta }}}_l} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_l^2{\mathit{\boldsymbol{\eta }}_l} + \mathit{\boldsymbol{F}}_{{\rm{s}}l}^{\rm{T}}\mathit{\boldsymbol{\dot \omega }} = 0. $ | (2) |
式中:ω=[ω1 ω2 ω3]T∈R3为航天器本体相对于惯性坐标系的角速度矢量;J∈R3×3为整体转动惯量矩阵;u∈R3为三轴控制力矩矢量;d∈R3为所受的环境干扰力矩矢量;Fsl∈R3×n为模态振动与本体转动耦合系数;n为模态阶数;ηl∈Rn为挠性模态坐标;l=1、l=2分别为板编号;ξl、Ωl分别为n维对角矩阵,表示挠性附件的模态阻尼比和频率矩阵;符号ω×为如下的反对称矩阵
| $ {\mathit{\boldsymbol{\omega }}^ \times } = \left[ {\begin{array}{*{20}{c}} 0&{ - {\omega _3}}&{{\omega _2}}\\ {{\omega _3}}&0&{ - {\omega _1}}\\ { - {\omega _2}}&{{\omega _1}}&0 \end{array}} \right]. $ |
采用ϑ∈R3表示航天器的三轴姿态角,分别为滚动角φ、俯仰角θ和偏航角ψ.考虑航天器作惯性定向飞行,则在x-y-z转序下的姿态运动学方程可表示为[19]
| $ \left[ {\begin{array}{*{20}{c}} {\dot \varphi }\\ {\dot \theta }\\ {\dot \psi } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \psi \sec \theta }&{ - \sin \psi \sec \theta }&0\\ {\sin \psi }&{\cos \psi }&0\\ { - \cos \psi \tan \theta }&{\sin \psi \tan \theta }&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\omega _x}}\\ {{\omega _y}}\\ {{\omega _z}} \end{array}} \right], $ | (3) |
记作
| $ {\mathit{\boldsymbol{J}}^ * }\left( {\pmb \vartheta} \right)\ddot {\pmb \vartheta} + \mathit{\boldsymbol{C}}\left( {{\pmb \vartheta} ,\dot {\pmb \vartheta}} \right)\dot {\pmb \vartheta} = {\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{D}}. $ | (4) |
式中:J*(ϑ)=GTJG,C(ϑ,
假设1 姿态角ϑ与姿态角速度
假设2 期望姿态角ϑd及其一阶和二阶导数已知且有界.
假设3 总干扰D有界,即||D||≤χ,其中χ为未知正常数.
本文的姿态控制目标可以表述为:设计控制器u使系统姿态角ϑ能够跟踪期望姿态角ϑd并使跟踪误差e=ϑ-ϑd具有预先给定的动态性能及稳态响应情况.
2 预设性能控制方法首先给出性能函数的定义.
定义1[13] 对于光滑函数ρ(t):R+→R,如果其满足如下条件:
1) ρ(t)单调递减且恒为正;
2)
通常可将性能函数设计为
| $ \rho \left( t \right) = \left( {{\rho _0} - {\rho _\infty }} \right){{\rm{e}}^{ - kt}} + {\rho _\infty }, $ | (5) |
式中ρ0、ρ∞、k分别为预先给定的正常数.
利用性能函数可以将跟踪误差表示为:
| $ \begin{array}{l} - {\delta _i}{\rho _i}\left( t \right) < {e_i}\left( t \right) < {\rho _i}\left( t \right),{e_i}\left( 0 \right) \ge 0;\\ - {\rho _i}\left( t \right) < {e_i}\left( t \right) < {\delta _i}{\rho _i}\left( t \right),{e_i}\left( 0 \right) < 0. \end{array} $ | (6) |
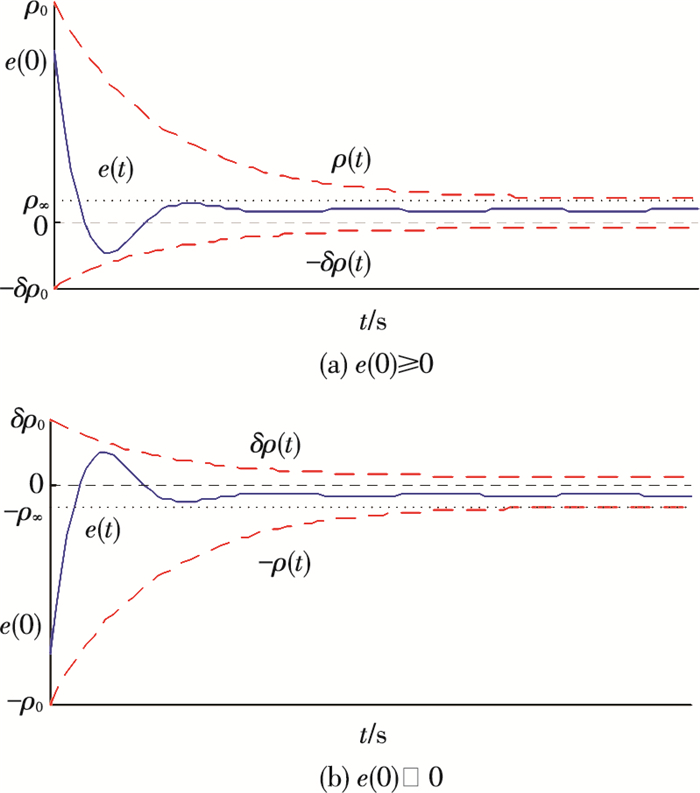
式中ei(t), i=1, 2, 3为航天器三轴姿态误差,0≤δi≤1.根据性能函数(5)和式(6)的形式可知,如果跟踪误差初值满足0≤|ei(0)|<ρi(0),则参数ki限制了跟踪误差的最小收敛速率,而ρi∞给定了允许的稳态跟踪误差的上界,同时系统响应的超调不会超过δiρi(t).因此,设计适当的性能函数ρi(t)及δi即可获得期望的系统误差响应.图 1给出了在性能函数ρ(t)及参数δ约束下误差响应曲线的范例.
|
图 1 预设跟踪误差响应曲线范例 Figure 1 An example of prescribed tracking error response curve |
为解决由式(6)表示的预设性能控制问题,采用一种误差变换方式将约束下的跟踪控制问题转化为无约束的稳定控制问题.定义函数Si(εi),具有以下性质.
性质1 Si(εi)光滑且严格单调递增.
性质2
性质3
其中εi∈(-∞, +∞)称为变换误差.满足上述条件的一个函数Si(εi)由下式给出:
| $ {S_i}\left( {{\varepsilon _i}} \right) = \left\{ \begin{array}{l} \frac{{{{\rm{e}}^{{\varepsilon _i}}} - {\delta _i}{{\rm{e}}^{ - {\varepsilon _i}}}}}{{{{\rm{e}}^{{\varepsilon _i}}} + {{\rm{e}}^{ - {\varepsilon _i}}}}},\;\;\;\;\;{{\rm{e}}_i}\left( 0 \right) \ge 0;\\ \frac{{{\delta _i}{{\rm{e}}^{{\varepsilon _i}}} - {{\rm{e}}^{ - {\varepsilon _i}}}}}{{{{\rm{e}}^{{\varepsilon _i}}} + {{\rm{e}}^{ - {\varepsilon _i}}}}},\;\;\;\;\;{{\rm{e}}_i}\left( 0 \right) < 0. \end{array} \right. $ | (7) |
根据Si(εi)的特性,式(6)可等价表示为
| $ {e_i}\left( t \right) = {\rho _i}\left( t \right){S_i}\left( {{\varepsilon _i}} \right), $ |
因为Si(εi)是严格单调递增的,所以存在反函数为
| $ {\varepsilon _i} = S_i^{ - 1}\left( {\frac{{{e_i}\left( t \right)}}{{{\rho _i}\left( t \right)}}} \right). $ | (8) |
如果能够控制εi有界,则可以保证式(6)成立,进而在性能函数ρi(t)的约束下使跟踪误差达到期望目标.此时系统(4)的跟踪控制问题便转化为以εi为变量的闭环系统的稳定控制问题.
考虑Si(εi)取式(7)的形式,则有
| $ {\varepsilon _i} = S_i^{ - 1}\left( {\frac{{{e_i}\left( t \right)}}{{{\rho _i}\left( t \right)}}} \right) = \left\{ \begin{array}{l} \frac{1}{2}\ln \frac{{{z_i} + {\delta _i}}}{{1 - {z_i}}},\;\;\;\;\;{e_i}\left( 0 \right) \ge 0;\\ \frac{1}{2}\ln \frac{{{z_i} + 1}}{{{\delta _i} - {z_i}}},\;\;\;\;\;{e_i}\left( 0 \right) < 0. \end{array} \right. $ | (9) |
式中zi=ei(t)/ρi(t).
注1 由式(9)知,对于ei(0)=0的情况,δi不能取为零.因为当δi=0时,将会使变换误差初值εi(0)趋近于无穷.
令εi对时间t求导可得
| $ {{\dot \varepsilon }_i} = \frac{{\partial S_i^{ - 1}}}{{\partial {z_i}}} \cdot {{\dot z}_i} = \frac{{\partial S_i^{ - 1}}}{{\partial {z_i}}} \cdot \frac{{{{\dot e}_i}{\rho _i} - {e_i}{{\dot \rho }_i}}}{{{\rho _i} \cdot {\rho _i}}} = {r_i}\left( {{{\dot e}_i} - \frac{{{e_i}{{\dot \rho }_i}}}{{{\rho _i}}}} \right), $ |
式中ri=(∂Si-1/∂zi)·(1/ρi)可通过式(9)计算获得,由于(∂Si-1/∂zi)>0和ρi(t)>0可知ri恒大于零,且只要误差ei(t)的轨迹严格限制在式(6)的范围内,则ri有界即满足r<ri<r,r和r为正常数.
进一步求εi对时间t的二阶导数有
| $ \begin{array}{l} {{\ddot \varepsilon }_i} = {{\dot r}_i}\left( {{{\dot e}_i} - \frac{{{e_i}{{\dot \rho }_i}}}{{{\rho _i}}}} \right) + {r_i}\left( {{{\ddot e}_i} - \frac{{{{\dot e}_i}{{\dot \rho }_i}{\rho _i} + {e_i}{{\ddot \rho }_i}{\rho _i} - {e_i}\dot \rho _i^2}}{{\rho _i^2}}} \right) = \\ \;\;\;\;\;\;{{\dot r}_i}\left( {{{\dot e}_i} - \frac{{{e_i}{{\dot \rho }_i}}}{{{\rho _i}}}} \right) - {r_i}\frac{{{{\dot e}_i}{{\dot \rho }_i}{\rho _i} + {e_i}{{\ddot \rho }_i}{\rho _i} - {e_i}\dot \rho _i^2}}{{\rho _i^2}} + \\ \;\;\;\;\;\;{r_i}\left( {{{\ddot \vartheta }_i} - {{\ddot \vartheta }_{{\rm{d}}i}}} \right), \end{array} $ |
式中ϑi、ϑdi(i=1, 2, 3)分别为航天器三轴的姿态角和期望姿态角.
取误差变量s∈R3为如下形式:
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{\lambda \varepsilon }} + \mathit{\boldsymbol{\dot \varepsilon }}, $ | (10) |
式中ε=[ε1, ε2, ε3]T,λ=diag[λ1, λ2, λ3]>0为待设计参数.考虑到模型(4)可化为
| $ \ddot {\pmb \vartheta} = - {\mathit{\boldsymbol{J}}^{ * - 1}}\left( {\pmb \vartheta} \right)\mathit{\boldsymbol{C}}\left( {{\pmb \vartheta} ,\dot {\pmb \vartheta} } \right)\dot {\pmb \vartheta} + {\mathit{\boldsymbol{J}}^{ * - 1}}\left({\pmb \vartheta} \right){\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{u + }}{\mathit{\boldsymbol{J}}^{ * - 1}}\left( {\pmb \vartheta}\right)\mathit{\boldsymbol{D}}, $ |
记A=-J*-1(ϑ)C(ϑ,
| $ \mathit{\boldsymbol{\dot s}} = \mathit{\boldsymbol{\lambda \dot \varepsilon }} + \mathit{\boldsymbol{\ddot \varepsilon }} = \mathit{\boldsymbol{V}} + \mathit{\boldsymbol{R}}\left( {\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{Bu}} + \mathit{\boldsymbol{\bar D}}} \right). $ | (11) |
式中:V=[v1, v2, v3]T.
系统(11)中存在不确定非线性项D,采用RBF神经网络进行逼近,即[20]
| $ \mathit{\boldsymbol{\bar D}} = {\mathit{\boldsymbol{W}}^{ * {\rm{T}}}}\mathit{\boldsymbol{h}}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{\mu }}. $ |
式中:x∈Ωx⊂Rq为神经网络输入向量;h(x)=[h1(x), h2(x), …, hj(x), …, hm(x)]T∈Rm.其中m为网络隐层节点数,hj(x)通常采用高斯基函数的形式,有
| $ {h_j}\left( \mathit{\boldsymbol{x}} \right) = \exp \left( { - \frac{{\left\| {\mathit{\boldsymbol{x}} - c} \right\|}}{{2b_j^2}}} \right),j = 1,2, \cdots m $ |
式中:cj为网络中第j个节点的中心向量,cj=[cj1, cj2, …, cjq]T;bj>0为节点j的基宽值.W*=[W1*, W2*, W3*]∈Rm×3网络的理想权值阵;μ∈R3为逼近误差,且满足||μ||≤μ*,μ*为未知的正常数.对于权值矩阵W∈Rm×3,理想情况的W*定义为
| $ {\mathit{\boldsymbol{W}}^ * } = \arg \mathop {\min }\limits_{\mathit{\boldsymbol{W}} \in {{\bf{R}}^{m \times 3}}} \left\{ {\mathop {\sup }\limits_{x \in {\mathit{\Omega }_x}} \left\| {\mathit{\boldsymbol{\bar D}} - {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{h}}\left( \mathit{\boldsymbol{x}} \right)} \right\|} \right\}. $ |
将神经网络输入取为x=[eT,
| $ \mathit{\boldsymbol{\hat {\bar D}}} = {{\mathit{\boldsymbol{\hat W}}}^{\rm{T}}}\mathit{\boldsymbol{h}}\left( \mathit{\boldsymbol{x}} \right), $ |
式中
综合以上分析过程,并考虑到逼近误差的上界μ*未知,提出如下自适应控制器:
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{B}}^{ - 1}}\left( { - \mathit{\boldsymbol{A}} - {\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{V}} - \mathit{\boldsymbol{\hat {\bar D}}} - {{\hat \mu }^2}\frac{\mathit{\boldsymbol{s}}}{{\hat \mu \left\| \mathit{\boldsymbol{s}} \right\| + \sigma }} - \mathit{\boldsymbol{Ks}}} \right), $ | (12) |
| $ {{\mathit{\boldsymbol{\dot {\hat W}}}}_i} = {\tau _{wi}}\left[ {{\mathit{\boldsymbol{s}}_i}\mathit{\boldsymbol{h}}\left( \mathit{\boldsymbol{x}} \right) - \beta {{\mathit{\boldsymbol{\hat W}}}_i}} \right],i = 1,2,3, $ | (13) |
| $ \dot {\hat \mu} = {\tau _\mu }\left( {\left\| \mathit{\boldsymbol{s}} \right\| - \gamma \hat \mu } \right). $ | (14) |
式中:
定理1 考虑挠性航天器姿态控制系统(4),通过误差变换(8)化为误差系统(11),如果将控制器u设计为式(12)的形式并采用式(13)、(14)的自适应律,则变换误差εi一致最终有界,且跟踪误差ei满足预设性能约束式(6).
证明 因为矩阵R对称正定且ri有界,可以选取Lyapunov函数为
| $ L = \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{s + }}\frac{1}{2}{\rm{tr}}\left( {{{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_w^{ - 1}\mathit{\boldsymbol{\tilde W}}} \right) + \frac{1}{2} \cdot \frac{1}{{{\tau _\mu }}}{{\tilde \mu }^2}. $ |
式中:
| $ \begin{array}{l} \dot L = {\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{\dot s}} + {\rm{tr}}\left( {{{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_w^{ - 1}\mathit{\boldsymbol{\tilde W}}} \right) + \frac{1}{{{\tau _\mu }}}\tilde \mu \dot {\tilde \mu} = \\ \;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\left[ {\mathit{\boldsymbol{V}} + \mathit{\boldsymbol{R}}\left( {\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{Bu}} + \mathit{\boldsymbol{\bar D}}} \right)} \right] + \sum\limits_{i = 1}^3 {\frac{1}{{{\tau _{wi}}}}\mathit{\boldsymbol{\tilde W}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot {\hat W}}}}_i}} + \\ \;\;\;\;\;\frac{1}{{{\tau _\mu }}}\tilde \mu \dot {\hat \mu} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\left[ { - {{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{h}}\left( \mathit{\boldsymbol{x}} \right) + \mu - {{\hat \mu }^2}\frac{s}{{\hat \mu \left\| \mathit{\boldsymbol{s}} \right\| + \sigma }} - \mathit{\boldsymbol{Ks}}} \right] + \\ \;\;\;\;\;\sum\limits_{i = 1}^3 {\mathit{\boldsymbol{\tilde W}}_i^{\rm{T}}\left[ {{\mathit{\boldsymbol{s}}_i}\mathit{\boldsymbol{h}}\left( \mathit{\boldsymbol{x}} \right) - \beta {{\mathit{\boldsymbol{\hat W}}}_i}} \right]} + \tilde \mu \left( {\left\| \mathit{\boldsymbol{s}} \right\| - \gamma \hat \mu } \right) \le - {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{Ks + }}\\ \;\;\;\;\;\left\| \mathit{\boldsymbol{s}} \right\|\hat \mu - {{\hat \mu }^2}\frac{{{{\left\| \mathit{\boldsymbol{s}} \right\|}^2}}}{{\hat \mu \left\| \mathit{\boldsymbol{s}} \right\| + \sigma }} - \beta \sum\limits_{i = 1}^3 {\mathit{\boldsymbol{\tilde W}}_i^{\rm{T}}{{\mathit{\boldsymbol{\hat W}}}_i}} - \gamma \tilde \mu \hat \mu . \end{array} $ | (15) |
应用Young不等式有:
| $ \begin{array}{l} - \beta \sum\limits_{i = 1}^3 {\mathit{\boldsymbol{\tilde W}}_i^{\rm{T}}{{\mathit{\boldsymbol{\hat W}}}_i}} \le - \frac{1}{2}\beta \sum\limits_{i = 1}^3 {\mathit{\boldsymbol{\tilde W}}_i^{\rm{T}}{{\mathit{\boldsymbol{\hat W}}}_i}} + \frac{1}{2}\beta \sum\limits_{i = 1}^3 {\mathit{\boldsymbol{W}}_i^{ * {\rm{T}}}\mathit{\boldsymbol{W}}_i^ * } ,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; - \gamma \tilde \mu \hat \mu \le - \frac{1}{2}\gamma {{\hat \mu }^2} + \frac{1}{2}\gamma {\mu ^{ * 2}}. \end{array} $ |
根据自适应律(14)可知
| $ \left\| \mathit{\boldsymbol{s}} \right\|\hat \mu - {{\hat \mu }^2}\frac{{{{\left\| \mathit{\boldsymbol{s}} \right\|}^2}}}{{\hat \mu \left\| \mathit{\boldsymbol{s}} \right\| + \sigma }} = \frac{{\left( {\hat \mu \left\| \mathit{\boldsymbol{s}} \right\|} \right) \cdot \sigma }}{{\hat \mu \left\| \mathit{\boldsymbol{s}} \right\| + \sigma }} < \sigma . $ |
进一步化简式(15)得
| $ \begin{array}{*{20}{c}} {\dot L \le - {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{Ks}} - \frac{1}{2}\beta \sum\limits_{i = 1}^3 {\mathit{\boldsymbol{\tilde W}}_i^{\rm{T}}{{\mathit{\boldsymbol{\tilde W}}}_i}} - \frac{1}{2}\gamma {{\tilde \mu }^2} + }\\ {\frac{1}{2}\beta \sum\limits_{i = 1}^3 {\mathit{\boldsymbol{W}}_i^{ * {\rm{T}}}\mathit{\boldsymbol{W}}_i^ * } + \frac{1}{2}\gamma {\mu ^{ * 2}} + \sigma .} \end{array} $ |
令
| $ {{\bf{N}}_1} = \left\{ {\mathit{\boldsymbol{s}} \in {{\bf{R}}^3}:\left\| \mathit{\boldsymbol{s}} \right\| \le \sqrt {\kappa /{\lambda _{\min }}\left( \mathit{\boldsymbol{K}} \right)} } \right\}, $ |
| $ {{\bf{N}}_2} = \left\{ {{{\mathit{\boldsymbol{\tilde W}}}_i} \in {{\bf{R}}^m}:\left\| {{{\mathit{\boldsymbol{\tilde W}}}_i} \le \sqrt {2\kappa /\beta } } \right\|} \right\}, $ |
| $ {{\bf{N}}_3} = \left\{ {\tilde \mu \in {\bf{R}}:\left| {\tilde \mu } \right| \le \sqrt {2\kappa /\gamma } } \right\}, $ |
其中λmin(K)为矩阵K的最小特征值.进而有变换误差εi一致最终有界,且收敛于
| $ {{\bf{N}}_4} = \left\{ {{\varepsilon _i} \in {\bf{R}}:\left| {{\varepsilon _i}} \right| \le \sqrt {\kappa /{\lambda _{\min }}\left( \mathit{\boldsymbol{K}} \right)} /{\lambda _i}} \right\}. $ |
再根据函数Si(εi)的性质,可得约束式(6),即挠性航天器姿态控制系统(4)的跟踪误差ei获得预先指定的动态性能及稳态响应.证毕.
4 仿真分析为验证本文所设计控制方法的有效性,将其应用到某挠性航天器姿态模型中进行仿真验证.截取两挠性帆板的前4阶模态,相应的姿态模型参数及姿态初值见表 1.
| 表 1 仿真参数 Table 1 Simulation parameters |
将d当作500 km轨道附近的环境干扰力矩,记n0为轨道角速度(n0≈0.001 1 rad/s),则d(Nm)可以假设为d=0.004 5[cos n0t+1, cos n0t+sin n0t, sin n0t+1]T.
姿态角ϑ需要跟踪的期望轨迹取ϑd(°)为
| $ {{\pmb \vartheta} _{\rm{d}}} = {\left[ {0.5\sin 0.1t,\sin 0.1t, - 0.5\sin 0.1t} \right]^{\rm{T}}}. $ |
要求系统稳态控制精度达到0.005 °.考虑将三轴姿态预期的跟踪控制性能设计为:1)稳态跟踪误差不超过0.005°;2)最小收敛速度限制为e-0.15t;3)系统响应无超调.据此可以确定性能函数ρi(t)和δi的取值,见表 2.
| 表 2 性能参数取值 Table 2 Performance parameter values |
注2 系统的收敛速度理论上可以设定为任意快,然而过快的收敛速度需要执行机构提供很大的控制力矩作用.因此,应根据实际的任务需求合理进行选取.
控制器参数选取为λ=diag[0.125, 0.125, 0.125]、K=diag[0.5, 0.1, 0.5]、σ=0.01;自适应增益选取为τwi=τμ=0.5、β=γ=0.01;将RBF神经网络隐含层的节点个数取为j=7,高斯基函数的中心表示为c=[c1, …, cj, …, c7],取值如下式所示,基宽bj=0.1.
| $ \mathit{\boldsymbol{c}} = \left[ {\begin{array}{*{20}{c}} { - 0.25}&{ - 0.17}&{ - 0.08}&0&{0.08}&{0.17}&{0.25}\\ { - 0.15}&{0.10}&{ - 0.05}&0&{0.05}&{0.10}&{0.15}\\ { - 0.20}&{ - 0.13}&{ - 0.07}&0&{0.07}&{0.13}&{0.20}\\ { - 0.03}&{ - 0.02}&{ - 0.01}&0&{0.01}&{0.02}&{0.03}\\ { - 0.15}&{ - 0.10}&{ - 0.05}&0&{0.05}&{0.10}&{0.15}\\ { - 0.03}&{ - 0.02}&{ - 0.01}&0&{0.01}&{0.02}&{0.03} \end{array}} \right] $ |
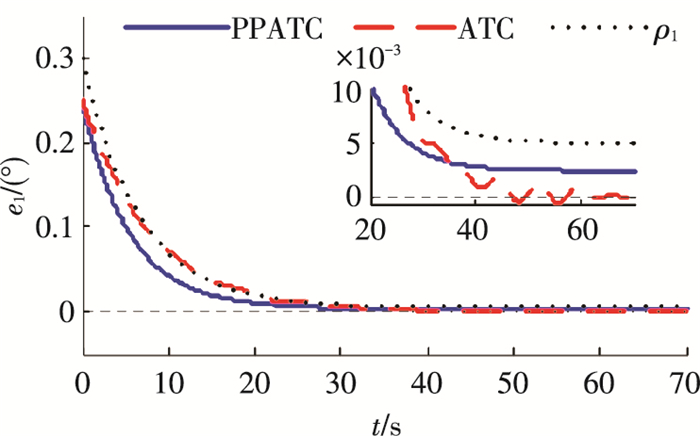
仿真结果如图 2~9所示.图 2~4给出了应用本文预设性能自适应跟踪控制器(12)~(14)的三轴姿态跟踪误差曲线,图中记为“PPATC”.
|
图 2 滚动轴姿态跟踪误差e1 Figure 2 Attitude tracking error e1 of roll axis |
|
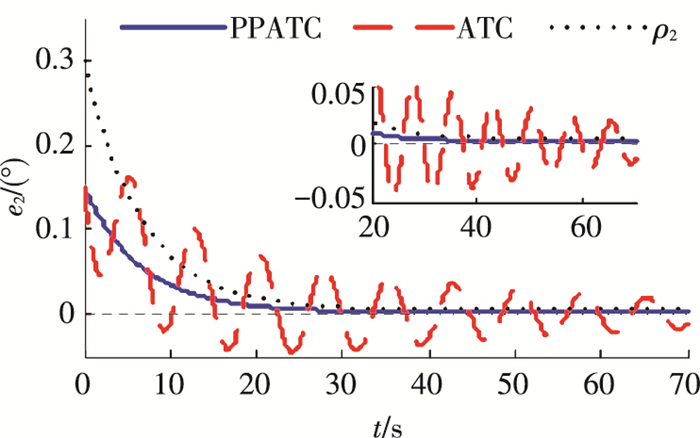
图 3 俯仰轴姿态跟踪误差e2 Figure 3 Attitude tracking error e2 of pitch axis |
|
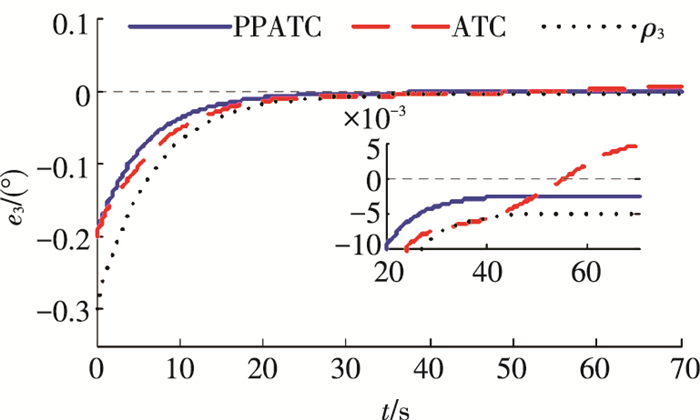
图 4 偏航轴姿态跟踪误差e3 Figure 4 Attitude tracking error e3 of yaw axis |
|
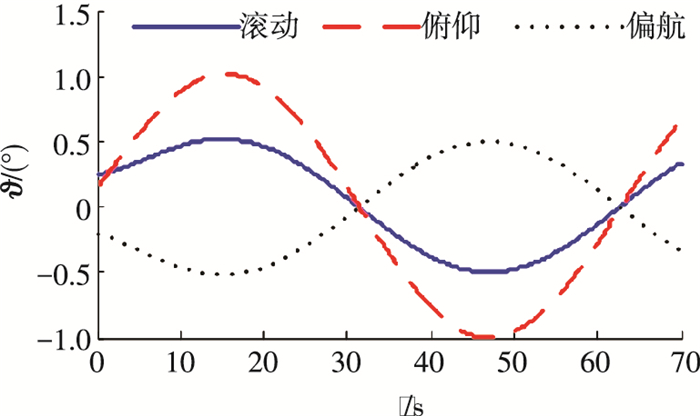
图 5 采用PPATC方法的姿态角 Figure 5 Attitude angles of PPATC method |
|
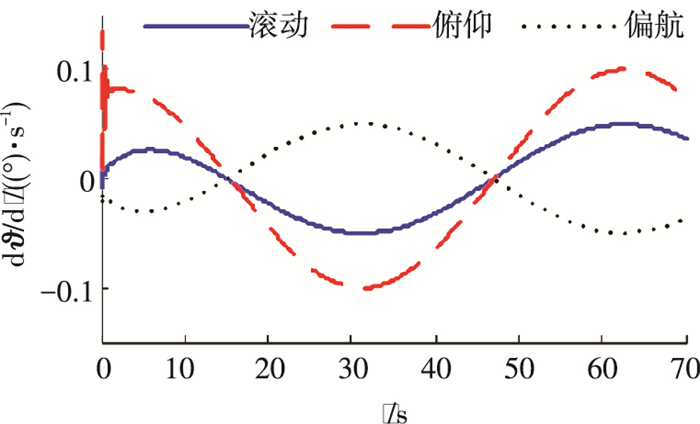
图 6 采用PPATC方法的姿态角速度 Figure 6 Attitude angular velocities of PPATC method |
|
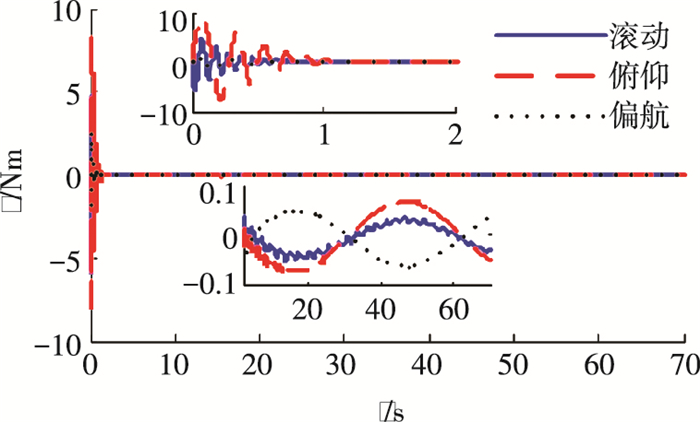
图 7 采用PPATC方法的控制力矩 Figure 7 Control torques of PPATC method |
|
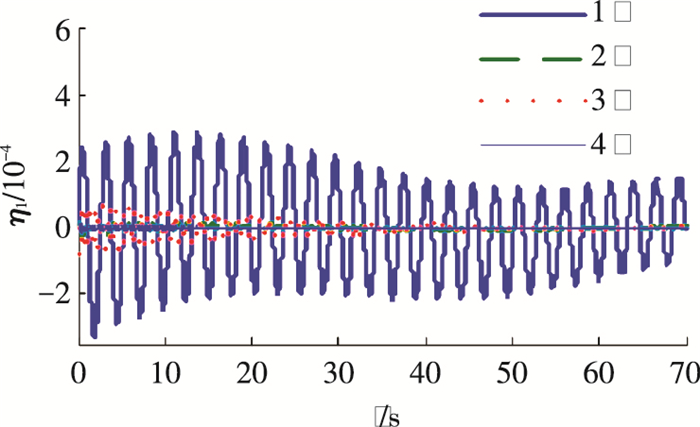
图 8 帆板1的模态坐标 Figure 8 Modal coordinates of solar array 1 |
|
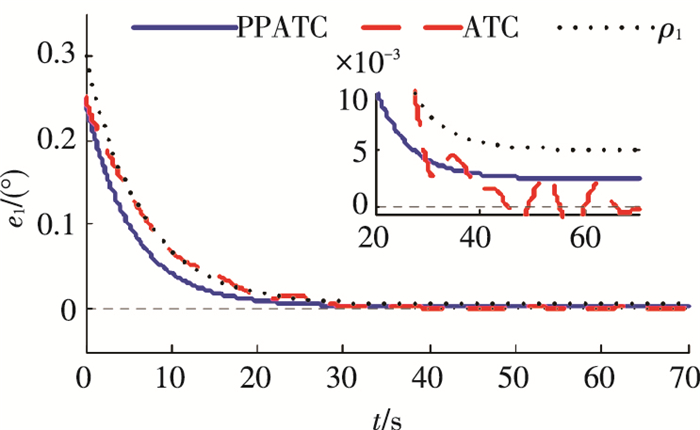
图 9 降低增益后的滚动轴姿态跟踪误差e1 Figure 9 Attitude tracking error e1 of roll axis after reducing the controller gain |
为了进行对比研究,同时给出在相同控制器形式及控制参数下未采用预设性能方法的仿真结果,称该控制器为自适应跟踪控制器,由下式给出,记为“ATC”.
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{B}}^{ - 1}}\left( { - \mathit{\boldsymbol{A}} + {{\pmb \vartheta} _{\rm{d}}} - \mathit{\boldsymbol{\lambda \dot e}} - \mathit{\boldsymbol{\hat {\bar D}}} - {{\hat \mu }^2}\frac{{{\mathit{\boldsymbol{s}}_e}}}{{\hat \mu \left\| {{\mathit{\boldsymbol{s}}_e}} \right\| + \sigma }} - \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{s}}_e}} \right),}\\ {{{\mathit{\boldsymbol{\dot {\hat W}}}}_i} = {\tau _{wi}}\left[ {{s_{ei}}\mathit{\boldsymbol{h}}\left( x \right),\beta {{\mathit{\boldsymbol{\hat W}}}_i}} \right],i = 1,2,3,}\\ {\dot {\hat \mu} = {\tau _\mu }\left( {\left\| {{\mathit{\boldsymbol{s}}_e}} \right\| - \gamma \hat \mu } \right),} \end{array} $ |
式中,se=[se1, se2, se3]T=λe+
从图 2~4可以看出,本文所提出的PPATC方法三轴姿态跟踪误差均保持在预先设定的由性能函数确定的界内,并获得了良好的动态过程以及期望的稳态控制精度.而在相同参数取值下,ATC方法姿态跟踪误差曲线存在较明显的振动且三轴的稳态控制精度不能满足指标要求.表明预设性能方法的引入不仅可以预先设定系统指标,使跟踪误差按期望要求变化,还可以减小对控制器参数选取的依赖性.
图 5~8分别给出了PPATC方法作用下的姿态角、姿态角速度、控制力矩和帆板1的模态坐标.可以看出,系统的姿态及姿态角速度均具有良好的跟踪性能,且帆板的挠性振动得到了抑制.
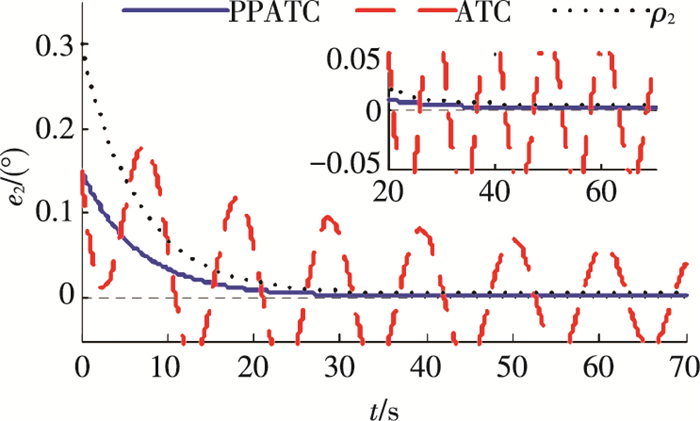
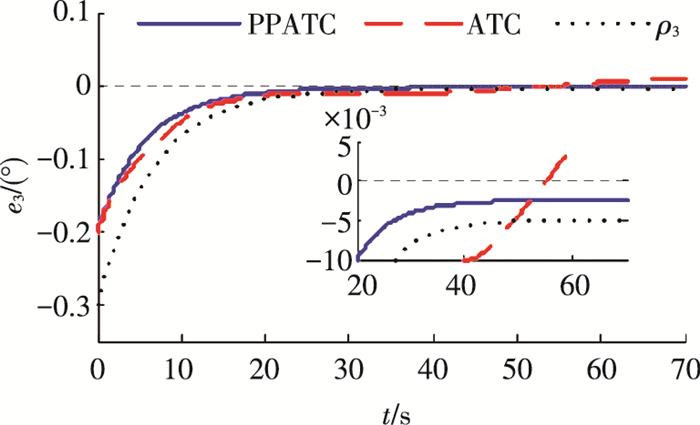
为进一步说明本文方法对控制参数的选取具有较小的依赖性,将控制增益K、自适应增益τwi和τμ取为原来的0.5倍进行仿真,得到的误差曲线如图 9~11所示.与图 2~4相比较可以看出,将控制增益与自适应增益减小后,ATC方法姿态跟踪精度有所降低且振动加剧,而PPATC方法得到的控制性能变化不大且仍能满足预先给定的性能指标.由此可知,预设性能方法降低了对控制增益大小的要求.
|
图 10 降低增益后的俯仰轴姿态跟踪误差e2 Figure 10 Attitude tracking error e2 of pitch axis after reducing the controller gain |
|
图 11 降低增益后的偏航轴姿态跟踪误差e3 Figure 11 Attitude tracking error e3 of yaw axis after reducing the controller gain |
1) 所提出的方法借助于预设性能的设计思路,可以预先给定姿态跟踪误差的最小收敛速度、最大超调和稳态精度,以保证系统性能.
2) 采用神经网络逼近与补偿未知干扰及挠性振动未建模动态,并引入对逼近误差上界的自适应估计,从而构成自适应控制器以保证系统稳定,同时一定程度减小了对未知上界的依赖.
3) 通过仿真对比分析,证明了该控制器可以有效抑制干扰及挠性振动的影响,使系统获得期望的姿态跟踪性能,并且对控制参数选取的依赖性较低.
| [1] |
刘敏, 徐世杰, 韩潮. 挠性航天器的退步直接自适应姿态跟踪控制[J].
航空学报, 2012, 33(9): 1697-1705.
LIU Min, XU Shijie, HAN Chao. Direct adaptive attitude tracking control of flexible spacecraft based on backstepping method[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(9): 1697-1705. |
| [2] |
刘敏, 徐世杰, 韩潮. 挠性航天器姿态机动直接自适应主动振动控制[J].
北京航空航天大学学报, 2013, 39(3): 285-289.
LIU Min, XU Shijie, HAN Chao. Active vibration control and attitude maneuver of flexible spacecraft via direct adaptive control method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(3): 285-289. DOI: 10.13700/j.bh.1001-5965.2013.03.020 |
| [3] |
AZADI M, FAZELZADEH S A, EGHTESAD M, et al. Vibration suppression and adaptive-robust control of a smart flexible satellite with three axes maneuvering[J].
Acta Astronautica, 2011, 69(5/6): 307-322.
DOI: 10.1016/j.actaastro.2011.04.001 |
| [4] |
HU Qinglei. Robust adaptive sliding mode attitude control and vibration damping of flexible spacecraft subject to unknown disturbance and uncertainty[J].
Transactions of the Institute of Measurement and Control, 2012, 34(4): 436-447.
DOI: 10.1177/0142331210394033 |
| [5] |
苗双全, 丛炳龙, 刘向东. 基于输入成形的挠性航天器自适应滑模控制[J].
航空学报, 2013, 34(8): 1906-1914.
MIAO Shuangquan, CONG Binglong, LIU Xiangdong. Adaptive sliding mode control of flexible spacecraft on input shaping[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(8): 1906-1914. DOI: 10.7527/S1000-6893.2013.0322 |
| [6] |
HU Qinglei, XIAO Bing. Adaptive fault tolerant control using integral sliding mode strategy with application to flexible spacecraft[J].
International Journal of Systems Science, 2012, 44(12): 2273-2286.
DOI: 10.1080/00207721.2012.702236 |
| [7] |
孙延超, 李传江, 姚俊羽, 等. 无需相对速度信息的多Euler-Lagrange系统自适应神经网络包含控制[J].
控制与决策, 2016, 31(4): 693-700.
SUN Yanchao, LI Chuanjiang, YAO Junyu, et al. Adaptive neural-network containment control of multiple Euler-Lagrange systems without using relative velocity information[J]. Control and Decision, 2016, 31(4): 693-700. DOI: 10.13195/j.kzyjc.2015.0198 |
| [8] |
XIAO Bing, HU Qinglei, ZHANG Youmin. Adaptive sliding mode fault tolerant attitude tracking control for flexible spacecraft under actuator saturation[J].
IEEE Transactions on Control Systems Technology, 2012, 20(6): 1605-1612.
DOI: 10.1109/tcst.2011.2169796 |
| [9] |
ZHONG Chenxing, GUO Yu, YU Zhen. A self-adjusting sliding-mode control based on RBF neural network for flexible spacecraft attitude[C]// Proceedings of the IEEE International Conference on Information and Automation(ICIA). Yinchuan, China: IEEE, 2013: 207-212. DOI: 10.1109/icinfa.2013.6720297.
http://www.researchgate.net/publication/271435987_A_self-adjusting_sliding-mode_control_based_on_RBF_neural_network_for_flexible_spacecraft_attitude
|
| [10] |
FAZLYAB A R, SABERI F F, KABGANIAN M. Adaptive attitude controller for a satellite based on neural network in the presence of unknown external disturbances and actuator faults[J].
Advances in Space Research, 2016, 57(1): 367-377.
DOI: 10.1016/j.asr.2015.10.026 |
| [11] |
孙延超. 挠性卫星姿态快速机动算法研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.
SUN Yanchao. Algorithm on rapid attitude maneuver for flexible satellite[D]. Harbin: Harbin Institute of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10213-1013036101.htm |
| [12] |
ZHANG Chao, SUN Yanchao, MA Guangfu, et al. Global sliding mode attitude control for flexible satellite with a rotating antenna[C]//Proceedings of the 34th Chinese Control Conference(CCC). Hangzhou, China: IEEE, 2015: 5337-5341. DOI: 10.1109/chicc.2015.7260473.
http://www.researchgate.net/publication/308833321_Global_sliding_mode_attitude_control_for_flexible_satellite_with_a_rotating_antenna
|
| [13] |
BECHLIOULISC P, ROVITHAKIS G A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance[J].
IEEE Transactions on Automatic Control, 2008, 53(9): 2090-2099.
DOI: 10.1109/tac.2008.929402 |
| [14] |
KOSTARIGKAA K, DOULGERI Z, ROVITHAKIS G A. Prescribed performance tracking for flexible joint robots with unknown dynamics and elasticity[C]// Proceedings of the IEEE International Conference on Robotics and Automation(ICRA). Saint Paul, MN: IEEE, 2012: 5365-5370. DOI: 10.1109/ICRA.2012.6224642.
http://ieeexplore.ieee.org/document/6224642/
|
| [15] |
NA Jing, CHEN Qiang, REN Xuemei, et al. Adaptive prescribed performance motion control of servo mechanisms with friction compensation[J].
IEEE Transactions on Industrial Electronics, 2014, 61(1): 486-494.
DOI: 10.1109/tie.2013.2240635 |
| [16] |
BU Xiangwei, WU Xiaoyan, ZHU Fujing, et al. Novel prescribed performance neural control of a flexible air-breathing hypersonic vehicle with unknown initial errors[J].
Isa Transactions, 2015, 59: 149-159.
DOI: 10.1016/j.isatra.2015.09.007 |
| [17] |
SUI Shuai, TONG Shaocheng, LI Yongming. Observer-based fuzzy adaptive prescribed performance tracking control for nonlinear stochastic systems with input saturation[J].
Neurocomputing, 2015, 158: 100-108.
DOI: 10.1016/j.neucom.2015.01.063 |
| [18] |
WU Shunan, RADICE G, SUN Zhaowei. Robust finite-time control for flexible spacecraft attitude maneuver[J].
Journal of Aerospace Engineering, 2014, 27(1): 185-190.
DOI: 10.1061/(ASCE)AS.1943-5525.0000247 |
| [19] |
李传江, 郭延宁, 张永合, 等. 基于时频域分析的轮控航天器姿态控制规律参数整定[J].
宇航学报, 2011, 32(11): 2319-2325.
LI Chuanjiang, GUO Yanning, ZHANG Yonghe, et al. Parameter tuning for the attitude control algorithm of wheel controlled spacecraft based on time and frequency domain analysis[J]. Chinese Journal of Astronautics, 2011, 32(11): 2319-2325. DOI: 10.3873/j.issn.1000-1328.2011.11.003 |
| [20] |
SUN Yanchao, WANG Wenjia, MA Guangfu, et al. Backstepping-based distributed coordinated tracking for multiple uncertain Euler-Lagrange systems[J].
Journal of Systems Engineering and Electronics, 2016, 27(5): 1083-1095.
DOI: 10.21629/JSEE.2016.05.16 |
 2018, Vol. 50
2018, Vol. 50


