现代战争的复杂多样性对制导武器的全方位攻击能力提出了更高要求，因而对带有攻击角约束导引律的研究受到了广泛关注^[1].近年来，国内外学者在此领域进行了大量研究.Kim等^[2]利用线性二次模型首次研究了攻击角约束问题.随后滑模控制理论被引入，变结构导引控制律不仅满足脱靶量需求，还实现了攻击角度约束^[3-4].由于传统终端滑模控制中普遍存在奇异问题，Song等^[5]采用一种改进的终端滑模面，使用自适应方法估计外部未知但有界扰动，提出一类自适应非奇异快速滑模导引律.Zhang等^[6]提出两类积分滑模导引律来保证视线角到期望角的有限时间收敛.Zhao等^[7]在设计滑模面时引入特定时变函数，使视线角收敛到期望角是有限时间的并且收敛时间可预知.与滑模控制方法不同，冯艳清等^[8]运用最优控制理论，在纵向和航向两个导引平面分别设计导引律，但仅在纵向平面上实现攻击角度约束.Tsalik等^[9]将相对运动方程在圆形标称弹道上线性化，使用圆形弹道内接角设计了一类有攻击角约束的最优导引律.Sun等^[10]应用连续非光滑控制方法使导弹满足攻击角约束的时间更快、精度更优.此外也有部分文献[11-13]在考虑攻击角约束的同时考虑了如攻击时间约束、视场角约束等复杂战况.

然而，现有研究多是基于二维平面导引动力学与运动学模型.三维导引模型间的相互耦合^[14]，使得设计有攻击角约束的三维导引律更为困难.另外，实战中为了扩展导弹的战术用途，制导律的设计还希望入射角有限时间收敛^[15].本文将针对有攻击角约束的三维有限时间导引律问题，通过引入用于估计目标加速度信息的非线性观测器，设计一种使三维视线角在有限时间内收敛至期望攻击角的导引律.

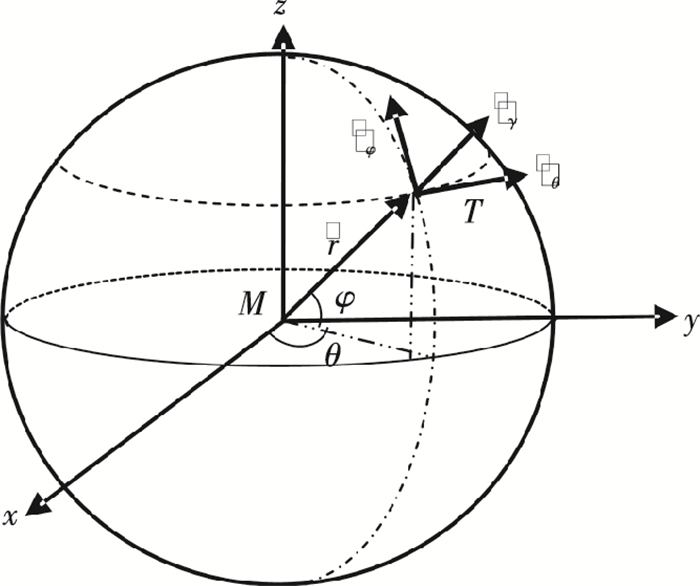
1 问题描述

考虑导弹和目标在三维空间的运动为质点运动，分别用M和T表示导弹和目标的质心.惯性系M-(x, y, z)建立在导弹初始位置，称由导弹指向目标的矢量$\vec r$为视线矢量，视线与惯性系的角度关系用视线偏角θ和视线倾角φ表示.建立视线球坐标系(r, θ, φ)，用(${{\overrightarrow{\pmb{e}}}_{r}}{,}{{\overrightarrow{\pmb{e}}}_{\theta }},{{\overrightarrow{\pmb{e}}}_{\varphi }}$)表示单位矢量，其中${{\overrightarrow{\pmb{e}}}_{\theta }}$沿经线方向，${{\overrightarrow{\pmb{e}}}_{\varphi }}$沿纬线方向，如图 1所示.令(a_Mr, a_Mθ, a_Mφ)为导弹加速度，(a_Tr, a_Tθ, a_Tφ)为目标加速度，则导弹与目标在视线球坐标系内的相对运动可用如下二阶非线性方程表示^[16]：

$ \ddot r - r{{\dot \varphi }^2} - r{{\dot \theta }^2}{\cos ^2}\varphi = {a_{Tr}} - {a_{Mr}}, $

(1)

$ r\ddot \theta \cos \varphi + 2\dot r\dot \theta \cos \varphi - 2\dot r\dot \varphi \dot \theta \sin \varphi = {a_{T\theta }} - {a_{M\theta }}, $

(2)

$ r\ddot \varphi + 2\dot r\dot \varphi + r{{\dot \theta }^2}\cos \varphi {\rm sin}\varphi = {a_{T\varphi }} - {a_{M\varphi }}. $

(3)

将(a_Mφ, a_Mθ)视作控制输入，将(a_Tφ, a_Tθ)视作扰动，令${x_1} = \dot \theta, {x_2} = \dot \varphi $，则式(2)、(3)可变为：

$ {{\dot x}_1} = - \frac{{2\dot r}}{r}{x_1} + 2{x_1}{x_2}\tan \varphi - \frac{1}{{r\cos \varphi }}\left( {{a_{M\theta }} - {a_{T\theta }}} \right), $

(4)

$ {{\dot x}_2} = - \frac{{2\dot r}}{r}{x_2} - x_1^2\cos \varphi \sin \varphi - \frac{1}{r}\left( {{a_{M\varphi }} - {a_{T\varphi }}} \right). $

(5)

本文的任务是通过设计(a_Mφ, a_Mθ)使得视线角速度($\dot \varphi, \dot \theta $)在有限时间内收敛到0，且视线角最终稳定于给定的期望入射角(θ_d, φ_d).因此，式(1)的a_Mr方向只需满足$\dot r$ < 0即可.下面给出有限时间稳定定理.

定理1^[17]  考虑非线性系统$\dot x$=f(x, t), f(0, t)=0.x∈Rⁿ，U为包含原点x=0的开区间，若存在一个在U上连续可微的正定函数V(x, t)满足${{\dot V}}$(x, t)+αV^λ(x, t)≤0，其中α > 0, λ∈(0, 1)，则该非线性系统在原点x=0处有限时间稳定，稳定时间为

$ T \le \frac{{{V^{1 - \lambda }}\left( {{x_0},0} \right)}}{{\alpha \left( {1 - \lambda } \right)}}. $

2 非线性观测器

实战中目标加速度信息通常难以获取，因此考虑基于导弹已知信息来估计目标加速度.对于系统(4)、(5)，可以改写为

$ \left\{ \begin{array}{l} {{\dot x}_1} = {F_1}\left( x \right) + {B_1}\left( {{a_{M\theta }} - {a_{T\theta }}} \right),\\ {{\dot x}_2} = {F_2}\left( x \right) + {B_2}\left( {{a_{M\varphi }} - {a_{T\varphi }}} \right). \end{array} \right. $

(6)

式中：${F_1}\left( x \right) =-\frac{{2\dot r}}{r}{x_1} + 2{x_1}{x_2}\tan \;\varphi, {B_1} = \frac{1}{{r\cos \;\varphi }}$，${F_2}\left( x \right) =-\frac{{2\dot r}}{r}{x_2}-x_1^2{\rm cos}\;\varphi {\rm sin}\;\varphi, {B_2} = {\rm{-}}\frac{1}{r}$.基于式(6)，设计非线性观测器^[18]形式如下：

$ \left\{ \begin{array}{l} {{\dot z}_1} = {F_1} + {B_1}\left( {{a_{M\theta }} - {{\hat a}_{T\theta }}} \right)\\ {{\hat a}_{T\theta }} = {c_1}\left( {{x_1} - {z_1}} \right), \end{array} \right. $

(7)

$ \left\{ \begin{array}{l} {{\dot z}_2} = {F_2} + {B_2}\left( {{a_{M\varphi }} - {{\hat a}_{T\varphi }}} \right),\\ {{\hat a}_{T\varphi }} = {c_2}\left( {{x_2} - {z_2}} \right). \end{array} \right. $

(8)

式中：c₁, c₂ > 0为观测器参数，z₁、z₂分别为观测器系统状态且z₁(0)=x₁(0), z₂(0)=x₂(0)，${\hat a_{T\theta }}$、${\hat a_{T\varphi }}$分别为观测器估计值，令观测误差ε_θ=a_Tθ-${\hat a_{T\theta }}$, ε_φ=a_Tφ-${\hat a_{T\varphi }}$，由式(6)~(8)可得

$ \left\{ \begin{array}{l} {{\dot {\hat a}}_{T\theta }} = {c_1}\left( {{{\dot x}_1} - {{\dot z}_1}} \right) = - {c_1}{B_1}{\varepsilon _\theta },\\ {{\dot {\hat a}}_{T\varphi }} = {c_2}\left( {{{\dot x}_2} - {{\dot z}_2}} \right) = - {c_2}{B_2}{\varepsilon _\varphi }. \end{array} \right. $

(9)

选取李雅普诺夫函数为

$ \hat V = \frac{1}{2}\left( {\dot {\hat a}_{T\theta }^2{{\cos }^2}\varphi + \dot {\hat a}_{T\varphi }^2} \right) = \frac{{\left( {c_1^2\varepsilon _\theta ^2 + c_2^2\varepsilon _\varphi ^2} \right)}}{{2{r^2}}}, $

(10)

对式(10)两边同时求导可得

$ \dot {\hat V} = \frac{{c_1^2\left( {{r^2}{\varepsilon _\theta }{{\dot \varepsilon }_\theta } - r\dot r\varepsilon _\theta ^2} \right) + c_2^2\left( {{r^2}{\varepsilon _\varphi }{{\dot \varepsilon }_\varphi } - r\dot r\varepsilon _\varphi ^2} \right)}}{{{r^4}}}. $

为了使$\dot {\hat V}$ < 0，一个充分条件为：

$ {r^2}{\varepsilon _\theta }{{\dot \varepsilon }_\theta } - r\dot r\varepsilon _\theta ^2 < 0, $

(11)

$ {r^2}{\varepsilon _\varphi }{{\dot \varepsilon }_\varphi } - r\dot r\varepsilon _\varphi ^2 < 0. $

(12)

下面仅以偏角θ方向的式(11)为例进一步推导，φ方向推导过程相同.考虑制导过程中r > 0，且${\varepsilon _\theta } = {\dot a_{T\theta }}-{\dot {\hat a}_{T\theta }} = {\dot a_{T\theta }} + {c_1}{B_1}{\varepsilon _\theta }$，代入${B_1} = \frac{1}{{r\cos \;\varphi }}$，式(11)等价于

$ \left\{ \begin{array}{l} {{\dot a}_{T\theta }} < \left( {\frac{{\dot r}}{r} + \frac{{{c_1}}}{{r\cos \varphi }}} \right){\varepsilon _\theta },{\varepsilon _\theta } > 0;\\ {{\dot a}_{T\theta }} > \left( {\frac{{\dot r}}{r} + \frac{{{c_1}}}{{r\cos \varphi }}} \right){\varepsilon _\theta },{\varepsilon _\theta } < 0. \end{array} \right. $

(13)

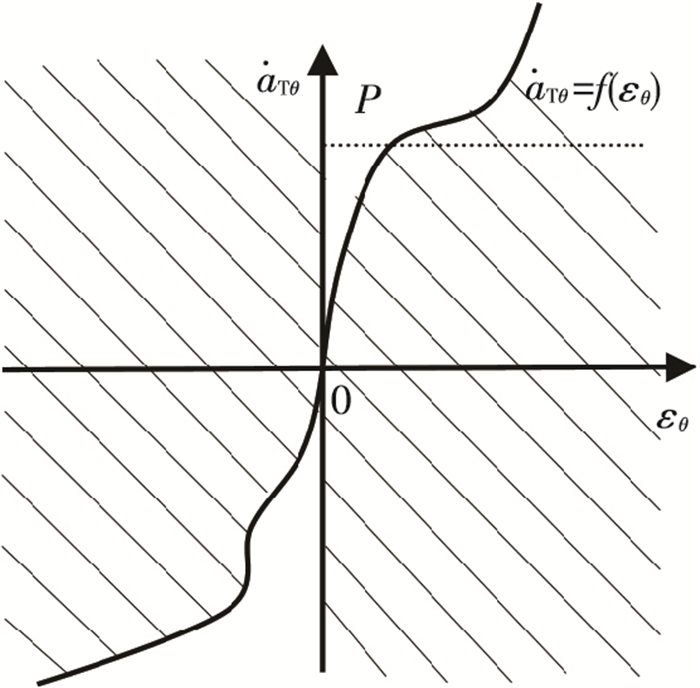
由式(13)可以看出，当目标加速度的变化值与跟踪误差始终落在如图 2所示的阴影区域内时，非线性观测器的观测误差是递减的.且特定${\dot a_{T\theta }}$对应的误差ε_θ将稳定于图中的P点.随r的减小斜率K_θ(t)逐渐增加|ε_θ|逐渐减小.因此当r趋于零时，|ε_θ|也将趋近于零.图中${\dot a_{T\theta }}$=f(ε_θ)=K_θ(t)ε_θ, K_θ(t)=$\frac{{\dot r}}{r} + \frac{{{c_1}}}{{r\cos \;\varphi }}$.倾角φ方向上，K_φ(t)=$\frac{{\dot r}}{r} + \frac{{{c_2}}}{r}$.

因此，当目标做匀变速运动，即${\dot a_{T\theta }}$, ${\dot a_{T\varphi }}$≡0，此时只需满足c₁ > -$\dot r$cos φ，c₂ > -$\dot r$，观测器将实现无误差跟踪；当目标做变加速运动，${\dot a_{T\theta }}$, ${\dot a_{T\varphi }}$随时间变化，因目标加速度变化通常可视为有界值，观测器估计值与真实值之间将一直存在误差.

3 有攻击角约束的有限时间收敛制导律设计

设θ_d、φ_d分别为视线的期望攻击偏角和倾角，希望通过设计制导律使得导弹可以在有限时间内以期望的攻击角攻击目标.由于两个方向导引律设计过程类似，此处仅以偏角θ方向详细说明，倾角φ方向仅给出结果.对式(4)选取滑模面^[19]：

$ {s_1} = {x_1} + {\beta _1}{\left| {{e_1}\left( t \right)} \right|^{{\gamma _1}}}{\mathop{\rm sgn}} \left( {{e_1}\left( t \right)} \right), $

(14)

式中β₁ > 0, γ₁∈(0, 1)，且e₁(t)=θ(t)-θ_d.对式(14)求导可得

$ {{\dot s}_1} = {{\dot x}_1} + {\beta _1}{\gamma _1}{\left| {{e_1}\left( t \right)} \right|^{{\gamma _1} - 1}}{x_1}. $

(15)

选取滑模趋近律为

$ {{\dot s}_1} = - \frac{{{\alpha _1}{\mathop{\rm sgn}} \left( {{s_1}} \right)}}{{r\cos \varphi }}{\left| {{s_1}} \right|^{{\eta _1}}}, $

(16)

式中α₁ > 0, η₁∈(0, 1)，则将式(4)、(16)代入式(15)中可得

$ \begin{array}{l} {a_{M\theta }} = {\beta _1}{\gamma _1}r{\left| {{e_1}\left( t \right)} \right|^{{\gamma _1} - 1}}{x_1}\cos \varphi + {\alpha _1}{\mathop{\rm sgn}} \left( {{s_1}} \right){\left| {{s_1}} \right|^{{\eta _1}}} - \\ \;\;\;\;\;\;\;\;\;2\dot r{x_1}\cos \varphi + 2\dot r{x_1}{x_2}\sin \varphi + {a_{T\theta }}. \end{array} $

(17)

对于在导引律(17)作用下，视线偏角θ的有限时间收敛分析可以分为两个阶段：滑模面s₁=0到达阶段和沿滑模面运动阶段.首先考虑滑模面到达阶段，选择正定李雅普诺夫函数为

$ V\left( {\dot \theta \left( t \right),\theta \left( t \right),t} \right) = s_1^2, $

对其求导可得

$ \dot V = 2{s_1}{{\dot s}_1} = - \frac{{2{\alpha _1}}}{{r\cos \left( \varphi \right)}}{V^{\frac{1}{2}\left( {{\eta _1} + 1} \right)}} < 0. $

考虑在末制导阶段满足r(t) < r(0), ∀t > 0，并且φ(t)∈($-\frac{\pi }{2}, \frac{\pi }{2}$), ∀t > 0，因此有0 < cos(φ(t)) < 1，由此可以得到

$ \dot V < - \frac{{2{\alpha _1}}}{{r\left( 0 \right)}}{V^{\frac{1}{2}\left( {{\eta _1} + 1} \right)}}. $

由定理1可知，到达平面的运动过程是有限时间稳定的，其稳定时间为

$ {T_{\theta 1}} \le \frac{{r\left( 0 \right){V^{\frac{1}{2}\left( {1 - {\eta _1}} \right)}}\left( {\dot \theta \left( 0 \right),\theta \left( 0 \right),0} \right)}}{{{\alpha _1}\left( {1 - {\eta _1}} \right)}}. $

下面考虑系统在平面内的运动.当系统达到s₁=0平面后，状态将沿该平面运动直到收敛到原点，此时平面满足s₁=x₁+β₁|e₁(t)|^γ₁sgn(e₁(t))=0，考虑${\dot e_1}\left( t \right) = \dot \theta = {x_1}$，因此该阶段运动的状态方程为

$ {{\dot e}_1}\left( t \right) = - {\beta _1}{\left| {{e_1}\left( t \right)} \right|^{{\gamma _1}}}{\mathop{\rm sgn}} \left( {{e_1}\left( t \right)} \right). $

选取李雅普诺夫函数为

$ \tilde V\left( {\theta \left( t \right),t} \right) = e_1^2, $

即

$ \dot {\tilde V} = 2{e_1}{{\dot e}_1} = - 2{\beta _1}{{\tilde V}^{\frac{1}{2}\left( {\gamma + 1} \right)}} < 0. $

(18)

由定理1可知，式(18)有限时间稳定于e₁=0处，此时x₁=${\dot e_1}$(t)=0.稳定时间为

$ {T_{\theta 2}} \le \frac{{{{\tilde V}^{\frac{1}{2}\left( {1 - {\gamma _1}} \right)}}\left( {\theta \left( 0 \right),0} \right)}}{{{\beta _1}\left( {1 - {\gamma _1}} \right)}}. $

综上所述，导引系统在视线偏角θ方向的稳定时间为

$ {T_\theta } \le {T_{\theta 1}} + {T_{\theta 2}}, $

同理可证得，对于视线倾角φ方向的角运动过程也是有限时间稳定的，其制导律为

$ \begin{array}{l} {a_{M\varphi }} = {\beta _2}{\gamma _2}r{\left| {{e_2}\left( t \right)} \right|^{{\gamma _2} - 1}}{x_2} + {\alpha _2}{\mathop{\rm sgn}} \left( {{s_2}} \right){\left| {{s_2}} \right|^{{\eta _2}}} - 2\dot r{x_2} - \\ \;\;\;\;\;\;\;\;\;rx_1^2\cos \varphi \sin \varphi + {a_{T\varphi }}, \end{array} $

其中

$ \left\{ \begin{array}{l} {s_2} = {x_2} + {\beta _2}{\left| {{e_2}\left( t \right)} \right|^{{\gamma _2}}}{\mathop{\rm sgn}} \left( {{e_2}\left( t \right)} \right),\\ {{\dot s}_2} = - \frac{{{\alpha _2}{\mathop{\rm sgn}} \left( {{s_2}} \right)}}{r}{\left| {{s_2}} \right|^{{\eta _2}}}. \end{array} \right. $

式中:β₂ > 0, α₂ > 0, γ₂∈(0, 1), η₂∈(0, 1), e₂(t)=φ(t)-φ_d.

结合有攻击角约束的有限时间收敛制导律设计，考虑目标加速度实战中不易获取，采用如下的复合制导律来处理有攻击角约束的三维有限时间制导问题：

$ \left\{ \begin{array}{l} {a_{M\varphi }} = {\beta _2}{\gamma _2}r{\left| {{e_2}\left( t \right)} \right|^{{\gamma _2} - 1}}{x_2} + {\alpha _2}{\mathop{\rm sgn}} \left( {{s_2}} \right){\left| {{s_2}} \right|^{{\eta _2}}} - \\ \;\;\;\;\;\;\;\;\;2\dot r{x_2} - rx_1^2\cos \varphi \sin \varphi + {{\hat a}_{T\varphi }},\\ {a_{M\theta }} = {\beta _1}{\gamma _1}r{\left| {{e_1}\left( t \right)} \right|^{{\gamma _1} - 1}}{x_1}\cos \varphi + {\alpha _1}{\mathop{\rm sgn}} \left( {{s_1}} \right){\left| {{s_1}} \right|^{{\eta _1}}} - \\ \;\;\;\;\;\;\;\;\;2\dot r{x_1}\cos \varphi + 2\dot r{x_1}{x_2}\sin \varphi + {{\hat a}_{T\theta }}. \end{array} \right. $

(19)

式中${\hat a_{T\varphi }}$、${\hat a_{T\theta }}$分别为式(7)、(8)的观测值.

当目标做变加速运动时，为分析观测误差对导引系统影响，将复合制导律(19)代入系统(4)、(5)可得

$ \left\{ \begin{array}{l} {{\dot x}_1} = - {\beta _1}{\gamma _1}{\left| {{e_1}\left( t \right)} \right|^{{\gamma _1} - 1}}{x_1} - \frac{{{\alpha _1}{\mathop{\rm sgn}} \left( {{s_1}} \right){{\left| {{s_1}} \right|}^{{\eta _1}}}}}{{r\cos \varphi }} + \frac{{{\varepsilon _\theta }}}{{r\cos \varphi }},\\ {{\dot x}_2} = - {\beta _2}{\gamma _2}{\left| {{e_2}\left( t \right)} \right|^{{\gamma _2} - 1}}{x_2} - \frac{{{\alpha _2}{\mathop{\rm sgn}} \left( {{s_2}} \right){{\left| {{s_2}} \right|}^{{\eta _2}}}}}{r} + \frac{{{\varepsilon _\varphi }}}{r}. \end{array} \right. $

(20)

式(20)右侧前两项保证了导引系统到达滑模面和滑模面内的有限时间运动.误差ε_φ和ε_θ对导引系统的影响表现为ε_θ/rcos φ与ε_φ/r.实际情况中，制导前期通常有|ε_θ|≪r、|ε_φ|≪r，制导后期由式(9)可知ε_θ和ε_φ将趋近于零.且在实际工程应用中，末端制导过程持续时间往往比较短，因此本文认为此影响可忽略，后文仿真将给出进一步数值分析.

4 数值仿真

选取导弹与目标的初始参数设置见表 1，为了验证本文所提方法的有效性，选取如下所示传统比例导引法作为对比.

$ \left\{ \begin{array}{l} {a_{M\theta }} = - {N_p}\dot r{x_1},\\ {a_{M\varphi }} = - {N_p}\dot r{x_2}. \end{array} \right. $

式中N_p≥2为量纲一的比例系数，仿真中选取典型值N_p=8^[16].复合导引律(19)各参数设置见表 2.

从表 1可计算视线初始角度为(φ_L0, θ_L0)=(65.9°, 26.6°)，设置期望入射角为(φ_Ld, θ_Ld)=(75°, 20°).假设导弹最大可用过载为10 g，分别选取匀变速和变加速两类目标进行仿真.由数值仿真可知，导引系统的有限时间稳定时间与目标运动状态无关.由所给各项参数，可计算两方向的理论稳定时间为：T_θ < 84.9 s, T_φ < 18.6 s.

1) 匀变速目标，选取目标加速度为a_Tθ=a_Tφ=2 g.

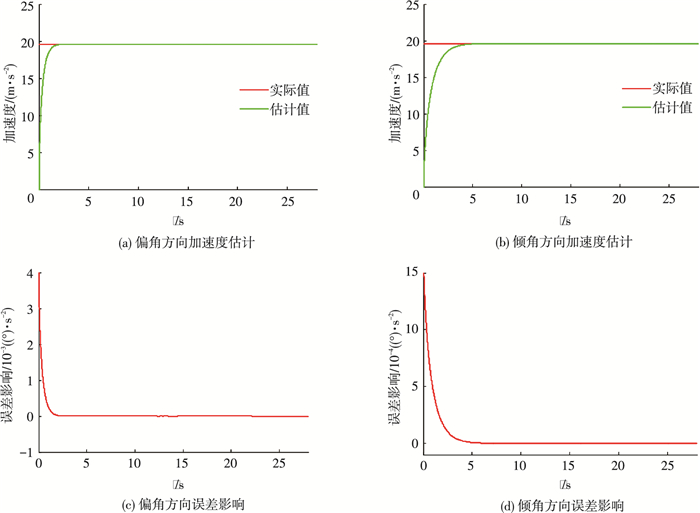
非线性观测器的仿真表现如图 3所示，其中偏角和倾角方向的误差影响图是对ε_θ/rcos φ和ε_φ/r两项进行仿真验证.仿真结果表明，针对均变速目标，非线性观测器将在较短时间内实现对目标加速度的稳定跟踪.即使在仿真前期观测器具有较大观测误差时，误差对导引系统的影响项ε_θ/r cos φ和ε_φ/r数量级仅为10^-4，且残存时间较短(5 s以内)，因此该项对有限时间导引过程的影响认定可忽略.

图 4为本文导引律与传统比例导引律之间的导引效果对比图.由图 4可知，仿真前期观测器误差对有限时间导引过程基本上不存在影响.与传统比例导引律相比，本文所提复合导引率可使系统的导引角在有效时间内收敛至期望攻击角度.

2) 变加速目标，选取目标加速度为a_Tθ=(1+0.5cos$\frac{t}{2}$)g, a_Tφ=0.5sin$\frac{t}{2}$g.

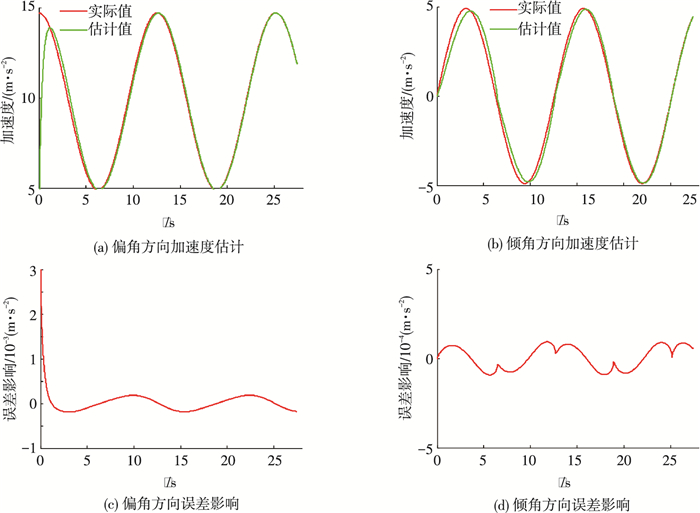
由图 5分析可知，当目标做变加速运动时，观测器对目标加速度的估计始终存在误差，但该误差随制导时间的增加而逐渐减少，并在大约15 s后，观测器观测值与真实值之间几乎没有偏差.观测器误差对导引系统的影响项ε_θ/rcos φ和ε_φ/r并未因弹目距离r的减少而增加，而是一直维持在10^-4量级，因此认为观测器误差对导引系统影响可以忽略不计.

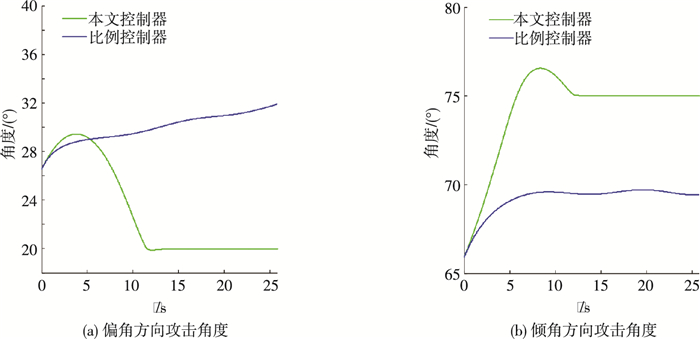
图 6表明，即使针对变加速目标，复合导引律(19)依然维持良好的有限时间稳定性能，非线性观测器带来的微小误差并未影响有限时间导引过程.与传统比例导引方法相比，本文研究结果可使导引角度在有限时间收敛至期望攻击角度.

通过仿真可知，在复合导引律(19)作用下，导弹对匀变速运动目标和变加速运动目标都实现了有效拦截并满足视线角有时间收敛至期望角的要求.与传统比例导引方法相比，本文所提复合导引律具有使弹目视线角在有限时间收敛至期望攻击角的优势.且对两类目标导引角度的有限收敛时间T_θ≈12 s，T_φ≈15 s，均符合理论值T_θ < 84.9 s, T_φ < 18.6 s.

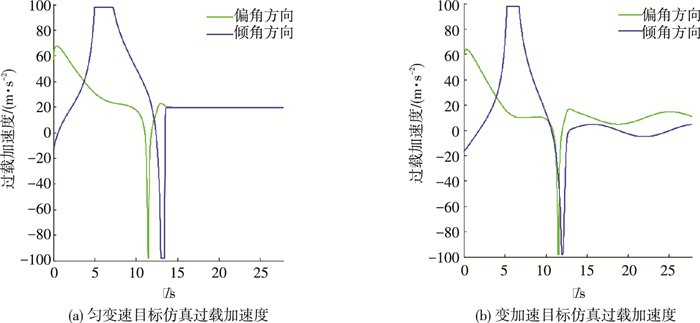
导引律对两类目标所产生的过载加速度变化情况如图 7所示.图 7表明，导引律对两类目标的制导过程中，过载加速度变化比较平缓，饱和程度低，符合实战需求.

5 结论

1) 引入了一类非线性观测器利用导弹已知信息估计目标加速度，分析了观测器稳定估测目标加速度信息的充分条件.结果显示，对匀加速目标，观测器最终可以实现稳定估计；针对变加速目标，观测器的观测误差对导引系统影响在实际工程应用中的影响较小，一般可忽略.

2) 对具有攻击角约束的三维导引问题，设计了一类滑模变结构有限时间导引控制率，使得弹目视线角可以在有限时间收敛于期望攻击角的有限时间导引律.通过使用给线性观测器，使得该导引律适用于目标加速度未知的复杂战场环境.

3) 针对变加速运动的复杂运动目标，非线性观测器的微小观测误差对导引系统有限时间收敛特性的显著性影响有待进一步研究和量化.