在航天技术的发展与应用中,卫星姿态控制问题得到了密切的关注与广泛的研究.滑模控制作为控制算法当中较为经典的一种,在卫星姿态控制领域得到了大量而广泛的研究与应用.传统的滑模控制存在结构简单、物理意义清晰的优点,为控制律的设计带来了极大的便利,然而,它却存在着终端收敛速率慢的严重缺陷,传统滑模面指数收敛的性质意味着状态在无穷远处才能严格到达平衡点.针对这一缺陷,国内外学者对于终端收敛速率性质优良的有限时间控制进行了深入的讨论与研究.
有限时间控制具有有限时间收敛的优良特性,然而该控制算法的奇异性问题极大程度的限制了该控制的发展与应用.文献[1]提出了一种非奇异性的饱和滑模有限时间控制律,但欠缺的是并没有考虑系统模型的鲁棒性;文献[2]针对卫星姿态机动问题提出了一种卫星鲁棒有限时间控制算法,并对于卫星的挠性附件进行了建模,同时考虑了挠性附件对于姿态系统的扰动,将卫星姿态运动学与动力学系统转化为Lagrange动力学模型,设计了一种对于系统模型具有鲁棒性的有限时间控制算法,但该文献并没有考虑控制力矩的饱和问题;在后续研究中,文献[3]针对卫星姿态跟踪控制问题设计了有限时间控制律,并提出了一种针对姿态跟踪控制的无奇异性有限时间滑模面.对于系统模型的不确定性、干扰力矩等扰动,针对滑模控制中存在的状态抖振问题,文献[4]针对高速航天器的姿态控制设计了连续终端滑模面,并给出了有限时间控制律;同时,文献[5]中基于对偶四元数为航天器编队飞行问题设计了有限时间控制器,针对滑模控制律中存在的状态抖颤问题设计了连续终端滑模面.文献[6]针对在太阳光压扰动下的卫星姿态控制设计了高阶有限时间滑模面,并设计了有限时间控制器.但是这些文献都缺少对于考虑控制力矩上限、系统模型存在不确定性的单星姿态有限时间控制的讨论.在其他控制领域,针对卫星自主轨道控制,文献[7]基于Lie群理论设计了有限时间控制器;文献[8]对于具有模型不确定性的离散线性系统设计了鲁棒有限时间控制器,在文献[8]中,线性矩阵不等式(LMI)被用于有限时间控制器的设计;文献[9-11]中研究了一阶与二阶系统的有限时间控制律,但这些对于线性系统的分析方法并不能够直接用于卫星姿态控制的非线性系统中.
在滑模控制方面,文献[12-13]对航天器姿态的稳定条件进行了分析,讨论了系统参数与有限稳定性之间的关系,但未考虑外部干扰对于系统的影响.文献[14-18]对滑模控制进行了研究,同时考虑了系统转动惯量的不确定性.文献[14-16]的控制对象主要是柔性机械臂,文献[17]主要针对航天器姿态跟踪控制进行研究,设计了一种鲁棒有限时间控制器,文献[18]解决了有限时间控制中的力矩饱和问题,但总的来说,这些文献对于力矩饱和、鲁棒性、外部扰动缺少统一讨论.
本文针对带有系统模型不确定性、外部干扰力矩、考虑控制力矩受限的卫星姿态控制问题,设计了一种三段式的无奇异性有限时间滑模面,基于角速度与四元数矢部反向时,欧拉轴指向不变的特性解决奇异性问题,保证了收敛速率与稳态精度,同时设计了鲁棒控制器实现系统状态在有限时间内收敛至本文所设计的滑模面;构造Lyapunov函数对本文提出的算法进行稳定性证明;最后通过数学仿真对本文提出的算法进行了有效性验证.
1 姿态动力学与运动学模型| $ \mathit{\boldsymbol{J\omega }} + {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }} = \mathit{\boldsymbol{u}} + \mathit{\boldsymbol{d}}. $ |
式中:J为卫星转动惯量矩阵且J为对称正定矩阵; ω为卫星角速度; u、d分别为控制力矩与干扰力矩且满足||d||≤d,三维向量叉乘算子r×的定义为
| $ {\mathit{\boldsymbol{r}}^ \times } = \left[ {\begin{array}{*{20}{c}} 0&{ - {r_3}}&{{r_2}}\\ {{r_3}}&0&{ - {r_1}}\\ { - {r_2}}&{{r_1}}&0 \end{array}} \right]. $ |
三维向量叉乘矩阵的奇异值具有如下性质:
| $ \lambda \left( {{\mathit{\boldsymbol{r}}^ \times }} \right) = 0,{\left\| \mathit{\boldsymbol{r}} \right\|_2},{\lambda _{\max }}\left( {{\mathit{\boldsymbol{r}}^ \times }} \right) = {\left\| \mathit{\boldsymbol{r}} \right\|_2}. $ |
基于欧拉轴/角与姿态四元数描述的卫星姿态运动学模型为[1-3]:
| $ \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot e}} = \frac{1}{2}{\mathit{\boldsymbol{e}}^ \times }\left( {{\mathit{\boldsymbol{I}}_3} - \cot \frac{\varphi }{2}{\mathit{\boldsymbol{e}}^ \times }} \right)\mathit{\boldsymbol{\omega }},}\\ {\dot \varphi = \frac{1}{2}{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{\omega }};} \end{array}} \right. $ |
| $ \left\{ \begin{array}{l} ~~~~~~{{\dot q}_0} = - \frac{1}{2}\mathit{\boldsymbol{q}}_v^{\rm{T}}\mathit{\boldsymbol{\omega }},\\ {{\mathit{\boldsymbol{\dot q}}}_v} = \frac{1}{2}\left( {{q_0}{\mathit{\boldsymbol{I}}_3} + \mathit{\boldsymbol{q}}_v^ \times } \right)\mathit{\boldsymbol{\omega }} = \frac{1}{2}\mathit{\boldsymbol{F\omega }}. \end{array} \right. $ |
式中矩阵F的奇异值满足:
| $ \lambda \left( \mathit{\boldsymbol{F}} \right) = \left| {{q_0}} \right|,1,{\lambda _{\max }}\left( \mathit{\boldsymbol{F}} \right) = 1. $ |
卫星姿态控制中经典滑模面定义如下:
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{\omega }} + k{\mathit{\boldsymbol{q}}_v},k > 0. $ |
该滑模面具有结构简单、易于设计控制律、物理意义清晰等优点,但其弊端在于指数收敛速率,即随着系统状态趋近于0,状态收敛速率急剧下降,在无穷远处状态才能够收敛于0.注意到该滑模面的物理意义是实现角速度与四元数矢部的反向,同时为了改进收敛速率下降过快的缺陷,本文提出的滑模面结构如下:
| $ \mathit{\boldsymbol{s}} = \left\{ \begin{array}{l} \mathit{\boldsymbol{\omega }} + {k_1}\mathit{\boldsymbol{e}},\;\;\;\;\;\;\;\left\| {{\mathit{\boldsymbol{q}}_v}} \right\| > \alpha ;\\ \mathit{\boldsymbol{\omega }} + {k_2}{\mathit{\boldsymbol{q}}_v},\;\;\;\;\;\;\beta < \left\| {{\mathit{\boldsymbol{q}}_v}} \right\| \le \alpha ;\\ \mathit{\boldsymbol{\omega }} + {k_3}{\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|^r}\mathit{\boldsymbol{e}},\;\left\| {{\mathit{\boldsymbol{q}}_v}} \right\| \le \beta . \end{array} \right. $ | (1) |
式中k1、k2、k3、α、β均为正常数,0.5 < r < 1.0.同时为满足在切换处角速度无突变,控制参数应满足:
| $ {k_1} = \alpha {k_2},{k_2} = {\beta ^{r - 1}}{k_3}. $ |
由式(1)可以看到本文提出的滑模面依然要求角速度与四元数的反向,同时,滑模面分为3段:ω+k1e为匀速段、ω+k2qv为减速段、ω+k3||qv||re为收敛段.一般来说为实现快速收敛的目标,系统状态应当尽可能的停留在匀速段,同时避免停留在角速度急剧下降的减速段,因此应当选择尽量小的α和尽量大的β.但值得注意的是为了避免奇异性问题,β应当足够小使得系统在到达收敛段之前实现角速度ω与四元数qv的反向,即
| $ \left\langle {\mathit{\boldsymbol{\omega }},{\mathit{\boldsymbol{q}}_v}} \right\rangle = {\mathit{\boldsymbol{\omega }}^{\rm{T}}}{\mathit{\boldsymbol{q}}_v}/\left( {\left\| {{\omega }} \right\|\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|} \right) = - 1. $ |
同时考虑到卫星控制力矩有限,选择过小的α会使得所需要的控制力矩趋于无穷大,因此α和β的选择应当在收敛速度和控制系统性能之间进行合理权衡.
接下来证明系统在滑模面(1)上是有限时间收敛的.由式(1)中匀速段与减速段的定义,可以得到匀速段与减速段的收敛时间均满足:
| $ {t_1} \le \left( {{\rm{ \mathsf{ π} }} - 2\arccos \sqrt {1 - {\alpha ^2}} } \right)/{k_1}, $ |
| $ {t_2} \le \left( {\ln \alpha - \ln \beta } \right)/\left( {{k_2}\sqrt {1 - {\alpha ^2}} } \right). $ |
在第3阶段收敛段,选取Lyapunov函数为
| $ {V_q} = \mathit{\boldsymbol{q}}_v^{\rm{T}}{\mathit{\boldsymbol{q}}_v}, $ |
对其求导可以得到
| $ \begin{array}{l} {{\dot V}_q} = 2\mathit{\boldsymbol{q}}_v^{\rm{T}}{{\mathit{\boldsymbol{\dot q}}}_v} = \mathit{\boldsymbol{q}}_v^{\rm{T}}\left( {{q_0}{\mathit{\boldsymbol{I}}_3} + \mathit{\boldsymbol{q}}_v^ \times } \right)\mathit{\boldsymbol{\omega }} = - {k_3}{q_0}{\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|^r}\mathit{\boldsymbol{q}}_v^{\rm{T}}\mathit{\boldsymbol{e}} = \\ \;\;\;\;\;\;\; - {k_3}{q_0}{\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|^{r + 1}} \le - {k_3}{q_0}V_q^{\frac{{r + 1}}{2}}. \end{array} $ |
考虑到在收敛段有
接下来设计控制律实现系统状态在有限时间内收敛至滑模面(1).本文所提出的有限时间控制律如下
| $ \mathit{\boldsymbol{u}} = \left\{ \begin{array}{l} - k{\left\| \mathit{\boldsymbol{s}} \right\|^p}{\mathit{\boldsymbol{s}}_e} - \frac{{{k_1}}}{2}\mathit{\boldsymbol{\hat J}}{\mathit{\boldsymbol{e}}^ \times }\left( {{\mathit{\boldsymbol{I}}_3} + \cos \frac{\varphi }{2}{e^ \times }} \right)\mathit{\boldsymbol{\omega }} - {l_1}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) + {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{\hat J\omega }},\left\| {{\mathit{\boldsymbol{q}}_v}} \right\| > \alpha ;\\ - k{\left\| \mathit{\boldsymbol{s}} \right\|^p}{\mathit{\boldsymbol{s}}_e} - \frac{{{k_2}}}{2}\mathit{\boldsymbol{\hat JF\omega }} - {l_2}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) + {{{\omega }}^ \times }\mathit{\boldsymbol{\hat J\omega }},\;\;\;\;\;\;\;\;\;\;\;\;\;\beta < \left\| {{\mathit{\boldsymbol{q}}_v}} \right\| \le \alpha ;\\ - k{\left\| \mathit{\boldsymbol{s}} \right\|^p}{\mathit{\boldsymbol{s}}_e} + \frac{{k_3^2}}{2}r{q_0}{\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|^{2r - 1}}\mathit{\boldsymbol{\hat Je}} - {l_3}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) + {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{\hat J\omega }},\;\;\;\left\| {{\mathit{\boldsymbol{q}}_v}} \right\| \le \beta . \end{array} \right. $ | (2) |
其中li定义如下
| $ \left\{ \begin{array}{l} {l_1} = \bar d + \lambda {\left\| \mathit{\boldsymbol{\omega }} \right\|^2} + \frac{{{k_1}}}{2}\lambda \left( {1 + \cot \frac{\varphi }{2}} \right)\left\| \mathit{\boldsymbol{\omega }} \right\|,\\ {l_2} = \bar d + \lambda {\left\| \mathit{\boldsymbol{\omega }} \right\|^2} + \frac{{{k_2}}}{2}\lambda \left\| \mathit{\boldsymbol{\omega }} \right\|,\\ {l_3} = \bar d + \lambda {\left\| \mathit{\boldsymbol{\omega }} \right\|^2} + \frac{{k_3^2}}{2}r\lambda \left| {{q_0}} \right|{\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|^{2r - 1}}. \end{array} \right. $ |
常数p满足1>p>0,se为s的单位方向向量,λ满足
| $ \lambda \ge {\lambda _{\max }}\left( {\mathit{\boldsymbol{\tilde J}}} \right). $ |
式中:
接下来对控制律(2)作用下的系统进行有限时间稳定证明.选取Lyapunov函数并对其求导为
| $ V = \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{Js}} \ge 0. $ | (3) |
在匀速段(||qv||>α)有
| $ \begin{array}{l} \dot V = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\dot s}} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\dot \omega }} + {k_1}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\dot e}} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }} + {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{d}} + \\ \;\;\;\;\;\frac{{{k_1}}}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{e}}^ \times }\left( {{\mathit{\boldsymbol{I}}_3} + \cot \frac{\varphi }{2}{\mathit{\boldsymbol{e}}^ \times }} \right)\mathit{\boldsymbol{\omega }} - k{\left\| \mathit{\boldsymbol{s}} \right\|^p}{\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{s}}_e} - \\ \;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{\tilde J\omega }} + {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{d + }}\frac{{{k_1}}}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\tilde J}}{\mathit{\boldsymbol{e}}^ \times }\left( {{\mathit{\boldsymbol{I}}_3} - \cot \frac{\varphi }{2}{\mathit{\boldsymbol{e}}^ \times }} \right)\mathit{\boldsymbol{\omega }} = \\ \;\;\;\;\; - \left( {\bar d + \lambda {{\left\| \omega \right\|}^2} + \frac{{{k_1}}}{2}\lambda \left( {1 + \cot \frac{\varphi }{2}} \right)\left\| \mathit{\boldsymbol{\omega }} \right\|} \right){\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) \le \\ \;\;\;\;\; - k{\left\| \mathit{\boldsymbol{s}} \right\|^{p + 1}} + {\lambda _{\max }}\left( {\mathit{\boldsymbol{\tilde J}}} \right)\left\| \mathit{\boldsymbol{s}} \right\|{\left\| \mathit{\boldsymbol{\omega }} \right\|^2} + \\ \;\;\;\;\;\frac{{{k_1}}}{2}\left( {1 + \cot \frac{\varphi }{2}} \right){\lambda _{\max }}\left( {\mathit{\boldsymbol{\tilde J}}} \right)\left\| \mathit{\boldsymbol{s}} \right\|\left\| \mathit{\boldsymbol{\omega }} \right\| - \\ \;\;\;\;\;\left( {\bar d + \lambda {{\left\| \mathit{\boldsymbol{\omega }} \right\|}^2} + \frac{{{k_1}}}{2}\lambda \left( {1 + \cot \frac{\varphi }{2}} \right)\left\| \mathit{\boldsymbol{\omega }} \right\|} \right)\left\| \mathit{\boldsymbol{s}} \right\| + \\ \;\;\;\;\;\bar d\left\| \mathit{\boldsymbol{s}} \right\| \le - k{\left\| \mathit{\boldsymbol{s}} \right\|^{p + 1}} \le - \mu {V^{\frac{{p + 1}}{2}}}. \end{array} $ | (4) |
在减速段(β<||qv||≤α)有
| $ \begin{array}{l} \dot V = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\dot s}} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\dot \omega }} + {k_2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot q}}}_v} = - k{\left\| \mathit{\boldsymbol{s}} \right\|^p}{\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{s}}_e} - \\ \;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{\tilde J\omega }} + {\mathit{\boldsymbol{s}}^{\rm{T}}}d + \frac{{{k_2}}}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\tilde JF\omega }} - \\ \;\;\;\;\;\left( {\mathit{\boldsymbol{\bar d}} + \lambda {{\left\| \mathit{\boldsymbol{\omega }} \right\|}^2} + \frac{{{k_2}}}{2}\lambda \left\| \mathit{\boldsymbol{\omega }} \right\|} \right){\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) \le - k{\left\| \mathit{\boldsymbol{s}} \right\|^{p + 1}} + \\ \;\;\;\;\;{\lambda _{\max }}\left( {\mathit{\boldsymbol{\tilde J}}} \right)\left\| \mathit{\boldsymbol{s}} \right\|{\left\| \mathit{\boldsymbol{\omega }} \right\|^2} + \frac{{{k_2}}}{2}{\lambda _{\max }}\left( {\mathit{\boldsymbol{\tilde J}}} \right)\left\| \mathit{\boldsymbol{s}} \right\|\left\| \mathit{\boldsymbol{\omega }} \right\| - \\ \;\;\;\;\;\left( {\bar d + \lambda {{\left\| \mathit{\boldsymbol{\omega }} \right\|}^2} + \frac{{{k_2}}}{2}\lambda \left\| \mathit{\boldsymbol{\omega }} \right\|} \right)\left\| \mathit{\boldsymbol{s}} \right\| + \bar d\left\| \mathit{\boldsymbol{s}} \right\| \le \\ \;\;\;\;\; - k{\left\| \mathit{\boldsymbol{s}} \right\|^{p + 1}} \le - \mu {V^{\frac{{p + 1}}{2}}}. \end{array} $ | (5) |
由式(4)、(5)可以看到系统状态将在有限时间内到达滑模面的匀速段与减速段.同时由上述假设,当系统进入收敛段时已满足角速度ω与四元数qv的反向,则有
| $ \begin{array}{l} \dot V = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\dot s = }}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\dot \omega }} + {k_3}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{Je}}\frac{{{\rm{d}}{{\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|}^r}}}{{{\rm{d}}t}} + {k_3}{\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|^r}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\dot e = }}\\ \;\;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }} + {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{d}} - \frac{{k_3^2}}{2}r{q_0}{\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|^{2r - 1}}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{Je}} = \\ \;\;\;\;\;\; - k{\left\| \mathit{\boldsymbol{s}} \right\|^p}{\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{s}}_e} - {\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{\tilde J\omega }} - \frac{{k_3^2}}{2}r{q_0}{\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|^{2r - 1}}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\tilde Je}} - \\ \;\;\;\;\;\;\left( {\bar d + \lambda {{\left\| \omega \right\|}^2} + \frac{{k_3^2}}{2}r\lambda \left| {{q_0}} \right|{{\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|}^{2r - 1}}} \right){\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathop{\rm sgn}} \left( \mathit{\boldsymbol{s}} \right) + \\ \;\;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{d}} \le - k{\left\| \mathit{\boldsymbol{s}} \right\|^{p + 1}} + {\lambda _{\max }}\left( {\mathit{\boldsymbol{\tilde J}}} \right)\left\| \mathit{\boldsymbol{s}} \right\|{\left\| \mathit{\boldsymbol{\omega }} \right\|^2} + \\ \;\;\;\;\;\;{\lambda _{\max }}\left( {\mathit{\boldsymbol{\tilde J}}} \right)\frac{{k_3^2}}{2}r\left| {{q_0}} \right|{\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|^{2r - 1}}\left\| \mathit{\boldsymbol{s}} \right\| - \\ \;\;\;\;\;\;\left( {\bar d + \lambda {{\left\| \mathit{\boldsymbol{\omega }} \right\|}^2} + \frac{{k_3^2}}{2}r\lambda \left| {{q_0}} \right|{{\left\| {{\mathit{\boldsymbol{q}}_v}} \right\|}^{2r - 1}}} \right)\left\| \mathit{\boldsymbol{s}} \right\| + \\ \;\;\;\;\;\;\bar d\left\| \mathit{\boldsymbol{s}} \right\| \le - k{\left\| \mathit{\boldsymbol{s}} \right\|^{p + 1}} \le - \mu {V^{\frac{{p + 1}}{2}}}. \end{array} $ | (6) |
在式(4)~(6)中
| $ \mu = k{\left( {2/{\lambda _{\max }}\left( \mathit{\boldsymbol{J}} \right)} \right)^{\frac{{p + 1}}{2}}}. $ |
在上述证明中用到了性质
由式(4)~(6)可以得到系统将在有限时间内收敛至滑模面(1).
3 考虑力矩受限的有限时间鲁棒控制算法由于所提出的控制律(2)并未考虑力矩饱和的情形,接下来将给出在输出力矩受限情况下的有限时间控制律.
首先改写控制律(2)为
| $ \mathit{\boldsymbol{u}} = \left\{ \begin{array}{l} - k{\left\| \mathit{\boldsymbol{s}} \right\|^p}{\mathit{\boldsymbol{s}}_e} + {\mathit{\boldsymbol{r}}_1},\;\;\;\;\left\| {{\mathit{\boldsymbol{q}}_v}} \right\| > \alpha ;\\ - k{\left\| \mathit{\boldsymbol{s}} \right\|^p}{\mathit{\boldsymbol{s}}_e} + {\mathit{\boldsymbol{r}}_2},\;\;\;\;\beta < \left\| {{\mathit{\boldsymbol{q}}_v}} \right\| \le \alpha ;\\ - k{\left\| \mathit{\boldsymbol{s}} \right\|^p}{\mathit{\boldsymbol{s}}_e} + {\mathit{\boldsymbol{r}}_3},\;\;\;\;\left\| {{\mathit{\boldsymbol{q}}_v}} \right\| \le \beta . \end{array} \right. $ |
假定控制力矩上限为u,设计合适的控制参数k1, k2, k3, α, β使得||ri||≤u,考虑力矩受限的有限时间控制律为
| $ \mathit{\boldsymbol{u}} = \left\{ \begin{array}{l} - {\rho _1}{\left\| \mathit{\boldsymbol{s}} \right\|^p}{\mathit{\boldsymbol{s}}_e} + {\mathit{\boldsymbol{r}}_1},\;\;\;\;\left\| {{\mathit{\boldsymbol{q}}_v}} \right\| > \alpha ;\\ - {\rho _2}{\left\| \mathit{\boldsymbol{s}} \right\|^p}{\mathit{\boldsymbol{s}}_e} + {\mathit{\boldsymbol{r}}_2},\;\;\;\;\beta < \left\| {{\mathit{\boldsymbol{q}}_v}} \right\| \le \alpha ;\\ - {\rho _3}{\left\| \mathit{\boldsymbol{s}} \right\|^p}{\mathit{\boldsymbol{s}}_e} + {\mathit{\boldsymbol{r}}_3},\;\;\;\;\left\| {{\mathit{\boldsymbol{q}}_v}} \right\| \le \beta . \end{array} \right. $ | (7) |
其中
| $ {\rho _i} = \left\{ \begin{array}{l} k,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\| {{\rho _i}{{\left\| \mathit{\boldsymbol{s}} \right\|}^p}{\mathit{\boldsymbol{s}}_e} + {\mathit{\boldsymbol{r}}_i}} \right\| \le \bar u;\\ \frac{{ - {{\left\| \mathit{\boldsymbol{s}} \right\|}^p}\mathit{\boldsymbol{s}}_e^{\rm{T}}{\mathit{\boldsymbol{r}}_i} + \sqrt {{{\left\| \mathit{\boldsymbol{s}} \right\|}^{2p}}{{\left( {\mathit{\boldsymbol{s}}_e^{\rm{T}}{\mathit{\boldsymbol{r}}_i}} \right)}^2} + {{\mathit{\boldsymbol{\bar u}}}^2} - {{\left\| {{\mathit{\boldsymbol{r}}_i}} \right\|}^2}} }}{{{{\left\| \mathit{\boldsymbol{s}} \right\|}^{2p}}}},{\rm{other}}{\rm{.}} \end{array} \right. $ |
通过式(7)可以看到,对控制力矩限幅是通过对控制律中比例项-k||s||pse进行限幅得到的,即在u不超过系统幅值的情况下对原控制律不作处理,而在超过系统幅值时对该比例项进行缩小使得||u||=u.
接下来对控制律(7)进行有限时间稳定性证明.选取Lyapunov函数如式(3)所示,对其求导并带入控制律(7),可以得到
| $ \dot V \le - {\rho _i}{\left\| \mathit{\boldsymbol{s}} \right\|^{p + 1}} \le - {\mu _i}{V^{\frac{{p + 1}}{2}}}, $ |
其中
| $ {\mu _i} = {\rho _i}{\left( {2/{\lambda _{\max }}\left( \mathit{\boldsymbol{J}} \right)} \right)^{\frac{{p + 1}}{2}}}, $ |
从而控制律(7)能够使系统在有限时间内收敛于滑模面(1).
4 仿真与分析本文以传统的滑模控制律作为对比[16]:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}} = - k\left( {\mathit{\boldsymbol{\omega }} + {k_1}{\mathit{\boldsymbol{q}}_v}} \right) - \frac{{{k_1}}}{2}\left( {{q_0}{\mathit{\boldsymbol{I}}_3} + \mathit{\boldsymbol{q}}_v^ \times } \right)\mathit{\boldsymbol{\omega }} - }\\ {\bar d{\mathop{\rm sgn}} \left( {\mathit{\boldsymbol{\omega }} + {k_1}{\mathit{\boldsymbol{q}}_v}} \right) + {\mathit{\boldsymbol{\omega }}^ \times }\mathit{\boldsymbol{J\omega }}.} \end{array} $ | (8) |
考虑到本文所提出算法在系统状态远离平衡点时对收敛速率提升较为明显,因此选取初始姿态角速度与四元数如下:
| $ \mathit{\boldsymbol{\omega }} = {\left[ {\begin{array}{*{20}{c}} { - 0.03}&{ - 0.04}&{0.05} \end{array}} \right]^{\rm{T}}}{\rm{rad}}/{\rm{s}}, $ |
| $ \mathit{\boldsymbol{q}} = {\left[ {\begin{array}{*{20}{c}} 0&{\sqrt 6 /6}&{\sqrt 3 /3}&{\sqrt 2 /2} \end{array}} \right]^{\rm{T}}}. $ |
同时考虑到选取较小的α能够使系统尽量停留在匀速阶段,同时应当使得系统在到达收敛段时实现角速度与四元数的反向,因此选取控制参数如下: α=0.2, β=0.02,r=2/3, p=1/2, λ=12,k1=0.05, k2=0.25, k3=0.0679, k=10.
最后,设置系统参数如下:J=diag(25, 30, 50) kg·m2,
|
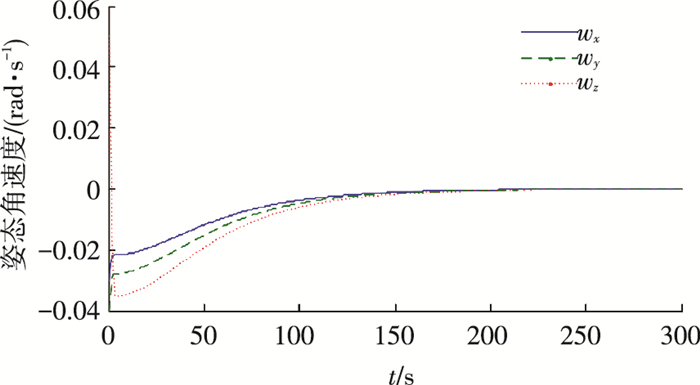
图 1 姿态角速度曲线 Figure 1 Curves of angular velocity |
|
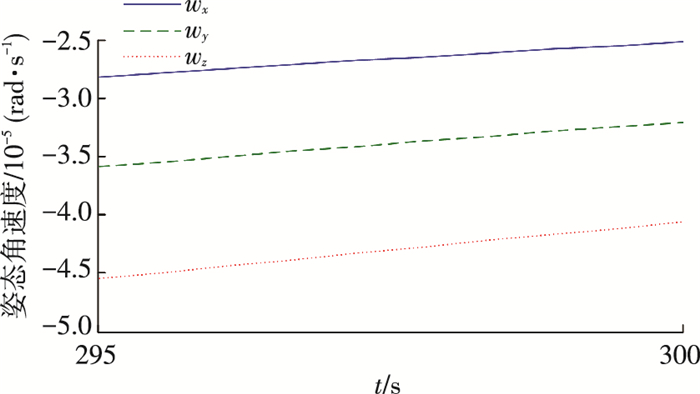
图 2 姿态角速度局部放大 Figure 2 Magnification of angular velocity |
|
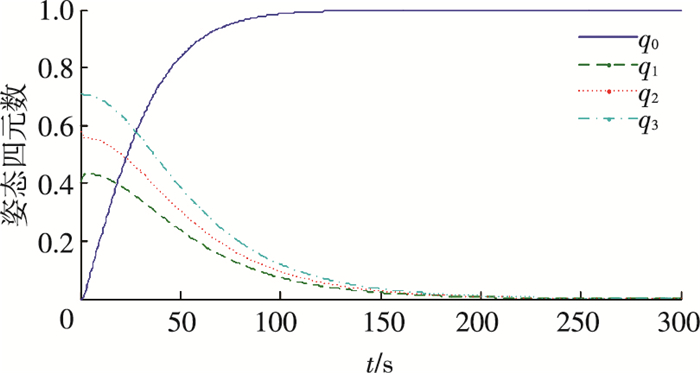
图 3 姿态四元数曲线 Figure 3 Curves of attitude quaternion |
|
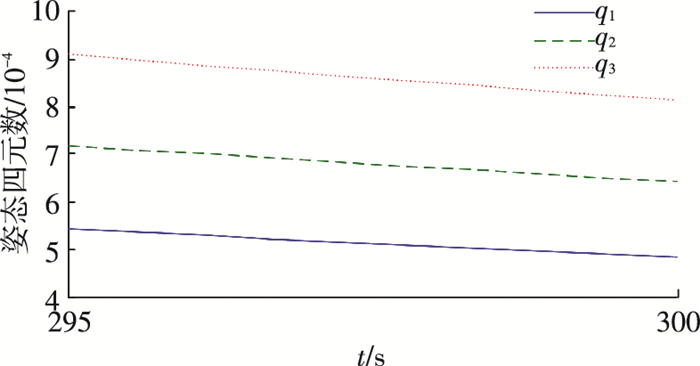
图 4 姿态四元数局部放大 Figure 4 Magnification of attitude quaternion |
|
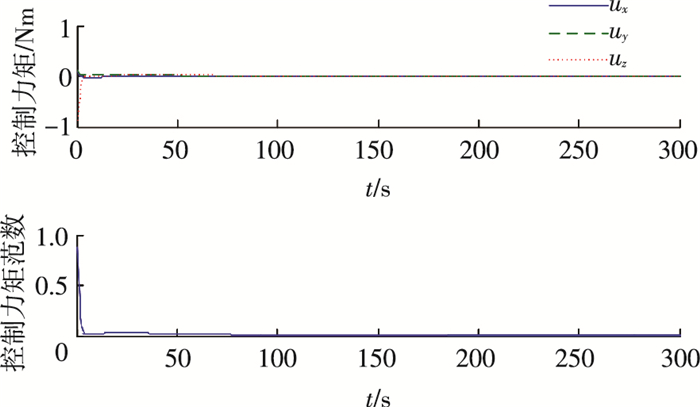
图 5 控制力矩及其范数曲线 Figure 5 Curves of control torque and the norm |
由图 1~5可以看到,虽然控制律(8)能够实现系统状态的收敛,但主要其存在两方面的问题:1)初始控制力矩过大,同时随着系统状态的减小控制力矩急剧下降,这就造成了初始阶段控制力矩容易出现饱和,随后又会出现控制力矩利用效率不高的问题;2)角速度下降过快导致了系统缓慢的状态收敛,由图 2可以看到系统在300 s处姿态角速度与姿态四元数的精度分别为4×10-5与9×10-4.
接下来给出本文提出的有限时间控制律(7)的仿真.首先由系统初始状态以及滑模参数的值可以得到系统由初始状态收敛至滑模面(1)的时间t0满足:
| $ {t_0} \le V_0^{1 - \frac{{p + 1}}{2}}/\mu \left( {1 + \frac{{p + 1}}{2}} \right) \approx 4.8. $ | (9) |
系统在匀速段、减速段、收敛段的收敛时间t1、t2、t3分别满足:
| $ {t_1} \le \left( {{\rm{ \mathsf{ π} }} - 2\arccos \left( {1 + {\alpha ^2}} \right)} \right)/{k_1} \approx 54.8, $ | (10) |
| $ {t_2} \le \left( {\ln \alpha - \ln \beta } \right)/\left( {{k_2}\sqrt {1 - {\alpha ^2}} } \right) \approx 9.4, $ | (11) |
| $ {t_3} \le {\beta ^{1 - r}}/{k_3}\left( {1 + \frac{{r + 1}}{2}} \right) \approx 22.9. $ | (12) |
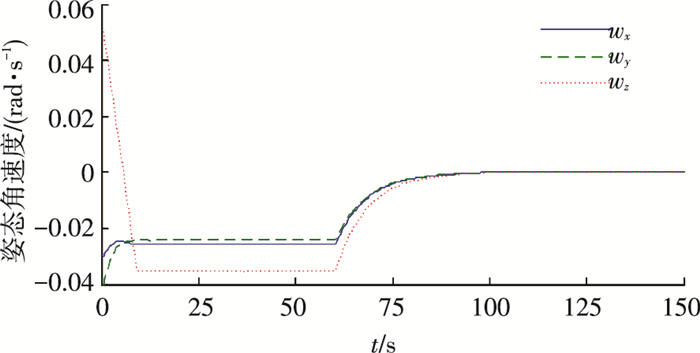
|
图 6 姿态角速度曲线 Figure 6 Curves of angular velocity |
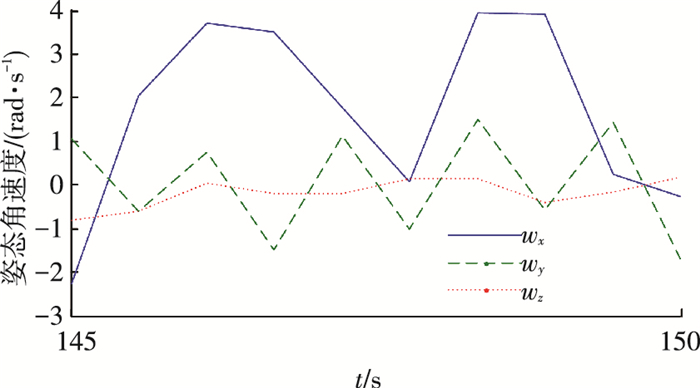
|
图 7 姿态角速度局部放大 Figure 7 Magnification of angular velocity |
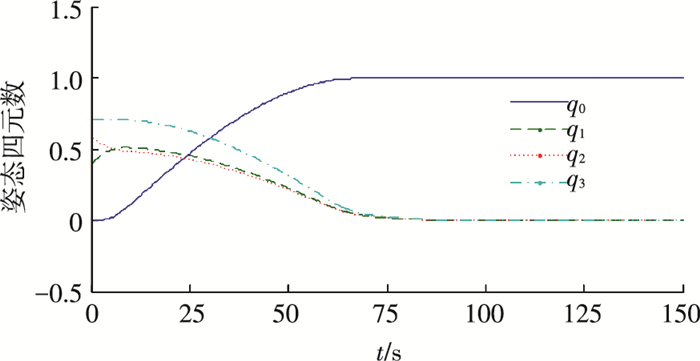
|
图 8 姿态四元数曲线 Figure 8 Curve of attitude quaternion |
|
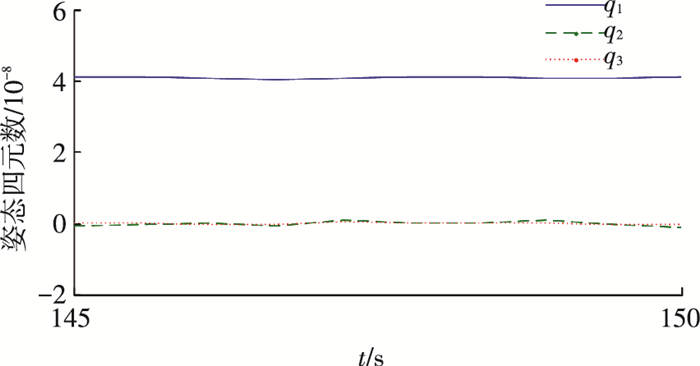
图 9 姿态四元数局部放大 Figure 9 Magnification of attitude quaternion |
|
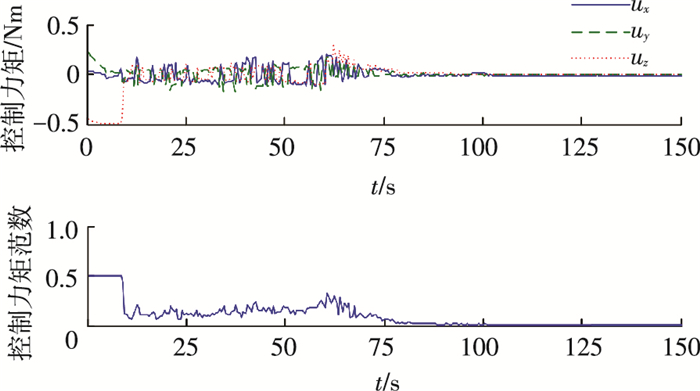
图 10 控制力矩及其范数曲线 Figure 10 Curves of control torque and the norm |
通过图 6、8可以看到本文提出的有限时间鲁棒控制律(7)能够实现系统在100 s处收敛至0,系统在5 s左右进入滑模面的匀速段,60 s左右进入减速段,这也印证了依据式(9)~(12)所估算的收敛时间,说明了本文给出的收敛时间估计算法的有效性.同时,在匀速段内控制力矩较小且角速度维持匀速状态,qv保持了较快的收敛速率,同时根据图 8可以得到在匀速段结束即60 s时q0为0.92,而经典滑模控制器在60 s处q0为0.85,对应的姿态角相差17.43°,这就说明控制器(7)能够避免角速度下降过快带来的收敛速率下降的问题,同时也能解决控制力矩利用率低下的问题.150 s处的姿态角速度与姿态四元数精度分别为6×10-7与4×10-8,高于经典滑模控制器在300 s处的精度,考虑到外部干扰力矩的存在,系统状态虽然不能绝对收敛至0,仍可具有较高的精度.与此同时,由图 10可以看到控制力矩全程未超过系统上限.
由于姿态四元数的收敛速率取决于姿态角速度,因此合理的规划姿态角速度轨迹是实现提升系统收敛速率的关键.控制器(7)能够在相同条件下大幅提升经典滑模控制器收敛速率的关键在于:1)系统应当尽可能长的处于匀速段,由图 10可以看到该阶段角速度保持恒定,从而四元数收敛速率得以维持,同时控制力矩较小,因此系统停留在该阶段能够使得控制力矩得到高效利用;2)系统应尽快进入滑模面(1)的收敛段,避免在指数收敛速率的减速段停留过长.
5 结论1) 本文所提出滑模面较经典滑模面提升收敛时间超过50%,提升收敛速率的关键在于匀速段与减速段,匀速段角速度恒定从而四元数收敛速率能够得以维持,而收敛段具有有限时间收敛的特性,这两个阶段是对于经典滑模面改进的关键.
2) 与经典滑模面类似,本文滑模面要求角速度与四元数矢部的反向,此时欧拉轴指向不变,这一点是解决奇异性问题的关键.
3) 本文所提出控制器对于位置干扰力矩与系统转动惯量不确定性具有鲁棒性,通过选择合适的控制参数,系统仍然能够拥有较高精度.
| [1] |
胡庆雷, 王辉, 石忠, 等. 航天器新型非奇异饱和终端滑模姿态控制[J].
宇航学报, 2015, 36(4): 430-437.
HU Qinglei, WANG Hui, SHI Zhong, et al. Novel non-singular saturated terminal sliding mode based attitude controller for spacecraft[J]. Journal of Astronautics, 2015, 36(4): 430-437. DOI: 10.3873/j.issn.1000-1328.2015.04.009 |
| [2] |
WU Shunan, RADICE G, SUN Zhaowei. Robust finite-time control for flexible spacecraft attitude maneuver[J].
Journal of Aerospace Engineering, 2014, 27(1): 185-190.
DOI: 10.1061/(ASCE)AS.1943-5525.0000247 |
| [3] |
WU Shunan, RADICE G, GAO Yongsheng, et al. Quaternion-based finite time control for spacecraft attitude tracking[J].
Acta Astronautica, 2011, 69(1/2): 48-58.
DOI: 10.1016/j.actaastro.2011.03.001 |
| [4] |
王剑颖, 梁海朝, 吴限德, 等. 高超声速飞行器连续终端滑模姿态控制方法[J].
哈尔滨工程大学学报, 2016, 37(2): 187-191.
WANG Jianying, LIANG Haizhao, WU Xiande, et al. Continuous terminal sliding mode attitude control for hypersonic aircrafts[J]. Journal of Harbin Engineering University, 2016, 37(2): 187-191. DOI: 10.11990/jheu.201411049 |
| [5] |
WANG Jianying, LIANG Haizhao, SUN Zhaowei, et al. Finite time control for spacecraft formation with dual number based description[J].
Journal of Guidance, Control and Dynamics, 2012, 35(3): 950-962.
DOI: 10.251/1.54277 |
| [6] |
LEE K W, SINGH S N. A higher-order sliding mode three-axis solar pressure satellite attitude control system[J].
Journal of Aerospace Engineering, 2016, 29(1): 670-684.
DOI: 10.1061/(ASCE)AS.1943-5525.0000509 |
| [7] |
LEE D, SANYAL A K, BUTCHER E A, et al. Finite-time control for body-fixed hovering of rigid spacecraft over an asteroid[C]//Proceedings of the 24th AAS/AIAA Space Flight Mechanics Meeting. Mexico: AIAA, 2014: 303-321.
https://arizona.pure.elsevier.com/en/publications/finite-time-control-for-body-fixed-hovering-of-rigid-spacecraft-o
|
| [8] |
RONTONDO D, NEJJARI F, PUIG V. Dilated LMI characterization for the robust finite time control of discrete time uncertain linear systems[J].
Automatica, 2016, 63: 16-20.
DOI: 10.1016/j.automatica.2015.10.003 |
| [9] |
LIShihua, DU Haibo, LIN Xiangze. Finite-time consensus algorithm for multi-agent systems with double-integrator dynamics[J].
Automatica, 2011, 47(8): 1706-1712.
DOI: 10.1016/j.automatica.2011.02.045 |
| [10] |
CHEN Gang, LEWIS F L, XIE Lihua. Finite-time distributed consensus via binary control protocols[J].
Automatica, 2011, 47(9): 1962-1968.
DOI: 10.1016/j.automatica.2011.05.013 |
| [11] |
JIANG Fangcui, WANG Long. Finite-time weighted average consensus with respect to a monotonic function application[J].
System & Control Letters, 2011, 60(9): 718-725.
DOI: 10.1016/j.sysconle.2011.05.009 |
| [12] |
DU Haibo, LI Shihua. Finite-time attitude stabilization for a rigid spacecraft using homogeneous method[J].
IFAC Proceedings Volumes, 2011, 44(1): 2620-2625.
DOI: 10.3182/20110828-6-IT-1002.01261 |
| [13] |
马克茂. 航天器连续非光滑姿态控制律设计[J].
宇航学报, 2012, 33(6): 713-719.
MA Kemao. Design of continuous non-smooth attitude control laws for spacecraft[J]. Journal of Aeronautics, 2012, 33(6): 713-719. DOI: 10.3873/j.issn.1000-1328.2012.06.005 |
| [14] |
FENG Yong, YU Xinghuo, MAN Zhihong. Non-singular terminal sliding mode control of rigid manipulators[J].
Automatica, 2002, 38(12): 2159-2167.
DOI: 10.1016/S0005-1098(02)00147-4 |
| [15] |
YU Shuanghe, YU X, SHIRINZADEH B. Continuous finite-time control for robotic manipulators[J].
Automatica, 2005, 41(11): 1957-1964.
DOI: 10.1016/j.automatica.2005.07.001 |
| [16] |
ZHAO Dongya, LI Shaoyuan, GAO Feng. A new terminal sliding mode control for robotic manipulators[J].
IFAC Proceedings Volumes, 2008, 41(2): 9888-9893.
DOI: 10.3182/20080706-5-KR-1001.01673 |
| [17] |
JIN Erdong, SUN Zhaowei. Robust controllers design with finite time convergence for rigid spacecraft attitude tracking control[J].
Aerospace Science and Technology, 2008, 12(4): 324-330.
DOI: 10.1016/j.ast.2007.08.001 |
| [18] |
HU Qinglei, XIAO Bing, SHI Peng. Tracking control of uncertain Euler Lagrange systems with finite time convergence[J].
International Journal of Robust and Nonlinear Control, 2015, 25(17): 3299-3315.
DOI: 10.1002/rnc.3263 |
 2018, Vol. 50
2018, Vol. 50


