现代航天技术的飞速发展对航天器姿态系统的响应速度和控制精度提出了越来越高的要求.现有的绝大多数航天器姿态控制设计方法都属于无限时间区间上的渐近控制方法,所得的结果中,闭环系统的状态最快的收敛速度为指数收敛[1-5].为了获得更好的收敛性能,有限时间控制理论便被引入到了航天器姿态控制设计中[6].所谓有限时间控制,就是使闭环系统的状态有限时间收敛的控制技术,它是一种时间最优的控制技术[7].除此以外,已有的研究成果表明,有限时间稳定闭环控制系统与非有限时间稳定闭环控制系统相比,具有更好的鲁棒性能和抗扰动性能[8-10].正因为如此,近年来,有限时间控制技术引起了控制专家和学者们的广泛兴趣,其在航天器姿态控制中的应用研究也得到了迅猛的发展[11-15].
需要指出的是,上述的文献均没有考虑输入死区非线性的影响.事实上,输入死区是广泛存在于航天器的执行机构(比如反作用力飞轮或推力器)中的一种典型非线性,而且输入死区非线性的存在会严重影响航天器姿态控制的性能[16].因此,输入死区非线性的影响是航天器高精度姿态控制设计中必须要考虑的一个重要因素.到目前为止,已有一些文献针对具有输入死区非线性的航天器姿态控制问题进行了研究.文献[17-18]针对具有模型不确定型、外部干扰和输入死区非线性的航天器姿态系统进行了鲁棒控制策略研究.所给的结果是在航天器的欧拉角较小,因而其控制系统模型可以写为一个线性系统加上非线性扰动形式的情况下获得的.文献[19]针对具有未知输入死区非线性的航天器姿态系统提出了一种自适应控制策略.该结果建立在用欧拉角表示的姿态运动学方程基础上,因而不适用于具有较大角度变化的航天器姿态控制.文献[16]针对输入死区非线性引入一个光滑的逆函数实现了对其影响的自适应补偿.文献[20]则考虑了执行机构同时含有输入死区和饱和非线性时航天器姿态的自适应控制问题.文献[16-20]仍然采用了无限时间区间上的渐近控制方法.考虑到有限时间控制技术重要的理论意义与实际应用价值,本文将进一步考虑含有不确定性和输入死区非线性的航天器姿态控制问题.基于时变滑模方法,提出一种有限时间姿态镇定控制算法,保证闭环系统的信号有界并且保证姿态误差在指定的时间内收敛到并以指定的精度保持在原点附近,并通过数值仿真来验证所提控制方法的有效性.
1 问题描述对航天器姿态运动的描述有多种方式,常见的包括经典的方向余弦、欧拉角和四元数等,以及后来发展起来的罗德里格参数(RPs)以及修正的罗德里格参数(MRPs).
修正的罗德里格参数定义如下:
| $ \sigma = \frac{{{q_v}}}{{1 + {q_0}}}, $ |
式中q=[q0 qvT]T∈R×R3为航天器本体坐标系相对于惯性坐标系的单位四元数,满足关系式:qTq=q0T+qvTqv=1.由修正的罗德里格参数描述的航天器姿态运动学方程如下:
| $ \dot \sigma = G\left( \sigma \right)\omega , $ | (1) |
式中,ω=[ω1 ω2 ω3]T为航天器的旋转角速率;矩阵G(σ)的定义如下:
| $ \mathit{\boldsymbol{G}}\left( \sigma \right) = \frac{1}{2}\left[ {\frac{{1 - {\sigma ^{\rm{T}}}\sigma }}{2}{I_3} + \mathit{\boldsymbol{S}}\left( \sigma \right) + \sigma {\sigma ^{\rm{T}}}} \right], $ | (2) |
其中
| $ \mathit{\boldsymbol{S}}\left( \sigma \right) = \left[ {\begin{array}{*{20}{c}} 0&{ - {\sigma _3}}&{{\sigma _2}}\\ {{\sigma _3}}&0&{ - {\sigma _1}}\\ { - {\sigma _2}}&{{\sigma _1}}&0 \end{array}} \right], $ | (3) |
矩阵G(σ)具有如下性质:
| $ {\sigma ^{\rm{T}}}\mathit{\boldsymbol{G}}\left( \sigma \right) = \left( {\frac{{1 + {\sigma ^{\rm{T}}}\sigma }}{4}} \right){\sigma ^{\rm{T}}}, $ | (4) |
| $ {\mathit{\boldsymbol{G}}^{\rm{T}}}\left( \sigma \right)\mathit{\boldsymbol{G}}\left( \sigma \right) = {\left( {\frac{{1 + {\sigma ^{\rm{T}}}\sigma }}{4}} \right)^2}{I_3}. $ | (5) |
很显然,从式(2)、(4)和(5)可以得知,矩阵G(σ)是一个正定对称矩阵.
航天器的姿态动力学方程如下:
| $ \mathit{\boldsymbol{J}}\dot \omega = - \mathit{\boldsymbol{S}}\left( \omega \right)\mathit{\boldsymbol{J}}\omega + u + {\tau _d}. $ | (6) |
式中:S(ω)的定义类似于式(3)中的S(σ);正定对称矩阵J∈R3×3为航天器的转动惯量矩阵;u=[u1 u2 u3]T为作用在航天器上的实际控制力矩,u=D(v), v=[v1 v2 v3]T表示控制力矩指令,即
| $ \mathit{\boldsymbol{D}}\left( v \right) = \left[ {\begin{array}{*{20}{c}} {{D_1}\left( {{v_1}} \right)}\\ {{D_2}\left( {{v_2}} \right)}\\ {{D_3}\left( {{v_3}} \right)} \end{array}} \right], $ | (7) |
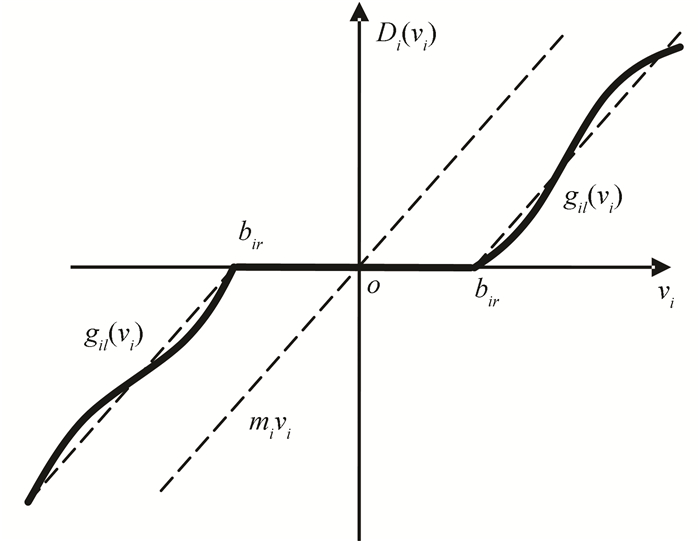
其中Di(·), i=1, 2, 3表示输入死区非线性,如图 1所示,Di(·)的表达式如下:
| $ {D_i}\left( {{v_i}} \right) = \left\{ \begin{array}{l} {g_{ir}}\left( {{v_i}} \right),\;\;\;\;\;{v_i} \ge {b_{ir}};\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;{b_{il}} < v < {b_{ir}};\\ {g_{il}}\left( {{v_i}} \right),\;\;\;\;\;{v_i} \le {b_{il}}. \end{array} \right. $ | (8) |
|
图 1 死区非线性示意 Figure 1 The dead-zone nonlinearity |
式中:bil、bir分别为输入死区的折点;gir(vi)、gil(vi)分别为连续函数;τd为干扰力矩,满足如下假设.
假设1 存在已知常数ρ0使得‖τd‖≤ρ0.
对于死区非线性,本文作如下假设.
假设2 gir(vi)、gil(vi)分别为未知函数,但存在已知的常数mi使之满足:
| $ \begin{array}{l} {g_{il}}\left( {{v_i}} \right) = {m_i}\left( {{v_i} - {b_{il}}} \right) + {\delta _{il}}\left( {{v_i}} \right),{v_i} \le {b_{il}},\\ {g_{ir}}\left( {{v_i}} \right) = {m_i}\left( {{v_i} - {b_{ir}}} \right) + {\delta _{ir}}\left( {{v_i}} \right),{v_i} \ge {b_{ir}}, \end{array} $ | (9) |
式中,δil(vi)、δir(vi)分别为未知但有界的函数,即存在已知常数δil和δir满足|δil(vi)|<δil,|δir(vi)|<δir.
假设3 参数bil、bir分别为未知,但是存在已知正常数bil1和bir1使之满足:
| $ \begin{array}{*{20}{c}} {0 < - {b_{il}} \le {b_{il1}},}\\ {0 < {b_{ir}} \le {b_{ir1}}.} \end{array} $ | (10) |
根据假设2和假设3,死区非线性的表达式(8)可以重新写成下述形式:
| $ {u_i} = {D_i}\left( {{v_i}} \right) = {m_i}{v_i} + {\Delta _i}\left( {{v_i}} \right), $ | (11) |
其中
| $ {\Delta _i}\left( {{v_i}} \right) = \left\{ \begin{array}{l} - {m_i}{b_{il}} + {\delta _{il}}\left( {{v_i}} \right),\;\;\;\;{v_i} \le {b_{il}};\\ - {m_i}{v_i},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{b_{il}} < {v_i} < {b_{ir}};\\ - {m_i}{b_{ir}} + {\delta _{ir}}\left( {{v_i}} \right),\;\;\;\;{v_i} \ge {b_{ir}}. \end{array} \right. $ |
于是,有
|Δi(vi)|≤ρi=mimax{bir1, bil1}+max{δil, δir}, 式中ρi为已知的正常数.
定义:
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {{m_1}}&0&0\\ 0&{{m_2}}&0\\ 0&0&{{m_3}} \end{array}} \right],\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}\left( v \right)\left[ {\begin{array}{*{20}{c}} {{\mathit{{{\varDelta} }}_1}\left( {{v_1}} \right)}\\ {{\mathit{{{\varDelta} }}_2}\left( {{v_2}} \right)}\\ {{\mathit{{{\varDelta} }}_3}\left( {{v_3}} \right)} \end{array}} \right], $ |
则
| $ \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{D}}\left( v \right) = \mathit{\boldsymbol{M}}v + \mathit{{ {\varDelta} }}\left( v \right), $ | (12) |
于是,航天器的姿态动力学方程可以写成:
| $ \mathit{\boldsymbol{J}}\dot \omega = - \mathit{\boldsymbol{S}}\left( \omega \right)\mathit{\boldsymbol{J}}\omega + \mathit{\boldsymbol{M}}v + d\left( v \right), $ | (13) |
式中,d(v)=τd+Δ(v).令
本文控制设计的目标是:在给定的假设1~假设3的条件下,针对航天器的姿态系统(1)~(13)设计合适的控制律,使得闭环系统状态有界,并且使得航天器的姿态在指定的时间(设为Tf>0)内到达并以指定的精度保持在原点附近.
2 控制设计受文献[21-22]的启发,本文采用时变滑模控制方法进行有限时间控制算法的设计.
定义期望的罗德里格参数变化规律由函数λ:R≥0→R3给出,该函数满足如下条件:
1) λ在[0, ∞)上二次连续可微;
2) 当t>T时,λ(t)=0;
3)
4) λ(0)=σ(0)且
定义跟踪误差为:
| $ \eta \left( t \right) = \sigma \left( t \right) - \lambda \left( t \right). $ | (14) |
构造时变滑模面如下:
| $ s\left( t \right) = \dot \eta \left( t \right) + C\eta \left( t \right), $ | (15) |
式中,C=diag(c1, c2, c3),ci>0为设计参数.设计滑模控制律如下:
| $ \begin{array}{l} v = {\left( {\mathit{\boldsymbol{G}}\left( \sigma \right){\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{M}}} \right)^{ - 1}}\left( { - \mathit{\boldsymbol{\dot G}}\left( \mathit{\boldsymbol{\sigma }} \right)\omega + \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{\sigma }} \right){\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{S}}\left( \omega \right)\mathit{\boldsymbol{J}}\omega - } \right.\\ \;\;\;\;\left. {C\mathit{\boldsymbol{G}}\left( \sigma \right)\mathit{\boldsymbol{\omega }} + \mathit{\boldsymbol{\ddot \lambda }} + C\dot \lambda - K{\mathop{\rm sgn}} \left( s \right)} \right), \end{array} $ | (16) |
其中
| $ {\mathop{\rm sgn}} \left( s \right) = \left[ {\begin{array}{*{20}{c}} {{\mathop{\rm sgn}} \left( {{s_1}} \right)}\\ {{\mathop{\rm sgn}} \left( {{s_2}} \right)}\\ {{\mathop{\rm sgn}} \left( {{s_3}} \right)} \end{array}} \right], $ |
K=diag(k1, k2, k3), ki≥ρ‖Gri(σ)J-1‖,这里,Gri(σ)表示G(σ)的第i行组成的行向量.
对于闭环系统有如下结果.
定理1 在假设1~假设3的条件下,由式(1)、(13)及(16)所组成的闭环系统的状态有界,并且状态σ满足:当t>T时,|σi(t)|=0.
证明 很容易求得:
| $ \eta \left( 0 \right) = \sigma \left( 0 \right) - \lambda \left( 0 \right) = 0, $ |
| $ \dot \eta \left( 0 \right) = \dot \sigma \left( 0 \right) - \dot \lambda \left( 0 \right) = 0, $ |
因此,
| $ s\left( 0 \right) = \dot \eta \left( 0 \right) + C\eta \left( 0 \right) = 0. $ | (17) |
由式(1)、(13)、(15)、(16)可得
| $ \begin{array}{*{20}{c}} {\dot s = \mathit{\boldsymbol{\ddot \eta }}\left( t \right) + C\dot \eta \left( t \right) = \mathit{\boldsymbol{\ddot \sigma }} + C\dot \sigma - \mathit{\boldsymbol{\ddot \lambda }} - C\dot \lambda ,}\\ {\mathit{\boldsymbol{\dot G}}\left( \sigma \right)\omega + \mathit{\boldsymbol{G}}\left( \sigma \right)\dot \omega + C\mathit{\boldsymbol{G}}\left( \sigma \right)\omega - \mathit{\boldsymbol{\ddot \lambda }} - C\dot \lambda = }\\ { - \left[ {\begin{array}{*{20}{c}} {{k_1}{\mathop{\rm sgn}} \left( {{s_1}} \right)}\\ {{k_2}{\mathop{\rm sgn}} \left( {{s_2}} \right)}\\ {{k_3}{\mathop{\rm sgn}} \left( {{s_3}} \right)} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{G}}_{r1}}\left( \sigma \right){\mathit{\boldsymbol{J}}^{ - 1}}d}\\ {{\mathit{\boldsymbol{G}}_{r2}}\left( \sigma \right){\mathit{\boldsymbol{J}}^{ - 1}}d}\\ {{\mathit{\boldsymbol{G}}_{r3}}\left( \sigma \right){\mathit{\boldsymbol{J}}^{ - 1}}d} \end{array}} \right].} \end{array} $ |
定义
| $ {V_i} = \frac{1}{2}s_i^2,i = 1,2,3 $ | (18) |
则有
| $ \begin{array}{l} {{\dot V}_i} = - {k_i}{s_i}{\mathop{\rm sgn}} \left( {{s_i}} \right) + {s_i}{\mathit{\boldsymbol{G}}_{ri}}\left( \sigma \right){\mathit{\boldsymbol{J}}^{ - 1}}d \le \\ \;\;\;\;\;\; - {k_i}\left| {{s_i}} \right| + \rho \left\| {{\mathit{\boldsymbol{G}}_{ri}}\left( \sigma \right){\mathit{\boldsymbol{J}}^{ - 1}}} \right\|\left| {{s_i}} \right| \le 0, \end{array} $ |
由式(17)、(18)可知,Vi(t0)=0.由此知
| $ 0 \le {V_i}\left( t \right) \le {V_i}\left( {{t_0}} \right) = 0, $ |
因此,Vi(t)≡0,故si≡0.由此及式(15)可知
| $ {{\dot \eta }_i} = - {c_i}{\eta _i}, $ |
故
| $ {\eta _i}\left( t \right) = {{\rm{e}}^{ - {c_i}t}}{\eta _i}\left( 0 \right) = 0, $ |
于是,有σi(t)=ηi(t)+λi(t)=λi(t).考虑到当t>T时,λi(t)=0,故当t>T时,σi(t)=0.
此外,很容易得知系统的状态σ和ω有界,证明详细过程这里不再赘述.
考虑到上述控制律中用到了不连续的符号函数,这可能会产生闭环系统的抖振现象.因此,本文用连续的饱和函数代替不连续的符号函数,改进设计滑模控制律如下
| $ \begin{array}{l} v = {\left( {\mathit{\boldsymbol{G}}\left( \sigma \right){\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{M}}} \right)^{ - 1}}\left( { - \mathit{\boldsymbol{\dot G}}\left( {{\sigma }} \right){{\omega }} + \mathit{\boldsymbol{G}}\left( {{\sigma }} \right){\mathit{\boldsymbol{J}}^{ - 1}}\mathit{\boldsymbol{S}}\left( {{\omega }} \right)\mathit{\boldsymbol{J}} \omega - } \right.\\ \;\;\;\;\left. {C\mathit{\boldsymbol{G}}\left( \sigma \right){{\omega }} + \mathit{\boldsymbol{\ddot \lambda }} + C\dot \lambda - K{\rm{SA}}{{\rm{T}}_\beta }\left( s \right)} \right), \end{array} $ | (19) |
其中
| $ {\rm{SA}}{{\rm{T}}_\beta }\left( s \right) = \left[ {\begin{array}{*{20}{c}} {{\rm{sa}}{{\rm{t}}_{{\beta _1}}}\left( {{s_1}} \right)}\\ {{\rm{sa}}{{\rm{t}}_{{\beta _2}}}\left( {{s_2}} \right)}\\ {{\rm{sa}}{{\rm{t}}_{{\beta _3}}}\left( {{s_3}} \right)} \end{array}} \right], $ |
式中, βi>0为设计参数.satβi(si)的定义如下:
| $ {\rm{sa}}{{\rm{t}}_{{\beta _i}}}\left( {{s_i}} \right) = \left\{ \begin{array}{l} \frac{{{s_i}}}{{{\beta _i}}},\;\;\;\;\;\;\;\;\;{\rm{if}}\;\;\left| {{s_i}} \right| < {\beta _i};\\ {\rm{sign}}\left( {{s_i}} \right),\;\;{\rm{if}}\;\;\left| {{s_i}} \right| \ge {\beta _i}. \end{array} \right. $ |
对于相应的闭环系统有如下结果.
定理2 任意给定常数εi>0, i=1, 2, 3,若设计参数满足βi/ci<εi,则在假设1~假设3的条件下,由式(1)、(13)、(19)组成的闭环系统的状态有界,并且状态σ满足:当t>T时,|σi(t)|<εi.
证明 由式(1)、(13)~(15)、(19)可得
| $ \dot s = - \left[ {\begin{array}{*{20}{c}} {{k_1}{\rm{sa}}{{\rm{t}}_{{\beta _1}}}\left( {{s_1}} \right)}\\ {{k_2}{\rm{sa}}{{\rm{t}}_{{\beta _2}}}\left( {{s_2}} \right)}\\ {{k_3}{\rm{sa}}{{\rm{t}}_{{\beta _3}}}\left( {{s_3}} \right)} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{G}}_{r1}}\left( \sigma \right){\mathit{\boldsymbol{J}}^{ - 1}}d}\\ {{\mathit{\boldsymbol{G}}_{r2}}\left( \sigma \right){\mathit{\boldsymbol{J}}^{ - 1}}d}\\ {{\mathit{\boldsymbol{G}}_{r3}}\left( \sigma \right){\mathit{\boldsymbol{J}}^{ - 1}}d} \end{array}} \right]. $ |
定义
| $ {V_i} = \frac{1}{2}s_i^2,\;\;i = 1,2,3 $ |
则有
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot V}}}_i} = - {k_i}s{\rm{sa}}{{\rm{t}}_{{\beta _i}}}\left( {{s_i}} \right) + s{\mathit{\boldsymbol{G}}_{ri}}\left( \sigma \right){\mathit{\boldsymbol{J}}^{ - 1}}d \le \\ \;\;\;\;\;\; - {k_i}s{\rm{sa}}{{\rm{t}}_{{\beta _i}}}\left( {{s_i}} \right) + \rho \left\| {{\mathit{\boldsymbol{G}}_{ri}}\left( \sigma \right){\mathit{\boldsymbol{J}}^{ - 1}}} \right\|, \end{array} $ |
很显然,如果|si|≥σi,则
由式(15)可知
| $ {{\dot \eta }_i}\left( t \right) = - {c_i}{\eta _i}\left( t \right) + {s_i}\left( t \right), $ |
由此可得
| $ \begin{array}{l} {\eta _i}\left( t \right) = {{\rm{e}}^{ - {c_i}t}}{\eta _i}\left( 0 \right) + \int_0^t {{{\rm{e}}^{ - {c_i}\left( {t - \tau } \right)}}{s_i}\left( \tau \right){\rm{d}}\tau } = \\ \;\;\;\;\;\;\;\;\;\;\int_0^t {{{\rm{e}}^{ - {c_i}\left( {t - \tau } \right)}}{s_i}\left( \tau \right){\rm{d}}\tau } , \end{array} $ |
于是有
| $ \begin{array}{*{20}{c}} {\left| {{\eta _i}\left( t \right)} \right| = \left| {\int_0^t {{{\rm{e}}^{ - {c_i}\left( {t - \tau } \right)}}{s_i}\left( \tau \right){\rm{d}}\tau } } \right| \le {\beta _i}\int_0^t {{{\rm{e}}^{ - {c_i}\left( {t - \tau } \right)}}{\rm{d}}\tau } = }\\ {\frac{{{\beta _i}}}{{{c_i}}}\left( {1 - {{\rm{e}}^{ - {c_i}t}}} \right) \le \frac{{{\beta _i}}}{{{c_i}}} \le {\varepsilon _i}.} \end{array} $ |
考虑到当t>T时,λ(t)=0,本文有当t>T时,σi(t)=ηi(t)+λi(t)=ηi(t).因此,当t>T时,即:|σi(t)|≤βi/ci<εi.
此外,很容易得知系统的状态σ和ω有界,证明过程这里不再赘述.
3 结果及分析本文针对某航天器进行姿态镇定控制的数学仿真以说明所提控制方法的有效性.为了避免控制律中使用不连续的符号函数导致系统抖振的问题,这里仅针对连续控制律(19)进行数学仿真.航天器的结构参数详见文献[23],其惯量矩阵标称值为
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {950}&{11}&5\\ {11}&{600}&{36}\\ 5&{36}&{360} \end{array}} \right]\left( {{\rm{kg}} \cdot {{\rm{m}}^2}} \right), $ |
干扰力矩设为
| $ {\tau _d} = \left[ {\begin{array}{*{20}{c}} {0.1\sin \left( {0.1t} \right)}\\ {0.2\sin \left( {0.1t + \frac{{\rm{ \mathsf{ π} }}}{2}} \right)}\\ {0.3\sin \left( {0.2t} \right)} \end{array}} \right]\left( {{\rm{N}} \cdot {\rm{m}}} \right). $ |
输入死区非线性的描述如式(8)、(9)所示,其中:m1=0.95, m2=1.00, m3=1.05, δ1l(v1)=0.2sin 2v1, δ2l(v2)=0.15cos 2.5v2, δ3l(v3)=0.1sin 3v3, δ1r(v1)=0.1cos v1, δ2r(v2)=0.2sin 2v2, δ3r(v3)=0.2sin 2.5v3, b1r=0.5, b2r=0.6, b3r=0.4, b1l=-0.6, b2l=-0.4, b3l=-0.5.
但是,在计算控制器参数时,本文仅仅知道mi的值,δil(vi)、δir(vi)绝对值的上界δil=δir=0.2和参数bil、bir绝对值的上界bil1=bir1=0.6.
设初始状态为:
| $ \sigma \left( 0 \right) = \left[ {\begin{array}{*{20}{c}} { - 0.128}\\ {0.515}\\ {0.128} \end{array}} \right],\;\;\;\;\omega \left( 0 \right) = \left[ {\begin{array}{*{20}{c}} {0.1}\\ { - 0.3}\\ {0.2} \end{array}} \right]{\rm{rad}} \cdot {{\rm{s}}^{ - 1}}. $ |
设计期望的罗德里格参数的变化规律如下:
| $ {\lambda _i}\left( t \right) = \left\{ \begin{array}{l} {a_{i0}} + {a_{i1}}t + {a_{i2}}{t^2} + {a_{i3}}{t^3},\;\;\;\;0 \le t \le {T_f};\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t > {T_f}. \end{array} \right. $ |
其中:
| $ {a_{i0}} = {\sigma _i}\left( 0 \right),{a_{i1}} = {{\dot \sigma }_i}\left( 0 \right), $ |
| $ {a_{i2}} = - 3\left( {{\sigma _i}\left( 0 \right)/T_f^2} \right) - 2\left( {{{\dot \sigma }_i}\left( 0 \right)/{T_f}} \right), $ |
| $ {a_{i3}} = 2\left( {{\sigma _i}\left( 0 \right)/T_f^3} \right) + {{\dot \sigma }_i}\left( 0 \right)/T_f^2.\;i = \left( {1,2,3} \right) $ |
其他控制参数设为:
| $ {k_i} = 1,{c_i} = 1,{\beta _i} = 0.001.\;i = \left( {1,2,3} \right) $ |
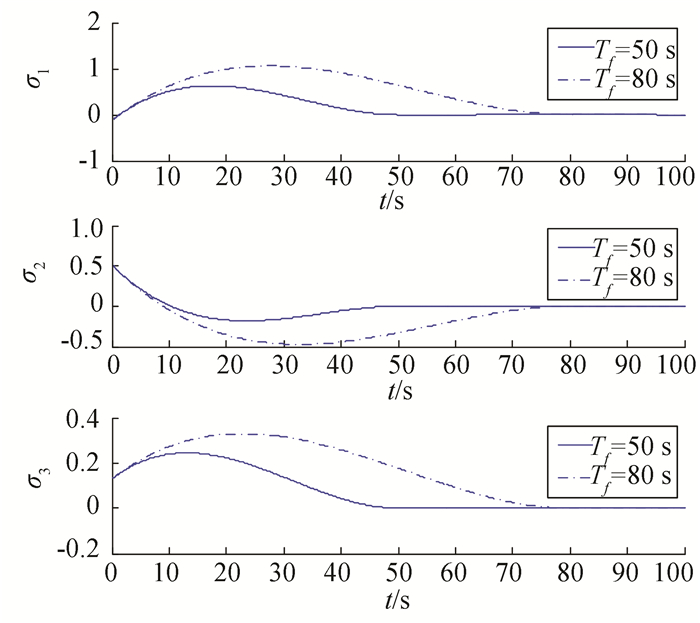
调整时间分别为Tf=50 s和Tf=80 s时的仿真结果如图 2~4所示.可以看出,随着调整时间的不同,航天器姿态的收敛速度不同,但是无论如何它们都能够以指定的时间收敛到并保持在零附近.
|
图 2 不同调整时间下的姿态MRPs变化曲线 Figure 2 Curves of MRPs with different settling 18:47:06 |

|
图 3 不同调整时间下的姿态角速率变化曲线 Figure 3 Curves of angular rates with different settling 18:47:13 |

|
图 4 不同调整时间下的控制力矩指令变化曲线 Figure 4 Curves of control torques with different settling time |
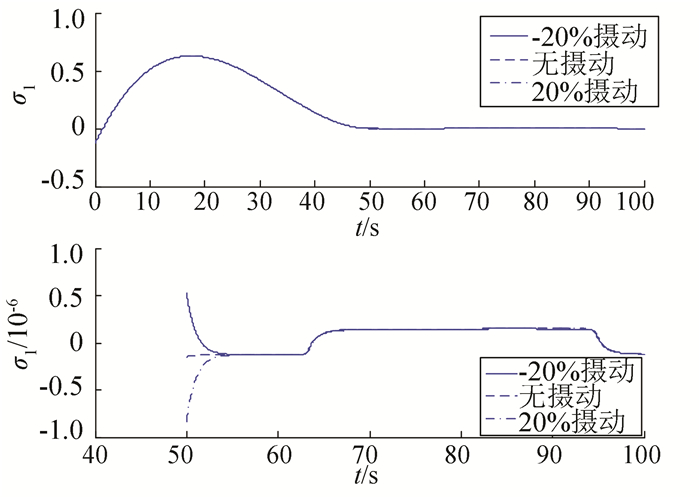
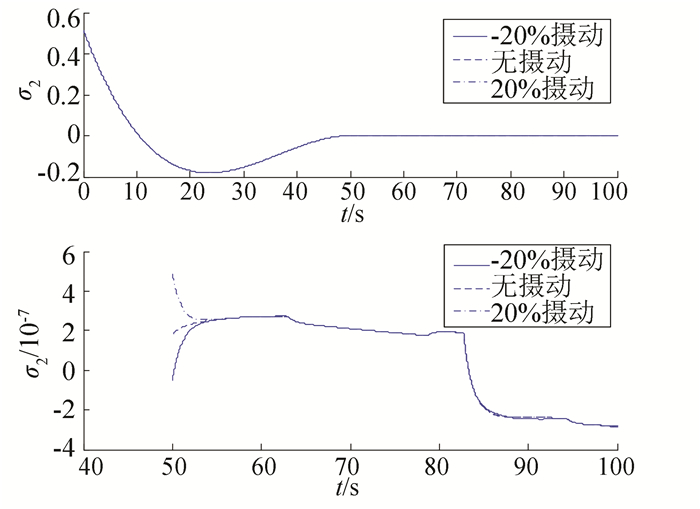
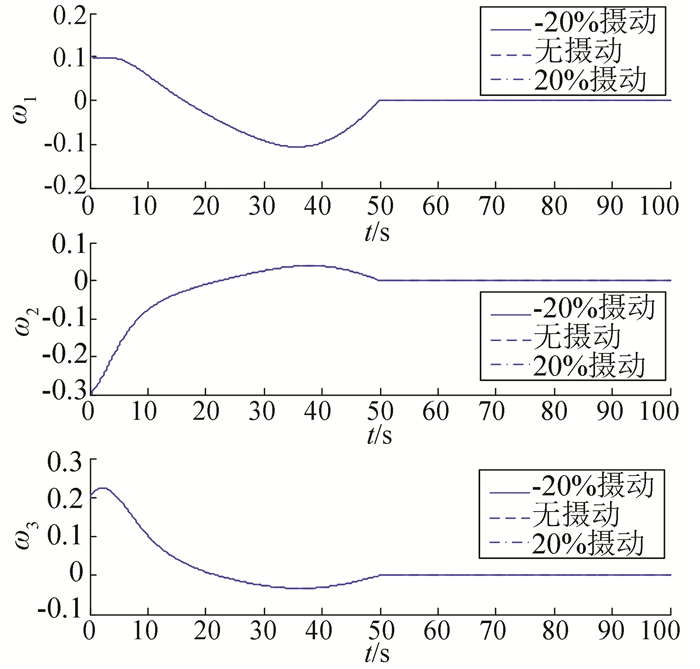
调整时间设为Tf=50 s,实际的惯量矩阵分别存在-20%摄动、无摄动、20%摄动情况下的仿真结果如图 5~9所示.从图中仿真结果可以看出,即使当转动惯量参数发生较大摄动时,姿态也能在指定的时间50 s内收敛到并保持在零附近,50 s后姿态控制精度小于10-6.同时,可以看出当转动惯量参数发生较大摄动时,除了控制力矩指令有一定的变化外,系统的姿态以及姿态角速率变化很小(它们的图像基本重合在一起),这说明所提出的控制方法对于参数的不确定性具有很好的鲁棒性.上述仿真结果说明了本文所提控制方法的有效性.
|
图 5 考虑参数摄动时的姿态σ1变化曲线 Figure 5 Curves of σ1 when considering parameter perturbations |
|
图 6 考虑参数摄动时的姿态σ2变化曲线 Figure 6 Curves of σ2 when considering parameter perturbations |

|
图 7 考虑参数摄动时的姿态σ3变化曲线 Figure 7 Curves of σ3 when considering parameter perturbations |
|
图 8 考虑参数摄动时的姿态角速度变化曲线 Figure 8 Curves of angular rates when considering parameter perturbations |

|
图 9 考虑参数摄动时的控制力矩指令变化曲线 Figure 9 Curvesof control torques when considering parameter perturbations |
1) 针对含有不确定性和输入死区非线性的航天器姿态控制问题,提出了一种有限时间镇定控制算法.
2) 引入了一个在指定时间内收敛到零的期望姿态变化曲线,并基于时变滑模方法设计了鲁棒控制算法使得实际姿态和期望姿态之间的偏差始终保持足够小,从而保证实际姿态在指定的时间内收敛到原点附近.
3) 理论分析表明设计控制律可以保证闭环系统的信号有界且实际姿态在指定的时间内收敛到并以指定的精度保持在原点附近;同时,仿真结果表明所提的控制方法可以实现航天器姿态的有限时间高精度控制,而且对于系统的不确定性具有良好的鲁棒性.
| [1] |
LI Chuanjiang, TEO K L, LI Bin, et al. A constrained optimal PID-like controller design for spacecraft attitude stabilization[J].
Acta Astronautica, 2012, 74: 131-140.
DOI: 10.1016/j.actaastro.2011.12.021 |
| [2] |
LUO Wencheng, CHU Y C, LING K V. Inverse optimal adaptive control for attitude tracking of spacecraft[J].
IEEE Transactions on Automatic Control, 2005, 50(11): 1639-1654.
DOI: 10.1109/TAC.2005.858694 |
| [3] |
Di GENNARO S. Output stabilization of flexible spacecraft with active vibration suppression[J].
IEEE Transactions on Aerospace and Electronic systems, 2003, 39(3): 747-759.
DOI: 10.1109/TAES.2003.1238733 |
| [4] |
WANG Bingquan, GONG Ke, YANG Di, et al. Fine attitude control by reaction wheels using variable-structure controller[J].
Acta Astronautica, 2003, 52(8): 613-618.
DOI: 10.1016/S0094-5765(02)00133-9 |
| [5] |
PUKDEBOON C, KUMAM P. Robust optimal sliding mode control for spacecraft position and attitude maneuvers[J].
Aerospace Science and Technology, 2015, 43: 329-342.
DOI: 10.1016/j.ast.2015.03.012 |
| [6] |
DU Haibo, LI Shihua, QIAN Chunjiang. Finite-time attitude tracking control of spacecraft with application to attitude synchronization[J].
IEEE Transactions on Automatic Control, 2011, 56(11): 2711-2717.
DOI: 10.1109/TAC.2011.2159419 |
| [7] |
丁世宏, 李世华. 有限时间控制问题综述[J].
控制与决策, 2011, 26(2): 161-169.
DING Shihong, LI Shihua. A survey for finite-time control problems[J]. Control and Decision, 2011, 26(2): 161-169. |
| [8] |
BHAT S P, BERNSTEIN D S. Continuous finite-time stabilization of the translational and rotational double integrators[J].
IEEE Transaction on Automatic Control, 1998, 43(5): 678-682.
DOI: 10.1109/9.668834 |
| [9] |
DING Shihong, LI Shihua, LI Qi. Stability analysis for a second-order continuous finite-time control system subject to a disturbance[J].
Journal of Control Theory and Applications, 2009, 7(3): 271-276.
DOI: 10.1007/s11768-009-8015-4 |
| [10] |
HONG Y, HUANG Jie, XU Yangsheng. On an output feedback finite-time stabilization problem[J].
IEEE Transaction on Automatic Control, 2001, 46(2): 305-309.
DOI: 10.1109/9.905699 |
| [11] |
ZHAO Lin, JIA Yingmin. Finite-time attitude tracking control for a rigid spacecraft using time-varying terminal sliding mode techniques[J].
International Journal of Control, 2015, 88(6): 1150-1162.
DOI: 10.1080/00207179.2014.996854 |
| [12] |
HE Xiaoyan, WANG Qingyun, YU Wenwu. Finite-time distributed cooperative attitude tracking control for multiple rigid spacecraft[J].
Applied Mathematics and Computation, 2015, 256: 724-734.
DOI: 10.1016/j.amc.2015.01.061 |
| [13] |
GAO Jiwei, CAI Yuanli. Robust adaptive finite time control for spacecraft global attitude tracking maneuvers[J].
Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2016, 230(6): 1027-1043.
DOI: 10.1177/0954410015602912 |
| [14] |
ZHONG Chenxing, GUO Yu, YU Zhen, et al. Finite-time attitude control for flexible spacecraft with unknown bounded disturbance[J].
Transactions of the Institute of Measurement and Control, 2016, 38(2): 240-249.
DOI: 10.1177/0142331214566223 |
| [15] |
SONG Zhankui, LI Hongxing, SUN Kaibiao. Finite-time control for nonlinear spacecraft attitude based on terminal sliding mode technique[J].
ISA transactions, 2014, 53(1): 117-124.
DOI: 10.1016/j.isatra.2013.08.008 |
| [16] |
WU Baolin, CAO Xibin, XING Lei. Robust adaptive control for attitude tracking of spacecraft with unknown dead-zone[J].
Aerospace Science and Technology, 2015, 45: 196-202.
DOI: 10.1016/j.ast.2015.05.014 |
| [17] |
HU Qinglei, MA Guangfu, XIE Lihua. Robust and adaptive variable structure output feedback control of uncertain systems with input nonlinearity[J].
Automatica, 2008, 44(2): 552-559.
DOI: 10.1016/j.automatica.2007.06.024 |
| [18] |
HU Qinglei. Variable structure output feedback control of a spacecraft under input dead-zone non-linearity[J].
Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2007, 221(2): 289-303.
DOI: 10.1243/09544100JAERO96 |
| [19] |
JASIM N F, JASIM I F. Robust adaptive control of spacecraft attitude systems with unknown dead zones of unknown bounds[J].
Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2012, 226(7): 947-955.
DOI: 10.1177/0959651812443926 |
| [20] |
HU Qinglei, LI Li, FRISWELL M I. Spacecraft anti-unwinding attitude control with actuator nonlinearities and velocity limit[J].
Journal of Guidance, Control, and Dynamics, 2015, 38(10): 2042-2050.
DOI: 10.2514/1.G000980 |
| [21] |
PARK K B, TSUJI T. Terminal sliding mode control of second-order nonlinear uncertain systems[J].
International Journal of Robust and Nonlinear Control, 1999, 9(11): 769-780.
DOI: 10.1002/(SICI)1099-1239(199909)9:11<769::AID-RNC435>3.0.CO;2-M |
| [22] |
SUN Liang. Passivity-based adaptive finite-time trajectory tracking control for spacecraft proximity operations[J].
Journal of Spacecraft and Rockets, 2015, 53(1): 46-56.
DOI: 10.2514/1.A33288 |
| [23] |
耿洁, 吕楠, 王韬, 等. 航天器的有限时间时变滑模姿态控制方法设计[J].
空间控制技术与应用, 2016, 42(4): 30-35.
GENG Jie, LV Nan, WANG Tao, et al. A novel finite-time sliding mode attitude controller for spacecraft[J]. Aerospace Control and Application, 2016, 42(4): 30-35. DOI: 10.3969/j.issn.1674-1579.2016.04.006 |
 2018, Vol. 50
2018, Vol. 50


