扑翼飞行器是一种模仿鸟类和昆虫飞行的新型飞行器,在军事和民用领域均蕴含着广阔的应用前景.鸟类和昆虫在翅膀结构与形态方面存在着很大的差异,其中鸟类翅膀相对较厚并具有一定的弯度,由肌肉、骨骼、羽毛以及关节构成;而昆虫翅膀较薄,上面分布了翅脉和柔性翅膜,并往往呈褶皱形态.飞行生物翅膀的这些历经数百万年自然进化获得的结构特征必然会对其飞行性能有着重要的影响.目前,关于不同厚度和弯度翼型的定常空气动力学特性已经有了较为深入的认识,然而这些经验仍不能直接应用到扑翼飞行的气动特性研究中.
为揭示翼型厚度和弯度对扑翼气动性能的影响规律,Bai等[1]研究了不同弯度翼型对仿生果蝇扑翼气动性能的影响,指出正向弯度翼型能有效提高扑翼升力和升阻比.Zhao等[2]对不同翼型厚度的扑翼在进行一维沉浮运动时的气动力及气动效率进行了数值计算,研究表明,随着翼型厚度的增大,扑翼推力和推进效率均逐渐增大,扑翼升力则无明显变化.Ashraf等[3]数值计算了具有不同翼型厚度和弯度的扑翼在沉浮-俯仰复合运动时的气动特性,发现推进效率随翼型厚度的增大呈先增大后减小的趋势,而翼型弯度对扑翼的推进性能影响很小.此外,Yu等[4]研究表明,不同厚度的扑翼的气动性能随着系统参数(雷诺数和斯特努哈尔数)的改变呈现出不同的变化趋势.综合上述研究结果表明,翼型厚度和翼型弯度对扑翼气动性能的影响还没有得到一致性的结论.国内方面, 宋笔峰等[5-6]通过求解三维非定常雷诺平均方程研究了不同翼型厚度和弯度对挥舞-俯仰复合运动中微型扑翼气动特性的影响,指出翼型厚度对扑翼升力影响很小,具有适当弯度的翼型可以改善扑翼的气动性能.冉景洪等[7-8]研究了不同翼型厚度和弯度的扑翼在等速上仰运动中的气动性能,结果表明厚度较小的翼型能获得较大的动态升阻比,且最大弯度位置对气动力影响较为显著.然而上述研究均没有求解扑翼的能耗和气动效率,亦没有充分研究扑翼的流场特征,并且他们采用的模型参数,如扑动幅值、转动幅值与鸟类和昆虫的实际运动参数相比存在较大差异.因此,有关大幅值扑动和转动条件下,不同翼型厚度和翼型弯度对扑翼气动特性的影响仍有待进一步研究.鉴于此,本文基于以往文献中鸟类和昆虫扑动规律的实验观测结果,运用计算流体力学方法建立并求解前飞扑翼的数值计算模型,对不同来流速度条件下,具有不同翼型厚度和翼型弯度的扑翼气动力、能耗、气动效率和流场结构进行系统研究,旨在为微型扑翼飞行器的气动设计提供一定的理论指导和技术参考.
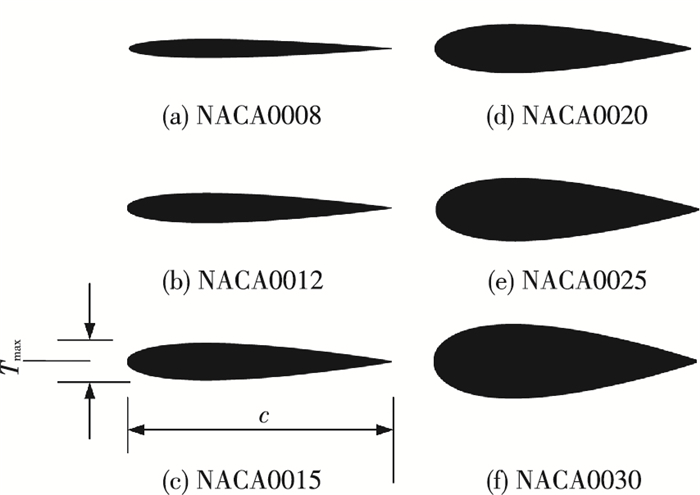
1 物理模型 1.1 翼型参数模型为研究翼型厚度和弯度对前飞扑翼气动性能的影响,选取NACA系列标准翼型作为研究对象,如图 1、2所示.图 1中Tmax为翼型最大厚度,c为翼型弦长,Tmax与c的比值定义为厚度比λ1,λ1变化范围为:8%~30%.在研究翼型弯度的过程中,翼型厚度保持15%c不变,且翼型最大弯曲位置距离前缘0.5c.图 2中Cmax为翼型中弧线至翼弦的最大距离,Cmax与c的比值表示翼型弯度λ2,当中弧线在翼弦上方时弯度为正,反之弯度为负.MNACA系列翼型由相应的NACA系列翼型沿着翼弦镜像得到.弯曲程度λ2翼变化范围为:-8%~8%.
|
图 1 不同厚度翼型 Figure 1 Airfoils with different thickness |

|
图 2 不同弯度翼型 Figure 2 Airfoils with different camber |
扑翼运动主要由包含沿扑动平面的往复平动和围绕旋转中心的周期性转动组成.扑翼运动模型示意图如图 3所示.图中XOY为惯性坐标系固定于地面,xoy为贴体坐标系固定于距前缘1/4弦长的翼型旋转中心处,β为扑动平面的倾角.

|
图 3 扑翼运动模型示意 Figure 3 Schematic of flapping wing motion |
扑翼运动规律采用简谐函数模型描述如下:
| $ \begin{array}{l} \;\;A\left( t \right) = {A_m}\cos \left( {2\pi ft} \right), \\ \alpha \left( t \right) = {\alpha _0}-{\alpha _m}\sin \left( {2\pi f + \varphi } \right). \end{array} $ |
式中:A(t)为瞬时扑动位移;Am为扑动位移幅值;f为扑动频率,f=1/T,其中T为扑动周期;α(t)为瞬时气动攻角;α0为初始气动攻角;αm为转动幅值;φ为扑动和转动之间相位差.扑翼各主要运动参数参照相关文献[9-10],具体设置如下:Am=1.25c,α0=π/12,αm=π/4,φ=0,β=5π/12.
2 计算方法前飞扑翼流场控制方程为非定常不可压缩黏性流体Navier-Stokes方程,具体形式如下:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\nabla \cdot \mathit{\boldsymbol{u}} = 0, \\ \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} + \mathit{\boldsymbol{u}} \cdot \nabla \mathit{\boldsymbol{u}} =-\nabla p + \frac{1}{{\mathit{Re}}}{\nabla ^2}\mathit{\boldsymbol{u}}. \end{array} $ |
式中:u为流体速度矢量,沿x和y方向的分量分别为u和v;p为流体动压;Re为雷诺数,定义为Re=ρUrefc/μ,其中ρ为流体密度,μ为流体粘性系数Uref为参考速度(定义为最大平动速度).
计算区域采用C型形式,如图 4所示.为更准确地捕捉流场信息以及考虑到翼型运动规律复杂性,采用混合网格形式对内外两层计算区域进行离散.通过动态网格技术设定内层计算区域与扑翼相同的运动规律,并采用结构化网格对其进行离散,此处网格紧贴翼型表面;外层计算区域采用非结构化网格进行离散,此处网格将随翼型的运动产生自适应弹性变形和动态局部重构.

|
图 4 计算区域与网格划分情况 Figure 4 Computational domain and grids |
假设前方来流均匀,在计算域的左侧边界AMC以及上、下两侧边界AB和CD设置Dirichlet边界条件:
| $ u = {U_\infty }, v = 0, p = {p_\infty }. $ |
式中U∞、p∞分别为无穷远的来流速度和压强.
右侧边界BD设定Neumman边界条件,边界上速度和压强变量梯度为0.翼型表面采用无滑移壁面边界条件.流体控制方程中对流项和扩散项分别采用二阶迎风格式和二阶中心差分格式进行离散,压力速度耦合方程采用SIMPLEC算法[11]进行分离求解.
翼型升力系数CL、阻力系数CD以及推力系数CT分别定义为:
| $ {C_L} = \frac{{{F_L}}}{{0.5\rho U_{{\rm{ref}}}^2cl}}, {C_D} = \frac{{{F_D}}}{{0.5\rho U_{{\rm{ref}}}^2cl}}, {C_T}{\rm{ = }}\frac{{{\rm{-}}{F_D}}}{{0.5\rho U_{{\rm{ref}}}^2cl}}. $ |
式中:FL、FD分别为瞬时升力和阻力;l为单位展长.
扑翼的能耗P(t)可定义如下:
| $ P\left( t \right) =- \left[{F\left( t \right) \cdot \dot A\left( t \right) + M\left( t \right) \cdot \dot \alpha \left( t \right)} \right]. $ |
式中:F(t)为沿着扑动平面方向的气动合力;M(t)为相对于转动中心的气动力矩.
扑翼运动所消耗的能量系数即可定义为
| $ {C_P} = \frac{{P\left( t \right)}}{{0.5\rho U_{{\rm{ref}}}^3c}}. $ |
扑翼一个扑动周期内的平均升力、推力和能耗系数分别为:
| $ {C_{Lm}} = \int_t^{t + T} {{C_L}} {\rm{d}}t, {C_{Tm}} = \int_t^{t + T} {{C_T}} {\rm{d}}t, {C_{Pm}} = \int_t^{t + T} {{C_P}} {\rm{d}}t. $ |
扑翼升举效率和推进效率分别为:
| $ {n_L} = \frac{{{C_{Lm}}}}{{{C_{Pm}}}}, {\eta _T}{\rm{ = }}\frac{{{C_{Tm}}}}{{{C_{Pm}}}}. $ |
首先,为验证本文数值方法及动网格模型计算前飞扑翼气动性能的正确性和有效性,选择Tuncer等[12]的实验结果以及Miao等[13]的数值结果进行分析验证.在以往的实验和计算模型中,研究了做沉浮运动的NACA0014翼型的气动性能,来流速度U∞保持恒定并以此为参考速度,来流马赫数Ma为0.1,Re为1×104,翼型攻角α0始终为零,扑动幅值Am为0.4c,扑动平面倾角β为π/2.图 5所示为本文求解得到的扑翼瞬时气动力系数与文献中的结果对比曲线.对比显示本文的计算结果与前人的实验和数值研究结果吻合较好.

|
图 5 气动力系数对比曲线 Figure 5 Comparison of aerodynamic force coefficient |
其次,针对本文具体的计算模型,为对网格方案的可靠性进行验证,通过不断调整翼型表面的网格节点数以及整个计算域的网格密度,对4种网格模型进行对比,见表 1.图 6所示为4种网格模型的试算分析结果,最终选择网格模型3对计算区域进行离散,翼型表面节点数为400,整个计算域初始网格约为6.3×104.
| 表 1 计算网格无关性验证 Table 1 Grid model test |

|
图 6 4种网格模型的阻力系数 Figure 6 Drag coefficients for four test grid models |
为研究翼型厚度对前飞扑翼气动性能的影响,基于刚性扑翼假设,采用层流计算模型求解了Re=1 000时,6种不同厚度的NACA系列标准对称翼型在3种不同来流速度条件下(前进比J=U∞/Uref,取J=0.10、0.25、0.50)的气动力、能耗、气动效率和流场结构变化情况.
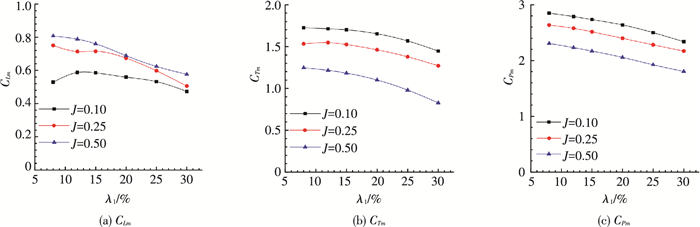
图 7所示为不同翼型厚度比λ1对扑翼时均升力系数(CLm)、时均推力系数(CTm)和时均能耗系数(CPm)的影响曲线.总体而言,3种不同来流速度条件下,扑翼CTm和CPm均随翼型厚度的增大而逐渐减小,而扑翼CLm随翼型厚度的变化趋势则稍有不同:当来流速度较大时(J为0.25、0.50),扑翼的CLm随着翼型厚度的增加逐渐减少;而当来流速度较小时(J为0.10),扑翼CLm随翼型厚度增加呈先增大后缓慢减小的趋势,并在λ1=12%处达到最大值.
|
图 7 扑翼时均气动力系数随翼型厚度的变化曲线 Figure 7 The variation of CLm, CTm, CPm with airfoil thickness |
图 8给出了翼型推进效率(ηT)和升举效率(ηL)随翼型厚度的变化情况.从图 8(a)中可以看出,当J=0.10、0.25时,随翼型厚度的增大,扑翼ηT呈先增大后减小的趋势,在λ1=20%时达到最大值,但总体变化程度较小;而当J=0.50时,扑翼ηT随λ1增大缓慢增大,在λ1=15%时达到峰值,而后则随翼型厚度的进一步增大而急剧减小,λ1=30%时的ηT与最大值相比下降了15.9%.另一方面,从图 8(b)中可以看出,不同来流速度条件下扑翼ηL变化趋势相近.ηL随λ1增大先缓慢增加,并在λ1=15%处达到峰值,而后随着翼型厚度的进一步增大,ηL缓慢减小.上述结果表明,来流速度较大时,翼型较薄的前飞扑翼具有更好的推进性能.

|
图 8 扑翼气动效率随翼型厚度的变化曲线 Figure 8 The variation of aerodynamic efficiencies with airfoil thickness |
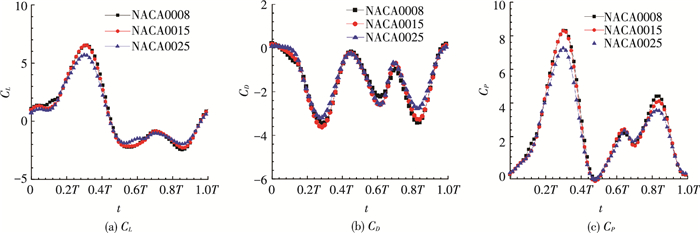
为具体分析翼型厚度对扑翼气动性能的影响以及扑翼周围流场变化情况,图 9给出了J=0.25时,一个扑动周期内3种具有不同翼型厚度的扑翼的瞬时升力系数(CL)、阻力系数(CD)和能耗系数(CP)的变化情况.图 10给出了相应的具有不同厚度翼型在一个扑动周期内不同特征时刻(0、0.25T、0.50T、0.75T)的表面压力系数Cp*(Cp*=(p-p∞)/(0.5ρUref2c)).
|
图 9 不同厚度翼型瞬时升阻力系数和能耗系数 Figure 9 Time histories of CL, CD, CP with different airfoil thickness during a flapping cycle |

|
图 10 不同时刻翼型表面压力系数分布情况 Figure 10 The Cp* of three airfoils with different thickness during a flapping cycle |
从图 9可知,翼型厚度的变化并未改变前飞扑翼流场的演变机制,不同翼型厚度的前飞扑翼的气动力系数和能耗系数有着同样的变化趋势.然而,扑翼气动力系数和能耗系数变化曲线的局部峰值在不同翼型厚度间存在显著差异.在下扑行程的前半程(0~0.25T)以及上挥行程的后半程(0.75T~1.00T),翼型厚度较小的扑翼能产生更大的升力和推力,但所需能耗亦最大.
对比图 10中具有不同翼型厚度的前飞扑翼表面压力分布差异可以看出,翼型厚度较薄的扑翼在下扑行程的前半程(0~0.25T),扑翼上、下表面间压力差较大,由此产生的升力和推力亦较大.翼型厚度的变化能显著影响扑翼前缘和尾缘处的压力分布.t=0.50T、0.75T时,翼型较薄的扑翼上表面高压区相比翼型较厚的扑翼分别距离扑翼尾缘和前缘更近.
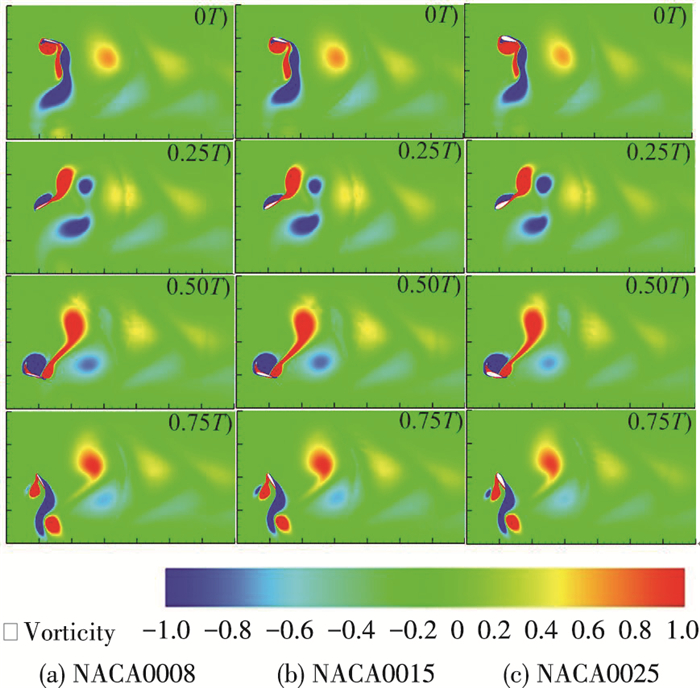
图 11给出了相应的具有不同翼型厚度的扑翼在一个扑动周期内不同特征时刻(0T、0.25T、0.50T、0.75T)流场中的涡量分布情况.总体而言,对应不同翼型厚度的扑翼尾流流场均呈现反卡门涡街形式,从而产生推力.具体来看,不同翼型厚度的扑翼前缘涡和尾缘涡基本同时从扑翼表面分离,各翼型所对应的扑翼流场尾涡结构亦基本一致;然而前缘涡的强度略有不同,翼型厚度的增加减弱了前缘涡强度并延迟了前缘涡的脱落.
|
图 11 不同厚度翼型一个周期内不同时刻的涡量图 Figure 11 The vorticity contour of three airfoils with different thickness during a flapping cycle |
本文为研究翼型弯度对扑翼气动性能的影响,基于刚性扑翼假设,采用层流计算模型求解了Re=1 000时,8种不同弯度翼型在不同来流速度条件下(J=0.10、0.25、0.50)的气动力、能耗、气动效率和流场结构变化情况.
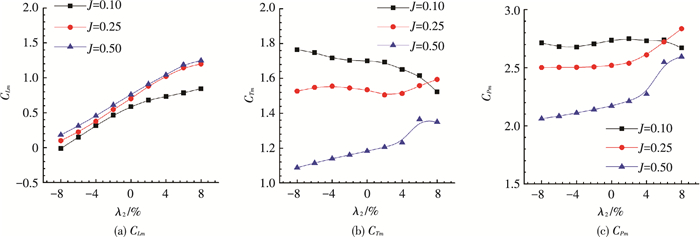
图 12所示为翼型弯度λ2对扑翼CLm、CTm和CPm的影响情况.研究发现,不同来流速度条件下扑翼CLm均随翼型弯度的增大而逐渐增大.Harbig等[14]在研究三维往复挥动扑翼气动性能过程中同样发现这一现象.扑翼CTm和CPm随翼型弯度变化的情况稍有不同:当来流速度较小时(J=0.10),随着翼型弯度由负向渐增为正向时,扑翼CTm逐渐减小,CPm则无明显变化;而当来流速度较大时(J=0.50),随着翼型弯度由负向渐变为正向,扑翼CTm和CPm均逐渐增大.
|
图 12 扑翼时均气动力系数随翼型弯度的变化曲线 Figure 12 The variation of CLm, CTm, CPm with airfoil camber |
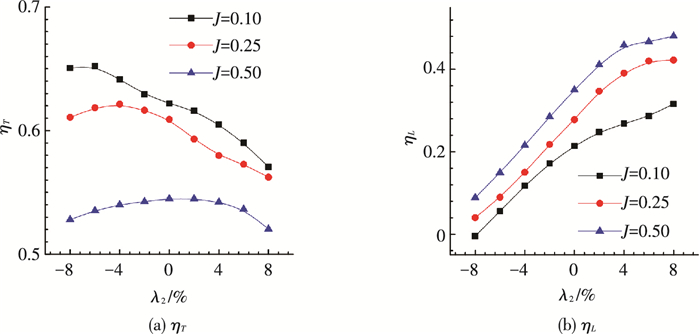
图 13给出了不同来流速度条件下扑翼ηT和ηL随翼型弯度λ2的变化情况.当来流速度较小时(J=0.10),扑翼ηT随翼型弯度的增大而逐渐降低;随着来流速度的增大(J=0.25、0.50),扑翼ηT随翼型弯度的增大先缓慢增大,随后逐渐降低.不同来流速度条件下扑翼ηL与图 12(a)中CLm有着相似的变化趋势,扑翼ηL随着翼型弯度的增大显著增大.
|
图 13 扑翼气动效率随翼型弯度的变化曲线 Figure 13 The variation of aerodynamic efficiencies with airfoil camber |
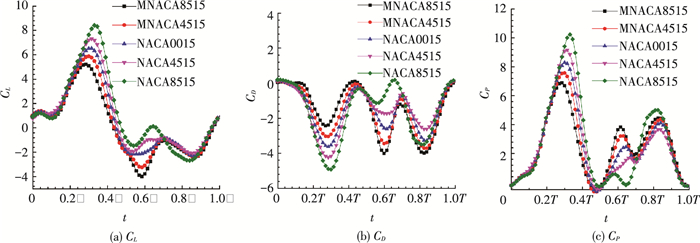
为具体分析翼型弯度对扑翼气动性能的影响,图 14给出了J=0.25时,一个扑动周期内5种具有不同翼型弯度的扑翼CL、CD和CP变化情况.在下扑行程中(0~0.50T), 具有正向弯度的扑翼翼型产生了更大的升力和推力;而在上挥行程中(0.50T~1.00T),具有负向弯度的扑翼翼型则产生了更大的推力.上述结果说明具有固定弯度的翼型很难同时提高前飞扑翼升力和推力,而动态柔性变形扑翼翼型可以克服这一问题,为同时提高扑翼翼型的升举效率和推进性能,设计主动变形扑翼翼型使其在上挥行程中具有负向弯曲变形而在下扑过程中具有正向弯曲变形[15].
|
图 14 不同弯度翼型瞬时升阻力系数和能耗系数 Figure 14 The time histories of CL、CD、CP with different airfoil camber during a flapping cycle |
图 15给出了J=0.25时,一个扑动周期内3种具有不同翼型弯度的扑翼在不同特征时刻的表面压力系数分布情况.总体而言,翼型弯度对扑翼上、下表面的压力分布有着显著的影响.当t=0.25T和t=0.75T时,具有正向翼型弯度扑翼的上、下表面压力分别均远低于和远高于具有负向翼型弯度扑翼.通过与图 10相对比可以看出,与翼型厚度相比,翼型弯度对前飞扑翼气动性能的影响更加显著.Thielicke等[16]在研究翅膀形态对鸟类扑翼气动性能的影响时也得出相同的结论.

|
图 15 不同弯度翼型在不同时刻表面压力系数分布情况 Figure 15 The Cp* of three airfoils with different camber during a flapping cycle |
为具体分析扑翼周围流场变化情况,图 16给出了相应的3种具有不同翼型弯度的扑翼在一个扑动周期内不同特征时刻(0、0.25T、0.50T、0.75T)流场涡量图.结果表明,不同翼型弯度扑翼尾流场均形成反卡门涡街,从而产生推力.通过比较不同翼型弯度扑翼间的流场涡量分布差异,发现翼型弯度改变了扑翼尾涡脱落方向,扑翼尾流中心线随翼型弯度的增大呈逐渐向右下方倾斜的趋势,从而产生更大的扑翼升力.这一现象正好可以解释图 14(a)中扑翼气动升力随翼型弯度增加而显著提高的结论.另一方面,翼型弯度还改变了扑翼尾涡的纵向间距.具有正向翼型弯度的扑翼相比负向翼型弯度扑翼所产生的尾涡纵向间距更大,从而产生更大的扑翼推力.Young[17]在研究翼型沉浮运动时的推进性能时同样得出类似的结论.

|
图 16 不同弯度翼型一个周期内不同时刻的涡量图 Figure 16 The vorticity contour of three airfoils with different camber during a flapping cycle |
1) 随着来流速度的增大,前飞扑翼推力、能耗和推进效率均逐渐减小,而扑翼升力和升举效率则逐渐而增大.
2) 翼型厚度的增加,降低了扑翼前缘涡强度并延迟了前缘涡的脱落;不同来流速度条件下,扑翼推力和能耗均随着翼型厚度的增大而逐渐减小.
3) 翼型弯度的增加,使得扑翼尾流中心线呈现向右下方倾斜的趋势,从而有利于扑翼升力的产生;翼型弯度能改变扑翼的有效气动攻角,正向翼型弯度可以显著提高扑翼升力和升举效率.
| [1] |
BAI Peng, CUI Erjie, ZHAN Huiling. Aerodynamic characteristics, power requirements and camber effects of the pitching-down flapping hovering[J].
Journal of Bionic Engineering, 2009, 6(2): 120-134.
DOI: 10.1016/S1672-6529(08)60109-2 |
| [2] |
ZHAO Liangyu, YANG Shuxing. Influence of thickness variation on the flapping performance of symmetric NACA airfoils in plunging motion[J].
Mathematical Problems in Engineering, 2010, 2010: 1-19.
DOI: 10.1155/2010/675462 |
| [3] |
ASHRAF M A, YOUNG J, LAI J C S. Reynolds number, thickness and camber effects on flapping airfoil propulsion[J].
Journal of Fluids and Structures, 2011, 27(2): 145-160.
DOI: 10.1016/j.jfluidstructs.2010.11.010 |
| [4] |
YU Minlin, WANG Z J, HU HUI. High fidelity numerical simulation of airfoil thickness and kinematics effects on flapping airfoil propulsion[J].
Journal of Fluids and Structures, 2013, 42: 166-186.
DOI: 10.1016/j.jfluidstructs.2013.06.001 |
| [5] |
杨文青, 宋笔锋, 宋文萍. N-S方程数值研究翼型对微型扑翼气动特性的影响[J].
计算力学学报, 2011, 28(2): 214-220.
YANG Wenqing, SONG Bifeng, SONG Wenping. The effect of airfoil to aerodynamic characteristics of flapping wing by numerical simulation on Navier-Stokes equations[J]. Chinese Journal of Computational Mechanics, 2011, 28(2): 214-220. DOI: 10.7511/jslx201102011 |
| [6] |
谢辉, 宋文萍, 宋笔锋. 基于CFD方法对微型扑翼翼型设计的研究[J].
空气动力学学报, 2009, 27(2): 227-233.
XIE Hui, SONG Wenping, SONG Bifeng. Airfoil design of a micro-flapping wing based on CFD[J]. Acta Aerodynamic Sinica, 2009, 27(2): 227-233. DOI: 10.3969/j.issn.02581825.2009.02.0-15 |
| [7] |
冉景洪, 刘子强, 白鹏. 相对厚度对低雷诺数流动中翼型动态气动力特性的影响[J].
空气动力学学报, 2008, 26(2): 78-185.
RAN Jinghong, LIU Ziqiang, BAI Peng. The effect of relative thickness to the dynamic aerodynamic characteristics about pitching airfoils[J]. Acta Aerodynamic Sinica, 2008, 26(2): 78-185. DOI: 10.3969/j.issn.0258-1825.2008.02.008 |
| [8] |
冉景洪, 刘子强, 白鹏. 相对弯度对低雷诺数流动中翼型动态气动力特性的影响[J].
计算力学学报, 2010, 27(1): 88-94.
RAN Jinghong, LIU Ziqiang, Bai Peng. The effect of relative camber to the dynamic aerodynamic characteristics about pitching airfoils[J]. Chinese Journal of Computational Mechanics, 2010, 27(1): 88-94. DOI: 10.7511/jslx20101015 |
| [9] |
YIN Bo, LUO Haoxiang. Effect of wing inertia on hovering performance of flexible flapping wings[J].
Physics of Fluids, 2010, 22(11): 111902.
DOI: 10.1063/1.3499739 |
| [10] |
TIAN Fangbao, LUO Haoxiang, SONG Jialei, et al. Force production and asymmetric deformation of a flexible flapping wing in forward flight[J].
Journal of Fluids and Structures, 2013, 36: 149-161.
DOI: 10.1016/j.jfluidstructs.2012.07.006 |
| [11] |
Van DOORMAAL J P, RAITHBY G D. Enhancements of the SIMPLE method for predicting incompressible fluid flows[J].
Numerical Heat Transfer, 1984, 7(2): 147-163.
DOI: 10.1080/01-495728408961817 |
| [12] |
TUNCER I H, KAYA M. Thrust generation caused by flapping airfoils in a biplane configuration[J].
Journal of Aircraft, 2003, 40(3): 509-515.
DOI: 10.2514/2.3124 |
| [13] |
MIAO J M, HO M H. Effect of flexure on aerodynamic propulsive efficiency of flapping flexible airfoil[J].
Journal of Fluids and Structures, 2006, 22(3): 401-419.
DOI: 10.1016/j.flui-dstructs.2005.11.004 |
| [14] |
HARBIG R R, SHERIDAN J, THOMPSON M C. Relationship between aerodynamic forces, flow structures and wing camber for rotating insect wing planforms[J].
Journal of Fluid Mechanics, 2013, 730: 52-75.
DOI: 10.1017/jfm.2013.335 |
| [15] |
HOKE C M, YOUNG J, LAI J C S. Effects of time-varying camber deformation on flapping foil propulsion and power extraction[J].
Journal of Fluids and Structures, 2015, 56: 152-176.
DOI: 10.1016/j.jfluidstructs.2015.05.001 |
| [16] |
THIELICKE W, STAMHUIS E J. The influence of wing morphology on the three-dimensional flow patterns of a flapping wing at bird scale[J].
Journal of Fluid Mechanics, 2015, 768: 240-260.
DOI: 10.1017/jfm.2015.71 |
| [17] |
YOUNG J. Numerical simulation of the unsteady aerodynamics of flapping airfoils[D]. Canberra: Australian Defence Force Academy, 2005.
https://www.researchgate.net/publication/258536896_Numerical_Simulation_of_the_Unsteady_Aerodynamics_of_Flapping_Airfoils
|
 2018, Vol. 50
2018, Vol. 50


