2. 空间智能控制技术上海市重点实验室(上海航天控制技术研究所),上海 201109
2. Key Laboratory of Space Intelligent Control Technology (Shanghai Aerospace Control Engineering Institute), Shanghai 201109, China
地球静止轨道(GEO)卫星可以实现对地面指定区域的持续观测,广泛应用于气象、测绘等领域.GEO卫星受到地球非球形摄动和三体引力的影响,定点位置会发生漂移,需要定期进行东西和南北位置保持,维持其固定轨位,因此燃耗是GEO卫星寿命的决定因素.近年来,电推进由于其高比冲、连续小推力特性[1]引起了国内外学者的广泛关注,包括地火转移[2-3]、轨道交会[4]、卫星编队[5]等,尤其在地球静止轨道卫星应用方面[6],全电推进将成为下一代GEO卫星的优选配置.
相对于传统GEO卫星的脉冲机动,电推进的连续小推力特性致使基于脉冲假设的非合作机动跟踪算法[7]性能退化.自适应滤波算法[8-9]引入系统噪声修正等变增益方法,虽可保证滤波误差的边界,但破坏了滤波系统的期望无偏特性,同时其偏保守的阈值设计导致导航系统在目标自由漂飞状态下处于次优滤波状态[10-11].文献[12]采用跟踪滤波器与DDF2滤波算法相结合,在目标进行短时间轨道机动时有较好效果,但对于长时间的主动变轨效果较差;交会多模型(IMM)[13-14]算法在所有的时刻都使用固定的模型集合进行目标跟踪,因此需要大量的模型来保证跟踪精度,而庞大的模型集合会带来巨大的计算量,并导致对非机动目标的跟踪性能有所下降.
电推进的连续小推力特性致使基于CW(clohessy-wiltshire)方程的经典相对导航算法期望有偏,两段状态估计法(two stage Kalman filter,TSKF)在稳态估计性能与机动跟踪响应间存在矛盾[15],针对该问题本文采用滤波误差理论对传统滤波系统性能衰减因素进行分析,提出一种自适应变维两段状态估计法,基于目标机动特性和无偏滤波器带宽设计自适应准则,自主重构观测阵并切换维度,实现对目标机动加速度的快速跟踪估计.
1 经典相对导航算法性能分析 1.1 电推进下相对运动建模在近圆轨道下,根据苛氏定理,考虑轨道环境摄动,得到两星相对运动动力学方程(CW方程).地球静止轨道的环境摄动力量级较小,通常在10-8 m/s2量级,远小于电推进所提供的机动加速度(典型电推进推力100 mN,卫星质量2 000 kg),将环境摄动用等效噪声近似,得到电推进下的相对运动描述为
| $ \left[ {\begin{array}{*{20}{c}} {\ddot x}\\ {\ddot y}\\ {\ddot z} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {2{\omega _{\dot z}}}\\ 0\\ { - 2{\omega _{\dot x}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ {\omega _y^2}\\ { - 3\omega _z^2} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {u_x^{\rm{t}}}\\ {u_y^{\rm{t}}}\\ {u_z^{\rm{t}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{w_x}}\\ {{w_y}}\\ {{w_z}} \end{array}} \right]. $ | (1) |
式中:[x y z]T为目标星在追踪星轨道坐标系的矢量坐标;ω为追踪星平均轨道角速度;[uxt uyt uzt]T为目标星的控制输入,上标t为目标星(target);[wx wy wz]T为环境摄动的等效噪声.
1.2 经典相对导航算法设计取系统状态
| $ \mathit{\boldsymbol{\dot X}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{Gw}}, $ | (2) |
其中:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&1&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1\\ 0&0&0&0&0&{2\omega }\\ 0&{ - {\omega ^2}}&0&0&0&0\\ 0&0&{3{\omega ^2}}&{ - 2\omega }&0&0 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{G}} = {\left[ {\begin{array}{*{20}{c}} {{0_{3 \times 3}}}&{{I_{3 \times 3}}} \end{array}} \right]^{\rm{T}}},\mathit{\boldsymbol{w}} = {\rm{diag}}\left( {\left[ {\begin{array}{*{20}{c}} {{w_x}}&{{w_y}}&{{w_z}} \end{array}} \right]} \right). $ |
式中: wx~N(0, σwx)、wy~N(0, σwy)、wz~N(0, σwz)分别为各轴的环境摄动的等效噪声.为了分析方便,设各轴加速度噪声相同,σwx=σwy=σwz=σw.
量测方程可表示为
| $ \mathit{\boldsymbol{Z}} = \left[ {\begin{array}{*{20}{c}} \rho \\ \psi \\ \theta \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\sqrt {{x^2} + {y^2} + {z^2}} }\\ {\arctan \frac{y}{{\sqrt {{x^2} + {z^2}} }}}\\ {\arctan \frac{{ - z}}{x}} \end{array}} \right] + \mathit{\boldsymbol{V}}. $ | (3) |
式中:ρ为两星的视线距;ψ为雷达测量航向角;θ为雷达测量俯仰角;V为雷达测量噪声.根据某实际系统取E[V, VT]=diag[(0.000 5ρ)2m2, (0.01/57.3)2rad2, (0.01/57.3)2rad2].
将式(3)转换至笛卡尔直角坐标系,与式(2)形成基于间接测量的相对导航系统[10],称为经典相对导航系统.
1.3 经典相对导航性能分析采用常值对式(1)的目标星机动特性进行建模,得电推进下相对导航模型为
| $ \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_{k + 1}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{X}}_k} + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{\gamma }}_k} + {\mathit{\boldsymbol{W}}_k},}\\ {{\mathit{\boldsymbol{Z}}_{k + 1}} = \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{X}}_{k + 1}} + {\mathit{\boldsymbol{V}}_{k + 1}}.} \end{array}} \right. $ |
式中,γk=[Δuxt Δuyt Δuzt]T为目标卫星未知机动.
为了便于分析,定义Δc=Bγ,由相对导航的递推过程对状态估计的有偏性进行分析,对估计误差取期望得
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_{k + 1}} = E\left[ {{\mathit{\boldsymbol{X}}_{k + 1}} - {{\mathit{\boldsymbol{\hat X}}}_{k + 1/k}}} \right] = \\ \;\;\;\;\;\;\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}k\mathit{\boldsymbol{H}}} \right){\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_k} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} c}}, \end{array} $ | (4) |
对式(4)展开,以后各时刻期望偏差为
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_{k + 1}} = {\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}k\mathit{\boldsymbol{H}}} \right)^l}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_k} + {\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}k\mathit{\boldsymbol{H}}} \right)^{l - 1}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} c}} + \\ \;\;\;\;\;\;\;\;\underbrace {{{\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}k\mathit{\boldsymbol{H}}} \right)}^{l - i}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} c}}}_{i = 2 \cdots l}. \end{array} $ | (5) |
有矩阵分析理论得,如果||(A-AkH)||<1,式(5)矩阵幂级数的和收敛,经过一段时间将收敛到极限值.
| $ \begin{array}{l} \mathop {\lim }\limits_{l \to \infty } {\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_{k + l}} = {\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}k\mathit{\boldsymbol{H}}} \right)^l}{\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}_k} + {\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}k\mathit{\boldsymbol{H}}} \right)^{l - 1}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} c}} + \\ \;\;\;\;\;\;\;\;\underbrace {{{\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}k\mathit{\boldsymbol{H}}} \right)}^{l - i}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} c}}}_{i = 2 \cdots l} = {\left( {\mathit{\boldsymbol{E}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}k\mathit{\boldsymbol{H}}} \right)^{l - 1}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} c}}. \end{array} $ |
对于稳定的卡尔曼滤波过程||(Φ-ΦkH)||<1,初值误差的Δk对期望的影响随着时间慢慢减弱,目标未知机动的偏差值经过一段时间后收敛在常值,导致状态估计值期望有偏.
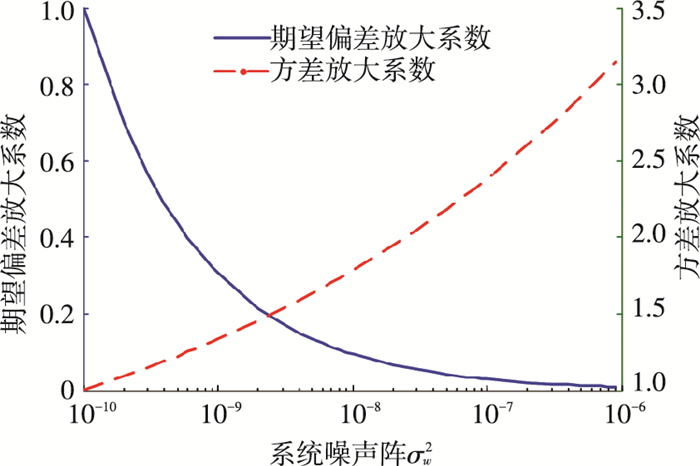
自适应滤波算法能够通过新息修正系统噪声阵Qk,以抑制期望偏差的上界,以Z轴相对速度估计为例,图 1分析了期望偏差放大系数与系统噪声阵的关系.修正系统噪声阵可以有效抑制滤波算法的期望偏差特性,但是系统噪声阵增加的同时牺牲了滤波系统的最优方差特性,经典相对导航算法的自适应规则难以实现两者的同步优化.
|
图 1 期望偏差/方差放大系数与系统噪声阵相关性仿真 Figure 1 Relation between error amplification factor of estimation bias and variance with σw2 |
经典相对导航算法对于机动目标跟踪存在系统误差,致使滤波估计有偏.最基本的解决方法是增广状态估计法,将加速度作为相对导航的滤波状态,改善滤波算法的估计特性.但随着向量维数的增加,计算变得复杂,通常引入两段状态估计法以简化计算,对于确定的、定常的未知机动,可取得与增广状态最优卡尔曼滤波等效的估计效果.
在目标的非机动区间,由于目标加速度估计的噪声影响,两段状态估计法性能较经典相对导航算法差.变维滤波器基于机动检测确定偏差滤波器的接入状态,但偏差滤波器的滤波跟踪响应时间直接决定于无偏滤波器的带宽.通常无偏滤波器为了保证非机动区间的滤波性能带宽较低,约2 000 s左右,极大影响了偏差滤波器的响应性能.为此,本文提出一种自适应两段状态估计法,修正偏差滤波器的观测阵递推方程,使其可在偏差滤波器新息异常初期快速进行目标跟踪.
定义有偏差状态Xk,经典相对导航系统组成无偏滤波器;偏差滤波器以无偏滤波器的新息为观测量,以目标机动加速度γk/k为估计量,递推方程为:
| $ {{\mathit{\boldsymbol{\bar \gamma }}}_{k/k - 1}} = {{\mathit{\boldsymbol{\bar \gamma }}}_{k - 1/k - 1}}, $ |
| $ {{\mathit{\boldsymbol{\bar \gamma }}}_{k/k}} = {{\mathit{\boldsymbol{\bar \gamma }}}_{k/k - 1}} + \bar K_k^\gamma \left( {{\mathit{\boldsymbol{Z}}_k} - {\mathit{\boldsymbol{H}}_k}{{\mathit{\boldsymbol{\bar X}}}_{k/k - 1}} - {\mathit{\boldsymbol{S}}_k}{{\mathit{\boldsymbol{\bar \gamma }}}_{k/k - 1}}} \right), $ |
| $ \mathit{\boldsymbol{\bar P}}_{k + 1/k}^\gamma = \mathit{\boldsymbol{\bar P}}_{k/k}^\gamma + \mathit{\boldsymbol{Q}}_k^\gamma , $ |
| $ \bar K_k^\gamma = \mathit{\boldsymbol{\bar P}}_{k/k - 1}^\gamma S_k^{\rm{T}}{\left[ {{\mathit{\boldsymbol{S}}_k}\mathit{\boldsymbol{\bar P}}_{k/k - 1}^\gamma \mathit{\boldsymbol{S}}_k^{\rm{T}} + {\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{\bar P}}_{k + 1/k}^X\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\mathit{\boldsymbol{R}}_k}} \right]^{ - 1}}, $ |
| $ \mathit{\boldsymbol{\bar P}}_{k/k}^\gamma = \left( {\mathit{\boldsymbol{I}} - \bar K_k^\gamma {\mathit{\boldsymbol{S}}_k}} \right)\mathit{\boldsymbol{\bar P}}_{k/k - 1}^\gamma , $ |
| $ {\mathit{\boldsymbol{S}}_k} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{U}}_k}, $ |
| $ {\mathit{\boldsymbol{U}}_k} = \mathit{\boldsymbol{S}}{\mathit{\boldsymbol{A}}_{k - 1}}{\mathit{\boldsymbol{V}}_{k - 1}} + {\mathit{\boldsymbol{B}}_{k - 1}}, $ |
| $ {\mathit{\boldsymbol{V}}_k} = \left( {\mathit{\boldsymbol{I}} - \bar K_k^X{\mathit{\boldsymbol{H}}_k}} \right){\mathit{\boldsymbol{U}}_k}, $ |
式中自适应因子S的引入用于调节雷达量测信息对滤波递推估计的修正作用,在目标机动的时刻,修正观测矩阵,取自适应规则为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{s}}_i} = \left\{ \begin{array}{l} {\zeta _i},\frac{{{\rm{d}}\left( {{f_{{\rm{pulse\_generator}}}}\left( t \right){\kappa _i}} \right)}}{{{\rm{d}}t}} \ne 0;\\ 1,\frac{{{\rm{d}}\left( {{f_{{\rm{pulse\_generator}}}}\left( t \right){\kappa _i}} \right)}}{{{\rm{d}}t}} = 0. \end{array} \right.}\\ {\left( {i = 1,2,3} \right)} \end{array} $ | (6) |
式中:ζi为自适应调节系数,与偏差滤波器的带宽和目标机动加速度的幅值相关,一般可取常值;fpulse_generator(t)κi为自适应开关调节函数,取为方波发生函数fpulse_generator(t)和机动状态检测κi乘积.对于典型的电推进机动平台,机动加速度区间取5×10-5 ~1×10-4 m/s2,可取ζi=0.5.
加速度估计是一个随机信号,用极大似然估计方法设计机动状态检测.对假设检验问题使用固定长度的滑动窗口方法,令L为窗口长度,在窗口内加速度估计
| $ {D_L}\left( i \right) = \sum\limits_{i = k - L + 1}^k {{{\bar \gamma }_{k/k - 1}}\left( i \right)} . $ |
统计项DL(k)在假设H0目标无机动时,DL(k)为零均值正态分布,其方差满足
| $ {\rm{Var}}\left[ {{D_L}\left( i \right)\left| {{\mathit{\boldsymbol{H}}_0}} \right.} \right] = \sigma _L^2\left( i \right) = \sum\limits_{i = k - L + 1}^k {\bar P_{k/k}^\gamma \left( {i,i} \right)} , $ | (7) |
式中,
由检测虚警率得到门限λH,当DL(k)≥λH时,判断目标机动.目标机动检测函数定义为
| $ {\kappa _i} = \left\{ \begin{array}{l} 0,{D_L}\left( i \right) \ge {\lambda _H};\\ 1,{D_L}\left( i \right) < {\lambda _H}. \end{array} \right.\left( {i = 1,2,3} \right) $ |
式中:0为目标机动,1为目标未机动.
系统状态真实估计表示为
| $ {{\mathit{\boldsymbol{\hat X}}}_{k/k}} = {{\mathit{\boldsymbol{\bar X}}}_{k/k}} + {\rm{NOT}}\left( {{\kappa _i}} \right){\mathit{\boldsymbol{V}}_k}{{\mathit{\boldsymbol{\bar \gamma }}}_{k/k}}, $ |
式中NOT(κi)为κi的非逻辑.
当si=1时本文算法即为传统两段状态估计法,与增广状态方程下的相对导航算法等效[15],系统完全可观且收敛性好.式(7)中自适应因子的引入使得算法在目标机动等时刻下更新观测阵,使其与式(6)中由机动加速度引起系统误差项
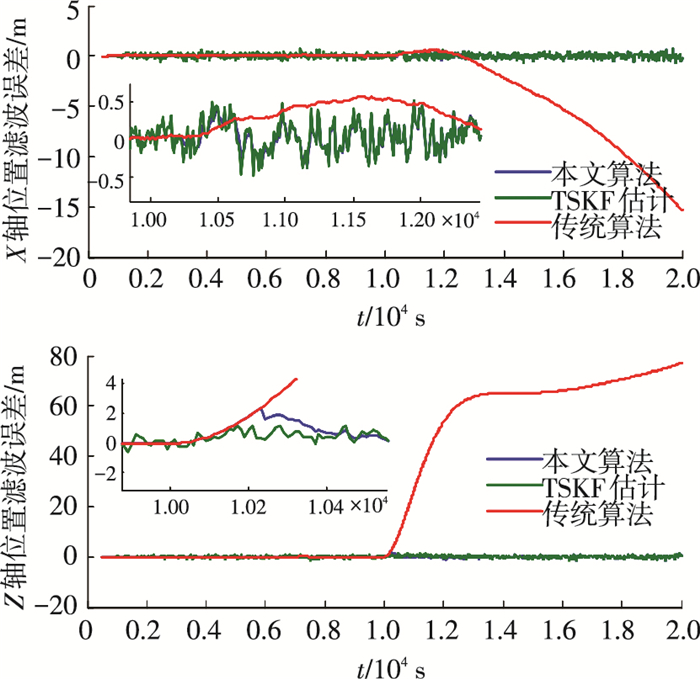
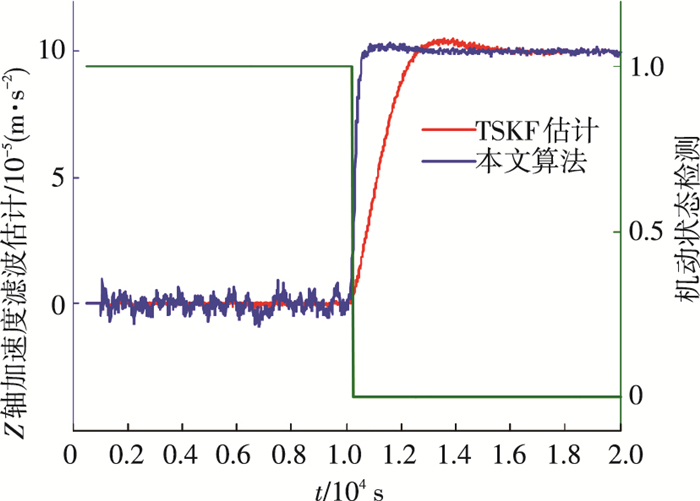
两星运行于地球静止轨道,初始距离10 km,相对运动面内尺寸2 km,面外尺寸1 km,仿真时间20 000 s.0~10 000 s目标卫星处于自由漂飞状态,10 000~20 000 s目标卫星在径向存在5×10-5 m/s2的连续机动.雷达测量噪声如式(3),目标卫星的相对位置和速度的跟踪估计如图 2~4所示;为了验证算法的适应性,10 000~20 000 s目标卫星在径向存在1×10-4 m/s2的连续机动跟踪情况如图 5所示.
|
图 2 目标相对位置估计误差 Figure 2 Target relative position estimation error |
|
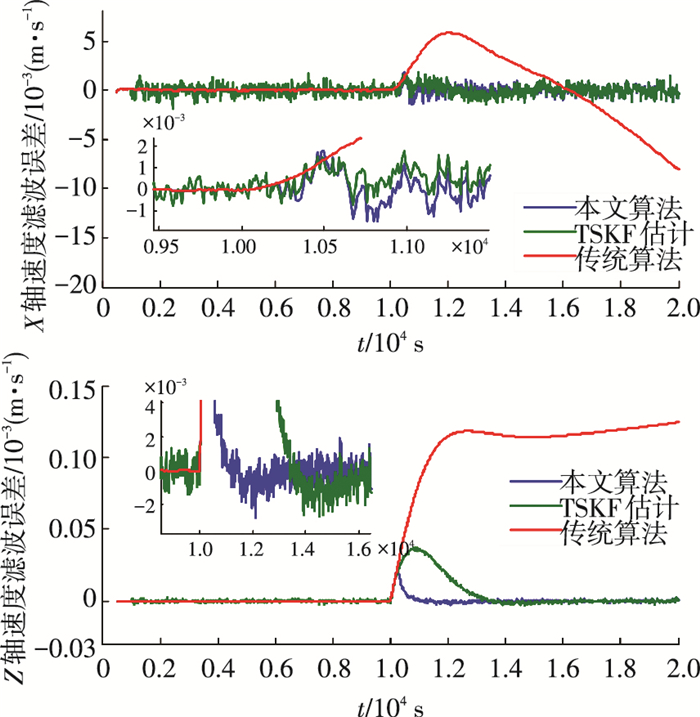
图 3 目标相对速度估计误差 Figure 3 Target relative velocity estimation error |
|
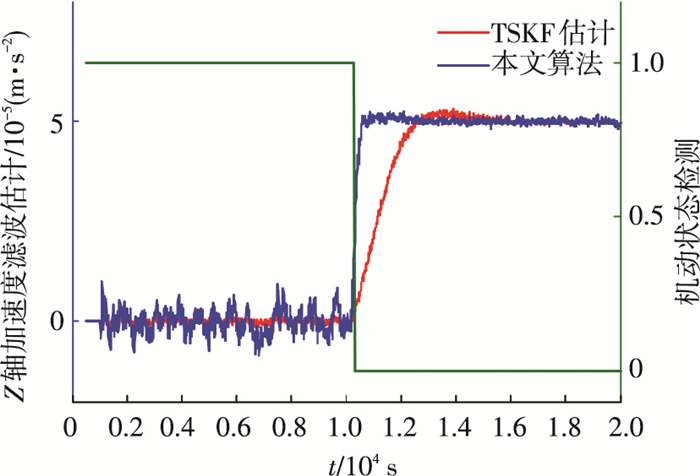
图 4 目标机动加速度跟踪估计(5×10-5 m/s2) Figure 4 Target manuever accelaration estimation(5×10-5 m/s2) |
|
图 5 目标机动加速度跟踪估计(1×10-4 m/s2) Figure 5 Target manuever accelaration estimation(1×10-4 m/s2) |
仿真可见,自适应两阶段状态估计在目标非机动区间与经典相对导航算法性能等效,相对速度估计精度1×10-4 m/s,在机动区间与两阶段状态估计算法(TSKF)性能等效,相对速度估计精度1×10-3 m/s.两阶段估计法跟踪性能受限于经典相对导航算法的带宽,与新息累积响应一致,对于典型的机动跟踪时间约2 000 s,本文提出的算法跟踪时间优于500 s,极大改善了目标机动跟踪过程中的估计性能.同时图 5的仿真表明,该算法跟踪响应性能稳定,对不同的目标机动特性具有一致的适应特性.
4 结论1) 本文针对GEO卫星跟踪非合作目标过程中,受到电推进的连续机动特性影响导致的经典相对导航滤波系统性能退化问题,开展了新型自适应机动目标跟踪算法的研究.给出了经典相对导航算法的模型与框架,分析了自适应滤波等滤波算法性能衰减的原因,提出了一种基于自适应二阶段状态法的相对导航算法设计方法,实现了对电推进机动目标相对运动状态的低噪声无偏估计.
2) 在存在低频未建模噪声的系统工况下进行仿真试验,结果显示,本文提出的滤波算法在目标非机动区间与经典相对导航算法性能等效,相对速度估计精度可达1×10-4 m/s;在机动区间与两阶段状态估计算法性能等效,相对速度估计精度可达1×10-3 m/s,跟踪时间优于500 s,跟踪性能提升约4~5倍,与理论分析结果一致.本文提出的导航算法性能优越,可推广应用至低轨以及椭圆轨道交会场景下的机动目标跟踪问题,具有极高的实用价值.
| [1] |
魏冰洁, 孙小箐, 王小永. 全电推进卫星平台现状与进展[J].
真空与低温, 2016, 22(5): 301-305.
WEI Bingjie, SUN Xiaoqing, WANG Xiaoyong. The review of all-electric propulsion platform on satallite[J]. Vacuum and Cryogenics, 2016, 22(5): 301-305. DOI: 10.3969/j.issn.1006-7086.2016.05.012 |
| [2] |
LIZIA P D, ARMELLIN R, BERNELLI-ZAZZERA F, et al. High order optimal control of space trajectories with uncertain boundary conditions[J].
Acta Astronautica, 2014, 93(1): 217-229.
DOI: 10.1016/j.actaastro.2013.07.007 |
| [3] |
HE Shengmao, ZHU Zhengfan, PENG Chao, et al. Optimal design of near-Earth asteroid sample-return trajectories in the Sun-Earth-Moon system[J].
Acta Mechanica Sinica, 2016, 32(4): 753-770.
DOI: 10.1007/s10409-015-0527-1 |
| [4] |
OH D Y, LANDAI D. Simple semi-analytic model for optimized interplanetary low-thrust trajectories using solar electric propulsion[J].
Journal of Spacecraft and Rockets, 2015, 50(3): 609-619.
DOI: 10.2514/1.A32326 |
| [5] |
XU Guangyan, WANG Xiaoying. Fuel optimal maneuver of passive and periodic circular-like satellite formation: legendre pseudospectral approach[C]//International Conference on Mechatronic Systems and Materials Application. Guangzhou, China: ICMSMA, 2013: 834-840. DOI: 10.4028/www.scientific.net/AMM.389.834.
|
| [6] |
崔铁敏, 唐福俊. 地球静止轨道卫星平台位保应用离子电推进系统方案[J].
真空与低温, 2009, 15(2): 90-94.
CUI Tiemin, TANG Fujun. The scheme of ion proplusion system on geosynchronous satellite for station keeping[J]. Vacuum and Cryogenics, 2009, 15(2): 90-94. DOI: 10.3969/j.issn.1006-7086.2009.02.006 |
| [7] |
李元凯, 敬忠良, 胡士强. 基于瞬态相对模型的轨道机动目标运动参数估计[J].
控制与决策, 2009, 24(7): 1059-1064.
LI Yuankai, JING Zhongliang, HU Shiqiang. Transient relative model based kinematical parameter estimation for orbital maneuvering target[J]. Control and Decision, 2009, 24(7): 1059-1064. DOI: 10.3321/j.issn.1001-0920.2009.07.019 |
| [8] |
LI Yuankai, JING Zhongliang, HU Shiqiang. Redundant adaptive robust tracking of active satellite and error evaluation[J].
IET Control Theory and Applications, 2010, 4(11): 2539-2553.
DOI: 10.1049/iet-cta.2009.0319 |
| [9] |
XI Tao, LI Jiancheng, PAN Weiquan. Nonlinear adaptive feedback control for spacecraft proximity formation flying[C]//2013 International Conference on Mechanical, Automotive and Materials Engineering. Hong kong: CMAME, 2013: 446-450. DOI: 10.4028//www.scientific.net/AMM.376.446.
|
| [10] |
SEO J, YU M J, PARK C G, et al. An extended robust Hinf filter for nonlinear constrained uncertain systems[J].
IEEE Transactions on Signal Precessing, 2006, 54(11): 4471-4475.
DOI: 10.1109/TSP.2006.880308 |
| [11] |
周朝霞, 任家栋, 曾庆双, 等. 测量最小分辨率特性下自主相对导航设计方法[J].
哈尔滨工业大学学报, 2015, 47(3): 49-53.
ZHOU Chaoxia, REN Jiadong, ZENG Qingshuang, et al. Autonomous relative navigation contrained by minimum measure resolution[J]. Journal of Harbin Institute of Technology, 2015, 47(3): 49-53. DOI: 10.11918/j.issn.0367-6234.2015.03.008 |
| [12] |
刘涛, 解永春. 空间非合作机动目标跟踪相对导航方法研究[J].
宇航学报, 2010, 31(5): 1338-1344.
LIU Tao, XIE Yongchun. A Relative navigation algorithm for a chaser tracking a non-cooperative maneuvering target in space[J]. Journal of Astronautics, 2010, 31(5): 1338-1344. DOI: 10.3873/j.issn.1000-1328.2010.05.014 |
| [13] |
KIM H S, PARK J G, LEE D. Adaptive fuzzy IMM algorithm for uncertain target tracking[J].
International Journal of Control Automation, and Systems, 2009, 7(6): 1001-1008.
DOI: 10.1007/s12555-009-0617-6 |
| [14] |
刘望生, 李亚安, 王明环. 复合K噪声下机动目标跟踪自适应UPF算法[J].
电工学报, 2012, 40(6): 1240-1245.
LIU Wangsheng, LI Yaan, WANG Minghuan. An adaptive UPF algorithm for tracking maneuvering target in compound K noise environment[J]. Acta Electronica Sinica, 2012, 40(6): 1240-1245. DOI: 10.3969/j.issn.0372-2112.2012.06.029 |
| [15] |
HU Yiming, QIN Yongyuan. Adaptive two-stage Kalman filter in the presence of random bias[C]// Proceedings of the 3rd IEEE International Conference on Computer Science and Information Technology. Guangzhou, China: IEEE, 2010, 6: 135-138. DOI: 10.1109/ICCSIT.2010.5563730.
|
 2018, Vol. 50
2018, Vol. 50


