2. 哈尔滨工业大学 智能控制与系统研究所,哈尔滨 150001
2. Research Institute of Intelligent Control and Systems, Harbin Institute of Technology, Harbin 150001, China
视觉跟踪,是计算机视觉研究重点之一,在运动目标识别、智能监视、图像标注、人机交互、飞行器导航等领域具有广阔的应用前景[1].尽管视觉跟踪算法已经取得巨大成就,但由于光照、噪声、复杂环境的影响,实时鲁棒的视觉跟踪算法仍然是一个难点.
为了提高视觉跟踪的实时性,Comaniciu等[2]提出了基于核密度梯度估计的视觉跟踪算法(mean shift,MS),该方法计算简单、实时性好,但要求目标的相邻帧间位移小且容易受干扰的影响,不适合复杂场景中运动目标的跟踪.基于粒子滤波的视觉跟踪方法[3](particle filter, PF)能够提高视觉跟踪效果,但是粒子滤波耗时大.为了结合两者的长处,Shan等[4]提出了基于MS改进的粒子滤波跟踪方法(mean shift particle filter,MSPF).该方法利用MS算法,将标准粒子滤波中重要性采样粒子集,移动到每个粒子的后验密度处,使粒子更接近于目标真实位置,从而提高了算法的实时性和鲁棒性,然而mean-shift是基于梯度下降的贪婪算法,容易收敛至局部最大值.
和声搜索[5] (harmony search,HS)是2001年首次公开提出的一种启发式智能优化算法,该算法基于和谐音乐的创作过程,结合遗传、模拟退火等算法思想,通过对和声记忆库的更新完成对解空间的搜索.一经提出就引起了广大专家学者的关注,提出的各种改进算法[6]广泛应用到工业、医疗、机器人、能源等各个方面[7].2010年,Fourie等[8]将和声搜索引入到视觉跟踪,提出了基于和声搜索视觉跟踪算法.2015年,Gao等[9]将差分进化和声搜索应用到视觉跟踪,并结合民主融合的多特征视觉跟踪策略,取得了良好的跟踪效果.
本文基于文献[4],将全局搜索能力更强的和声搜索引入到基于粒子滤波的视觉跟踪算法的框架下,通过和声搜索改进粒子滤波视觉跟踪的粒子准确性,提高粒子滤波视觉跟踪算法的鲁棒性.
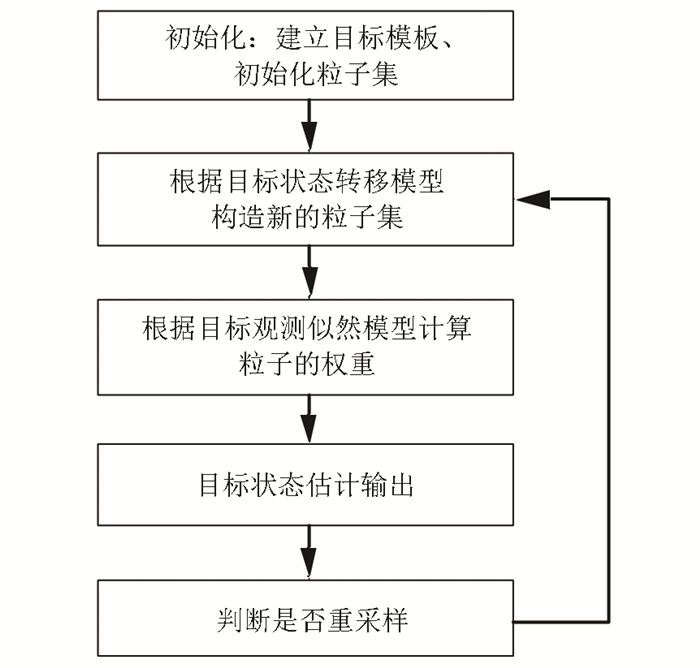
1 基于粒子滤波的视觉跟踪框架基于粒子滤波的视觉跟踪算法包含3个基本步骤:目标状态转移、粒子的加权和目标状态估计输出.图 1给出了基于粒子滤波的视觉跟踪流程图,有关粒子滤波视觉跟踪算法的理论推导和详细步骤,可详见文献[3, 10-11].
|
图 1 基于粒子滤波的视觉跟踪流程 Figure 1 The flat of visual tracking based on PF |
在视觉跟踪中,重要性采样函数的建立是粒子滤波设计中非常关键的一步.然而选取最优的重要性采样函数在实际中很难实现,常常将系统的状态转移模型作为先验分布.一般地,粒子滤波采用随机游走模型.
2 和声搜索粒子滤波视觉跟踪 2.1 和声搜索算法HS算法是一种类比音乐创作提出的现代启发式智能进化算法.基本和声搜索的[6]计算步骤如下.
Step1 定义问题与参数值.主要是定义目标函数f(x)、和声记忆库的大小HMS,和声记忆库考虑概率HMCR,基音调整概率PAR,和声微调步长bw和停止标准(一般的为最大迭代次数NI).
Step2 初始化和声记忆库.在和声向量Xj的各个分量xij上界UBi和下界LBi之间随机产生HMS个和声向量,即
| $ \begin{array}{l} {x_{ij}} = L{B_i} + {\rm{rand}}\left( {0,1} \right) \times \left( {{\rm{U}}{{\rm{B}}_i} - {\rm{L}}{{\rm{B}}_i}} \right),\\ \;\;\;\;\;\;j = 1,2, \cdots ,{\rm{HMS}} \end{array} $ |
并计算其目标函数f(Xj),一并构成和声记忆库HM.每个和声向量Xj构成一个解向量为
| $ {\rm{HM}} = \left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{21}}}& \cdots &{{x_{n1}}}\\ {{x_{12}}}&{{x_{22}}}& \cdots &{{x_{n2}}}\\ \vdots&\vdots&\cdots&\vdots \\ {{x_{1{\rm{HMS}}}}}&{{x_{2{\rm{HMS}}}}}& \cdots &{{x_{n{\rm{HMS}}}}} \end{array}\left| {\begin{array}{*{20}{c}} {f\left( {{\mathit{\boldsymbol{X}}^1}} \right)}\\ {f\left( {{\mathit{\boldsymbol{X}}^2}} \right)}\\ \vdots \\ {f\left( {{\mathit{\boldsymbol{X}}^{{\rm{HMS}}}}} \right)} \end{array}} \right.} \right]. $ |
Step3 生成一个新的和声.和声搜索算法通过记忆考虑、基音调整和随机考虑来生成一个新的和声.在记忆考虑中,新的和声向量通过随机继承和声记忆库的解向量得到;在基音调整中,新的和声向量利用记忆考虑的和声向量叠加一个随机的步长得到;在随机考虑中,新的和声向量在向量空间随机产生,三者通过随机数指导进行.
Step4 更新和声记忆库.计算新产生的和声向量的目标函数,若优于当前HM最差的目标函数,则替换最差和声向量和目标函数.
Step5 检查是否达到算法终止条件.根据终止条件判断是否重复执行step3~5.最后选择和声记忆库中最好的目标函数对应的和声向量作为问题的解向量.
本文所采用和声搜索是Mahdavi等[12]提出的改进版和声搜索(IHS).与基本和声搜索的不同,主要表现在基音调整概率PAR和和声微调步长bw两个参数的自适应.
| $ \begin{array}{*{20}{c}} {{\rm{PAR}}\left( {gn} \right) = {\rm{PA}}{{\rm{R}}_{\min }} + \frac{{{\rm{PA}}{{\rm{R}}_{\max }} - {\rm{PA}}{{\rm{R}}_{\min }}}}{{{\rm{NI}}}} \times gn,}\\ {bw\left( {gn} \right) = b{w_{\max }}{{\rm{e}}^{c \times gn}},}\\ {c = \frac{{\ln \left( {b{w_{\min }}/b{w_{\max }}} \right)}}{{{\rm{NI}}}}.} \end{array} $ |
式中:gn为和声搜索迭代次数; NI为最大迭代次数; PAR(gn)、bw(gn)分别为第gn次迭代时PAR值; PARmax、PARmin分别为PAR设定的最大值和最小值; bwmax、bwmin分别为bw设定的最大值和最小值.
2.2 和声搜索粒子滤波 2.2.1 基本框架粒子滤波跟踪结果精确性依赖于目标的状态转移模型,然而在实践中很难获得目标精确的状态转移模型,特别是在视觉跟踪中,经常采用通用运动模型[13]代替目标的实际模型,这需要大量的粒子来近似表示目标的后验分布.为解决该问题,本文通过和声搜索改进粒子滤波的重要性采样函数,利用当前最新观测信息,提高粒子滤波视觉跟踪的效果.
在视觉跟踪中,和声搜索的目标函数定义为目标的参考表观模型和候选区域表观模型的观测似然概率[3],即
| $ f\left( \mathit{\boldsymbol{x}} \right) = \mathop {\arg \max }\limits_X p\left( {\mathit{\boldsymbol{Z}}_k^i\left| {\mathit{\boldsymbol{X}}_k^i} \right.} \right). $ |
式中:argmax为最大值; p(Zk|Xki)为观测似然模型; Zk为k时刻观测向量; Xki为k时刻第i个粒子的状态.
本文采用Bhattacharyya距离度量颜色核直方图来计算粒子的观测似然概率:
| $ D\left[ {\mathit{\boldsymbol{p}},\mathit{\boldsymbol{q}}} \right] = \sqrt {1 - \sum\limits_{u = 1}^B {\sqrt {{p^u}{q^u}} } } , $ |
| $ p\left( {\mathit{\boldsymbol{Z}}_k^i\left| {\mathit{\boldsymbol{X}}_k^i} \right.} \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} \sigma }}{{\rm{e}}^{ - {D^2}\left[ {\mathit{\boldsymbol{p}},\mathit{\boldsymbol{q}}} \right]/2{\mathit{\boldsymbol{\sigma }}^2}}}. $ |
式中:D[*]为Bhattacharyya距离; σ为观测方差; p、q分别为候选和参考的颜色核直方图; B为颜色量化等级,本文采用HSV颜色空间,B=6×6×6;pu、qu分别为第u个bin的直方图,给定当前视觉目标状态,其中p可以通过如下方式求得:
| $ p = {\left[ {{p^u}} \right]_{u = 1,2, \cdots ,B}}, $ |
| $ p_l^u = C\sum\limits_{m = 1}^M {k\left( {\left\| {\frac{{l - {l_m}}}{h}} \right\|} \right)\delta \left( {b\left( {{l_m}} \right) - u} \right)} . $ |
式中:lm为当前状态的视觉目标中心; l为区域像素位置; M为像素总数; h为区域的小; k(*)为核函数(选择Epanechnikov核); δ(*)为Kronecker Delta函数; C为归一化常数.
对于每一个粒子,通过记忆考虑、基因变异、随机变异等和声搜索算子结合当前候选模型的观测似然概率,将粒子移动观测概率较高的区域,而改善重要性采样函数.显然,该基本算法存在着计算量大、不符合贝叶斯估计理论等问题,需要对该算法进行优化.
2.2.2 算法优化1) 参数优化.为了减少计算量同时也为了避免粒子通过过多的和声搜索移动到同一位置,保持粒子集的多样性,在基于和声搜索粒子滤波的视觉跟踪中,采用比和声搜索视觉跟踪算法[8]更为宽泛的和声搜索迭代停止条件和更适合粒子滤波框架下的和声搜索参数.同样采用和声搜索视觉跟踪算法选用3个迭代停止标准:1)最大迭代次数NI; 2)空迭代数目ider; 3)最差解和最好解向量图像距离Tpecison、最好解的目标函数Tquality.通过实验发现,一般的取NI=10,HMS=2能在滤波精度和时间上取得较好的平衡.在文献[8-9]基础上,视觉跟踪算法主要的参数如下:NI=10,ider=5,Tpecison=5像素,Tquality=0.7.
2) 权重补偿和更新.由于和声搜索粒子滤波在滤波中对每个粒子都通过和声搜索进行了迭代寻优,改变了粒子在状态空间的位置,使得新的粒子集不再服从后验分布.这样就使粒子滤波的理论基础贝叶斯估计不再成立.为解决该问题,类似文献[4],对和声搜索移动后粒子的权重进行补偿更新,使新的粒子集与移动前的粒子集服从同一分布.更新后粒子权重为
| $ w_k^i = \frac{{p\left( {X_k^i} \right)}}{{q\left( {\tilde X_k^i} \right)}}p\left( {{Z_k}\left| {X_k^i} \right.} \right). $ | (1) |
式中:p(Xki)为k时刻和声搜索移动后粒子Xki分布,q(
| $ p\left( {\mathit{\boldsymbol{X}}_k^i} \right) = \frac{1}{N}\sum\limits_{j = 1}^N {G\left( {\mathit{\boldsymbol{X}}_k^j,\mathit{\Sigma }} \right)\left( {\mathit{\boldsymbol{X}}_k^i} \right)} , $ | (2) |
| $ q\left( {\mathit{\boldsymbol{X}}_k^i} \right) = \frac{1}{N}\sum\limits_{j = 1}^N {G\left( {\mathit{\boldsymbol{\tilde X}}_k^j,\mathit{\tilde \Sigma }} \right)\left( {\mathit{\boldsymbol{\tilde X}}_k^i} \right)} . $ | (3) |
式中:G(*)为高斯分布; Σ、
将式(2)、(3)带入式(1)有
| $ w_k^i = \frac{{\sum\limits_{j = 1}^N {G\left( {\mathit{\boldsymbol{X}}_k^j,\mathit{\Sigma }} \right)\left( {\mathit{\boldsymbol{X}}_k^i} \right)} }}{{\sum\limits_{j = 1}^N {G\left( {\mathit{\boldsymbol{\tilde X}}_k^j,\mathit{\tilde \Sigma }} \right)\left( {\mathit{\boldsymbol{\tilde X}}_k^i} \right)} }}p\left( {{\mathit{\boldsymbol{Z}}_k}\left| {\mathit{\boldsymbol{X}}_k^i} \right.} \right), $ | (4) |
若令
| $ \mathit{\boldsymbol{\lambda }}_k^i = \frac{{\sum\limits_{j = 1}^N {G\left( {\mathit{\boldsymbol{X}}_k^j,\mathit{\Sigma }} \right)\left( {\mathit{\boldsymbol{X}}_k^i} \right)} }}{{\sum\limits_{j = 1}^N {G\left( {\mathit{\boldsymbol{\tilde X}}_k^j,\mathit{\tilde \Sigma }} \right)\left( {\mathit{\boldsymbol{\tilde X}}_k^i} \right)} }}, $ |
则式(4)可改为
| $ w_k^i = \lambda _k^ip\left( {{\mathit{\boldsymbol{Z}}_k}\left| {\mathit{\boldsymbol{X}}_k^i} \right.} \right). $ | (5) |
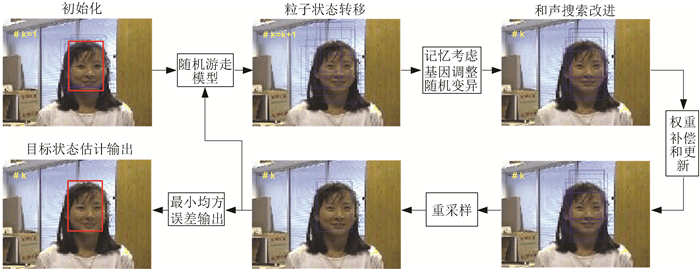
综上所述,图 2、算法1分别给出了基于和声搜索的粒子滤波的视觉跟踪算法的流程和详细步骤.
|
图 2 基于和声搜索的粒子滤波视觉跟踪流程 Figure 2 The flat of visual tracking based on HSPF |
算法1 (基于和声搜索粒子滤波的视觉跟踪算法).
1) 初始化.令k=1,在初始帧手动选择参考目标Xc,建立参考区域表观模型;同时,由p(X1)得到初始状态样本集
2) 粒子状态转移.根据随机游走模型和粒子Xk-1i计算粒子
| $ \tilde X_k^i = X_{k - 1}^i + w. $ |
3) 对每个粒子
| $ \left[ {\mathit{\boldsymbol{X}}_k^iw_k^i} \right] = {\rm{HS}}\left( {\mathit{\boldsymbol{\tilde X}}_{k - 1}^i,w_{k - 1}^i} \right), $ |
式中HS表示和声搜索算子.
4) 对粒子Xki权值wki归一化为
| $ w_k^i = w_k^i/\sum\limits_{i = 1}^N {w_k^i} . $ |
对粒子进行重采样为
| $ \left[ {\mathit{\boldsymbol{X}}_k^i\frac{1}{N}} \right] = {\rm{Resampling}}\left( {\mathit{\boldsymbol{X}}_k^i,w_k^i} \right), $ |
式中Resampling为重采样算子.
5) 目标状态的估计输出.k时刻目标状态估计为
| $ {{\mathit{\boldsymbol{\hat X}}}_k} = \frac{1}{N}\sum\limits_{i = 1}^N {\mathit{\boldsymbol{X}}_k^i} . $ |
6) 令k=k+1返回粒子状态转移.
3 实验为了更好地说明算法的有效性,本文将从数值仿真和视觉跟踪实验验证本文的算法.实验环境为Intel@ Core(TM)i7 CPU 3.6 GHz 8 G RAM计算机,算法开发均使用Matlab平台.
3.1 数值仿真对于经典的运动模型和观测模型[4]为:
| $ \begin{array}{*{20}{c}} {x\left( k \right) = 0.5x\left( {k - 1} \right) + \frac{{25x\left( {k - 1} \right)}}{{1 + x\left( {k - 1} \right)}} + }\\ {8\cos \left( {1.2\left( {k - 1} \right)} \right) + w\left( k \right),}\\ {z\left( k \right) = \frac{{x{{\left( k \right)}^2}}}{{20}} + v\left( k \right).} \end{array} $ |
式中:运动噪声w(k)服从高斯分布N(0, 10);观测噪声v(k)服从高斯分布N(0, 1);仿真步数为60步,状态初值x(1)=1.实验评价采用均方根误差(root mean square error, RMSE)来评价算法的滤波精度.
| $ {\rm{RMSE}} = \sqrt {\frac{1}{k}\sum\limits_{k = 1}^K {{{\left\| {x_k^F - x_k^T} \right\|}^2}} } , $ |
为克服随机模拟带来的影响,实验运行100次,可获得均方根误差的统计量,M=100为:
| $ {\rm{RMSE}}\left( {{\rm{mean}}} \right) = {\rm{mean}}\left( {{\rm{RMSE}},M} \right), $ |
| $ {\rm{RMSE}}\left( {{\rm{var}}} \right) = {\rm{var}}\left( {{\rm{RMSE}},M} \right). $ |
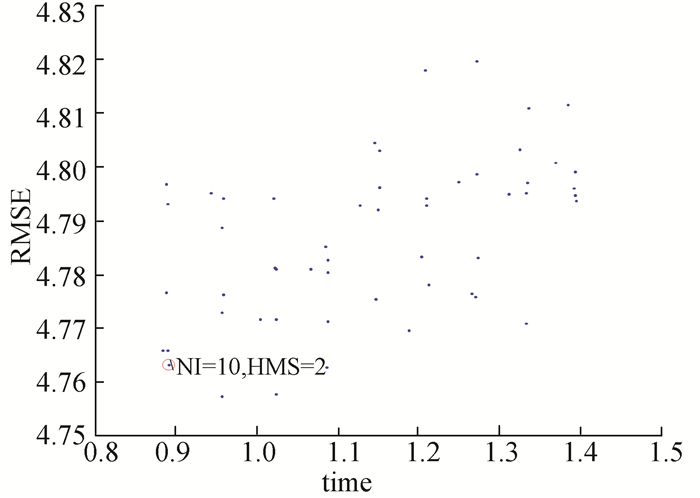
图 3给出了不同NI、HMS所对应的HSPF(粒子数为100)结果,其中,NI={6,10,20, 30, 50, 100},HMS={2, 3,4,5, 6, 7, 8, 9, 10}.从图中可以看出,本文所选取的参数为NI=10,HMS=2距原点最近,即算法所用的时间和误差均较小,能够较好地平衡算法的快速性和准确性.图 4给出了k=[1, 60]时间内,PF(粒子数为500)和HSPF(粒子数为100,NI=10HMS=2)在第6次运行时相应的状态估计结果所示.
|
图 3 不同NI、HMS所对应的HSPF结果 Figure 3 Simulation results of HSPF of different NI and HMS |
|
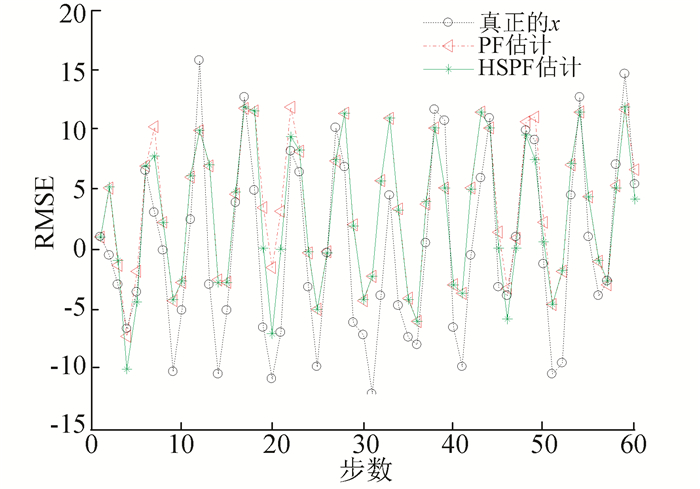
图 4 PF、HSPF状态估计结果示意 Figure 4 State estimation of PF and HSPF |
从图 4可以看到,基于HSPF的系统状态估计的准确度比基于标准PF的系统状态估计要高,特别是在第20步,HSPF比PF明显更靠近真实状态;表 1给出了两种状态估计算法在100次重复实验后均方根误差的均值和方差的统计表.
| 表 1 PF、HSPF仿真结果比较 Table 1 Comparison of simulation results of PF and HSPF |
由表 1可以看出,HSPF比PF滤波精度提升1.8%,而HSPF仅用少量的粒子数(100)就获得比标准粒子滤波(粒子数为500)更高的滤波精度,这是因为利用和声搜索改善了重要性采样函数,但由于HSPF本身的HS操作使得运行时间比PF稍长.
3.2 视觉跟踪实验在视觉跟踪实验中,将本文的算法(HSPF)与基于粒子滤波的视觉跟踪算法[3] (PF)、基于和声搜索的视觉算法[8] (HS)、基于Mean-Shift的视觉跟踪算法[2] (MS)、基于Mean-Shift的改进的粒子视觉跟踪算法[4] (MSPF)、分布场视觉跟踪算法[15] (distribution fields tracking,DFT)、多示例视觉跟踪算法[16] (multiple instance learning,MIL)进行对比.
3.2.1 实验细节测试视频来源于著名评价标准[17]中的CarDark、Sylvester、Matrix、Skating1、Jogging2、David3、Carscale、Suv、Liquor等序列,跟踪序列描述见表 2.为实现公平比较,DFT和MIL采用作者源码,其他算法实验中观测似然模型均采用Bhattacharyya系数衡量的核颜色直方图,状态转移模型为随机游走模型[13].实验中,PF采样粒子数目均为500,HSPF和MFPF采样粒子数目均为100.为加快程序实验速度,PF、HS、HSPF在计算颜色直方图时,仅统计在指定区域均匀采样的颜色,均匀采样点个数100,而由于MS状态估计位置与每个像素相关,因此在MS、MSPF采用全像素计算核颜色直方图.为了直观表示实验结果,实验评价采用常用目标状态的中心位置偏差和跟踪的精确率.在精确率的阈值本文取∂=20像素.实验的结果如图 5、6所示.
| 表 2 跟踪序列描述 Table 2 Description of tracking sequences |

|
图 5 视觉跟踪结果 Figure 5 Tracking results of sequences |
|
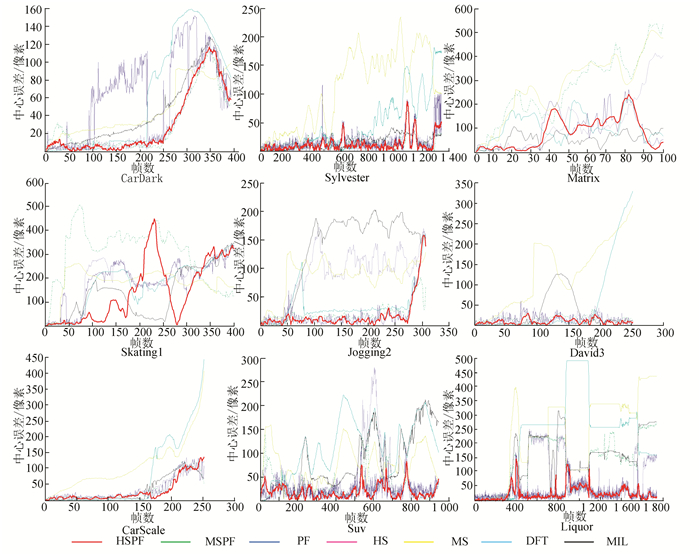
图 6 视觉跟踪算法中心误差结果 Figure 6 Tracking results of center error of visual tracking methods |
图 5给出了7种算法在序列CarDark、Sylvester、Matrix、Skating1、Jogging2、David3、Carscale、Suv、Liquor(由上至下)等序列视觉跟踪结果.由图 5可以看到MS容易陷于局部最优值,常常跟丢目标(Sylvester第950帧、Matrix第53帧、Carscale第158帧).HS比MS具有更强的全局搜索能力,但容易受到相似物体的干扰(Jogging2第57帧、Liquor第517帧),在目标被遮挡时,性能明显下降(Suv第547帧).PF在遮挡情况,能够利用历史信息,较好跟踪目标(David3第136帧),不易受到相似物体干扰.MSPF虽然改善了MS算法陷于局部最优值的弊病(Sylvester第450帧),但并没有完全克服(Matrix第25帧),DFT以其优秀的目标能力获得较好跟踪,但在光照剧烈变化(Sylvester第950帧)、快速运动(Carscale第170帧)性能出现明显下降、多示例则在目标出现遮挡时(Suv第547帧)、相似物体(Liquor第517帧),常常跟丢目标,而本文提出的基于HSPF,有效地实现了目标视觉跟踪.当出现光照变化(Matrix第2帧)、自身旋转(Sylvester第450帧)、遮挡(Liquor第1237帧)、快速运动(Liquor第1423帧)的情况下,本文的视觉跟踪算法仍然较好地跟踪目标.
3.2.3 定量分析图 6显示了序列各种算法的跟踪中心误差.从图 6可以看出本文算法在大多数的情况下,优于其他跟踪误差.
表 3显示了各个算法的跟踪精确率,精确率越高,跟踪算法越好.从表中可知,HSPF具有较高的跟踪精确率.
| 表 3 跟踪精确率 Table 3 The accuracy of tracking methods |
由定性和定量分析可知,HSPF能够在摄像机运动、自身旋转、遮挡等复杂环境稳定进行目标跟踪,在9个序列中获得了较好的跟踪效果,具有较强的鲁棒性.而在9个序列中,均采用了相同的状态转移模型,这与目标的实际运动模型不一致,PF相比,HSPF利用和声搜索结合当前的观测来改进重要采样函数,使采样粒子更靠近目标的真实位置,提高跟踪精度,同时具有PF等贝叶斯估计的优势,能够利用目标的先验信息克服因遮挡、模糊等噪声的影响,提高跟踪的稳定性.与MSPF相比,HSPF具有更强全局搜索能力,避免陷入局部最小值,在目标快速运动时跟踪性能.综上所述,HSPF能够利用HS的全局搜索能力提高PF重要性采样分布适应目标场景的变化,同时也能利用贝叶斯估计特性提高噪声的抗干扰性.
4 结论1) 和声搜索较好地利用当前观测信息,提高重要性采样函数对系统状态转移模型的鲁棒性.
2) 通过对和声搜索参数进行了优化,较好地平衡了视觉跟踪实时性和精确性的要求,并对粒子的权重进行补偿,满足了粒子滤波的理论基础贝叶斯估计.
3) 对比实验表明,相较于粒子滤波、和声搜索、Mean-Shift改进的粒子滤波、分布场、多示例等视觉跟踪算法,和声搜索粒子滤波视觉跟踪算法展现出更强的鲁棒性能.
| [1] |
YILMAZ A, JAVED O, SHAH M. Object tracking: a survey[J].
ACM Computing Surveys, 2006, 38(4): 1-45.
DOI: 10.1145/1177352.1177355 |
| [2] |
COMANICIU D, RAMESH V, MEER P. Kernel-based object tracking[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(5): 564-575.
DOI: 10.1109/TPAMI.2003.1195991 |
| [3] |
NUMMIARO K, KOLLER-MEIER E, GOOL V L. An adaptive color-based particle filter[J].
Image and Vision Computing, 2003, 21(1): 99-110.
DOI: 10.1016/S0262-8865(02)00129-4 |
| [4] |
SHAN Caifeng, TAN Tieniu, WEI Yucheng. Real-time hand tracking using a mean shift embedded particle filter[J].
Pattern Recognition, 2007, 40(7): 1958-1970.
DOI: 10.1016/j.patcog.2006.12.012 |
| [5] |
GEEM Z W, KIM J H, LOGANATHAN G V. A new heuristic optimization algorithm: harmony search[J].
Simulation: Transactions of The Society for Modeling and Simulation International, 2001, 76(2): 60-68.
DOI: 10.1177/003754970107600201 |
| [6] |
ALIA O M, MANDAVA R. The variants of the harmony search algorithm: an overview[J].
Artificial Intelligence Review, 2011, 36(1): 49-68.
DOI: 10.1007/s10462-010-9201-y |
| [7] |
MANJARRES D, LANDA-TORRES I, GIL-LOPEZ S, et al. A survey on applications of the harmony search algorithm[J].
Engineering Applications of Artificial Intelligence, 2013, 26(8): 1818-1831.
DOI: 10.1016/j.engappai.2013.05.008 |
| [8] |
FOURIE J, MILLS S, GREEN R. Harmony filter: A robust visual tracking system using the improved harmony search algorithm[J].
Image and Vision Computing, 2010, 28(12): 1702-1716.
DOI: 10.1016/j.imavis.2010.05.006 |
| [9] |
GAO Mingliang, LI Lili, SUN Xianming, et al. Face tracking based on differential harmony search[J].
IET Computer Vision, 2015, 9(1): 98-109.
DOI: 10.1049/iet-cvi.2014.0035 |
| [10] |
ARULAMPALAM M, MASKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J].
IEEE Transactions on Signal Processing, 2002, 50(2): 174-188.
DOI: 10.1109/78.978374 |
| [11] |
ZHOU Shaohua, CHELLAPPA R, MOGHADDAM B. Visual tracking and recognition using appearance-adaptive models in particle filters[J].
IEEE Transactions on Image Processing, 2004, 13(11): 1491-1506.
DOI: 10.1109/TIP.2004.836152 |
| [12] |
MAHDAVI M, FESANGHARY M, DAMANGIR E. An improved harmony search algorithm for solving optimization problems[J].
Applied Mathematics and Computation, 2007, 188(2): 1567-1579.
DOI: 10.1016/j.amc.2006.11.033 |
| [13] |
LI X R, JILKOV V P. Survey of maneuvering target tracking. Part Ⅰ. dynamic models[J].
IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1333-1364.
DOI: 10.1109/TAES.2003.1261132 |
| [14] |
LI Tiancheng, VILLARRUBIA G, SUN Shudong, et al. Resampling methods for particle filtering: identical distribution, a new method, and comparable study[J].
Frontiers of Information Technology and Electronic Engineering, 2015, 16(11): 969-984.
DOI: 10.1631/FITEE.1500199 |
| [15] |
SEVILLA-LARA L, LEARNED-MILLER E. Distribution fields for tracking[C]// Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Providence, RI: IEEE, 2012: 1910-1917. DOI: 10.1109/CVPR.2012.6247891.
|
| [16] |
BABENKO B, YANG M H, BELONGIE S. Robust object tracking with online multiple instance learning[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1619-1632.
DOI: 10.1109/TPAMI.2010.226 |
| [17] |
WU Yi, LIM J, YANG M H. Object tracking benchmark[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848.
DOI: 10.1109/TPAMI.2014.2388226 |
 2018, Vol. 50
2018, Vol. 50


