2. 哈尔滨工业大学 智能控制与系统研究所,哈尔滨 150001
2. Research Institute of Intelligent Control and Systems, Harbin Institute of Technology, Harbin 150001, China
随着人类对太空探索日渐深入,所需执行空间的任务相应变得复杂,在完成各类空间任务的过程中,空间机器人发挥着不可替代的作用[1].自由漂浮空间机器人(FFSM)是一种基座处于自由状态的空间机器人,在执行任务的过程中,其基座固连航天器停止运行,处于“自由漂浮”的状态[2].这种“自由漂浮”状态对完成特定空间任务、减小航天器损耗、延长卫星寿命有着重要的意义,因此国内外许多学者[3-4]对FFSM系统机械结构、动力学建模以及控制问题进行了相关研究.
对FFSM系统的轨迹规划研究有直接法和间接法两种主要方法.直接法将连续最优控制问题转化为非线性离散规划问题直接进行数值求解,收敛速度快、对初值要求低[5].2006年Huang等[6]以粒子蚁群算法为基础解决了FFSM时间最优控制问题.2013年李适[7]利用Gauss伪谱法完成了FFSM时间燃料最优控制,并利用协态映射引理证明了解的可行性.间接法利用哈密顿函数推导出最优控制一阶必要条件,并通过数值计算的方法求得最优解.该方法求解精度高,但收敛速度慢, 对初值依赖强.2009年Yokoyama等[8]通过间接法得到受风力约束的飞行机器人点到点最优路径.
伪谱法是一种直接方法,基于正交多项式的根进行配点,应用较为广泛的有Lobatto伪谱法、Gauss伪谱法和Radau伪谱法[9-10].在应用形式上,伪谱法有两种主要形式:p法和h法.p法仅通过增加多项式阶数来提高精度,高阶多项式微分矩阵求解困难和收敛速度慢导致该方法有很大的局限性;h法将整个过程分段,在每段内用低阶多项式近似,通过增加分段的个数来提高收敛速度.然而,分段个数过多会使得误差变大,影响解的精确性[11-12].
本文在Gauss伪谱法和Radau伪谱法的基础上,将h法和p法的优点结合在一起设计出hp自适应Radau伪谱法.该方法对分段个数、每段的宽度、以及在每段上多项式的阶数进行配置,可以显著提高计算效率和求解精度.Han等[13]用hp自适应RPM解决了飞行器再入轨迹规划问题.本文将hp自适应RPM算法应用到FFSM系统,完成空间机械臂的轨迹规划问题.
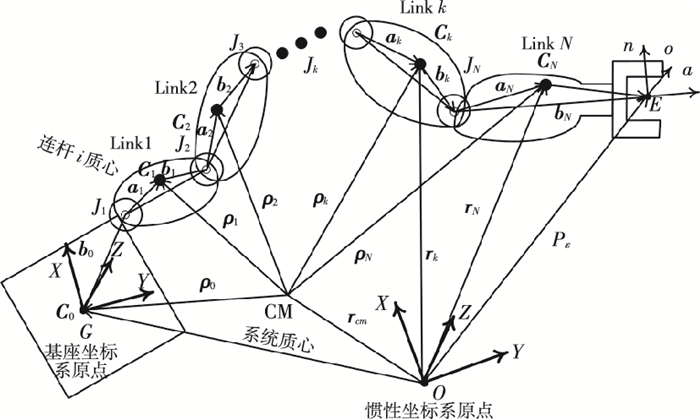
1 FFSM系统动力学建模惯性坐标系下FFSM系统模型如图 1所示,ρi为系统质心到连杆i质心的矢量,ri为连杆i质心到惯性坐标系原点O的矢量,pi为关节i在惯性坐标系中的位置矢量.
|
图 1 FFSM系统模型 Figure 1 The model of FFSM system |
由图 1可知连杆k的质心矢量ρk满足:
| $ \begin{array}{*{20}{c}} {\sum\limits_{k = 0}^n {{m_k}{\mathit{\boldsymbol{\rho }}_k}} = \mathit{\boldsymbol{0}},}\\ {{\mathit{\boldsymbol{\rho }}_k} - {\mathit{\boldsymbol{\rho }}_{k - 1}} = {\mathit{\boldsymbol{b}}_{k - 1}} + {\mathit{\boldsymbol{a}}_k}.\left( {k = 1, \cdots ,N} \right)} \end{array} $ |
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\rho }}_k} = \sum\limits_{i = 0}^n {{\mathit{\boldsymbol{v}}_{ik}}} ,\\ {{\mathit{\boldsymbol{\dot \rho }}}_k} = \sum\limits_{i = 0}^n {{\mathit{\boldsymbol{\omega }}_i} \times {\mathit{\boldsymbol{v}}_{ik}}} , \end{array} \right.\left( {k = 0, \cdots ,n} \right) $ | (1) |
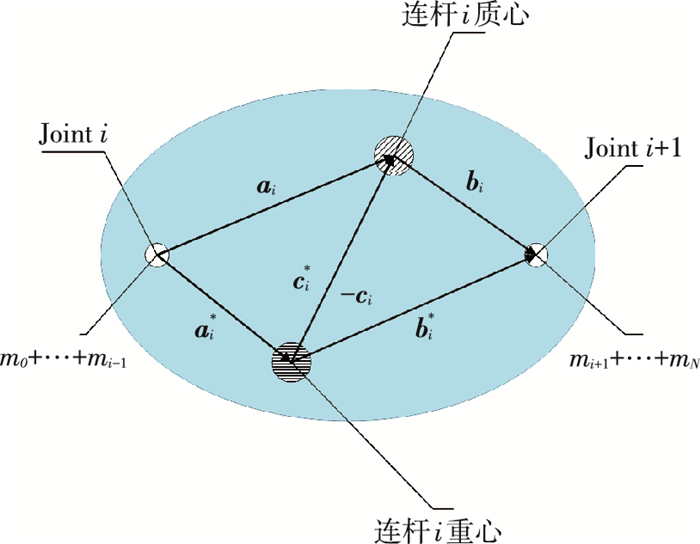
|
图 2 增广体定义 Figure 2 The definition of augment body |
其中
| $ {\mathit{\boldsymbol{v}}_{ik}} = \left\{ \begin{array}{l} \mathit{\boldsymbol{b}}_i^ * ,\;\;\;\;\;i < k;\\ \mathit{\boldsymbol{c}}_i^ * ,\;\;\;\;\;i = k;\\ - \mathit{\boldsymbol{a}}_i^ * ,\;\;\;i > k. \end{array} \right. $ |
不失一般性,假设惯性坐标系原点和系统质心重合即rcm为0.由式(1)可以得到末端执行器的角速度、线速度和角动量为:
| $ {\mathit{\boldsymbol{\omega }}_E} = {\mathit{\boldsymbol{\omega }}_0} + \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{z}}_i}{{\mathit{\boldsymbol{\dot q}}}_i}} , $ | (2) |
| $ {{\mathit{\boldsymbol{\dot r}}}_E} = \sum\limits_{i = 0}^n {{\mathit{\boldsymbol{\omega }}_i} \times {\mathit{\boldsymbol{v}}_{in}} + {\mathit{\boldsymbol{\omega }}_n} \times {\mathit{\boldsymbol{r}}_n}} , $ | (3) |
| $ \begin{array}{l} \mathit{\boldsymbol{h}} = \sum\limits_{k = 0}^n {\left( {{\mathit{\boldsymbol{I}}_k}{\mathit{\boldsymbol{\omega }}_k} - {m_k}\left( {\sum\limits_{j = 0}^n {{\mathit{\boldsymbol{v}}_{jk}}} \times \sum\limits_{i = 0}^n {{v_{ik}}} \times {\mathit{\boldsymbol{\omega }}_i}} \right)} \right)} = \\ \;\;\;\;\;\sum\limits_{j = 0}^N {\sum\limits_{i = 0}^N {{\mathit{\boldsymbol{D}}_{ij}}{\mathit{\boldsymbol{\omega }}_i}..} } \end{array} $ | (4) |
其中Dij为
| $ {\mathit{\boldsymbol{D}}_{ij}} = \left\{ {\begin{array}{*{20}{l}} { - M\left\{ { - \mathit{\boldsymbol{a}}_i^* \cdot \left. {\mathit{\boldsymbol{b}}_i^*} \right){\mathit{\boldsymbol{1}}} - \mathit{\boldsymbol{a}}_i^*\mathit{\boldsymbol{b}}_i^*} \right\},\;\;\;\;\;\;\;\;\;\;\;i < j;}&{}\\ {{\mathit{\boldsymbol{I}}_i} + \sum\limits_{k = 0}^N {{m_k}\left\{ {\left( {{\mathit{\boldsymbol{v}}_{ik}} \cdot {\mathit{\boldsymbol{v}}_{ik}}} \right){\mathit{\boldsymbol{1}}} - {\mathit{\boldsymbol{v}}_{ik}}{\mathit{\boldsymbol{v}}_{ik}}} \right\}} ,\;\;\;i = j;}&{}\\ { - M\left\{ {\mathit{\boldsymbol{b}}_i^* \cdot \left( { - \mathit{\boldsymbol{a}}_i^*} \right){\mathit{\boldsymbol{1}}} - \mathit{\boldsymbol{b}}_i^*\left( { - \mathit{\boldsymbol{a}}_i^*} \right)} \right\},\;\;\;i > j.}&{} \end{array}} \right. $ |
式中1为单位并矢.
由于ivik是在第i个关节坐标系中定义,因此要得到惯性坐标系的表达式,需要将连杆坐标系中的表达式转换到惯性坐标系.根据文献[14],可以求得由基座坐标系和关节坐标系到惯性坐标系的转移矩阵T0、Ti为:
| $ \begin{array}{l} {\mathit{\boldsymbol{T}}_0}\left( {\mathit{\boldsymbol{e}},n} \right) = \left( {{n^2} - {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{e}}} \right)\mathit{\boldsymbol{1}} + 2\mathit{\boldsymbol{e}}{\mathit{\boldsymbol{e}}^{\rm{T}}} + 2n{\mathit{\boldsymbol{e}}^ \times },\\ {\mathit{\boldsymbol{T}}_i}\left( {\mathit{\boldsymbol{e}},n,{\mathit{\boldsymbol{q}}_1} \cdots {\mathit{\boldsymbol{q}}_i}} \right) = {\mathit{\boldsymbol{T}}_0}{\left( {\mathit{\boldsymbol{e}},n} \right)^0}{\mathit{\boldsymbol{T}}_i}\left( {{\mathit{\boldsymbol{q}}_1} \cdots {\mathit{\boldsymbol{q}}_i}} \right), \end{array} $ | (5) |
式中e、n分别为欧拉参数,随基座转轴单位向量a和转角θ变化,满足:
| $ \mathit{\boldsymbol{e}}\left( {\mathit{\boldsymbol{a}},\theta } \right) = \mathit{\boldsymbol{a}}\sin \left( {\theta /2} \right), $ |
| $ n\left( {\mathit{\boldsymbol{a}},\theta } \right) = \cos \left( {\theta /2} \right). $ |
由式(5)可知,转移矩阵T0是随基座运动不断变化的量,需要实时更新;新的转移矩阵可利用如下公式求取:
| $ \mathit{\boldsymbol{\dot e}} = \frac{1}{2}{\left[ {{\mathit{\boldsymbol{e}}^ \times } + n} \right]^0}{\mathit{\boldsymbol{\omega }}_0}, $ |
| $ \dot n = \frac{1}{2}{\mathit{\boldsymbol{e}}^{{\rm{T0}}}}{\mathit{\boldsymbol{\omega }}_0}. $ |
式(2)、(3)在惯性坐标系中表示为:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot r}}}_E} = {\mathit{\boldsymbol{T}}_0}\left\{ {{}^0{\mathit{\boldsymbol{J}}_{11}}^0{\mathit{\boldsymbol{\omega }}_0} + {}^0{\mathit{\boldsymbol{J}}_{12}}^{{\mathit{\boldsymbol{\dot q}}}_m}} \right\},\\ {\mathit{\boldsymbol{\omega }}_E} = {\mathit{\boldsymbol{T}}_0}\left\{ {^0{\mathit{\boldsymbol{\omega }}_0} + {}^0{\mathit{\boldsymbol{J}}_{22}}{{\mathit{\boldsymbol{\dot q}}}_m}} \right\}, \end{array} $ | (6) |
其中:
| $ {}^0{\mathit{\boldsymbol{J}}_{11}} = - \sum\limits_{i = 0}^n {{{\left( {{}^0{\mathit{\boldsymbol{T}}_i}{}^i{{\mathit{\boldsymbol{v'}}}_{in}}} \right)}^ \times }} ,{}^0{\mathit{\boldsymbol{J}}_{22}} = {}^0{\mathit{\boldsymbol{F}}_n}, $ |
| $ {}^0{\mathit{\boldsymbol{J}}_{12}} = - \sum\limits_{i = 0}^n {{{\left( {{}^0{\mathit{\boldsymbol{T}}_i}{}^i{{\mathit{\boldsymbol{v'}}}_{in}}} \right)}^ \times }} {}^0{\mathit{\boldsymbol{F}}_i}, $ |
| $ {}^0{\mathit{\boldsymbol{F}}_j} = \left[ {\begin{array}{*{20}{c}} {{}^0{\mathit{\boldsymbol{T}}_1}{}^1{\mathit{\boldsymbol{z}}_1}}&{{}^0{\mathit{\boldsymbol{T}}_2}{}^2{\mathit{\boldsymbol{z}}_2}}&{, \cdots ,}&{{}^0{\mathit{\boldsymbol{T}}_j}{}^j{\mathit{\boldsymbol{z}}_j}}&{0, \cdots ,0} \end{array}} \right]. $ |
式(6)带入拉格朗日方程得到系统动力学方程[15]:
| $ {\mathit{\boldsymbol{H}}_q}\left( {{\mathit{\boldsymbol{q}}_m}} \right){{\mathit{\boldsymbol{\ddot q}}}_m} + {\mathit{\boldsymbol{C}}_q}\left( {{\mathit{\boldsymbol{q}}_m},{{\mathit{\boldsymbol{\dot q}}}_m}} \right){{\mathit{\boldsymbol{\dot q}}}_m} = \mathit{\boldsymbol{\mu }}. $ | (7) |
式中:Hq为N×N的对称正定惯量矩阵;Cq为N×1的离心力和哥氏力矩阵;μ为N×1的控制力矩向量;qm=[q1 q2 … qn]T为各关节转角状态矩阵.各矩阵计算如下:
| $ {\mathit{\boldsymbol{H}}_q}\left( {{\mathit{\boldsymbol{q}}_m}} \right) = \mathit{\boldsymbol{H}}_\omega ^{\rm{T}}\left( {\mathit{\boldsymbol{I}} + M\sum\limits_{k = 0}^N {{\mathit{\boldsymbol{H}}_k}} } \right){\mathit{\boldsymbol{H}}_\omega }, $ |
| $ {\mathit{\boldsymbol{H}}_\omega } = {\left[ {\begin{array}{*{20}{c}} {{}^0{\mathit{\boldsymbol{D}}^{ - 1}}{}^0{\mathit{\boldsymbol{D}}_q}}&\mathit{\boldsymbol{F}}&{{\mathit{\boldsymbol{F}}_2}} \end{array}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{H}}_k} = {{\mathit{\boldsymbol{\tilde V}}}_k}\mathit{\boldsymbol{\tilde V}}_k^{\rm{T}},{{\mathit{\boldsymbol{\tilde V}}}_k} = {\left[ {\begin{array}{*{20}{c}} {{v_{0k}}}&{{v_{1k}}}&{{v_{2k}}} \end{array}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{C}}_q}\left( {{\mathit{\boldsymbol{q}}_m},{{\mathit{\boldsymbol{\dot q}}}_m}} \right){{\mathit{\boldsymbol{\dot q}}}_m} = {\mathit{\boldsymbol{H}}_q}\left( {{\mathit{\boldsymbol{q}}_m}} \right){{\mathit{\boldsymbol{\dot q}}}_m} - \frac{\partial }{{\partial {\mathit{\boldsymbol{q}}_m}}}\left( {\frac{1}{2}\mathit{\boldsymbol{\dot q}}_m^{\rm{T}}{\mathit{\boldsymbol{H}}_q}\left( {{\mathit{\boldsymbol{q}}_m}} \right){{\mathit{\boldsymbol{\dot q}}}_m}} \right). $ |
将式(7)转化成状态方程形式
| $ \mathit{\boldsymbol{\dot X}} = f\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{U}},t} \right), $ |
其中:
| $ \mathit{\boldsymbol{U}} = \mathit{\boldsymbol{\mu }}, $ |
| $ \mathit{\boldsymbol{X = }}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\theta }}_m}}\\ {{{\mathit{\boldsymbol{\dot q}}}_m}} \end{array}} \right], $ |
| $ f\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{U}},t} \right) = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{0}}&\mathit{\boldsymbol{E}}\\ \mathit{\boldsymbol{0}}&{ - \mathit{\boldsymbol{H}}_q^{ - 1}{\mathit{\boldsymbol{C}}_q}} \end{array}} \right]\mathit{\boldsymbol{X}} + \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{0}}\\ {\mathit{\boldsymbol{H}}_q^{ - 1}} \end{array}} \right]\mathit{\boldsymbol{U}}. $ | (8) |
边界约束为
| $ \mathit{\boldsymbol{E}}\left( {\mathit{\boldsymbol{X}}\left( {{t_0}} \right),{t_0},\mathit{\boldsymbol{X}}\left( {{t_f}} \right),{t_f}} \right) = 0. $ | (9) |
路径约束为
| $ \mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{X}}\left( \tau \right),\mathit{\boldsymbol{U}}\left( \tau \right),\tau } \right) \le 0. $ | (10) |
考虑到时间最优、燃料最优和基座扰动,定义如下目标函数[16]:
| $ \begin{array}{l} \mathit{\boldsymbol{J}} = \alpha {\mathit{\boldsymbol{J}}_1} + \beta {\mathit{\boldsymbol{J}}_2} + \gamma {\mathit{\boldsymbol{J}}_3} = \\ \;\;\;\;\;\;\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {\mathit{\boldsymbol{X}}\left( {{t_0}} \right),{t_0},\mathit{\boldsymbol{X}}\left( {{t_f}} \right),{t_f}} \right) + \int_{{t_0}}^{{t_f}} {\mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},t} \right){\rm{d}}t} , \end{array} $ |
其中
| $ \mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{X}}\left( t \right),\mathit{\boldsymbol{U}}\left( t \right),t} \right) = \alpha + \beta {\mathit{\boldsymbol{U}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{U}}\left( t \right). $ |
式中:α、β、γ分别为相关系数;J1、J2、J3分别为时间最优、燃料最优和基座稳定性目标函数.
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{J}}_1} = \int_{{t_0}}^{{t_f}} {{\rm{d}}t} ,\\ {\mathit{\boldsymbol{J}}_2} = \int_{{t_0}}^{{t_f}} {{\mathit{\boldsymbol{u}}^{\rm{T}}}\left( t \right)u\left( t \right){\rm{d}}t} ,\\ {\mathit{\boldsymbol{J}}_3} = \int_{{t_0}}^{{t_f}} {\mathit{\boldsymbol{\omega }}_0^{\rm{T}}\left( t \right){\mathit{\boldsymbol{\omega }}_0}\left( t \right){\rm{d}}t} . \end{array} \right. $ | (11) |
将时间[to, tf]分成S段,0=t0 < t1 < … < tS=tf,变量t∈[ts-1, ts].通过如下变换将变量t转化为变量τ∈[-1, 1]为
| $ \tau = \frac{{2t - \left( {{t_s} + {t_{s - 1}}} \right)}}{{{t_s} - {t_{s - 1}}}},\left( {{t_{s - 1}} < t < {t_s}} \right) $ | (12) |
式中x(s)(τ)、μ(s)(τ)分别为时间区间s内的状态变量和控制变量.标准Bolza最优控制问题可以描述为
| $ \begin{array}{l} {\mathit{\boldsymbol{J}}^{\left( s \right)}} = \alpha \mathit{\boldsymbol{J}}_1^{\left( s \right)} + \beta \mathit{\boldsymbol{J}}_2^{\left( s \right)} + \gamma \mathit{\boldsymbol{J}}_3^{\left( s \right)} = \\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {\mathit{\boldsymbol{X}}\left( { - 1} \right),{t_0},\mathit{\boldsymbol{X}}\left( 1 \right),{t_f}} \right) + \sum\limits_{s = 1}^S {\frac{{{t_s} - {t_{s - 1}}}}{2}\int_{ - 1}^1 {\mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},\tau } \right){\rm{d}}\tau } } , \end{array} $ |
其中
| $ \mathit{\boldsymbol{J}}_1^{\left( s \right)} = \sum\limits_{s = 1}^S {\frac{{{t_s} - {t_{s - 1}}}}{2}\int_{ - 1}^1 {{\rm{d}}\tau } } , $ |
| $ \mathit{\boldsymbol{J}}_2^{\left( s \right)} = \sum\limits_{s = 1}^S {\frac{{{t_s} - {t_{s - 1}}}}{2}\int_{ - 1}^1 {{\mathit{\boldsymbol{u}}^{\left( s \right)}}{{\left( \tau \right)}^{\rm{T}}}{\mathit{\boldsymbol{u}}^{\left( s \right)}}\left( \tau \right){\rm{d}}\tau } } , $ |
| $ \mathit{\boldsymbol{J}}_3^{\left( s \right)} = \sum\limits_{s = 1}^S {\frac{{{t_s} - {t_{s - 1}}}}{2}\int_{ - 1}^1 {{\mathit{\boldsymbol{\omega }}^{\left( s \right)}}{{\left( \tau \right)}^{\rm{T}}}{\mathit{\boldsymbol{\omega }}^{\left( s \right)}}\left( \tau \right){\rm{d}}\tau } } , $ |
且满足
| $ \frac{{{\rm{d}}{\mathit{\boldsymbol{x}}^{\left( s \right)}}\left( \tau \right)}}{{{\rm{d}}\tau }} = \frac{{{t_s} - {t_{s - 1}}}}{2}f\left( {{\mathit{\boldsymbol{x}}^{\left( s \right)}}\left( \tau \right),{\mathit{\boldsymbol{x}}^{\left( s \right)}}\left( \tau \right),\tau ;{t_{s - 1}},{t_s}} \right), $ |
| $ \frac{{{\rm{d}}{\mathit{\boldsymbol{x}}^{\left( s \right)}}\left( \tau \right)}}{{{\rm{d}}\tau }} = \frac{{{t_s} - {t_{s - 1}}}}{2}f\left( {{\mathit{\boldsymbol{x}}^{\left( s \right)}}\left( \tau \right),{\mathit{\boldsymbol{x}}^{\left( s \right)}}\left( \tau \right),\tau ;{t_{s - 1}},{t_s}} \right), $ |
| $ \mathit{\boldsymbol{E}}\left( {{\mathit{\boldsymbol{X}}^{\left( 1 \right)}}\left( { - 1} \right),{\tau _0},{\mathit{\boldsymbol{X}}^{\left( S \right)}}\left( 1 \right),{\tau _f}} \right) = 0, $ |
由连续性条件可得
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {t_s^{ - 1}} \right) = \mathit{\boldsymbol{x}}\left( {t_s^{ + 1}} \right),\\ \mathit{\boldsymbol{u}}\left( {t_s^{ - 1}} \right) = \mathit{\boldsymbol{u}}\left( {t_s^{ + 1}} \right). \end{array} \right. $ |
Radau伪谱法离散点选择基于Legendre-Gauss-Radau(LGR)节点,该类节点散落在半开区间[-1,1)或(-1,1]内.本文利用LGR节点进行离散处理,且仅包含-1边界点.第s段中的状态变量xi(s)由多项式近似[17]:
| $ \begin{array}{l} {\mathit{\boldsymbol{x}}^{\left( s \right)}}\left( \tau \right) \approx {\mathit{\boldsymbol{X}}^{\left( s \right)}}\left( \tau \right) = \sum\limits_{i = 0}^{{N_s}} {\mathit{\boldsymbol{L}}_i^{\left( s \right)}\left( \tau \right){\mathit{\boldsymbol{X}}^{\left( s \right)}}\left( {{\tau _i}} \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 0}^{{N_s}} {\mathit{\boldsymbol{L}}_i^{\left( s \right)}\left( \tau \right)\mathit{\boldsymbol{X}}_i^{\left( s \right)}} , \end{array} $ | (13) |
| $ \mathit{\boldsymbol{L}}_i^{\left( s \right)}\left( \tau \right) = \prod\limits_{j = 0,j \ne i}^{{N_s} + 1} {\frac{{\tau - \tau _j^{\left( s \right)}}}{{{\tau _i} - \tau _j^{\left( s \right)}}}} .\;\;\;\left( {i = 0,1, \cdots ,{N_s}} \right) $ |
式中:τ∈[-1, 1],(τ0(s), …, τNs-1(s))为s段内LGR节点;τNs(s)=1为s段的终点;Li(s)(τ)为拉格朗日基函数.
在Radau伪谱法中,假设最后一个点没有控制,控制变量离散化为:
| $ \begin{array}{l} {\mathit{\boldsymbol{u}}^{\left( S \right)}}\left( \tau \right) \approx {\mathit{\boldsymbol{U}}^{\left( S \right)}}\left( \tau \right) = \sum\limits_{i = 0}^{{N_s} - 1} {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over L} }}_i^{\left( S \right)}\left( \tau \right){\mathit{\boldsymbol{U}}^{\left( S \right)}}\left( {{\tau _i}} \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 0}^N {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over L} }}_i^{\left( s \right)}\left( \tau \right)\mathit{\boldsymbol{U}}_i^{\left( s \right)}} , \end{array} $ |
| $ \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over L} }}_i^{\left( s \right)}\left( \tau \right) = \prod\limits_{j = 0,j \ne i}^{{N_s} - 1} {\frac{{\tau - \tau _j^{\left( S \right)}}}{{{\tau _i} - \tau _j^{\left( S \right)}}}} ,\;\;\;\left( {i = 0,1, \cdots ,{N_s} - 1} \right) $ |
式中Ui(s)为在Nk个LGR节点处近似值.状态方程式(8)的离散形式为
| $ \begin{array}{*{20}{c}} {\sum\limits_{i = 0}^{{N_s} - 1} {\mathit{\boldsymbol{H}}_{k,i}^{\left( s \right)}\mathit{\boldsymbol{X}}_k^{\left( s \right)}} = \frac{{{t_s} - {t_{s - 1}}}}{2}f\left( {\mathit{\boldsymbol{X}}_k^{\left( s \right)},\mathit{\boldsymbol{U}}_k^{\left( s \right)},\tau _k^{\left( s \right)};{t_{k - 1}},{t_k}} \right),}\\ {\left( {k = 0,1, \cdots ,{N_s} - 1} \right).} \end{array} $ | (14) |
其中
| $ \mathit{\boldsymbol{H}}_{k,i}^{\left( s \right)} = \mathit{\boldsymbol{\dot L}}_i^{\left( s \right)}\left( {{\tau _k}} \right),\left\{ \begin{array}{l} i = 0,1, \cdots ,{N_s} - 1,\\ k = 0,1, \cdots ,{N_s} - 1,\\ s = 1,2, \cdots ,S. \end{array} \right. $ |
为第s段的Radau伪谱微分矩阵.同时目标函数离散形式为
| $ \begin{array}{l} \mathit{\boldsymbol{J}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {\mathit{\boldsymbol{X}}_1^{\left( 1 \right)},{t_0},\mathit{\boldsymbol{X}}_{Ns + 1}^{\left( s \right)},{t_s}} \right) + \\ \;\;\;\;\;\;\sum\limits_{s = 1}^S {\sum\limits_{j = 0}^{{N_s} - 1} {\frac{{{t_s} - {t_{s - 1}}}}{2}\mathit{\boldsymbol{\omega }}_j^{\left( s \right)}\mathit{\boldsymbol{g}}\left( {\mathit{\boldsymbol{X}}_j^{\left( s \right)},\mathit{\boldsymbol{U}}_j^{\left( s \right)},\mathit{\boldsymbol{\tau }}_j^{\left( s \right)}} \right)} } , \end{array} $ |
式中ωj(s)(i=1, …, Ns)为LGR权重,可通过下式离线计算得到:
| $ {\mathit{\boldsymbol{\omega }}_1} = \frac{2}{{{N^2}}}, $ |
| $ {\mathit{\boldsymbol{\omega }}_k} = \frac{1}{{\left( {1 - {\tau _k}} \right){{\left( {{{\dot p}_{N - 1}}\left( {{\tau _k}} \right)} \right)}^2}}}.\;\;\;\;\left( {k = 2, \cdots ,N - 1} \right). $ |
由式(9)~(13)可得边界条件、路径约束和连续性条件离散形式为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{E}}\left( {\mathit{\boldsymbol{X}}_0^{\left( 1 \right)},{t_0},\mathit{\boldsymbol{X}}_{{N_S} + 1}^{\left( 1 \right)},{t_S}} \right) = 0,\\ \mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{X}}_j^{\left( s \right)},\mathit{\boldsymbol{U}}_j^{\left( s \right)},\tau _j^{\left( s \right)}} \right) \le 0,\\ \mathit{\boldsymbol{X}}_{{N_s}}^{\left( s \right)} = \mathit{\boldsymbol{X}}_0^{\left( {s + 1} \right)},\\ \mathit{\boldsymbol{U}}_{{N_s}}^{\left( s \right)} = \mathit{\boldsymbol{U}}_0^{\left( {s + 1} \right)}. \end{array} \right. $ |
第s段内节点为[t0(s), t1(s), …, tNs-1(s)]∈[ts-1, ts],取两两节点的中间点为
| $ \bar t_j^{\left( s \right)} = \frac{{t_j^{\left( s \right)} + t_{j + 1}^{\left( s \right)}}}{2}.\;\;\;\left( {j = 0,1, \cdots ,{N_s} - 1} \right) $ |
定义X、U分别为状态变量x和控制变量u在中间点处的取值,其值由拉格朗日插值多项式计算得到:
| $ {{\mathit{\boldsymbol{\bar X}}}^{\left( s \right)}} = {\left[ {\mathit{\boldsymbol{x}}\left( {\bar t_0^{\left( s \right)}} \right),\mathit{\boldsymbol{x}}\left( {\bar t_1^{\left( s \right)}} \right), \cdots ,\mathit{\boldsymbol{x}}\left( {\bar t_{{N_s} - 1}^{\left( s \right)}} \right)} \right]^{\rm{T}}}, $ |
| $ {{\mathit{\boldsymbol{\bar U}}}^{\left( s \right)}} = {\left[ {\mathit{\boldsymbol{u}}\left( {\bar t_0^{\left( s \right)}} \right),\mathit{\boldsymbol{u}}\left( {\bar t_1^{\left( s \right)}} \right), \cdots ,\mathit{\boldsymbol{u}}\left( {\bar t_{{N_s} - 1}^{\left( s \right)}} \right)} \right]^{\rm{T}}}, $ |
上式带入到式(14)中,并定义s段内的误差矩阵R(s)如下
| $ {\mathit{\boldsymbol{R}}^{\left( s \right)}} = \left| {{{\mathit{\boldsymbol{\bar H}}}^{\left( s \right)}}{{\mathit{\boldsymbol{\bar X}}}^{\left( s \right)}} - \frac{{{t_s} - {t_{s - 1}}}}{2}f\left( {{{\mathit{\boldsymbol{\bar X}}}^{\left( s \right)}},{{\mathit{\boldsymbol{\bar U}}}^{\left( s \right)}},{{\mathit{\boldsymbol{\bar \tau }}}^{\left( s \right)}};{t_{s - 1}},{t_s}} \right)} \right|. $ |
式中:R(s)为一个Ns×1的矩阵;R(s)中的元素为在节点tj(s)(j=0, 1, …, Ns-1)处的误差,定义s段内误差的最大值[18]为
| $ e_{\max }^{\left( s \right)} = \mathop {\max }\limits_{j = 0 \cdots {N_s} - 1} {\mathit{\boldsymbol{R}}^s}\left[ j \right]. $ |
定义εd为容忍误差,若emax(s) < εd,表明在s段内,配点处状态满足精度要求,可停止该段内的迭代计算.若emax(s)>εd,则需要细分时间段或增加时间段内配点个数来减少误差,达到精度要求.当所有时间段内误差均满足要求,则停止迭代,得到最优解.
4.2 细分区间或增加配点准则当s段内精度不满足要求,定义s段内各点曲率[16]为
| $ {k^{\left( s \right)}}\left( {{\tau _i}} \right) = \frac{{\left| {\mathit{\boldsymbol{\ddot X}}_m^{\left( s \right)}\left( {{\tau _i}} \right)} \right|}}{{\left| {{{\left[ {1 + \mathit{\boldsymbol{\ddot X}}_m^{\left( s \right)}\left( {{\tau _i}} \right)} \right]}^{3/2}}} \right|}}, $ |
令
| $ {r_s} = \frac{{k_{\max }^{\left( s \right)}}}{{{{\bar k}^{\left( s \right)}}}}. $ |
式中kmax(k)、k(k)分别为s区间内各点曲率的最大值和平均值.
定义临界值参数rmax,若rs < rmax,表明该区间内比较平滑,可以通过增加节点个数来提高精度;若rs>rmax,说明s段内振荡较大,需要对该区间重新划分.
4.2.1 增加节点个数计算若rs < rmax,需要增加s段内节点个数,增加的节点个数Nsf为
| $ {N_{sf}} = {\rm{ceil}}\left( {{{\log }_{10}}\left( {e_{\max }^{\left( s \right)}} \right) - {{\log }_{10}}\left( {{\varepsilon _d}} \right)} \right) + 1. $ |
修正后节点的数量为
| $ {N_s} = {N_{s0}} + {N_{sf}}. $ |
式中:Ns0为修正前节点的个数,ceil(·)为取整运算.
4.2.2 区间细分个数及位置计算若rs>rmax,对s段细分,子区间的数量nk由如下公式计算:
| $ {n_k} = 2 * {\rm{ceil}}\left( {{{\log }_{10}}\left( {e_{\max }^{\left( s \right)}} \right) - {{\log }_{10}}\left( {{\varepsilon _d}} \right)} \right). $ |
子区间的位置通过曲率密度函数ρ(τ)求取[19], 定义
| $ \rho \left( \tau \right) = c{k^{\left( s \right)}}{\left( \tau \right)^{1/3}}, $ |
c为常数,且满足
| $ \int_{ - 1}^1 {\rho \left( \tau \right){\rm{d}}\tau } = 1. $ |
定义节点分配函数为
| $ F\left( \tau \right) = \int_{ - 1}^\tau {\rho \left( \zeta \right){\rm{d}}\zeta } , $ |
第i个子区间起点和终点分别为τi-1和τi,满足
| $ F\left( {{\tau _i}} \right) = \frac{i}{{{n_k}}}.\;\;\;\;\left( {1 \le i \le {n_k}} \right) $ |
本文以两连杆FFSM系统为例,分别应用GPM和hp-RPM进行轨迹规划仿真,并对两方法进行比较,系统参数见表 1,状态约束见表 2.
| 表 1 FFSM系统参数 Table 1 The FFSM parameters |
| 表 2 状态约束 Table 2 The state constraint |
控制变量满足约束为:
| $ \begin{array}{*{20}{c}} { - 10 \le {\mu _1} \le 10,}\\ { - 8 \le {\mu _2} \le 8.} \end{array} $ |
选取目标函数各相关系数为:
| $ \alpha = 0.7,\beta = 0.1,\gamma = 2, $ |
取初始时刻节点个数P=10,分段个数S=1,容忍误差εd=1×10-3.
在CPU为Inter i5-3230、操作系统Windows7 32位、内存4 G的电脑上,应用MATLAB2014a进行仿真实验.选取相同的初始节点个数,用GPM和hp-RPM方法进行计算.计算时间见表 3,仿真结果如图 3~6所示.
| 表 3 耗时比较 Table 3 Comparison of time-consumtion |
|
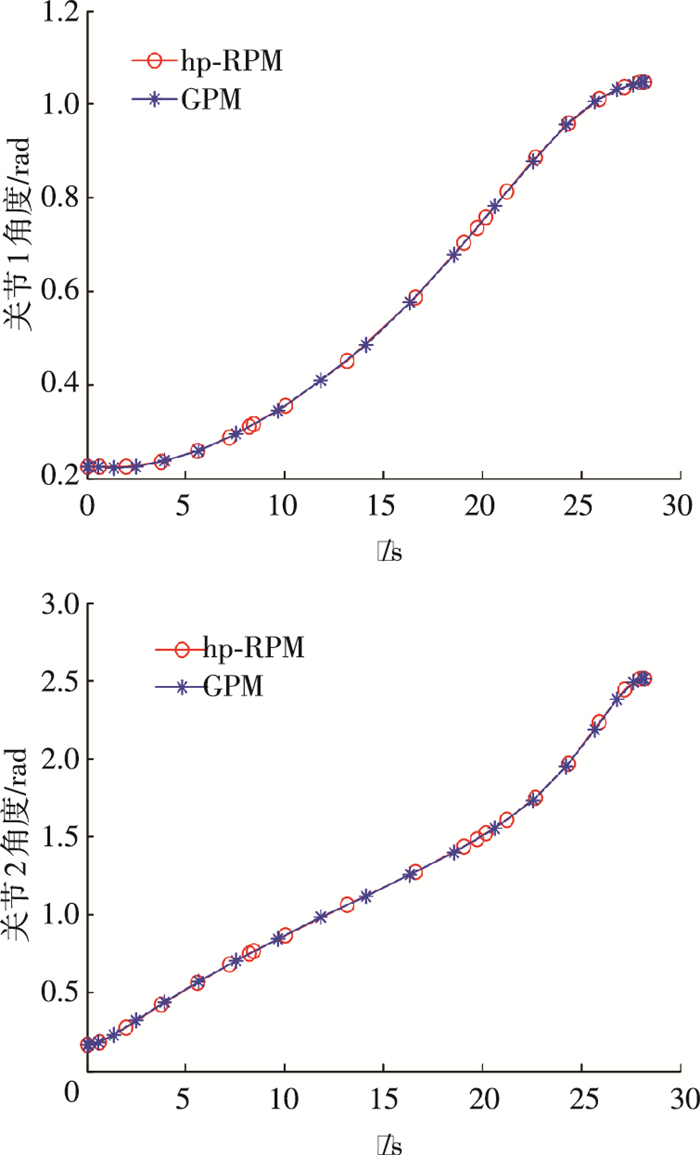
图 3 关节1、关节2角度变化曲线 Figure 3 Angle change curve of joint 1 and joint 2 |

|
图 4 关节1、关节2角速度变化曲线 Figure 4 Angle velocity change curve of joint 1 and joint 2 |
|
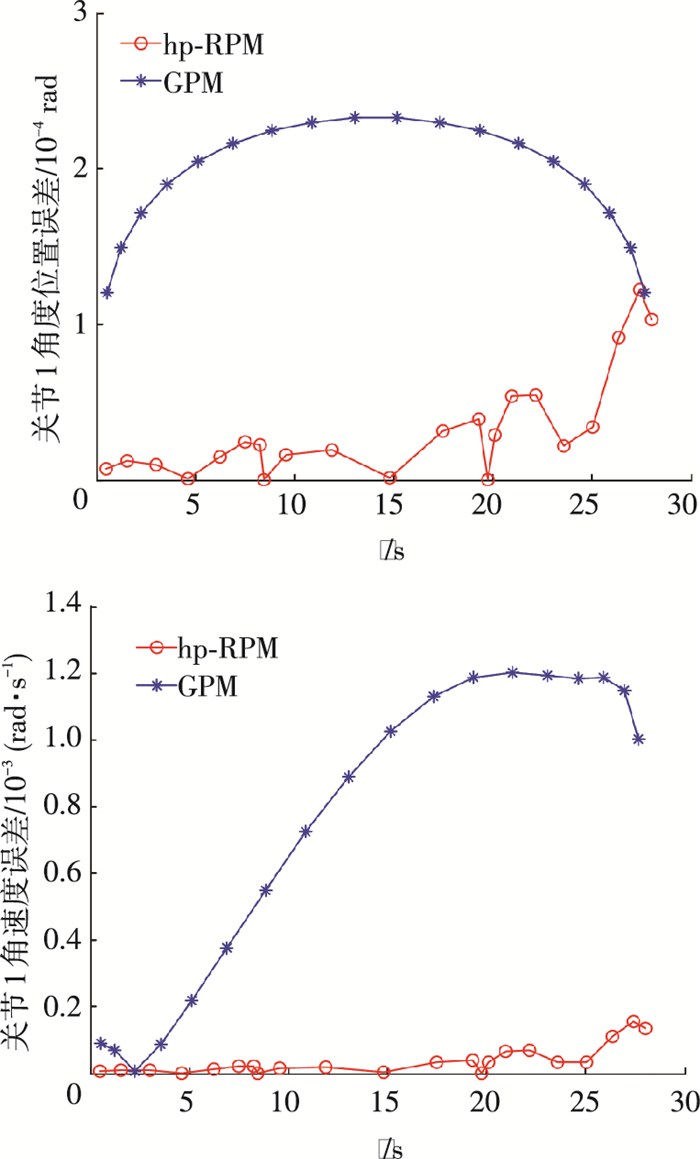
图 5 关节1位置和角速度误差曲线 Figure 5 Position and angular velocity error curve of joint 1 |
|
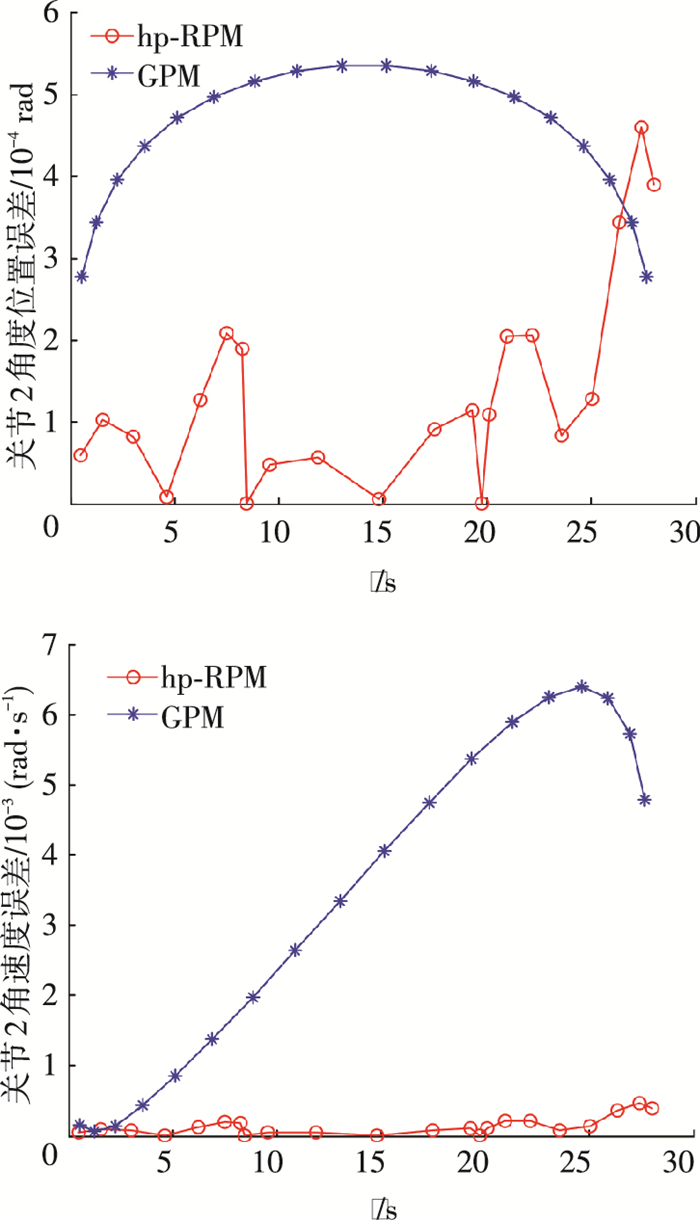
图 6 关节2位置和角速度误差曲线 Figure 6 Position and angular velocity error curve of joint 2 |
图 3、4为两关节角度、角速度的变化曲线,可以看出用两种方法进行轨迹规划时得到的两关节角度、角速度轨迹曲线在趋势和平滑度上是一致的.但在整个运动过程中两者的配点选取有很大差别,例如在7、20 s时,hp-RPM配点个数明显多于GPM,相对应的误差曲线在此时有明显变大的趋势,这也表明hp-RPM可以根据当前误差对子区间内节点个数进行重配置来减少误差.
图 5、6为位置误差和角速度误差曲线,可以看出hp-RPM在求解过程中精度明显高于GPM,在各个计算节点上的精度均满足要求;而用GPM进行求解时,出现精度不满足要求的情况.
观察图 5、6位置误差曲线,可知在即将到达目标位置时,利用hp-RPM规划出的位置误差曲线有较大的振荡趋势,在实际应用时会对FFSM正常工作产生一定的影响.产生这种现象的一个重要原因是在进行节点配置时,最后一个节点没有施加控制量,导致在即将到达目标位置时系统出现不受控情况.因此,在实际设计跟踪控制器时需要对末端振荡进行充分考虑,通过对末端状态的单独控制消除影响.
6 结论1) 针对普通Gauss伪谱法求解轨迹规划问题的缺点,本文提出了hp-RPM来解决FFSM系统点到点的轨迹规划问题.该方法通过求解每次迭代过程的误差,来决定下一次迭代时子区间及其节点个数.
2) 不同于传统的GPM,hp-RPM通过细分子区间避免了求解过程中出现高阶多项式,显著的减少了计算时间,从而解决了普通伪谱法中求解精度和计算效率之间的矛盾.在系统精度要求较高的情况下,hp-RPM通过计算每次迭代的误差来决定是否继续进行迭代计算,从而保证了精度要求,有着重要的实际意义.
3) 在两连杆FFSM系统中对hp-RPM方法进行了仿真验证,仿真结果表明hp-RPM在计算速度上明显高于GPM,并且在计算过程中hp-RPM通过改变区间及节点个数来提高计算精度.
| [1] |
SKAAR S B, RUOFF C F.
Teleoperation and Robotics in Space[M]. Reston, VA: American Institute of Aeronautics and Astronautics, 1994.
|
| [2] |
LILLY K W, BONAVENTURA C S. A generalized formulation for simulation of space robot constrained motion[C]//Proceedings of 1995 IEEE International Conference on Robotics and Automation. Nagoya, Japan: IEEE, 1995, 3: 2835-2840. DOI: 10.1109/ROBOT.1995.525685.
|
| [3] |
VAFA Z, DUBOWSKY S. The kinematics and dynamics of space manipulators: the virtual manipulator approach[J].
International Journal of Robotics Research, 1990, 9(4): 3-21.
DOI: 10.1177/027836499000900401 |
| [4] |
LIANG Bin, XU Yangsheng, BERGERMAN M. Mapping a space manipulator to a dynamically equivalent manipulator[J].
Journal of Dynamic Systems, Measurement, and Control, 1998, 120(1): 1-7.
DOI: 10.1115/1.2801316 |
| [5] |
GARG D, PATTERSON M, HAGER W W, et al. A unified framework for the numerical solution of optimal control problems using pseudospectral methods[J].
Automatica, 2010, 46(11): 1843-1851.
DOI: 10.1016/j.automatica.2010.06.048 |
| [6] |
HUANG Panfeng, XU Yangsheng. PSO-based time-optimal trajectory planning for space robot with dynamic constraints[C]//Proceedings of ROBIO'6 IEEE International Conference on Robotics and Biomimetics. Kunming, China: IEEE, 2006: 1402-1407. DOI: 10.1109/ROBIO.2006.340134.
|
| [7] |
李适. 空间机器人路径优化与鲁棒跟踪控制[D]. 哈尔滨: 哈尔滨工业大学, 2013.
LI Shi. Path optimization and robust tracking control for spacemanipulator[D]. Harbin: Harbin Institute of Technology. 2013. |
| [8] |
YOKOYAMA N, OCHI Y. Path planning algorithms for skid-to-turn unmanned aerial vehicles[J].
Journal of Guidance, Control, and Dynamics, 2009, 32(5): 1531-1543.
DOI: 10.2514/1.41822 |
| [9] |
DARBY C L, HAGER W W, RAO A V. An hp-adaptive pseudospectral method for solving optimal control problems[J].
Optimal Control Applications and Methods, 2011, 32(4): 476-502.
DOI: 10.1002/oca.957 |
| [10] |
COTTRILL G C, HARMON F G. Hybrid Gauss pseudospectral and generalized polynomial chaos algorithm to solve stochastic trajectory optimization problems[C]//AIAA Guidance, Navigation, and Control Conference. Portland, Oregon: AIAA, 2011: 6572. DOI: 10.2514/6.2011-6572.
|
| [11] |
HUNTINGTO G T, BENSON D, RAO A V. A comparison of accuracy and computational efficiency of three pseudospectral methods[J].
AIAA Guidance, Navigation, and Control Conference and Exhibit, 2007.
DOI: 10.2514/6.2007-6405 |
| [12] |
BENSON D A, HUNTINGTO G T, THORVALDSEN T P, et al. Direct trajectory optimization and costate estimation via an orthogonal collocation method[J].
Journal of Guidance Control and Dynamics, 2006, 29(6): 1435-1440.
DOI: 10.2514/1.20478 |
| [13] |
HAN Peng, SHAN Jiayuan, MENG Xiuyun. Re-entry trajectory optimization using an hp-adaptive Radau pseudospectralmethod[J].
Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2013, 227(10): 1623-1636.
DOI: 10.1177/0954410012461745 |
| [14] |
DUBOWSKY S, PAPADOPOULOS E. The kinematics, dynamics, and control of free-flying and free-floating space robotic systems[J].
IEEE Transactions on Robotics and Automation, 1993, 9(5): 531-543.
DOI: 10.1109/70.258046 |
| [15] |
SAHA S K. A unified approach to space robot kinematics[J].
IEEE Transactions on Robotics and Automation, 1996, 12(3): 401-405.
DOI: 10.1109/70.499822 |
| [16] |
HAN Peng, SHAN Jiayuan. Re-entry trajectory optimization using a multiple-interval Radau pseudospectral method[J].
Journal of Beijing Institute of Technology, 2013, 22(1): 20-27.
DOI: 10.3969/j.issn.1004-0579.2013.01.004 |
| [17] |
刘瑞帆, 于云峰, 闫斌斌. 基于改进hp自适应伪谱法的高超声速飞行器上升段轨迹规划[J].
西北工业大学学报, 2016, 34(5): 790-797.
LIU Ruifan, YU Yunfeng, YAN Binbin. Ascent phase trajectory optimization for hypersonic vehicle based on hp-adaptive pseudospectral method[J]. Journal of Northwestern Polytechnical University, 2016, 34(5): 790-797. DOI: 10.3969/j.issn.1000-2758.2016.05.008 |
| [18] |
GARG D, HAGER W W, RAO A V. Pseudospectral methods for solving infinite-horizon optimal control problems[J].
Automatica, 2011, 47(4): 829-837.
DOI: 10.1016/j.automatica.2011.01.085 |
| [19] |
ZHAO Yiming, TSIOTRAS P. Density functions for mesh refinement in numerical optimal control[J].
Journal of Guidance Control & Dynamics, 2015, 34(1): 271-277.
DOI: 10.2514/1.45852 |
 2018, Vol. 50
2018, Vol. 50



