多目标跟踪就是在杂波等干扰导致量测的不确定性条件下估计目标的数目、状态信息,并维持目标的航迹[1-2].传统的多目标跟踪方法是对每个目标分配一个独立的滤波器进行跟踪[3-4],然后再使用数据关联技术将每个滤波器与正确量测进行关联[5-6],从而得到各个目标独立的航迹关联信息, 但是由于计算量太大,实际应用中很难实现.基于随机有限集(RFS)的PHD滤波器将目标和量测均看作随机有限集[7-8],减少了数据关联的计算量,但却无法提供目标的航迹关联信息.
为解决PHD滤波的航迹关联问题,Panta等[9]提出了标记高斯混合PHD(GM-PHD)滤波算法,在有效估计多目标数目和状态的同时,还能关联出不同目标的航迹,但此方法在目标相互靠近时航迹关联的错误率很高.因此,Yazdian-Dehkordi等[10-12]提出了惩罚高斯项权值法(PGM-PHD),提高了邻近目标的跟踪精度.此后,Wang等[13]又提出了合作惩罚高斯项权值法(CPGM-PHD),通过修正同一目标的高斯项的权重,可以实现目标估计和量测的一对一对应关系,从而更好地区分并提取目标各自的航迹信息,但此方法在权值分配过程中仍存在一些问题.同时当遇到实际中杂波大等复杂环境时,所有量测均参与到目标的滤波跟踪,导致此方法的计算效率低,实时性差.
为了实现高效的PHD航迹关联算法,本文引入了量测划分的思想,降低了杂波量测对于计算时间的影响.同时,针对CPGM-PHD滤波器中的问题,采用了改进的高斯项权值分配方法,可以更精准地实现各目标的航迹关联.通过仿真实验对比,可以看出本算法在复杂跟踪环境中,无论是在计算效率还是跟踪精度上都有较好的表现.
1 PHD和GM-PHD滤波器由于多目标状态空间和量测空间都是高维的,贝叶斯滤波器在实际中难以实现.在泊松RFS假设的前提下,Mahler[6]用RFS的一阶矩,即概率假设密度(PHD,又称强度函数)近似多目标后验概率密度,得到PHD滤波器.
1.1 PHD滤波器假设vk(x)和vk|k-1(x)分别表示k时刻多目标后验概率密度pk(X)和预测概率密度pk|k-1 (X)的PHD函数.在满足如下假设的前提下:
假设1 每个目标的运动和产生的量测都是相互独立的.
假设2 杂波RFS是服从泊松分布的,且独立于由目标产生的量测RFS.
假设3 预测多目标状态RFS也是服从泊松分布的.
由此, 可以得到PHD滤波器的递推公式(本文暂不考虑衍生目标情况),即:
| $ {v_{k\left| {k - 1} \right.}}\left( \mathit{\boldsymbol{x}} \right) = \int {{p_{S,k}}\left( \zeta \right){f_{k\left| {k - 1} \right.}}\left( {\mathit{\boldsymbol{x}}\left| \zeta \right.} \right){v_{k - 1}}\left( \zeta \right){\rm{d}}\zeta } + {\gamma _k}\left( \mathit{\boldsymbol{x}} \right), $ |
| $ \begin{array}{l} {v_k}\left( \mathit{\boldsymbol{x}} \right) = \left[ {1 - {p_{D,k}}\left( \mathit{\boldsymbol{x}} \right)} \right]{v_{k\left| {k - 1} \right.}}\left( \mathit{\boldsymbol{x}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{z \in {Z_k}} {\frac{{{p_{D,k}}\left( \mathit{\boldsymbol{x}} \right)g\left( {\mathit{\boldsymbol{z}}\left| \mathit{\boldsymbol{x}} \right.} \right){v_{k\left| {k - 1} \right.}}\left( \mathit{\boldsymbol{x}} \right)}}{{{\kappa _k}\left( z \right) + \int {{p_{D,k}}\left( \zeta \right)g\left( {\mathit{\boldsymbol{z}}\left| \zeta \right.} \right){v_{k\left| {k - 1} \right.}}\left( \zeta \right){\rm{d}}\zeta } }}} . \end{array} $ |
式中:pS, k(ζ)、pD, k(ζ)分别为目标状态ζ在k时刻的存活概率和检测概率;fk|k-1 (·)为k时刻单目标状态转移概率密度函数;γk(·)为k时刻新生目标随机集Γk的PHD;g(·)为k时刻单传感器单目标似然函数;κk(·)为k时刻杂波随机集Υk的PHD[14].
1.2 GM-PHD滤波器GM-PHD滤波利用多个高斯项的加权和近似目标强度函数,并随时间变化递推实现数目变化的多目标跟踪[15],是PHD滤波器在线性高斯条件下的闭合解,因此需要满足以下假设.
假设4 目标的状态模型和量测模型都是线性高斯的.
假设5 目标的存活概率和检测概率是相互独立且与状态无关.
假设6 新生目标强度函数可描述为若干高斯混合加权和形式.
由此,可以得到GM-PHD的递推公式,先验强度函数表示为高斯加权和的形式为
| $ {v_{k - 1}}\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^{{J_{k - 1}}} {w_{k - 1}^iN\left( {\mathit{\boldsymbol{x}};\mathit{\boldsymbol{m}}_{k - 1}^i,\mathit{\boldsymbol{P}}_{k - 1}^i} \right)} , $ |
式中wk-1i为在时刻k-1高斯项的权值.于是,k时刻的预测强度函数可表示为
| $ {v_{k\left| {k - 1} \right.}}\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^{{J_{k\left| {k - 1} \right.}}} {w_{k\left| {k - 1} \right.}^iN\left( {\mathit{\boldsymbol{x}};\mathit{\boldsymbol{m}}_{k\left| {k - 1} \right.}^i,\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}^i} \right)} . $ |
当在时刻k得到的量测集Zk,则此时多目标的后验强度函数可表示为
| $ {v_k}\left( \mathit{\boldsymbol{x}} \right) = \left( {1 - {p_{D,k}}} \right){v_{k\left| {k - 1} \right.}}\left( \mathit{\boldsymbol{x}} \right) + \sum\limits_{z \in {Z_k}} {\sum\limits_{i = 1}^{{J_{k\left| {k - 1} \right.}}} {w_k^i\left( \mathit{\boldsymbol{z}} \right)N\left( {\mathit{\boldsymbol{x}};\mathit{\boldsymbol{m}}_{k\left| k \right.}^i,\mathit{\boldsymbol{P}}_{k\left| k \right.}^i} \right)} } , $ |
式中wki(z)为第i个高斯项的权值,计算公式为
| $ w_k^i\left( z \right) = \frac{{{p_{D,k}}w_{k\left| {k - 1} \right.}^ig\left( {\mathit{\boldsymbol{z}}\left| {{\mathit{\boldsymbol{x}}^i}} \right.} \right)}}{{{\kappa _k}\left( \mathit{\boldsymbol{z}} \right) + {p_{D,k}}\sum\limits_{i = 1}^{{J_{k\left| {k - 1} \right.}}} {w_{k\left| {k - 1} \right.}^ih\left( {\mathit{\boldsymbol{z}}\left| {{\mathit{\boldsymbol{x}}^i}} \right.} \right)} }}. $ |
针对GM-PHD滤波算法的问题,本文采用高效的分类检索的椭球门限方法将量测集有效划分,同时针对CPGM-PHD算法权值惩罚过程中出现的相同标记目标高斯项惩罚遗漏的情况加以改进,并且在高斯项合并过程中, 结合目标标记减少目标状态的提取误差,从而提高邻近目标的跟踪精度.
2.1 分类检索的椭球门限量测划分方法PHD滤波的量测划分是将每一步得到的量测集划分成已存在目标,新生目标以及杂波的量测等3个部分,采用分类检索的椭球门限方法,可以有效地节省在量测划分中的算法复杂度.其主要思路为:首先将量测集,按照空间维度做分类检索,提取出量测集的每一维度的信息; 然后通过重叠坐标系的建立和判断,得到在此重叠系坐标下的量测信息,此过程可以有效地通过目标预测和量测噪声的协方差信息,筛选进入椭球门限判断的量测数目,从而有效地降低量测划分的算法复杂度.
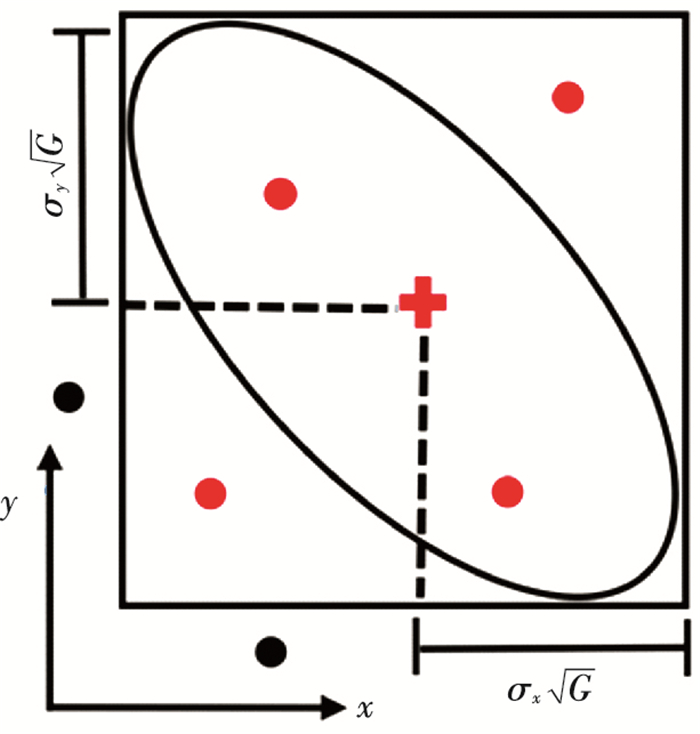
考虑一个椭球相切坐标系,其坐标轴相切于椭球区域[16-17],椭球区域的中心是预测目标的位置,则每一个量测落在此坐标系中是落在椭球门限里的必要条件[18],如图 1所示.
|
图 1 椭球门限相切坐标系 Figure 1 The circumscribing coordinate of the ellipsoidal gate |
此坐标系的坐标轴大小由新息协方差矩阵S和椭球门限值
| $ \mathit{\boldsymbol{S}} = \mathit{\boldsymbol{\hat C}} + \mathit{\boldsymbol{C}} = \mathit{\boldsymbol{HP}}{\mathit{\boldsymbol{H}}^{\rm{T}}} + \mathit{\boldsymbol{R}}, $ |
| $ \mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {\sigma _{S,1}^2}& \cdots &{}\\ \vdots&\ddots&\vdots \\ {}& \cdots &{\sigma _{S,{n_{\dim }}}^2} \end{array}} \right], $ |
| $ G = - 2\ln \left( {1 - {p_G}} \right), $ |
| $ {\Delta _d}: = \left| {{z_d} - {{\hat z}_d}} \right|, $ |
| $ \hat z = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{m}}_{k\left| {k - 1} \right.}}, $ |
| $ {\Delta _d} < \sqrt G \cdot {\sigma _{S,d}},d \in \left\{ {1, \cdots ,{n_{\dim }}} \right\}. $ |
在大多数多目标跟踪情况中,无论是目标预测的协方差还是量测噪声的协方差相对较小,因此由协方差构成的重叠坐标系区域大小明显小于整体的跟踪区域.针对在重叠坐标系区域内的量测点再做椭球门限判断,将大幅减少计算时间.分类检索的椭球门限划分法就是先根据量测和预测目标的协方差对所有量测做初步的筛选,使得进入椭球门限判断的量测数目明显减少,再利用经典的椭球门限方法对量测进行有效划分.
首先,将量测集按照维度分类,然后根据预测的目标位置确定检索区域,对所有实际得到的量测点进行检索,如图 2所示.如果实际量测的位置小于预测目标位置,则需要判断量测坐标系的上限是否大于预测坐标系的下限为
| $ {z_d} + {\sigma _d}\sqrt G > {{\hat z}_d} - {{\hat \sigma }_d}\sqrt G , $ |

|
图 2 量测检索判断 Figure 2 The sort and decision of measurement |
或者如果实际量测的位置大于预测量测位置
| $ {z_d} - {\sigma _d}\sqrt G < {{\hat z}_d} + {{\hat \sigma }_d}\sqrt G . $ |
从预测目标位置出发去考虑此判断条件,可以得到下式,从而依次判断每一个实际得到的量测点是否满足此条件
| $ \left| {{z_d} - {{\hat z}_d}} \right| < \left[ {\mathop {\max }\limits_i \left( {{\sigma _{i,d}}} \right) + {{\hat \sigma }_d}} \right]\sqrt G . $ |
按照每一维度信息进行分类检索,每一维度不符合判断标准的量测就直接去除,再进入下一维度检索判断,直到所有维度都在重叠坐标系区域的量测点才是需要进行椭球门限判断的量测.
椭球门限的判断准则如下
| $ \mathit{\boldsymbol{Z}}\left( {k,G} \right) = \left\{ {\mathit{\boldsymbol{z}}:\left( {\mathit{\boldsymbol{z}} - {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{m}}_{k\left| {k - 1} \right.}}} \right)\mathit{\boldsymbol{S}}_k^{ - 1}\left( {\mathit{\boldsymbol{z}} - {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{m}}_{k\left| {k - 1} \right.}}} \right) \le G} \right\}. $ |
在每一时刻的量测集中,首先将量测分为已存在目标的量测和剩余的量测为:
| $ {D_{S,k}}\left( \mathit{\boldsymbol{z}} \right) = \left\{ {d_{S,k}^1\left( \mathit{\boldsymbol{z}} \right), \cdots ,d_{S,k}^i\left( \mathit{\boldsymbol{z}} \right), \cdots ,d_{S,k}^{{J_{S,k\left| {k - 1} \right.}}}\left( \mathit{\boldsymbol{z}} \right)} \right\}, $ |
| $ d_{S,k}^i\left( \mathit{\boldsymbol{z}} \right) = {\left( {\mathit{\boldsymbol{z}} - {\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{m}}_{\mathit{\boldsymbol{S}},k\left| {k - 1} \right.}^i} \right)^{\rm{T}}}{\left( {\mathit{\boldsymbol{S}}_{S,k}^i} \right)^{ - 1}}\left( {\mathit{\boldsymbol{z}} - {\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{m}}_{\mathit{\boldsymbol{S}},k\left| {k - 1} \right.}^i} \right), $ |
| $ \mathit{\boldsymbol{S}}_{S,k}^i = {\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{P}}_{S,k\left| {k - 1} \right.}^i\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\mathit{\boldsymbol{R}}_k}, $ |
| $ {\mathit{\boldsymbol{Z}}_{S,k}} = \left\{ {\mathit{\boldsymbol{z}}\left| {{D_{S,k}}\left( \mathit{\boldsymbol{z}} \right)} \right. \le G,\mathit{\boldsymbol{z}} \in {\mathit{\boldsymbol{Z}}_k}} \right\}, $ |
| $ {\mathit{\boldsymbol{Z}}_{re,k}} = {\mathit{\boldsymbol{Z}}_k}\backslash {\mathit{\boldsymbol{Z}}_{S,k}}. $ |
而剩余的量测集包含了新生目标的量测和杂波量测为:
| $ {D_{\gamma ,k}}\left( \mathit{\boldsymbol{z}} \right) = \left\{ {d_{\gamma ,k}^1\left( \mathit{\boldsymbol{z}} \right), \cdots ,d_{\gamma ,k}^j\left( \mathit{\boldsymbol{z}} \right), \cdots ,d_{\gamma ,k}^{{J_{\gamma ,k\left| {k - 1} \right.}}}\left( \mathit{\boldsymbol{z}} \right)} \right\}, $ |
| $ d_{\gamma ,k}^i\left( \mathit{\boldsymbol{z}} \right) = {\left( {\mathit{\boldsymbol{z}} - {\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{m}}_{\gamma ,k - 1}^j} \right)^{\rm{T}}}{\left( {\mathit{\boldsymbol{S}}_{\gamma ,k}^j} \right)^{ - 1}}\left( {\mathit{\boldsymbol{z}} - {\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{m}}_{\gamma ,k - 1}^j} \right), $ |
| $ \mathit{\boldsymbol{S}}_{\gamma ,k}^j = {\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{P}}_{\gamma ,k - 1}^j\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\mathit{\boldsymbol{R}}_k}, $ |
| $ {\mathit{\boldsymbol{Z}}_{\gamma ,k}} = \left\{ {\mathit{\boldsymbol{z}}\left| {{D_{\gamma ,k}}\left( \mathit{\boldsymbol{z}} \right)} \right. \le G,\mathit{\boldsymbol{z}} \in {\mathit{\boldsymbol{Z}}_{re,k}}} \right\}. $ |
再根据新生目标的预测值将剩余量测进行划分得到新生目标的量测和杂波量测.
2.2 权值重新分配的GM-PHD航迹关联方法在多目标跟踪问题中,假定量测和目标是一对一的对应关系,因此同一个目标将不能同时把多个量测作为它的目标估计进行输出.然而在GM-PHD滤波器中,当多个量测距离一个目标较近,而距离其他目标较远时就会违背这一假设[19].CPGM-PHD滤波通过修正同一目标的高斯分量的权重,可以实现目标估计和量测的一对一关系.然而,在其权重分配过程中,忽略了同一标记可能有不同临时目标的情况,这样会出现遗漏目标权值没有正确分配的错误,导致在目标靠近情况下,跟踪精度的下降.
假定在k时刻的更新步骤中,所有预测目标的权值构成了权值矩阵W,归一化的权值构成了归一化的权值矩阵W,矩阵元素 < m, n>代表了目标xkm被量测zkn更新后的权值.假设wk, updatedm, n、wk, updatedm, n分别为xkm, n的权值及归一化权值,则
| $ w_{k,{\rm{updated}}}^{m,n} = {p_{D,k}}w_{k\left| {k - 1} \right.}^mN\left( {\mathit{\boldsymbol{z}}_k^n;\eta _{k\left| {k - 1} \right.}^m;S_k^m} \right), $ |
| $ \bar w_{k,{\rm{updated}}}^{m,n} = \frac{{w_{k,{\rm{updated}}}^{m,n}}}{{{\kappa _k}\left( {\mathit{\boldsymbol{z}}_k^n} \right) + \sum\limits_{i = 1}^{{J_{k\left| {k - 1} \right.}}} {w_{k,{\rm{updated}}}^{i,n}} }}. $ |
当多个目标相互靠近时,若多个量测更靠近某一目标时,归一化权值矩阵中目标对应的多个高斯项的权值之和将大于1,此时这个目标的各个高斯项的权值需要被重新分配.
在CPGM-PHD滤波方法中,先找出权值最大高斯项的标记目标,若满足其所有高斯项权值之和大于1的条件,将对权值矩阵W中所有与权值最大目标标记相同的其他高斯项的权值进行惩罚,再对惩罚后的权值重新归一化.然而这种做法忽略了一种情况:若同一目标高斯项权值之和小于1,但是同一标记的不同预测目标的高斯项权值之和大于1.按照原来的方法这些高斯项权值就不会被重新分配,会遗漏这些目标.因此需要对这些遗漏的目标进行修复,即对有相同标记的所有高斯项权值进行惩罚.
首先,在归一化权值矩阵W中找到权值最大的高斯分量为
| $ \left\langle {{m^ * },{n^ * }} \right\rangle = \mathop {{\mathop{\rm argmax}\nolimits} }\limits_{m \in I,\forall n = 1:{N_k}} \left( {\bar w_k^{m,n}} \right), $ |
式中Nk为所有预测目标的高斯项个数.
然后,改进的权值重新分配方法将在目前的归一化权值矩阵W中,找到与最大权值的高斯项有相同标记的所有高斯项,并计算它们的权值之和为:
| $ \mathit{\Theta } = \left\{ {i\left| {l_{k - 1}^i} \right. = l_{k - 1}^{{m^ * }},i \in I} \right\}, $ |
| $ \mu = \sum\limits_{n = 1}^{{N_k}} {\bar w_k^{{m^ * },n}} ,\forall {m^ * } \in \mathit{\Theta }. $ |
如果所选目标的高斯项权值之和大于1,这个目标的所有高斯项权值按照下式重新分配:
| $ \lambda = \left( {1 - \frac{\mu }{\sigma }} \right) \times \left( {1 - \bar w_k^{{m^ * },{n^ * }}} \right), $ |
| $ w_{k,{\rm{updated}}}^{m,n} = \left\{ \begin{array}{l} w_k^{m,n}\left\{ \begin{array}{l} n \ne {n^ * },\\ m \ne {m^ * },l_k^{m,n} \ne l_k^{{m^ * },{n^ * }},\forall n = 1:{N_k},n \ne {n^ * }; \end{array} \right.\\ \lambda \times w_k^{m,n}\left\{ \begin{array}{l} m = {m^ * },\forall n = 1:{N_k},n \ne {n^ * };\\ m \ne {m^ * },l_k^{m,n} = l_k^{{m^ * },{n^ * }},\forall n = 1:{N_k},n \ne {n^ * }. \end{array} \right. \end{array} \right. $ |
| $ \bar w_{k,{\rm{updated}}}^{m,n} = \frac{{w_{k,{\rm{updated}}}^{m,n}}}{{{\mathit{\boldsymbol{\kappa }}_k}\left( {\mathit{\boldsymbol{z}}_k^n} \right) + \sum\limits_{i = 1}^{{J_{k\left| {k - 1} \right.}}} {w_{k,{\rm{updated}}}^{i,n}} }}, $ |
式中σ为归一化权值矩阵W当前目标的高斯项个数.重复上述计算过程,直到当前标记目标的所有高斯项权值之和均小于1.
最后,利用此方法继续检测其他目标,直到所有目标的高斯项归一化权值之和都小于1,这表明每一个预测目标都按照量测一对一的对应关系进行跟踪滤波,从而减小了相邻目标的状态提取误差,提高了邻近目标的跟踪精度.
2.3 MP-CPGM-PHD算法的实现步骤本文提出的基于量测划分的权值重新分配的GM-PHD改进算法(MP-CPGM-PHD),其算法步骤可以归纳如下.
步骤1 初始化.假设初始时刻目标强度函数v0(x)是J0个高斯项的混合形式,对每个高斯项分配一个独特的标记l0, 初始强度函数和目标标记集为:
| $ \begin{array}{*{20}{c}} {{v_0}\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^{{J_0}} {w_0^iN\left( {\mathit{\boldsymbol{x}};\mathit{\boldsymbol{m}}_0^i,\mathit{\boldsymbol{P}}_0^i} \right)} ,}\\ {{T_0} = \left\{ {l_0^1, \cdots ,l_0^{{J_0}}} \right\}.} \end{array} $ |
步骤2 预测步.对k时刻的已存在目标和新生目标进行预测.k时刻预测的强度函数也是高斯和形式,则预测的高斯项将与k-1时刻的标记相同,新生目标的高斯项将分配新的标记,则预测目标强度函数和目标标记集为:
| $ \begin{array}{l} {v_{k\left| {k - 1} \right.}}\left( \mathit{\boldsymbol{x}} \right) = {p_{S,k}}\sum\limits_{i = 1}^{{J_{S,k\left| {k - 1} \right.}}} {w_{k - 1}^iN\left( {\mathit{\boldsymbol{x}};\mathit{\boldsymbol{m}}_{S,k\left| {k - 1} \right.}^i,\mathit{\boldsymbol{P}}_{S,k\left| {k - 1} \right.}^i} \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^{{J_{\gamma ,k}}} {w_{\gamma ,k - 1}^jN\left( {\mathit{\boldsymbol{x}};\mathit{\boldsymbol{m}}_{\gamma ,k - 1}^j,\mathit{\boldsymbol{P}}_{\gamma ,k - 1}^j} \right)} , \end{array} $ |
| $ {T_{k\left| {k - 1} \right.}} = {T_{k - 1}} \cup \left\{ {l_{\gamma ,k}^1, \cdots ,l_{\gamma ,k}^j, \cdots ,l_{\gamma ,k}^{{J_{\gamma ,k}}}} \right\},j = \left[ {1,{J_{\gamma ,k}}} \right]. $ |
步骤3 更新步.对k时刻得到的量测集Zk,按照分类检索的椭球门限量测划分方法将量测集划分为ZS, k是已存在目标量测集,Zγ, k是新生目标量测集.更新后的存活目标和新生目标的强度函数为:
| $ {v_{k\left| k \right.}}\left( \mathit{\boldsymbol{x}} \right) = {v_{S,k\left| k \right.}}\left( \mathit{\boldsymbol{x}} \right) + {v_{\gamma ,k\left| k \right.}}\left( \mathit{\boldsymbol{x}} \right), $ |
| $ \begin{array}{l} {v_{S,k\left| k \right.}}\left( \mathit{\boldsymbol{x}} \right) = \left( {1 - {p_{D,k}}} \right){v_{S,k\left| {k - 1} \right.}}\left( \mathit{\boldsymbol{x}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{z \in {Z_{S,k}}} {\sum\limits_{i = 1}^{{J_{S,k\left| {k - 1} \right.}}} {w_{S,k\left| k \right.}^i\left( \mathit{\boldsymbol{z}} \right)N\left( {\mathit{\boldsymbol{x}};\mathit{\boldsymbol{m}}_{S,k\left| k \right.}^i,\mathit{\boldsymbol{P}}_{S,k\left| k \right.}^i} \right)} } , \end{array} $ |
| $ \begin{array}{l} {v_{\gamma ,k\left| k \right.}}\left( \mathit{\boldsymbol{x}} \right) = \left( {1 - {p_{D,k}}} \right){\gamma _k}\left( \mathit{\boldsymbol{x}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{z \in {Z_{\gamma ,k}}} {\sum\limits_{j = 1}^{{J_{\gamma ,k}}} {w_{S,k\left| k \right.}^j\left( \mathit{\boldsymbol{z}} \right)N\left( {\mathit{\boldsymbol{x}};\mathit{\boldsymbol{m}}_{\gamma ,k\left| k \right.}^j,\mathit{\boldsymbol{P}}_{\gamma ,k\left| k \right.}^j} \right)} } , \end{array} $ |
| $ \begin{array}{l} {w_{k\left| k \right.}}\left( \mathit{\boldsymbol{z}} \right) = \\ \;\;\;\frac{{{p_{D,k}}{w_{k\left| {k - 1} \right.}}N\left( {\mathit{\boldsymbol{z}};{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{m}}_{k\left| {k - 1} \right.}},{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}}\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\mathit{\boldsymbol{R}}_k}} \right)}}{{{\mathit{\boldsymbol{\kappa }}_k}\left( \mathit{\boldsymbol{z}} \right) + {p_{D,k}}\sum\limits_{\varphi = 1}^\varepsilon {w_{k\left| {k - 1} \right.}^\varphi N\left( {\mathit{\boldsymbol{z}};{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{m}}_{k\left| {k - 1} \right.}},{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}}\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\mathit{\boldsymbol{R}}_k}} \right)} }}, \end{array} $ |
| $ {\mathit{\boldsymbol{m}}_{k\left| k \right.}}\left( \mathit{\boldsymbol{z}} \right) = {\mathit{\boldsymbol{m}}_{k\left| {k - 1} \right.}} + {\mathit{\boldsymbol{K}}_k}\left( {\mathit{\boldsymbol{z}} - {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{m}}_{k\left| {k - 1} \right.}}} \right), $ |
| $ {\mathit{\boldsymbol{P}}_{k\left| k \right.}} = \left[ {I - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{H}}_k}} \right]{\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}}, $ |
| $ {\mathit{\boldsymbol{K}}_k} = {\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}}\mathit{\boldsymbol{H}}_k^{\rm{T}}{\left( {{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}}\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\mathit{\boldsymbol{R}}_k}} \right)^{ - 1}}. $ |
式中:Kk为在k时刻的卡尔曼增益矩阵,参数ε∈{JS, k|k-1, Jγ, k}.在更新步中,由同一个高斯项更新的多个高斯项将会与预测时刻的标记相同,则更新后的目标标记集为
| $ \begin{array}{l} {T_k} = {T_{k\left| {k - 1} \right.}} \cup \left\{ {T_{k - 1}^{{z_1}}, \cdots ,T_{k - 1}^z\left| {{\mathit{\boldsymbol{Z}}_{S,k}}} \right|} \right\} \cup \\ \;\;\;\;\;\;\left\{ {{{\left\{ {l_{\gamma ,k}^1, \cdots ,l_{\gamma ,k}^{{J_{\gamma ,k}}}} \right\}}^{{z_1}}}, \cdots ,{{\left\{ {l_{\gamma ,k}^1, \cdots ,l_{\gamma ,k}^{{J_{\gamma ,k}}}} \right\}}^z}\left| {{\mathit{\boldsymbol{Z}}_{\gamma ,k}}} \right|} \right\}. \end{array} $ |
步骤4 高斯项的合并与删减.在原始的GM-PHD算法的高斯项合并删减过程中并没有考虑距离相近目标的情况.当式(2)中距离差Δ不大于合并阈值U时,多个高斯项将会合并成一个高斯项.而在目标相互靠近的情况下,不同目标高斯项的距离很容易小于合并门限,此时如果其他目标中权值高的高斯项被合并,就会导致目标状态估计的错误,使得跟踪精度降低.改进的高斯项合并删减方法利用标记高斯项和高斯项权值比例的思路,可以保证不同目标的大权值高斯分量不会被合并.
| $ j = \mathop {{\mathop{\rm argmax}\nolimits} }\limits_{i \in I} \left( {w_k^i} \right),I = \left\{ {i:1 \le i \le {J_k},w_k^i > {T_{th}}} \right\}, $ | (1) |
| $ \Delta = {\left( {\mathit{\boldsymbol{m}}_k^i - \mathit{\boldsymbol{m}}_k^j} \right)^{\rm{T}}}{\left( {\mathit{\boldsymbol{P}}_k^i} \right)^{ - 1}}\left( {\mathit{\boldsymbol{m}}_k^i - \mathit{\boldsymbol{m}}_k^j} \right),i \in I, $ | (2) |
| $ \mathit{\Xi } = \left\{ \begin{array}{l} \left\{ i \right\},\Delta \le U,w_k^i < r,w_k^j < r,i,j \in I;\\ \;\;\;\;\;\Delta \le U,l_k^i = l_k^j,i,j \in I;\\ \left\{ j \right\},\Delta > U. \end{array} \right. $ | (3) |
式中:U为可合并权重阈值; r为可合并权重上限阈值,一般可取值在0~0.5之间, 即:
| $ {{\tilde w}_k} = \sum\limits_{i \in \mathit{\Xi }} {w_k^i} , $ |
| $ {{\mathit{\boldsymbol{\tilde m}}}_k} = \frac{1}{{{{\tilde w}_k}}}\sum\limits_{i \in \mathit{\Xi }} {w_k^i\mathit{\boldsymbol{m}}_k^i} , $ |
| $ {{\mathit{\boldsymbol{\tilde P}}}_k} = \frac{1}{{{{\tilde w}_k}}}\sum\limits_{i \in \mathit{\Xi }} {w_k^i\left[ {\mathit{\boldsymbol{P}}_k^i + \left( {{{\mathit{\boldsymbol{\tilde m}}}_k} - \mathit{\boldsymbol{m}}_k^i} \right){{\left( {{{\mathit{\boldsymbol{\tilde m}}}_k} - \mathit{\boldsymbol{m}}_k^i} \right)}^{\rm{T}}}} \right]} . $ |
步骤5 目标状态提取.当高斯项合并删减步骤结束后的强度函数如下
| $ {v_k}\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^{{{\tilde J}_k}} {\tilde w_k^iN\left( {\mathit{\boldsymbol{x}};\mathit{\boldsymbol{\tilde m}}_k^i,\mathit{\boldsymbol{\tilde P}}_k^i} \right)} , $ |
可以得到每个目标的状态提取和相应的标记为:
| $ \mathop {{\mathit{\boldsymbol{X}}_k}}\limits^ \gg = \left\{ {\mathit{\boldsymbol{\tilde m}}_k^i;\tilde w_k^i > {w_{Th}},i = 1, \cdots ,{{\tilde J}_k}} \right\}, $ |
| $ \mathop {{\mathit{\boldsymbol{T}}_k}}\limits^ \gg = \left\{ {l_k^i;\tilde w_k^i > {w_{Th}},i = 1, \cdots ,{{\tilde J}_k}} \right\}. $ |
本文对所提的MP-CPGM-PHD滤波算法的有效性进行验证.选取一多目标跟踪问题进行仿真,为了不失多目标航迹关联问题的一般性,即有效仿真实际跟踪问题中多目标相互交叉的情况,假设在二维监控区域-500, 500 m× -500, 500 m内共有4个目标,仿真时间为100 s,目标状态向量定义为xk=[x1, k, x2, k, x3, k, x4, k]T,其中:[x1, k, x2, k]T为目标位置信息,[x3, k, x4, k]T为目标速度信息.目标运动方程和传感器量测方程都满足线性高斯条件:
| $ {\mathit{\boldsymbol{x}}_k} = \left[ {\begin{array}{*{20}{c}} 1&0&T&0\\ 0&1&0&T\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]{\mathit{\boldsymbol{x}}_{k - 1}} + \left[ {\begin{array}{*{20}{c}} {{T^2}/2}&0\\ 0&{{T^2}/2}\\ T&0\\ 0&T \end{array}} \right]{\mathit{\boldsymbol{w}}_k}, $ |
| $ {\mathit{\boldsymbol{z}}_k} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&1&0&0 \end{array}} \right]{\mathit{\boldsymbol{x}}_k} + {\mathit{\boldsymbol{v}}_k}. $ |
式中:采样周期T=1 s,过程噪声和量测噪声都是零均值的高斯白噪声,其协方差矩阵分别为Q =diag([0.4, 0.4])和R=diag([400, 400]).杂波均匀分布在整个观测区域内,杂波强度服从泊松分布λc=15×10-4,目标的存活概率pS, k和检测概率pD, k分别为0.99、0.98[13].本文中设定的可合并权重阈值设为U=4,可合并权重上限阈值设为r=0.3,高斯项修剪阈值T=10-5, 最大高斯项个数Jmax=100.本文使用的椭球门限中,量测落入确认区域概率为pG=0.99.目标的初始状态见表 1.
| 表 1 目标初始状态 Table 1 Initial values of target state |
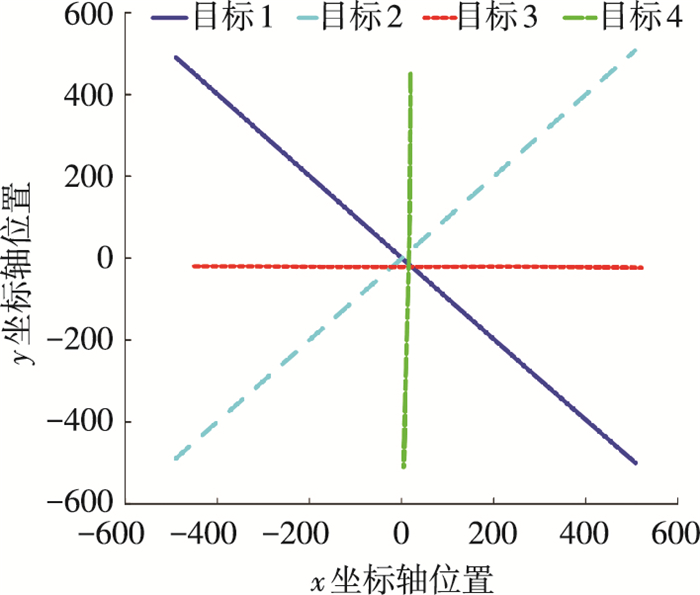
图 3显示了目标的真实运动轨迹.在相同的仿真场景下,通过对比以下3种滤波算法的仿真结果来验证本文算法的优势:传统的标记GM-PHD滤波算法[9]、CPGM-PHD滤波算法[13]和本文提出的MP-CPGM-PHD滤波算法.
|
图 3 目标真实运动轨迹 Figure 3 True trajectories of 4 targets |
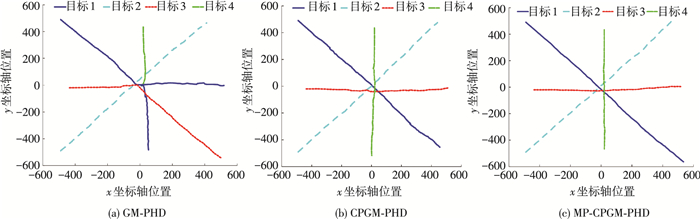
图 4显示了3种滤波算法的估计航迹图,从图 4(a)中可以明显看出,标记的GM-PHD算法在目标位置相互靠近时会出现目标航迹识别的错误,目标航迹标记1就错误地分配给航迹3和4,导致了航迹关联的错误;而在图 4(b)中CPGM-PHD滤波算法通过对于相邻目标权值分配的调整,多目标相互靠近时的航迹区分已经相对明显,但目标靠近区域的误差明显还是较大,而从图 4(c)中可以看出,本文提出的算法能更加精准地估计区分多目标航迹,尤其在多目标航迹相互交叉的部分,能够更有效地区分航迹标识,从而得到准确的区分航迹信息,由此提高了航迹关联的正确率.
|
图 4 3种算法的跟踪航迹对比 Figure 4 Comparison of estimated tracks between 3 algorithms |
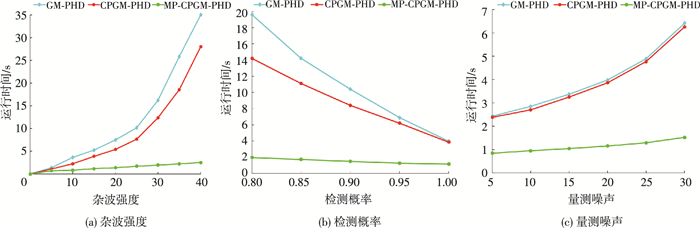
针对本文提出的分类检索的椭球门限的量测划分方法对于算法计算效率的提升进行验证,图 5对比了3种滤波算法在不同杂波强度、检测概率、量测噪声下的运行时间.
|
图 5 不同跟踪条件下的3种滤波算法运行时间对比 Figure 5 Comparison of the 3 filter algorithms running time under different tracking conditions |
从图 5(a)中可以看出,随着杂波强度的不断增大,GM-PHD算法和CPGM-PHD算法的运行时间增加地非常剧烈,这是由于对于每一个量测都要对预测目标进行滤波更新,增加了算法的计算负担,在高杂波强度的情况下,算法的实时性很差.而本算法由于引入了有效的量测划分方法,在每一步都对于目标跟踪滤波的量测加以筛选,避免了无用的杂波量测对于计算负担的影响,在运行时间上节省了很多,在高杂波强度下依然能很好地保持算法的实时性.从图 5(b)、(c)中可以看出,随着检测概率的降低和量测噪声的增大,3种算法的运行时间都有明显的增加,而MP-CPGM-PHD算法的运行时间一直处在相对最低的水平,可见此算法在检测概率较低和量测噪声较大的环境下依然可以有效提高航迹关联算法的计算效率.
3.2.3 跟踪精度针对本文提出的权值重新配的GM-PHD航迹关联方法对于跟踪精度的提升进行验证.为了评价算法的多目标跟踪效果,这里采用最优子模式分配(optimal subpattern assignment,OSPA)距离对多目标跟踪估计性能进行评价.具体参数设置如下:截断距离c=100,阶数p=2[20]以及目标平均估计误差(mean number of targets estimation error,NTE)作为跟踪性能的评价指标.本仿真实验均进行了50次蒙特卡洛仿真得到3种滤波算法的OSPA距离和NTE距离.
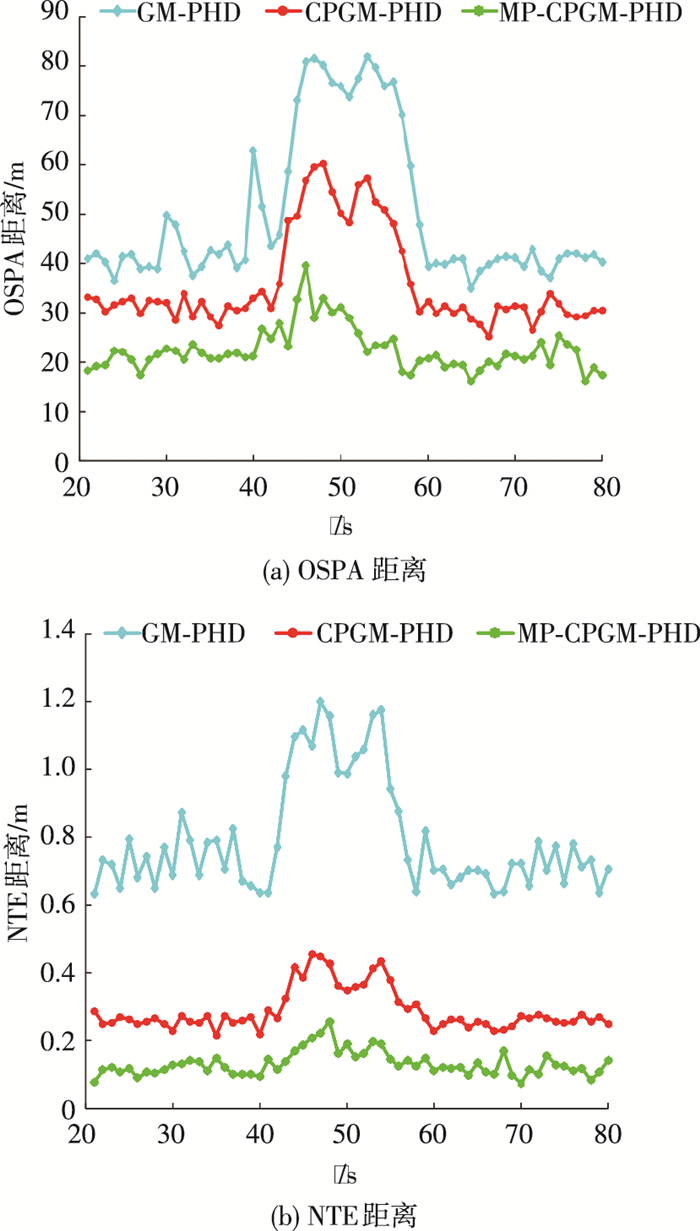
图 6显示了3种滤波算法的OSPA距离和NTE距离对比图.明显地看出,本算法的跟踪精度指标都明显优于前两种算法,尤其在多目标位置距离相近时,GM-PHD算法的跟踪精度下降的特别厉害,CPGM-PHD虽然有一定的改进,但还是有些目标的状态被遗漏地估计,所以本算法通过调整邻近目标高斯成分的权值大小,提高了相邻目标航迹的区分效果,弥补了CPGM-PHD算法中对遗漏目标的权值处理缺失,有效地减少了多目标的跟踪误差,特别是在目标相互靠近的情况下.本算法的OSPA距离和NTE距离相比于CPGM-PHD算法减少30%左右,相比于传统GM-PHD算法更是减少超过了50%,由此可以验证本文算法有效地提高了多目标跟踪精度.
|
图 6 3种算法的估计误差对比 Figure 6 Comparison of estimated error between 3 algorithms |
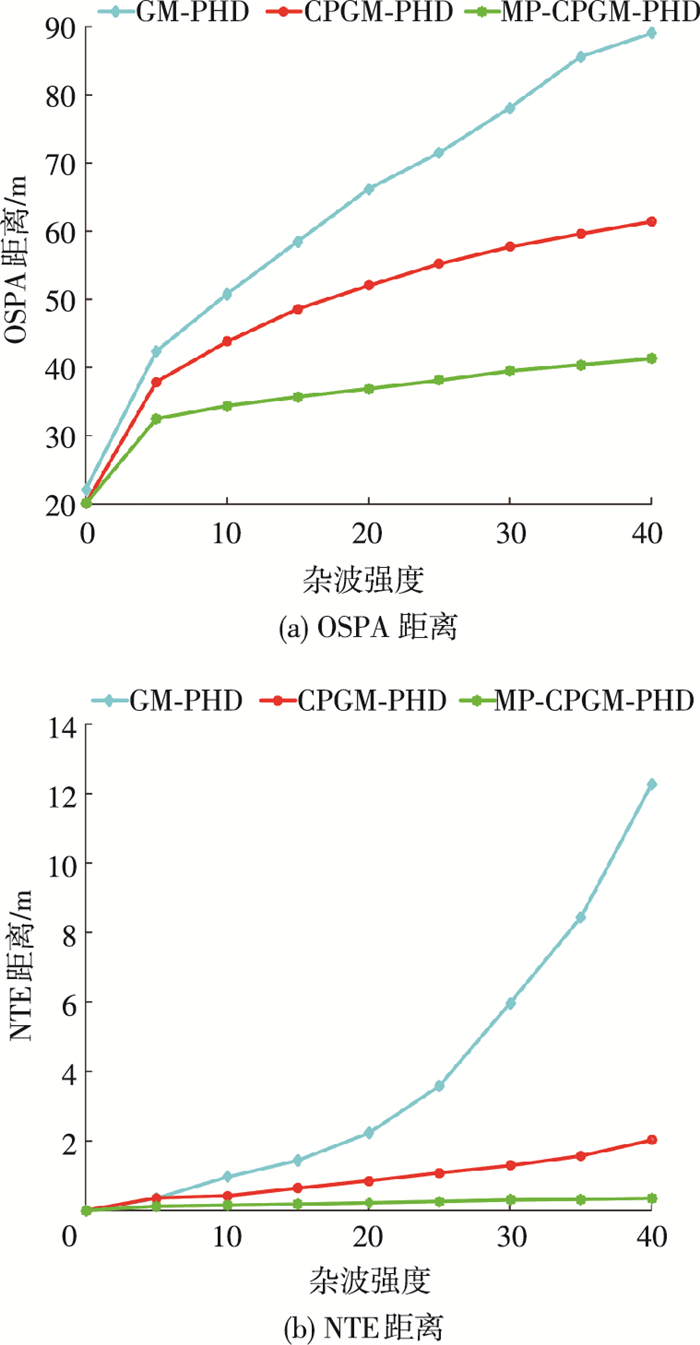
图 7对比了在不同杂波环境下3种滤波算法的OSPA距离和NTE距离.杂波强度从0~40,按照每5.0依次递加,其他参数没有变化.从图 7(a)、(b)可以看出,由于GM-PHD算法没有对于靠近目标高斯项权值的重新分配,导致在杂波强度增大的时候,跟踪误差也增加的越来越明显.而CPGM-PHD滤波算法通过修正同一目标的高斯分量的权重大小,可以实现目标估计和量测的准确对应关系,从而实现相对较小的跟踪误差.本文提出的MP-CPGM-PHD算法弥补了权值分配中的遗漏目标缺失处理,无论是OSPA距离还是NTE距离都是最优的,且随着杂波强度的不断增加,跟踪误差依然保持很低的水平,从而验证了本文算法在高强度的复杂跟踪环境中可有效提高航迹关联算法的跟踪精度.
|
图 7 不同杂波强度下的跟踪精度对比 Figure 7 Comparison of track accuracy under different clutter rates |
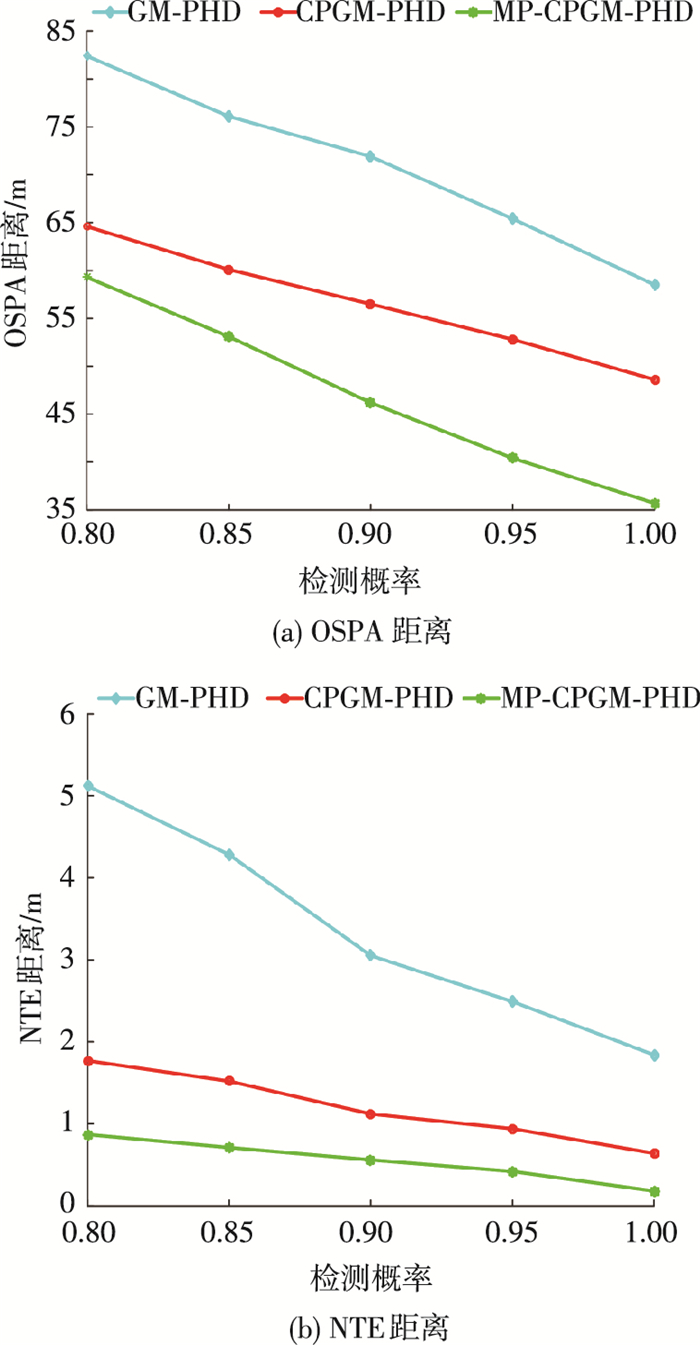
图 8对比了在不同检测概率下3种滤波算法的OSPA距离和NTE距离.检测概率从0.8~1.0,按照每0.5依次递加,其他参数没有变化.从图 8(a)、(b)可以看出,随着检测概率的增加,3种算法的跟踪精度有着一定程度地提高,但同时本算法在检测概率下降的情况下依然可以保持相对较好的跟踪效果.在OSPA距离方面,随着检测概率的增大,本文算法的OSPA距离下降了45%左右,相比于其他两种传统算法,下降趋势更加明显,并且在检测概率较低的情况下依然可以维持较好的估计误差.在NTE距离方面,传统GM-PHD和CPGM-PHD滤波方法在检测概率较低的情况下,NTE距离成倍的增加,严重影响了跟踪效果,而本文提出的MP-CPGM-PHD算法的NTE距离虽然也有一定程度地增加,但是在可接受的跟踪误差范围之内.
|
图 8 不同检测概率下的跟踪精度对比 Figure 8 Comparison of track accuracy under different detection probabilities |
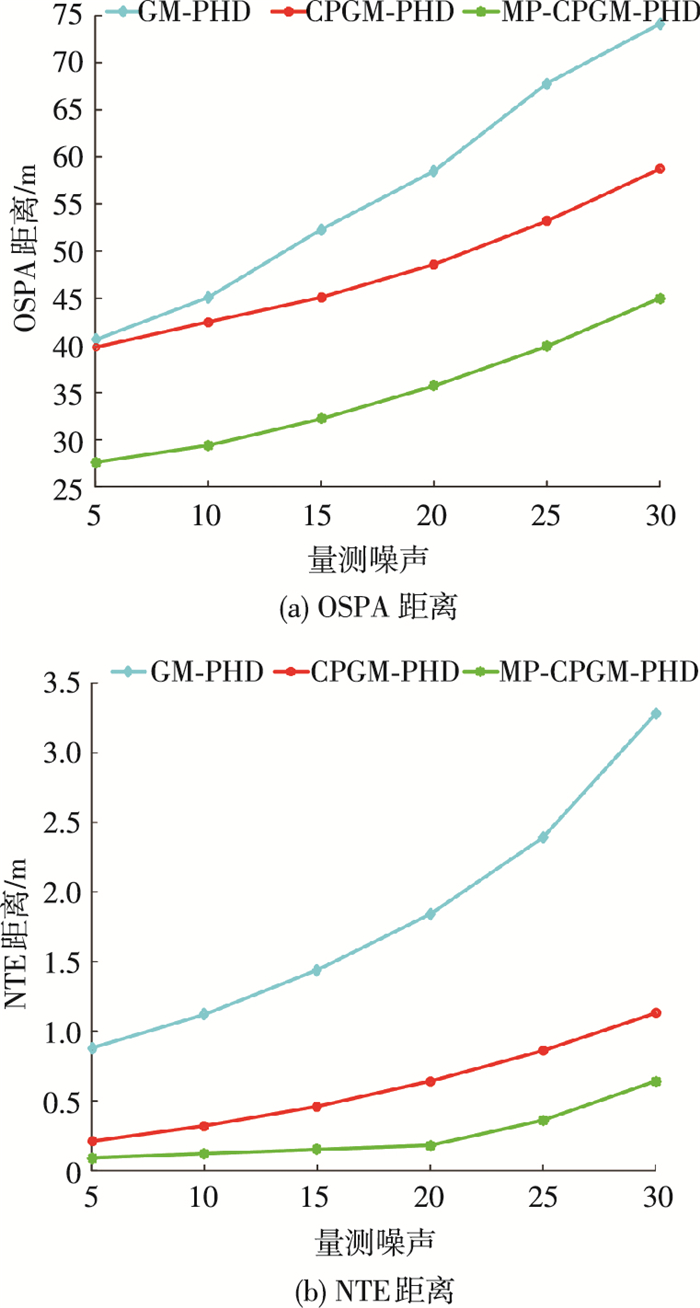
图 9对比了在不同量测噪声情况下3种算法的OSPA距离和NTE距离.量测噪声的标准差从5~30,按照每5.0依次递加,其他参数没有变化.从图 9(a)、(b)可以看出,随着量测噪声的增加,3种算法的OSPA距离和NTE距离有一定程度地增加,但本算法在量测噪声较大的情况下,依然可以得到相对较小的跟踪误差,主要是因为在量测划分方法中引入了重叠坐标系初步筛选的思想,而重叠坐标系是由量测噪声的标准差决定的,因此在每次筛选时考虑了量测噪声的影响,降低了量测划分的误差,从而在高量测噪声的情况下,依然可以有较好的跟踪精度.
|
图 9 不同量测噪声下的跟踪精度对比 Figure 9 Comparison of track accuracy under different measurement noise |
在OSPA距离方面,本文算法随着量测噪声的增加,相较于两种传统算法OSPA距离减少超过了30%,并且在大噪声情况下的OSPA距离也维持在较低的水平.在NTE距离方面,与GM-PHD算法相比更是下降了75%以上,跟踪精度明显得到了有效的改善.
因此,从仿真的结果分析中可以看出,本文提出的算法在复杂跟踪环境下,如杂波强度增大,检测概率变低,以及量测噪声变大,相比于传统GM-PHD算法,在跟踪精度和计算效率上都有明显提高.
4 结论1) 提出了分类检索的椭球门限量测划分方法,应用在GM-PHD航迹关联算法中,减少了杂波对于状态估计的干扰,提高了航迹关联算法的计算效率,使得算法的平均运行时间下降超过了50%.
2) 提出了改进的权值重新分配的协作惩罚GM-PHD航迹关联算法,通过调整邻近目标高斯成分的权值大小,有效提高了相邻目标的跟踪精度,算法的跟踪误差与传统算法相比减少了30%以上.大量仿真实验表明,在复杂跟踪环境下,相比于标准GM-PHD和CPGM-PHD滤波器,本文方法在估计精度和计算效率上都有明显提高.
| [1] |
BLACKMAN S. Multiple hypothesis tracking for multiple target tracking[J].
IEEE Transactions on Aerospace and Electronic Systems Magazine, 2004, 19(1): 5-18.
DOI: 10.1109/MAES.2004.1263228 |
| [2] |
LIU Qin, TAN C C, WU Jie, et al. Towards differential query services in Cost-Efficient Clouds[J].
IEEE Transactions on Parallel & Distributed Systems, 2014, 25(6): 1648-1658.
DOI: 10.1109/TPDS.2013.132 |
| [3] |
LIU Long, JI Hongbing, FAN Zhenhua. Improved Iterated-corrector PHD with Gaussian mixture implementation[J].
IEEE Transaction on Signal Processing, 2015, 114(1): 89-99.
DOI: 10.1016/j.sigpro.2015.01.007 |
| [4] |
杨峰, 王永齐, 粱彦, 等. 面向快速多目标跟踪的协同PHD滤波器[J].
系统工程与电子技术, 2014, 36(11): 2113-2121.
YANG Feng, WANG Yongqi, LIANG Yan, et al. Collaborative PHD filter for multi-target tracking[J]. Systems Engineering and Electronics, 2014, 36(11): 2113-2121. DOI: 10.3969/j.issn.1001-506X.2014.11.01 |
| [5] |
章涛, 来燃, 吴仁彪, 等. 观测最优分配的GM-PHD多目标跟踪算法[J].
信号处理, 2014, 30(12): 1419-1426.
ZHANG Tao, LAI Ran, WU Renbiao, et al. Measurements optimal assigned GM-PHD multi-target tracking algorithm[J]. Journal of Signal Processing, 2014, 30(12): 1419-1426. DOI: 10.3969/j.issn.1003-0530.2014.12.001 |
| [6] |
MAHLER R. Multi-target Bayes filtering via first-order multi-target moments[J].
IEEE Transactions on Aerospace and Electronic System, 2003, 39(4): 1152-1178.
DOI: 10.1109/TAES.2003.1261119 |
| [7] |
MAHLER R. PHD filters of higher order in target number[J].
IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(4): 1523-1543.
DOI: 10.1109/TAES.2007.4441756 |
| [8] |
WANG Yan, MENG Huadong, ZHANG Hao, et al. Track probability hypothesis density filter for multi-target tracking[C] //Proceedings of the Radar Conference(RADAR). Kansas City, MO: IEEE, 2011: 612-615. DOI: 10.1109/RADAR.2011.5960610.
|
| [9] |
PANTA K, CLARK D E, VO B N. Data association and track management for the Gaussian mixture probability hypothesis density filter[J].
IEEE Transaction on Aerospace and Electronic Systems, 2009, 45(3): 1003-1016.
DOI: 10.1109/TAES.2009.5259179 |
| [10] |
YAZDIAN-DEHKORDI M, ROJHANI O R, AZIMIFAR Z. Visual target tracking in occlusion condition: a GM-PHD-based approach[C]//Proceedings of the 16th CSI International Symposium on Artificial Intelligence and Signal Processing(AISP). Shiraz: IEEE, 2012: 538-541. DOI: 10.1109/AISP.2012.6313805.
|
| [11] |
YAZDIAN-DEHKORDI M, AZIMIFAR Z, MASNADI-SHIRAZI M A. Penalized Gaussian mixture probability hypothesis density filter for multiple target tracking[J].
IEEE Transaction on Signal Processing, 2012, 92(5): 1230-1242.
DOI: 10.1016/j.sigpro.2011.11.016 |
| [12] |
YAZDIAN-DEHKORDI M, AZIMIFAR Z, MASNADI-SHIRAZI M A. Competitive Gaussian mixture probability hypothesis density filter for multiple target tracking in the presence of ambiguity and occlusion[J].
IET Radar, Sonar & Navigation, 2012, 6(4): 251-262.
DOI: 10.1049/iet-rsn.2011.0038 |
| [13] |
WANG Yan, MENG Huadong, LIU Yimin, et al. Collaborative penalized Gaussian mixture PHD tracker for close target tracking[J].
IEEE Transaction on Signal Processing, 2014, 102(1): 1-15.
DOI: 10.1016/j.sigpro.2014.01.034 |
| [14] |
张洪建. 基于有限集统计学的多目标跟踪算法研究[D]. 上海: 上海交通大学, 2009.
ZHANG Hongjian. Finite-set statics based multiple target tracking[D]. Shanghai: Shanghai Jiao Tong University, 2009. |
| [15] |
VO B N, MA W K. The Gaussian mixture probability hypothesis density filter[J].
IEEE Transaction on Signal Processing, 2006, 54(11): 4091-4104.
DOI: 10.1109/TSP.2006.881190 |
| [16] |
章涛, 吴仁彪. 自适应门限GM-CPHD多目标跟踪算法[J].
数据采集与处理, 2014, 29(4): 549-554.
ZHANG Tao, WU Renbiao. Adaptive gating GM-CPHD for multi-target tracking[J]. Journal of Data Acquisition and Processing, 2014, 29(4): 549-554. DOI: 10.3969/j.issn.1004-9037.2014.04.009 |
| [17] |
NGUYEN V D, CLAUSSEN T. Reducing computational complexity of gating procedures using sorting algorithms[C] // Proceedings of the 16th International Conference on Information Fusion. Istanbul: IEEE, 2013: 1707-1713.
|
| [18] |
NGUYEN V D. Small-target radar detection and tracking within the Pitas Hard-and Software Environment[J].
Communications in Computer and Information Science, 2012, 318(1): 347-358.
DOI: 10.1007/978-3-642-33161-9_52 |
| [19] |
LEI Ming, JING Zhongliang, Dong Peng. Extended GM-PHD filter for multi-target tracking in nonlinear/non-Gaussian system[C]//Proceedings of the 17th International Conference on Information Fusion, Salamanca: IEEE, 2014: 1-8.
|
| [20] |
SCHUHMACHER D, VO B T, VO B N. A consistent metric for performance evaluation of multi-object filter[J].
IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457.
DOI: 10.1109/TSP.2008.920469 |
 2018, Vol. 50
2018, Vol. 50


