接收机实时精密单点定位RT-PPP中,精准的位置测量至少需要亚纳秒级的实时卫星钟差数据.但是,导航卫星提供的实时广播星历中的钟差精度只达到10 ns级,不能满足RT-PPP中对钟差数据的精度要求;而IGS(international global navigation satellite system service)数据分析中心提供的亚纳秒级精密钟差产品是后处理数据,具有一定的发布时延,无法满足RT-PPP中实时性要求.因此,折中RT-PPP中高精度和实时性的需求,利用历史精密钟差数据对当前时刻的卫星钟差进行精准预报,具有重要的工程意义.
星载原子钟时频特性极为复杂,并且极易受到外界环境影响,因此高精度钟差预报一直是卫星导航定位领域和时频领域中的一个难题.国内外学者开展了大量的研究,将多种预测模型运用到了钟差预报中.二次项模型(second order polynomia,SP)是依据原子基准时频的频漂特性建立的钟差拟合模型,模型简单且易于实现,能够得到钟差的变化趋势,但预报精度不高[1-2].卡尔曼滤波需基于准确的噪声方差先验知识[3],但钟差数据中非线性噪声方差的估计是一个难点,基于Hadamard方差的卡尔曼滤波模型在铷钟钟差预报中取得较好的效果,但对铯钟钟差的预报精度不高[4].支持向量机是基于机器学习理论的一种分类学习模型[5-6],基于线性核函数的最小二乘支持向量机在预报呈振荡分布的钟差数据时取得了较好的效果,但其核函数参数的选取对钟差预报精度影响很大,目前尚未有可靠的理论进行指导[7].人工神经网络模型具有较强的非线性拟合能力[8],在钟差短期预报中具有较高的精度,但模型层次过于复杂,在学习样本数量有限时,精度难以保证[9].上述模型方法在钟差预报中取得了一定的成果,但尚存在改进空间.
灰色理论模型是一种利用微分拟合进行二次建模的方法,研究表明星载原子钟钟差的变化规律符合灰色系统理论的特点[10].并且,基于灰色理论的算法样本需求小,模型表达式简单,便于工程应用.文献[10]对GM(1, 1)模型的指数系数与卫星钟差预报精度的关系做了详细研究,指出模型指数系数为恒定常量是预报误差源之一.文献[11]提出了调节GM(1, 1)模型中的指数系数和常数系数可以显著提升钟差预报精度,但并未系统地提出系数优化方法.
本文在上述研究的基础上,首先分析了GM(1, 1)模型存在的缺点,然后对其建模方法进行优化设计,并引入粒子群参数自适应寻优方法,建立灰色自适应粒子群PGM(1, 1)预测模型,并将其运用到导航卫星精密钟差预报中进行研究.本文采用第1天的历史精密钟差数据自适应建模,进行第2天的实时预报实验,实验结果表明,算法对卫星钟差的预报精度可达到亚纳秒级,可为RT-PPP提供高精度的钟差数据.
1 GM(1, 1)预测模型 1.1 GM(1, 1)预测模型基本形式常用的灰色预测模型是单变量的一阶预测模型—GM(1, 1)模型.设原始量测数据为
| $ {\mathit{\boldsymbol{x}}^{\left( 0 \right)}} = \left\{ {{x^{\left( 0 \right)}}\left( 1 \right),{x^{\left( 0 \right)}}\left( 2 \right), \cdots ,{x^{\left( 0 \right)}}\left( n \right)} \right\}. $ |
一次累加原始量测数据x(0),进而生成一次累加序列(accumulation generation operator, 1-AGO),记为
| $ {\mathit{\boldsymbol{x}}^{\left( 1 \right)}} = \left\{ {{x^{\left( 1 \right)}}\left( 1 \right),{x^{\left( 1 \right)}}\left( 2 \right), \cdots ,{x^{\left( 1 \right)}}\left( n \right)} \right\}, $ |
式中
为建立灰色原始数据的白化方程,对1-AGO序列进行背景值的紧邻数据生成,生成的序列记为
| $ {\mathit{\boldsymbol{z}}^{\left( 1 \right)}} = \left\{ {{z^{\left( 1 \right)}}\left( 2 \right),{z^{\left( 1 \right)}}\left( 3 \right), \cdots ,{z^{\left( 1 \right)}}\left( n \right)} \right\}, $ |
式中z(1)(k)=0.5× x(1)(k)+x(1)(k-1),k=1, 2, …, n.
首先, 根据新生成的序列x(1)和z(1),建立GM(1, 1)灰色模型的微分方程和白化微分方程分别为:
| $ \frac{{{\rm{d}}{x^{\left( 1 \right)}}\left( t \right)}}{{{\rm{d}}t}} = a{x^{\left( 1 \right)}}\left( t \right) + b, $ |
| $ {x^{\left( 0 \right)}}\left( k \right) = a{z^{\left( 1 \right)}}\left( k \right) + b, $ |
式中待辨识的拟合参数A =[a b]Τ可以通过最小二乘法得到.令:
| $ \mathit{\boldsymbol{y}} = {\left[ {\begin{array}{*{20}{c}} {{x^{\left( 0 \right)}}\left( 2 \right)}&{{x^{\left( 0 \right)}}\left( 3 \right)}& \cdots &{{x^{\left( 0 \right)}}\left( n \right)} \end{array}} \right]^{\rm{T}}}, $ |
| $ \mathit{\boldsymbol{L}} = {\left[ {\begin{array}{*{20}{c}} {{z^{\left( 1 \right)}}\left( 2 \right)}&{{z^{\left( 1 \right)}}\left( 3 \right)}& \cdots &{{z^{\left( 1 \right)}}\left( n \right)}\\ 1&1& \cdots &1 \end{array}} \right]^{\rm{T}}}, $ |
则可得到A的最小二乘法解为
| $ \mathit{\boldsymbol{\hat A}} = {\left( {{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}}} \right)^{ - 1}}{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{y}}. $ |
然后, 根据测量初值、拟合参数a和b可得微分方程的数值解为
| $ {{\hat x}^{\left( 1 \right)}}\left( t \right) = \left( {{x^{\left( 1 \right)}}\left( 1 \right) + b/a} \right){{\rm{e}}^{a\left( {t - 1} \right)}} - b/a, $ |
由x(1)(1)=x(0)(1),上式对应的离散时间序列解为
| $ {{\hat x}^{\left( 1 \right)}}\left( {k + 1} \right) = \left( {{x^{\left( 0 \right)}}\left( 1 \right) + b/a} \right){{\rm{e}}^{ak}} - b/a. $ |
最后,通过对得到的1-AGO序列进行反向差分处理
| $ {{\hat x}^{\left( 0 \right)}}\left( {k + 1} \right) = \left( {1 - {e^{ - a}}} \right)\left( {{x^{\left( 0 \right)}}\left( 1 \right) + b/a} \right){{\rm{e}}^{ak}}. $ |
信息不完全的、小样本的不确定性灰色系统通常可采用GM(1, 1)模型进行表述,但对其建模方式进行分析,可知该模型存在以下不足:
1) 在GM(1, 1)预测模型建立时至少要求具有4个量测数据,但在卫星钟差预测时,过多的建模数据将使得旧信息的影响始终存在,因而对预测精度产生了影响.求解辨识系数a和b的方法是最小二乘法,其本质是等权值拟合所有的量测数据,并没有区分新、旧信息的贡献,未体现出灰色理论新信息优先的原理.
2) 不同特征的序列,与之相应的背景值的不同建立方法对GM(1, 1)模型的预测精度有较大的影响.通常使用两个相邻的1-AGO序列数据点的平均值作为背景值,即z(1)(k)=0.5× x(1)(k)+x(1)(k-1),这种构造方式简单,但使得GM(1, 1)模型对于变化较为剧烈的序列适应性较差.文献[12]给出了适用于呈现指数型变化的数据序列的背景值构造方法,其背景值构造形式为
3) GM(1, 1)预测实质上是一种外推法,是用指数曲线拟合累加生成序列,研究表明拟合系数a和b对预测效果有直接影响.a为发展系数,其大小和符号反映了序列的发展态势;b为灰作用量,其反映了外在扰动量的大小.传统的GM(1, 1)模型将拟合系数视为不变,使求解过程简洁明了,但随着预测空间和时间历元的变化,发展系数和灰作用量必然会随之改变.因此当序列变化剧烈,尤其是呈近指数变化时,预测误差较大.
4) GM(1, 1)模型在解算白化微分方程的数值解时,选取第1个量测数据作为初始条件,即第1个量测数据点必定在拟合曲线上,但第1个量测数据是与预测点相距最远最旧的信息,因而这与新信息优先的灰色理论基本原理相矛盾.
1.3 GM(1, 1)模型的改进通过分析GM(1, 1)模型所存在的缺陷,从下列4个方面对其进行相应的改进.
1.3.1 遗忘因子最小二乘法的引入依据灰色理论新信息优先的原理,距离预测点较远的旧信息对未来预测点的影响逐渐降低甚至消失,但靠近预测点的新信息会对预测结果产生较大的影响.从而,利用衰减记忆的最小二乘法对预测模型进行改进,以量测数据与预测点的距离为依据来设计遗忘因子,则带遗忘因子的系数矩阵计算式为
| $ \mathit{\boldsymbol{\hat A}} = {\left( {{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{WL}}} \right)^{ - 1}}{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{Wy}}, $ |
式中,W为对角渐消阵,对角元素为渐消遗忘因子.以指数型因子表征量测数据点与预测点间的距离范数,可确保W对角渐消阵的正定性,W =diag(e-(n-1), e-(n-2)…,e-(n-n)),n为序列长度.
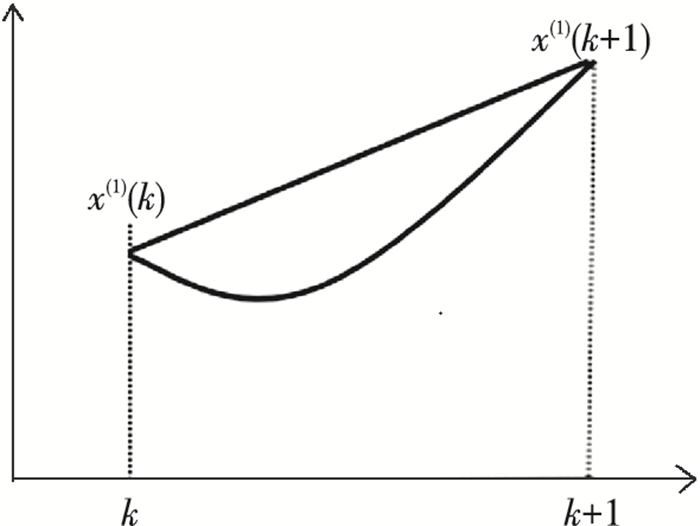
1.3.2 背景值的构造GM(1, 1)模型背景值建立的误差源是由于采用紧邻的两个1-AGO数据点连接成的直边梯形面积代替其原始曲边梯形面积,而出现了滞后误差,如图 1所示,越剧烈变化的数据序列,其滞后误差也越大.依据序列特点,对紧邻的两个1-AGO数据点进行自适应加权平均得到新的背景值,即
| $ {z^{\left( 1 \right)}}\left( k \right) = \omega {x^{\left( 1 \right)}}\left( k \right) + \left( {1 - \omega } \right){x^{\left( 1 \right)}}\left( {k - 1} \right),0 \le \omega \le 1 $ |
|
图 1 GM(1, 1)背景值误差源示意 Figure 1 GM(1, 1) background value error source |
式中,权值ω的最优解可以通过自适应算法求得.该背景值具有更小的滞后误差,对剧烈变化的序列具有更佳的适应性.
1.3.3 系数优化因子的引入为了确定拟合系数和函数形态的变化关系,对白化微分方程式求偏导可得:
| $ \frac{{{\partial ^2}{{\hat x}^0}\left( k \right)}}{{\partial {k^2}}} = {a^2}{{\hat x}^0}\left( k \right), $ |
| $ \frac{{\partial {{\hat x}^0}\left( k \right)}}{{\partial b}} = \frac{{\left( {1 - {e^{ - a}}} \right)}}{a} \times {{\rm{e}}^{a\left( {k - 1} \right)}}. $ |
GM(1, 1)模型的数据序列均为非负序列即
系数优化是基于最小二乘拟合的自适应调节,使模型更加适应于拟合剧烈变化的数据序列,如近指数型序列.一方面要抑制发散趋势使拟合总体误差减小,另一方面又不能引起函数形态的畸变,由此在预测值求解式中引入发展系数优化因子λ和灰作用量优化因子θ.
| $ {{\hat x}^{\left( 0 \right)}}\left( {k + 1} \right) = \left( {1 - {{\rm{e}}^{ - \lambda a}}} \right)\left( {{x^{\left( 0 \right)}}\left( 1 \right) + \theta b/a} \right){{\rm{e}}^{\lambda ak}}. $ |
式中,经数值试验系数优化因子的有效范围为λ∈(0, 2], θ∈(0, 2], 同时要满足λa∈(
求解微分方程时,可任意选取1-AGO序列中的量测数据点作为初值,可得其对应的时间序列解为
| $ \begin{array}{*{20}{c}} {{{\hat x}^{\left( 1 \right)}}\left( {k + 1} \right) = \left( {{x^{\left( 0 \right)}}\left( 1 \right) + b/a} \right){e^{a\left( {k + 1 - l} \right)}} - b/a.}\\ {\left( {k = 1,2, \cdots ,n,1 \le l \le k} \right)} \end{array} $ |
据新信息优先的原理,1-AGO序列中最新的量测量可选取为初值进行预测求解,可得微分方程的解为
| $ {{\hat x}^{\left( 1 \right)}}\left( {k + 1} \right) = \left( {{x^{\left( 1 \right)}}\left( k \right) + b/a} \right){{\rm{e}}^a} - b/a.\left( {k = 1,2, \cdots ,n} \right) $ |
本文在上述对GM(1, 1)模型建模方法进行优化设计的基础上,引入粒子群参数自适应寻优方法,建立了灰色自适应粒子群PGM(1, 1)预测模型(particle swarm optimization-grey model).
2.1 PGM(1, 1)预测模型的构建设原始量测数据为
| $ {\mathit{\boldsymbol{x}}^{\left( 0 \right)}} = \left\{ {{x^{\left( 0 \right)}}\left( 1 \right),{x^{\left( 0 \right)}}\left( 2 \right), \cdots ,{x^{\left( 0 \right)}}\left( n \right)} \right\},\left( {k = 1,2, \cdots ,n} \right) $ |
对应的1-AGO序列为:
| $ {\mathit{\boldsymbol{x}}^{\left( 1 \right)}} = \left\{ {{x^{\left( 1 \right)}}\left( 1 \right),{x^{\left( 1 \right)}}\left( 2 \right), \cdots ,{x^{\left( 1 \right)}}\left( n \right)} \right\} $ |
| $ {x^{\left( 1 \right)}}\left( k \right) = \sum\limits_{i = 1}^k {{x^{\left( 0 \right)}}\left( i \right)} ,\left( {k = 1,2, \cdots ,n} \right) $ |
背景值由1-AGO序列进行一次紧邻数据自适应寻优生成.
| $ {\mathit{\boldsymbol{z}}^{\left( 1 \right)}} = \left\{ {{z^{\left( 1 \right)}}\left( 2 \right),{z^{\left( 1 \right)}}\left( 3 \right), \cdots ,{z^{\left( 1 \right)}}\left( n \right)} \right\}. $ |
式中, z(1)(k)=ωx(1)(k)+ (1-ω) x(1)(k-1).其中:k=2, 3, …, n;ω为自适应权值, 0≤ω≤1.
依据新生成的数列,可得到PGM(1, 1)的微分方程及白化微分方程为:
| $ \frac{{{\rm{d}}{x^{\left( 1 \right)}}\left( t \right)}}{{{\rm{d}}t}} = a{x^{\left( 1 \right)}}\left( t \right) + b, $ | (1) |
| $ {x^{\left( 0 \right)}}\left( k \right) = a{z^{\left( 1 \right)}}\left( k \right) + b. $ | (2) |
式中, 拟合初始参数A =[a b]Τ由衰减记忆的最小二乘法辨识得到,则A的估计值为
| $ \mathit{\boldsymbol{\hat A}} = {\left( {{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{WL}}} \right)^{ - 1}}{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{Wy}}. $ |
求解微分方程式(1),可得其初始数值解为
| $ {{\hat x}^{\left( 1 \right)}}\left( t \right) = \left( {{x^{\left( 1 \right)}}\left( 1 \right) - b/a} \right){{\rm{e}}^{a\left( {t - 1} \right)}} + b/a. $ |
以1-AGO序列中任意值为初始条件,式(1)的初始时间序列解为
| $ \begin{array}{*{20}{c}} {{{\hat x}^{\left( 1 \right)}}\left( {k + 1} \right) = \left( {{x^{\left( 0 \right)}}\left( l \right) + b/a} \right){{\rm{e}}^{a\left( {k + 1 - l} \right)}} - b/a,}\\ {\left( {k = 1,2, \cdots ,n,1 \le l \le k} \right)} \end{array} $ |
式中,x(1)(l)为1-AGO序列中的第l个值.如果选取l=1,上式为采用初值进行预测的模型;如果选取l=k,上式为采用最新的预测值或量测量进行预测的模型.反向差分并引入系数优化因子可得预测值为
| $ \begin{array}{*{20}{c}} {{{\hat x}^{\left( 0 \right)}}\left( {k + 1} \right) = \left( {1 - {{\rm{e}}^{ - \lambda a}}} \right)\left( {{x^{\left( 0 \right)}}\left( l \right) + \theta b/a} \right){{\rm{e}}^{\lambda a\left( {k - l} \right)}},}\\ {\left( {k = 1,2, \cdots ,n} \right)} \end{array} $ | (3) |
式中,λ∈(0, 2],θ∈(0, 2],同时λa∈(
通过自适应算法求解出最佳的优化因子组合φbest=[ωbest, λbest, θbest],代入式(3)计算可得优化模型的预测值.
2.2 模型精度检测模型精度的检验标准选择使用平均相对误差[13],这适用于各数据采样点量测精度相当的序列,然而对采样点量测精度变化有区分度的序列,使用平均相对误差作为精度检验标准,将会使得在参数寻优过程中,量测精度较低的采样点对预测误差函数的影响权值与量测精度高的采样点一致,无法保证参数自适应寻优的效果.因此,本文中精度检验的标准选择使用归一化的平均相对误差,即利用采样点量测精度为权值对平均相对误差进行归一化平均[14],为
| $ \sigma = \frac{1}{n}\sum\limits_{k = 1}^n {q\left( k \right)\left( {\frac{{\left| {\hat x_i^{\left( 0 \right)}\left( k \right) - x_i^{\left( 0 \right)}\left( k \right)} \right|}}{{x_i^{\left( 0 \right)}\left( k \right)}}} \right)} ,\left( {k = 1,2, \cdots ,n} \right) $ |
式中,q(k)为采样点量测精度值,若q(k)=1则各采样点精度一致.本文实验中以精密星历的钟差数据点精度作为权值进行归一化.
2.3 自适应优化因子的求解算法粒子群优化算法(particle swarm optimization, PSO)是一类随机全局优化技术,通过粒子间的相互作用发现复杂搜索空间中的最优区域.由于其收敛速度快,参数调整较为简单,概念明确且较容易编程实现,在工程中应用广泛.因此,本文参数自适应寻优选用PSO算法,其原理如下[14].
假设有m个粒子组成的一个微粒群,分布在D维的搜索空间中,第i个粒子的飞行速度和位置分别为vi=[vi1 vi2 … viD]和si=[si1 si2 … siD],其中i=1, 2, …, m.根据对环境的适应度将群体中的微粒移动到更好的区域,每个粒子的位置就是一个潜在的解.在每次迭代中,粒子通过跟踪两个“极值”更新自己.第1个极值是粒子本身所找到的最优解,即个体极值pibest=[pi1, pi2, …, piD];第2个极值是整个种群中所找到的最优解,即全局极值pgbest=[pg1, pg2, …, pgD].对每一代粒子,在找到这两个最优值时,粒子根据下式来更新自己的速度和位置为
| $ \begin{array}{*{20}{c}} {\left\{ \begin{array}{l} {v_{il}} = w{v_{id}} + {c_1}{r_1}\left( {{p_{id}} - {s_{id}}} \right) + {c_2}{r_2}\left( {{s_{gl}} - {s_{gl}}} \right),\\ {s_{il}} = {s_{id}} + {v_{id}}. \end{array} \right.}\\ {\left( {i = 1,2, \cdots ,m,d = 1,2, \cdots ,D} \right)} \end{array} $ |
式中:正常数c1、c2分别为加速系数,通常取值范围在[2,4]之间; r1、r2分别为在范围[0, 1]内变化的随机数; w为惯性权值.为改善PSO算法的全局和局部搜索能力本文采用惯性权值非线性递减策略[15]即
| $ w=\left( {{w_{{\rm{start}}}} - {w_{{\rm{end}}}}} \right){\left( {\frac{t}{{{t_{\max }}}}} \right)^2} + \left( {{w_{{\rm{start}}}} - {w_{{\rm{end}}}}} \right){\left( {\frac{{2t}}{{{t_{\max }}}}} \right)^2} + {w_{{\rm{start}}}}. $ |
式中:wstart、wend分别为惯性权值的上限和下限;t、tmax分别为迭代次数和迭代上限.
采用PSO算法求解最优因子组合的步骤如下.
Step 1 按微粒群的规模n生成初始群体(φ1, φ2, …, φn),惯性权值上、下限wmax和wmin,加速系数c1、c2,最大允许迭代次数tmax,以及各个微粒的初始位置和初始速度;其中φi=[ωi, λi, θi]T.
Step 2 以模型平均相对误差最小为准则对参数进行优化,其目标函数为
| $ \min f\left( {{\varphi _i}} \right) = \frac{1}{n}\sum\limits_{k = 1}^n {q\left( k \right)\left( {\frac{{\left| {\hat x_i^{\left( 0 \right)}\left( {{\varphi _i},k} \right) - x_i^{\left( 0 \right)}\left( k \right)} \right|}}{{x_i^{\left( 0 \right)}\left( k \right)}}} \right)} , $ |
式中,
Step 3 各微粒将当前适应值和其个体历史最好适应值进行比较,以此得到全局历史最好适应度值;
Step 4 依据个体和全局历史最优值更新各微粒的速度和位置.
Step 5 当适应度值到达精度标准时停止搜索,输出搜索结果,否则,返回Step2继续搜索;若达到迭代次数上限,适应度值还未收敛,表明本文的模型算法已失效,需另选其他模型进行计算.
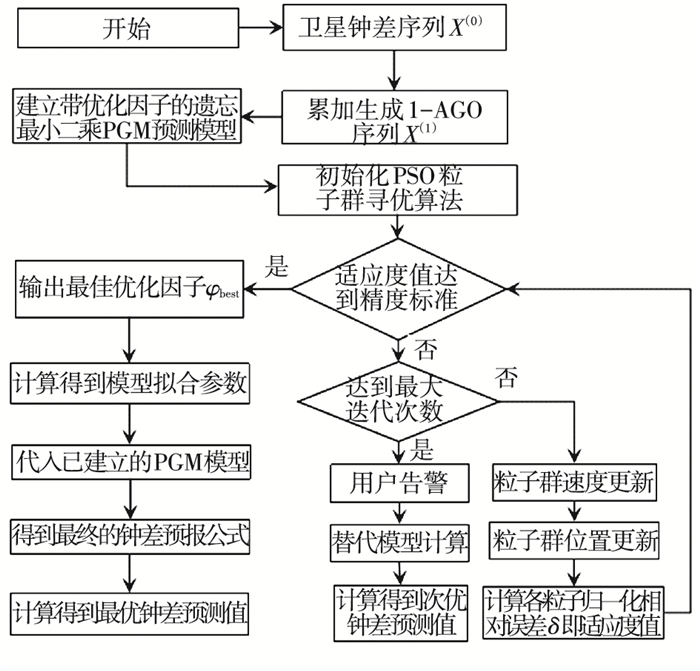
2.4 PGM(1, 1)模型卫星钟差预测流程图 2所示为灰色粒子群自适应卫星钟差预测方法的计算流程,其具体步骤如下.
|
图 2 PGM(1, 1)算法流程 Figure 2 PGM(1, 1) algorithm flow chart |
Step 1 依据待预测序列的特点对其进行预处理,处理后的序列为非负序列.
Step 2 一次累加预处理后的序列生成1-AGO序列.
Step 3 依据原始序列和1-AGO序列建立预测模型,PSO算法初始化后,计算各粒子初始归一化平均相对误差.
Step 4 将归一化平均相对误差最小作为寻优准则,PSO算法自适应训练出最优的组合优化因子φbest;若达到最大迭代上限还未得到训练结果,则本文的钟差预报方法失效,需对精密定位用户进行告警,并采用其他钟差预报模型进行替代.
Step 5根据最优的组合优化因子φbest计算拟合参数a和b.
Step 6 形成最终的序列预测公式,并依据预测公式计算钟差序列预测值.
3 实验验证IGS提供的精密钟差产品分为快速精密星历钟差和事后精密星历钟差,快速精密星历钟差具有1 d左右的发布延迟,其钟差数据精度可达0.5 ns以内;而事后精密星历钟差具有13 d以上的延迟,但其精度最高,可达0.3 ns以内[16].快速精密星历钟差已满足实时精密单点定位的精度要求,且能表征星载原子钟钟差的变化规律.因此,本文经过两种星历钟差精度和发布时延的折中,选用快速精密星历钟差数据进行PGM(1, 1)模型的实验仿真.
本文所使用的实验数据是2015年12月1日至12月2日的GPS快速精密星历钟差数据,将12月1日的钟差数据作为历史进行PGM(1, 1)建模自适应优化,形成最终的钟差预测公式后,再对12月2日的钟差数据进行预报.数据采样间隔与IGS精密星历保持一致,为15 min.GPS星载原子钟钟差与其自身物理结构和运行环境密切相关,所表现出的钟差变化各有其特点,因此,本文选取5颗钟差变化典型的GPS卫星进行PGM(1, 1)模型的钟差预报实验,见表 1;同时选取GM(1, 1)模型和二次多项式SP模型作为对照组进行预报结果比较.
| 表 1 精密星历数据选取一览 Table 1 Precise clock error experimental data list |
由表 2可知,PGM模型对铷钟钟差的平均预报残差都在0.1 ns以内,对铯钟钟差的平均预报残差约为0.5 ns,预报残差标准差均在0.5 ns左右,由此导致的伪距测量误差均为厘米级,而IGS快速精密星历的平均精度亦在0.5 ns左右,证明了本文预测方法的有效性.同时,铯钟比铷钟时频稳定性差,钟差量测精度偏低,导致其钟差数据序列不够平稳,因此相应的PRN 27卫星钟差预报精度也偏低,进一步说明预测序列的变化趋势对PGM模型的预报精度影响较小,而序列的平稳程度对模型预报精度有较大的影响.
| 表 2 PGM模型预报精度统计 Table 2 PGM model forecasting accuracy statistics |
由表 3可知,GM模型的预报残差平均值在1~5 ns之间,预报残差标准差在0.5~2.5 ns之间,由此导致的平均伪距测量误差在1~2 m之间,但在预报PRN 01卫星钟差时出现了误差发散的情况,预报残差平均值达到72 ns.SP模型预报精度在60~400 ns之间,由此导致的平均伪距测量误差在18~125 m之间,而且针对不同的卫星钟差序列预测精度有较大差别.因此,GM模型的总体预报精度优于SP模型.
| 表 3 GM模型和SP模型预报精度统计 Table 3 GM model forecasting accuracy statistics |
对比表 2、3中各模型的预报结果,PGM模型平均预报残差达到了亚纳级,比GM模型的平均相对误差降低73%~97%,较SP模型平均相对误差降低两个数量级.GM模型在预报PRN 01卫星钟差时出现了误差发散的情况,SP模型预报的多颗卫星钟差精度差异较大,说明传统模型对不同的钟差序列敏感性有较大差异.PGM模型对各颗卫星钟差预报精度较高,证明依据预测序列的特点,引入PSO参数自适应寻优方法可改善传统模型的适应性和收敛性.
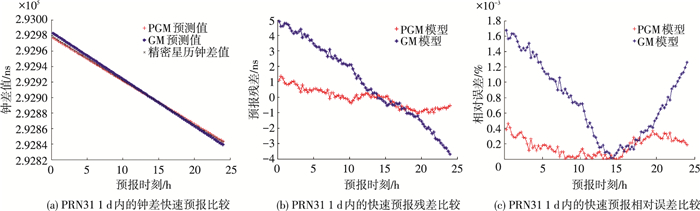
图 3为PRN 31卫星的钟差预报结果图,其余各颗卫星的钟差预报结果与之类似.如图 3所示PGM模型1 d内各历元的预报残差稳定在1 ns以内,由此造成的伪距测量误差在厘米级,预报精度相较GM模型有较大提升,且预报数据序列较GM模型更加平稳,进一步证明了PGM模型性能优于GM模型,能为RT-PPP提供实时高精度的钟差预报数据.
|
图 3 PRN31 PGM和GM预报结果比较 Figure 3 PRNN31 PGM and GM forecasting result comparison |
1) 本文提出的PGM(1, 1)预测模型针对GM(1, 1)模型在建模方式上的不足,引入了带遗忘因子的最小二乘法,由此旧信息对预测结果的影响权值较小,而新信息对预测结果有较大的影响权值,有效提升了模型的预测精度.同时,依据预测序列的特点引入组合优化因子,对模型的背景值、发展系数以及灰作用量进行粒子群自适应寻优,使得模型预测精度进一步提升,并具备更好的适应性和收敛性.
2) 由于卫星钟差序列各数据点量测精度不一致,采用归一化平均相对误差作为模型自适应精度检测的标准,由此避免以平均相对误差为标准时,相对误差大的低量测精度钟差数据点湮没相对误差小的高量测精度钟差数据点,显著降低了不稳定钟差数据序列的预测误差.
3) GPS卫星钟差预报实验表明,本文提出的PGM(1, 1)预测模型,其预报精度相对于常规GM(1, 1)和SP模型有了较大提升且所需训练样本小,平均预报残差达到了亚纳秒级,能够满足RT-PPP对实时高精度钟差数据的需求.
| [1] |
SENIOR K, KOPPANG P, RAY J. Developing an IGS time scale[J].
IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2003, 50(6): 585-593.
DOI: 10.1109/FREQ.2001.956188 |
| [2] |
JONSSON P, EKLUNDH L. Seasonality extraction by function fitting to time-series of satellite sensor data[J].
IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(8): 1824-1832.
DOI: 10.1109/TGRS.2002.802519 |
| [3] |
赵思浩, 陆明泉, 冯振明. 基于自适应卡尔曼滤波的GNSS矢量锁定环路[J].
哈尔滨工业大学学报, 2012, 44(7): 139-143.
ZHAO Sihao, LU Mingquan, FENG Zhenming. GNSS vector lock loop based on adaptive Kalman filter[J]. Journal of Harbin Institute of Technology, 2012, 44(7): 139-143. DOI: 10.11918/j.issn.0367-6234.2012.07.027 |
| [4] |
HOWE D A, BEARD R L, GREENHALL C A, et al. Enhancements to GPS operations and clock evaluations using a "total" Hadamard deviation[J].
IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2005, 52(8): 1253-1261.
DOI: 10.1109/TUFFC.2005.1509784 |
| [5] |
SONG Qing, HU Wenjie, XIE Wenfang. Robust support vector machine with bullet hole image classification[J].
IEEE Transactions on Systems, Man, and Cybernetics, 2002, 32(4): 440-448.
DOI: 10.1109/TSMCC.2002.807277 |
| [6] |
颜根廷, 马广富, 肖余之. 一种混合核函数支持向量机算法[J].
哈尔滨工业大学学报, 2007, 39(11): 1704-1706.
YAN Genting, MA Guangfu, XIAO Yuzhi. Support vector machines based on hybrid kernel function[J]. Journal of Harbin Institute of Technology, 2007, 39(11): 1704-1706. DOI: 10.3321/j.issn:0367-6234.2007.11.006 |
| [7] |
雷雨, 赵丹宁. 基于最小二乘支持向量机的钟差预报[J].
大地测量与地球动力学, 2013, 33(2): 91-95.
LEI Yu, ZHAO Danning. Clockerror prediction using least squares support vector machines[J]. Journal of Geodesy and Geodynamics, 2013, 33(2): 91-95. |
| [8] |
魏微, 高谦. 改进的BP神经网络模型预测充填体强度[J].
哈尔滨工业大学学报, 2013, 45(6): 90-95.
WEI Wei, GAO Qian. Strength prediction of backfilling bodybased on modified BP neural network[J]. Journal of Harbin Institute of Technology, 2013, 45(6): 90-95. DOI: 10.11918/j.issn.0367-6234.2013.06.016 |
| [9] |
郭承军, 滕云龙. 神经网络在卫星钟差短期预报中的应用研究[J].
测绘科学, 2011, 36(4): 198-200.
GUO Chengjun, TENG Yunlong. Application of neural network in satellite clock bias short-term prediction[J]. Science of Surveying and Mapping, 2011, 36(4): 198-200. |
| [10] |
郑作亚, 陈永奇, 卢秀山. 灰色模型修正及其在实时GPS卫星钟差预报中的应用研究[J].
天文学报, 2008, 49(3): 306-320.
ZHENG Zuoya, CHEN Yongqi, LU Xiushan. An improved greymodel for the prediction of real-time GPS satellite clock bias[J]. ACTA Astronomica Sinica, 2008, 49(3): 306-320. DOI: 10.15940/j.cnki.0001-5245.2008.03.012 |
| [11] |
路晓峰, 杨志强, 贾小林, 等. 灰色系统理论的优化方法及其在卫星钟差预报中的应用[J].
武汉大学学报:信息科学版, 2008, 33(5): 492-495.
LU Xiaofeng, YANG Zhiqiang, JIA Xiaolin, et al. Parameter optimization method of graysystem theory for the satellite clock error predicating[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 492-495. |
| [12] |
吕林正, 吴文江. 灰色模型GM(1, 1)优化探讨[J].
系统工程理论与实践, 2001, 21(8): 92-96.
LU Linzheng, WU Wenjiang. Research on the optimization of grey model GM(1, 1)[J]. System Engineering Theory and Practice, 2001, 21(8): 92-96. DOI: 10.3321/j.issn:1000-6788.2001.08.018 |
| [13] |
朱晓菲, 王国华, 张欣豫, 等. 基于遗传新陈代谢灰色模型的电子设备故障预测模型[J].
现代电子技术, 2014, 37(1): 86-89.
ZHU Xiaofei, WANG Guohua, ZHANG Xinyu, et al. Research on failure of electronic equipment based on genetic metabolism grey model[J]. Modern Electronics Technique, 2014, 37(1): 86-89. DOI: 10.16652/j.issn.1004-373x.2014.01.019 |
| [14] |
张朝飞, 罗建军, 徐兵华, 等. 基于灰色理论的新陈代谢自适应多参数预测方法[J].
上海交通大学学报, 2017, 51(8): 970-976.
ZHANG Zhaofei, LUO Jianjun, XU Binghua, et al. Metabolism adaptive multi-parameter prediction method based on grey theory[J]. Journalof Shanghai Jiao Tong University, 2017, 51(8): 970-976. DOI: 10.16183/j.cnki.jsjtu.2017.08.011 |
| [15] |
陈贵敏, 贾建援, 韩琪. 粒子群优化算法的惯性权值递减策略研究[J].
西安交通大学学报, 2006, 40(1): 53-56.
CHEN Guimin, JIA Jianyuan, HAN Qi. Study on the strategy of decreasing inertia weight in particle swarm optimization algorithm[J]. Journal of Xi'an Jiao Tong University, 2006, 40(1): 53-56. DOI: 10.3321/j.issn:0253-987X.2006.01.013 |
| [16] |
汪平, 许家琨, 沈国康, 等. IGS快速精密星历与事后精密星历的定位精度分析[J].
海洋测绘, 2015, 35(5): 32-34.
WANG Ping, XU Jiakun, SHEN Guokang, et al. Positioning accuracy analysis between IGS rapid precise ephemeris and final precise ephemeris[J]. Hydrographic Surveying and Charting, 2015, 35(5): 32-34. DOI: 10.3969/j.issn.1671-3044.2015.05.008 |
 2018, Vol. 50
2018, Vol. 50


