随着仿真技术在现代工程设计中的广泛应用,模型确认已经成为国内学者的研究热点.模型确认是指从模型的用途出发,客观地评估模型在多大程度上能够准确描述真实物理世界的过程[1-3].开展模型确认工作,首先需要建立科学合理的模型确认指标.模型确认指标是指用于度量模型预测与试验结果之间差异程度的指标[4-5].
在实际工程中,由于模型本身、模型参数、物理试验结果和试验数据信息等4个方面都会受到各种不确定性因素的影响,因此模型确认工作也具有一定的不确定性[6-9].目前,不确定性条件下的模型确认方法很多.文献[10]将其分为:假设检验法[11-12]、贝叶斯因子法[13-15]、频率指标[2, 16]和面积指标[17-18]等.这些方法主要适用于一维或多维独立输出模型确认,而不适合多维相关输出模型确认问题.为此,文献[19]提出了基于多维概率积分转换(probability integral transformations, PIT)的PIT面积指标和t-pooling方法,文献[20]提出了基于马氏距离(Mahalanobis distance, MD)的MD面积指标和MD-pooling方法.
已有这些方法均建立在概率方法之上,仅适合于随机不确定性模型确认问题.然而,在工程实际中,所建的多输出模型往往既含有随机输入变量,又含有区间输入变量,这类模型称为随机-区间混合不确定性多输出模型.关于这类模型确认方法,目前还鲜有研究.在随机-区间混合不确定性多输出模型中,随机变量和区间变量之间可能相互独立,也可能存在相关性.本文所研究的随机-区间混合不确定性多输出模型,是指随机输入变量和区间输入变量共存且相互独立这类模型,运用概率理论和区间分析方法,对它的确认方法进行研究.
1 MD面积指标针对随机不确定性多输出模型确认问题,文献[20]提出了适用于单个确认点的MD面积指标.
设Y =(Y1, …, Ym)为m(m>1)维模型随机输出向量,μ、Σ和FY(y1, …, ym)分别为输出向量Y的均值向量、协方差矩阵和联合分布函数. y =(y1, …, ym)为来自FY(y1, …, ym)的任一样本观察值.则Y到μ的马氏距离被定义为
| $ R\left( {\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{\mu }}} \right) = \sqrt {{{\left( {\mathit{\boldsymbol{Y}}{\rm{ - }}\mathit{\boldsymbol{\mu }}} \right)}^{\rm{T}}}{\sum ^{{\rm{ - }}1}}\left( {\mathit{\boldsymbol{Y}}{\rm{ - }}\mathit{\boldsymbol{\mu }}} \right){\rm{,}}} $ | (1) |
样本观察值y到μ的马氏距离为
| $ r\left( {\mathit{\boldsymbol{y}},\mathit{\boldsymbol{\mu }}} \right) = \sqrt {{{\left( {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{\mu }}} \right)}^{\rm{T}}}{\sum ^{ - 1}}\left( {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{\mu }}} \right)} . $ |
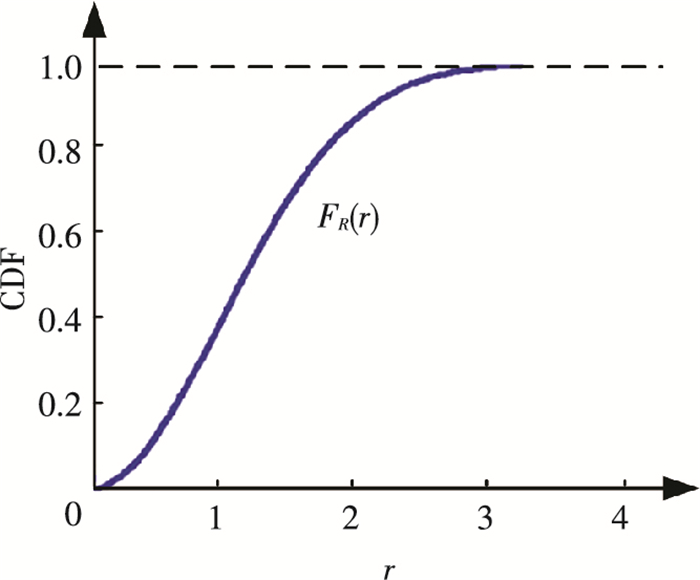
式中Y为随机输出向量.由式(1)可知,R(Y, μ)为一维随机变量.设R(Y, μ)的CDF记为FR(r)=P{R≤r},则FR(r)曲线如图 1所示.
|
图 1 随机变量CDF对应的马氏距离CDF Figure 1 CDF of MD distribution for a random variable |
由图 1可知,输出向量Y通过式(1)被转变成一维随机变量R(Y, μ).由于式(1)含有Y的均值向量和协方差矩阵,因此FR(r)综合了Y的均值向量和协方差矩阵的信息.运用MD的这一性质,文献[20]提出的多维相关响应量模型确认指标为
| $ {\rm{d}}\left( {F, S} \right) = \int_0^\infty {\left| {{F^m}\left( r \right){\rm{-}}{S^e}\left( r \right)\left| {{\rm{d}}r} \right.\;} \right.} . $ | (2) |
式中:Fm(r)为多维输出模型响应量到它的均值向量μ的MD分布函数;Se(r)为对应的试验响应量到模型响应量均值向量μ的经验MD分布函数.式(2)实质上表示Fm(r)曲线和Se(r)曲线之间的面积差,即如图 2中的阴影部分的面积.

|
图 2 多维相关响应量模型确认的MD面积指标 Figure 2 MD area validation metric for models with multiple correlated responses |
当模型与物理试验完全相同时,式(2)将趋于零;当模型与物理试验不一致时,且它们之间的差异越大,式(2)的计算结果也就越大.因此,通过式(2)计算结果的大小可以评估不同多输出模型在描述真实物理过程的准确性程度.
2 混合不确定性多输出模型确认指标 2.1 随机-区间混合不确定性多输出模型设含随机-区间混合不确定性no维输出模型的表达式定义为
| $ Z_i^m = {g_i}\left( {\mathit{\boldsymbol{X}}, \mathit{\boldsymbol{Y}}} \right){\rm{, }}\;\;\left( {i = 1, \ldots, {n_o}} \right)\; $ | (3) |
式中:X =(X1, X2, …, XnR)为nR维随机输入向量;fX(x)为随机向量X的联合概率密度函数;fXi(xi)(i=1, …, nR)为第i维随机变量Xi的边缘概率密度函数;Y =(Y1, Y2, …, YnI)为nI维区间输入向量;[YjL, YjU](j=1, …, nI)为第j维区间变量Yj的取值区间;YjL、YjU分别为第j维区间变量的下、上界,且X和Y相互独立.no维模型输出向量Zm=(Z1m, Z2m, …, Zmno)可通过式(3)获得.
当随机向量X取任意一个实现值x*时,X的随机不确定性对输出变量的影响将会被消除,模型输出响应量的不确定性则来自区间向量Y,这种情况下的模型输出响应量为多维区间变量,即Zm|(X = x*)=(Z1m|x*, Z2m|x*, …, Zmno|x*),其中第k维区间输出变量Zkm|x*的取值区间可表示为[ZkmL, ZkmU](k=1, …, no),ZkmL、ZkmU分别为第k维区间输出变量的下、上界.当随机向量X按照fX(x)在其取值范围内取全部实现值时,模型输出响应量Zm|X为no维随机区间变量,则它的上界ZmU|X和下界ZmL|X均为no维随机变量.因此,随机-区间混合不确定多输出模型确认问题即转化为:X取x*时,模型与试验输出响应量的多维随机区间变量之间的差异程度比较.
2.2 随机-区间混合不确定性多输出模型确认指标由上述分析可知,当X按照它的fX(x)在其取值范围内取全部实现值时,模型响应量Zm|X的下、上界皆为no维随机变量.设μL、ΣL分别为模型响应量下界ZmL|X的均值向量和协方差矩阵,则模型响应量下界ZmL|X到μL的MD定义为
| $ {R^{mL}}({\mathit{\boldsymbol{Z}}^{mL}}\left| \mathit{\boldsymbol{X}} \right.,\mathit{\boldsymbol{\mu}}{^L}) = \sqrt {{{({\mathit{\boldsymbol{Z}}^{mL}}\left| \mathit{\boldsymbol{X}} \right.{\rm{ - }}\mathit{\boldsymbol{\mu }}{^L})}^{\rm{T}}}{{(\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{^L})}^{{\rm{ - }}1}}({\mathit{\boldsymbol{Z}}^{mL}}\left| \mathit{\boldsymbol{X}} \right.{\rm{ - }}\mathit{\boldsymbol{\mu }}{^L})} , $ | (4) |
模型响应量上界ZmU|X到μL的MD定义为
| $ {R^{mU}}\left( {{\mathit{\boldsymbol{Z}}^{mU}}\left| \mathit{\boldsymbol{X}} \right.,\mathit{\boldsymbol{\mu }}{^L}} \right) = \sqrt {{{({\mathit{\boldsymbol{Z}}^{mU}}\left| \mathit{\boldsymbol{X}} \right.{\rm{ - }}\mathit{\boldsymbol{\mu }}{^L})}^{\rm{T}}}{{\left( {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{^L}} \right)}^{{\rm{ - }}1}}({\mathit{\boldsymbol{Z}}^{mU}}\left| \mathit{\boldsymbol{X}} \right.{\rm{ - }}\mathit{\boldsymbol{\mu }}{^L})} . $ | (5) |
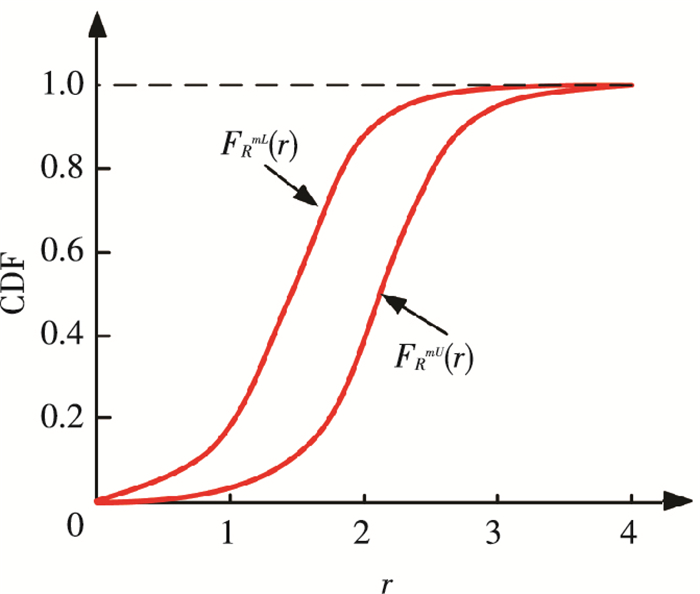
设RmL(ZmL|X, μL)和RmU(ZmU|X, μL)的分布函数分别为FRmL(r)=P{RmL≤r}和FRmU(r)=P{RmU≤r},它们如图 3所示.
|
图 3 模型响应量的上下限MD分布函数曲线 Figure 3 The MD CDF curves of the upper and the lower bounds of the model responses |
同理,相应的试验响应量下界ZeL|X到模型响应量下界均值向量μL的MD定义为
| $ {R^{eL}}\left( {{\mathit{\boldsymbol{Z}}^{eL}}\left| \mathit{\boldsymbol{X}} \right.,\mathit{\boldsymbol{\mu }}{^L}} \right) = \sqrt {{{({\mathit{\boldsymbol{Z}}^{eL}}\left| \mathit{\boldsymbol{X}} \right.{\rm{ - }}\mathit{\boldsymbol{\mu }}{^L})}^{\rm{T}}}{{\left( {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{}}^L}} \right)}^{{\rm{ - }}1}}({\mathit{\boldsymbol{Z}}^{eL}}\left| \mathit{\boldsymbol{X}} \right.{\rm{ - }}\mathit{\boldsymbol{\mu }}{^L})} , $ | (6) |
试验响应量上界ZeU|X到模型响应量下界均值向量μL的MD定义为
| $ {R^{eU}}({\mathit{\boldsymbol{Z}}^{eU}}\left| \mathit{\boldsymbol{X}} \right.,\mathit{\boldsymbol{\mu }}{^L}) = \sqrt {{{({\mathit{\boldsymbol{Z}}^{eU}}\left| \mathit{\boldsymbol{X}} \right.{\rm{ - }}\mathit{\boldsymbol{\mu }}{^L})}^{\rm{T}}}{{(\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}{^L})}^{ - 1}}({\mathit{\boldsymbol{Z}}^{eU}}\left| \mathit{\boldsymbol{X}} \right.{\rm{ - }}{\mathit{\boldsymbol{\mu }}^L})} . $ | (7) |
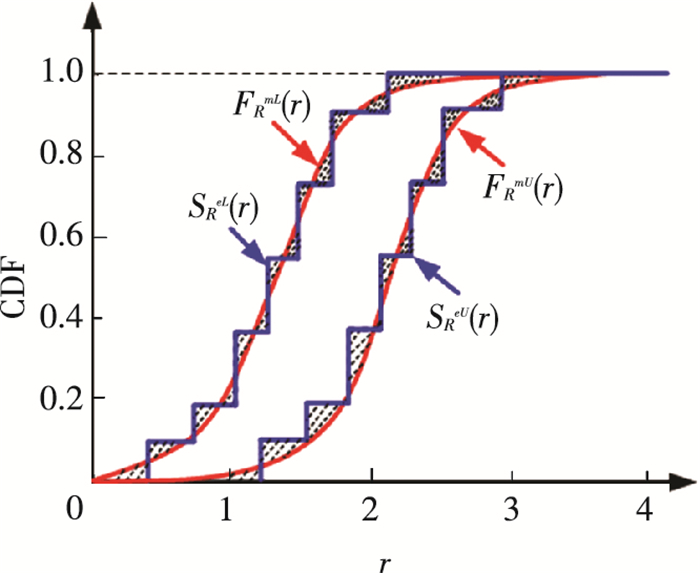
设ReL(ZeL|X, μL)和ReU(ZeU|X, μL)的经验分布函数分别为SReL(r)=P{ReL≤r}和SReU(r)=P{ReU≤r},它们如图 4中的阶梯线所示.
|
图 4 模型和试验响应量上、下界MD分布函数和经验MD分布函数 Figure 4 MD CDF and empirical MD CDF curves of the upper and the lower bounds of the model and experimental responses |
在随机输入变量取现实值的情况下,如果所建的多输出模型与物理试验完全一致,那么模型与试验响应量上、下界的MD分布函数和经验MD分布函数曲线应该完全重合,即图 4中的两条曲线与两条阶梯线之间阴影部分的面积应该为零.如果所建的模型与物理试验存在差异,那么模型与试验响应量上、下界的MD分布函数和经验MD分布函数也会存在差异,且它们的差异越大,图 4中阴影部分的面积也就越大.因此,根据模型与试验响应量上、下界的MD分布函数和经验MD分布函数曲线之间的面积大小,可以定量地评估所建模型的准确性程度.为此,本文提出的模型确认指标的表达式为
| $ \begin{array}{l} {\rm{d}}\left( {{F^m}, {S^e}} \right) = \;\\ \int_0^{ + \infty } {\left\{ {\left| {{F_{{R^{mL}}}}\left( r \right){\rm{-}}{S_{{R^{eL}}}}\left( r \right)} \right| + \left| {{F_{{R^{mU}}}}\left( r \right){\rm{-}}{S_{{R^{eU}}}}\left( r \right)} \right|\;} \right\}{\rm{d}}r.} \end{array} $ | (8) |
对式(8)进一步分析可以看出,本文提出的新指标具有下列数学性质.
性质1 非负性.由于式(8)的被积函数为非负函数,因此本文提出的新指标d(Fm, Se)也为非负数.
性质2 对称性.由于
| $ \begin{array}{l} d\left( {{F^m}, {S^e}} \right) = \int_0^{ + \infty } {\left\{ {\left| {{F_{{R^{mL}}}}\left( r \right){\rm{-}}{S_{{R^{eL}}}}\left( r \right)} \right| + \left| {{F_{{R^{mU}}}}\left( r \right){\rm{-}}{S_{{R^{eU}}}}\left( r \right)} \right|\;} \right\}} \;{\rm{d}}r = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int_0^{ + \infty } {\left\{ {\left| {{S_{{R^{eL}}}}\left( r \right){\rm{-}}{F_{{R^{mL}}}}\left( r \right)} \right| + \left| {{S_{{R^{eU}}}}\left( r \right){\rm{ - }}{F_{{R^{mU}}}}\left( r \right)} \right|} \right\}} {\rm{d}}r = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{d}}\left( {{S^e}, {\rm{ }}{F^m}} \right){\rm{, }} \end{array} $ |
所以新指标d(Fm, Se)具有对称性.
性质3 理想模型的指标值趋零性.当且仅当随机-区间混合不确定性多输出模型与物理试验完全一致时,如果X按照fX(x)在其取值范围内取全部实现值,且样本量趋于无穷,则模型与试验响应量上、下界的MD分布函数和经验MD分布函数曲线重合, 即d(Fm, Se)趋于零.
2.4 指标的求解运用Monte Carlo数字模拟法,新指标的求解过程主要包括以下7个步骤.
步骤1 获取模型随机输入变量的实现值.根据随机输入变量X的联合概率密度fX(x),产生样本容量为MRm的模型输入随机变量的实现值xi=(xi1, xi2, …, xinR)(i=1, …, MRm).
步骤2 获取模型区间输入变量样本.将模型的区间输入变量Y =(Y1, Y2, …, YnI)在其取值区间内均匀的离散成NI个样本yk=(yk1, yk2, …, yknI),(k=1, …, NI).
步骤3 求解多输出模型响应量的区间集.对于模型的随机输入变量X的每一个实现值xi=(xi1, xi2, …, xinR)(i=1, …, MRm),根据区间输入变量Y的NI个样本yk=(yk1, yk2, …, yknI)(k=1, …, NI),计算对应的模型响应量Zm|(X = xi),进而求得与X = xi对应的模型输出响应量的区间集[zmL|xi, zmU|xi](i=1, …, MRm).
步骤4 求解模型输出响应量上、下界的经验MD分布函数.依据步骤3求得的MRm个不同的模型输出响应量区间上、下界zmU|xi和zmL|xi,计算区间下界集zmL|xi (i=1, …, MRm)的均值向量μL和协方差矩阵ΣL,然后根据式(4)、(5)求解模型输出响应量区间上、下界ZmU|X和ZmL|X的经验MD分布函数FRmL(r)和FRmU(r).
步骤5 求解试验输出响应量的区间集.按照X的联合概率密度fX(x)选取样本容量为MRe的输入向量试验样本xj=(xj1, xj2, …, xjnR)(j=1, …, MRe),分别固定每个试验样本xj,通过试验得到与区间变量向量Y的NI个样本yk=(yk1, yk2, …, yknI)(k=1, …, NI)对应的输出响应量观测值Ze (X = xj),并求解对应于X = xj的试验输出响应量的区间集[zeL|xj, zeU|xj](j=1, …, MRe).
步骤6 求解试验输出响应量上、下界的马氏距离经验分布函数.依据步骤5求得的MRe个不同的试验输出响应量的区间上、下界zeU|xj和zeL|xj,根据式(6)、(7)求得试验输出响应量的上、下界经验MD分布函数SReL(r)和SReU(r).
步骤7 通过式(8)计算模型确认指标d(Fm, Se).
3 算例分析下面通过一个数字算例和一个工程算例,验证本文所提指标的可行性和有效性.
3.1 数字算例在本算例中,物理试验数据由式(9)产生,式中x∈[0, 6]为区间变量,θ(θ=1.5)为模型参数,ε1~N(0, 0.22)、ε2~N(0, 0.22)分别为两个试验响应量的测量误差.设测量误差ε1与ε2之间的相关系数为ρε1, ε2=0.5.ρε1, ε2的表达式为
| $ {\rho _{{\varepsilon _1}, {\varepsilon _2}}} = \frac{{\;{\rm{Cov}}({\varepsilon _1}, {\varepsilon _2})}}{{\sqrt {D({\varepsilon _1})} \sqrt {D({\varepsilon _2})} }}. $ |
选取与物理试验对应的7个模型(见表 1),它们被分为3组来验证新指标的可行性和有效性.
| $ \begin{array}{l} y_1^e\left( {x, \theta } \right) = {\rm{sin}}(2x{\rm{-}}0.5{\rm{ \mathsf{ π} }})\theta + {\varepsilon _1}, \\ y_2^e\left( {x, \theta } \right) = {\rm{cos}}(0.25{\rm{ \mathsf{ π} }}x)\theta + 0.2x + {\varepsilon _2}. \end{array} $ | (9) |
| 表 1 3个测试组的模型 Table 1 Formulas of mathematical models in three test cases |
第1组测试包括3个模型.模型1与式(9)相同,是一个完全正确的模型;模型2与式(9)中的参数θ有差异;模型3与式(9)相比,不仅参数θ发生了变化,而且试验响应量测量误差的相关系数也发生了变化.由此可推断出模型1优于模型2,模型2优于模型3.这组测试的目的是在随机-区间混合不确定性多输出模型的参数或相关性存在差异的情况下,讨论所建指标的可行性和有效性.
在本组测试中,模型的随机输入变量的样本容量MRm为10 000,试验随机输入变量的样本容量MRe为1 000,区间输入变量样本量NI为300,按照本文提出的指标求解方法和步骤,计算第1组测试中的3个模型的指标值,计算结果见表 2.
| 表 2 数字算例的模型确认指标计算结果 Table 2 Model validation metric results of the numerical test case |
由表 2可以看出,模型1的指标值最小(0.085 7),模型2次之(2.472 8),而模型3的指标值最大(5.440 9).通过3个指标的计算结果,可以清晰地判断出模型1优于模型2,模型2优于模型3,这一判断结论与定性分析的结论完全一致.此外,依据指标的数学性质的性质3可知,模型1的指标值应该收敛于0,但表 2中模型1的指标值为0.085 7,并不为零.产生这一问题的原因为:在指标求解过程中,FRmL(r)、FRmU(r)、FRmL(r)和FRmU(r)均是通过有限样本估计所得,这必然会产生一定的误差.如果进一步增大样本容量,FRmL(r)、FRmU(r)、FRmL(r)和FRmU(r)的计算结果将会趋于理论值,这样指标的计算结果就会趋于零.由此可见,对于参数或相关性存在差异的随机-区间混合不确定性多输出模型,所建指标能够有效地度量不同模型与物理试验之间的差异程度,正确地判断不同模型之间的优劣.
3.1.2 测试2第2组测试包括2个模型.与试验模型相比,模型4和模型5均将参数θ作为随机变量.模型4和模型5中参数θ的均值与试验模型的参数θ相同,皆为1.5,但模型4中θ的方差比模型5的小.由此可推断出模型4优于模型5.第2组测试的目的是在模型参数的分布函数存在很小差异时,验证所建指标是否能够有效判断不同模型之间的优劣.
同理,可求得第2组测试中的2个模型的指标值,计算结果见表 2.由表 2可知,模型4的指标值(0.451 0)小于模型5的指标值(0.725 7),由此可判断出模型4优于模型5,这一判断结论与定性分析的结论完全吻合.因此,对于参数的分布函数存在很小差异的随机-区间混合不确定性多输出模型,所建的指标也能够正确地判断不同模型之间的优劣.
3.1.3 测试3第3组测试也包括2个模型.与试验模型相比,模型6和模型7中随机输入变量与式(9)完全相同,但区间变量发生了变化.模型6中变量x的区间下限大于式(9)中x的区间下限,模型7中区间变量x的区间上限小于模型6中区间变量x的区间上限.因此模型6优于模型7.第3组测试的目的是在模型区间变量的取值区间发生变化时,验证所建指标是否能够有效判断不同模型之间的优劣.
同理,可求得第3组测试中的2个模型的指标值,计算结果见表 2.由表 2可以看出,模型6的指标值(0.926 6)小于模型7的指标值(3.143 5),由此可以判断出模型6优于模型7,这一判断结论与定性分析的结论完全吻合.因此,对于区间变量的取值区间存在差异的随机-区间混合不确定性多输出模型,所建指标也能够正确地判断不同模型之间的优劣.
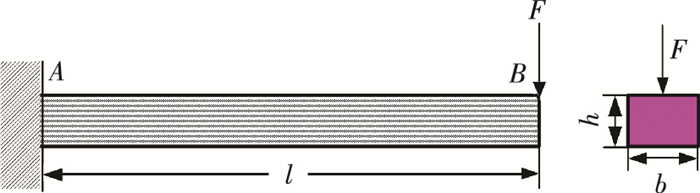
3.2 工程算例如图 5所示的矩形截面悬臂梁,自由端承受集中力F∈[1 000, 1 500],截面宽度b=50 mm,截面厚度h=37 mm,梁的长度l~N(2, 0.022),弹性模量E~N(206.8, 162).输出响应量为梁固定端A点的正应力σA(GPa)、自由端B点处截面的转角θB(rad)和挠度yB(m),它们试验数据由式(10)产生,它们的测量误差分别为εθ~N(0, 0.0032)、εy~N(0, 0.0032)、εσ~N(0, 0.012).
| $ \left\{ \begin{array}{l} {\sigma _A} = \frac{{6Fl}}{{b{h^2}}} + {\varepsilon _\sigma }{\rm{, }}\\ {y_B} = \frac{{4F{l^3}}}{{Eb{h^3}}}\; + {\varepsilon _y}{\rm{, }}\\ {\theta _B} = \frac{{6F{l^2}}}{{Eb{h^3}}} + {\varepsilon _\theta }. \end{array} \right. $ | (10) |
|
图 5 悬臂梁结构 Figure 5 Diagram of the cantilever beam |
为节约试验费用,假设建立了6个的悬臂梁模型,这些模型的形式与式(10)相同,但在输入变量存在差异,具体见表 3.为了便于研究,这6个模型被分为两组.第1组包括模型1、模型2和模型3,第2组包括模型4、模型5和模型6.与物理试验相比,第1组中3个模型的区间输入变量的取值区间与试验模型相同,但输入随机变量的分布函数的参数相互之间存在一定差异,第2组中3个模型的随机变量的分布函数与物理试验相同,但区间变量的取值区间相互不同.由表 3中数据可以判断出,在第1组模型中,模型1优于模型2,模型2优于模型3;在第2组模型中,模型4优于模型5,模型5优于模型6.
| 表 3 悬臂梁输入变量的参数分布 Table 3 Distribution parameters of inputs of the cantilever beam |
同算例1相似,MRm为10 000,MRe为1 000,NI为500,这两组模型确认指标计算结果见表 4.
| 表 4 悬臂梁模型确认指标计算结果 Table 4 Model validation metric results of the cantilever beam |
由表 4可以看出,对于第1组模型,模型1的指标值(0.065 2)小于模型2的指标值(1.197 2),模型2的指标值(1.197 2)小于模型3的指标值(4.713 9),由此可判断出:模型1优于模型2,模型2优于模型3;对于第2组模型,由指标计算结果可判断出:模型4优于模型5,模型5优于模型6.由此可见,这两组模型指标值的判断结论与定性分析结论完全吻合,从而再次验证了本文所提指标的可行性和有效性.
3.3 模型确认指标的风险分析虽然上述分析结果表明,在样本充足的情况下,新指标能够有效解决随机-区间混合不确定性多输出模型确认问题.但是样本量匮乏时,运用新指标进行模型确认存在一定的风险.下面以算例2的第1组模型为例,分两种情况进行讨论.
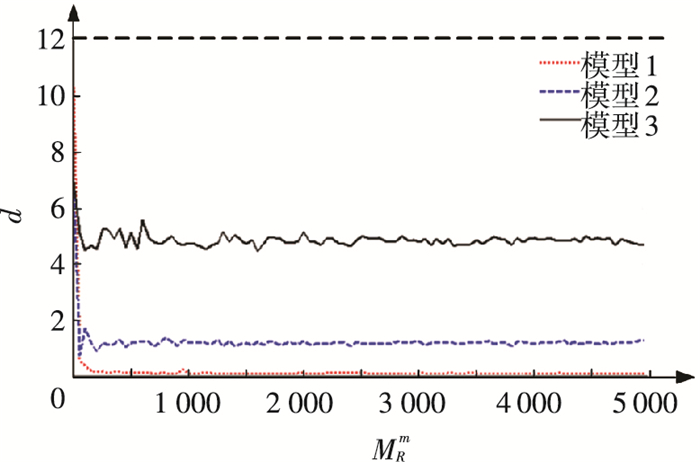
3.3.1 MRe固定,MRm变化在保持NI为500情况下,当MRm发生变化时,d随MRm的变化情况如图 6所示.
|
图 6 模型确认指标d随MRm的变化曲线 Figure 6 Model validation metric d versus the MRm |
由图 6可以看出,随着MRm的增大,指标值d迅速减小,波动幅度也趋于减小.当MRm < 50时,由于求解模型响应量区间上、下限MD分布函数时存在较大误差,使得3个模型的指标值很不稳定,并存在相互重叠的现象.因此,在MRm较少的情况下,运用新指标对不同模型的优劣进行评判,可能存在错判、误判风险.但当MRm>100时,指标值d开始趋于收敛.这一现象表明随着MRm的不断增大,模型响应量区间上限界的MD分布函数的计算结果趋于它们的理论解.由此可见,运用新指标进行模型确认时,要尽量获得充足的模型输入变量样本,以减少由于计算原因而导致的错判误判风险.
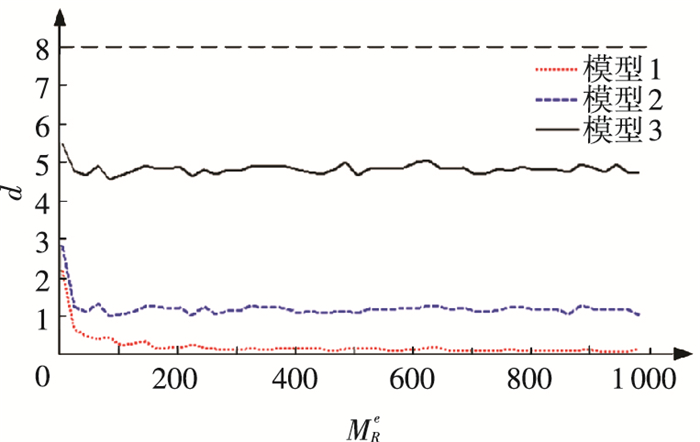
3.3.2 MRm固定,MRe变化在保持NI为500的情况下,当MRe发生变化时,d随MRe的变化情况如图 7所示.
|
图 7 模型确认指标d随MRe的变化曲线 Figure 7 Model validation metric d versus the MRe |
由图 7可以看出,随着MRe的增大,d同样迅速减小并趋于收敛.当MRe < 100时,由于在求解试验响应量区间上、下限的经验MD分布函数时存在较大误差,使得3个模型的指标值很不稳定.因此,在试验样本较少的情况下,运用新指标对不同模型的优劣进行评判,会存在一定的错判、误判风险.但当MRe>100时,d开始趋于稳定并收敛,并能够客观地评估不同模型与试验的一致性.
由上述分析可知,为了控制新指标的错判、误判风险,在模型确认时,首先要保证能够获得有效的样本.由于不同领域的科学问题所建的多输出模型是不同的,对应的模型确认指标达到稳定收敛状态所需的有效样本量也是不同的.因此,在模型确认时,有效样本量的大小要根据具体问题来确定.当样本量取使指标值达到稳定收敛状态的样本量时,就能够防止错判、误判问题的发生,保证所选择的随机-区间混合不确定性多输出模型的正确性.
4 结论1) 对于随机-区间混合不确定性下的多输出模型,当它的随机输入变量按照其联合概率密度在其取值范围内取所有实现值时,模型输出响应量则为多维随机区间变量.因此,随机-区间混合不确定性多输出模型确认的实质上就是比较模型与试验输出响应量的多维随机区间变量之间的差异程度.
2) 运用概率方法和区间理论,将随机不确定性多输出模型的MD面积指标,推广到随机-区间混合不确定性多输出模型确认中.将模型与试验输出多维随机区间变量上、下界的MD分布函数和经验MD分布函数之间的面积差异,定义为新指标,解决了随机和区间变量共存条件下多输出模型在描述真实物理试验时的准确性评估方法问题.
3) 研究结果表明,在样本充足的情况下,所提的新指标在随机-区间混合不确定性多输出模型确认方面可行有效,但它也有一定的局限性.当样本量较少时,运用新指标对不同模型的优劣进行评判时,存在一定的错判误判风险.
| [1] |
OBERKAMPF W L, SINDIR M N, CONLISK A T. Guide for the verification and validation of computational fluid dynamics simulations: AIAA-G-077-1998[R]. Reston, VA: American Institute of Aeronautics and Astronautics, 1998.
|
| [2] |
OBERKAMPF W L, BARONE M F. Measures of agreement between computation and experiment: validation metrics[J].
Journal of Computational Physics, 2006, 217(1): 5-36.
DOI: 10.1016/j.jcp.2006.03.037 |
| [3] |
OBERKAMPF W L, ROY C J.
Verification and validation in scientific computing[M]. New York, USA: Cambridge University Press, 2010.
|
| [4] |
MESSER M, PANCHAL J H, KRISHNAMURTHY V, et al. Model selection under limited information using a value of information based indicator[J].
Journal of Mechanical Design, 2010, 132(12): 121008.
DOI: 10.1115/1.4002751 |
| [5] |
XIONG Ying, CHEN Wei, TSUI K L, et al. A better understanding of model updating strategies in validating engineering models[J].
Compute Methods in Applied Mechanics and Engineering, 2009, 189(15/16): 1327-1337.
DOI: 10.1016/j.cma.2008.11.023 |
| [6] |
BAYARRI M J, BERGER J O, PAULO R, et al. A framework for validation of computer models[J].
Technometrics, 2007, 49(2): 138-154.
DOI: 10.1198/004017007000000092 |
| [7] |
KENNEDY M C, O'HAGAN A. Bayesian calibration of computer models[J].
Journal of the Royal Statistical Society, 2001, 63(3): 425-464.
DOI: 10.1111/1467-9868.00294 |
| [8] |
ARENDT P D, APLEY D W, CHEN Wei, et al. Improving identifiability in model calibration using multiple responses[J].
Journal of Mechanical Design, 2012, 134(10): 100909.
DOI: 10.1115/1.4007573 |
| [9] |
NECPÁLOVÁ M, ANEX R P, FIENEN M N, et al. Understanding the DayCent model: calibration, sensitivity, and identifiability through inverse modeling[J].
Environmental Modelling & Software, 2015, 66: 110-130.
DOI: 10.1016/j.envsoft.2014.12.011 |
| [10] |
LIU Yu, CHEN Wei, ARENDT P, et al. Toward a better understanding of model validation metrics[J].
Journal of Mechanical Design, 2011, 133(7): 071005.
DOI: 10.1115/1.4004223 |
| [11] |
BURANATHITI T, CAO Jian, CHEN Wei, et al. Approaches for model validation: methodology and illustration on a sheet metal flanging process[J].
Journal of Manufacturing Science and Engineering-Transactions of the ASME, 2006, 128(2): 588-597.
DOI: 10.1115/1.1807852 |
| [12] |
REBBA R, MAHADEVAN S. Validation of models with multivariate output[J].
Reliability Engineering and System Safety, 2006, 91(8): 861-871.
DOI: 10.1016/j.ress.2005.09.004 |
| [13] |
张保强, 陈国平, 郭勤涛. 模型确认热传导挑战问题求解的贝叶斯方法[J].
航空学报, 2011, 32(7): 1202-1209.
ZHANG Baoqiang, CHEN Guoping, GUO Qintao. Solution of model validation thermal challenge problem using a Bayesian method[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(7): 1202-1209. |
| [14] |
REBBA R, MAHADEVAN S. Model predictive capability assessment under uncertainty[J].
AIAA Journal, 2006, 44(10): 2376-2384.
DOI: 10.2514/1.19103 |
| [15] |
MAHADEVAN S, REBBA R. Validation of reliability computational models using Bayes networks[J].
Reliability Engineering and System Safety, 2005, 87(2): 223-232.
DOI: 10.1016/j.ress.2004.05.001 |
| [16] |
OBERKAMPF W L, TRUCANO T G. Verification and validation in computational fluid dynamics[J].
Progress in Aerospace Sciences, 2002, 38(3): 209-272.
DOI: 10.1016/S0376-0421(02)00005-2 |
| [17] |
FERSON S, OBERKAMPF W L. Validation of imprecise Probability models[J].
International Journal of Reliability and Safety, 2009, 3(1): 3-22.
DOI: 10.1504/IJRS.2009.026832 |
| [18] |
FERSON S, OBERKAMPF W L, GINZBURG L. Model validation and predictive capability for the thermal challenge problem[J].
Computer Methods in Applied Mechanics and Engineering, 2008, 197(29/30/31/32): 2408-2430.
DOI: 10.1016/j.cma.2007.07.030 |
| [19] |
LI Wei, CHEN Wei, JIANG Zhen, et al. New validation metrics for models with multiple correlated responses[J].
Reliability Engineering and System Safety, 2014, 127: 1-11.
DOI: 10.1016/j.ress.2014.02.002 |
| [20] |
ZHAO Lufeng, LU Zhenzhou, YUN Wanying, et al. Validation metric based on Mahalanobis distance for models with multiple correlated responses[J].
Reliability Engineering and System Safety, 2017, 159: 80-89.
DOI: 10.1016/j.ress.2016.10.016 |
 2018, Vol. 50
2018, Vol. 50


