大力开发和利用清洁、无污染、可再生新能源是人类面对能源需求和经济社会可持续发展能做出的唯一选择.风能是新能源领域中技术最成熟、规模最大、最具开发条件和最有发展前景的新能源.风力机是将风能转换成机械能、电能或热能的能量转换装置.风力机主要有两种型式:水平轴风力机(horizental axis wind turbine,HAWT)和垂直轴风力机(vertical axis wind turbine,VAWT)[1-4].尽管HAWT相比VAWT有更高的风能利用率和更成熟的开发技术,但VAWT运转与风向无关,振动小、噪音低、环境友好、安全性高、结构简单、便于安装和维护维修等优点,近年来受到各国研究人员的广泛关注和高度重视,成为当前风力发电领域的一个研究热点[5].本文即以结构简单、加工容易、成本低廉,整个叶片都可产生较高扭矩,风能利用效率高的H型垂直轴风力机(H type vertical axis wind turbine,H-VAWT)为对象,研究其不同设计参数(实度、翼型和展弦比)对H-VAWT叶尖损失的影响.帮助H-VAWT设计者设计叶片时是否要增加叶尖小翼或增大叶片展弦比作出决策.
通过数值计算及实验研究,人们发现VAWT叶尖与风扇、螺旋桨等旋转机械叶片叶尖以及飞机机翼翼尖的流动相似,非常复杂[6].由于叶片吸力面上的压力小于压力面上的压力,流线从叶尖上方或下方由压力面流向吸力面,以致叶尖部分的流动既有沿叶片翼型的环向绕流,又有叶尖端部的绕流,不同方向的绕流又会相互干扰,形成典型的复杂三维流动.由于叶尖上方或下方的绕流使得叶尖部分的压差减少,叶片表面的压力系数分布沿着展长方向的分布出现不同,叶片叶尖部分对整体力矩的贡献降低,以致整体H-VAWT的效率减小,这一损失是由叶尖处的流动带来的,即称为叶尖损失.
由于叶尖处的流场是3D的,其损失不能由基于2D的叶素理论或动量理论来确定,从现有的文献看,一些研究者为了更准确的估计H-VAWT的气动性能,对2D理论或其他理论方法,用相应的叶尖损失因数来估计,如prandtl、Goldsteins和Glauert等叶尖损失因数[7-8].
对实际3D H-VAWT,为了改善其叶尖的流动情况,减少叶尖的流动损失,人们提出了各种不同形式的叶尖小翼概念,即在叶尖加装上不同形式的小翼、导流板以改变叶尖流场,使叶尖的流动接近于2D流动[9-12];有的研究者提出加大展弦比的概念,加大叶片展弦比是在不改变叶尖流动的情况下,使叶尖损失的能量占整体来流风能的比率减少,从而使其功率效率与无限展长模型的差减小.但由于不同的VAWT等旋转机械以及机翼,所选实度不同、翼型各异,增加叶尖小翼或加大展弦比是否有作用,在什么情况下有作用及作用程度,这些对希望通过增加叶尖小翼或加大展现比以改善旋转机械或机翼气动性能的研究或设计来讲,都是迫切需要解决的问题,而目前尚未发现有人对此进行研究.本文即通过数值计算对比分析,回答了上述问题,不仅给实际H-VAWT叶片设计提供参考,亦给其他旋转机械叶片或飞机机翼设计提供借鉴.
1 计算方法及计算对比模型 1.1 计算方法有许多的方法和理论用于预测风力机的性能、模拟其流场,例如动量理论模型、涡模型、瀑布模型、面元法和CFD方法.动量理论模型、涡模型和瀑布模型为准稳态方法,其计算需要翼型的数据库,对H-VAWT性能计算特别需要低雷诺数和低尖速比下的较宽攻角范围的升力系数CL和阻力系数CD数据,这些方法只能用作设计过程的评估,不能模拟H-VAWT三维非稳态流场,没有办法使用其用作翼型参数的设计,另外双流管模型不适合高尖速比和高实度的H-VAWT流场计算;涡模型是许多研究者认为计算比较准确的模型,但是它们需要消耗较多计算机时,且在一些情况下会出现不收敛问题.面元法尽管较涡模型更准确,较CFD方法更简单,但它是基于应用势流理论,其模型没有考虑在实际流动中不可忽略的流体黏性.
相比上述方法,CFD方法凭借其可计算动态失速、考虑黏性影响、三维非稳态流动以及阻力的影响等特点,在计算风力机流场方面具有更大的优势,尽管相对需要消耗较大计算机时,但这种方法随着计算机计算能力的高速发展越来越流行[6].
本文应用收敛性和稳定性较好的CFD分析软件CFX模拟H-VAWT非稳态三维流场,并通过普遍使用和可靠性得到验证的k-ω SST(Menter’s shear stress transport, menter, 1994)湍流模型[13-14]求解其时均N-S方程(URANS),得到需要的H-VAWT气动性能参数(力矩系数Cm或功率系数Cp)和流场分布.
CFD计算前对不同三维模型的的建立和网格划分通过CATIA和ICEM软件完成,为减少计算负担,所建模型均为上半模型,底面设置为对称面,其中网格生成示例如图 1所示.

|
图 1 计算模型网格划分示例 Figure 1 The sample of calculating grids generation |
由于实际H-VAWT的长度是有限的,故叶尖损失是不可避免的,又由于叶尖或翼尖不能从叶片或机翼上割裂出来,所以不管是计算还是实验都很难把孤立的叶尖损失准确的求出来.为了量化叶尖损失,取两种计算模型:有限展长(finite blade length,FBL)模型和相应的无叶尖损失的无限展长(infinite blade length,INFBL)模型.两种不同叶片模型生成的H-VAWT的气动性能(用功率系数Cp表示)相比较所得的相对差值记为该FBL H-VAWT气动性能的最大改善比率(式(1)).本文通过比较不同设计参数(实度和翼型)生成的H-VAWT在不同尖速比下气动性能的相对差值或最大改善比率来分析各个参数对叶尖损失的影响情况,为实际的FBL H-VAWT是否需要增加叶尖小翼等改善叶尖损失措施提供准确的参考依据.
| $ \eta = \;\frac{{\Delta {C_p}\;}}{{{C_{p{\rm{FBL}}}}}}\; = \frac{{{C_{p{\rm{INFBL}}}}{\rm{-}}{C_{p{\rm{FBL}}}}}}{{{C_{p{\rm{FBL}}}}}}\; \times 100\% . $ | (1) |
式中:CpINFBL、CpFBL分别为无限和有限展长H-VAWT功率效率.
需要指出的是,本文计算用的CpFBL均为展弦比μ=7.5的FBL H-VAWT的气动性能,且不同设计参数所生成的H-VAWT在不同尖速比下的CpFBL是不同的,也就是说所得到的气动性能的最大改善比率均是基于H-VAWT各自原有气动性能的基础上的.
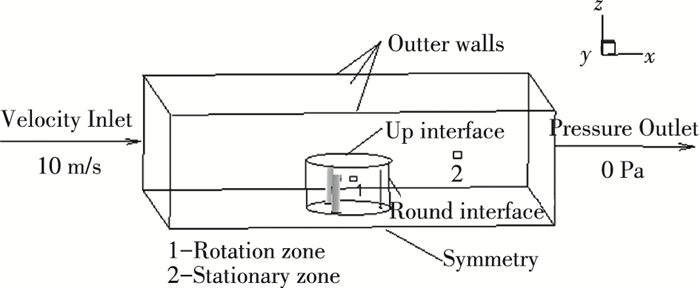
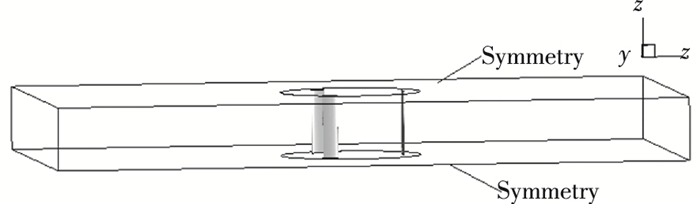
FBL计算模型示例和边界条件设置如图 2所示,INFBL计算模型示例如图 3所示.该模型包裹叶片的旋转域及外静止域与叶片等高,上、下面均设为对称面以实现INFBL模型.
|
图 2 FBL H-VAWT模型示例及边界条件 Figure 2 The FBL H-VAWT geometry sample and bounday conditions |
|
图 3 INFBL H-VAWT模型示例 Figure 3 The INFBL H-VAWT geometry sample |
在改进叶尖损失的方法上,文献[5-7]关于不同外形的叶尖小翼对H-VAWT叶尖损失的改进效果进行了研究,本文不再赘述.为了全面的总结H-VAWT设计参数对其叶尖损失的影响,本文更详细的研究和分析了展弦比对叶尖损失的影响及改进效果,通过对8种不同展弦比所生成的FBL H-VAWT在同一尖速比(λ=1.5)下的气动性能进行计算对比,总结了其对改善叶尖损失的影响,亦为H-VAWT设计提供了相应的参考依据.本文所有计算模型的基本尺寸为:叶片弦长c=400 mm,叶轮直径D=2.5 m.
进口自由来流风速V∞=10 m/s,压力出口设置为0 Pa.
2 实度(σ)对H-VAWT叶尖损失的影响本文计算了5种实度H-VAWT(0.32~1.60)在不同尖速比下气动性能的相对差值情况, 如图 4所示.

|
图 4 不同实度H-VAWT η-λ曲线 Figure 4 η-λ curves for different solidity H-VAWT |
从图 4可以看出:1)不论大实度还是小实度H-VAWT,当尖速比较高时,相对差值较大,特别是λ>1.00时(图 4的正值表示INFBL H-VAWT优于FBL H-VAWT的气动性能,反之则相反);当λ < 1.00时,相对差值为负,即INFBL H-VAWT差于FBL H-VAWT的气动性能,特别是实度较小的情况. 2)不论是低尖速比还是高尖速比,当实度较小时,其Cp值的相对差值大都小于实度较大的情况,另有大实度所对应的曲线较小实度的情况较陡,也就是说实度越大对H-VAWT的叶尖损失的影响越大.
从以下3个方面进行分析:1)不同实度H-VAWT在低尖速比下的叶尖损失情况.2)不同实度H-VAWT在高尖速比下的叶尖损失情况.3)同一实度H-VAWT在不同尖速比下的叶尖损失情况.
为了分析不同实度、不同尖速比下FBL&INFBL H-VAWT气动性能的变化情况,先推导Cp与Cm的关系.
| $ \begin{array}{l} {C_p} = \frac{{{P_{{\rm{turbine}}}}}}{{{P_{{\rm{wind}}}}}}\;\; = \frac{{M\omega }}{{\frac{1}{2}\rho {V^3}A}} = \frac{{M\omega \cdot{R}}}{{\frac{1}{2}\rho {V^3}A\cdot{R}}} = \\ \frac{M}{{\frac{1}{2}\rho {V^2}A\cdot{R}}}\cdot\frac{{\omega R}}{V} = {C_m}\cdot\lambda {\rm{, }} \end{array} $ | (2) |
| $ \overline {{C_p}} \; = \overline {{C_m}} \cdot\lambda {\rm{, }} $ | (3) |
| $ \overline {{C_m}\;} = \frac{{{C_m}\left( {{\rm{max}}} \right) + {C_m}\left( {{\rm{min}}} \right)}}{2}. $ | (4) |
式中:CpINFBL为H-VAWT功率; CpFBL为来流风功率; M为H-VAWT转动力矩; ω为转动角速度; λ为转动尖速比; V为自由来流风速; ρ为空气密度; A为H-VAWT迎风面积; R为转动半径.
由式(2)可知,Cp与Cm的关系与λ成正比,若固定λ,Cp与Cm的趋势完全相同,即FBL&INFBL H-VAWT模型的Cm的对比情况与Cp的对比情况相同,为了计算软件读取方便,下文亦由Cm代替Cp进行对比情况分析.
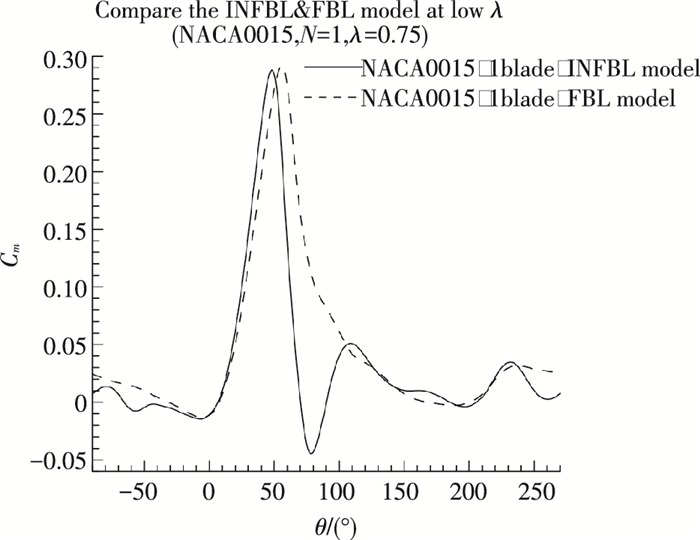
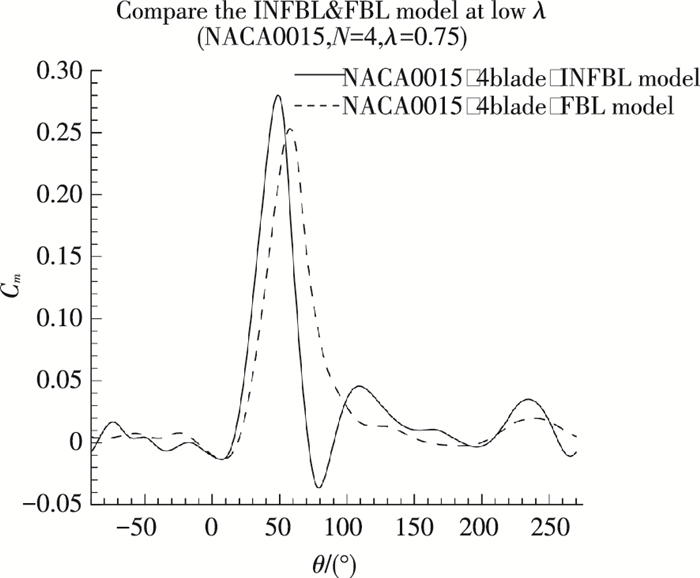
2.1 不同实度H-VAWT在低尖速比下的叶尖损失情况图 5、6分别给出了小实度(N=1)和大实度(N=4)在λ=0.75下FBL&INFBL H-VAWT在旋转一周过程中其中一个叶片的Cm对比情况.
|
图 5 INFBL&FBL H-VAWT在低尖速比下的Cm对比情况(N=1, λ=0.75) Figure 5 Cm VS azimuth angles curves for INFBL&FBL H-VAWT with small solidity at low tip speed ratio(N=1, λ=0.75) |
|
图 6 INFBL&FBL H-VAWT在低尖速比下的Cm对比情况(N=4, λ=0.75) Figure 6 Cm VS azimuth angles curves for INFBL&FBL H-VAWT with large solidity at low tip speed ratio(N=4, λ=0.75) |
从图 5、6可以看出,尽管INFBL H-VAWT在旋转一周过程中的最大Cm值均优于FBL H-VAWT(小实度H-VAWT,其相差不太明显;大实度H-VAWT,最大Cm值相差较明显),但最小Cm值在低尖速比情况下变差很多,以致在H-VAWT旋转一周过程中的Cm平均值变差.
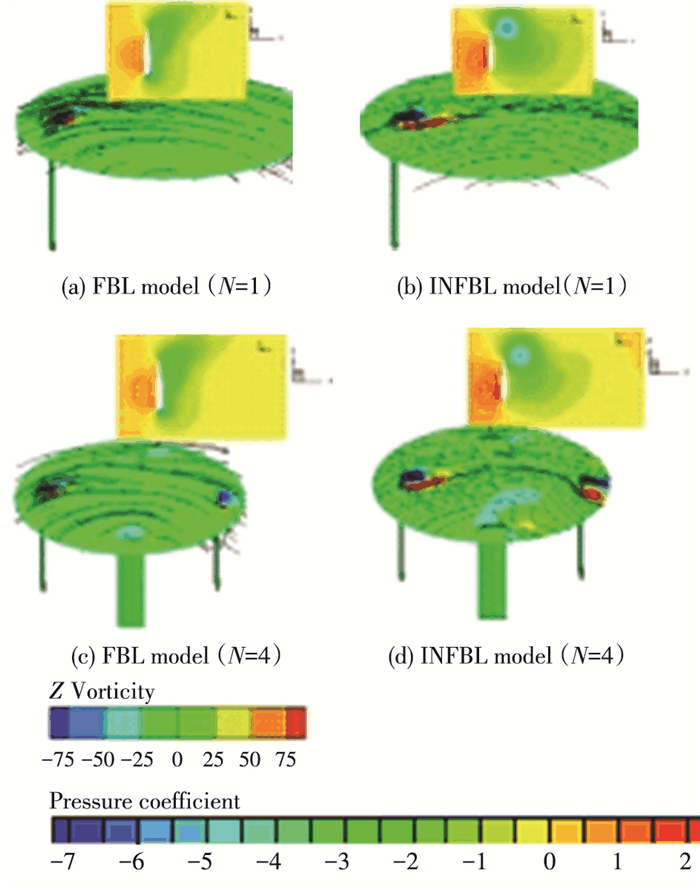
为了更好的理解INFBL H-VAWT最小Cm值变差的原因,图 7给出了最小Cm值所在方位角(从图 5、6看均约为90°)处叶尖所截平面z方向的涡量和压力系数云图,从图 7中可以看到,叶片翼型在该方位角处有很强的分离现象,这是由于根据式(5),当λ较小时,该最小Cm值所在的90°方位角处的翼型攻角为大于失速角的某一攻角,在该攻角下,分离涡向叶片翼型前缘移动,流动出现大分离现象.
| $ \begin{array}{l} \alpha = {\rm{arctan}}\left( {\frac{{{V_\infty }{\rm{sin}}\;\theta }}{{\omega R + {V_\infty }{\rm{cos}}\;\theta }}} \right) = {\rm{arctan}}(\frac{{{\rm{sin}}\;\theta }}{{\frac{{\omega R}}{{{V_\infty }}} + {\rm{cos}}\;\theta }})\\ = \;{\rm{arctan}}(\frac{{\;{\rm{sin}}\;\theta }}{{\lambda + {\rm{cos}}\;\theta }}){\rm{, }} \end{array} $ | (5) |
|
图 7 INFBL&FBL H-VAWT叶尖截面上(Z/H≈0.967)涡量和压力系数云图(λ=0.75) Figure 7 The vorticity and pressure coefficient contours of the blade tip sitted surface for INFBL&FBL H-VAWT(Z/H≈0.967, λ=0.75) |
式中θ为H-VAWT旋转过程中不同位置所处的方位角.
从图 7亦可以看到,FBL相比INFBL H-VAWT(不论小实度或大实度)来讲,叶尖的流动对分离涡起到干扰作用,延迟了流动分离,高压区域更靠近叶片翼型后缘,使得压差方向偏向旋转方向,这对H-VAWT旋转力矩的贡献是有利的,有利于增大Cm的最小值,这即是INFBL H-VAWT相比FBL H-VAWT最小Cm值在低尖速比情况下变差的原因.由于H-VAWT起动时其尖速比是比较低的,由上述分析可知,在低尖速比下,增加叶尖小翼或加大叶片展弦比对H-VAWT气动性能是起不到改善作用的,因此改善叶尖损失的措施对H-VAWT自起动性能是不利的.
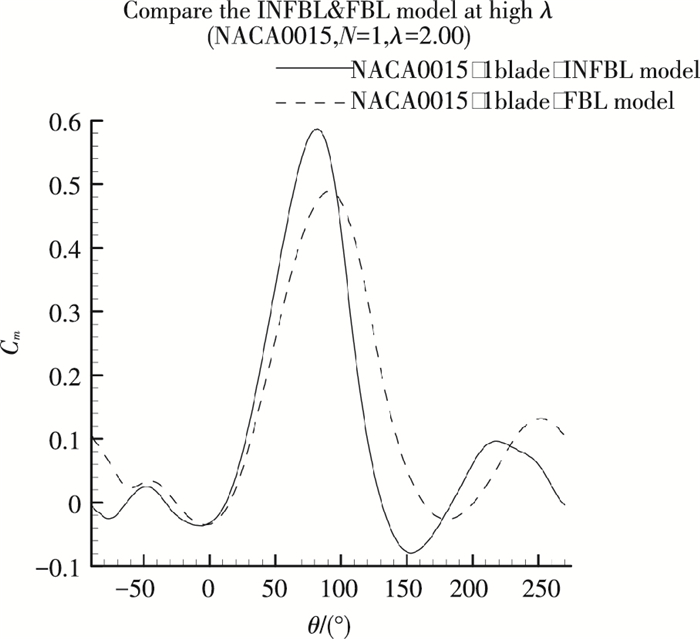
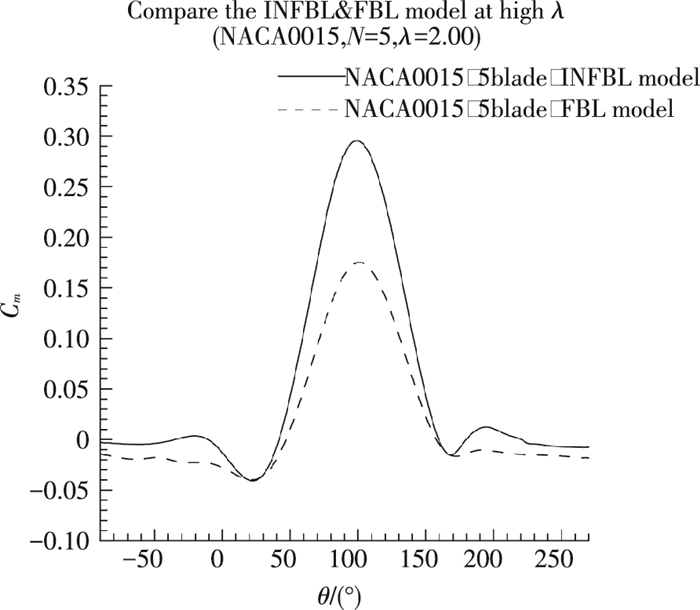
2.2 不同实度H-VAWT在高尖速比下的叶尖损失情况图 8、9分别给出了小实度(N=1)和大实度(N=5)FBL&INFBL H-VAWT在高尖速比(λ=2.00)下旋转一周过程中的其中一个叶片的Cm对比情况.
|
图 8 小实度INFBL&FBL H-VAWT高尖速比下的Cm对比情况(N=1,λ=2.00) Figure 8 Cm VS azimuth angles curves for INFBL&FBL H-VAWT with small solidity at high tip speed ratio(N=1, λ=2.00) |
|
图 9 大实度INFBL&FBL H-VAWT高尖速比下的Cm对比情况(N=5,λ=2.00) Figure 9 Cm VS azimuth angles curves for INFBL&FBL H-VAWT with large solidity at high tip speed ratio(N=5, λ=2.00) |
从图 8、9可以看出,大实度所生成的H-VAWT相比小实度的情况来讲,不仅最大Cm值改善幅度较大,最小Cm值没有像小实度H-VAWT那样变得较差,即大实度H-VAWT在旋转一周过程中所对应的平均Cm值有更多的改善,也就是说由于叶片之间的相互影响,实度越大,对H-VAWT的叶尖损失影响较大,特别是尖速比较高时.
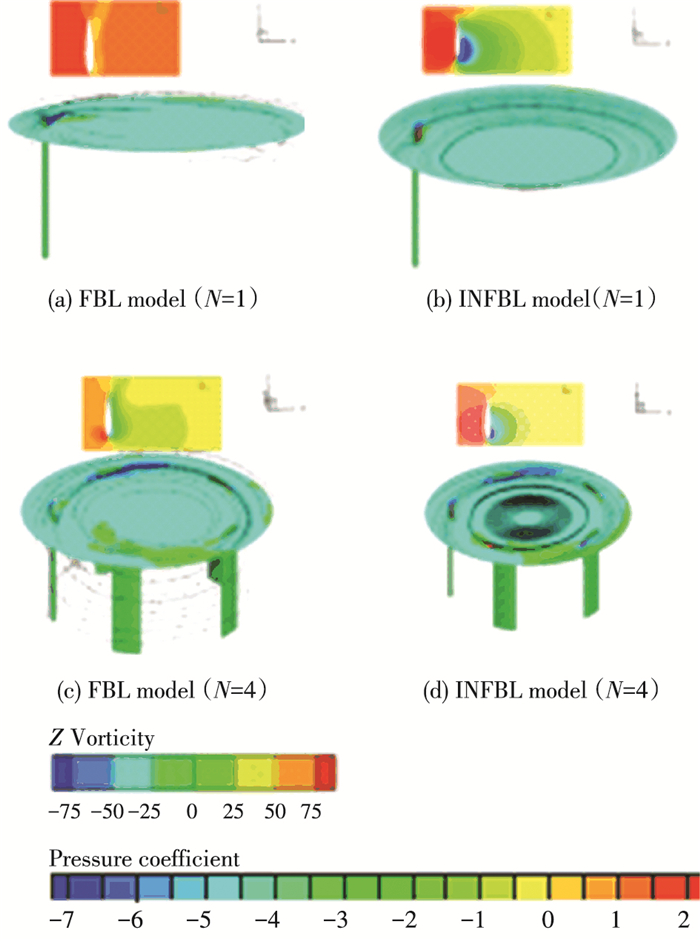
根据式(5),当尖速比较高时,叶片翼型的攻角范围较小,在最小Cm值所在的方位角处,其流动分离现象较低尖速比情况减弱,从图 8、9亦可以看到,INFBL H-VAWT的最小Cm值虽然像不同实度H-VAWT在低尖速比下的叶尖损失情况下亦会有减少,但不太明显,其最大Cm值对其平均Cm值有决定性的影响,为更好的理解该最大Cm值所在方位角(约为90°)处的流场特性,图 10给出了相应叶尖截面上z方向的涡量和压力云图.
|
图 10 INFBL&FBL H-VAWT叶尖截面上(Z/H≈0.967)涡量和压力系数云图(λ=2.00) Figure 10 The vorticity and pressure coefficient contours of the blade tip sitted surface of for INFBL&FBL H-VAWT(Z/H≈0.967, λ=2.00) |
从图 10中可以看到,不管小实度还是大实度H-VAWT,其在90°方位角处的叶片上压力云图的变化趋势是相同的:INFBL H-VAWT和FBL H-VAWT相比,除了压力面压力升高、高压区域向叶片翼型后缘移动之外,吸力面相比有更明显的低压区域,且低压区域向前缘移动.其原因是当尖速比较高时,叶片翼型的攻角在同一方位角处相比尖速比较低时较小,叶片吸力面的附着涡对叶片的气动性能是有利的,可保证失速攻角下的最佳气动性能,从流场分布和计算结果看,对FBL H-VAWT来讲,叶尖流动对这些附着涡有一定的破坏作用,使得压力面压力降低、吸力面压力升高,压差降低,又加上其压力面高压区更靠近叶片翼型前缘,致使压差方向偏向旋转中心,因此无论从压差的大小还是方向,其均不利于对旋转方向的分力或旋转扭矩的贡献.
2.3 同一实度H-VAWT在不同尖速比下的叶尖损失情况本文即综合不同实度H-VAWT在低尖速比下的叶尖损失情况和不同实度H-VAWT在高尖速比下的叶尖损失情况,详细讨论同一实度H-VAWT在不同尖速比下的叶尖损失情况.
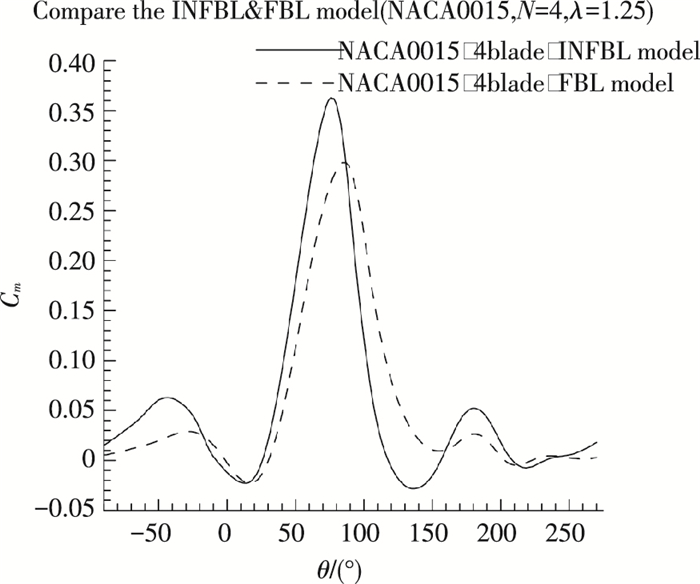
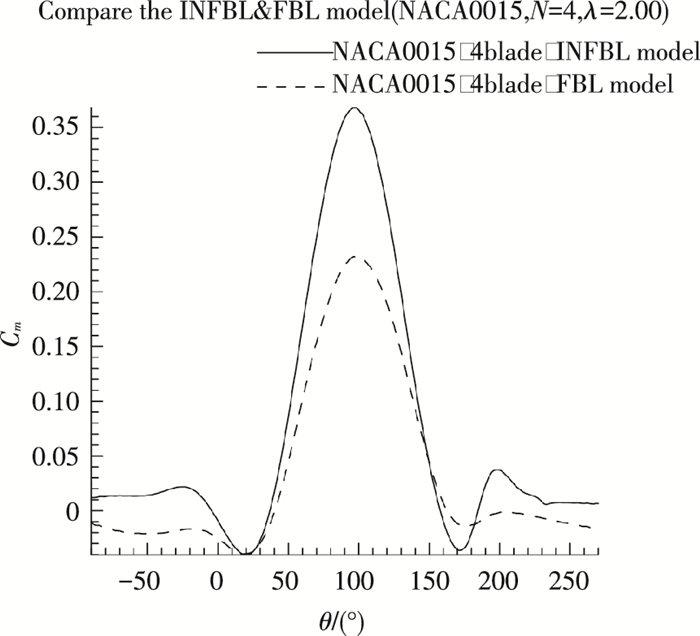
图 11、12给出同一实度(N=4)INFBL&FBL H-VAWT在不同尖速比(λ=1.25和λ=2.00)下的Cm对比情况.
|
图 11 INFBL&FBL H-VAWT在同一实度(N=4)下的Cm对比情况(λ=1.25) Figure 11 Cm VS azimuth angles curves for INFBL&FBL H-VAWT with the same solidity(λ=1.25) |
|
图 12 INFBL&FBL H-VAWT在同一实度(N=4)下的Cm对比情况(λ=2.00) Figure 12 Cm VS azimuth angles curves for INFBL&FBL H-VAWT with the same solidity(λ=2.00) |
从图 11、12可以看出,不论是低尖速比(λ=1.25)还是较高尖速比(λ=2.00),INFBL H-VAWT的最大Cm值都优于FBL H-VAWT的最大Cm值,最小Cm值都差于FBL H-VAWTT的最小Cm值,其原因与最大Cm值和最小Cm值所在方位角处所对应的叶片翼型的攻角有关.根据翼型气动特性,最大Cm值所对应的翼型攻角在失速攻角附近,最小Cm值出现在在叶片翼型失速之后某一大攻角处,也就是说对FBL H-VAWT来讲,叶尖上方或下方的绕流对出现最大Cm值的失速攻角的流场有破坏作用,而对出现最小Cm值的较大攻角的流场可起到延迟流动分离的作用,尖速比越高,前者现象越明显,尖速比越低,后者现象越明显.
从图 4还可以看出,当尖速比为1.75时,某些实度H-VAWT气动性能的相对差值差于其他尖速比下的情况,其原因是H-VAWT的最大Cp值是在λ=1.75时得到的(本文给出的都是Cp的相对差值,因篇幅所限,原始Cp值没有给出),尽管INFBL相比FBL H-VAWT,其在λ=1.75下旋转一周过程中的最大Cm值尽管有所改善,但其改善幅度较小,而其最小Cm值相比较差,故平均Cm值改善较小,也就是说,当H-VAWT运行在最佳气动性能所对应的尖速比时,H-VAWT的气动性能的最大改善比率较小,但这与实度有关,实度不同,最佳气动性能所对应的尖速比是不同的[15].
从图 4和本文相同实度的INFBL&FBL H-VAWT在不同尖速比下Cm的对比情况可以得出:对同一实度的H-VAWT,当尖速比较小时,叶尖上方或下方的绕流对H-VAWT的气动性能的影响是有利的,增加叶尖小翼或加大叶片的展弦比对H-VAWT的气动性能的改善不利;当尖速比较大时,由于相同方位角处叶片翼型的攻角较小,叶尖上方或下方的绕流对H-VAWT的气动性能的影响是不利的,带来叶尖损失,可以通过增加叶尖小翼或加大叶片的展弦比来改善H-VAWT的气动性能.
综上所述,相同尖速比下,实度越大,其H-VAWT叶尖损失的影响就越大,同一实度对叶尖损失的影响随着尖速比的增大而增大.
当H-VAWT实度较大(σ≥0.96)时,有必要通过增加叶尖小翼或加大叶片展弦比来改善H-VAWT气动性能,只是H-VAWT气动性能在低尖速比时,改善不明显甚或会变差.
不论是大实度还是小实度H-VAWT,当H-VAWT工作在较高尖速比(λ≥1.60)的情况下,其可以通过增加叶尖小翼或加大叶片展弦比来改善H-VAWT的气动性能,但由于H-VAWT起动时尖速比较低,使得增加改善措施后其起动性能变差,增加了改善H-VAWT起动性能的负担;当其工作在低尖速比的情况下,不适合增加叶尖小翼或增加展弦比来改善H-VAWT的气动性能.
3 翼型对H-VAWT叶尖损失的影响 3.1 不同厚度NACA对称翼型对H-VAWT叶尖损失的影响为了研究翼型对H-VAWT叶尖损失的影响,本文首先以风力机常用的NACA对称翼型为例,
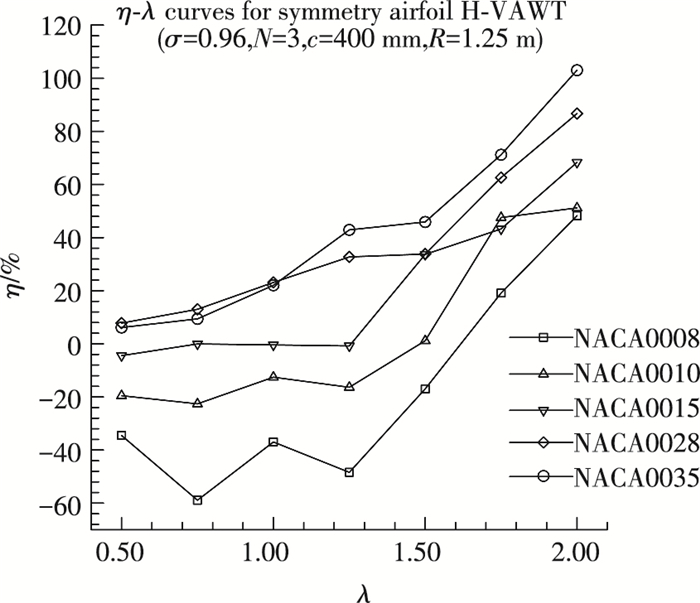
计算并分析了其不同厚度的对称翼型所生成的INFBL&FBL H-VAWT在不同尖速比下气动性能的相对差值情况,如图 13所示.
|
图 13 不同厚度的NACA对称翼型所生成的H-VAWT的η-λ曲线 Figure 13 η-λ curves for different thickness NACA symmetry airfoils generating H-VAWT |
从图 13可以看出:1)不论翼型的厚度如何,尖速比越高,其相对差值越大,即在高尖速比(λ≥1.60)下,最好使用叶尖小翼或加大叶片展弦比来改善H-VAWT的气动性能.2)不论是在高尖速比或低尖速比下,厚翼型所对应的相对差值较薄翼型情况较大,也就是说厚翼型所生成的H-VAWT,最好使用叶尖小翼或加大叶片展弦比来改善H-VAWT的气动性能.3)当翼型较薄时,若其生成的H-VAWT工作在低尖速比下,由其相对差值可知:INFBL H-VAWT更差于FBL H-VAWT的气动性能.其原因是低尖速比相比于高尖速比,其叶片翼型的攻角在相同方位角处的值更大,更易造成薄翼型失速,从同一实度H-VAWT在不同尖速比下的叶尖损失情况分析可知,低尖速比下的平均Cm值取决于H-VAWT旋转一周过程中的最小Cm值,由于薄翼型更差的失速特性,使得其所生成的INFBL H-VAWT最小Cm值更差,也就是说,薄翼型生成的H-VAWT,当其工作在低尖速比下时,不宜使用叶尖小翼或过大的展弦比.
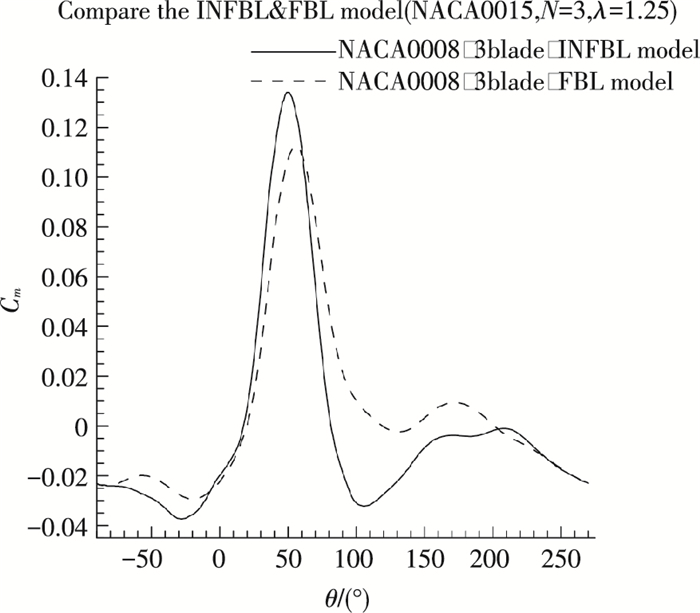
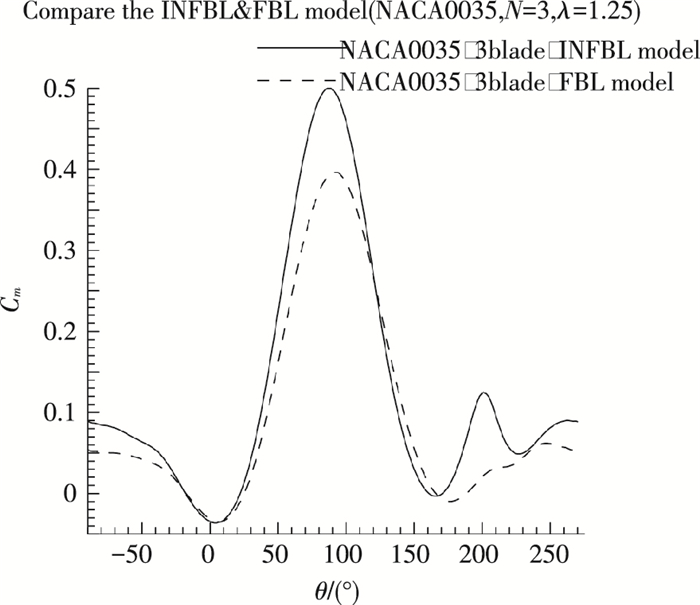
为了更好的理解薄翼型和厚翼型所生成的INFBL&FBL H-VAWT在旋转一周过程中具体气动性能的对比情况,图 14、15分别给出了薄翼型NACA0008和厚翼型NACA0035所生成的INFBL&FBL H-VAWT在较小尖速比(λ=1.25)下的Cm对比情况.
|
图 14 薄翼型(NACA0008)所生成的INFBL&FBL H-VAWT的Cm对比情况(λ=1.25) Figure 14 Cm VS azimuth angles curves for INFBL&FBL H-VAWT generated by thin airfoil NACA0008(λ=1.25) |
|
图 15 厚翼型(NACA0035)所生成的INFBL&FBL H-VAWT的Cm对比情况(λ=1.25) Figure 15 Cm VS azimuth angles curves for INFBL&FBL H-VAWT generated by thick airfoil NACA0035(λ=1.25) |
从图 14、15可以看出,尽管薄翼型和厚翼型所生成的H-VAWT的最大Cm值都有所改善,其在旋转一周过程中的最小Cm值的改善情况相差较大,对薄翼型所生成的H-VAWT,其最小的Cm改善情况差于厚翼型所生成的H-VAWT.从图 10和式(5)尖速比对叶片翼型攻角影响,可以预测尖速比越小,薄翼型所生成的H-VAWT的Cm的最小值的对比情况会更差于厚翼型的情况.
3.2 非对称翼型对H-VAWT叶尖损失的影响为了更全面的分析总结不同翼型对H-VAWT叶尖损失的影响,本文以两种厚度的非对称翼型(厚度为15%、21%,翼型为:NACA4415、TW11515-OBA642A、NACA652-215、NACA4421、LS0421(MOD))所生成的H-VAWT为例,研究其对H-VAWT叶尖损失的影响如图 16所示.

|
图 16 不同非对称翼型所生成的H-VAWT η-λ曲线 Figure 16 η-λ curves for different asymmetry airfoils generating H-VAWT |
从图 16可以看出:1)与图 13结论类似,不论在高尖速比或低尖速比下,厚非对称翼型所生成的H-VAWT的气动性能大都比薄非对称翼型的情况改善的要好,除了NACA4415所生成的H-VAWT情况以外.2)当翼型厚度相同,H-VAWT气动性能的改善比率与其翼型外形有关,特别是翼型较薄时.3)与不同厚度NACA对称翼型对H-VAWT叶尖损失的影响类似,当λ < 1.00时,INFBL H-VAWT的气动性能亦差于FBL H-VAWT的气动性能,即当尖速比较小时,不适合使用叶尖小翼或加大叶片的展弦比改善H-VAWT气动性能.3)由于与图 14、15所给出的对比图类似,非对称翼型所生成的INFBL&FBL H-VAWT的Cm和其他图形的对比情况不再累赘给出.
综上所述,不论在高尖速比或是低尖速比下,H-VAWT的叶片翼型越厚,对其叶尖损失的影响就越大,也就是说厚翼型所生成的H-VAWT更适合增加叶尖小翼或加大展弦比改善其气动性能.
与非对称翼型对H-VAWT叶尖损失的影响结论相同:不论翼型的厚度如何,尖速比越高,其对H-VAWT叶尖损失的影响就越大,也就是说高尖速比下更适合增加叶尖小翼或加大展弦比改善其气动性能.
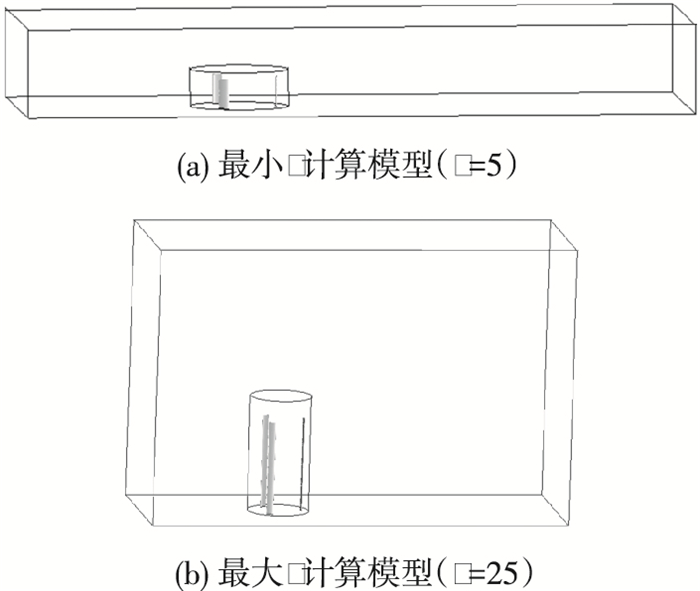
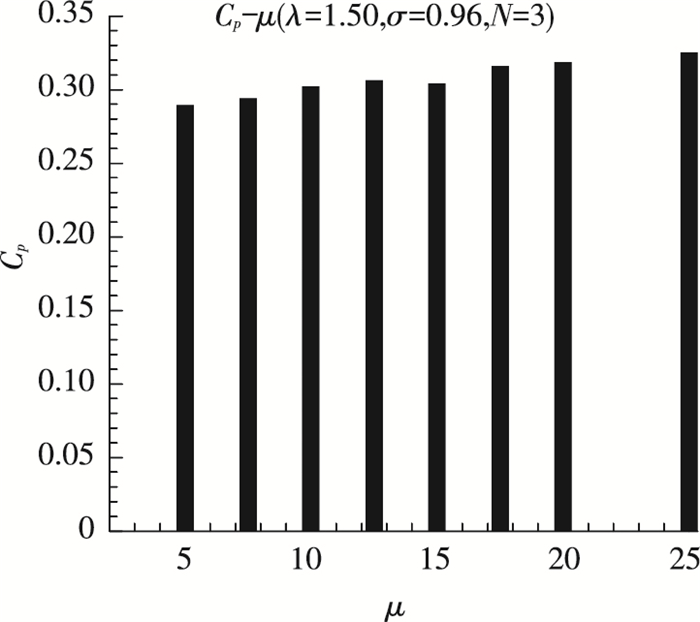
4 展弦比(μ)对H-VAWT叶尖损失的影响本文计算了8个不同展弦比(5~25)下H-VAWT的Cp值,通过对比分析,总结了展弦比对其叶尖损失的影响情况.图 17给出了最小展弦比(μ=5)和最大展弦比(μ=25)的H-VAWT计算模型,从图 17中可以看出,计算域(旋转域和静止域)随着叶片的长度都有所改变以确保计算结果的准确性.图 18给出了所有模型的计算结果.
|
图 17 最小和最大展弦比(μ=5 & 25,H=1 m & 5 m,c=0.4 m)H-VAWT计算域的上半模型 Figure 17 The half calculating model for the minimum and maximum aspect ratio(μ=5 & 25, H=1 m & 5 m, c=0.4 m) |
|
图 18 Cp-μ(λ=1.50,σ=0.96,N=3) Figure 18 Cp-μ(λ=1.50, σ=0.96, N=3) |
从图 18可以看出,当展弦比较大时,其H-VAWT的Cp值有缓慢增加(从0.289 350 ~ 0.325 659),即叶尖损失随着叶片展弦比的增加(叶片弦长固定,长度增加)越来越小.需要指出的是,属于实际3D流动现象的叶尖损失不可能完全避免,H-VAWT效率增加的原因不是叶尖损失得到了真正的改善,而是其所占整体来流风能的比率下降了,从图 19给出的不同展弦比下H-VAWT (相同实度,相同来流风速和尖速比)的叶尖涡量图和其计算公式亦可以看出,除以叶片展弦比以后的叶尖涡的强度越来越小了,但并不是叶尖涡真正的减少了.

|
图 19 叶尖平面上的涡的强度等值线云图(λ=1.50, σ=0.96, N=3) Figure 19 Vorticity contours of the blade tip sitted surface(λ=1.50, σ=0.96, N=3) |
从图 18计算结果可以看到,通过增加叶片展弦比来减小叶片损失占整体来流的风能的比率,从而提高H-VAWT功率系数这种方式是有限的,它不像水平轴风力机(HAWT),由于其叶尖离旋转中心距离较远,叶尖部分的气动性能对力矩的贡献相比H-VAWT更为重要,通过增加展弦比可使HAWT气动性能改善的更为明显;此外增大叶片的展弦比会受到高径比、实度(对固定的迎风面积,增加叶片长度会减少叶轮直径,会影响实度,影响H-VAWT的气动性能)的要求或限制,H-VAWT的展弦比不能太大,5 < μ < 20即可.
综上所述,基于展弦比对H-VAWT的叶尖损失改善的有限性,又根据H-VAWT所要求的输出功率,叶轮高径比(H/D)取值范围(大约0.5~2.0)、实度的取值范围(大约0.20~1.28)[16]、结构强度和材料的限制,也从图 19的涡的等值线云图,可以得出:H-VAWT的展弦比没有必要特别大,5 < μ < 20即可,对小型H-VAWT,由于其通常运行在低尖速比下,上述范围还可以更小一些.
5 结论1) 不论H-VAWT是大实度还是小实度、薄翼型还是厚翼型,其对H-VAWT叶尖损失的影响随尖速比的增加而增加,当H-VAWT工作在尖速比较小的情况下,一般不适合增加叶尖小翼或使用过大的展弦比叶片,在较高尖速比下(λ≥1.60),更适合使用改善叶尖损失的措施来改善H-VAWT的气动性能;另外尽管增加叶尖小翼或加大叶片的展弦比可以改善工况下H-VAWT的气动性能,从其低尖速比下(叶片翼型攻角比较大)的气动性能改善情况可以看出,其对H-VAWT自起动性能是不利的.
2) 当H-VAWT实度较大(σ≥0.96)时,可以通过增加叶尖小翼或增加展弦比来改善H-VAWT气动性能.
3) 较厚翼型所生成的H-VAWT通过增加叶尖小翼或加大叶片展弦比大都比薄翼型所生成的H-VAWT的气动性能在相同情况下有明显的改善.
4) 由于叶尖损失不可能消失,尽管展弦比越大,其所占能量损失比例会越小,但通过该方法对H-VAWT气动性能的改善是有限的,基于输出功率(与迎风面积有关)、叶轮高径比(H/D)取值范围(大约0.5~2.0)、实度的取值范围(大约0.20~1.28)以及结构强度和材料的要求或限制等,展弦比在5 ≤μ≤20范围内较合适.
| [1] |
伊恩·帕拉斯基沃尤(Ion). 垂直轴风力机原理与设计[M]. 李春, 叶舟, 高伟, 等译. 上海: 上海科学技术出版社, 2013.
PARASCHIVOIU I. Wind turbine design with emphasis on darrieus concept[M]. LI Chun, YE Zhou, GAO Wei, et al. Shanghai: Shanghai science and Technology Press, 2013. |
| [2] |
CARRINGAN T J. Aerodynamic shape optimization of a vertical axis wind turbine[D]. Arlington: University of Texas at Arlington, 2010.
|
| [3] |
ATHEARN F J, RIGHTER R W. Wind energy in america: a history[J].
The Western Historical Quarterly, 1999, 27(4): 546.
DOI: 10.2307/970571 |
| [4] |
MAXWELL J F, MCGOWAN J M, ROGERS A L.
Wind energy explained[M]. Chichester, UK: John Wiley & Sons, Ltd., 2009.
|
| [5] |
ENGSTRÖM S. Trends and development in wind power technology[J].
Elforsk, Stockholm, Sverige, 2010.
|
| [6] |
SORAGHAN C, LEITHEAD W, JAMIESON P, et al. Influence of lift to drag ratio on optimal aerodynamic performance of straight blade vertical axis wind turbines[C]//Proceedings of European Wind Energy Association Annual Conference. Vienna: [s. l. ], 2013.
|
| [7] |
WALKER S N. Performance and optimum design analysis/computation for propeller type wind turbines[D]. Corvallis: Oregon State University, 1976.
|
| [8] |
BRANLARD E. Wind turbine tip-loss corrections[D]. Lyngby Campus: Technical University of Denmark, 2011.
|
| [9] |
GASPARONI L. Effect of winglets on a vertical-axis wind turbine[D]. Veneto, Reg: Università degli studi di Padova, 2012.
|
| [10] |
ISLAM M, FARTAJ A, CARRIVEAU R. Analysis of the design parameters related to a fixed-pitch straight-bladedvertical axis wind turbine[J].
Wind Engineering, 2008, 32(5): 491-507.
DOI: 10.1260/030952408786411903 |
| [11] |
AMATO F, BEDON G, CASTELLI M R, et al. Numerical analysis of the influence of tip devices on the power coefficient of a VAWT[C]//Proceedings of International Conference on Mechanical, Industrial, and Manufacturing Engineering. Copenhagen, Denmark: World Academy of Science, Engineering and Technology, 2013(78): 387-394.
|
| [12] |
李寿图. 几种典型状况下垂直轴风力机气动特性及流场分析[D]. 兰州: 兰州理工大学, 2014. DOI: 10.7666/d.Y2566801.
LI Shoutu. Aerodynamic character and flow field analyzation of vertical axis wind turbine under the several typical conditions[D]. Lanzhou: Lanzhou University of Thechnology, 2014. DOI: 10.7666/d.Y2566801. |
| [13] |
ISLAM M, CARRIVEAU R, FARTAJ A. Performance analyses of a fixed-pitch straight-bladed VAWT with selected low Reynolds number airfoils[J].
International Journal of Environmental Studies, 2012, 69(2): 289-298.
DOI: 10.1080/00207233.2012.663226 |
| [14] |
CASTELLI M R, SIMIONI G, BENINI E. Numerical analysis of the influence of airfoil asymmetry on VAWT performance[J].
World Academy of Science, Engineering and Technology, 2012, 61: 263-272.
|
| [15] |
ROH S C, KANG S H. Effects of a blade profile, the Reynolds number, and the solidity on the performance of a straight bladed vertical axis wind turbine[J].
Journal of Mechanical Science and Technology, 2013, 27(11): 3299-3307.
DOI: 10.1007/s12206-013-0852-x |
| [16] |
AHMADI-BALOUTAKI M, CARRIVEAU R, TING D S K. Straight-bladed vertical axis wind turbine rotor design guide based on aerodynamic performance and loading analysis[J].
Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2014, 228(7): 742-759.
DOI: 10.1177/0957650914538631 |
 2018, Vol. 50
2018, Vol. 50


