2. 中国科学院太空应用重点实验室(中国科学院空间应用工程与技术中心),北京 100094
2. Key Laboratory of Space Utilization (Technology and Engineering Center for Space Utilization, Chinese Academy of Sciences), Beijing 100094, China
人类航天活动的逐渐频繁,使得目前空间中存在的失效航天器日益增多,对失效航天器进行相应空间操作如维修、补给、抓捕等,可使其工作寿命延长、回收关键零部件或减少太空垃圾,这对航天技术的长远发展意义重大.在这一过程中,需要运用航天器近距离交会对接技术使得追踪星接近失效目标[1].在交会对接任务中,失效目标由于在空间中呈翻滚状态,同时不能提供信息且不可控制,对接近过程尤其是近距离接近过程造成许多困难,相比于合作目标,对失效目标的接近危险程度更高,复杂程度也更高.所以,对于接近失效目标的任务,航天器间出现碰撞的可能性更大.为了更安全地接近失效目标,就必须对其接近轨迹的安全性进行分析,规避碰撞风险.
针对这一问题,国内外学者尝试用多种方法判别碰撞,主要分为区域判定法(Box法)和碰撞概率法.Box法主要思想是对区域进行划分,将进入设定预警区域的行为均视为危险[2].近年来,国内学者分别对碰撞概率显示表达式及灵敏度分析[3]、碰撞模型及概率快速算法[4]和碰撞概率的数值计算方法[5]进行了较为深入的研究,国外学者则对空间碎片与航天器间的碰撞概率[6]、近地微小碎片间的碰撞概率[7],紧急情况下最大碰撞概率[8]和高斯误差分布下的球形航天器间碰撞概率[9]分别展开了研究.
前期的碰撞研究,包括航天器间或空间碎片间,主要是以被研究目标初始位置相距较远为前提进行碰撞预警或碰撞概率计算,主要起到轨道预报的作用.而对于交会对接的最后段,对目标安全走廊内碰撞问题研究较少,然而在对失效目标的最后抓捕段,接近危险程度高,所以最后对碰撞预警、碰撞预判和碰撞规避的需求也同样存在.张大伟等[10]将人工势函数法与椭圆蔓叶线函数结合,提出了目标安全走廊内的制导方法,但对于安全走廊内的碰撞判断问题,目前还未有较为全面细致的方法.
为了对空间翻滚目标安全走廊内的碰撞问题进行判断,本文参考Box法的思想,建立了目标安全走廊锥面模型及追踪星位置误差椭球模型,通过判断椭球是否与锥面相交来判断安全走廊内的运动是否危险.将锥面模型首先射影变换为圆柱面,并将同样变换施加到椭球面上,再将变换所得的圆柱面和椭球变换后对应的曲面分别向平面投影,并标准化,得平面标准圆与椭圆.由于射影变换与仿射变换空间曲面、曲线位置不变,利用平面曲线位置判据,可以判别标准圆与椭圆的位置关系,反推获得原锥面与误差椭球的位置关系,从而判断是否存在碰撞危险.
1 问题描述为方便问题描述,采用如下坐标系:ECI坐标系,记为I系;目标航天器LVLH坐标系,记为L系.
1.1 非合作目标安全走廊模型由文献[11]可知轴对称自由刚体在惯性空间绕它对质心的动量矩HI作圆锥运动,HI为守恒量,在惯性空间方向不变.虽然航天器一般不满足轴对称性质,但此处不需关心目标星在空间中具体运动规律,只需确定它在空间中可能扫过的范围即可.
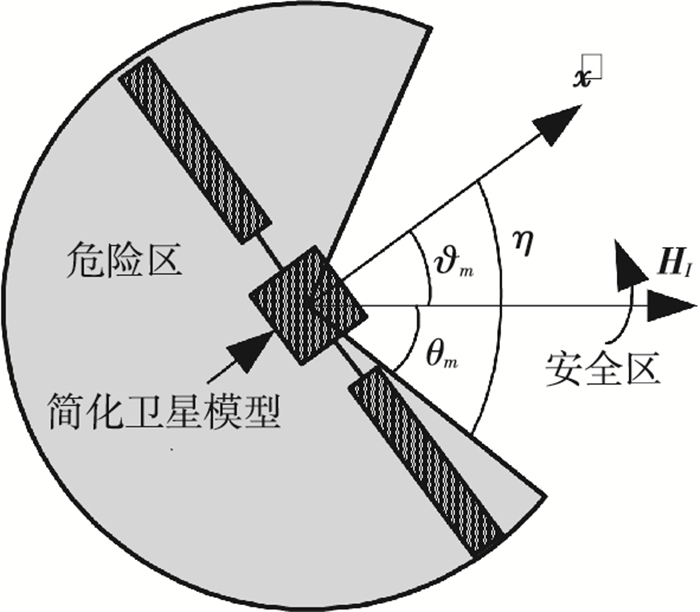
本文以空间中带大附件的翻滚目标为目标星,为方便建模,将目标星简化为主体为立方体、两侧带长方体帆板的对称卫星,其平面图如图 1中简化卫星模型所示.
|
图 1 目标安全区平面示意 Figure 1 Plan sketch of the target safe zone |
假设目标星的最大惯量主轴所在方向为
图 1中对于不围绕最大惯量主轴旋转的目标,同理,确定目标转轴到其两侧边缘夹角和最大章动角,按照旋转规律确定安全锥面即可.
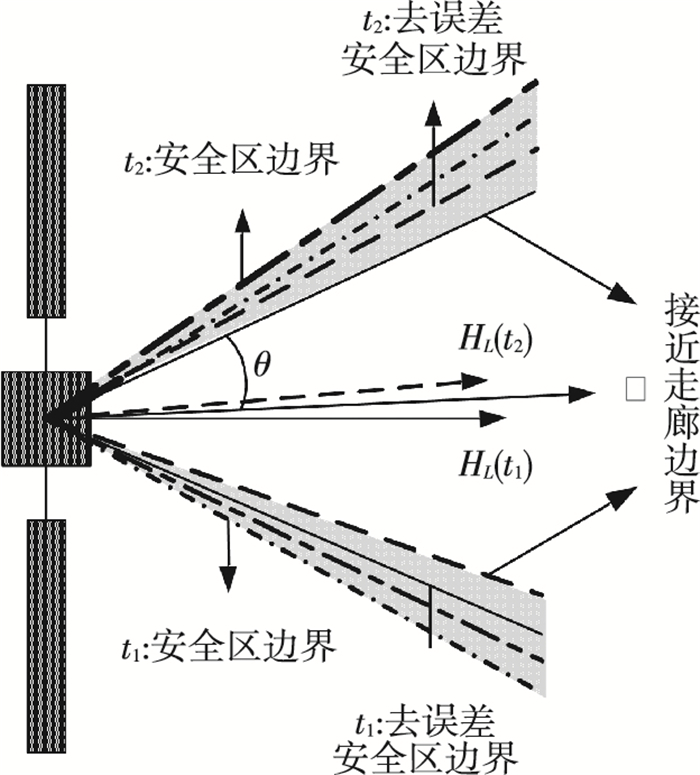
虽然HI在I系中为常矢量,但由于接近问题许多情况下要在L系下考虑.记L系下的目标自旋角动量为HL,I系到L系的转换矩阵为CIL,则有:HL= CIL HI.由于CIL是随时间变化的,经分析可知,HL的运动规律为绕L系z轴做圆锥运动,运动周期等于目标星轨道周期,因此,安全走廊的设计应考虑时间因素.对于追踪星在目标安全区内停留的时间段t1~t2,HL在L系中的方向是变化的,如图 2所示.
|
图 2 目标安全走廊平面示意 Figure 2 Plan sketch of the target safe corridor |
图 2中的长点划线和短点划线分别表示t1时刻与t2时刻目标的安全区,考虑到对目标建模过程中可能存在测量误差或近似误差,取误差角ε(ε>0),去掉误差角ε后,实线表示t1时刻的去误差安全区边界,虚线表示t2时刻的去误差安全区边界.对于追踪星在目标安全走廊内飞行时间相对较短的情况,即HL (t1)与HL(t2)有较大交集时,可取HL (t1)与HL (t2)的交集作为安全走廊,交集所形成的新锥面的中心线方向及半锥角可取为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{n}} = {\mathit{\boldsymbol{H}}_L}\left( {\frac{{{t_1} + {t_2}}}{2}} \right)/\left\| {{\mathit{\boldsymbol{H}}_L}\left( {\frac{{{t_1} + {t_2}}}{2}} \right)} \right\|,\\ \theta = {\theta _m} - \varepsilon - \arccos \left( {\frac{{{\mathit{\boldsymbol{H}}_L}\left( {{t_1}} \right) \cdot {\mathit{\boldsymbol{H}}_L}\left( {{t_2}} \right)}}{{\left\| {{\mathit{\boldsymbol{H}}_L}\left( {{t_1}} \right)} \right\|\left\| {{\mathit{\boldsymbol{H}}_L}\left( {{t_2}} \right)} \right\|}}} \right)/2. \end{array} \right. $ |
通过取交集作为安全走廊的方法,可在计算过程中使得走廊中心线n在L系下固定,方便追踪星的运动规律设计,同时使得安全结果更为保守.带大附件失效目标一般为高轨道卫星,轨道周期相对较长,使用该方法一般可行.但对某些特殊情况,如目标轨道太低,或在走廊内停留时间太长,导致HL (t1)与HL(t2)交集过小或不存在交集的情况,则该方法不再适用,此时必须考虑HL的时变性.
1.2 追踪星位置误差模型在L系下,追踪星的状态可由位置r和速度v表示,设x为追踪星在安全走廊内的标称状态,x为实际状态:x = (rT, vT)T,x = (rT, vT)T.记状态误差矢量为δx,则有:δx = x - x = (δrT, δvT)T;记状态误差协方差为P,P是一个6×6的实对称矩阵,则根据线性系统的描述函数理论可得航天器标称状态和协方差的传播方程组:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot {\bar x}}}\left( t \right) = \mathit{\boldsymbol{F\bar x}}\left( t \right) + \mathit{\boldsymbol{Bu}},\\ \mathit{\boldsymbol{\dot P}}\left( t \right) = \mathit{\boldsymbol{FP}}\left( t \right) + \mathit{\boldsymbol{P}}\left( t \right){\mathit{\boldsymbol{F}}^{\rm{T}}}, \end{array} \right. $ |
式中,u为航天器所受合外力.由文献[12]可知,随机变量x位于以标称状态矢量x为球心的一个超椭球内,此椭球的椭球面可表示为
| $ {\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\bar x}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{P}}^{ - 1}}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\bar x}}} \right) = {l^2}, $ |
式中,l为马氏距离常数,该式所描述是航天器6维全状态空间误差超椭球.为判断航天器与目标安全走廊的位置关系,还需将位置误差子椭球从超椭球中提取出来.矩阵P是6×6的实对称矩阵,可被划分为对应δr和δv的对称矩阵块:
| $ \mathit{\boldsymbol{P}} = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{rr}}}&{{\mathit{\boldsymbol{P}}_{rv}}}\\ {{\mathit{\boldsymbol{P}}_{vr}}}&{{\mathit{\boldsymbol{P}}_{vv}}} \end{array}} \right),{\mathit{\boldsymbol{A}}_{rr}} = \mathit{\boldsymbol{P}}_{rr}^{ - 1}/{l^2}, $ | (1) |
式中,Arr即为位置误差子椭球的对应矩阵.
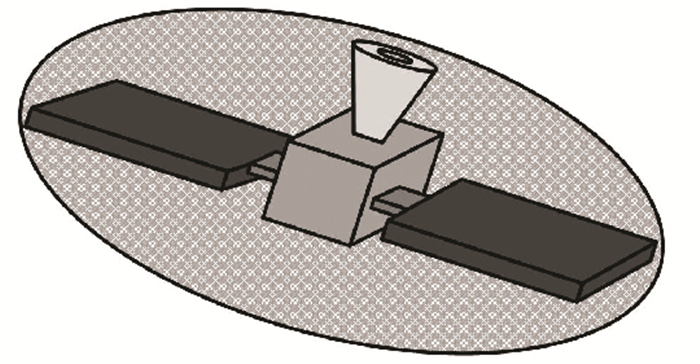
为了补偿追踪星自身形状或姿态对位置误差椭球的影响,尤其是在误差椭球的边缘处消除由于追踪星形状或姿态引起的不确定因素,使得误差椭球能够涵盖所有协方差为P下的追踪星上任一点的可能位置,根据追踪星的星体特征对追踪星作星体包络椭球U,如图 3所示.
|
图 3 追踪星星体包络椭球 Figure 3 Envelope ellipsoid of the chaser |
由图 3可知,追踪星上所有的点均在椭球U内.设椭球U的最长轴为u,标称位置误差椭球的最短轴为a,对式(1)作如下处理:
| $ k = a/\left( {u + a} \right),\;\;\;\mathit{\boldsymbol{A}} = {k^2}{\mathit{\boldsymbol{A}}_{rr}}, $ |
用处理后的A表示追踪星位置误差椭球,会在Arr表示的标称位置误差椭球基础上,扩大椭球半轴,使得新椭球完全涵盖星体包络椭球U,借此消除追踪星星体形状或姿态对后续判断结果的影响.因此,追踪星位置误差椭球为
| $ {\left( {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{\bar r}}} \right)^{\rm{T}}}\mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{\bar r}}} \right) - 1 = 0. $ |
设锥面顶点为O1,以n所在直线为中心线,设以中心线为法线且与锥面仅相交于O1的平面为投影平面.以O1为坐标原点建立O1x1y1z1坐标系,记为S1系,其中,z轴沿着中心线方向,x与y轴在投影平面上,构成右手坐标系.
在S1系下,目标航天器的安全锥面走廊可表示为
| $ \left\{ \begin{array}{l} {x^2} + {y^2} = {\left( {h\tan \theta } \right)^2},\\ z = h, \end{array} \right. $ |
式中,θ为锥面走廊半锥角,消去h则可得锥面走廊公式为
| $ \frac{{{x^2} + {y^2}}}{{{{\tan }^2}\theta }} - {z^2} = 0. $ | (2) |
设X = (x, y, z, 1),则用二次型XB0XT=0的形式表示式(2),则可得S1系下表示锥面对应矩阵B0为
| $ {\mathit{\boldsymbol{B}}_0} = \left( {\begin{array}{*{20}{c}} {1/{{\tan }^2}\theta }&0&0&0\\ 0&{1/{{\tan }^2}\theta }&0&0\\ 0&0&{ - 1}&0\\ 0&0&0&0 \end{array}} \right). $ |
(注:为方便表达,后续用矩阵符号表示对应曲面或曲线,如:B0为锥面)
由于位置误差椭球在L系下求出,定义L系到S1系的坐标转换矩阵为CL1,则表征误差椭球大小的矩阵A和对应标称位置r在S1系下的表达式为
| $ \mathit{\boldsymbol{A}} = \mathit{\boldsymbol{C}}_L^1\mathit{\boldsymbol{AC}}_L^{1{\rm{T}}},\;\;\;{{\mathit{\boldsymbol{\bar r}}}_1} = \mathit{\boldsymbol{C}}_L^1\mathit{\boldsymbol{\bar r = }}{\left( {{{\mathit{\boldsymbol{\bar r}}}_{1x}},{{\mathit{\boldsymbol{\bar r}}}_{1y}},{{\mathit{\boldsymbol{\bar r}}}_{1z}}} \right)^{\rm{T}}}, $ |
将A转换为二次型:XAXT=0,则可得四阶矩阵:A =diag (A, -1),A为S1系下表示误差椭球的矩阵.此时椭球中心在O1处,为了正确表达误差椭球在S1系下的位置,需要将椭球中心从O1处平移至r1处,对A所表示的椭球作以下代换:
| $ \left\{ \begin{array}{l} f = \mathit{\boldsymbol{X\bar A}}{\mathit{\boldsymbol{X}}^{\rm{T}}},\\ f' = f\left( {\mathit{\boldsymbol{X}} - {{\mathit{\boldsymbol{\bar r}}}_1}} \right). \end{array} \right. $ |
式中,f′对应的二次型矩阵记为A0,A0为S1系下的中心为r1的椭球.
1.4 两曲面可能存在的位置关系为明确计算所得的目标锥面安全走廊和追踪星位置误差椭球在空间中可能存在的位置关系,应讨论空间中椭球与锥面的位置关系,结合安全走廊内碰撞问题的背景,除去椭球与锥面外离、椭球与锥面外切、以及锥顶点在椭球上或椭球内的情况,共有如下几种情况:1)椭球在锥面内;2)椭球与锥面仅有1个切点;3)椭球与锥面有2个以上切点;4)椭球与锥面有1个切点,2个交面;5)椭球与锥面有1个交面;6)椭球与锥面有2个交面.
参考Box法的思想,若判断安全走廊内是否存在碰撞风险,应判断追踪星是否进入了危险区域.显然,对于目标安全走廊内的飞行问题,走廊外部的区域全部视为危险区域,只有追踪星轨迹全部处于走廊内部才视为安全.因此,目标安全走廊内的碰撞判断问题,与判断走廊锥面与追踪星位置误差椭球的位置关系是等价的,考虑上述可能存在的位置关系,将走廊锥面与误差椭球位置关系简化为3种:内含、内切与相交,并与碰撞判断结果一一对应,见表 1.
| 表 1 曲面位置判断与碰撞结果判断对应关系 Table 1 The corresponding relation between determinations of surface position and the collision |
需要说明的是,在判断出曲面相交后,对应的碰撞判断结果是可能碰撞,而非一定碰撞.由于追踪星位置误差椭球是一定概率阈值内,追踪星在标称位置附近的实际位置的集合.所以,若误差椭球与锥面相交,是说明在一定概率下产生碰撞,而非绝对碰撞,而概率的大小跟P有关,此处不做深入讨论,此处仅认为两曲面相交有碰撞可能,为危险情况,以此为目标星在安全走廊内的标称轨迹规划及设计提供评估轨迹安全性的参考.
2 碰撞判断代数判据由于直接判断空间中锥面与椭球面的位置关系较为困难,因此本文利用射影定理,即经射影变换,原曲面间的位置关系不改变的原理[13],将原问题做如下变换:1)将锥面射影变换成圆柱面,并将变换同样施加到椭球面上;2)在圆柱面的垂直面投影,得到圆柱面和椭球射影变换后曲面所对应的两条平面二次曲线.由此,利用平面二次曲线间的代数判据,判断两二次曲线间的位置关系,从而获得原问题的解.
2.1 走廊锥面与误差椭球位置问题的转化为判断圆锥面与椭圆面间的位置关系,需对其进行射影变换.应注意的是,在变换前应检查S1系的xy平面是否穿过或切于椭球A0,若xy平面与A0有交点,由客观特征可直接判断A0与B0相交,不需再进行变换.由于A0为椭球,故xy平面与A0若存在交点,则相交所得曲线必为椭圆或一个点.令椭球A0中的z坐标为0,得到曲线f×为
| $ {f^ \times }:\left\{ \begin{array}{l} f = \left[ {x,y,z,1} \right]{\mathit{\boldsymbol{A}}_0}{\left[ {x,y,z,1} \right]^{\rm{T}}}\\ z = 0, \end{array} \right., $ |
若f×是实椭圆或一个点,则说明xy平面与A0相交,可得A0与B0相交,结束计算.
若xy平面与A0无交点,取过S1系原点O1的平面F使F与B0只交于O1,做射影变换P使F变为无穷远平面. B0变换为标准圆柱面,记为B1,同时椭球A0变换为新的曲面,记为A1.
在本文中,取
| $ {\mathit{\boldsymbol{B}}_1} = \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{B}}_0}{\mathit{\boldsymbol{M}}^{\rm{T}}},{\mathit{\boldsymbol{A}}_1} = \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{A}}_0}{\mathit{\boldsymbol{M}}^{\rm{T}}}, $ |
这样,原锥面B0和椭球A0就分别变换为了柱面B1和曲面A1,因射影变换原位置关系不变的特性,A0与B0的位置关系问题就转换为了A1与B1的位置关系问题.
直接判定A1与B1的位置关系仍不容易,但由于B1为柱面,故可以通过向底面投影判断曲面间有无交点.由B1的形式可看出,该圆柱面的母线是沿z方向的,因此将A1与B1分别向xy平面投影,记投影后曲线分别为CA与CB.
由上述易知圆柱面的投影曲线CB的形式为:x2+y2-1=0.为求出投影曲线CA,做如下计算:
| $ {C_A}:\left\{ \begin{array}{l} f = \mathit{\boldsymbol{X}}{\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{X}}^{\rm{T}}} = 0,\\ \frac{{\partial f}}{{\partial z}} = 0. \end{array} \right. $ |
该方程组消去变量z后,即得到曲线CA,经实验可得,当xy平面与A0不相交时,CA为椭圆(此处自动满足该条件).设X′=[x, y, 1],则CA可化为平面二次型X′A2X′T=0,得矩阵A2,同理可得CB对应的二次型矩阵B2.
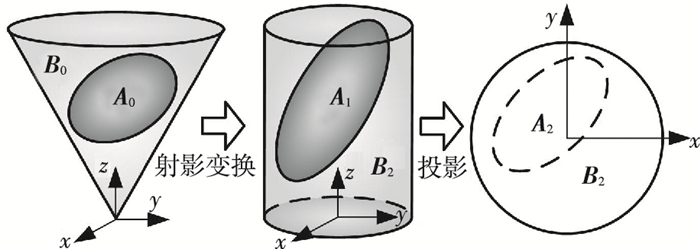
由此,在A0不与xy平面相交情况下,原锥面B0与椭球A0的位置判断问题可转化为平面圆B2与椭圆A2的位置判断问题,过程如图 4所示.
|
图 4 椭球与锥面位置问题的平面转化过程 Figure 4 Process of transforming the position relation problem between the cone and the ellipsoid to planar one |
| $ \begin{array}{l} \mathit{\boldsymbol{A}}:\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1,\;\;\;\left( {0 < a \le b,1 \le b} \right)\\ \mathit{\boldsymbol{B}}:{\left( {x - {x_0}} \right)^2} + {\left( {y - {y_0}} \right)^2} = 1, \end{array} $ | (3) |
其对应的二次型矩阵分别为:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {1/{a^2}}&0&0\\ 0&{1/{b^2}}&0\\ 0&0&{ - 1} \end{array}} \right],\mathit{\boldsymbol{B = }}\left[ {\begin{array}{*{20}{c}} 1&0&{ - {x_0}}\\ 0&1&{ - {y_0}}\\ { - {x_0}}&{ - {y_0}}&{ - 1 + x_0^2 + y_0^2} \end{array}} \right], $ |
可由其广义特征多项式f (λ) =det(λA +B)来判断圆与椭圆的关系.
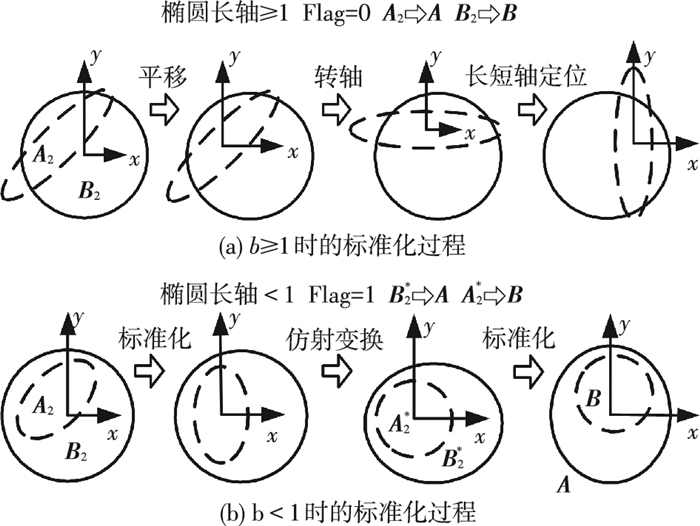
由图 4可知,投影后,坐标原点在B2即单位圆的中心,为使A2与B2满足式(3)中的形式,应使坐标原点平移至椭圆中心,并使得y轴对应椭圆的长轴方向.
在式(3)中,需满足b≥1(b为椭圆长轴),才能使用位置判据.但事实上,投影后的椭圆CA的长轴不一定满足该条件,此处需分类讨论,并引入标志位Flag进行区分.对于b≥1的情况,需进行曲线标准化过程,标准化后的A2和B2分别对应式(3)中的A和B,并记Flag=0,过程如图 5(a)所示.对于b < 1的情况,在经标准化后,还需将椭圆CA仿射变换为圆CA*,同时圆CB仿射变换为椭圆CB*,再次经标准化后,CA*和CB*分别对应的矩阵A2*和B2*此时分别对应式(3)中的B和A,记Flag=1,如图 5(b)所示.
|
图 5 投影后椭圆与圆的标准化过程 Figure 5 The standardization process of the ellipse and the circle obtained after projection |
结合安全走廊内碰撞判断的客观存在条件,不考虑A与B相离或外切的情况,并将重合视为内切的1种,则对应广义特征函数f(λ)=det (λA + B) =0的解,根据文献[14]中的结论,可得以下位置代数判据.
判据1 f(λ)有虚根
判据2 f(λ)有3个相异负根,均属于(-∞,-a2],但至多一个为-a2
判据3 f(λ)有负重根,均属于(-∞,-a2],但至多一个为-a2
判据4 f(λ)有3个相异负根,且其中两个属于[-a2, 0)
判据5 f(λ)有负重根,属于(-a2, 0)
判据6 f(λ)的解刚好为{-a2, -a2, -b2/a2},若a2>b
由上述位置判据,可判断平面上A与B的位置情况,获得二次曲线A2和B2或A2*和B2*的位置关系,进一步反推二次曲面A1和B1的关系,从而获得原问题目标安全走廊A0和航天器误差椭球B0的位置关系.
3 安全走廊内碰撞判断主要步骤于追踪星于无控翻滚失效目标安全走廊内的碰撞可能性判断问题,其判断主要步骤如下.
步骤1 根据两航天器的动力学特性和外形特征,建立目标安全走廊圆锥面模型与误差椭球模型.
步骤2 建立S1系,并记S1系下圆锥面与误差椭球的二次型对应矩阵分别为B0与A0.
步骤3 将z =0带入A0所在方程,得曲线f×,判断f×是否为实椭圆或一个点,若是,则说明xy平面与A0有交点,B0与A0相交,计算结束.
步骤4 将B0射影变换为标准圆柱面,同时A0进行相同变换,记变换后分别为B1和A1.
步骤5 将B1和A1分别向xy平面投影,得圆CB和椭圆CA.
步骤6 将椭圆标准化,并在圆上施加同样的变换,得变换后两曲线对应二次型矩阵A2和B2.
步骤7 判断A2长轴,若长轴大于等于1,将A2和B2分别对应标准椭圆A与标准单位圆B,记符号Flag=0,并跳至步骤9.
步骤8 将A2仿射变换为圆,并在B2上施加相同变换成为椭圆,重复步骤6,标准化后分别记为A2*和B2*,并分别对应标准单位圆B和标准椭圆A,记符号Flag=1.
步骤9 定义广义特征函数f(λ)=det (λA +B),获得f(λ) =0的解,根据平面圆与椭圆位置代数判据获得A与B的位置关系.
步骤10 根据A与B的位置关系获得原问题A0与B0的位置关系:
1) A与B相交
2) B内切于A
3) B内含于A
为验证文中提出的目标安全走廊内碰撞判断方法,取表 1中内含、内切、相交情况中各一种进行仿真计算.
4.4.1 内含| 表 2 曲面二次型矩阵参数(内含) Table 2 Quadratic matrix parameters of the surface(included) |
| 表 3 曲面判定过程及结果(内含) Table 3 Process and result of position relation determination between surfaces(included) |
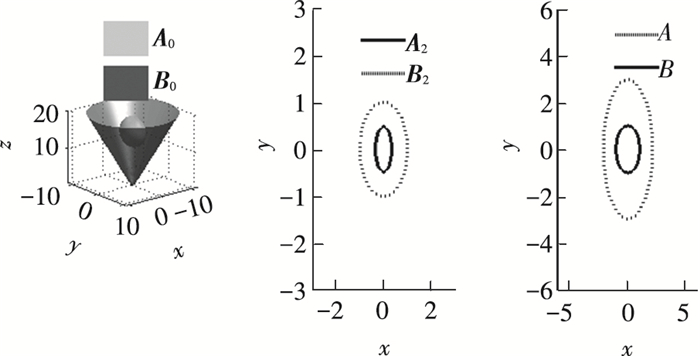
|
图 6 判断椭球内含于锥面的过程 Figure 6 The process for determining the ellipsoid included in the cone |
| 表 4 曲面二次型矩阵参数(内切) Table 4 Quadratic matrix parameters of the surface(tangent) |
| 表 5 曲面判定过程及结果(内切) Table 5 Process and result of position relation determination between surfaces(tangent) |
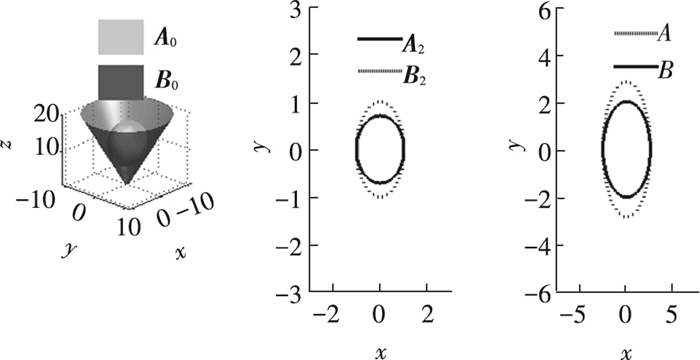
|
图 7 判断椭球内切于锥面的过程 Figure 7 The process for determining the ellipsoid internally tangent in the cone |
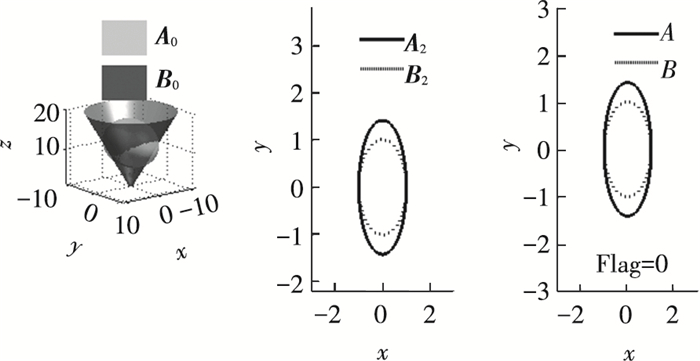
| 表 6 曲面二次型矩阵参数(相交) Table 6 Quadratic matrix parameters of the surface(intersected) |
| 表 7 曲面判定过程及结果(相交) Table 7 Process and result of position relation determination between surfaces(intersected) |
|
图 8 判断椭球相交于锥面的过程 Figure 8 The process for determining the ellipsoid intersected in the cone |
在内含、内切仿真中,由图 6、7可看出,曲面A0和B0经射影变换和投影后,平面单位圆B2半径大于平面椭圆A2长轴,故进行了安全走廊内碰撞判断的步骤8,将问题重新规划,使得A2对应判据标准圆B,B2对应判据标准椭圆A,并记Flag=1.而在相交中,A2长轴大于B2半径,则A2和B2分别对应A和B,同时Flag=0.比较内切、相交并结合图 7、8可发现,其平面判断结果是相同的,但因Flag值的不同,其曲面判断结果是不同的,这是因为A0和B0经射影变换后,原锥面变换为单位圆B2,虽然在平面上B2与A2属内切关系,但还原到曲面上,两者可能是相交的,对于平面内含的结果也同样如此.因此在判断过程中记录Flag的值并用于最终结果判断是必要的.
上述3组仿真可看出,将锥面与椭球的位置关系问题变换为平面圆与椭圆的问题进行判断是可行的,平面曲线的判断结果经过Flag值的辨别可用于反推曲面的判断结果,其判断结果准确.
4.2 目标安全走廊内碰撞判断仿真假设目标星为运行在轨道高度为R=26 115 km圆轨道上的空间翻滚对称失效卫星,其外形可以简化为非合作目标安全走廊模型中卫星模型,计算可得目标星轨道周期为T=2π
| $ {\mathit{\boldsymbol{H}}_L}\left( {{t_1}} \right) = {\left( {\sin \left( {{\rm{ \mathsf{ π} /30}}} \right),cos\left( {{\rm{ \mathsf{ π} /30}}} \right),0} \right)^{\rm{T}}}, $ |
则计算可得
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{n}} = {\mathit{\boldsymbol{H}}_L}\left( {\frac{{{t_1} + {t_2}}}{2}} \right)/\left\| {{\mathit{\boldsymbol{H}}_L}\left( {\frac{{{t_1} + {t_2}}}{2}} \right)} \right\| = {\left( {0,1,0} \right)^{\rm{T}}},\\ \theta = {\theta _m} - \varepsilon - \arccos \left( {\frac{{{\mathit{\boldsymbol{H}}_L}\left( {{t_1}} \right) \cdot {\mathit{\boldsymbol{H}}_L}\left( {{t_2}} \right)}}{{\left\| {{\mathit{\boldsymbol{H}}_L}\left( {{t_1}} \right)} \right\|\left\| {{\mathit{\boldsymbol{H}}_L}\left( {{t_2}} \right)} \right\|}}} \right)/2 = {\rm{ \mathsf{ π} /6}}. \end{array} \right. $ |
假设追踪星在目标星L系下的初始位置为r0=(0, 170, 0)T,假定追踪星在L系下以速度v=0.1(m/s)沿-y轴匀速接近目标星,则追踪星标称位置为r =(0, 170-vt, 0)T,标称速度为v =(0, -v, 0)T,t为追踪星在走廊内的飞行时间,设T为当前时刻,则有:t=T-t1≤t2-t1.取追踪星星体包络椭球最长半轴u=3 m.设追踪星初始误差相关参数为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{vv}}\left( 0 \right) = {{10}^{ - 6}}{{\left( {\begin{array}{*{20}{c}} 1&0&0\\ 0&4&0\\ 0&0&1 \end{array}} \right)}^{\rm{T}}},{\mathit{\boldsymbol{P}}_{rr}}\left( 0 \right) = {{10}^{ - 4}}{{\left( {\begin{array}{*{20}{c}} 4&0&0\\ 0&{100}&0\\ 0&0&4 \end{array}} \right)}^{\rm{T}}},}\\ {{\mathit{\boldsymbol{P}}_{vr}}\left( 0 \right) = {\mathit{\boldsymbol{P}}_{rv}}\left( 0 \right) = {{\left( {{0_{3 \times 3}}} \right)}^{\rm{T}}}.\;\;\;\;\;\;\;\;\left( {l = 3} \right)} \end{array} $ |
为方便作图,在仿真过程中,用追踪星位置误差椭球的包络线替代误差椭球.由文献[15]可知,追踪星运动过程中误差椭球的包络方程为
| $ \left\{ \begin{array}{l} F = {\left( {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{\bar r}}} \right)^{\rm{T}}}\mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{r}} - \mathit{\boldsymbol{\bar r}}} \right) - 1 = 0,\\ \frac{{\partial F}}{{\partial t}} = 0. \end{array} \right. $ |
追踪星动力学过程采用C-W方程,采用上述仿真条件,则追踪星在目标误差走廊内的运动轨迹及位置误差椭球的包络仿真结果如图 9所示.
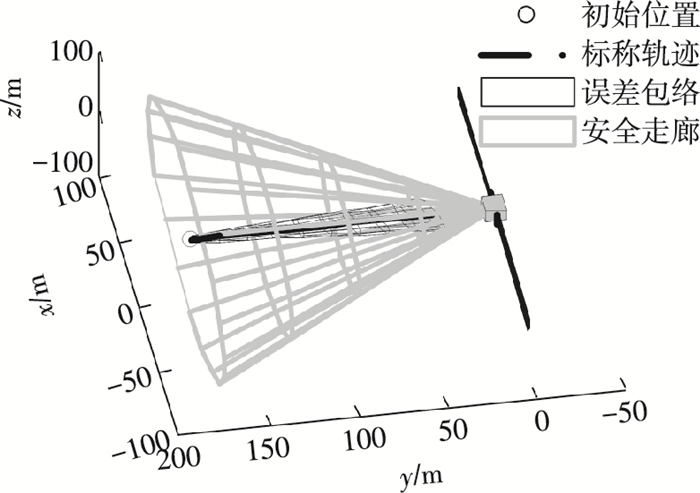
|
图 9 追踪星在安全走廊内运动轨迹及误差包络(1) Figure 9 The trajectory and the position error envelope of the chaser in safe corridor (1) |
由于篇幅有限,此处仅平均选取t1到t2内的5个时间点,计算在每个时间点位置误差椭球与安全走廊锥面的位置关系,见表 8.
| 表 8 广义特征方程根及判断结果(1) Table 8 Roots of generalized characteristic equation and the relevant determination results (1) |
表 8中的结果反映了5个时刻分别对应的走廊锥面与误差椭球变换后的所得平面曲线的广义特征方程的根值及曲面间位置判断结果,结合图 9可看出,走廊锥面与误差椭球位置判断结果正确,走廊锥面始终包含追踪星误差椭球,接近过程中无碰撞危险,该轨迹是安全的.
将追踪星的运动规律改为r0=(-70, 150, 0)T,v =(0.5v, -v, 0)T,则追踪星在L系下的标称位置为r =(-70+0.5vt, 150-vt, 0)T,其他条件不变,再次仿真可得追踪星在目标误差走廊内的运动轨迹及位置误差椭球的包络,如图 10所示.
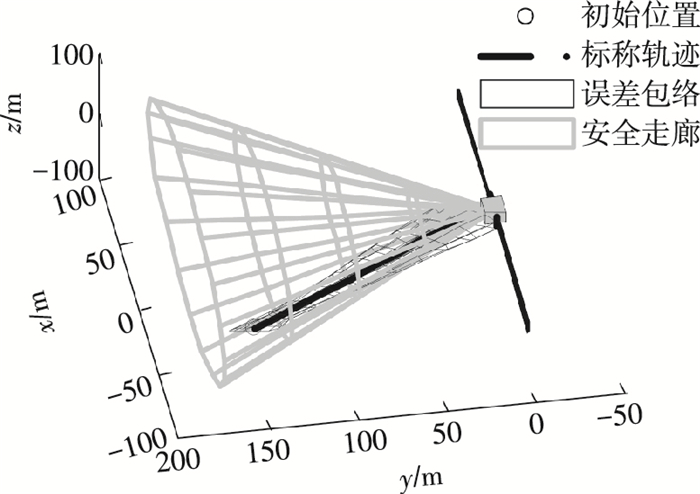
|
图 10 追踪星在安全走廊内运动轨迹及误差包络(2) Figure 10 The trajectory and the position error envelope of the chaser in safe corridor (2) |
同样选取t1到t2内的5个时间点,可得对应广义特征方程根及判断结果见表 9.
| 表 9 广义特征方程根及判断结果(2) Table 9 Roots of generalized characteristic equation and the relevant determination results (2) |
表 9给出了对应图 10中追踪星轨迹中平均5个时刻的目标走廊锥面与追踪星位置误差椭球变换后所得平面曲线的广义特征方程的根及判断结果.在时刻1、2,追踪星误差椭球仍包含在走廊锥面内,轨迹暂时安全.在时刻3后,开始出现共轭虚根,说明椭球与锥面已经开始出现相交情况,而在时刻5,此时追踪星误差椭球已经穿越S1系xy平面,不需要再进行变换,直接可判断椭球与锥面相交.从时刻1到时刻5,两曲面的位置关系是渐变的,误差椭球也是逐渐穿过xy平面的,说明该算例的判断结果是正确的.该算例中,追踪星在目标安全走廊内的标称轨迹是危险的,对于这种情况,应重新对轨迹进行设计,或采取避撞机动措施.
综上所述,锥面与椭球位置判定方法可以准确地运用在目标安全走廊内的碰撞判断问题中.当给定追踪星在目标安全走廊内的标称轨迹后,可以判断出给定初始误差参数下的安全走廊与误差椭球的位置判断结果.根据判断结果,可以判定该标称轨迹是安全或危险,当判定该轨迹危险时,可对标称轨迹重新设计或采取机动措施避撞.
5 结论1) 通过在目标LVLH系下建立目标安全走廊锥面模型与追踪星位置误差椭球,可将走廊内的碰撞判断问题转化为两曲面位置关系的判定问题.
2) 通过将锥面射影变换为圆柱面、椭球射影变换为二次曲面,再经由平面投影和曲线标准化后,可将锥面与椭球面的位置判定问题转化为平面单位圆与椭圆的位置判定问题.
3) 利用平面曲线位置判据的平面圆与椭圆位置关系判定结果,可反推出原锥面与椭球的位置关系,进而对应目标走廊内的碰撞判断结果.
4) 数值仿真结果说明了文中提出的方法可以准确地判断锥面与椭球面在空间中的位置关系,并且可以运用在追踪星于目标安全走廊飞行过程中.通过判定飞行过程中目标走廊锥面与追踪星位置误差椭球的位置关系,从而判定追踪星标称轨迹是否安全.
| [1] |
SUN Liang, HUO Wei. Robust adaptive control of spacecraft proximity maneuvers under dynamic coupling and uncertainty[J].
Advances in Space Research, 2015, 56(10): 2206-2217.
DOI: 10.1016/j.asr.2015.08.029 |
| [2] |
白显宗, 陈磊, 张翼, 等. 空间目标碰撞预警技术研究综述[J].
宇航学报, 2013, 34(8): 1027-1039.
BAI Xianzong, CHEN Lei, ZHANG Yi, et al. Survey on collision assessment and warning techniques for space object[J]. Journal of Astronautics, 2013, 34(8): 1027-1039. DOI: 10.3873/j.issn.1000-1328.2013.08.001 |
| [3] |
白显宗. 空间目标轨道预报误差与碰撞概率问题研究[D]. 长沙: 国防科学技术大学, 2013.
BAI Xianzong. Research on orbital prediction error and collision probability of space objects[D]. Changsha: National University of Defense Technology, 2013. |
| [4] |
安喜彬, 秦伟伟, 黄志兵, 等. 空间碎片碰撞概率数值计算方法[J].
计算机应用, 2016, 36(S2): 325-327.
AN Xibin, QIN Weiwei, HUANG Zhibing, et al. Computing method for space debris collision probability[J]. Journal of Computer Application, 2016, 36(S2): 325-327. |
| [5] |
吴波. 空间目标交会期间碰撞概率研究[D]. 郑州: 解放军信息工程大学, 2011.
WU Bo. Research on collision probability between space objects during encounter[D]. Zhengzhou: PLA Information Engineering University, 2011. |
| [6] |
LIDTKE A A, LEWIS H G, ARMELLIN R, et al. Considering the collision probability of active debris removal missions[J].
Acta Astronautica, 2016, 131: 10-17.
DOI: 10.1016/j.actaastro.2016.11.012 |
| [7] |
LETIZIA F, COLOMBO C, LEWIS H G. Small debris fragments contribution to collision probability for spacecraft in low earth orbits[C]//Iaass Conference. Friedrichshafen: ISSF, 2014: 379-387. DOI: 10.1007/978-3-319-15982-9_45.
|
| [8] |
REITER J A, SPENCER D B. Trading spacecraft propellant use and mission performance to determine the optimal collision probability in emergency collision avoidance scenarios[C]//International Astronautical Congress. Guadalajara, Mexico: IAF, 2016: IAC-16. A6. 7. 5.
|
| [9] |
SERRA R, ARZELIER D, JOLDES M, et al. Fast and accurate computation of orbital collision probability for short-term encounters[J].
Journal of Guidance Control & Dynamics, 2016, 39(5): 1-13.
DOI: 10.2514/1.G001353 |
| [10] |
张大伟, 宋申民, 裴润, 等. 非合作目标自主交会对接的椭圆蔓叶线势函数制导[J].
宇航学报, 2010, 31(10): 2259-2268.
ZHANG Dawei, SONG Shenmin, PEI Run, et al. Ellipse cissoid-based potential function guidance for autonomous rendezvous and docking with non-cooperative target[J]. Journal of Astronautics, 2010, 31(10): 2259-2268. DOI: 10.3873/j.issn.1000-1328.2010.10.005 |
| [11] |
赵育善, 师鹏.
航天器飞行动力学建模理论与方法[M]. 北京: 北京航空航天大学出版社, 2012: 44-53.
ZHAO Yushan, SHI Peng. Theory and method of spacecraft flight dynamics modeling[M]. Beijing: Beihang University Press, 2012: 44-53. |
| [12] |
BRYSON J.
Applied optimal control[M]. London: Taylor & Francis Group, 1975: 309-311.
|
| [13] |
WANG Wenping, WANG Jiaye, KIM M S. An algebraic condition for the separation of two ellipsoids[J].
Computer Aided Geometric Design, 2001, 18(6): 531-539.
DOI: 10.1016/S0167-8396(01)00049-8 |
| [14] |
刘洋, 申立勇. 判别平面上两个椭圆位置关系的代数条件[J].
计算机辅助设计与图形学学报, 2003, 15(5): 555-560.
LIU Yang, SHEN Liyong. An algebraic condition for classifying the positional relationship of two planar ellipses[J]. Journal of Computer-Aided Design & Computer Graphics, 2003, 15(5): 555-560. DOI: 10.3321/j.issn:1003-9775.2003.05.009 |
| [15] |
石昊, 赵育善, 师鹏. 航天器近距离相对运动的轨迹偏差分析[J].
北京航空航天大学学报, 2017, 43(3): 636-644.
SHI Hao, ZHAO Yushan, SHI Peng. Analysis of trajectory deviation for spacecraft relative motion in close-range[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(3): 636-644. DOI: 10.13700/j.bh.1001-5965.2016.0641 |
 2018, Vol. 50
2018, Vol. 50


