2. 中国航天科工集团第三研究院 无人机技术研究所, 北京 100074;
3. 北京空天技术研究所, 北京 100074
2. UAV Technology Institute, The Third Academy of CASIC, Beijing 100074, China;
3. Beijing Aerospace Technology Institute, Beijing 100074, China
吸气式高超声速飞行器由于自身复杂的动力学特性和大跨度的飞行包线, 呈现出多学科耦合、强非线性以及强不确定性的特点[1].此外, 当燃油当量比指令过大, 会引发超燃冲压发动机的热阻塞问题, 需要考虑控制输入饱和问题.基于线性化模型进行控制器设计[2-5], 无法实现飞行器的大范围控制.在以往研究中, 多种非线性控制方法多应用于高超声速飞行器[6-7], 已取得较好的效果.对于严反馈形式的飞行动力学模型, 反步法控制策略由于递推思路清晰且实现简单, 在飞行控制中受到学者们广泛的关注.
文献[8-9]针对弹性高超声速飞行器设计了一种基于反步法的鲁棒自适应控制器, 文中用鸭翼来辅助攻角跟踪期望航迹角, 升降舵控制跟踪角速度, 并将弹性模态视为内动态, 取得较好的控制效果, 但理论上, 鸭翼和升降舵指令之间存在代数环问题, 会引起系统的震荡.文献[10-11]针对含有非匹配不确定性的模型设计了抗干扰反演控制器, 但均没有考虑气动弹性的影响.文献[12-14]针对弹性高超声速飞行器, 设计基于滑模方法的反演控制器, 但都没有同时考虑攻角/推力耦合和控制输入受限问题.文献[15]以推力和升降舵为控制变量设计了无人机鲁棒自适应控制器, 能够有效处理无人机推力饱和以及参数不确定问题.而对于飞行器机体弹性振动, 由于其主要激励源来自于舵面产生的控制力, 文献[16]指出, 通过采用多舵面联合控制, 可实现在满足对刚体运动控制的同时避免激励指定的低阶弹性运动模态, 能够有效抑制弹性振动.
本文将解决考虑输入饱和与气动参数不确定的弹性高超声速飞行器模型的非线性控制问题, 对速度和高度子系统分别进行控制器设计, 采用动态逆和反步法分别设计虚拟控制量和实际控制量, 利用自适应律估计含有不确定性的气动参数, 根据Lyapunov稳定性理论设计考虑输入受限的混合自适应律, 以解决燃油当量比指令饱和问题, 采用鸭翼与升降舵联动控制策略消除控制舵面对一阶弹性模态的激励, 并利用非线性微分观测器来获取虚拟指令的微分信号, 最后通过仿真对比验证了所设计控制器的有效性.
1 高超声速飞行器动力学模型弹性高超声速飞行器纵向运动方程描述如下[9]:
| $ \left\{ \begin{array}{l} \dot V = \frac{1}{m}\left( {T\cos \alpha - D - mg\sin \left( {\theta - \alpha } \right)} \right),\\ \dot h = V\sin \left( {\theta - \alpha } \right),\\ \dot \alpha = q + \frac{1}{{mV}}\left( { - T\sin \alpha - L + mg\cos \left( {\theta - \alpha } \right)} \right),\\ \dot \theta = q,\\ \dot q = {M_y}/{I_{yy}},\\ {{\ddot \eta }_i} = - 2{\xi _i}{\omega _i}{{\dot \eta }_i} - \omega _i^2{\eta _i} + {N_i}. \end{array} \right. $ |
式中:5个刚体状态变量包括:速度V、高度h、攻角α、俯仰角θ、俯仰角速率q; 6个弹性变量包括:前三阶弹性模态ηi(i=1, 2, 3)以及相应的速度变量
| $ \left\{ \begin{array}{l} T \approx \bar qS\left[ {{C_{T,\mathit{\Phi }}}\left( \alpha \right) + {C_T}\left( \alpha \right) + C_T^\eta \mathit{\boldsymbol{\eta }}} \right],\\ L \approx \bar qS{C_L}\left( {\alpha ,{\delta _e},{\delta _c},\mathit{\boldsymbol{\eta }}} \right),\\ D \approx \bar qS{C_D}\left( {\alpha ,{\delta _e},{\delta _c},\mathit{\boldsymbol{\eta }}} \right),\\ M \approx {z_T}T + \bar qS\bar c{C_M}\left( {\alpha ,{\delta _e},{\delta _c},\mathit{\boldsymbol{\eta }}} \right),\\ {N_i} \approx \bar qS\left[ {N_i^{{\alpha ^2}}{\alpha ^2} + N_i^\alpha \alpha + N_i^{{\delta _e}}{\delta _e} + N_i^{{\delta _c}}{\delta _c} + } \right.\\ \;\;\;\;\;\;\;\left. {N_i^\eta \mathit{\boldsymbol{\eta }}} \right],i = 1,2,3. \end{array} \right. $ |
式中:升降舵偏角δe、鸭翼δc、燃油当量比Φ分别为控制输入; q为飞行动压; S、c分别为气动参考面积和平均气动弦长; zT为推力偏心臂长; 气动力和力矩系数拟合函数形式如下:
| $ \left\{ \begin{array}{l} {C_{T,\mathit{\Phi }}}\left( \alpha \right) = C_T^{\mathit{\Phi }{\alpha ^3}}{\alpha ^3} + C_T^{\mathit{\Phi }{\alpha ^2}}{\alpha ^2} + C_T^{\mathit{\Phi }\alpha }\alpha + C_T^\mathit{\Phi },\\ {C_T}\left( \alpha \right) = C_T^3{\alpha ^3} + C_T^2{\alpha ^2} + C_T^1\alpha + C_T^0,\\ {C_M}\left( {\alpha ,\delta ,\mathit{\boldsymbol{\eta }}} \right) = C_T^{{\alpha ^2}}{\alpha ^2} + C_M^\alpha \alpha + C_M^{{\delta _e}}{\delta _e} + C_M^{{\delta _c}}{\delta _c} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;C_M^0 + C_M^\eta \mathit{\boldsymbol{\eta }},\\ {C_L}\left( {\alpha ,\delta ,\mathit{\boldsymbol{\eta }}} \right) = C_L^\alpha \alpha + C_L^{{\delta _e}}{\delta _e} + C_L^{{\delta _c}}{\delta _c} + C_L^0 + C_L^\eta \mathit{\boldsymbol{\eta }},\\ {C_D}\left( {\alpha ,\delta ,\mathit{\boldsymbol{\eta }}} \right) = C_D^{{\alpha ^2}}{\alpha ^2} + C_D^\alpha \alpha + C_D^{\delta _e^2}\delta _e^2 + C_D^{{\delta _e}}{\delta _e} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;C_D^{\delta _c^2}\delta _c^2 + C_D^{{\delta _c}}{\delta _c} + C_D^0 + C_D^\eta \mathit{\boldsymbol{\eta }},\\ C_j^\mathit{\boldsymbol{\eta }} = \left[ {\begin{array}{*{20}{c}} {C_j^{{\eta _1}}}&0&{C_j^{{\eta _2}}}&0&{C_j^{{\eta _3}}}&0 \end{array}} \right],j = T,M,L,D\\ N_i^\mathit{\boldsymbol{\eta }} = \left[ {\begin{array}{*{20}{c}} {N_i^{{\eta _1}}}&0&{N_i^{{\eta _2}}}&0&{N_i^{{\eta _3}}}&0 \end{array}} \right],i = 1,2,3. \end{array} \right. $ |
式中, Ni(·)、CT(·)、CM(·)、CL(·)、CD(·)均为拟合得到的气动系数.
本文拟采用鸭翼舵面与升降舵联动的控制策略, 达到如下目的:1)通过选取联动控制增益为kec=-CLδe/CLδc, 消除控制舵面与升力的耦合, 避免非最小相位特性; 2)选择合理的鸭翼的布局位置, 调整Niδc的值, 满足Niδe+kecNiδc=0, 以消除控制舵面对一阶模态的激励.
鸭翼和升降舵联动控制避免了控制输入对一阶弹性模态的激励, 弹性方程中与α有关的项可视为外部激励力, 从而不影响一阶弹性模态的稳定性, 其稳定性依靠自身的结构阻尼可保证.二、三阶弹性模态频率较高, 控制增益对二、三阶弹性模态影响较小, 其稳定性也能依靠自身的结构阻尼保证.
2 控制器设计在本文的设计中, 将高超声速飞行器纵向通道分解为速度子系统和高度子系统, 其中速度子系统由燃油当量比控制, 高度子系统由鸭翼舵面和升降舵面进行联动控制.
2.1 速度子系统采用自适应动态逆控制方法设计速度子系统.将推力表达式代入速度动力学方程, 速度跟踪误差的动力学方程为
| $ \begin{array}{l} m\dot {\tilde V} = \frac{1}{2}\rho {V^2}S\left[ {{C_{T,\mathit{\Phi }}}\left( \alpha \right)\mathit{\Phi } + {C_T}\left( \alpha \right)} \right]\cos \alpha - \\ \;\;\;\;\;\;\;\;\frac{1}{2}\rho {V^2}S{C_D} - mg\sin \gamma - m{{\dot V}_r}. \end{array} $ | (1) |
定义不确定参数向量θ1∈ R14如下:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\theta }}_1} = \left[ {C_T^{\mathit{\Phi }{\alpha ^3}},C_T^{\mathit{\Phi }{\alpha ^2}},C_T^{\mathit{\Phi }\alpha },C_T^\mathit{\Phi },C_T^3,C_T^2,C_T^1,C_T^0,} \right.}\\ {{{\left. {C_D^{{\alpha ^2}},C_D^\alpha ,C_D^{\delta _e^2},C_D^{{\delta _e}},C_D^{\delta _c^2},C_D^{{\delta _c}},C_D^{\delta _e^2},C_D^0,m} \right]}^{\rm{T}}}.} \end{array} $ |
式(1)可写成为
| $ m\dot {\tilde V} = \mathit{\boldsymbol{\theta }}_1^{\rm{T}}\left[ {{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right)\mathit{\Phi } - {\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)} \right], $ | (2) |
其中, φ1(x, u, yr)、B1(x)分别为如下形式:
| $ \begin{array}{l} {\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right) = \bar qS\left[ {{\mathit{\boldsymbol{0}}_{1 \times 4}}, - {\alpha ^3}\cos \alpha , - {\alpha ^2}\cos \alpha , - \alpha \cos \alpha ,} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left. { - \cos \alpha ,{\alpha ^2}\alpha ,\delta _e^2,{\delta _e},1,\left( {g\sin \gamma + {{\dot V}_r}} \right)/\bar qS} \right]^{\rm{T}}}, \end{array} $ |
| $ {\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right) = \bar qS{\left[ {{\alpha ^3}\cos \alpha ,{\alpha ^2}\cos \alpha ,\alpha \cos \alpha ,\cos \alpha ,{\mathit{\boldsymbol{0}}_{1 \times 12}}} \right]^{\rm{T}}}. $ |
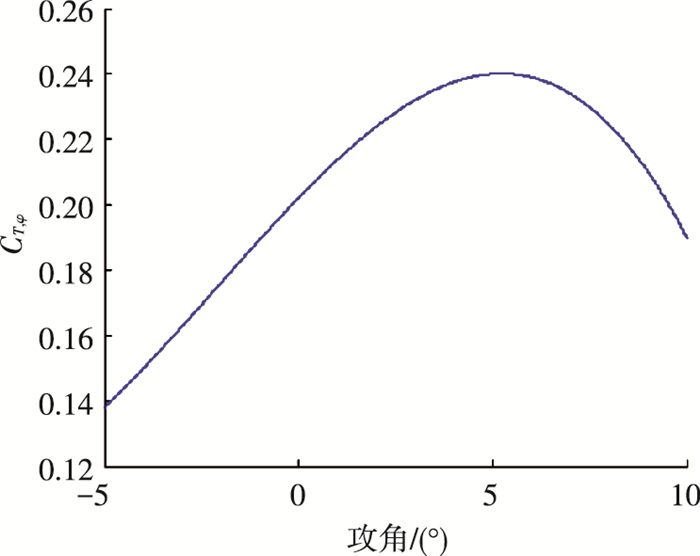
从图 1可知, 在给定的攻角范围内, CT, Φ(α)≠0, 从而推出, 对于所有给定范围内的攻角和动压, θ1T B1(x)≠0均成立.
|
图 1 CT, Φ(α)随攻角的变化范围 Figure 1 CT, Φ(α) as a function of angle of attack |
参数θ1的估计值记为
| $ {W_V}\left( {\tilde V,{{\mathit{\boldsymbol{\tilde \theta }}}_1}} \right) = \frac{{{\sigma _1}}}{2}\left( {m{{\tilde V}^2} + \mathit{\boldsymbol{\tilde \theta }}_1^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1^{ - 1}{{\mathit{\boldsymbol{\tilde \theta }}}_1}} \right). $ | (3) |
式中:σ1>0为以比例因子, Γ1∈ R14×14为对角正定矩阵.自适应更新律和控制指令取如下形式:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot {\hat \theta} }}}_1} = - \tilde V{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1}\left[ {{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right)\mathit{\Phi } - {\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)} \right],\\ \mathit{\Phi } = \frac{1}{{\mathit{\boldsymbol{\hat \theta }}_1^{\rm{T}}{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right)}}\left[ { - {k_1}\tilde V + {\mathit{\boldsymbol{\varphi }}_1}{{\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\hat \theta }}}_1}} \right]. \end{array} $ | (4) |
式中, k1>0为反馈增益.对Lyapunov方程(3)进行求导, 并将式(4)代入, 可得
| $ \begin{array}{*{20}{c}} {{{\dot W}_V} = {\sigma _1}\tilde V\mathit{\boldsymbol{\theta }}_1^{\rm{T}}\left[ {{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right)\mathit{\Phi } - {\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)} \right] + }\\ {{\sigma _1}\mathit{\boldsymbol{\tilde \theta }}_1^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1^{ - 1}{{\mathit{\boldsymbol{\dot {\tilde \theta} }}}_1} = - {\sigma _1}{k_1}{{\tilde V}^2},} \end{array} $ | (5) |
易知, WV为正定且径向无界的函数,
为了维持超燃冲压发动机的正常工作, 燃油当量比需要限制在一定的范围之内.记最大可用燃油当量比为Φ, 此外, 燃油当量比指令必须为正, 因此燃油当量比满足Φ∈[0, Φ].
假设1 速度参考指令Vr对燃油当量比指令的需求不会违反燃油当量比的限制.
假设1可以描述为方程(2)可以达到平衡状态时, 即
| $ \mathit{\boldsymbol{\theta }}_1^{\rm{T}}\left[ {{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right)\mathit{\Phi } - {\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)} \right] = 0, $ | (6) |
式(6)成立时, Φ∈[0, Φ].
由图 1易知, 在本文研究的攻角范围内, 有θ1TB1(x)>0成立, 因此由(6)可以推出
| $ \frac{{\mathit{\boldsymbol{\theta }}_1^{\rm{T}}{\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)}}{{\mathit{\boldsymbol{\theta }}_1^{\rm{T}}{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right)}} \in \left[ {0,\mathit{\bar \Phi }} \right]. $ | (7) |
显然, 由式(7)推导出如下两个不等式成立:
| $ \mathit{\boldsymbol{\theta }}_1^{\rm{T}}{\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right) \ge 0, $ | (8) |
| $ \mathit{\boldsymbol{\theta }}_1^{\rm{T}}{\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right) \le \mathit{\boldsymbol{\theta }}_1^{\rm{T}}{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right)\mathit{\bar \Phi }. $ | (9) |
下面, 分别从燃油当量比超出上边界Φ和下边界0两种情况来分析.
1) Φ=Φ如果控制解算得到的燃油当量比指令大于等于Φ, 则根据控制律(4)有
| $ \frac{1}{{\mathit{\boldsymbol{\hat \theta }}_1^{\rm{T}}{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right)}}\left[ { - {k_1}\tilde V + {\mathit{\boldsymbol{\varphi }}_1}{{\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\hat \theta }}}_1}} \right] \ge \mathit{\bar \Phi }, $ |
即
| $ {\mathit{\boldsymbol{\varphi }}_1}{\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)^{\rm{T}}}{{\mathit{\boldsymbol{\hat \theta }}}_1} - \mathit{\boldsymbol{\hat \theta }}_1^{\rm{T}}{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right)\mathit{\bar \Phi } \ge {k_1}\tilde V, $ | (10) |
此时, 有Φ=Φ, 代入方程(5)可得
| $ \begin{array}{l} {{\dot W}_V} = {\sigma _1}\tilde V\left[ {\mathit{\boldsymbol{\theta }}_1^{\rm{T}}{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right)\mathit{\bar \Phi } - \mathit{\boldsymbol{\theta }}_1^{\rm{T}}{\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)} \right] + \\ \;\;\;\;\;\;\;{\sigma _1}\mathit{\boldsymbol{\tilde \theta }}_1^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1^{ - 1}{{\mathit{\boldsymbol{\dot {\tilde \theta} }}}_1}. \end{array} $ | (11) |
下面将从
当
| $ {{\dot W}_V} = {\sigma _1}\tilde V\left[ {\mathit{\boldsymbol{\dot \theta }}_1^{\rm{T}}{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right)\mathit{\bar \Phi } - \mathit{\boldsymbol{\dot \theta }}_1^{\rm{T}}{\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)} \right] \le - {k_1}{\sigma _1}{{\tilde V}^2}, $ |
因此,
当
| $ {{\dot W}_V} = {\sigma _1}\tilde V\left[ {\mathit{\boldsymbol{\theta }}_1^{\rm{T}}{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right)\mathit{\bar \Phi } - \mathit{\boldsymbol{\theta }}_1^{\rm{T}}{\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)} \right] \le 0, $ |
因此,
2) Φ=0.当控制解算的燃油当量比指令为负, 则根据控制律(4)有
| $ \frac{1}{{\mathit{\boldsymbol{\hat \theta }}_1^{\rm{T}}{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right)}}\left[ { - {k_1}\tilde V + {\mathit{\boldsymbol{\varphi }}_1}{{\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\hat \theta }}}_1}} \right] \le 0, $ | (12) |
此时, 将Φ=0代入方程(5)有
| $ {{\dot W}_V} = {\sigma _1}\tilde V\left[ { - \mathit{\boldsymbol{\theta }}_1^{\rm{T}}{\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)} \right] + {\sigma _1}\mathit{\boldsymbol{\tilde \theta }}_1^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1^{ - 1}{{\mathit{\boldsymbol{\dot {\tilde \theta} }}}_1}. $ | (13) |
当
| $ \begin{array}{*{20}{c}} {{{\dot W}_V} = {\sigma _1}\tilde V\left[ { - \mathit{\boldsymbol{\theta }}_1^{\rm{T}}{\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)} \right] + {\sigma _1}\mathit{\boldsymbol{\tilde \theta }}_1^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1^{ - 1}{{\mathit{\boldsymbol{\dot {\tilde \theta} }}}_1} = }\\ { - {\sigma _1}\tilde V\mathit{\boldsymbol{\hat \theta }}_1^{\rm{T}}{\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right) \le - {k_1}{\sigma _1}{{\tilde V}^2},} \end{array} $ |
成立.
当
| $ {{\dot W}_V} = - {\sigma _1}\tilde V\mathit{\boldsymbol{\theta }}_1^{\rm{T}}{\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right) \le 0. $ |
综上所述, 控制律和自适应律可选取为如下形式:
| $ \mathit{\Phi } = \frac{1}{{\mathit{\boldsymbol{\hat \theta }}_1^{\rm{T}}{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right)}}\left[ { - {k_1}\tilde V + {\mathit{\boldsymbol{\varphi }}_1}{{\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\hat \theta }}}_1}} \right], $ |
| $ {{\mathit{\boldsymbol{\dot {\hat \theta} }}}_1} = \left\{ \begin{array}{l} \;\;\;\;\;\;0,\;\;\;\;\;\;\;{\rm{if}}\;\mathit{\Phi } < 0\;{\rm{and}}\;\tilde V \ge 0;\\ \;\;\;\;\;\;0,\;\;\;\;\;\;\;{\rm{if}}\;\mathit{\Phi } \ge \mathit{\bar \Phi }\;{\rm{and}}\;\tilde V \le 0;\\ - \tilde V{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1}\left[ {{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{x}} \right)\mathit{\Phi } - {\mathit{\boldsymbol{\varphi }}_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{y}}_r}} \right)} \right],其他. \end{array} \right. $ |
式中k1>0, Γ1= Γ1-1>0, 则能够保证
采用递推形式的自适应反步法对高度子系统进行控制, 采用鸭翼与升降舵联动控制的策略.
2.2.1 高度控制以弹道倾角γ=θ-α作为虚拟控制变量对高度进行跟踪.当γ较小时, 有sinγ≈γ成立, 高度跟踪误差的动态方程可表示为
| $ \dot {\tilde h} = V\sin \gamma - {{\dot h}_r} \approx V\gamma - {{\dot h}_r}. $ |
选取航迹角指令为
| $ {\gamma _d} = - {k_2}\tilde h + {{\dot h}_r}/V, $ | (14) |
式中, k2>0.定义航迹角跟踪误差为
| $ \dot {\tilde h} = - {k_2}V\tilde h + V\tilde \gamma . $ | (15) |
定义Lyapunov函数
| $ {{\dot W}_h} = - {k_2}V{{\tilde h}^2} + V\tilde \gamma \tilde h. $ | (16) |
选择攻角α实现航迹角的稳定跟踪控制.航迹角的误差方程为
| $ \begin{array}{l} \dot {\tilde \gamma} = \frac{1}{{mV}}\left[ {\bar qSC_L^\alpha \alpha + T\sin \alpha - mg\cos \gamma + } \right.\\ \;\;\;\;\;\left. {\bar qS\left( {C_L^{{\delta _e}}{\delta _e} + C_L^{{\delta _c}}{\delta _c} + C_L^0} \right) - mV{{\dot \gamma }_{cmd}}} \right]. \end{array} $ | (17) |
从式(17)可以看到, 由于Tsin α项中包含了α的非线性项, 为了使得式(17)满足严反馈形式, 需要对攻角非线性项进行处理.本文采用对qSCLαα+Tsinα进行一阶泰勒展开的方式.
定义α的参数化函数如下
| $ f\left( {\alpha ,x} \right) = \bar qSC_L^\alpha \alpha + T\sin \alpha . $ |
为保证发动机正常工作, 攻角必须保持在很小的变化范围.在初始攻角附近的选择常值α*, 将f(α, x)绕α*进行一阶泰勒展开得到:
| $ f\left( {\alpha ,x} \right) = f\left( {{\alpha ^ * },x} \right) + f'\left( {{\alpha ^ * },x} \right)\left( {\alpha - {\alpha ^ * }} \right) + o\left( {\alpha - {\alpha ^ * }} \right), $ |
作为α-α*的高阶项, o(α-α*)可以近似为零.
不确定性参数向量ϑ2, 向量φ2(x, yr, u)和B2(x, yr, u)定义如下:
| $ {\vartheta _2} = {\left[ {{c_3}\left( {{\alpha ^ * }} \right),{c_4}\left( {{\alpha ^ * }} \right),{c_1}\left( {{\alpha ^ * }} \right) + C_L^0,{c_2}\left( {{\alpha ^ * }} \right),m} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{\varphi }}_2}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{y}}_r},\mathit{\boldsymbol{u}}} \right) = \bar qS{\left[ {0,0,1,\mathit{\Phi },\left( { - g\cos \gamma - V{{\dot \gamma }_{cmd}}} \right)/\bar qS} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{B}}_{\rm{2}}}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{y}}_r},\mathit{\boldsymbol{u}}} \right) = \bar qS{\left[ {1,\mathit{\Phi ,}{\rm{0}}\mathit{,}{\rm{0}}\mathit{,}{\rm{0}}} \right]^{\rm{T}}}. $ |
航迹角误差方程重新表示为
| $ \dot {\tilde \gamma} = \frac{1}{{mV}}\vartheta _2^{\rm{T}}\left[ {{\mathit{\boldsymbol{B}}_2}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{y}}_r},\mathit{\boldsymbol{u}}} \right)\left( {\alpha - {\alpha ^ * }} \right) - {\mathit{\boldsymbol{\varphi }}_2}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{y}}_r},\mathit{\boldsymbol{u}}} \right)} \right]. $ | (18) |
选择Lyapunov方程为
| $ {W_\gamma } = \frac{1}{2}m{{\tilde \gamma }^2} + \frac{1}{2}\vartheta _2^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_2^{ - 1}{{\tilde \vartheta }_2}. $ |
设计自适应律和攻角虚拟指令为:
| $ {{\dot {\hat \vartheta} }_2} = - \frac{{\tilde \gamma }}{V}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_2}\left[ {{\mathit{\boldsymbol{B}}_2}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{y}}_r},\mathit{\boldsymbol{u}}} \right)\left( {\alpha - {\alpha ^ * }} \right) - {\mathit{\boldsymbol{\varphi }}_2}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{y}}_r},\mathit{\boldsymbol{u}}} \right)} \right], $ | (19) |
| $ {\alpha _d} = {\alpha ^ * } + \frac{{ - {k_3}\tilde \gamma - {V^2}\tilde h + \hat \vartheta _2^{\rm{T}}{\mathit{\boldsymbol{\varphi }}_2}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{y}}_r},\mathit{\boldsymbol{u}}} \right)}}{{\hat \vartheta _2^{\rm{T}}{\mathit{\boldsymbol{B}}_2}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{y}}_r},\mathit{\boldsymbol{u}}} \right)}}. $ | (20) |
式中kγ为设计参数.定义攻角误差为
| $ {{\dot W}_\gamma } = - \frac{{{k_3}}}{V}{{\tilde \gamma }^2} - V\tilde h\tilde \gamma + \frac{{f'\left( {{\alpha ^ * },x} \right)}}{V}\tilde \gamma \tilde \alpha . $ | (21) |
攻角跟踪误差动态为
| $ \dot {\tilde \alpha} = q - \dot \gamma - {{\dot \alpha }_d}. $ | (22) |
定义Lyapunov函数为
| $ {{\dot W}_\alpha } = \tilde \alpha \left( {q - \dot \gamma - {{\dot \alpha }_d}} \right). $ | (23) |
角速率的指令设计如下:
| $ {q_d} = - {k_4}\tilde \alpha + \dot \gamma + {{\dot \alpha }_d} - \frac{{f'\left( {{\alpha ^ * },x} \right)}}{V}\tilde \gamma . $ | (24) |
定义角速率跟踪误差为
| $ \tilde q = q - {q_d}, $ | (25) |
将式(24)、(25)代入式(23)中可得
| $ {{\dot W}_\alpha } = - {k_4}{{\tilde \alpha }^2} - \frac{{f'\left( {{\alpha ^ * },x} \right)}}{V}\tilde \gamma \tilde \alpha + \tilde q\tilde \alpha . $ | (26) |
俯仰角速度的误差动态为
| $ \dot {\tilde q} = \frac{{{z_T}T + \bar qS\bar c\left( {C_M^\alpha \alpha + C_M^{{\delta _e}}{\delta _e} + C_M^{{\delta _c}}{\delta _c} + C_M^0} \right)}}{{{I_{yy}}}} - {{\dot q}_d}. $ |
定义不确定参数向量ϑ3, 向量φ3(x, yr, u)和B3(x)如下:
| $ \begin{array}{l} {\vartheta _3} = \frac{S}{{{I_{yy}}}}\left[ {\bar cC_M^{{\delta _e}},{z_T}C_T^{\mathit{\Phi }{\alpha ^3}},{z_T}C_T^{\mathit{\Phi }{\alpha ^2}},{z_T}C_T^{\mathit{\Phi }\alpha },{z_T}C_T^\mathit{\Phi },{z_T}C_T^\mathit{3},} \right.\\ \;\;\;\;\;\;\;{\left. {\left( {{z_T}C_T^2 + \bar cC_M^{{\alpha ^2}}} \right),\left( {{z_T}C_T^1 + \bar cC_M^\alpha } \right),\left( {{z_T}C_T^0 + \bar cC_M^0} \right)} \right]^{\rm{T}}}, \end{array} $ |
| $ {\mathit{\boldsymbol{\varphi }}_3}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{y}}_r},\mathit{\boldsymbol{u}}} \right) = - \bar q{\left[ {0,{\alpha ^3}\mathit{\Phi },{\alpha ^2}\mathit{\Phi ,}\alpha \mathit{\Phi ,\Phi },{\alpha ^3},{a^2},\alpha ,1} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{B}}_3}\left( x \right) = {\left[ {\bar q,{\mathit{\boldsymbol{0}}_{1 \times 8}}} \right]^{\rm{T}}}. $ |
俯仰角速度的误差动态重新写为
| $ \dot {\tilde q} = \vartheta _3^{\rm{T}}\left[ {{\mathit{\boldsymbol{B}}_3}\left( \mathit{\boldsymbol{x}} \right){\delta _e} - {\mathit{\boldsymbol{\varphi }}_3}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{y}}_r},\mathit{\boldsymbol{u}}} \right)} \right] - {{\dot q}_d}. $ |
定义Lyapunov函数为
| $ {W_q} = \frac{1}{2}{{\tilde q}^2} + \frac{1}{2}\tilde \vartheta _3^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_3^{ - 1}{{\tilde \vartheta }_3}. $ | (27) |
设计参数估计自适应律和舵面指令为
| $ {{\dot {\tilde \vartheta} }_3} = - \tilde q{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_3}\left[ {{\mathit{\boldsymbol{B}}_3}\left( \mathit{\boldsymbol{x}} \right){\delta _e} - {\mathit{\boldsymbol{\varphi }}_3}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{y}}_r},\mathit{\boldsymbol{u}}} \right)} \right], $ | (28) |
| $ {\delta _e} = \frac{{ - {k_5}\tilde q + {{\dot q}_d} + \hat \vartheta _3^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_3}\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{y}}_r}} \right)}}{{\tilde \vartheta _3^{\rm{T}}{\mathit{\boldsymbol{B}}_3}\left( \mathit{\boldsymbol{x}} \right)}}, $ | (29) |
对式(27)进行求导, 并将自适应律(28)和升降舵指令(29)代入可得
| $ {{\dot W}_q} = - {k_5}{{\tilde q}^2} - \tilde q\tilde \alpha . $ | (30) |
从式(14)、(20)和式(24)可以看出, 各参考指令表达式都非常复杂.为了避免重复求导困难, 引入文献[13]提出的基于双曲正弦函数的微分跟踪器来估计参考指令的微分信号.将γd, αd和qd信号通过如下微分跟踪器:
| $ \left\{ \begin{array}{l} \dot {\bar \gamma} = {\chi _1},\\ {{\dot \chi }_1} = R_1^2\left[ { - {a_{11}}\sinh \left( {{l_{11}}\left( {\bar \gamma - {\gamma _d}} \right)} \right) - {a_{12}}\sinh \left( {{l_{12}}{\chi _1}/{R_1}} \right)} \right]; \end{array} \right. $ |
| $ \left\{ \begin{array}{l} \dot {\bar \alpha} = {\chi _2},\\ {{\dot \chi }_2} = R_2^2\left[ { - {a_{21}}\sinh \left( {{l_{21}}\left( {\bar \alpha - {\alpha _d}} \right)} \right) - {a_{22}}\sinh \left( {{l_{22}}{\chi _2}/{R_2}} \right)} \right]; \end{array} \right. $ |
| $ \left\{ \begin{array}{l} \dot {\bar q} = {\chi _3},\\ {{\dot \chi }_3} = R_3^2\left[ { - {a_{31}}\sinh \left( {{l_{31}}\left( {\bar q - {q_d}} \right)} \right) - {a_{32}}\sinh \left( {{l_{32}}{\chi _3}/{R_3}} \right)} \right]. \end{array} \right. $ |
式中:Ri>0, ai1>0, ai2>0, li1>0, li2>0(i=1, 2, 3);γ、α、q均收敛于γd、αd、qd、χ1、χ2、χ3均逼近于
定义系统的Lyapunov函数如下:
| $ W = {W_V} + {W_h} + {W_\gamma } + {W_\alpha } + {W_q}, $ |
对W进行求导, 联合式(16)、(21)、(26)和(30)以及速度子系统结论可知
| $ \begin{array}{l} \dot W = {{\dot W}_V} + {{\dot W}_h} + {{\dot W}_\gamma } + {{\dot W}_\alpha } + {{\dot W}_q} = \\ \;\;\;\;\;\;{{\dot W}_V} - {k_2}V{{\tilde h}^2} - \frac{{{k_3}}}{V}{{\tilde \gamma }^2} - {k_4}{{\tilde \alpha }^2} - {k_5}{{\tilde q}^2} \le 0, \end{array} $ |
即
为了验证所设计控制器的有效性, 针对吸气式高超声速飞行器非线性模型进行闭环系统仿真.考虑实际燃油当量比限制在[0, 1]范围内, 升降舵和鸭翼限制在±20°范围内.鸭翼与升降舵进行联动控制, 满足kec=-CLδe/CLδc, 且Niδe+kecNiδc=0.
仿真初始状态参数见表 1.
| 表 1 仿真状态初值 Table 1 Initial conditions |
α*选取为表 1中的初始攻角.为了测试控制器的抗饱和性能, 参考指令Vref由幅值分别为27.4 m/s和18.3 m/s的阶梯信号通过二阶滤波器生成, 滤波器自然频率ωf1=1 rad/s, 阻尼比ζf1=0.9.其中, 27.4 m/s阶跃指令将会引起燃油当量比饱和.参考指令href由幅值为60 m/s为的阶跃信号通过二阶滤波器产生, 其滤波器自然频率ωf2 =0.3 rad/s, 阻尼比ζf2 =0.9.考虑参数不确定性, 将自适应估计参数的初始值在其真值30%范围内随机选取.控制器参数取为:
| $ {k_1} = 200,{k_2} = 1 \times {10^{ - 4}},{k_3} = 5 \times {10^{ - 6}},{k_4} = 4,{k_5} = 8. $ |
自适应律参数为:
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1} = 1 \times {10^{ - 6}} \times {{\bf{I}}_{16 \times 16}},{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_2} = 0.01 \times {{\bf{I}}_{5 \times 5}},{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_3} = \\ \;\;\;\;\;\;0.0001 \times {{\bf{I}}_{10 \times 10}}, \end{array} $ |
微分跟踪器参数为:
| $ {R_1} = 5,{R_2} = 12,{R_3} = 14, $ |
| $ {a_{11}} = {a_{21}} = {a_{31}} = {a_{12}} = {a_{22}} = {a_{132}} = 2, $ |
| $ {l_{11}} = {l_{21}} = {l_{31}} = {l_{12}} = {l_{22}} = {l_{132}} = 3. $ |
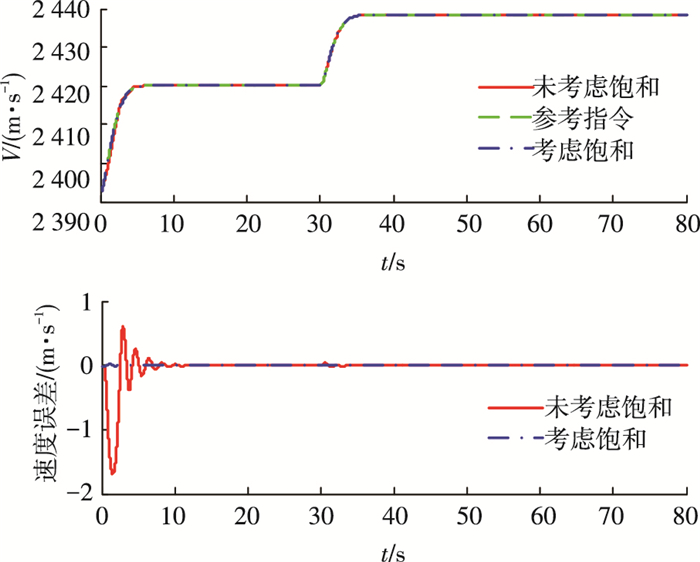
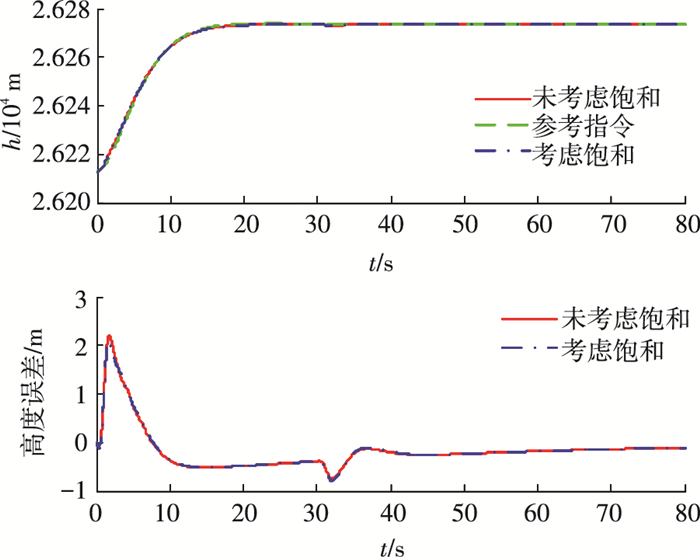
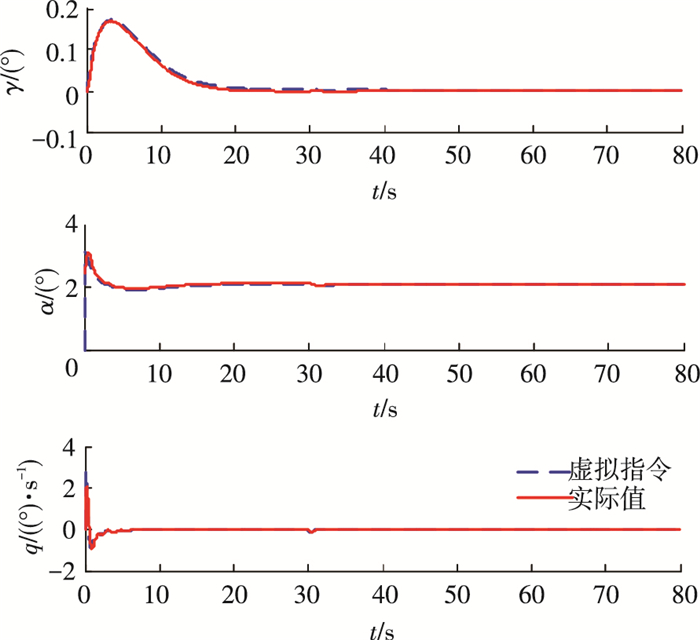
对未考虑以及考虑输入饱和两种情况的进行仿真对比, 仿真结果如图 2~8所示.由图 2、3的仿真曲线可知, 在未确切知道飞行器气动参数时, 速度和高度均具有良好的跟踪效果, 超调量很小, 且稳态误差收敛至0.图 4给出了航迹角、攻角和俯仰角速率的参考指令曲线和实际跟踪曲线, 可以看出, 航迹角、攻角和角速率等均能实现对名义参考指令的良好跟踪, 且航迹角、攻角最终到达稳态值, 角速率最终收敛到零, 从而验证了控制器的效果.
|
图 2 速度和速度跟踪误差仿真结果 Figure 2 Velocity tracking and tracking error |
|
图 3 高度和高度跟踪误差仿真结果 Figure 3 Altitude tracking and tracking error |
|
图 4 航迹角、攻角和俯仰角速率仿真结果 Figure 4 Results of flight-path angle, angle of attack and pitch rate |
|
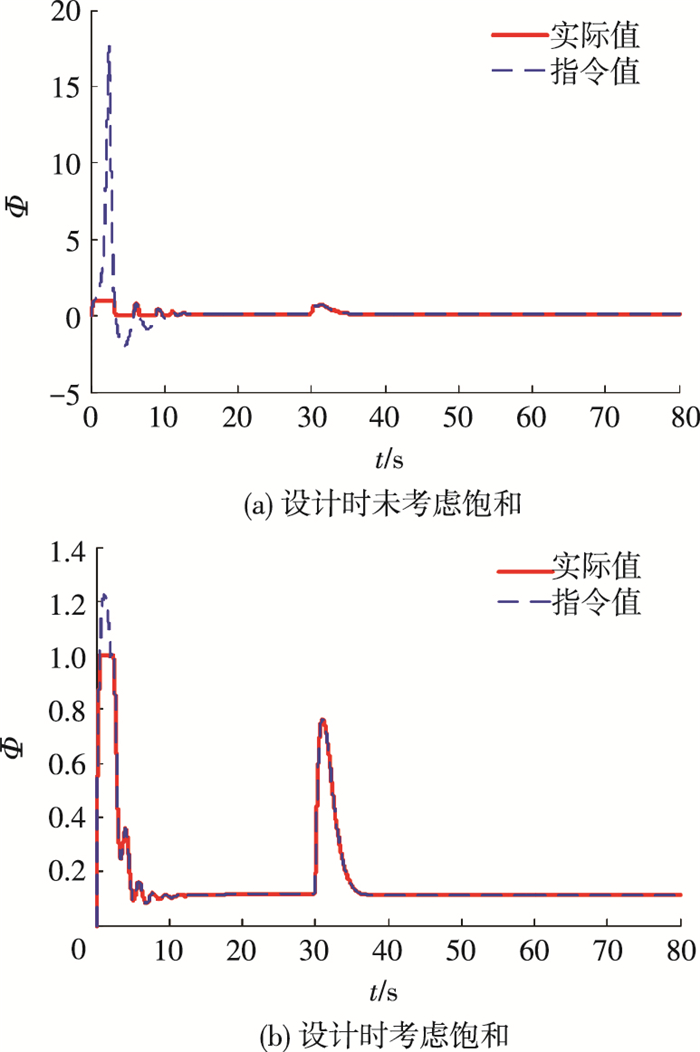
图 5 燃油当量比仿真曲线 Figure 5 Simulation results of equivalence ratio |
|
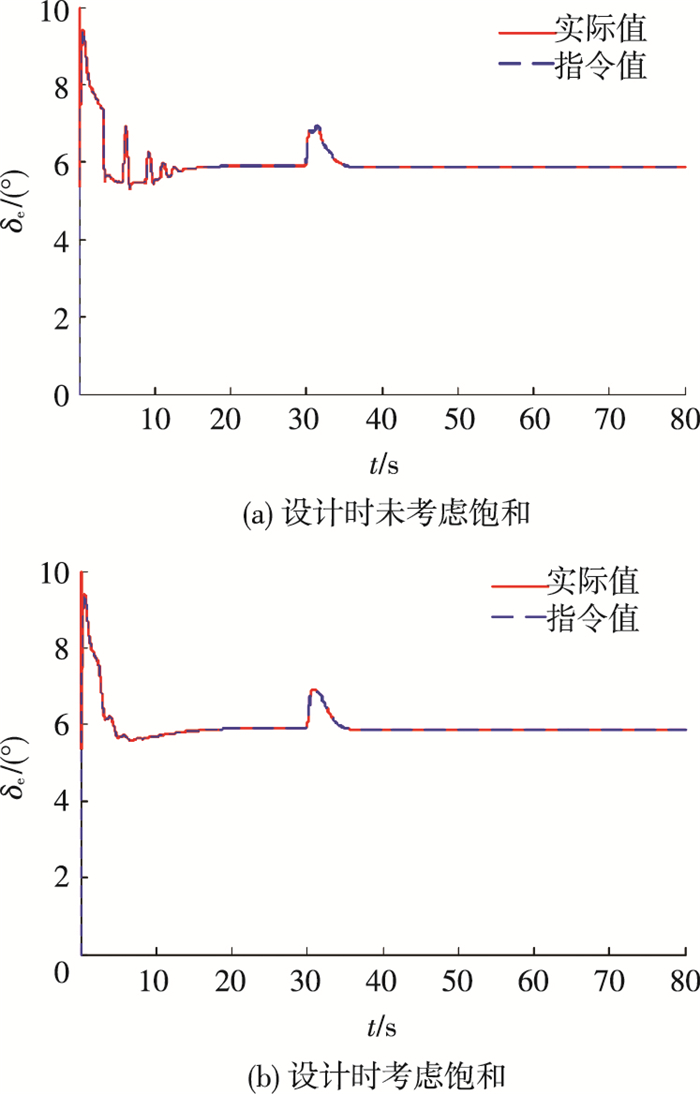
图 6 升降舵仿真曲线 Figure 6 Simulation results of elevator deflection |
|
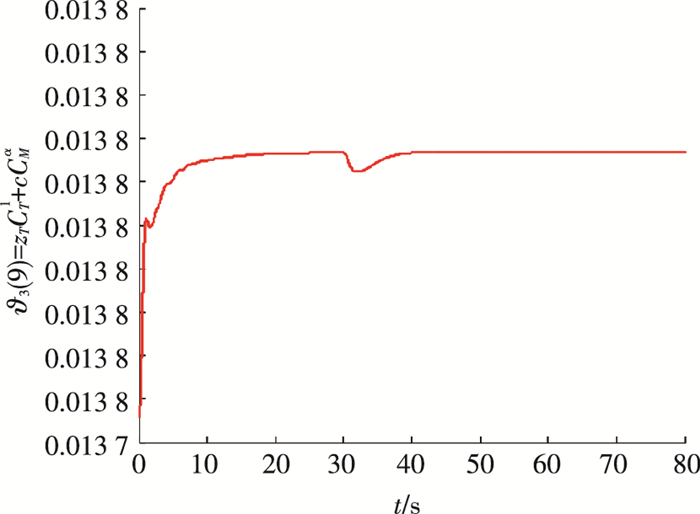
图 7
参数估计值 |
|
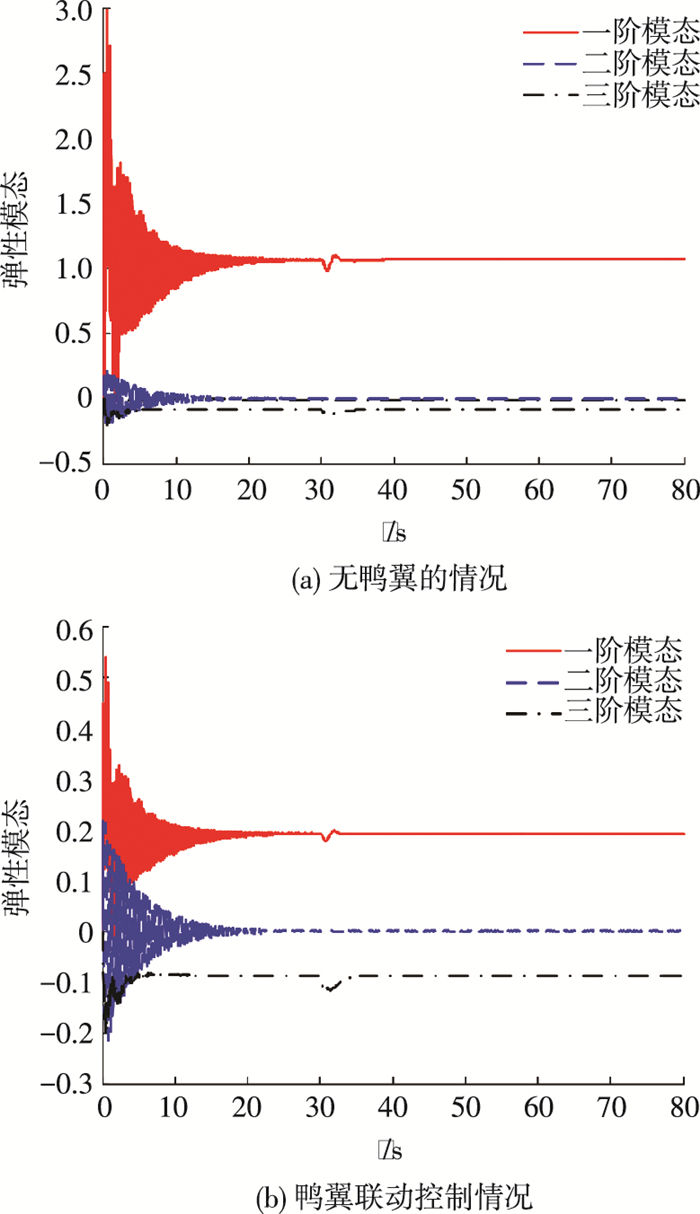
图 8 弹性模态仿真结果 Figure 8 Simulation results of elastic modes |
由图 5、6可以看出, 输入饱和主要出现在燃油当量比的仿真结果中, 且出现在速度指令变化较大的0~10 s阶段, 而升降舵未出现饱和现象, 且由图 2可知, 在饱和阶段, 速度控制跟踪性能受到一定的影响, 出现较大的震荡.同时, 综合图 2、5和图 6可知, 与未考虑输入饱和设计相比, 本文设计的抗饱和策略极大程度上减小了燃油当量比饱和时间和指令幅值, 并显著减小了速度跟踪曲线在饱和区的震荡幅值和震荡时间, 能够有效的处理速度指令过快引起的燃油当量比输入饱和问题.从图 3、6可以看出, 对燃油当量比的饱和处理, 可以降低升降舵的震荡现象, 但是对高度跟踪性能影响较小.
图 7代表性的给出了不确定性参数ϑ3(9)=zTCT1+cCMα的实时估计曲线, 可见, 在不确定性参数真值未知的情况, 参数估计值能保持有界并较快的收敛到常值.
由图 8可知, 在没有采用鸭翼配合控制情况下, 一阶弹性模态虽然也能保持收敛, 但是其震荡幅值较大, 且对刚体运动较为敏感, 最后的稳态值也维持在较大的数值.采用鸭翼配合时, 其震荡幅值大幅减弱, 且对刚体运动的变化响应较小, 最后的稳态值保持在较小的幅值, 这对于飞行器都是非常有利的.从图中还可以看出, 二、三阶弹性模态受刚体运动影响较小, 能够靠自身的结构阻尼保持稳定.
5 结论1) 在速度控制设计中考虑了油门实际限幅, 所提出的自适应控制律在油门饱和情况下可以保证系统李雅普诺夫稳定性, 并能有效改善饱和情况下系统的跟踪性能.
2) 为解决模型参数不确定性问题, 根据Lyapunov稳定性理论设计了实时参数估计自适应律和各级虚拟控制指令, 根据LaSalle不变集原理, 采用所提出的控制策略可保证闭环系统的所有信号都是稳定的, 所有虚拟控制量的跟踪误差能够渐进收敛, 实时参数估计误差是收敛的.通过引入跟踪微分器获得虚拟控制指令的导数, 解决了反步法求导复杂的问题.
3) 本文采用鸭翼和升降舵联动的控制策略避免了控制舵面对选定弹性模态的激励, 从而保证了弹性模态的能够在较短的时间内迅速收敛.
| [1] |
BOLENDER M A, DOMAN D B. Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J].
Journal of Spacecraft and Rockets, 2007, 44(2): 374-387.
DOI: 10.2514/1.23370 |
| [2] |
SCHMIDT D K. Optimum mission performance and multivariable flight guidance for airbreathing launch vehicles[J].
Journal of Guidance, Control, and Dynamics, 1997, 20(6): 1157-1164.
DOI: 10.2514/2.4171 |
| [3] |
BUSCHEK H, CALISE A J. Uncertainty modeling and fixed-order controller design for a hypersonic vehicle model[J].
Journal of Guidance, Control, and Dynamics, 1997, 20(1): 42-48.
DOI: 10.2514/2.4031 |
| [4] |
GREGORY I M, CHOWDHRY R S, MCMINN J D, et al. Hypersonic vehicle model and control law development using H∞ and μ synthesis[J].
NASA Technical Memorandum 4562, 1994: 1-24.
DOI: 10.2514/6.1992-5010 |
| [5] |
SIGTHORSSON D O, JANKOVSKY P, SERRANI A, et al. Robust linear output feedback control of an airbreathing hypersonic vehicle[J].
Journal of Guidance, Control, and Dynamics, 2008, 31(4): 1052-1066.
DOI: 10.2514/1.32300 |
| [6] |
PARKER J T, SERRANI A, YURKOVICH S, et al. Control-oriented modeling of an airbreathing hypersonic vehicle[J].
Journal of Guidance, Control, and Dynamics, 2007, 30(3): 856-869.
DOI: 10.1016/j.ast.2012.07.004 |
| [7] |
ZONG Qun, WANG Jie, TIAN Bailing, et al. Quasi-continuous high-order sliding mode controller and observer design for flexible hypersonic vehicle[J].
Aerospace Science and Technology, 2013, 27(1): 127-137.
DOI: 10.1016/j.ast.2012.07.004 |
| [8] |
FIORENTINI L, SERRANI A, BOLENDER M, et al. Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles[J].
Journal of Guidance, Control, and Dynamics, 2009, 32(2): 401-417.
DOI: 10.2514/1.39210 |
| [9] |
FIORENTINI L. Nonlinear adaptive controller design for airbreathing hypersonic vehicle[D]. Columbus, Ohio: Ohio State University, 2010.
|
| [10] |
后德龙, 王青, 王通. 高超声速飞行器抗干扰反步滑模控制[J].
北京航空航天大学学报, 2014, 40(1): 80-85.
HOU Delong, WANG Qing, WANG Tong. Disturbance rejection sliding mode control of hypersonic vehicle based on backstepping method[J]. Journal of Beijing Universaty of Aeronautics and Astronautics, 2014, 40(1): 80-85. |
| [11] |
路遥, 董朝阳, 王青. 高超声速飞行器自适应反步控制器设计[J].
航空学报, 2015, 36(3): 970-978.
LU Yao, DONG Chaoyang, WANG Qing. Adaptivebackstepping controller design for hypersonic vehicle[J]. Acta Aeronautica et Astrounautic Sinica, 2015, 36(3): 970-978. DOI: 10.7527/S1000-6893.2014.0255 |
| [12] |
卜祥伟, 吴晓燕, 陈永兴, 等. 吸气式高超声速飞行器鲁棒反演控制器设计[J].
固体火箭技术, 2014, 37(6): 743-748.
BU Xiangwei, WU Xiaoyan, CHEN Yongxing, et al. Robust backstepping controller design for air-breathing hypersonic vehicles[J]. Journal of Solid Rocket Technology, 2014, 37(6): 743-748. DOI: 10.7673/j.issn.1006-2793.2014.06.002 |
| [13] |
BU Xiangwei, WU Xiaoyan, ZHANG Rui, et al. Tracking differentiator design for the robust backstepping control of a flexible air-breathing hypersonic vehicle[J].
Journal of the Franklin Institute, 2015, 352(4): 1739-1765.
DOI: 10.1016/j.jfranklin.2015.01.014 |
| [14] |
李静, 左斌, 段洣毅, 等. 输入受限的吸气式高超声速飞行器自适应Terminal滑模控制[J].
航空学报, 2012, 33(2): 220-233.
LI Jing, ZUO Bin, DUAN Miyi, et al. Adaptive Terminal sliding mode control for air-breathing hypersonic vehicle under control input saturations[J]. Acta Aeronautica et Astrounautic Sinica, 2012, 33(2): 220-233. |
| [15] |
GAVILAN F, VAZQUEZ R, ACOSTA J A, et al. Adaptive control for aircraft longitudinal dynamics with thrust saturation[J].
Journal of Guidance, Control, and Dynamics, 2015, 38(4): 651-661.
DOI: 10.2514/1.G000028 |
| [16] |
PARKER J T, SERRANI A, YURKOVICH S, et al. Control-oriented modeling of an air-breathing hypersonic vehicle[J].
Journal of Guidance, Control, and Dynamics, 2007, 30(3): 856-869.
DOI: 10.2514/1.27830 |
 2018, Vol. 50
2018, Vol. 50


