近年来皮纳卫星发展迅速, 多颗皮纳卫星组成星群后, 能力大大提高, 甚至可完成传统大卫星无法实现的任务[1].皮纳卫星及星群具有广阔应用前景, 但应用时要求地面系统具有高度自动管理能力, 特别是基于遥测数据分析的异常检测-故障诊断能力.首先, 单颗卫星包含上百维实时遥测, 星群的设计增加了大量遥测数据; 其次, 皮纳卫星多采用商用器件, 寿命设计较短, 性能退化或状态的切换导致数据漂移[2]; 最后, 皮纳卫星的监控人员少, 实时而自动的地面系统需求十分迫切.
传统边界检查方法操作简单, 但存在难以适应数据概念漂移, 无法检测非越界故障等问题[3].近年来数据挖掘方法被应用到遥测数据异常检测中, ESA开发的Novelty Detection System (NDS)[4]和GSOC开发的Automated Telemetry Health Monitoring System (ATHMoS)[5]均能适应数据的趋势变化, 并发现非越界故障, 但限于处理单维数据(下文称单维属性), 无法满足皮纳卫星及星群多维数据异常检测要求.
特征变换和特征选择均可对多维数据进行降维.目前特征变换在异常检测领域应用较多[6-12], 此类方法通过主成分分析, 捕捉遥测数据主要特征实现降维, 并在主要特征空间内检测异常.主要特征由遥测数据多个属性组合, 发现异常后追踪原因不直观.当数据出现概念漂移, 特征发生变化, 之前设定的特征空间失效.Keller等[13]举例证明此类算法无法发现某些非主要特征属性的异常.特征选择方法通过搜索相关性, 在多个子空间上检测全空间被覆盖和单维无法发现的异常点[14], 适合多潜在相关性的皮纳卫星及星群.由于每个子空间内数据维度低, 物理意义明确, 可采用聚类异常检测方法, 方便追踪故障原因.但传统基于特征选择和聚类的异常检测算法存在运算复杂、实时性不强等问题[15].
针对皮纳卫星遥测数据多维、存在概念漂移的特点, 和实时、自动化异常检测的要求, 本文提出一种基于相关子空间的两阶段聚类遥测数据异常检测方法, 该方法可获得遥测数据低维相关子空间, 并通过聚类算法实现快速自动的异常检测.
1 算法原理及实现系统包含相关子空间搜索和基于两阶段聚类的遥测数据异常检测两部分, 其中两阶段聚类包含在线、离线阶段, 系统结构如图 1所示.
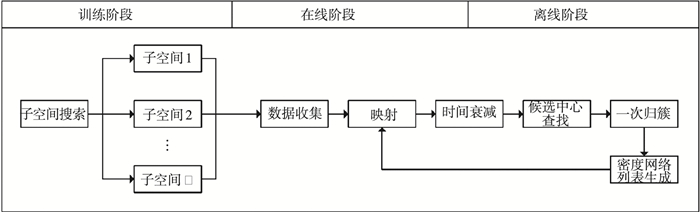
|
图 1 皮纳卫星遥测数据异常检测系统的结构 Figure 1 Structure of telemetry monitoring system for nano-satellites |
相关子空间搜索是为了区分分布密集和稀疏的属性, 其中密集单维属性自成子空间.而对趋向均匀分布的单维属性, 采取二维(或多维)子空间内相关属性互相监督的方式检测异常.每个子空间数据结构见表 1.
| 表 1 子空间数据向量的结构 Table 1 Structure of subspace data vector |
两阶段聚类包括在线、离线阶段, 处理对象为子空间搜索获得的相关子空间.在线阶段检测单点异常, 包括数据收集和映射单元.在线阶段结束后, 时间衰减单元用于减少或去除早期数据对当前聚类的影响.离线阶段检测集体异常和关联异常, 包括簇中心查找、融合归簇与密度网格列表生成单元.
1.1 子空间搜索子空间搜索自下而上, 以熵为量化指标[16], 区分属性密集程度.
首先, 遍历遥测数据所有属性的熵, 定义为
| $ H\left( \mathit{\boldsymbol{X}} \right) =-\sum\limits_{x \in \mathit{\boldsymbol{X}}} {p\left( x \right){\rm{ln}}\;p\left( x \right)} . $ |
式中:X为每个属性离散的随机变量总体, 将归一化后的属性范围分为等长的间隔; x为X在固定间隔内的输出; p(x)是对应的概率质量函数.
其中单维属性的熵低于阈值ε(一般取相同范围的均匀分布数据的熵的0.15), 为密集属性, 放入子空间划分的列表.
剩余属性分布相对稀疏, 采用联合熵和兴趣度概念[13], 判断两维子空间是否存在簇, 联合熵定义为
| $ {\rm{Interest(}}\mathit{\boldsymbol{A}}{\rm{) = }}\sum\limits_{{\mathit{\boldsymbol{X}}_i} \in \mathit{\boldsymbol{A}}} {H\left( {{\mathit{\boldsymbol{X}}_i}} \right)-H({\mathit{\boldsymbol{X}}_1}, {\mathit{\boldsymbol{X}}_2}, \ldots, {\mathit{\boldsymbol{X}}_n})} {\rm{ }} $ |
式中A为包含多个属性Xi的子空间.
联合熵值低且兴趣度高的稀疏属性对组成候选子空间, 采用聚类算法(DPC算法, 详见下文)验证相关性, 簇中心发现成功则将属性对放入子空间划分的列表.皮纳卫星遥测数据多有潜在相关, 此时一般可将所有属性划分完毕.如有遗留属性, 仍可在全空间更高维度内检索, 过程同上.
皮纳卫星遥测数据通过检索单维和两维空间, 一般可实现子空间全划分.按两维子空间搜索计算, 子空间搜索时间复杂度为O(n+l2), n为全空间维度, l为稀疏空间维度.
1.2 两阶段聚类遥测数据异常检测两阶段聚类遥测数据异常检测以相关子空间为对象, 分为在线、离线阶段.
1.2.1 在线阶段在线阶段数据收集单元用于累积数据点的权重ω, 即相同数据点出现的次数.新数据点(ω=0)到达时, 映射单元将数据存入网格索引[17], 并依据上一次离线阶段给出的密度网格列表, 判断新数据点属于正常点、候选异常点或重要异常点.密度网格列表在离线阶段产生, 分为高密、低密网格列表.映射到高密网格的点属正常点; 映射到低密网格的点属候选异常点, 系统标记异常; 剩余点属重要单点异常, 系统预警并标记异常.
皮纳卫星在任务切换和性能衰减时, 遥测数据呈现概念漂移.在线阶段结束后, 将本次在线收集的数据和旧数据以数据点权重相加的方式合并, 采用时间衰减单元应对概念漂移, 衰减公式为
| $ {\omega _{i, {t_c}}} = {\lambda ^{{t_c}-{t_x}}}*{\omega _{i, {t_x}}}. $ |
式中:tc为当前时标; tx为上次时间衰减的时标.当数据点的权重低于阈值γ时, 系统删除该点.定义数据存留期是权重为1且其后不在出现的数据点, 系统保留该点的时间长度.经计算存留期为logλ(γ).如λ选择0.9, 阈值γ选择0.7, 使数据存留期为3个卫星测控周期.这组阈值的选择适用于稳定时间保持3个周期以上的数据, 出现概念漂移, 聚类稳定的速度小于3个周期(实际使用中为1个周期).时间衰减单元可以减少或去除早期数据对当前聚类的影响.
1.2.2 离线阶段离线阶段包含3个单元, 即簇中心查找、一次归簇和密度网格列表生成.
1) 簇中心查找.密度峰值聚类算法(density peak clustering, DPC)[18]是一种基于密度和距离的聚类算法, 适合于静态高斯分布数据的簇中心查找.其基本思想是作为簇中心的点, 本地密度大, 且距离其余簇中心远.算法需要每个数据点的本地密度ρi和最小距离δi, 本地密度ρi定义为
| $ {\rho _i} = \sum\limits_{j \ne i} {\chi ({d_{ij}}-{d_c}) \times {\omega _j}} . $ |
式中:当x < 0时, χ(x) = 1, 当x ≥ 0时, χ(x) = 0;dc为截断距离; ωj为数据点权重; ρi为数据点i的本地密度.DPC算法[15]给出了截断距离dc的计算方法.
最小距离δi定义为
| $ {\delta _i} = \left\{ {\begin{array}{*{20}{c}} {{\rm{max}}({d_{ij}}), }&{{\rho _i} = {\rm{max}}\left( \rho \right);}\\ {\mathop {{\rm{min}}}\limits_{j:{\rho _j} > {\rho _i}} ({d_{ij}}), }&{{\rm{else}}.} \end{array}} \right. $ |
式中dij为数据点i和j之间的欧几里德距离.
DPC算法处理静态数据有优势[15], 但应用到动态的遥测数据上存在两个问题.其一, DPC算法需计算每个数据点的密度和距离, 运算复杂度为O(n2).其二, 簇中心通过画出密度距离决策图(δi-ρi)人工选定, 无客观标准, 难以自动化.
本单元采取以下步骤在有异常标记的数据点中判断是否有候选簇中心.
步骤1 利用网格索引的本地密度ρ计算.在线阶段建立的网格索引使每个数据点的查找范围从全局缩减为该点所在网格及相邻网格.计算复杂度降低为O(kn), 其中k为邻近网格包含的最大数据点个数, 相比数据点个数n极小.
步骤2 根据本地密度标准筛选
| $ \rho > {\lambda ^{{t_c}-{t_x}}}{\rho _\alpha }, $ |
使低密度点不进入距离计算步骤.其中ρα是上个离线阶段归簇成功的数据点密度升序排列后的α分位点, 一般认为α=5%是合理值.
步骤3 相对高密度点间计算最小距离β, 并选择距离密度积β×ρ最大的m个点作为候选中心, 为下个归簇单元使用.根据相关子空间维度1~2维, 从遥测数据属性的物理意义判断, m值选择3~5为合理区间.
簇中心查找范围为异常标记的数据点集, 避免了全局查找, 同时利用网格索引和密度筛选降低了DPC算法的复杂度, 适合于动态数据的快速簇中心查找.
2) 一次归簇单元.本单元按照以下步骤进行每个数据点的归簇.
步骤4 从空间的一角开始建立空间上连续的有序数据点队列, 其中部分数据点包含簇属性(候选中心和上次归簇的密集区域点), 其余点无簇属性.
步骤5 按照队列确定每个点的簇属性, 判断过程如下:属性的临近点(dc空间范围内), 赋予目前不存在的最大负值作为簇属性; 存在有簇属性的单独临近点(dc空间范围内), 跟随赋予该簇属性.
步骤6 存在有簇属性的多个临近点(dc空间范围内):该点密度符合上式, 说明该点不属于边界点, 跟随赋予最接近0值的簇属性, 同时将其余异簇属性的临近点跟随赋予该值; 否则, 该点簇为边界点, 属性不变.
步骤7 簇属性为正值的点成功归簇, 簇属性没有或为负值, 则没有归簇.
本单元将新数据点归簇和旧数据属性同时完成.邻近簇相互融合, 聚类结果具有较高鲁棒性.因为每个数据点仅查询一次而非递归, 时间复杂度较低, 称为一次归簇单元.此时发现的新簇, 可能属于数据的集体故障, 需要被提取分析.
3) 密度网格列表.密度网格列表生成单元, 按照在线阶段的映射需求, 给出高密列表和低密列表.定义如下:
定义1 高密列表.dc网格内, 存在归属相同簇的点覆盖面积大于阈值(一般取50%);
定义2 低密列表.dc网格内, 存在归属相同簇的点, 但覆盖面积小于阈值(一般取50%).
50%的覆盖面积可以保障处于高密列表的新到数据点与当前簇的最远距离不超过0.77dc, 符合归簇要求.
1.3 小结在相关子空间搜索的基础上, 本文提出了基于两阶段聚类的异常检测方法.与传统两阶段聚类算法不同, 在线阶段增加单点异常的实时检测功能.离线阶段精确提取数据的集体异常, 并提供在线阶段映射所用的密度网格索引.针对动态遥测数据, 簇中心查找单元采用局部更新降低了聚类算法的时间和内存消耗, 候选中心的参数阈值具有动态自适应能力.一次归簇单元更新所有点的簇属性, 并整合集体异常点.密度网格列表的生成使在线阶段为离线阶段提高效率、离线阶段为在线阶段提供准确性得以循环.算法满足实时、自动化的异常检测要求.
2 结果与分析本文在Matlab R2010b中, 采用人工数据集DS0和ZDPS-1A卫星实时遥测数据DS1对算法功能和性能进行了验证.人工数据集DS0由6×105个两维数据点组成, 其中10%属于离散点, 数据密集区域每1 100点发生位置偏移, 簇的数量从1变为3并循环.ZDPS-1A卫星是浙江大学微小卫星中心2010年9月成功发射的试验型皮纳卫星.DS1包含2010年9月到2011年12月的3.121 63×105个133维实时遥测数据, 其中90维是数字量(单元的开关标识等), 43维是模拟量(温度、电流等).模拟量是异常检测的重点和难点.
2.1 子空间搜索子空间搜索用的训练数据集为DS1, 2010年9月到11月的模拟量部分.划分后生成12维单维密集属性和19对两维相关子空间(存在多对一), 在两维下实现子空间全划分.
以太阳电池电流和太阳敏感器采样值为例, 单维熵分别是1.58和1.45, 属稀疏属性, 无法自成子空间.两者联合熵为2, 兴趣度为0.199, DPC算法发现两个簇中心, 划入两维相关子空间, 此子空间数据落点图和两维属性的密度直方图如图 2所示, 发现了A和B两个异常点.
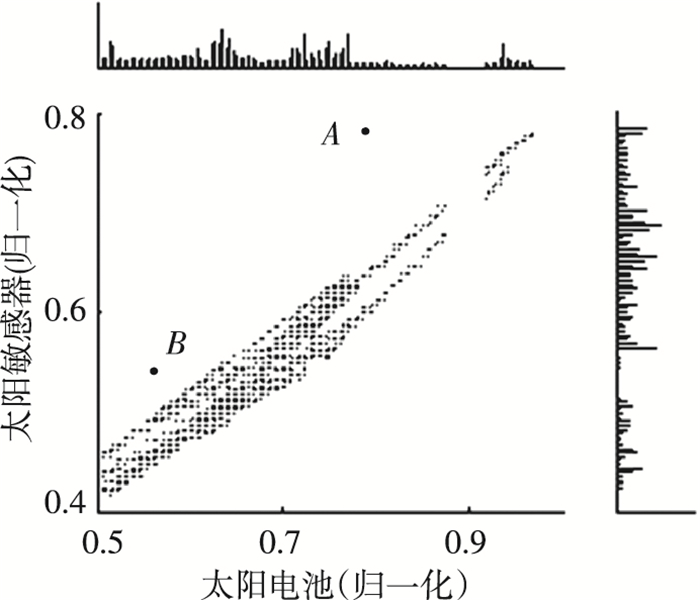
|
图 2 相关子空间的异常 Figure 2 Anomalies in correlative subspace |
经训练集DS0和DS1验证, 在线阶段实现了10 kHz速率的两维数据流处理, 满足实时遥测异常检测需求, DS1中重要异常点检测率达到95%.在线阶段实现了数据量压缩, 经权重累积后DS1的平均数据量是原始数据的37%, 映射后异常点标记的平均数据量是原始数据的9%.
离线阶段用于发现集体异常, 即新簇.图 3显示, DS0处于簇数量从1个变为3个的过程, 如图 3(a)所示.首次出现的两个簇, 簇中数据点权重低且分布稀疏, 如图 3(b)所示.本文提出的算法完整保留了不同密度的簇.图 3(c)、(d)分别为使用两组参数的DBSCAN聚类结果, 由于3个簇的密度不同, 固定参数的DBSCAN无法形成稳定的簇形状.图 3(e)使用了DPC算法, 因为边界的定义较为严苛, 也产生了多个簇.由于候选中心与边界点的筛选阈值具自适应, 本文提出的算法在动态数据发生变化时捕捉新簇的准确性更高, 簇的形状相对稳定.
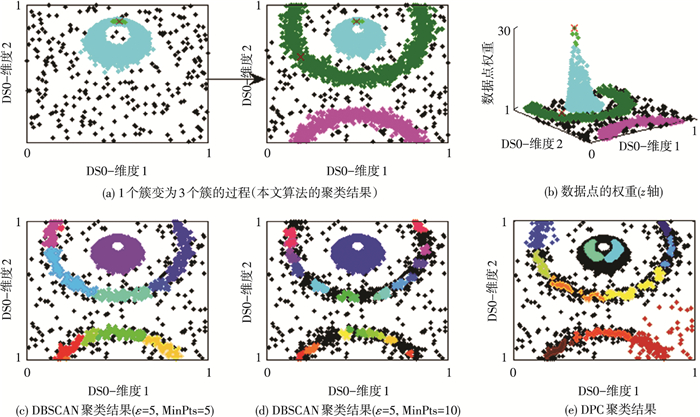
|
图 3 动态训练集数据归簇结果比较(本文算法、DBSCAN、DPC) Figure 3 Clustering result comparison between proposed algorithm, DPC and DBSCAN of DS0 |
在软件环境为MatlabR2010b, 处理器为i5@3.10 GHz、内存4 GB的PC上, 采用DPC、DBSCAN和本文提出的算法, 在训练集DS0上测试.每1 100个点进行一次阶段循环, 离线阶段的时间消耗如图 4所示.第82周期前, DPC算法的时间消耗保持相对稳定; 第82周期, 簇数量的变化导致时间消耗上升到2.816 s; 全过程DPC算法平均时间消耗为1.770 s.DBSCAN的时间消耗保持平稳, 平均为0.760 s.本文提出的算法, 只在簇数量变化时出现一次时间消耗尖峰(2.580 s), 映射单元和局部簇中心查找的算法设计使其后曲线迅速回落, 平均值为0.510 s.相比DBSCAN和DPC算法更低.本文提出的算法能快速适应异常, 恢复稳定的时间消耗.
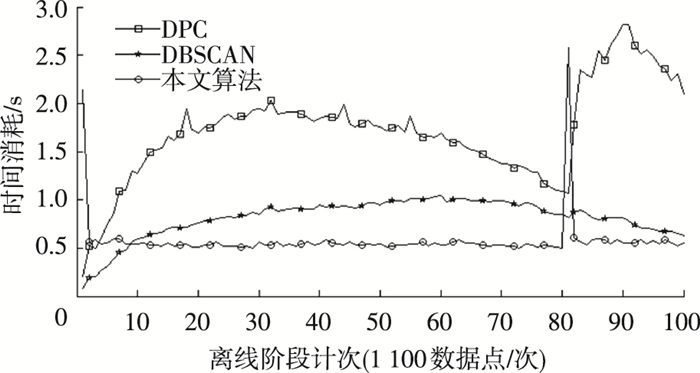
|
图 4 离线阶段动态时间消耗比较(本文算法、DBSCAN、DPC) Figure 4 Offline phase time consumption comparison between proposed algorithm, DPC and DBSCAN of DS0 |
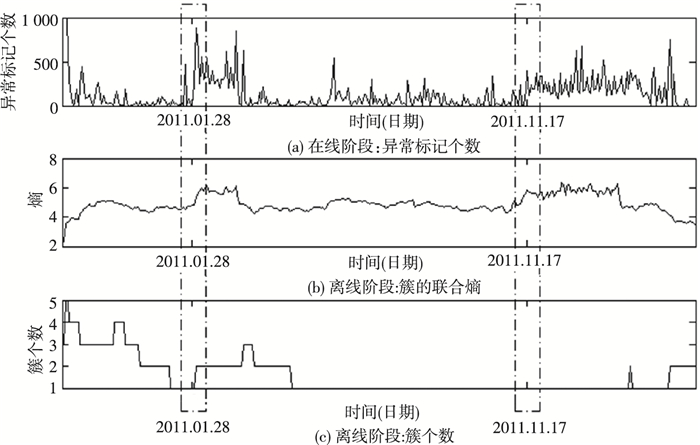
为实现自动化异常检测, 3个过程参数指标被用于判断异常, 见表 2.应用到太阳敏感器和太阳电池的子空间后, 指标变化如图 5所示.
| 表 2 异常检测的特征指标 Table 2 Indicators for anomaly detection |
|
图 5 用于异常检测的3个指标曲线(2010年9月到2012年1月) Figure 5 Curves of three indicators for anomaly detection in 2010.09 to 2012.01 |
3个指标中, 簇的联合熵反应了簇内数据的稀疏程度, 是关键指标; 异常标记个数和簇个数作为辅助指标.本文采用Grubbs准则(显著性水平0.05)对异常标记个数和簇的联合熵进行指标异常与否的判断; 簇个数指标状态明确可直接判读.除初始状态外, 结合3个指标, 两个明显的突变被发现, 分别位于2011年1月28日和2011年11月17日.
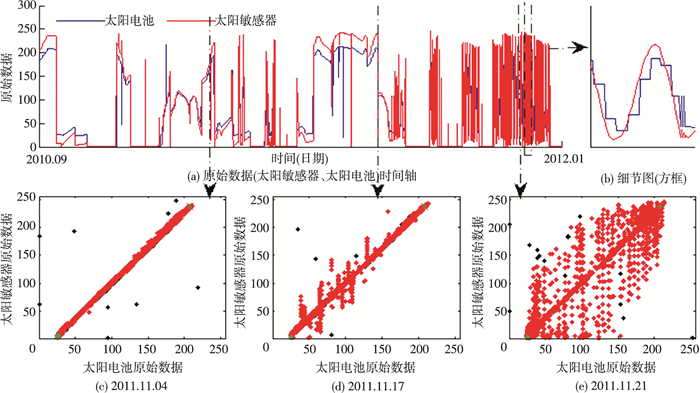
2011年1月22日, Grubbs准则显示异常标记个数指标有异动; 2011年1月28日的在线阶段有882个异常点没有落在数据密集区域; 2011年1月29日时, 一个新簇产生.该簇提供了一个特征:当太阳电池数据保持0值时, 太阳敏感器在它的数据范围内大幅跳变, 如图 6所示.当天数据显示太阳电池在正常的变化周期内, 而太阳敏感器的采样结果在任何范围内都存在跳变, 应定义为太阳敏感器出现故障.

|
图 6 2011年1月27日异常及发展 Figure 6 Anomaly on 2011.01.27 and clustering results |
由于太阳敏感器的数据没有越界, 当时的地面监控系统没有发现这个故障.直到1个月后, 故障蔓延使姿控系统的磁强计数据错误标示变为“1”, 才发现故障并进行重启.
2011年11月10日, Grubbs准则显示簇的联合熵指标有异动; 2011年11月17日出现现象为簇发生扩散, 产生类似叶子的形状, 如图 7所示.根据现象, 找到簇扩散时间段内的数据, 发现两维属性的变化周期缩短; 细节图显示, 两个传感器参数具有不同的采样参数设置, 采样时延和平滑程度存在差异.当时卫星转速过快, 产生了相关性降低的情况.这个现象由卫星状态转变引起, 数据发生了概念漂移, 而非传感器发生故障.算法适应了簇密度降低这一情况.
|
图 7 2011年11月17日异常及发展 Figure 7 Anomaly on 2011.11.17 and clustering results |
从检测结果看出, 3个指标能满足了皮纳卫星自动化异常检测的要求.离线阶段的聚类结果一定程度上精确定位了异常数据, 帮助故障原因分析.
3 结论1) 本文提供了一种新的异常检测方法用于皮纳卫星的遥测数据, 方法基于相关子空间的两阶段密度聚类.相关子空间的划分实现子空间内属性的相互监督.两阶段密度聚类算法分为在线、离线阶段.在线阶段通过网格索引实时发现单点异常, 离线阶段通过聚类挖掘数据的集体异常及其特征.算法通过时间衰减单元平衡概念漂移与早期数据参考性.
2) 人工数据集和ZDPS-1A卫星的实际数据集的实验表明, 在线阶段能实时处理10 kHz的流量数据, 发现95%的单点异常, 满足皮纳卫星实时遥测数据异常检测的一般需求.对更高速的遥测数据, 需通过增强硬件或降低采样率保持系统处理能力.离线阶段的聚类适应了ZDPS-1A卫星快速转动导致的数据漂移, 维持稳定的簇形态, 并相比现有系统提前一个月抓取到姿控系统程序跑飞引起的太阳敏感器数据紊乱.
3) 算法的两阶段系统结构, 符合卫星一轨只有部分时间处于测控范围内的现状, 适用于地面监控系统.与现有异常检测系统相比, 本文提供了完整的多维数据异常检测解决方案.灵活适应环境或卫星状态引起的变化, 更为符合皮纳卫星星座组网的发展方向.
| [1] |
赵炜渝, 白保存, 金仲和. 皮纳卫星应用与特点分析[J].
国际太空, 2013(3): 36-40.
ZHAO Weiyu, BAI Baocun, JIN Zhonghe. Application and characteristics of Pico-satellite[J]. Space International, 2013(3): 36-40. |
| [2] |
GAMA J, ŽLIOBAITĖ I, BIFET A, et al. A survey on concept driftadaptation[J].
ACM Computing Surveys (CSUR), 2014, 46(4): 1-37.
DOI: 10.1145/2523813 |
| [3] |
彭喜元, 庞景月, 彭宇, 等. 航天器遥测数据异常检测综述[J].
仪器仪表学报, 2016, 37(9): 1929-1945.
PENG Xiyuan, PANG Jingyue, PENG Yu, et al. Review on anomaly detection of spacecraft telemetrydata[J]. Chinese Journal of Scientific Instrument, 2016, 37(9): 1929-1945. DOI: 10.3969/j.issn.0254-3087.2016.09.003 |
| [4] |
MARTÍNEZ-HERAS J A, DONATI A, KIRSCH M G F, et al. New telemetry monitoring paradigm with noveltydetection[C]//SpaceOps 2012 Conference. Stockholm: AIAA, 2012: 11-15. DOI: 10.2514/6.2012-1275123.
|
| [5] |
O'MEARA C, SCHLAG L, FALTENBACHER L, et al. ATHMoS: automated telemetry health monitoring system at GSOC using outlier detection and supervised machine learning[C]//Proceedings of the 14th International Conference on Space Operations. [S. I. ]: AIAA, 2016: 2347. DOI: 10.2514/6.2016-2347.
|
| [6] |
钱威, 周军, 张国勇, 等. 基于主成分分析的卫星遥测回归方法: CN105590026A[P]. 2016-05-18.
QIAN Wei, ZHOU Jun, ZHANG Guoyong, et al. Satellite telemetryregression based on principal component analysis: CN105590026A[P]. 2016-05-18. |
| [7] |
朱宁, 冯志刚, 王祁. 基于KPCA和SVM的火箭发动机试验台故障诊断方法[J].
哈尔滨工业大学学报, 2009, 41(3): 81-84.
ZHU Ning, FENG Zhigang, WANG Qi. Fault diagnosis of rocket engine ground testing bed based on KPCA and SVM[J]. Journal of Harbin Institute of Technology, 2009, 41(3): 81-84. DOI: 10.3321/j.issn:0367-6234.2009.03.020 |
| [8] |
INUI M, KAWAHARA Y, GOTO K, et al. Adaptive limit checking for spacecraft telemetry data using kernel principal component analysis[J].
Transactions of the Japan Society for Aeronautical & Space Sciences Space Technology Japan, 2009, 7(ists26): Pf_11-Pf_16.
DOI: 10.2322/tstj.7.Pf_11-Pf_16 |
| [9] |
YAIRI T, TAGAWA T, TAKATA N. Telemetry monitoring by dimensionality reduction and learning hidden markov model[C]//Proceedings of the International Symposium on Artificial Intelligence, Robotics and Automation in Space. Turin, Italy: [s. n. ], 2012.
|
| [10] |
MOHAMMAD B R, HUSSEIN W M. A novel approach of health monitoring and anomaly detection applied to spacecraft telemetry based on PLSDA multivariate latent technique[C]//Proceedings of the 15th International Workshop on Research and Education in Mechatronics (REM). El Gouna, Egypt: IEEE, 2014: 1-6. DOI: 10.1109/rem.2014.6920243.
|
| [11] |
PAN Dawei, LIU Datong, ZHOU Jun, et al. Anomaly detection for satellite power subsystem with associated rules based on Kernel Principal ComponentAnalysis[J].
Microelectronics Reliability, 2015, 55(9/10): 2082-2086.
DOI: 10.1016/j.microrel.2015.07.010 |
| [12] |
YAIRI T, KAWAHARA Y, FUJIMAKI R, et al. Telemetry-mining: a machine learning approach toanomaly detection and fault diagnosis for space systems[C]//Second IEEE International Conference on Space Mission Challenges for Information Technology. Pasadena, CA: IEEE, 2006: 468-476. DOI: 10.1109/SMC-IT.2006.79.
|
| [13] |
KELLER F, MULLER E, BOHM K. HiCS: high contrast subspaces for density-based outlier ranking[C]//Proceedings of the 28th International Conference on Data Engineering(ICDE). Washington, DC: IEEE, 2012: 1037-1048. DOI: 10.1109/ICDE.2012.88.
|
| [14] |
ZIMEKA, SCHUBERT E, KRIEGEL H P. A survey on unsupervised outlier detection in high-dimensional numerical data[J].
Statistical Analysis and Data Mining, 2012, 5(5): 363-387.
DOI: 10.1002/sam.11161 |
| [15] |
AZEVEDO D R, AMBRÓSIO A M, VIEIRA M. Applying data mining for detecting anomalies in satellites[C]//Proceedings of the 9th Dependable Computing Conference (EDCC). Sibiu, Romania: IEEE, 2012: 212-217. DOI: 10.1109/EDCC.2012.19.
|
| [16] |
CHENG C H, FU A W, ZHANG Y. Entropy-based subspace clustering for mining numerical data[C]// Proceedings of the 5th ACM SIGKDD international conference on Knowledge discovery and data mining. New York, NY: ACM, 1999: 84-93. DOI: 10.1145/312129.312199.
|
| [17] |
RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J].
Science, 2014, 344(6191): 1492-1496.
DOI: 10.1126/science.1242072 |
| [18] |
杨阳, 吉根林, 鲍培明. 基于网格索引的时空轨迹伴随模式挖掘算法[J].
计算机科学, 2016, 43(1): 107-110.
YANG Yang, JI Genlin, BAO Peiming. Algorithm for miningad joint patternof spatial-temporal trajectory basedon gridindex[J]. Computer Science, 2016, 43(1): 107-110. DOI: 10.11896/j.issn.1002-137X.2016.1.025.j.issn.1002-137X2016.1.025 |
 2018, Vol. 50
2018, Vol. 50


