深度卷积神经网络(deep convolutional neural network, CNN)利用结构深度的优势在计算机视觉如图像分类[1-2]、目标识别[3]、目标探测[4]等应用中取得了较大的成功, 故CNN结构的加深是深度学习的重要研究内容.2012年, Krizhevsky等[1]首次将CNN应用于计算机视觉的模型具有8层网络, 2014年, Simonyan等[5]将网络加深至19层, 2015年Szegedy等[2]设计了22层的深度网络, He等[6]将网络加深至152层.随着网络的加深, 梯度消失/溢出的问题越来越突出, 网络较浅时, 非线性层数较少, 传递到网络底层时梯度变化较少, 能够驱动参数更新; 而网络较深时, 非线性层数较多, 传递到网络底层的梯度会消失/溢出, 无法驱动底层参数[7].传统常用的非线性变换如sigmoid、tanh等, 容易形成梯度消失/溢出.
2010年, Nair等[8]提出线性修正单元(rectified linear unit, ReLU), ReLU具有单侧抑制、相对宽阔的兴奋边界等特点, 不仅能够缓解梯度消失/溢出问题, 还能够加速模型收敛速度、提高模型学习精度.但ReLU对负数输入的处理造成了部分神经元死亡, 使得梯度不能在负数部分传播; 且当输入为正数时, 输出保持输入不变, 使函数输出的平均值始终大于零, 形成了偏移现象(bias shift), 限制了学习速率和学习精度[1, 8].在ReLU的基础上, Mass等[9]提出弱修正线性单元(leaky ReLU, LReLU)以避免零梯度问题, 但LReLU对坡度因子较为敏感; He等[10]针对损失函数对不同坡度因子不可导的特点提出了参数修正线性单元(parametric ReLU, PReLU), 但模型容易过拟合; Xu等[11]提出随机弱线性修正单元(randomized LReLU, RReLU), 使得模型一定程度上减缓偏移现象; Clevert等[12]提出指数线性单元(exponential linear unit, ELU), 但存在左软饱和现象, 且其指数级变化使得饱和点更接近零点, 而饱和点之后的梯度较难传递[7].
针对ReLU函数存在的零梯度问题与偏移现象, 本文提出了SLU(softplus linear unit)函数.实验结果证明, 无论是监督学习还是非监督学习, 基于SLU的模型均具有更好的特征学习能力和更高的分类精度.
1 ReLU及相关改进单元自2012年Krizhevsky等[1]首次将ReLU作为激活函数应用于神经网络模型并取得突破后, 很多学者针对ReLU存在的零梯度问题和偏移现象进行了改进, 以期进一步提升神经网络性能.对ReLU的改进方法主要有LReLU、PReLU、RReLU和ELU.
1.1 ReLU函数ReLU的定义如[8]
| $ {y_i} = \left\{ {\begin{array}{*{20}{c}} {{x_i}, }&{{x_i} \ge 0;}\\ {0, }&{{x_i} < 0.} \end{array}} \right. $ |
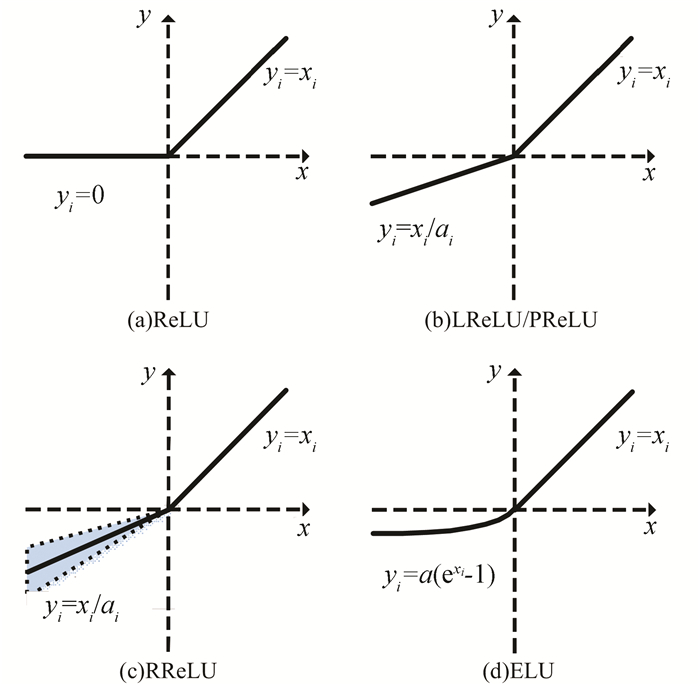
式中:xi为第i个输入, yi为相对应的输出.如图 1(a)所示, 当输入为正数时, 输出保持输入不变, 当输入为负数时, 输出为零, 故ReLU函数输出平均值大于零, 存在偏移现象, 影响模型的收敛速率和学习效果.
|
图 1 ReLU及其改进函数示意 Figure 1 Shape of ReLU and variants |
LReLU的定义为[9]
| $ {y_i} = \left\{ \begin{array}{l} {x_i},\;\;\;\;\;\;{x_i} \ge 0;\\ {x_i}/{\alpha _i},\;{x_i} < 0. \end{array} \right. $ | (1) |
式中αi为坡度因子, 取值范围为(1, +∞), 取值越大, 对负数部分的修正越小, 如图 1(b)所示, 图中取αi=10.坡度因子的存在一定程度上可以减缓偏移现象, 但LReLU对坡度因子较为敏感, αi的取值影响模型的收敛速率和学习效果.
1.3 PReLU函数PReLU是LReLU的改进形式[10], 其表达式与LReLU一致, 如式(1), 但其坡度因子αi并非固定值, 而是通过后向传播学习得到, 灵活可变, 其取值范围同样为(1, +∞).PReLU在修正偏移现象的同时调整函数在零点的值, 使函数在整个定义域内连续可导, 但变化的坡度因子在增加计算量的同时容易导致模型的过拟合.
1.4 RReLU函数RReLU是LReLU的随机形式[11], 其定义为
| $ {y_i} = \left\{ \begin{array}{l} {x_i},\;\;\;\;\;\;{x_i} \ge 0;\\ {x_i}/{\alpha _i},\;{x_i} < 0. \end{array} \right. $ |
式中坡度因子αi从标准正态分布中随机取值, 如
| $ {\alpha _i} \sim U\left( {l,u} \right). $ |
RReLU在较小数据集上可一定程度上防止过拟合, 但其在较大数据集上的表现并不理想.
1.5 ELU函数ELU的定义为[12]
| $ {y_i} = \left\{ \begin{array}{l} {x_i},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_i} \ge 0;\\ \alpha \left( {{\rm{exp}}\left( {{x_i}} \right) - 1} \right),{x_i} < 0. \end{array} \right. $ |
ELU对正数部分的处理与ReLU一致, 而对负数部分的处理与sigmoid函数相似, Clevert等[12]证明了ELU传递的常规梯度更接近自然梯度(nature gradient), 而自然梯度是利用Fisher信息矩阵、Hessian矩阵或者Gauss-Newton矩阵梯度求取的更新方向; 神经网络后向传播中的梯度更接近自然梯度意味着迭代次数更少、学习速率更快、精度更高.但ELU在处理负数部分时存在软饱和现象, 且其指数级变化使得饱和点更接近零点, 梯度在饱和点之后的负数部分较难传递, 梯度可传递范围较窄.
2 改进的SLU函数由ReLU及相关改进单元可知, ReLU存在零梯度问题和偏置现象, 影响神经网络的收敛速度和学习效果; 根据文献[12]所证“输出均值接近零的激活函数能够提升神经网络性能”原理, 本文对ReLU进行改进, 提出SLU单元, 并在理论上说明SLU的优越性.文献[12]中对“输出均值接近零的激活函数能够提升神经网络性能”原理进行了详细的证明, 因其过程较为晦涩繁琐, 此处并不进行赘述.
Softplus函数可以看作是ReLU函数的平滑校正[13-14], 定义为
| $ {\rm{softplus}}\left( x \right) = {\rm{log}}\left( {{\rm{exp}}\left( {x + 1} \right)} \right), $ | (2) |
对式(2)求导可得
| $ \sigma \left( x \right) = \frac{{1}}{{{\rm{exp}}\left( {-x} \right) + 1}}. $ | (3) |
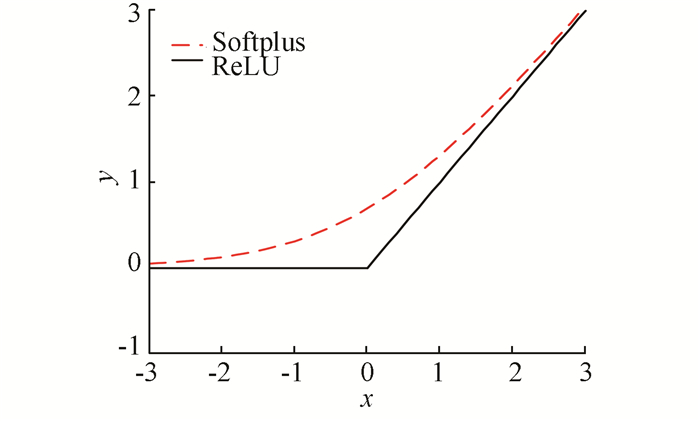
式(3)为饱和函数Sigmoid的定义.Softplus与ReLU相似, 具有单侧抑制、相对宽阔的兴奋边界等优点, 如图 2所示, 相比于ReLU, 其优势在于其在定义域内连续可导, 使得梯度可在整个定义域内传播, 更接近生物特性.
|
图 2 Softplus和ReLU函数 Figure 2 Softplus and ReLU function |
输入为负数时, ReLU单元输出为零, 导致零梯度问题; 且正数输入时, 单元输出为正, 使得ReLU输出平均值为正数, 存在偏移现象.本文利用softplus处理ReLU负数输入部分, 使得负数输入时的输出为负, 可以避免的零梯度问题, 且一定程度上修正整个函数的输出接近于零.改进的修正线性单元函数SLU的一般形式可以定义为
| $ {\rm{SLU}}\left( \mathit{\boldsymbol{x}} \right) = \left\{ \begin{array}{l} \beta x,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x{\rm{ }} \ge 0;\\ \alpha {\rm{log}}\left( {{{\rm{e}}^x} + 1} \right) - \gamma ,x < 0. \end{array} \right. $ |
式中:β为坡度因子, β越大, 正数部分坡度越陡, 较陡的坡度在深度学习中容易导致梯度溢出; α为影响负数部分的饱和位置, α越大, 饱和点越靠近零点, 在训练过程中越容易导致梯度消散; γ为调节负数输入时, 函数向下偏离横轴的距离, γ越大, 偏离横轴的距离越大, 一定范围内, 激活函数的平均值越接近零.SLU的导数为
| $ {\rm{SLU}}\prime \left( \mathit{\boldsymbol{x}} \right) = \left\{ \begin{array}{l} \beta ,\;\;\;\;\;\;\;\;\;\;\;\;\;x \ge 0;\\ \alpha \frac{1}{{\left( {{{\rm{e}}^{ - x}} + 1} \right)}},x < 0. \end{array} \right. $ | (4) |
由式(4)可见, SLU'(x)的负数部分为Sigmoid函数与α的乘积.为保证信息前向传播与梯度后向传播的连续平稳, 令函数SLU(x)在0点处连续且可导, 可得
| $ \begin{array}{l} \left\{ \begin{array}{l} {\rm{SLU}}\left( \mathit{\boldsymbol{x}} \right)\left| {_{x = {0^ + }}} \right. = 0, \\ {\rm{SLU}}\left( \mathit{\boldsymbol{x}} \right)\left| {_{x = {0^-}}} \right. = \alpha {\rm{log}}2-\gamma, \\ {\rm{SLU}}{\left( \mathit{\boldsymbol{x}} \right)_{\left| {x = {0^ + }} \right.}} = {\rm{SLU}}\left( \mathit{\boldsymbol{x}} \right)\left| {_{x = {0^-}}} \right., \\ {\rm{SLU}}\prime {\left( \mathit{\boldsymbol{x}} \right)_{\left| {x = {0^ + }} \right.}} = \beta, \\ {\rm{SLU}}\prime \left( \mathit{\boldsymbol{x}} \right)\left| {_{x = {0^ - }}} \right. = \frac{\alpha }{2}, \\ {\rm{SLU}}\prime \left( \mathit{\boldsymbol{x}} \right)\left| {_{x = {0^ + }}} \right. = {\rm{SLU}}\prime \left( \mathit{\boldsymbol{x}} \right)\left| {_{x = {0^ - }}} \right., \end{array} \right.\\ \end{array} $ | (5) |
解式(5)可得
| $ \left\{ \begin{array}{l} \gamma = \alpha {\rm{log}}\;2, \\ \beta = \frac{\alpha }{2}. \end{array} \right. $ |
在CNN的后向传播过程中, 经过多次非线性变换后, 传递到网络底层的梯度会变大/变小, 变化的速度是以激活函数导数为底、以非线性变换层数为指数的幂的值[7].为减缓梯度在传递过程中出现的消失/溢出现象, 令β=1, 则α=2, γ=2log 2, SLU可精确定义为
| $ {\rm{SLU}}\left( \mathit{\boldsymbol{x}} \right) = \left\{ \begin{array}{l} x,\;\;\;\;\;\;\;\;\;\;\;\;\;\;x \ge 0;\\ 2{\rm{log}}\frac{{{{\rm{e}}^x} + 1}}{2},x < 0. \end{array} \right. $ | (6) |
式(6)为SLU函数的精确形式, 也是本文后续用于训练时的函数.
设参数概率模型为p(x; ω), 令x+为正数输入, x-为负数输入, ω为输入x的概率.经过SLU进行非线性变换后, 输出均值mSLU(x)为
| $ {m_{{\rm{SLU}}}}\left( \mathit{\boldsymbol{x}} \right) = \sum \omega {f_{{\rm{SLU}}}}\left( \mathit{\boldsymbol{x}} \right) = \sum \omega {x^ + } + \sum \omega 2{\rm{log}}\frac{{{{\rm{e}}^{{x^-}}} + 1}}{2}. $ | (7) |
经过ReLU进行非线性变换后, 输出均值mReLU(x)为
| $ {m_{{\rm{ReLU}}}}\left( \mathit{\boldsymbol{x}} \right) = \sum \omega {f_{{\rm{ReLU}}}}\left( \mathit{\boldsymbol{x}} \right) = \sum \omega {x^ + }. $ | (8) |
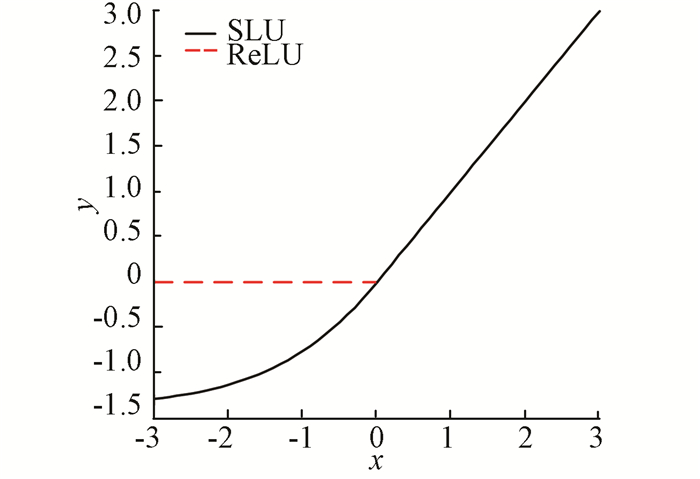
显然, 式(7)、(8)中的权重ω为正, 所以ReLU的输出均值mReLU(x)始终为正; 式(7)的第1项为正数, 第2项为负数, 一定程度上可以修正输出值接近于零.所以, 相比于ReLU函数, SLU的输出平均值更接近零.如图 3所示, SLU函数为黑色实线, ReLU函数为红色线段, SLU函数相比ReLU均值更接近于零.
|
图 3 SLU和ReLU函数 Figure 3 SLU and ReLU function |
本文分别从监督学习与非监督学习的角度对激活函数进行分析, 首先构建深度自编码(deep autoencoder)模型在MNIST数据集上进行监督学习, 利用模型的重建误差描述其对图像特征的学习能力; 其次构建了网中网(network in network, NiN)卷积神经网络模型在CIFAR-10上进行非监督学习, 利用模型的分类概率损失、top1误差与top5误差描述模型的学习能力.
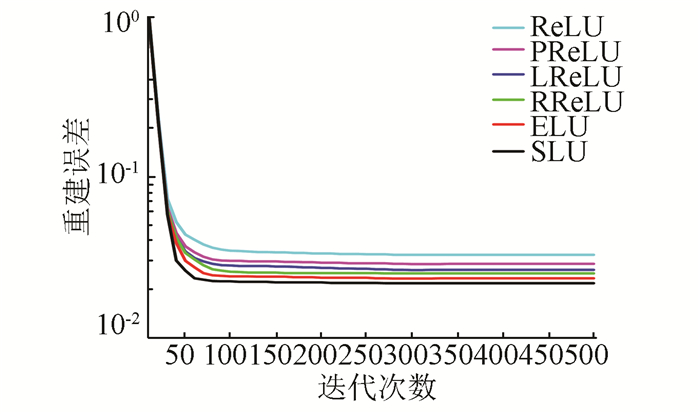
3.1 MNIST本文构建了深度自编码模型对MNIST数据集进行无监督学习.MNIST手写数字识别数据集含有0~9共10类手写阿拉伯数字, 包括60 000个训练数据和10 000个测试数据, 图像灰度级为8, 分辨率为28×28[15].深度自编码模型的自编码部分共有4层编码层, 单元数分别设置为1 000、500、250和30, 每层编码层后面对应相应的解码层; 利用随机梯度下降法训练模型, 对编码后的数据进行批量规范化, 每批大小为128;利用Dropout以增强稀疏性和鲁棒性, 概率设置为0.2;学习速率设置为0.001, 动量设置为0.9.模型在MNIST数据集上的重建误差如图 4所示.
|
图 4 不同激活函数下深度自编码重建误差 Figure 4 Reconstruction error of deep atouencoder with different activations |
由图 4可知, 与其他模型相比, 基于SLU模型的重建误差最小, 重建精度最高, 误差在迭代80余次后趋于平稳, 收敛速度稍快, 说明其特征学习能力较好; 其余模型的重建误差由低到高依次为ELU、RReLU、LReLU、PReLU与ReLU, 且ReLU在迭代接近100次时, 重建误差趋于平稳, 收敛速度稍慢.在数据集MINST上的深度自编码学习验证了基于SLU模型的无监督学习能力.
3.2 CIFAR-10本文构建了NiN[16]模型在数据集CIFAR-10[17-18]上进行监督学习.CIFAR-10含有60 000张彩色图像, 包括50 000张训练图像和10 000测试图像, 可被分为10类, 图片分辨率为32×32.
3.2.1 模型构建及参数设置NiN模型是常用的深度卷积神经网络模型之一.与一般CNN模型不同的是, NiN利用多层感知层进行非线性变换, 再与卷积层和池化层共同组成NiN区块[16].本文构建的NiN模型含有3个NiN区块与一个分类层, 3个NiN区块依次相连学习图像, 最后利用softmax分类层进行分类.每个NiN区块含有4层网络, 依次为卷积层、两层感知层和池化层, 每个NiN区块后设置规则化层.NiN模型架构见表 1.
| 表 1 NiN模型架构 Table 1 NiN network structure |
权重衰减值设置为0.000 5, 最小批规范化大小为100, 动量设置为0.9;学习速率初始值为0.5, 并在30次迭代后降为0.1, 40次迭代后降为0.02;非线性变换阶段分别利用ReLU、LReLU、PReLU、RReLU、ELU、SLU这6种激活函数进行处理, 并令LReLU的坡度因子αi=5.5[11].
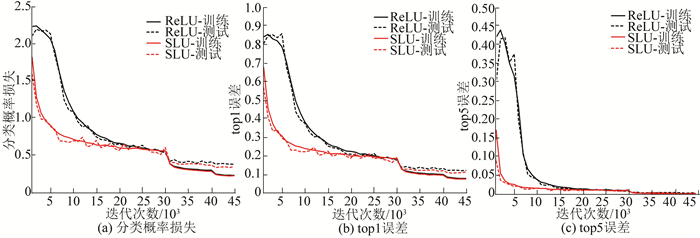
3.2.2 实验过程与结果分析利用模型构建及参数设置中所述NiN模型及其参数在数据集CIFAR-10上进行监督训练, 记录基于不同激活函数的NiN模型的分类概率损失、top1和top5误差, 比较ReLU与SLU的迭代过程如图 5所示; 比较LReLU与SLU的迭代过程如图 6所示; 比较PReLU与SLU的迭代过程如图 7所示; 比较RReLU与SLU的迭代过程如图 8所示; 比较ELU与SLU的迭代过程如图 9所示.
|
图 5 基于ReLU与SLU函数NiN模型的迭代过程比较 Figure 5 Convergence curves for training and test sets of ReLU and SLU activation based models |
|
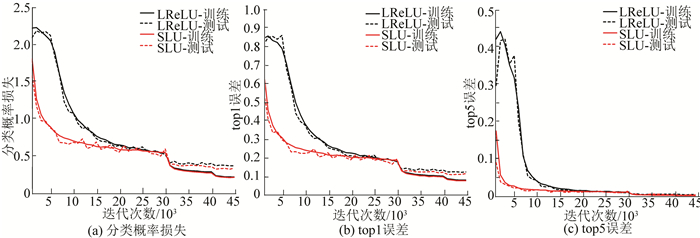
图 6 基于LReLU与SLU函数NiN模型的迭代过程比较 Figure 6 Convergence curves for training and test sets of LReLU and SLU activation based models |
|
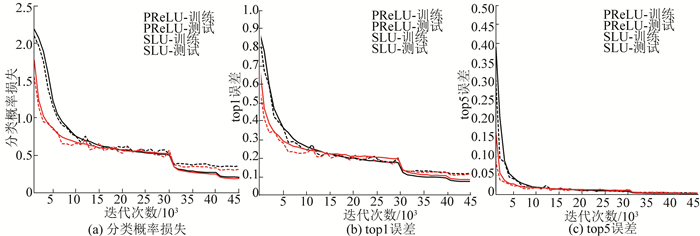
图 7 基于PReLU与SLU函数NiN模型的迭代过程比较 Figure 7 Convergence curves for training and test sets of PReLU and SLU activation based models |
|
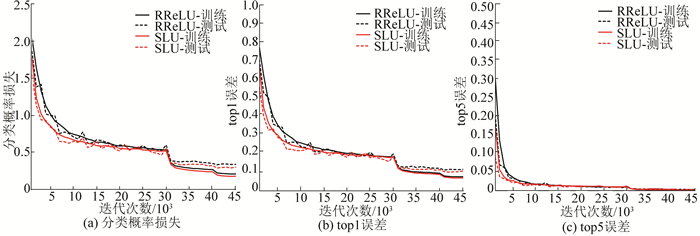
图 8 基于RReLU与SLU函数NiN模型的迭代过程比较 Figure 8 Convergence curves for training and test sets of RReLU and SLU activation based models |
|
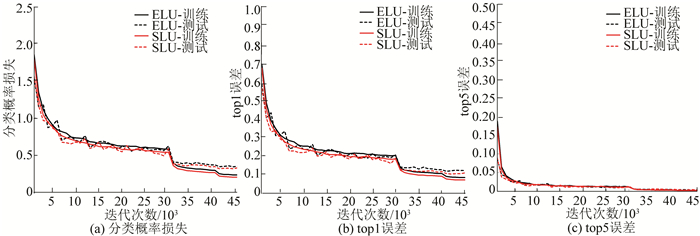
图 9 基于ELU与SLU函数NiN模型的迭代过程比较 Figure 9 Convergence curves for training and test sets of ELU and SLU activation based models |
由图 5~9可知, 相比于ReLU、LReLU、PReLU、RReLU和ELU函数, SLU的收敛速度均有不同程度的加快, 图 5中所示与ReLU函数的对比尤为明显; 与ReLU、LReLU、RReLU和ELU函数相比, SLU分类概率损失、top1和top5的训练误差与测试误差均较小; 与PReLU函数相比, SLU分类概率损失、top1和top5的测试误差均较小, 但训练误差稍大, 这是因为PReLU模型容易导致过拟合, 所以PReLU训练误差较小.
基于不同激活函数NiN模型的最终分类概率损失的训练值与测试值见表 2; top1训练误差与测试误差见表 3; top5训练误差与测试误差见表 4.
| 表 2 基于不同激活函数NiN模型的分类概率损失 Table 2 Classification loss of NiN models |
| 表 3 基于不同激活函数NiN模型的top1误差 Table 3 Top1 error rate of NiN models |
| 表 4 基于不同激活函数NiN模型的top5误差 Table 4 Top5 error rate of NiN models |
由表 2~4可知, 所有NiN网络不同指标下的训练误差均比测试误差小, 说明网络在训练过程中有过拟合现象, 尤其是PReLU函数, 其在分类概率损失、top1误差与top5误差的训练指标均为最小, 但测试指标相对较高, 过拟合现象较其他激活函数严重.利用ReLU激活函数的NiN网络的训练误差与测试误差均最高, 可见其他5类激活函数在ReLU的基础上都有不同程度的改进, 基于文中所提SLU函数的NiN网络的分类概率损失、top1误差与top5误差的测试指标分别为0.34%、10.02%、0.28%, 均小于基于其他5种函数的测试误差, 且相比其余最好性能的ELU激活函数误差分别减少了2.9%、5.1%、4.5%.显然, 模型增加的参数与步骤提高了模型精度, 但也增加了时间消耗.本文记录了基于不同激活函数的NiN模型迭代至收敛的时间进行比较, 并比较了调用激活函数的次数和时间, 见表 5.需要说明的是, 实验所用处理器为Intel(R)Core(TM)i5-4590, CPU主频为3.3 GHz, 显卡为AMD系列, 实验并未调用GPU.实验时间仅作为本文所有实验横向比较参考依据.
| 表 5 基于不同激活函数NiN模型的时间消耗 Table 5 Time-consuming of NiN models |
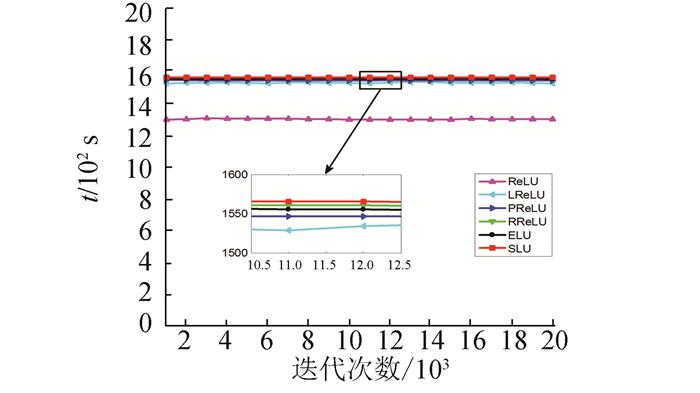
由表 5可知, 与ReLU相比, 其改进函数LReLU、PReLU、RReLU、ELU和SLU模型的运行总时间均有不同程度的增加, 但5种改进的函数相互之间增加的时间与总时间相比并不明显, 平均每迭代千次耗时分别为13 041、15 302、15 318、15 363、15 353、15 373 s; 6种模型对激活函数的调用次数均为445 500次, 平均调用时间分别为0.068 5、0.084 1、0.084 3、0.084 5、0.084 4、0.084 5 s.选取基于不同激活函数的NiN模型每迭代千次的时间进行比较, 如图 10所示.
|
图 10 基于不同激活函数NiN模型时间消耗 Figure 10 The time of NiN models with different activations |
通过表 5与图 10可知, 相比于其他改进函数, SLU的消耗时间并没有明显增加.这是因为SLU模型虽然增加了参数, 带来了一定的时间消耗, 但是对比模型的总参数量及时间消耗, 增加的时间消耗极微.考虑到模型对精度的提升, 本文认为这样的时间消耗是值得的.
4 结论1) 本文针对ReLU函数存在的零梯度问题和偏移现象, 根据“输出均值接近零的激活函数能够提升神经网络学习性能”原理提出SLU, 利用softplus对ReLU的负数部分进行改进, 再根据SLU对正数部分的处理调整负数部分的参数, 最后建立了深度自编码模型和网中网模型, 分别从无监督和有监督方面验证了改进单元的学习能力.
2) 实验结果表明:基于SLU的模型的收敛速度和学习精度均比其他几类算法有不同程度的提升; 相比于整个模型而言, 函数增加的参数并没有消耗过多的时间.基于SLU函数的模型具有较好的特征学习能力和较高的分类精度.
| [1] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe, Nevada: Curran Associates Inc., 2012: 1097-1105. DOI: 10.1145/3065386.
|
| [2] |
SZEGEDY C, LIU Wei, JIA Yangqing, et al. Going deeper with convolutions[C]//Proceeding of the IEEE Conference on Computer Vision and Pattern Recognition. Boston, MA: IEEE, 2015: 1-9. DOI: 10.1109/CVPR.2015.7298594.
|
| [3] |
GIRSHICK R, DONAHUE J, DARRELL T, et, al. Rich feature hierarchies for accurate object detection and semantic segmentation[C]//Proceeding of the IEEE Conference on Computer Vision and Pattern Recognition. Columbus, OH: IEEE, 2014: 580-587. DOI: 10.1109/CVPR.2014.81.
|
| [4] |
WANG Naiyan, LI Siyi, GUPTA A, et al. Transferring rich feature hierarchies for robust visual tracking[EB/OL]. (2015-01-19)[2015-04-23]. http://arxiv.org/abs/1501.04587.
|
| [5] |
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[EB/OL]. (2014-09-04)[2015-04-10]. http://arxiv.org/abs/1409.1556.
|
| [6] |
HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[EB/OL]. (2015-12-10). http://arxiv.org/abs/1512.03385.
|
| [7] |
TROTTIER L, GIGUÈRE P, CHAIB-DRAA B. Parametric exponential linear unit for deep convolutional neural networks[EB/OL]. (2016-05-30)[2018-01-10]. http://arxiv.org/abs/1605.09332.
|
| [8] |
NAIR V, HINTON G E. Rectified linear units improve restricted boltzmann machines[C]//Proceedings of the 27th International Conference on Machine Learning. Haifa, Israel:, Omnipress, 2010: 807-814.
|
| [9] |
MAAS A L, HANNUN A Y, NG A Y. Rectifier nonlinearities improve neural network acoustic models[C]//Proceeding of the 30th International Conference on Machine Learning. Atlanta, GA: [s. n. ], 2013.
|
| [10] |
HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification[C]//Proceedings of the IEEE International Conference on Computer Vision. Santiago, Chile: IEEE, 2015: 1026-1034. DOI: 10.1109/ICCV.2015.123.
|
| [11] |
XU Bing, WANG Naiyan, CHEN Tianqi, et al. Empirical evaluation of rectified activations in convolutional network[EB/OL]. (2015-05-05)[2015-11-27]. http://arxiv.org/abs/1505.00853.
|
| [12] |
CLEVERT D A, UNTERTHINER T, HOCHREITER S. Fast and accurate deep network learning by exponential linear units (elus)[EB/OL]. (2015-11-23)[2016-02-22]. http://arxiv.org/abs/1511.07289.
|
| [13] |
GLOROT X, BORDES A, BENGIO Y. Deep sparse rectifier neural networks[C]//Proceeding of the 14th International Conference on Artificial Intelligence and Statistics. Fort Landerdale, FL: [s. n. ], 2011: 315-323.
|
| [14] |
SENIOR A, LEI Xin. Fine context, low-rank, softplus deep neural networks for mobile speech recognition[C]// Proceeding of IEEE International Conference on Acoustic, Speech and Signal Processing. Florence, Italy: IEEE, 2014: 7644-7648. DOI: 10.1109/ICASSP.2014.6855087.
|
| [15] |
LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J].
Proceedings of the IEEE, 1998, 86(11): 2278-2324.
DOI: 10.1109/5.726791 |
| [16] |
LIN Min, CHEN Qiang, YAN Shuicheng. Network in network[EB/OL]. (2013-12-16)[2014-03-04] http://arxiv.org/abs/1312.4400.
|
| [17] |
LEE C Y, XIE S, GALLAGHER P W, et al. Deeply-supervised nets[C]//Proceeding of the 18th International Conference on Artificial Intelligence and Statistics. San Diego, California: [s. n. ], 2015.
|
| [18] |
刘凯, 张立民, 范晓磊. 改进卷积波尔兹曼机的图像特征深度提取[J].
哈尔滨工业大学学报, 2016, 48(5): 155-159.
K ai, ZHANG Limin, FAN Xiaolei. New image deep feature extraction based on improved CEBM[J]. Journal of Harbin Institute of Technology, 2016, 48(5): 155-159. DOI: 10.11918/j.issn.0367-6234.2016.05.025 |
 2018, Vol. 50
2018, Vol. 50


