旋翼是直升机最重要的升力部件[1], 旋翼旋转时桨叶的叶尖处于高动压区, 桨叶载荷和旋翼系统的总体性能高度地依赖于桨尖涡的强度和相对于旋翼的位置[2-3]; 桨-涡干扰(BVI)是造成桨叶上局部产生较大的非定常气动载荷, 并导致旋翼振动水平增加以及旋翼脉冲噪声产生的主要因素[4-7].因而, 研究直升机旋翼桨叶的尾迹和桨尖涡的形成和演化, 对于提升旋翼的气动性能、降低直升机噪声和振动具有重要的指导意义.
旋翼气动载荷预测的数学模型广泛地依赖于对桨叶桨尖涡特性的经验性观测[8-9].如:速度场和黏性核尺寸的试验测量数据可以用于发展桨尖涡结构的模型.反映旋涡流动的测量可促进旋翼尾迹数学模型的进一步发展成熟[10-11], 并应用于先进桨叶的设计, 有助于消除诸如振动气动载荷和BVI诱导旋翼噪声等不利的旋涡诱导的旋翼气动现象.
目前, 粒子图像测速仪(PIV)测量方法在旋翼流动测量中取得了广泛应用[12-15], 基本获得了试验条件下旋翼的诱导速度分布、桨尖涡的形成发展过程等.但是大多数试验的PIV测量系统采样频率较低, 而且部分试验的桨尖马赫数偏小[12], 不利于桨尖涡特性的精细化分析; 而且国内对于涡核中心判定、涡核流动数据提取以及涡核模型拟合等少有提及.
本文针对上述问题, 采用了TR-PIV技术[16]作为旋翼流场测量的研究工具, 在桨尖马赫数相似的情况下用高频粒子图像测速仪进行了桨尖涡精细化测量试验, 获得了悬停状态下旋翼桨尖涡生成和变化过程.同时, 本文还采用了更加精细合理的数据处理方法, 从而能更加准确地诠释旋翼悬停状态下的桨尖涡特性.
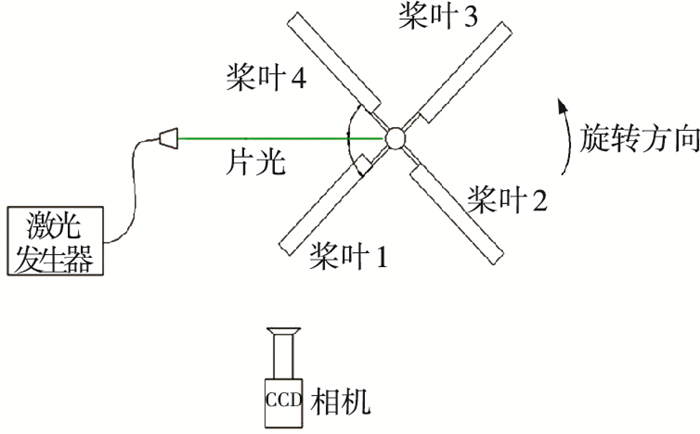
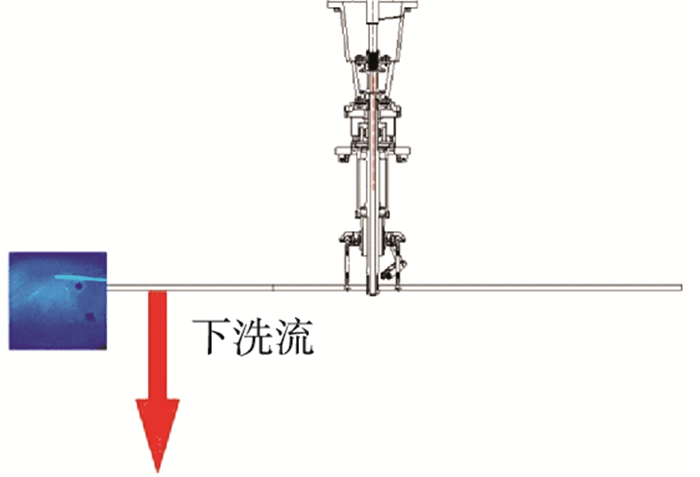
1 试验简介试验在中国空气动力研究与发展中心的Φ5 m立式风洞的开口试验段中进行.直升机模型垂直升降试验台[17-18](以下简称试验台)额定转速2 100 r/min, 桨尖马赫数Mt为0.64.旋翼模型直径为2 m, 桨毂为无铰式结构, 翼型为NACA23012, 矩形桨尖, 桨叶扭转角为-8°.图 1为旋翼模型在Φ5 m立式风洞的试验照片.悬停试验采用定总距θ7和定拉力系数的方式进行, 采用旋翼方位角外触发同步采集流场图像如图 2所示.拍摄视场相对于旋翼的位置如图 3所示, 图中阴影部分为拍摄视场, 其左上角为测量坐标的零点, 该点相对于桨毂中心的位置约为(-1 260 mm, 120 mm).需要注意的是拍摄视场中桨尖部分与模型示意图并未对齐, 反映了桨叶在气动载荷下的弹性变形.

|
图 1 试验照片 Figure 1 Test picture |
|
图 2 桨叶编号与触发采集方位角示意(俯视) Figure 2 Schematic diagram of blade number and acquisition triggering azimuth (top view) |
试验中所采用的TR-PIV相机分辨率为1 024像素×1 024像素, 有效视场为340 mm×340 mm, 采集频率为1 120 Hz, 触发信号由旋翼轴轴端编码器同步触发产生, 旋翼模型旋转90°能采集到8对图像, 使用LAVISION公司的DaVis软件进行数据后处理.激光片光由双脉冲Nd:YAG激光器、导光臂和片光头组成, 其单脉冲最大能量为30 mJ, 波长为527 nm, 光腰约在0.5~3.0 m范围内连续可调.示踪粒子由乙二醇与丙二醇的混合液蒸发产生[13], 粒子释放前经过粒子沉降室沉淀过滤掉大直径的示踪粒子, 促使示踪粒子的平均直径足够小, 从而尽可能提高示踪粒子的跟随性.
|
图 3 拍摄视场相对于旋翼位置示意 Figure 3 Sketch map of viewing field relative to the rotor |
旋翼悬停状态时其气动环境可认为是周期变化的, 故可用某一片桨叶旋转90°方位角的流场特性代表其他桨叶的流场特性, 图 4为旋翼悬停状态桨叶不同方位角的涡量云图和速度矢量图(拉力系数为0.01, 对应总距约为8°).

|
图 4 旋翼悬停状态桨叶不同方位角的涡量云图和速度矢量图 Figure 4 Vorticity contours and velocity vector picture of different blades azimuth angel at hovering status |
由图 4(a)可以看出, 依据矢量箭头, 可以初步确定3片桨叶(1#、2#、3#桨叶)的桨尖涡位置从上往下依次约为(178 mm, -86 mm)、(246 mm, -137 mm)、(301 mm, -256 mm), 且三者的涡龄角依次为11.25°、101.25°、191.25°, 桨尖涡呈现向下向里的运动规律; 结合其他7幅不同方位角的流场图, 可以看出, 同一个桨尖涡随着涡龄角的增加, 逐渐向下向里移动, 直至耗散; 同时, 在ψ=90°时能明显看到后1片桨叶(3#桨叶)的桨尖涡已基本耗散.但若要从该试验得到准确的桨尖涡特性, 还需对试验结果进行精细化处理, 包括精细化的涡核中心判定、涡核流动数据提取以及涡核模型拟合等.
2.1 桨尖涡的涡核中心(CV)宏观上, 旋翼桨尖涡是呈螺旋形的三维涡线, 悬停时桨尖涡系向旋翼下方移动.基于PIV的桨尖涡识别及定位的目的是在PIV测量得到的平面速度矢量中将与测量平面相交的桨尖涡涡核识别出来, 并确定其中心位置坐标.
从平面上的速度矢量中一般可以依据速度矢量的旋转分布(矢量箭头或流线)识别漩涡.依据旋转的速度矢量来辨别漩涡比较直观, 但是当漩涡叠加上迁移速度时其旋转中心位置会发生变化, 典型如图 5所示(拉力系数为0.01, 对应总距为8°), 桨尖涡有向旋翼下方迁移的速度, 采用流线旋转中心定位的中心实际距离真正的涡量中心有大约6.1 mm的误差(大约是涡核半径的1/4), 因此不能采用速度矢量旋转中心来确定涡核中心(CV)位置, 而要采用实践中更准确的涡量判据.

|
图 5 漩涡叠加上迁移速度后其旋转中心位置与涡量中心位置的差别 Figure 5 The difference between rotation center position and vorticity center position of the vortex under translational velocity |
涡量的定义为ω=∇×V, 其二元z分量为
| $ {\omega _\mathit{z}} = \frac{{{\rm{d}}\mathit{v}}}{{{\rm{d}}\mathit{x}}} - \frac{{{\rm{d}}\mathit{u}}}{{{\rm{d}}\mathit{y}}}. $ |
涡核是涡量集中的区域, 因而理想的涡核模型是在涡核中心处涡量达到峰值, 可根据涡量集中的区域识别桨尖涡, 使用涡量的极值判断涡核中心位置.但是PIV测量结果中的涡量是离散化的, 通过搜寻各节点涡量中的最大值来判断涡核中心位置存在离散误差.此外实际的涡核自身不稳定或者受到扰动后可能存在变形, 一般也不容易通过人工判读涡核中心.因此一般采用加权平均公式来计算涡量中心从而来定义涡核中心, 对于二维问题, 涡量中心采用下式来确定[19]:
| $ {\rm{CV}} = \frac{{{\sum _k}{{({\omega _z})}_k}\cdot({x_k}, {y_k})}}{{{\sum _k}{{({\omega _z})}_k}}}, $ |
式中k为参与计算网格节点总数目.
2.1.1 不同涡龄角相同拉力系数桨尖涡轨迹图 6为旋翼运行1/4圈测量得到的瞬态桨尖涡涡核位置构成的连续轨迹(拉力系数为0.01), 可以看到1#、2#桨叶的桨尖涡轨迹有良好的连续性, 但是2#、3#桨叶的桨尖涡轨迹有间断, 这说明悬停旋翼的流场其中存在着某些干扰因素使得各个叶片的桨尖涡轨迹不是稳定重复性的, 存在涡核随机跳动(jitter)现象.本文受限于样本数量还不充足, 无法反映涡核随机跳动的统计分析结果, 这在未来的工作中可以通过获取大样本数据库进行分析来完成.

|
图 6 不同桨叶相同拉力系数桨尖涡轨迹测量值 Figure 6 Blade tip vortex position result under different blades and same thrust coefficient |
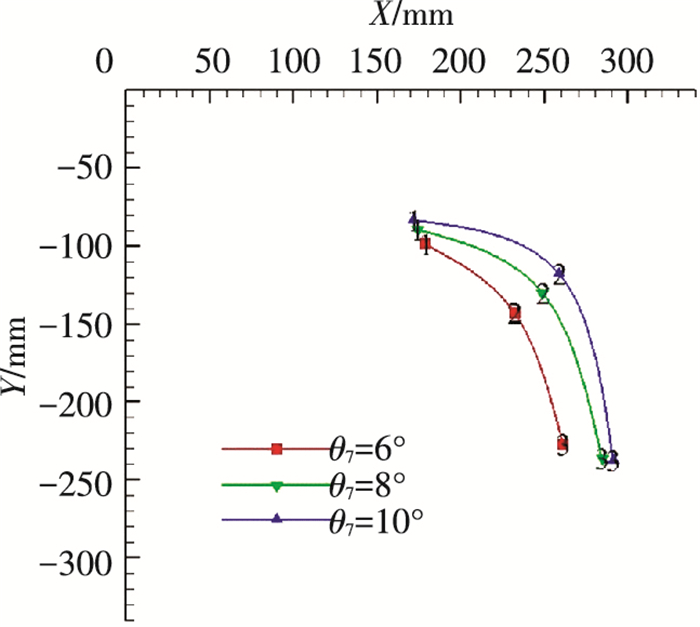
图 7为旋翼在方位角11.25°时测量得到的不同总距情况下的瞬态桨尖涡涡核位置, 每条曲线有3个点, 从上往下分别为1#、2#、3#桨叶在该方位角情况下对应的涡核位置.由图 7可以明显看出, 不同旋翼总距时, 其涡核位置层次清晰, 有缓慢向右上方移动的趋势; 且随着旋翼总距增大, 1#桨叶涡核位置缓慢上移, 这主要由总距增大旋翼挥舞增大造成; 而增大总距情况下, 桨尖涡收缩速度加剧, 其下降速度亦加快.
|
图 7 不同总距相同方位角桨尖涡位置测量值 Figure 7 Blade tip vortex position result under different collective pitches and the same azimuth angle |
在实际的桨尖涡内部流动中, 其漩涡结构是分层的, 主要分为3个区域:最内部的区域1为分层的层流流动; 区域2为层流和湍流的混合区域; 区域3为完全发展的湍流区域[20].区域1内的周向诱导速度分布类似于刚体旋转运动, 区域2为过渡区域, 区域3的周向诱导速度为符合B-S定理的势流区域.
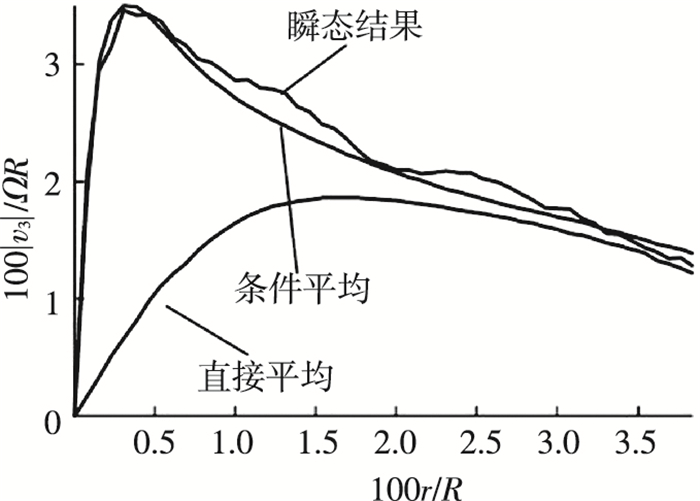
由于桨尖涡测量结果的非周期性, 直接将各时刻的测量结果平均将会抹平桨尖涡特性, 使涡核半径增大而涡强度减小.图 8[20]为各种处理方法得到的桨尖涡切向诱导速度, 直接平均处理得出的桨尖涡切向诱导速度峰值显著小于直接从瞬态测量中提取的结果.为了得到具有统计意义的周期性结果, 需要对各瞬态的测量结果条件平均:将不同时刻的测量结果以各自涡核中心为基准点进行平均, 或从各瞬态测量结果中提取涡核半径和涡强度平均.取周向诱导速度最大的半径位置即为桨尖涡涡核半径.
|
图 8 从条件平均、直接平均、瞬态结果中提取的诱导速度分布 Figure 8 Induced velocity extracted from conditional average, direct average, and transient result |
涡核中心确定后, 将绕桨尖涡流动的速度矢量减去涡核中心的速度矢量, 可得到绕涡核中心的周向诱导速度分布, 简单地可以取0°、90°、180°、270°象限方向的周向诱导速度分布来获得涡核尺寸和最大诱导速度[20], 但是这种方法获得的涡核尺寸和最大诱导速度不确定度较大.
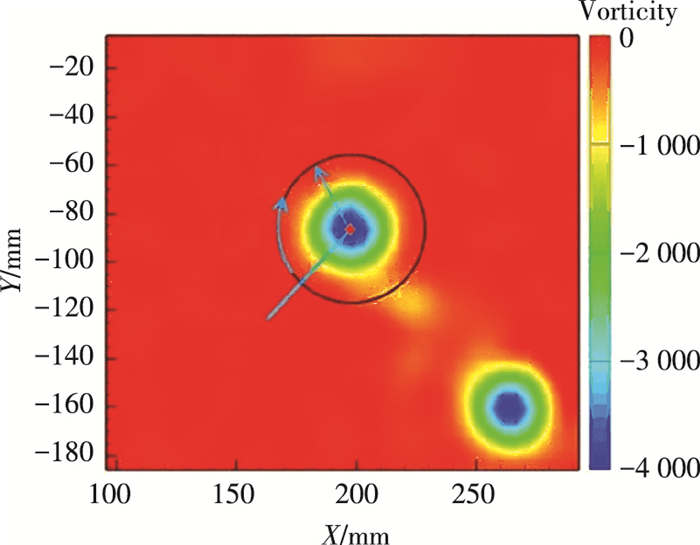
因此采用基于环量分析的方法, 来更加合理、可靠地确定涡核尺寸和最大诱导速度参数.从涡量-环量-诱导速度关系(详见图 9)可知
| $ \mathit{\Gamma }=\iint{\omega \cdot \text{d}A=}\oint{v}\cdot \text{d}s. $ |
|
图 9 典型取11.25°涡龄角桨尖涡的涡量-环量-诱导速度关系 Figure 9 The relationship between vorticity, circulation and induced velocity extracted from 11.25° wake age |
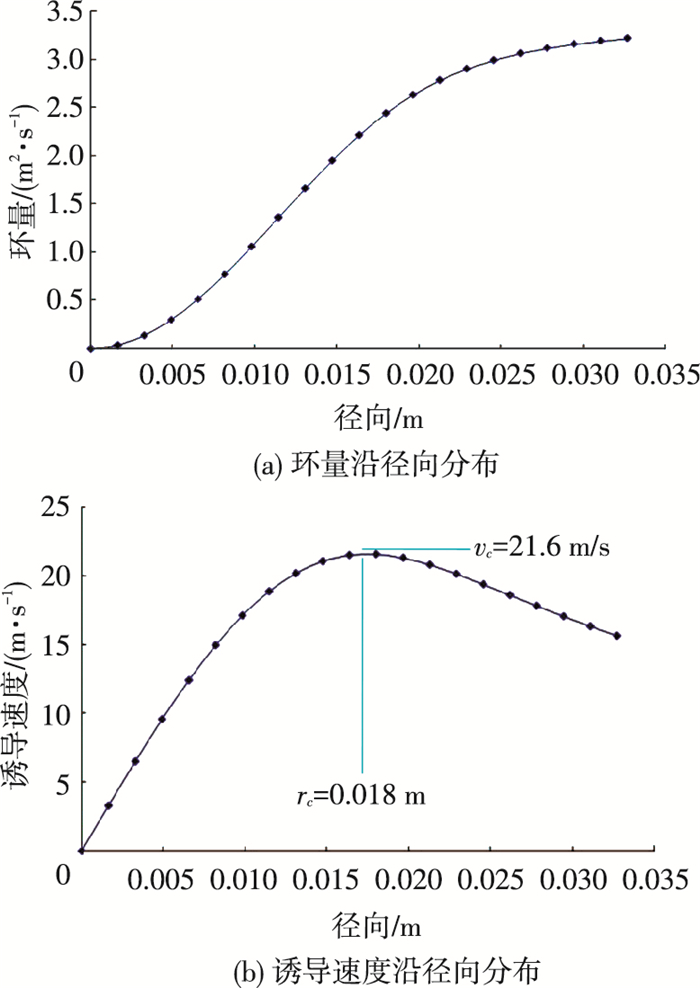
因此通过涡量的面积积分可以获得不同积分半径下的环量, 以11.25°涡龄角状态为例(拉力系数为0.01, 对应总距为8°), 图 10(a)获得了环量沿径向分布曲线, 再根据下式就可以获得周向诱导速度随半径的变化曲线, 如图 10(b)曲线的极值点对应的就是涡核半径rc(0.018 m)和最大诱导速度vc(21.6 m/s).
| $ v = \mathit{\Gamma }/2{\rm{ \mathit{ π} }}r. $ |
|
图 10 11.25°涡龄角状态下桨尖涡环量和诱导速度沿径向分布 Figure 10 The blade tip vortex circulation and induced velocity distribution along the radial distribution at 11.25° wake age status |
图 11、12为旋翼运行1/4圈测量得到的涡核最大诱导速度和桨尖涡涡核半径的变化曲线.可以看出涡核最大诱导速度随涡龄角有缓慢减小趋势, 桨尖涡涡核半径随涡龄角有缓慢增大趋势.这主要是由于桨尖涡形成后, 随着桨尖涡的发展和耗散, 桨尖涡环量逐渐减小, 导致涡核最大诱导速度逐渐减小, 进而引起离心力减小, 故涡核半径逐渐增大.而不同涡龄角的涡核半径和诱导速度跳动可能与流场环境的不稳定性有关.

|
图 11 涡核最大诱导速度变化 Figure 11 The change of vortex core max induced velocity |

|
图 12 涡核半径变化 Figure 12 The change of vortex core radius |
根据文献[12]的研究, 通用的Vatistas等[22]涡核模型计算诱导速度公式为
| $ v = \frac{{r\mathit{\Gamma }}}{{2{\rm{ \mathit{ π} }}{{({r^{2n}} + r_c^{2n})}^{1/n}}}}, $ |
式中rc为涡核半径, 对应于周向诱导速度最大的半径位置.不同的n值对应了不同的轴向诱导速度分布, 即不同的涡核模型, n=1对应的是Scully涡核模型, n=2时近似于Lamb-Oseen涡核模型, n=∞对应的是Rankine涡核模型.
图 13为11.25°涡龄角状态下拟合出的曲线, 其横纵坐标均进行了量纲一的处理,

|
图 13 11.25°涡龄角状态下拟合出的曲线 Figure 13 Fitting curves at 11.25° wake age status |
图 14为旋翼运行1/4圈测量得到的不同总距时不同桨叶桨尖涡拟合出的桨尖涡模型n值变化曲线(其中, 图 14(c)中涡龄角大于213.75°的桨尖涡已耗散掉或超出有效视场, 故3#桨叶的桨尖涡n值仅有前3个点).不同总距时, 桨尖涡模型n值不为定值, 而呈现出不同幅度的波动情况.涡龄角为11.25°~90.00°(1#桨叶)和191.25°~258.75°(3#桨叶)时桨尖涡n值波动幅度相对较大, 而涡龄角为101.25°~180.00°(2#桨叶)时n值波动幅度相对较小, 表明桨尖涡在形成和耗散阶段其桨尖涡模型n值不稳定, 而在桨尖涡稳定存在阶段其桨尖涡n值相对稳定, 这可能与桨尖涡生成和衰减阶段的不稳定性有关.而且随着桨尖涡的发展, 其n值呈现出缓慢减小的趋势, 其桨尖涡模型向着Scully涡靠近.上述分析结果对于旋翼尾迹方法中的涡核修正计算有较大的参考意义.

|
图 14 不同总距时拟合出的n值变化 Figure 14 Fitting curves of the n value at different θ7 |
1) TR-PIV设备采样频率远高于普通PIV设备, 在0°~90°方位角能采集8对图像, 有利于旋翼悬停状态下流场的精细化处理和分析.
2) 采用基于涡量加权平均的方法来计算涡核中心位置可以消除涡核中心平移速度的影响, 其结果优于依据速度矢量的判读方法; 并据此得到了不同桨叶相同拉力系数和不同总距相同涡龄角的桨尖涡轨迹特性.
3) 采用基于环量分析的方法可以更加合理地确定涡核尺寸和最大诱导速度, 其结果优于依据周向诱导速度分布来判读的方法.
4) 桨尖涡发展演化过程中, 桨尖涡涡核半径随涡龄角有缓慢增大趋势, 涡核最大诱导速度随涡龄角有缓慢减小趋势.桨尖涡在不同发展阶段具有不同的涡核模型n参数, 总体来说桨尖涡在初始和稳定阶段更类似于Lamb-Oseen涡, 在衰减阶段n值减小逐渐向Scully涡靠近.此外桨尖涡在不同发展阶段n的波动程度不同, 可能与桨尖涡生成和衰减阶段的不稳定性有关.
| [1] |
JOHNSON W.
Helicopter theory[M]. Princeton: Princeton University Press, 1980.
|
| [2] |
BHAGWAT M J, RAMASAMY M, CARADONNA F X. Fundamental characterization of spanwise loading and trailed wake vortices[R]. AMRDEC Redstone Arsenal United States, 2016.
|
| [3] |
LEISHMAN J G, BAGAI A. Challenges in understanding the vortex dynamics of helicopter rotor wakes[J].
AIAA Journal, 1998, 36(7): 1130-1140.
DOI: 10.2514/2.510 |
| [4] |
KITAPLIOGLU C, CARADONNA F X. Aerodynamics and acoustics of blade-vortex interaction using an independently generated vortex[C]//Aeromechanics Specialists Conference on Aerodynamics, Acoustics and Dynamics. San Francisco, CA: [s. n. ], 1994.
|
| [5] |
WITTMER K S, DEVENPORT W J. Effects of perpendicular blade-vortex interaction, Part 1:Turbulence Structure and Development[J].
AIAA Journal, 1999, 37(7): 805-812.
DOI: 10.2514/2.7527 |
| [6] |
史勇杰, 招启军, 徐国华. 旋翼桨-涡干扰气动特性计算及参数影响研究[J].
航空学报, 2010, 31(6): 1106-1114.
SHI Yongjie, ZHAO Qijun, XU Guohua. Numerical calculation and parametric study of aerodynamics of rotor blade-vortex interaction[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(6): 1106-1114. |
| [7] |
宋辰瑶. 基于尾迹分析的旋翼旋转噪声计算及桨-涡干扰噪声研究[D]. 南京: 南京航空航天大学, 2010: 75-97. DOI: 10.7666/d.d167153.
SONG Chenyao. Computation of Rotational noise and research of blade-vortex interaction noise for rotors based upon wake analysis[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010: 75-97. DOI: 10.7666/d.d167153. |
| [8] |
LANDGREBE A J. An analytical method for predicting rotor wake geometry[J].
Journal of the American Helicopter Society, 1969, 14(4): 20-32.
DOI: 10.2514/6.1969-196 |
| [9] |
JOHNSON W. A general free wake geometry calculation for wings and rotors[C]// Proceedings of the 51th Annual Forum of the AHS International. [S. l. ]: [s. n. ], 1995: 137-153.
|
| [10] |
李攀, 陈仁良. 旋翼桨尖涡模型及其参数确定方法研究[J].
空气动力学学报, 2009, 27(3): 296-302.
LI Pan, CHEN Renliang. Research on rotor tip vortex model and the method for determining its parameter[J]. Acta Aerodynamica Sinica, 2009, 27(3): 296-302. DOI: 10.3969/j.issn.0258-1825.2009.03.006 |
| [11] |
李攀, 陈仁良. 旋翼桨尖涡模型及其在自由尾迹分析中的影响[J].
航空学报, 2009, 27(3): 2010-1523.
LI Pan, CHEN Renliang. Rotor tip vortex model and its effect on free-vortex wake analysis[J]. Acta Aeronautica et Astronautica Sinica, 2009, 27(3): 2010-1523. |
| [12] |
MILLUZZO J, LEISHMAN J G. Development of the turbulent vortex sheet in the wake of a hovering rotor[C]//Proceedings of the 69th Annual Forum Proceedings of the American Helicopter Society. Fairfax Virginia: AHS, 2013.
|
| [13] |
杨永东, 武杰. 悬停旋翼桨尖涡的试验研究[J].
实验流体力学, 2008, 22(3): 36-39.
YANG Yongdong, WU Jie. Investigation of hovering rotor tip vortex[J]. Journal of Experiments in Fluid Mechanics, 2008, 22(3): 36-39. DOI: 10.3969/j.issn.1672-9897.2008.03.008 |
| [14] |
袁红刚, 李进学, 杨永东, 等. 悬停状态下旋翼尾迹测量试验研究[J].
空气动力学学报, 2010, 28(3): 306-309.
YUAN Honggang, LI Jinxue, YANG Yongdong, et al. Test investigation of measuring wake geometry for helicopter rotors in hover[J]. Acta Aerodynamica Sinica, 2010, 28(3): 306-309. DOI: 10.3969/j.issn.0258-1825.2010.03.012 |
| [15] |
李春华, 曹金华, 吴裕平. 直升机旋翼流场特性PIV试验分析[J].
直升机技术, 2012(1): 6-10.
LI Chunhua, CAO Jinhua, WU Yuping. PIV experimental investigation on flow field for helicopter rotor[J]. Helicopter Technique, 2012(1): 6-10. DOI: 10.3969/j.issn.1673-1220.2012.01.002 |
| [16] |
余俊, 万津津, 施鎏鎏, 等. 基于连续式激光光源的TR-PIV测试技术[J].
上海交通大学学报, 2009, 43(8): 1254-1257.
YU Jun, WAN Jinjin, SHI Liuliu, et al. TR-PIV measurement technology using continuous laser illumination[J]. Journal of Shanghai Jiaotong University, 2009, 43(8): 1254-1257. DOI: 10.3321/j.issn:1006-2467.2009.08.014 |
| [17] |
黄明其, 兰波, 杨永东, 等. Φ5 m立式风洞直升机垂直升降试验台研制[J].
实验流体力学, 2013, 27(5): 94-97.
HUANG Mingqi, LAN Bo, YANG Yongdong, et al. The development of helicopter vertical flight test rig in Φ5 m vertical wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(5): 94-97. DOI: 10.3969/j.issn.1672-9897.2013.05.018 |
| [18] |
黄明其.
直升机风洞试验[M]. 北京: 国防工业出版社, 2014: 81-83.
HUANG Mingqi. Helicopter wind tunnel test[M]. Beijing: National Defence Industry Press, 2014: 81-83. |
| [19] |
BROOKS T F, Van Der WALL B G, RICHARD H, et al. Rotor wake vortex definition-initial evaluation of 3-C PIV results of the hart-Ⅱ study[C]//Proceedings of the 28th European Rotorcraft Forum. Bristol England: [s. n], 2002: 17-20.
|
| [20] |
BURLEY C L, BROOKS T F, Van Der WALL B, et al. Rotor wake vortex definition using 3C-PIV measurements: corrected for vortex orientation[C]//Proceedings of the 9th AIAA/CEAS Aeroacoustics Conference and Exhibit. Hilton Head, SC: AIAA, 2003: 12-14.
|
| [21] |
BHAGWA M J, LEIHMAN J G. Generalized viscous vortex core model for application to free-vortex wake and aeroacoustic calculations[C]//Annual Forum Proceedings-American Helicopter Society. [S. l. ]: American Helicopter Society, Inc, 2002, 58(2): 2042-2057.
|
| [22] |
VATISTAS G H, KOZEL V, MIH W C. Asimpler model for concentrated vortices[J].
Experiments in Fluids, 1991, 11(1): 73-76.
DOI: 10.1007/BF00198434 |
 2018, Vol. 50
2018, Vol. 50


