水下滑翔机是一种将传统的浮标技术与水下机器人技术相结合而研制成的新型无人水下机器人, 以其能耗低、成本低、航程远和噪声小等优势在科学研究、资源探测和军事侦查等领域具有广阔的应用前景[1].自1989年Henry首先提出“水下滑翔机”的概念以来, 各式各样的水下滑翔机根据不同的需求而产生.由于圆碟形水下滑翔机扁平且高度对称的特殊外形使其在低速时具有优良的灵活性和操纵性, 国内外许多学者对此类滑翔机产生了浓厚的兴趣并进行了相关的理论研究和仿真实验.
日本“Pteroa”系列航行器[2-4]的相关样机实验对圆碟形水下滑翔机的水动力特性进行了定量的研究; 上海交通大学[5]结合其自主研发的圆碟形水下滑翔机所开展的研究和仿真, 进一步论证了在低速环境下其具有良好的操纵性和运动稳定性; 赵宝强等[6-7]对圆碟形水下滑翔机进行的三维定常运动仿真, 从理论上验证了其水下运动的稳定性和灵活性; 大连海事大学[8]所开展的圆碟形水下滑翔机实验则对其滑行性能进行实验研究并验证了其水下滑翔的可能; 但与当今世界主流的水下滑翔机相比, 圆碟型水下滑翔机具有良好操纵性的同时也具有湿表面积较大、黏性阻力较大、升阻比较低、经济性较差等诸多缺点.
为改善圆碟形水下滑翔机的水动力性能, 提高滑翔经济性, 本文提出一种飞翼式碟形自主水下滑翔机, 具体为其纵向剖面为大升力翼型剖面, 横向剖面为水滴形, 提高滑翔机升力的同时减小阻力.目前国内外对此类水下滑翔机的研究相对较少, 本文采用实验和数值仿真相结合的方法分析了该型水下滑翔机的流体动力特性, 并以此为基础进行运动学仿真获得其相关运动规律, 结论可为新型水下滑翔机的改进和设计提供参考.
1 数学模型的建立 1.1 坐标系与运动参数为更好的确定水下滑翔机的位置和姿态, 本文定义两个参考系即惯性坐标系E0-xiyizi和随体坐标系e0-xbybzb.如图 1所示, 惯性坐标系原点E0固定在水面, 坐标轴zi正方向竖直向下, 轴xi和yi正交于轴zi; 随体坐标系原点e0固定在水下滑翔机浮心CB处, 坐标轴xb指向潜器正前方, 轴yb指向正右侧, 轴zb垂直于平面xb-e0-yb方向向下[9].
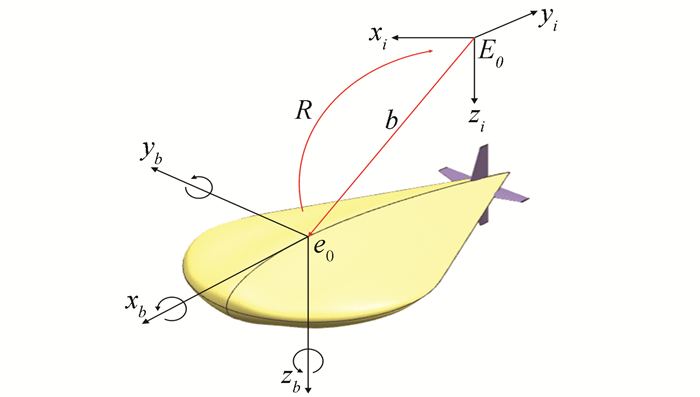
|
图 1 水下滑翔机参考坐标系 Figure 1 Reference coordinate of underwater glider |
水下滑翔机在惯性系下的位置参数表示为b = [x, y, z]T和θ = [φ, θ, φ]T; 在随体坐标系中转换速度和角速度分别表示为V= [u, v, w]T和Ω= [p, q, r]T, 利用惯性系和随体系之间的转换矩阵可得知[10]:
| $ \begin{array}{l} \mathit{\boldsymbol{\dot b}} = \mathit{\boldsymbol{RV}} = \\ \left[ \begin{array}{l} c\left( \psi \right)c\left( \theta \right)\;\;\; - s\left( \psi \right)c\left( \varphi \right) + c\left( \psi \right)s\left( \theta \right)s\left( \varphi \right)\\ s\left( \psi \right)c\left( \theta \right)\;\;c\left( \psi \right)c\left( \varphi \right) + s\left( \varphi \right)s\left( \theta \right)s\left( \psi \right)\\ - s\left( \theta \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;c\left( \theta \right)s\left( \varphi \right) \end{array} \right.\\ \left. \begin{array}{l} s\left( \psi \right)s\left( \varphi \right) + c\left( \psi \right)c\left( \varphi \right)s\left( \theta \right)\\ - c\left( \psi \right)s\left( \varphi \right) + s\left( \theta \right)s\left( \psi \right)c\left( \varphi \right)\\ \;\;\;\;\;\;\;\;\;\;\;c\left( \theta \right)c\left( \varphi \right) \end{array} \right]\mathit{\boldsymbol{V}}, \end{array} $ | (1) |
| $ \mathit{\boldsymbol{\dot \theta }}{\rm{ = }}\left[{\begin{array}{*{20}{c}} 1&{s\left( \varphi \right){\rm{tan}}\left( \theta \right)}&{c\left( \varphi \right){\rm{tan}}\left( \theta \right)}\\ 0&{c\left( \varphi \right)}&{-s\left( \varphi \right)}\\ 0&{s\left( \varphi \right){\rm{sec}}\left( \theta \right)}&{c\left( \varphi \right){\rm{sec}}\left( \theta \right)} \end{array}} \right]\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}. $ | (2) |
式中:φ为横滚角; θ为俯仰角; ψ为偏航角; c(·)=cos(·), s(·)=sin(·).
1.2 动力学模型水下滑翔机主要由传感器模块、浮力驱动模块、平移质量块、驱动模块、控制模块和通信记录模块组成; 滑行速度0.5 ~1.0 m/s, 主要通过内部质量块控制其运动姿态, 水下滑翔机内部质量块分布如图 2所示.
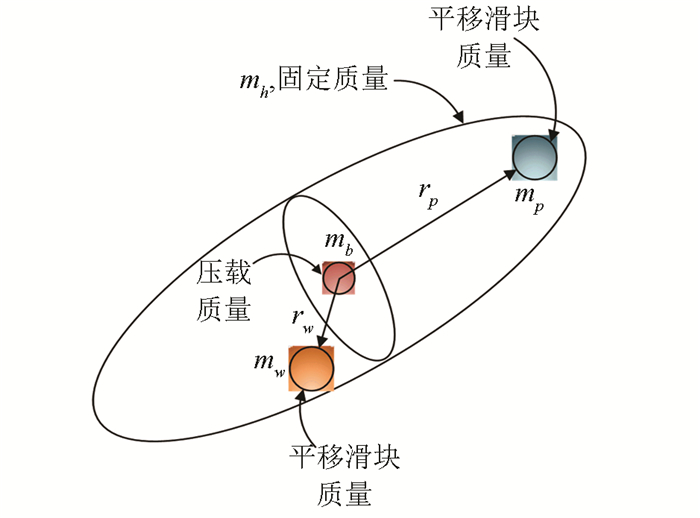
|
图 2 水下滑翔机主体质量分布 Figure 2 Mass distribution of the underwater glider |
水下滑翔机总质量m为
m=mh+mw+mp+mb.
式中:mh为固定质量, 主要包括外壳、控制系统等非运动部件质量; mp为纵向平移滑块质量, 用于调节滑翔机俯仰角, 体坐标系下矢径为rp=[rpx, rpy, rpz]T; mw为横向平移滑块质量, 用于调节滑翔机横滚角, 实现转弯运动, 体坐标系下矢径为rw=[rwx, rwy, rwz]T; mb为浮力驱动系统压载质量, 位于水下滑翔机浮心处, 实现滑翔机下潜或上浮运动.则根据多体动力学原理可知水下滑翔机惯性系下动力学方程为[11-12]
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot p}} = \sum\limits_{i = 1}^m {{f_{{\rm{exti}}}}}, \\ {\bf{ \pmb{\mathit{\dot π}} }} = \left( {\sum\limits_{i = 1}^m {\left( {{\mathit{\boldsymbol{r}}_i} \times {\mathit{\boldsymbol{f}}_{{\rm{exti}}}}} \right)} } \right. + \sum\limits_{j = 1}^n {{{\bf{ \pmb{\mathit{ π}} }}_{{\rm{exti}}}}}, \\ {{\mathit{\boldsymbol{\dot p}}}_p} = {m_p}g\mathit{\boldsymbol{k}} + \sum\limits_{k = 1}^K {{\mathit{\boldsymbol{f}}_{{\rm{move}} \sim {\rm{mass}}}}}, \\ {{\mathit{\boldsymbol{\dot p}}}_\mathit{b}} = {m_b}g\mathit{\boldsymbol{k}} + \sum\limits_{k = 1}^K {{\mathit{\boldsymbol{f}}_{{\rm{ballast}} \sim {\rm{mass}}}}}, \\ {{\mathit{\boldsymbol{\dot p}}}_\mathit{w}} = {m_w}g\mathit{\boldsymbol{k}} + \sum\limits_{k = 1}^K {{\mathit{\boldsymbol{f}}_{{\rm{move}} \sim {\rm{mass}}}}} . \end{array} \right. $ | (3) |
式中:p、π分别为水下滑翔机在惯性系下的动量和动量矩; pp、pb、pw分别为纵向平移滑块、压载滑块以及横向平移滑块在惯性系中的动量; fexti、πexti分别为作用在水下滑翔机上的外力和力矩; ri为外力作用点在惯性系内的矢径.
令P、Π分别为水下滑翔机系统在随体系中的动量和动量矩; Pp、Pb、Pw分别为纵向平移滑块、压载滑块以及横向平移滑块在随体系中的动量; R为随体系到惯性系转换矩阵, 则有
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{p}} = \mathit{\boldsymbol{RP}}, \\ {\bf{ \pmb{\mathit{ π}} }} = \mathit{\boldsymbol{R \boldsymbol{\varPi} }} + \mathit{\boldsymbol{b}} \times \mathit{\boldsymbol{p}}, \\ {\mathit{\boldsymbol{p}}_p} = \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{P}}_p}, {\rm{ }}\\ {\mathit{\boldsymbol{p}}_b} = \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{P}}_b}, {\rm{ }}\\ {\mathit{\boldsymbol{p}}_w} = \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{P}}_w}. \end{array} \right. $ | (4) |
将式(4)对时间求导可得到动力学表达式如下:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot p}} = \mathit{\boldsymbol{R}}\left( {\mathit{\boldsymbol{\dot P}} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times \mathit{\boldsymbol{P}}} \right){\rm{ }}, \\ {\bf{ \pmb{\mathit{\dot π}} }} = \mathit{\boldsymbol{R}}\left( {\mathit{\boldsymbol{ \boldsymbol{\dot \varPi} }} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times \mathit{\boldsymbol{ \boldsymbol{\varPi} }}} \right) + \mathit{\boldsymbol{RV}} \times \mathit{\boldsymbol{p}} + \mathit{\boldsymbol{b}} \times \mathit{\boldsymbol{p}}, \\ {{\mathit{\boldsymbol{\dot p}}}_p} = \mathit{\boldsymbol{R}}\left( {{{\mathit{\boldsymbol{\dot P}}}_p} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times {\mathit{\boldsymbol{P}}_p}} \right), \\ {{\mathit{\boldsymbol{\dot p}}}_b} = \mathit{\boldsymbol{R}}\left( {{{\mathit{\boldsymbol{\dot P}}}_b} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times {\mathit{\boldsymbol{P}}_b}} \right), \\ {{\mathit{\boldsymbol{\dot p}}}_w} = \mathit{\boldsymbol{R}}({{\mathit{\boldsymbol{\dot P}}}_w} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \times {\mathit{\boldsymbol{P}}_w}). \end{array} \right. $ | (5) |
将式(5)代入式(3)中得到水下滑翔机系统在随体系下动力学方程为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot P}} = \mathit{\boldsymbol{P}} \times {\bf{\Omega }} + {\mathit{\boldsymbol{R}}^{\rm{T}}}\sum\limits_{i = 1}^m {{\mathit{\boldsymbol{f}}_{{\rm{exti}}}}} ,\\ \mathit{\boldsymbol{ \boldsymbol{\dot \varPi} }} = \mathit{\boldsymbol{ \boldsymbol{\varPi} }} \times \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} + \mathit{\boldsymbol{P}} \times \mathit{\boldsymbol{V}} + {\mathit{\boldsymbol{R}}^{\rm{T}}}\left( {\sum\limits_{i = 1}^m {\left( {{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{r}}} \right)} \times {\mathit{\boldsymbol{f}}_{{\rm{exti}}}}} \right)\\ \;\;\;\;\;\;\;\; + {\mathit{\boldsymbol{R}}^{\rm{T}}}\sum\limits_{j = 1}^n {{{\bf{ \pmb{\mathit{ π}} }}_{{\rm{exti}}}}} ,\\ {{\mathit{\boldsymbol{\dot P}}}_p} = {\mathit{\boldsymbol{P}}_p} \times \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} + {m_p}g\left( {{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{k}}} \right) + {\mathit{\boldsymbol{R}}^{\rm{T}}}\sum\limits_{k = 1}^K {{f_{{\rm{move}} \sim {\rm{mass}}}}} ,\\ {{\mathit{\boldsymbol{\dot P}}}_b} = {\mathit{\boldsymbol{P}}_b} \times \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} + {m_b}g\left( {{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{k}}} \right) + {\mathit{\boldsymbol{R}}^{\rm{T}}}\sum\limits_{k = 1}^K {{f_{{\rm{ballast}} \sim {\rm{mass}}}}} ,\\ {{\mathit{\boldsymbol{\dot P}}}_w} = {\mathit{\boldsymbol{P}}_w} \times \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} + {m_w}g\left( {{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{k}}} \right) + {\mathit{\boldsymbol{R}}^{\rm{T}}}\sum\limits_{k = 1}^K {{f_{{\rm{move}} \sim {\rm{mass}}}}} . \end{array} \right. $ | (6) |
式中前两项即为水下滑翔机六自由度动力学方程, 式(1)、(2)共同构成系统运动学方程.
2 流动特性分析为了更好地说明该型水下滑翔机(模型1)的水动力特性, 本文将其与传统水下滑翔机Seaglider(模型2)和主流圆碟形水下滑翔机(模型3)共同进行流体动力仿真, 并对仿真结果进行对比分析, 水下滑翔机几何参数见表 1.
| 表 1 模型几何参数 Table 1 Geometric parameters of models |
对水下滑翔机流动特性的分析其实就是对于Navier-Stokes方程的求解, 此外考虑到3种水下滑翔机表面曲率变化较大, 对网格质量要求较高, 故选用SST-kω湍流模型对其在不可压缩条件下进行流体动力仿真, 其流动控制方程[13-14]为:
| $ \nabla \cdot U = 0, $ | (7) |
| $ \rho \frac{{{\rm{d}}U}}{{{\rm{d}}t}} = \rho g-\nabla p + \mu \;{\nabla ^2}U. $ | (8) |
式中:U为流体速度; ρ为流体的密度; p为流体的压力; μ为流体的动力黏性系数.
湍流强度k方程为
| $ \frac{{\partial \rho k}}{{\partial t}} + \nabla \left( {\rho kU} \right) = \nabla [(\mu + \frac{{{\mu _z}}}{{{\sigma _k}}})\nabla k] + {p_k} -{b_k}\rho k\omega . $ | (9) |
湍流频率ω方程为
| $ \frac{{\partial \rho \omega }}{{\partial t}} + \nabla \left( {\rho \omega U} \right) = \nabla [(\mu + \frac{{{\mu _z}}}{{{\sigma _k}}})\nabla \omega] + a\frac{\omega }{k}{p_k} -{b_\omega }\rho k{\omega ^2}. $ | (10) |
式中:pk为层流速度梯度所产生的的湍流动能; σk、σw分别为湍流能量的普朗特数; μz为涡黏度, μz=-ρk/ω.
2.1.2 网格划分本文仅以模型1网格划分为例, 其余模型网格划分方法与其基本一致.整体计算域如图 3所示:流域长度为12L, 直径为6L, 其中L为滑翔机长度, 流域边界为速度入口, 滑移壁面边界和压力出口条件, 滑翔机表面为不滑移边界; 网格形式为混合结构网格[15], 即在滑翔机表面附近曲率复杂的区域采用非结构网格划分, 其表面进行加密细化, 而对于外部流场处则采用质量较高的结构化网格, 保证网格质量的同时降低网格数量, 网格总数300万, 保证网格质量不低于0.6.
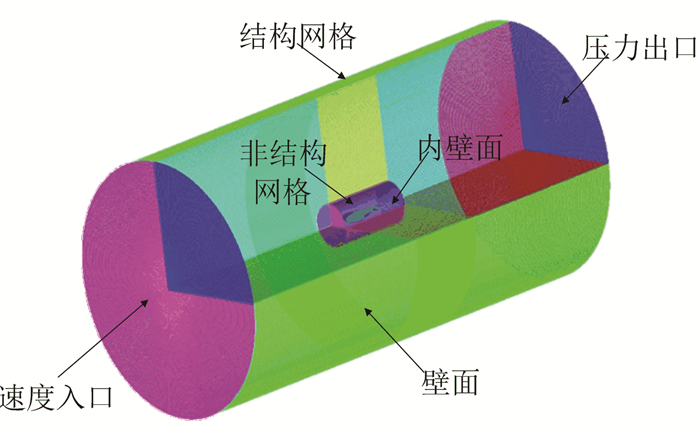
|
图 3 网格划分图 Figure 3 Mesh generation of underwater glider |
为验证数值计算的准确性, 本文按照上述方法计算模型1在航速0.5 m/s, 攻角0°~21°(间隔3°)工况下的阻力系数、升力系数、俯仰力矩系数以及升阻比, 并和实验数据进行对比, 结果如图 4所示.
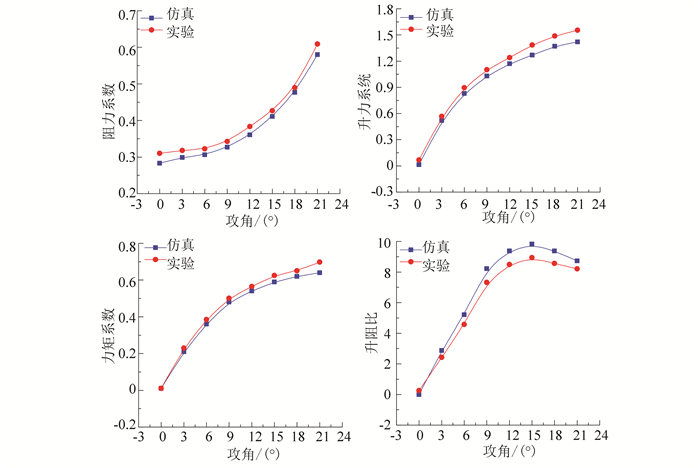
|
图 4 水动力性能数值模拟验证 Figure 4 Verification of numerical simulation results |
由图 4可知:对于阻力系数、升力系数、俯仰力矩系数以及升阻比, 数值计算结果与实验结果变化规律一致, 且其最大相对误差分别为9.12%、8.21%、8.35%和9.01%, 均小于10%, 验证了上述数值计算方法的可靠性.
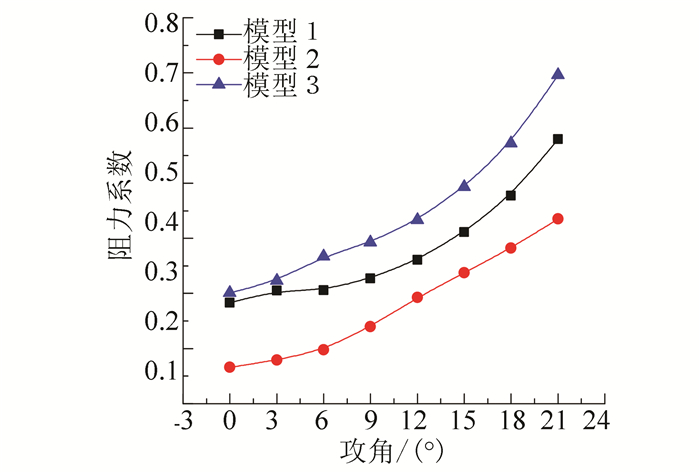
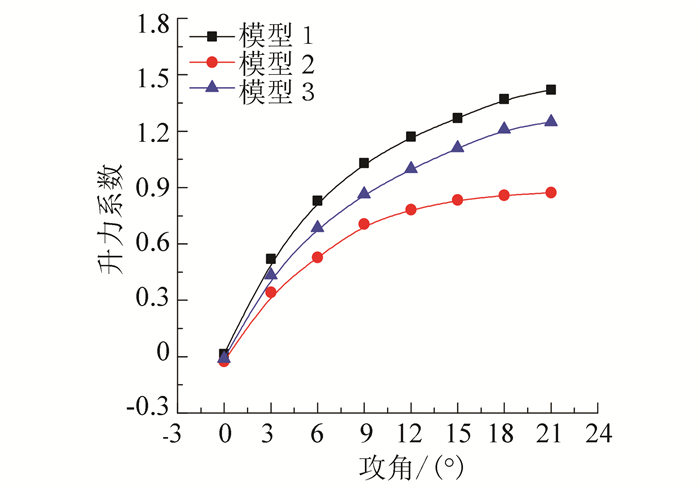
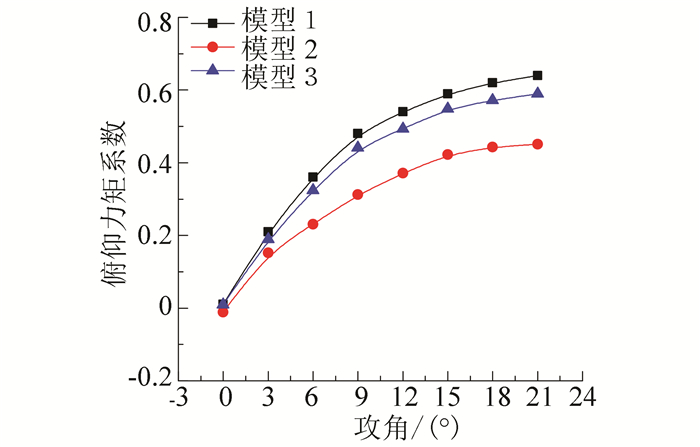
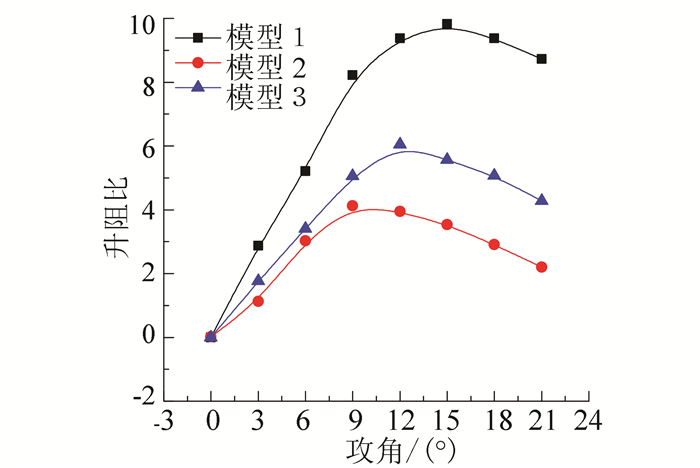
2.3 仿真结果分析基于上述数值计算方法对以上3种水下滑翔机在航速0.5 ~1.0 m/s(间隔0.25 m/s), 攻角0°~21°(间隔3°)工况下的阻力特性, 升力特性和升阻比进行数值仿真, 由于工况较多此处以航速0.5 m/s为例, 仿真结果如图 5~8所示.由图 5可知, 3种模型的阻力系数均与攻角呈二次函数关系, 且均随着攻角的增加而增大; 此外在同一攻角下模型3的阻力系数最大, 模型2最小, 且相比模型1和模型3, 模型2的阻力系数随攻角增加相对缓慢, 模型3增长最快.由此可说明模型2的低阻层流外壳具有非常好的阻力特性, 模型1其次, 模型3最差.由图 6、7可知, 3种模型的升力系数和力矩系数变化规律相似, 均随着攻角的增加而增大, 且各自增长速率均随攻角增长而逐渐减慢; 由于模型1和模型3采用扁平式设计, 其在升力作用面上的投影面积远大于模型2, 因此在相同攻角下模型1和模型3的升力系数和力矩系数远大于模型2的相应系数; 而与模型3相比, 由于模型1采用大升力的飞翼式外形设计, 因此在相同攻角下模型1具有更优良的升力特性; 由图 8可知, 3种模型的升阻比均随攻角呈先增加后减小的趋势, 且在0°~9°小攻角范围内升阻比与攻角呈线性关系; 模型1的最大升阻比约为9.8左右, 出现在15°攻角附近, 远大于其余2种模型, 具有最佳的滑翔经济性能.
|
图 5 阻力系数曲线 Figure 5 Drag cofficient over the angle of attack |
|
图 6 升力系数曲线 Figure 6 Lift cofficient over the angle of attack |
|
图 7 俯仰力矩系数曲线 Figure 7 Moment cofficient over the angle of attack |
|
图 8 升阻比曲线 Figure 8 Lift drag ratio over the angle of attack |
在水下滑翔机外形设计中, 升阻比和俯仰力矩是衡量滑翔机水动力性能的重要指标, 在增加升阻比的同时尽量减小水动力对滑翔机的俯仰力矩, 以保持其运动稳定性.为了综合描述滑翔机的水动力性能本文采用文献[16]中的水动力性能加权公式为
| $ {\rm{max}}\left\{ {{\omega _1}\frac{{{F_L}\left( \alpha \right)}}{{{F_D}\left( \alpha \right)}} + {\omega _2}\frac{1}{{{M_\theta }\left( \alpha \right)}}} \right\}. $ | (11) |
式中:FL(α)、FD(α)、Mθ(α)分别为3种模型的升力、阻力以及俯仰力矩; ω1、ω2分别为水动力加权系数, ω1=0.6, ω2=0.4;利用式(11)本文计算出3种模型综合水动力性能参数见表 2.
| 表 2 综合水动力性能对照表 Table 2 The hydrodynamic performance comparisons |
由表 2可知, 模型1的加权系数最高, 远大于其余2种模型, 即飞翼式碟形自主水下滑翔机具有最优的综合水动力性能, 水下工作效率最高.
3 滑翔运动仿真考虑水下滑翔机的实际运动形式并根据动力学与运动学方程, 带入质量、附加质量、排水质量以及各项水动力系数, 进一步推导出动力学方程的微分形式并编写相应运动仿真程序对水下滑翔机锯齿滑翔运动和螺旋滑翔运动进行运动仿真分析; 滑翔机水动力系数和几何参数见表 3、4, 其余高阶水动力耦合系数可由表 3中系数推导得出, 本文不做详细介绍.
| 表 3 无因次水动力系数 Table 3 Hydrodynamic cofficient of the model |
| 表 4 水下滑翔机几何参数 Table 4 Geometric parameters of the underwater glider |
锯齿滑翔运动是水下滑翔机最主要的运动模式之一, 主要通过滑翔机净浮力, 升力和阻力之间的配合使其稳定运动, 具有能量消耗低、续航能力强等显著优点.本文利用ode45算法对其运动微分方程进行求解, 以Input=[mb, rpy, rpx, δr, δs]为控制量, 式中δr为尾翼垂直翼舵角右舵为正, δs为尾翼水平翼舵角下舵为正; 并假设纵向、横向移动滑块以及压载质量变化为匀速过程, 定义纵向和横向移动滑块的速度为0.02 m/s, 压载质量变化速度为0.14 kg/s, 调节过程用时10 s, 初始参数取Initial=[u, v, w, p, q, r, x, y, z, φ, θ, ψ]数值均为0;以Input=[0.7 kg, 0.1 m, 0m, 0°, 0°]水下滑行490 s, 以Input=[-0.7kg, -0.1m, 0m, 0°, 0°]滑行490 s, 滑行1 000 s为一个周期, 共仿真3 000 s, 仿真结果如图 9所示.
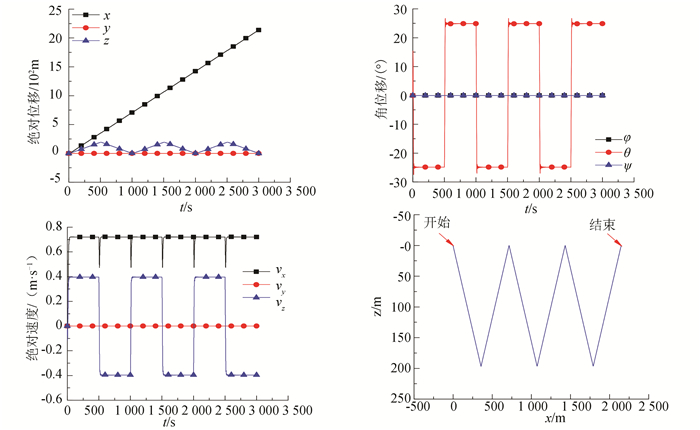
|
图 9 锯齿滑翔仿真结果 Figure 9 Simulation results of sawtooth motion |
由图 9可知:仿真过程中水下滑翔机前进速度0.72 m/s, 垂向速度0.39 m/s, 俯仰角θ稳定在25°, 500 s时达到最大下潜深度193.85 m, 最大前进位移2 138.34 m.
3.2 螺旋滑翔运动螺旋滑翔运动是水下滑翔机回转时所采取的典型运动, 主要通过净重力和升力组成的向心力使滑翔机回转, 与舵翼回转方式相比具有更低的能耗.本文控制量取Input=[0.7kg, 0.1m, 0.1m, 0°, 0°], 调节过程用时10 s, 初始参数Initial=[u, v, w, p, q, r, x, y, z, φ, θ, ψ]均设为0, 总仿真时间2 000 s, 仿真结果如图 10所示.
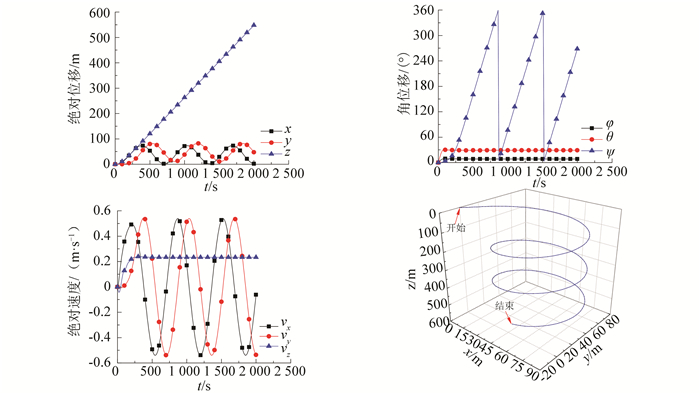
|
图 10 螺旋滑翔仿真结果 Figure 10 Simulation results of spiral motion |
由图 10可知:仿真过程中该型水下滑翔机稳定地进行螺旋滑翔, 回转半径79.54 m, 回转螺距145.13 m, 滑翔总速度0.56 m/s, 垂向稳定速度0.26 m/s, 横滚角φ稳定在10°, 俯仰角ψ稳定在30°, 2000 s时下潜深度527.95 m.
4 结论1) 建立了确定该型水下滑翔机流动特性的数值模拟方法, 数值计算结果与实验结果具有较好的一致性, 验证了所采用数值方法的可靠性和准确性.
2) 与传统水下滑翔机Seaglider和主流圆碟形水下滑翔机相比, 该型水下滑翔机具有更优的综合水动力性能和滑翔经济性.
3) 该型水下滑翔机可以稳定地完成锯齿滑翔和螺旋滑翔运动, 且滑翔过程中其速度、位移、俯仰角等运动参数除改变滑翔模式时存在短时间波动外, 其余时刻没有明显波动, 表明该型水下滑翔机具有一定的运动稳定性, 从理论上验证了其水下航行的可能.
| [1] |
刘立栋, 张宇文. 基于浮力补偿的水下无人平台低速状态最优控制研究[J].
兵工学报, 2013, 34(5): 644-648.
LIU Lidong, HANG Yuwen. Buoyancy compensation-based optimal control of UUV low-speed state[J]. Acta Armamentarii, 2013, 34(5): 644-648. |
| [2] |
URA T, OTSUBO S. Design of unmanned untethered submersible for quick swimming[J].
Journal of Society of Naval Architects of Japan, 1987, 162: 110-117.
DOI: 10.2534/jjasnaoe1968.1987.162-110 |
| [3] |
FU JII T, URA T. Control with neural network for autonomous underwater vehicle:application to longitudinal motion control[J].
Journal of the Society of Naval Architects of Japan, 1989, 166: 503-511.
DOI: 10.2534/jjasnaoe1968.1988.163-204 |
| [4] |
FU JII T, URA T. Neural-network based adaptive control systems for AUVs[J].
Engineering Applications of Artificial Intelligence, 1991, 4(4): 309-318.
DOI: 10.2534/jjasnaoe1968.1989.166-503 |
| [5] |
张怀新, 潘雨村. 圆碟形潜水器阻力性能研究[J].
上海交通大学学报, 2006, 40(6): 978-982.
ZHANG Huaixin, PAN Yucun. The resistance performance of a dish-shaped underwater vehicle[J]. Journal of Shanghai JiaoTong University, 2006, 40(6): 978-982. DOI: 10.3321/j.issn:1006-2467.2006.06.023 |
| [6] |
赵宝强. 碟形水下滑翔机动态稳定性建模仿真研究[J].
舰船科学技术, 2016, 38(7): 82-86.
ZHAO Baoqiang. Study of modeling and simulation of dish-underwater glider dynamic stability[J]. Ship Science and Technology, 2016, 38(7): 82-86. DOI: 10.3404/j.issn.1672-7619.2016.07.018 |
| [7] |
赵宝强, 王晓浩, 姚宝恒, 等. 碟形水下滑翔机三维定常建模分析[J].
海洋技术学报, 2014, 33(1): 11-18.
ZHAO Baoqiang, WANG Xiaohao, YAO Baoheng, et al. Three-dimensional steady motion model and analysis und erwater gliders[J]. Journal of Ocean Technology, 2014, 33(1): 11-18. |
| [8] |
张心曙, 繆国平, 黄国梁, 等. 碟形潜水器水动力性能研究[J].
上海交通大学学报, 2003, 37(8): 1186-1188.
ZHANG Xinshu, MIAO Guoping, HUANG Guoliang, et al. Hydrodynamic characteristics of a dish-shaped under water vehicle[J]. Journal of Shanghai Jiao Tong University, 2003, 37(8): 1186-1188. DOI: 10.3321/j.issn:1006-2467.2003.08.011 |
| [9] |
ZHANG Shaowei, YU Jiancheng, ZHANG Aiqun, et al. Spiraling motion of underwater gliders:modeling, analysis and experimental results[J].
Ocean Engineering, 2013, 60(3): 1-13.
DOI: 10.1016/j.oceaneng.2012.12.023 |
| [10] |
HE Wei, CHEN Yuhao, YIN Zhao. Adaptive neural network control of an uncertain robot with full-state constraints[J].
IEEE Transactions on Cybernetics, 2016, 46(3): 620-629.
DOI: 10.1109/TCYB.2015.2411285 |
| [11] |
CHEN Mou, GE Shuzhi. Adaptive neural output feedback control of uncertain nonlinear systems with unknown hysteresis using disturbance observer[J].
IEEE Transactions on Industrial Electronics, 2015, 62(12): 7706-7716.
DOI: 10.1109/TIE.2015.2455053 |
| [12] |
HUA Jing, Li Yimin, ZHANG Kun, et al. Observer based adaptive fuzzy control of class of nonlinear systems with unknown symmetric nonlinear[J].
Applied Mathematical Modelling, 2015, 40(7/8): 4370-4379.
DOI: 10.1016/j.apm.2015.11.013 |
| [13] |
胡志强, 林扬, 谷海涛. 水下机器人粘性类水动力数值计算方法研究[J].
机器人, 2007, 29(2): 145-150.
HU Zhiqiang, LIN Yang, GU Haitao. On numerical computation of viscous hydrodynamics of unmanned underwayter vehicle[J]. Robot, 2007, 29(2): 145-150. DOI: 10.3321/j.issn:1002-0446.2007.02.009 |
| [14] |
WANG Shuxin, SUN Xiujun, WANG Yanhui, et al. Dynamic modeling and motion simulation for a winged hybrid-driven underwater glider[J].
China Ocean Engineering, 2011, 25(1): 97-112.
DOI: 10.1007/s13344-011-0008-7 |
| [15] |
SMITH R, SCHWAGER M, SMITH S L, et al. Persistent ocean monitoring with underwater gliders:adapting sampling resolution[J].
Journal of Field Robotics, 2011, 28(5): 714-741.
DOI: 10.1002/rob.20405 |
| [16] |
谷海涛, 林扬, 胡志强, 等. 基于代理模型的水下滑翔机机翼设计优化方法[J].
机械工程学报, 2009, 45(12): 7-14.
GU Haitao, LIN Yang, HU Zhiqiang, et al. Surrogate models based optimization methods for the design of underwater glider wing[J]. Journal of Mechanical Engineering, 2009, 45(12): 7-14. DOI: 10.3091/JME.2009.12.007 |
 2018, Vol. 50
2018, Vol. 50


