国内外学者对小球入水问题已经开展了大量研究.实验观察是早期研究小球入水的主要手段, Richardson[1]、May[2-4]和Gilbarg等[5]实验探究了入水空泡的形成、发展、闭合和溃灭的演化过程受小球物理特性、环境压力以及流体介质特性的影响规律.随着光学测量科学的发展, 马庆鹏等[6]基于高速摄像技术, 开展了不同抨击速度和不同表面润湿性的小球入水实验研究, 对比分析了入水过程小球质心的运动特性和动力特性.基于有限体积法的数值计算算法的建立和高性能集群计算机并行运算技术的发展, 数值仿真成为研究入水流场特性的重要方法, Abraham等[7]通过数值模拟分析了小球入水多相流动特性, 得到了阻力系数随介质表面张力、流动状态以及小球入水速度的变化规律.
针对小球入水问题的研究, 虽然已经取得了许多有价值的成果, 但是对于旋转小球入水的研究较少, Truscott等[8-9]采用实验的方式探究了旋转小球入水流场特性, 发现了旋转小球入水后呈现马格努斯效应的曲线轨迹[10]和旋转小球低速入水产生楔形劈尖的现象; 总结了量纲一的升力和阻力变化规律.近年来随着破障炮弹的研制需要, 弹体入水和水中弹道的稳定性研究引起学者们的广泛关注.顾建农等[11]实验研究了高速旋转弹丸水平入水, 实验结果表明半球形弹头弹道稳定性较好.旋转半球头与旋转小球机理一致, 旋转小球入水特性的探索是研究旋转弹体入水的基础, 由于受实验条件的限制, 已公开的关于高速旋转体入水问题的研究很少.为深入研究旋转体入水空泡特性, 本文采用数值模拟方法来探究高速旋转小球入水过程空泡特性.
1 数值计算方法 1.1 控制方程及其求解本文基于VOF均值多相流模型并采用动计算域技术对小球入水过程进行数值模拟.低弗劳德数旋转小球的数值模拟可以忽略空化现象, 且假设流体不可压缩并忽略整个运动过程中的热效应.默认小球为刚体, 故忽略流固耦合, 只考虑流体与刚体之间的摩擦力.VOF多相流模型对各相单独处理为可变密度的介质, 对流体微团中的各相流体采用体积分数表示, 各相之间共享压力场、速度场且忽略各相之间的相对滑移.任一流体微团各相之间的体积分数关系为
αair+αwater=1,
式中αair、αwater分别为空气、水的体积分数.定义汽水交界面为αinterf=0.5.
流体中混合连续介质的质量守恒方程为
ρmix(∇·v)=0.
流体中混合连续介质的动量守恒方程为
| $ {\rho _{{\rm{mix}}}}\frac{{{\rm{d}}\mathit{\boldsymbol{u}}}}{{{\rm{d}}t}} = {\rho _{{\rm{mix}}}}\mathit{\boldsymbol{f}} + {\rm{div}}\mathit{\boldsymbol{\sigma }}{\rm{, }} $ |
其中
| $ \mathit{\boldsymbol{\sigma }} =- p\mathit{\boldsymbol{I}} + 2{\mu _{{\rm{mix}}}}\mathit{\boldsymbol{E}} + [\mu \prime-\frac{2}{3}({\mu _{{\rm{mix}}}} + {\mu _{{\rm{turb}}}})]{\rm{ }}\mathit{\boldsymbol{E}}\cdot\mathit{\boldsymbol{EI}}. $ |
式中:u为速度矢量; σ为应力张量; I为单位张量; E为应变率张量; p为流体静压; μturb为湍流黏度; ρmix为混合介质密度, 其中ρmix=αairρair+αwaterρwater; μmix为混合介质动力黏度, 其中μmix=αairμair+αwaterμwater; μ′为第二黏度系数; 根据本文假设可知μ′可忽略不计, 即
| $ \mathit{\boldsymbol{\sigma }} =-p\mathit{\boldsymbol{I}} + 2{\mu _{{\rm{mix}}}}\mathit{\boldsymbol{E}}-\frac{2}{3}({\mu _{{\rm{mix}}}} + {\mu _{{\rm{turb}}}})\mathit{\boldsymbol{E}}\cdot\mathit{\boldsymbol{EI}}. $ |
本文雷诺数范围为Re=4.0×104~3.5×105, 即小球附近流场以及尾迹区域为湍流区, 所以必须考虑因湍流引起的附加黏性力.参考Versteeg等[12]对不同湍流模型使用推荐和Abraham等[7]计算所采用的湍流数值模型, 经过分析对比选择Shear StressTurbulence(SST)湍流模型, 大量案例证明该湍流模型能够满足复杂流体流动要求.SST湍流模型为两参变量k-ω模型, 其中k为湍动能, ω为湍流耗散率.Menter[13]定义湍流黏度为
| $ {\mu _{{\rm{turb}}}} = \frac{{{a_1}\rho k}}{{{\rm{max}}({a_1}\omega, S{F_2})}}. $ |
式中:a1=0.31;
| $ {S_{ij}} = \frac{1}{2}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right), $ |
| $ {\rm{ar}}{{\rm{g}}_2} = {\rm{max}}\left( {{\rm{}}2\frac{{\sqrt k }}{{0.09\omega y}};500\frac{v}{{{y^2}\omega }}} \right). $ |
式中, ν=μ/ρ为流体动力黏度.
方程中的参量k和ω由下面两个传输方程联合求解:
| $ \frac{{D\left( {\rho k} \right)}}{{Dt}} = p- {\beta ^*}\rho k\omega + {\rm{div}}[({\mu _{{\rm{mix}}}} + {\sigma _k}{\mu _{{\rm{turb}}}}){\rm{div}}k], $ |
| $ \begin{array}{l} \frac{{{\rm{ }}D\left( {\rho \omega } \right)}}{{Dt}} = \gamma \frac{\omega }{k}p- \beta \rho {\omega ^2} + {\rm{div}}[({\mu _{{\rm{mix}}}} + {\sigma _\omega }{\mu _{{\rm{turb}}}}){\rm{div}}\omega )] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2\left( {1 -{F_1}} \right)\rho {\sigma _{{\omega ^2}}}\frac{1}{\omega }{\rm{div}}k{\rm{div}}\omega . \end{array} $ |
本文采用有限体积法[12]对流体的控制方程进行空间和时间离散.计算域内的压力和速度场的耦合采用SIMPLEC(semi-implicit method for pressure-linked equations consistent)算法; 压力场的空间离散选择Body Force Weighted格式; 忽略空化影响, 选择Geo-Reconstruct对各相体积率进行离散; 考虑到SIMPLEC算法有更好的收敛性, 选择Second Order Upwind格式对动量方程进行离散处理; 湍动能方程和湍流耗散率方程都选用First Order Upwind格式进行离散; 瞬态方程选用First Order Implicit进行离散.
1.2 模型建立弗劳德数(Froude number)
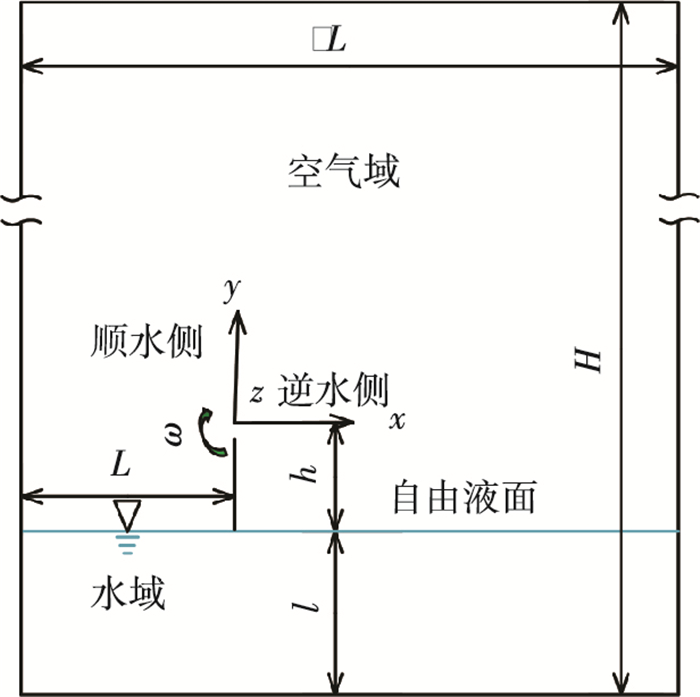
本文中使用均质小球, 图 1是初始计算域几何示意图, 定义小球右侧为顺水侧、左侧为逆水侧.将小球重心作为坐标原点, 各几何参数值见表 1.图 2是计算域网格划分和边界条件的设置, 图 2(a)、(b)分别是xoy平面的网格和yoz平面的网格.计算域网格划分时, 考虑到小球会出现马格努斯效应, 所以对偏转轨迹区域的网格进行加密; 计算得到入水空泡完全闭合后偏转轨迹在x方向的投影长度为5d, 故对计算域进行预先加宽处理避免计算域的宽度对计算的影响, 如图 2(a)中所示.初始旋转小球切向线速度vω和竖直方向的速度v的大小同一数量级, 所以划分网格时应保证微元体的长、宽、高是同一数量级.经过大量探索得到Y+=20时, 计算得到的小球近壁面网格能够很好的捕获流场细节.为提高小球附近的压力场、速度场以及汽水交界面的精度, 对小球附近5d区域进行加密处理, 并形成以该区域为中心向外逐渐过渡的流场网格.本文计算域总共划分为235.5万个微元体.
|
图 1 计算域几何示意 Figure 1 Schematic of the computational domain |
| 表 1 计算域的几何参数 Table 1 Geometry parameters of computational domain |

|
图 2 计算网格和边界示意 Figure 2 Sketch of mesh and boundary conditions |
本文对高速旋转小球入水应用两次动计算域技术, 实现小球在计算域内部高速旋转而随外流域xoy平面内平动.嵌入六自由度UDF和编写相关UDF分别计算小球受力和实现网格更新.小球旋转角速度(335 rad/s)恒定不变, 通过设置不同入水速度v和不同的比重s(s=Gball/Gwater)来研究小球入水空泡特性, 计算变量见表 2.
| 表 2 计算变量 Table 2 Computational variables |
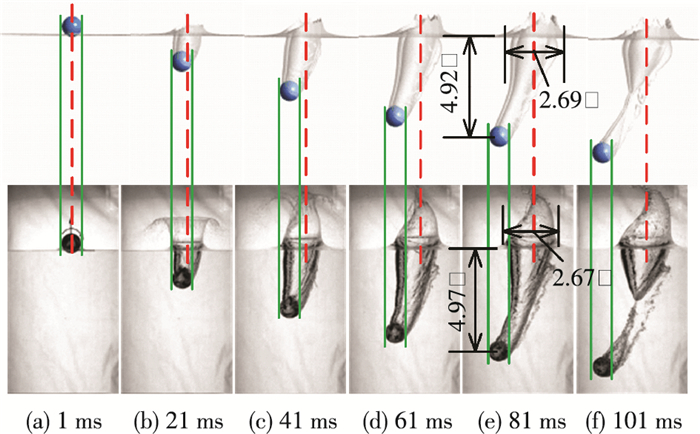
旋转入水问题的理论研究尚不成熟, 没有形成完整的理论体系, 所以本文通过与文献[9]的实验结果对比分析, 验证数值计算方法的正确性.选取文献[9]中某一实验参数, 即小球直径d=57.2 mm、旋转角速度Ω=199 rad/s、入水速度v0=5.45 m/s, 此时弗劳德数Fr0=7.3、旋转数Sp0=1.1.计算时取长、宽、高分别为600 mm×400 mm×800 mm的长方体流域, 其中小球几何位置关系和网格的分布规律如图 1、2所示一致.
图 3是数值计算空泡形态与文献中实验结果的对比.图中第1行是数值计算的空泡形态, 第2行是实验的空泡形态.图 3(a)是小球入水1 ms时的空泡形态对比, 之后每相邻两张图之间的时间间隔为Δt=20 ms, 图中虚线为入水点的空泡中心.图 3(e)中的两组尺寸表明小球入水后81 ms数值模拟结果的空泡形态和试验结果一致.通过对比分析小球从穿过自由液面到空泡深闭合结束的数值模拟结果和试验结果可以较好的吻合.
|
图 3 数值模拟空泡形态与文献中实验对比 Figure 3 Comparison of the cavity shape between simulation and experiment |
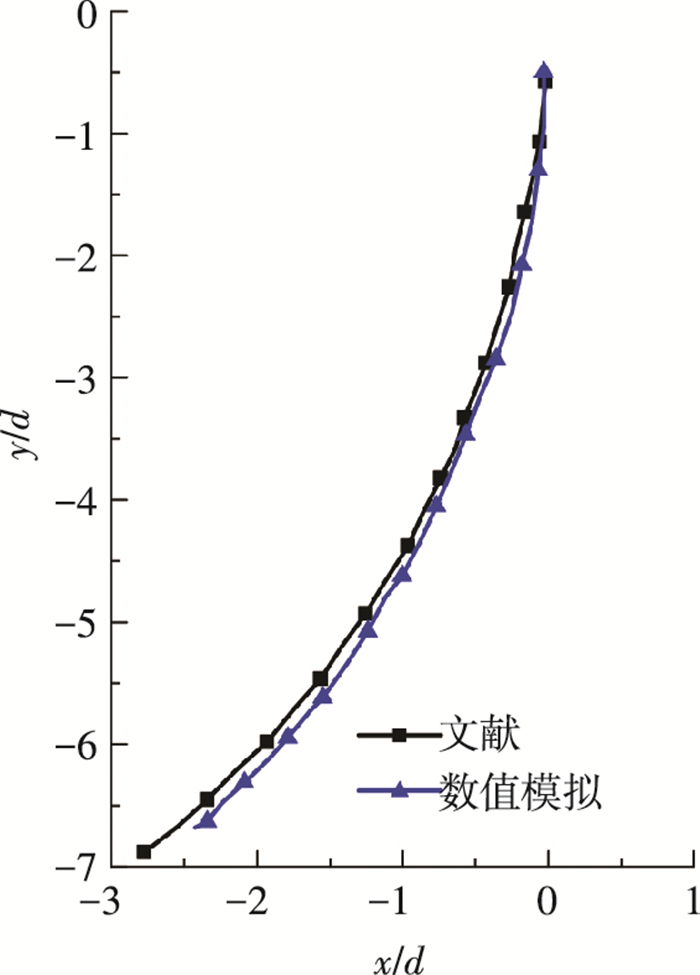
图 4为数值计算与实验过程小球的运动轨迹对比, 以小球触水瞬间的球心坐标为运动起点, 将球心在x方向和y方向的位移归一化, 其中d为小球直径, 从图中可看出数值模拟的轨迹和试验结果高度一致.
|
图 4 数值模拟轨迹与文献中实验对比 Figure 4 Comparison of the trajectory between simulation and experiment |
图 5是数值计算与实验在水平方向的速度u和竖直方向的速度v的对比, 从图中可以看出数值计算得到的水平和竖直方向的速度与实验结果具有较好的一致性.通过以上对空泡形态、轨迹曲线和速度曲线验证了数值计算方法的有效性.

|
图 5 数值模拟速度与文献中实验对比 Figure 5 Comparison of the velocity simulation and experiment |
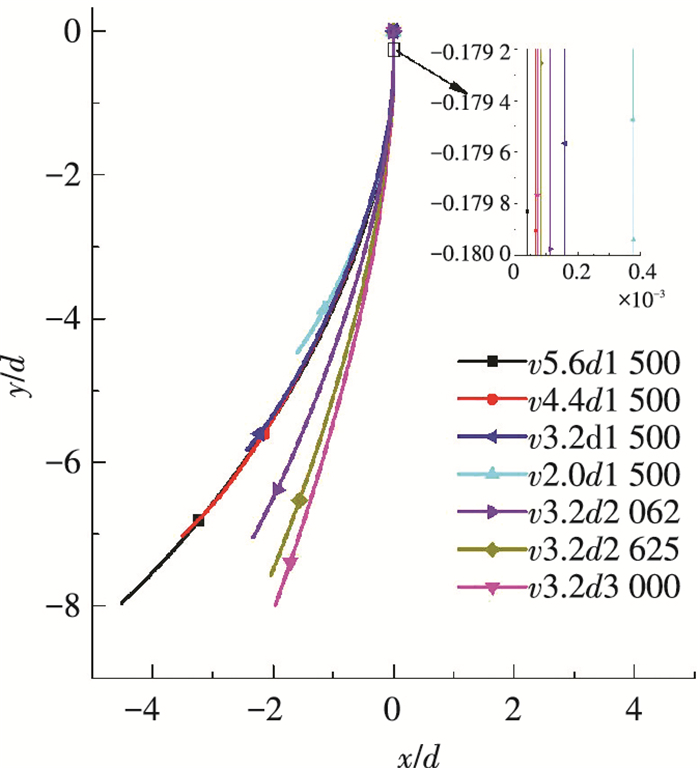
图 6入水轨迹对比是不同的触水速度和不同比重的小球入水轨迹变化的规律(小球旋转速度保持不变).从图中可以看到入水后的旋转小球在马格努斯力的作用下轨迹发生偏转, 相同比重不同触水速度的小球入水前期轨迹基本相同, 受闭合冲击载荷作用均出现相对前期较大幅度的偏转; 相同入水速度比重大的小球轨迹曲率小.从局部放大图中还可以发现入水初期小球有逆升力方向偏移的现象.
|
图 6 入水轨迹对比 Figure 6 Comparison of the trajectory |
入水初期旋转小球的表面绝大部份暴露在空气域中, 可知ρmix的值远小于入水后的值, 因为马格努斯力FM正比于ρmix[16], 所以旋转小球入水初期受到的马格努斯力可以忽略不计.高速旋转小球不断将顺水侧的介质引入逆水侧, 导致在顺水侧形成侧空穴(如图 7所示), 而在逆水侧由于水的填塞形成局部高压.
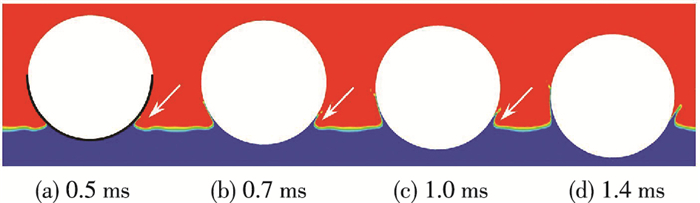
|
图 7 入水初期侧空穴 Figure 7 Side cavity at the initial stage of water entry |
图 8是取xoy平面与小球表面交线的下半部分圆弧线(如图 7(a)中所示)归一化后得到的压力分布, 从图中可以明显看到逆水侧在水的填塞作用下形成的局部高压.所以受到侧空穴和逆水侧局部高压相互作用的旋转小球在入水初期出现了逆升力方向偏移的现象.逆升力偏移距离随小球速度和比重的增加而减小, 因为速度和比重越大的小球, 其运动状态越难改变.
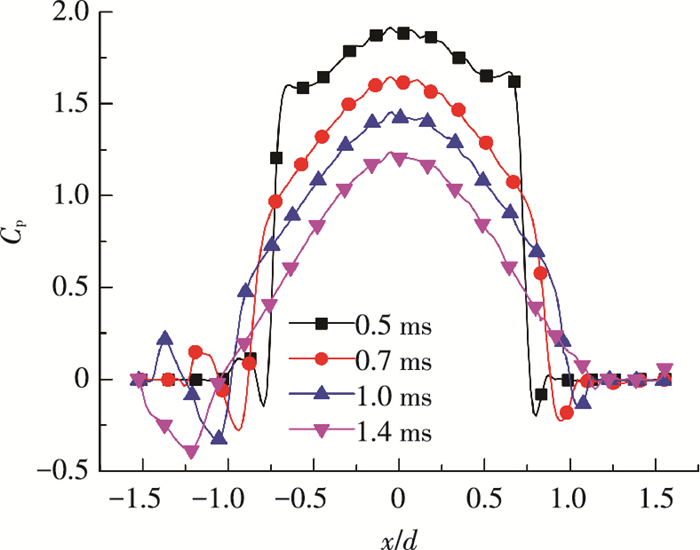
|
图 8 球面压力分布 Figure 8 Pressure distribute on the sphere's face |
图 9是旋转小球入水初期升力系数随时间变化规律, 图 9(a)、(b)分别展示了不同速度和不同比重的旋转小球.图 9(a)中可以看到小球入水后先受到逆升力的作用, 且入水速度大的小球, 入水后最先达到最大逆升力点p, 最大逆升力值小, 持续时间短.这是由于旋转小球触水后0.25d距离范围内受到逆升力方向的力的作用, 超过这一距离后, 侧空穴在顺水侧介质的扶正作用下对小球的影响减小, 且小球有较大的沾湿面积比后马格努斯升力作用增加.因此速度大的小球历经侧空穴影响的时间短, 逆升力产生的冲量小, 故小球逆升力偏移距离小.上述两个因素导致了小球入水初期出现逆升力偏移现象.本文所研究范围内比重的变化对逆偏移现象的影响不明显.
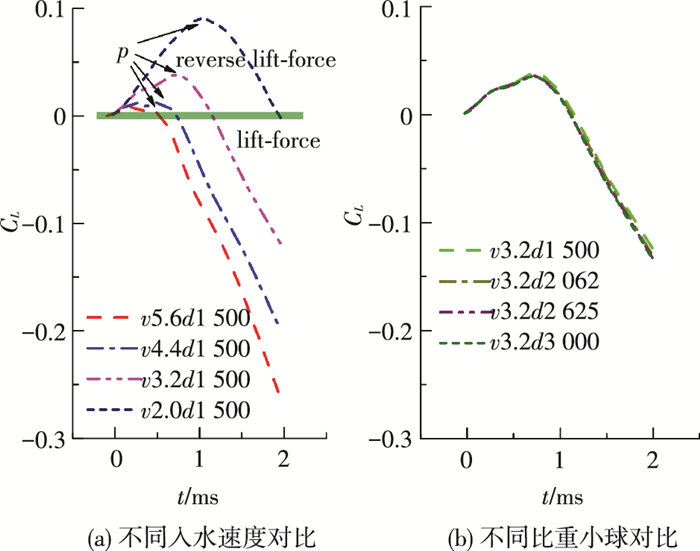
|
图 9 入水初期升力系数对比 Figure 9 Comparison of left coefficient |
图 10对比了不同速度和比重的小球入水后5 ms时的空泡形态.可以发现不同速度的小球入水深度不同且速度越大入水深度越深; 空泡直径不同, 速度大的空泡直径大, 因为背压相同时, 触水后速度大的小球给其周围相邻介质的动量大, 相同区域介质的速度越大, 所以空泡半径较大; 楔形劈尖不同, 速度越大楔形劈尖越完整, 图 10(b)中楔形劈尖没有完全形成, 只是形成了一股垂直射流, 而v2.0d1500中还没有形成楔形劈尖.楔形劈尖的强弱直接关系到下文中凸起的形成和空泡纵向闭合.
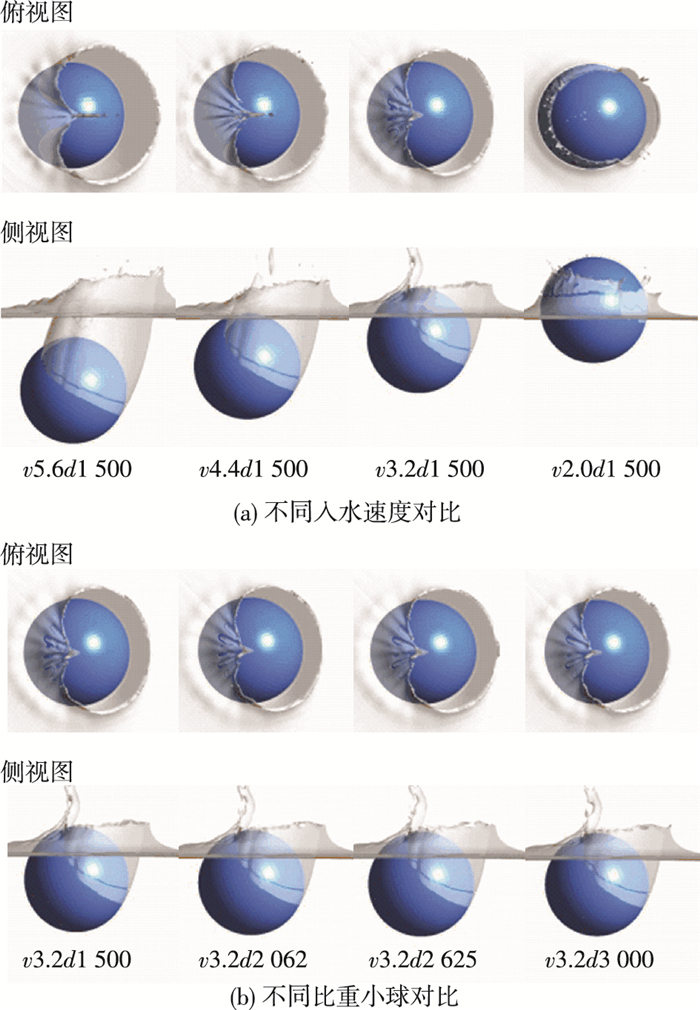
|
图 10 入水5 ms时的空泡形态进行对比 Figure 10 Comparison of cavity shape at 5 ms |
逆水侧流体介质在黏性力的作用下附着在小球壁面上随小球一起转动, 当黏性力和表面张力不足以克服由于小球旋转引起的离心力时, 流体介质从小球壁面脱落.未脱落的流体介质与小球抨击水面后形成相水幕相互撞击, 出现了如图 10(b)中的垂直射流现象.本文研究范围内可以忽略比重对入水冲击阶段的空泡形态、入水深度和楔形劈尖的影响.
图 11是不同触水速度和不同比重的旋转小球入水后空泡闭合时的空泡形态的侧面对比.图中空泡闭合深度Hp以及空泡最大直径dp随入水速度的增加而呈现非线性增大, 同时可以看出在本文研究范围内比重对空泡闭合深度和最大空泡直径的影响可以忽略不计.旋转小球与其附近的介质进行能量交换后, 获得能量的介质将小球附近的介质排开形成空泡, 因为能量交换是非线性的过程[12], 所以最大直径dp呈现出非线性的特性.从图中还可以得到, 最大尾空泡直径dtail随着触水速度和比重的增加而增大.
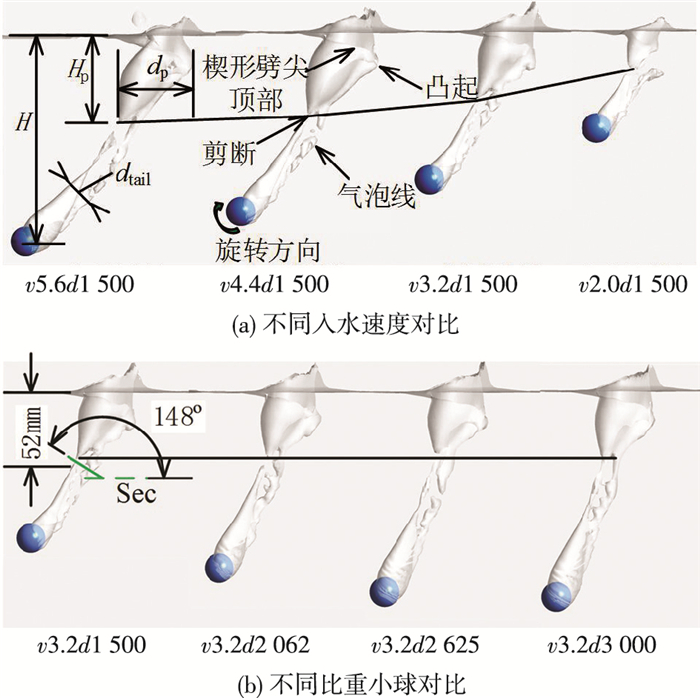
|
图 11 空泡发生横向闭合时的空泡形态对比 Figure 11 Comparison of cavity shape at transverse closure |
图 12是Hp/H(H为自由液面到小球球心处的深度)和dp/Hp随速度的变化规律, 可以发现图中Hp/H和dp/Hp约为定值, 经过拟合后得Hp/H≈0.43、dp/Hp≈0.85.这一结果与Lee等[17]等试验和理论推导Hp/H≈1/3~1/2的结论相符.
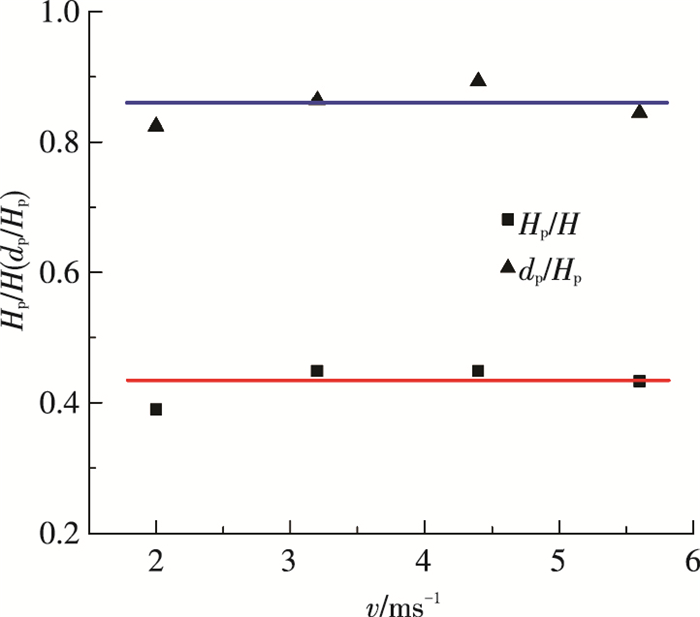
|
图 12 闭合深度和最大空泡直径变化规律 Figure 12 Change law of closure depth and the maximum diameter |
图 13是尾空泡直径归一化(dtail/r)随小球触水速度和比重的变化而变化的规律, 即尾空泡直径随着触水速度和比重增加而成线性增大, 结合表 2中可知, 在保证动量成线性增减的前提条件下两者的线性斜率一致, 经过处理斜率为k≈0.75.结合表 2和图 13尾空泡变化对比, 分别通过改变速度和比重来保证触水时动量相同的前提下, 通过增加比重得到的尾空泡直径比通过增大速度得到的尾空泡要大.因为角速度相同时改变速度的大小只改变动量(P=mv)的大小而不改变角动量(L=mr2ω)的值, 而改变比重的大小不仅改变动量的大小同时也改变角动量的大小.故相同触水动量, 质量大的小球尾空泡直径dtail更大.
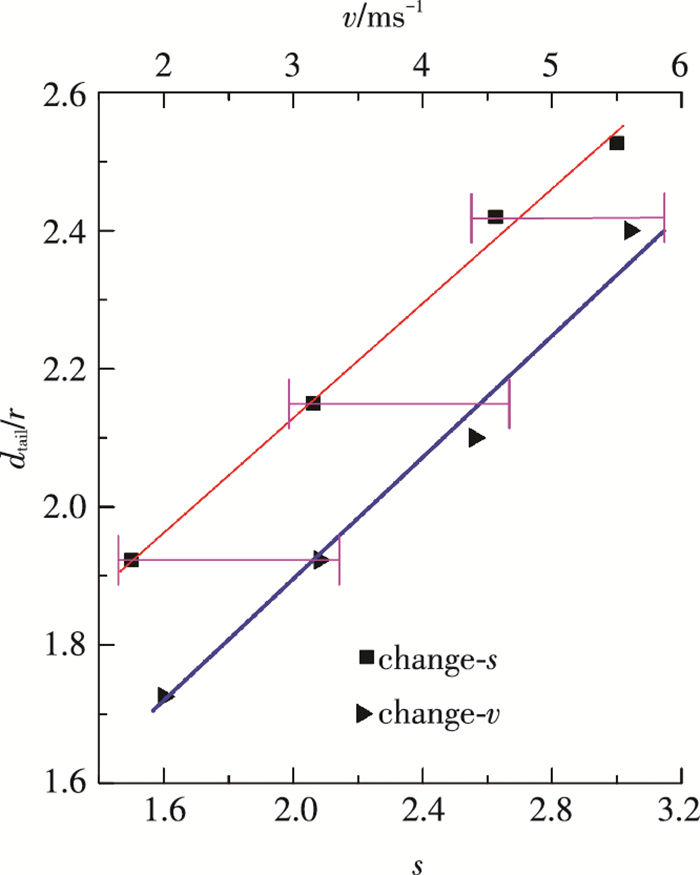
|
图 13 尾空泡变化对比 Figure 13 Comparison of the diameter of the tail cavity |
图 14是高速旋转小球入水后凸起形成的相图.从图中可以看到在离心力的作用下, 附着在球面的流体介质从分离点切线方向飞出抨击空泡壁面形成凸起(如图 11所示).发生横向闭合后, 闭合点附近凸起率先破碎成小气泡, 随后凸起部分相继破碎成小气泡形图 11中的气泡线.
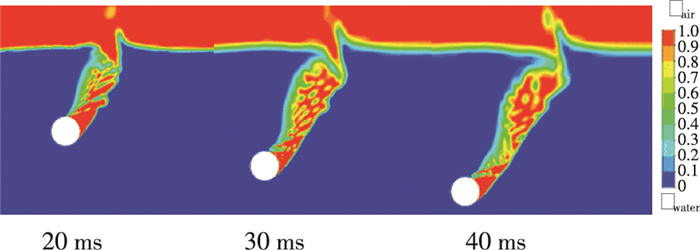
|
图 14 凸起的形成 Figure 14 Formation of the cavity bulge |
图 15是取图 11(b)(v3.2d1 500)中距离自由液面52 mm且与水平方向夹角为148°的截面(该截面为空泡截断点截面)上空泡形态变化.对比发现45、50 ms时凸起已经形成, 随着时间的推移发生纵向剪断即纵向闭合(如55 ms), 形成3个小的空泡带; 在水压的作用下空泡带不断收缩减小, 凸起所形成的空泡带破碎成小气泡形成气泡线, 此时空泡为两条气泡带; 最后两条气泡带不断收缩到空泡完全闭合即横向闭合.
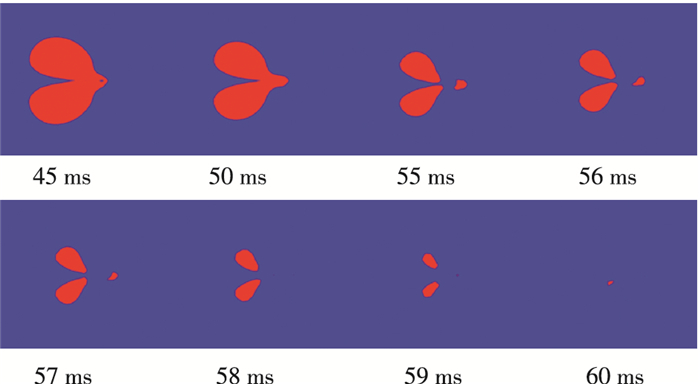
|
图 15 对比不同时刻闭合截面的空泡形态 Figure 15 Comparison of the cavity shape of the closed transverse section for the different time |
1) 建立了小球高速旋转入水数值模拟方法, 数值计算结果与实验结果有较好的一致性, 验证了所采用的数值方法的正确性与可靠性.
2) 在入水深度0.25d范围内, 小球出现逆升力方向偏移的现象, 逆偏移距离随入水速度和比重的增加而减小, 且速度对逆升力方向偏移的影响比比重对其的影响更大.相同比重不同触水速度入水前期轨迹基本相同, 而相同速度条件下比重越大的小球轨迹曲率越小.
3) 小球入水速度越大所楔形劈尖越完整且强度越强.由闭合截面上的空泡形态特性可知, 旋转小球入水先发生纵向闭合, 随后凸起收缩拉断后发生横向闭合(即深闭合), 且纵向闭合与楔形劈尖强弱一致.
4) 空泡发生横向闭合时, 空泡闭合深度Hp以及空泡最大直径dp都随着触水速度的增加而呈现非线性增大, 最大尾空泡直径dtail随着触水速度和比重的增加而增大.相同触水动量, 质量大的小球尾空泡直径dtail大.
| [1] |
RICHARDSON E G. The impact of a solid on a liquid surface[J].
Proceedings of the Physical Society, 1948, 61(4): 352.
DOI: 10.1088/0959-5309/61/4/308 |
| [2] |
MAY A, WOODHULL J C. Drag coefficients of steel spheres entering water vertically[J].
Journal of Applied Physics, 1948, 19(12): 1109-1121.
DOI: 10.1063/1.1715027 |
| [3] |
MAY A, WOODHULL J C. The virtual mass of a sphere entering water vertically[J].
Journal of Applied Physics, 1950, 21(12): 1285-1289.
DOI: 10.1063/1.1699592 |
| [4] |
MAY A. Effect of surface condition of a sphere on its water-entry cavity[J].
Journal of Applied Physics, 1951, 22(10): 1219-1222.
DOI: 10.1063/1.1699831 |
| [5] |
GILBARG D, ANDERSON R A. Influence of atmospheric pressure on the phenomena accompanying the entry of spheres into water[J].
Journal of Applied Physics, 1948, 19(2): 127-139.
DOI: 10.1063/1.1698377 |
| [6] |
马庆鹏, 何春涛, 王聪, 等. 球体垂直入水空泡实验研究[J].
爆炸与冲击, 2014, 34(2): 174-180.
MA Qingpeng, HE Chuntao, WANG Cong, et al. Experimental investigation on vertical water-entry cavity of sphere[J]. Explosion and Shock Waves, 2014, 34(2): 174-180. DOI: 10.11883/1001-1455(2014)02-0174-07 |
| [7] |
ABRAHAM J, GORMAN J, RESEGHETTI F, et al. Modeling and numerical simulation of the forces acting on a sphere during early-water entry[J].
Ocean Engineering, 2014, 76: 1-9.
DOI: 10.1016/j.oceaneng.2013.11.015 |
| [8] |
TRUSCOTT T T, TECHET A H. Cavity formation in the wake of a spinning sphere impacting the free surface[J].
Physics of Fluids, 2006, 18(9): 91113-91113.
DOI: 10.1063/1.2335903 |
| [9] |
TRUSCOTT T T, TECHET A H. Water entry of spinning spheres[J].
Journal of Fluid Mechanics, 2009, 625: 135-165.
DOI: 10.1017/S0022112008005533 |
| [10] |
GRAFF G Y, MOORE F G. Empirical method for predicting the Magnus characteristics of spinning shells[J].
AIAA Journal, 1977, 15(10): 1379-1380.
DOI: 10.2514/3.60803 |
| [11] |
顾建农, 张志宏, 王冲, 等. 旋转弹头水平入水空泡及弹道的实验研究[J].
兵工学报, 2012, 33(5): 540-544.
GU Jiannong, ZHANG Zhihong, WANG Chong, et al. Experimental research for cavity and ballistics of a rotating bullet entraining water levelly[J]. Acta Armamentarii, 2012, 33(5): 540-544. |
| [12] |
VERSTEEG H K, MALALASEKERA W.
An introduction to computational fluid dynamics:the finite volume method[M]. 2rd. [S.l.]: Pearson Education, 2007.
|
| [13] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J].
AIAA Journal, 1994, 32(8): 1598-1605.
DOI: 10.2514/3.12149 |
| [14] |
WATTS R G, FERRER R. The lateral force on a spinning sphere:Aerodynamics of a curveball[J].
American Journal of Physics, 1987, 55(1): 40-44.
DOI: 10.1119/1.14969 |
| [15] |
ALAWAYS L W, HUBBARD M. Experimental determination of baseball spin and lift[J].
Journal of Sports Sciences, 2001, 19(5): 349-358.
DOI: 10.1080/02640410152006126 |
| [16] |
潘慧炬. 马格努斯效应的力学模型[J].
浙江体育科学, 1995, 17(3): 16-19.
PAN Huijun. Mechanical model of magnus effect[J]. Zhejiang Sport Science, 1995, 17(3): 16-19. |
| [17] |
LEE M, LONGORIA R G, WILSON D E. Cavity dynamics in high-speed water entry[J].
Physics of Fluids (1994-present), 1997, 9(3): 540-550.
DOI: 10.1063/1.869472 |
 2018, Vol. 50
2018, Vol. 50


