2. 上海交通大学 船舶海洋与建筑工程学院, 上海 200240
2. School of Naval Architecture, Ocean & Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China
风能作为一种清洁、丰富而又可持续的新能源受到世界各国的广泛关注, 海洋中巨大的风力资源促使研究人员将风电研究的重点转移到离岸深海, 海上风电技术成为一项蓬勃发展的产业并且能够解决由于化石能源的消耗和日益枯竭而带来的环境恶化和能源短缺问题, 从而达到促进全球经济健康发展的目的.在深水区, 油气开发产业已经成功使用spar型平台, 并且spar型平台显示出良好的水动力性能.基于此, spar平台作为一个可靠的概念应用于海上浮式风力机.
挪威国家石油公司(Statoil)[1]提出“Hywind”即2.3 MW spar浮式风力机概念并于2009年6月将实型机安装在海况恶劣的挪威西海岸, “Hywind Demo”安装有西门子风电的变速风机并且是世界上第1个兆瓦级浮式风力机.美国国家可再生能源实验室(NREL)[2]提出了5 MW spar浮式风力机概念, 这是一个典型的公用工程规模、多兆瓦的风力机, 同时也被作为欧洲上风向风力机综合研究计划的参考模型.Jonkman[3]将其开发的水动力计算模块与气-伺服-弹性数值模拟软件FAST模块结合起来, 实现对海上浮式风力机(FOWT)运动响应的时域耦合计算.Jonkman等[4]比较研究了3种浮式风力机即ITI驳船型、TLP型和OC3-Hywinds风力机在模型开发的异同点并分别进行了载荷分析.Karimirad等[5]对NREL 5 MW spar型概念风力机在极端海况条件下、停机状态时的动态响应进行了计算分析, 验证该风力机在恶劣海况下的生存能力.Coulling等[6]对DeepCwind半潜式风力机在动态风和二阶差频波浪绕射力作用下的总体响应进行了研究, 结果表明二阶差频波浪绕射力增加了导缆孔张力响应的低频相关性.Roald等[7]评估了二阶波浪力对OC3-HYWind spar型风力机和缅因大学的张力腿型风力机概念的重要性.Karimirad[8]对5 MW spar型风力机在只有波浪条件和风浪共同作用条件下进行了耦合计算分析, 结果表明二阶波浪力对平台纵荡运动和锚链张力响应的影响不大, 但是对垂荡运动有明显影响.Bayati等[9]探讨了二阶波浪力对半潜浮式风力机的影响, 结果表明二阶差频波浪力与较低的平台固有频率共同作用下, 会激发平台较大的运动响应, 尤其在恶劣海况不能忽视二阶差频载荷的影响.Borg等[10]研究了垂直轴半潜式风力机的长期总体响应, 得出平台的总体运动响应和系泊线张力不一定只有以最高风速特征为50年一遇的海洋气象条件所决定的结论.
当前关于spar浮式风力机的研究较多, 但关于其在恶劣海况下的生存情况以及二阶波浪力对平台运动响应及锚链张力的影响的研究较少.本文针对设计出的6 MW spar型海上浮式风力机, 利用Sesam软件获得考虑二阶波浪力计算时所需的二次传递函数QTF, 利用气-液-固-弹性数值模拟软件FAST对风力机整体进行时域耦合数值计算, 考察spar浮式风力机的总体运动响应、锚链张力及机舱加速度等.
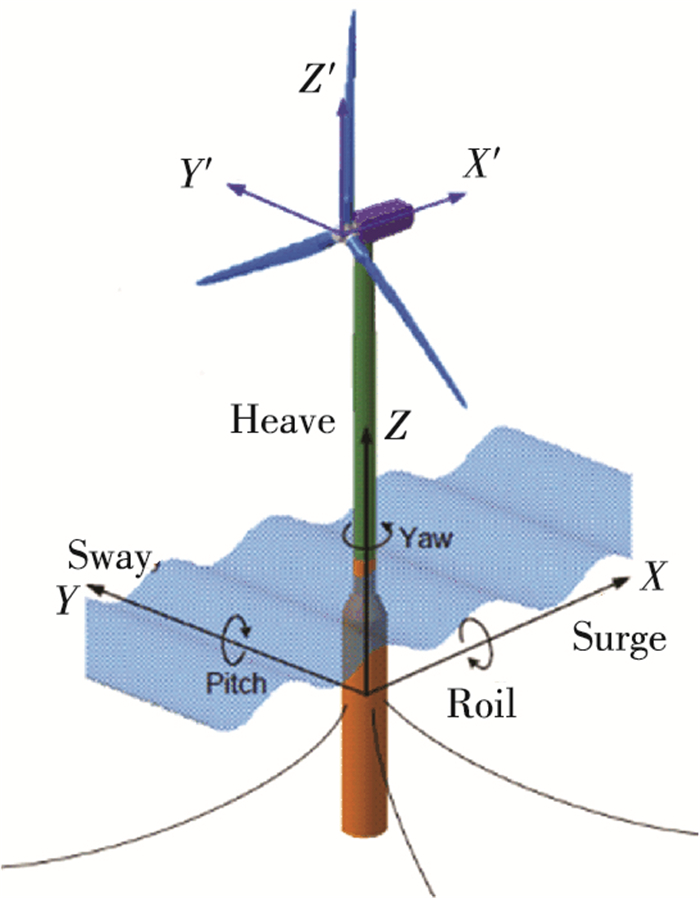
1 6 MW spar型风力机参数当前国内外spar浮式风力机实型机的发展仍未成熟, 仅Statoil公司计划在2017年建成拥有5个spar风力机的风场并投入商业使用.本文设计出针对100 m水深条件的新型6 MW spar型浮式风力机, 其示意图和坐标系如图 1、2所示, 并对该风力机在50年一遇海况条件下进行数值模拟计算, 验证其在恶劣海况下的生存能力.

|
图 1 6 MW浮式风力机示意 Figure 1 Specifications of the 6 MW floating wind turbine |
|
图 2 坐标系和平台自由度 Figure 2 The coordinate system and platform DOF |
风机采用传统的水平轴风力发电机组, 其特点是上风向三叶片、中速永磁型, 并且采用具有NACA及DU系列改型的翼型的叶片.塔架材料采用Q345钢, 塔身高度为83.706 m.具体参数见表 1.
| 表 1 6 MW风机和塔架的总体参数 Table 1 Overall parameters of the 6 MW wind turbine |
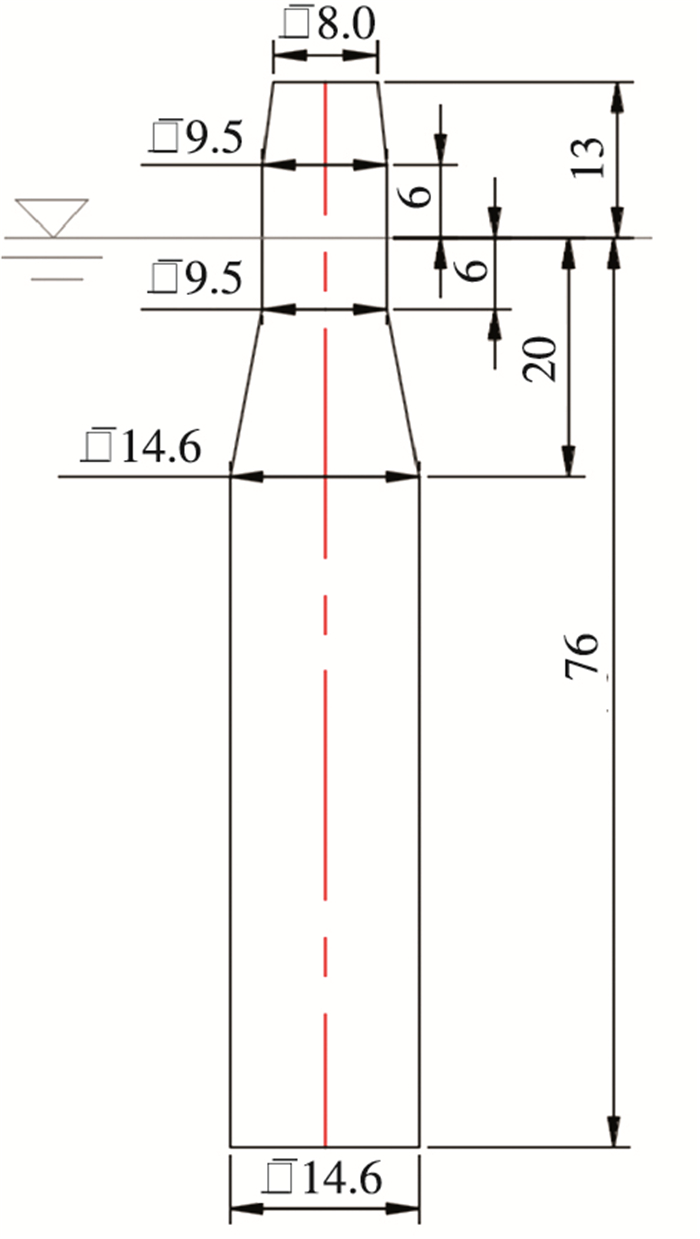
Spar型平台有着小水线面和大排水量的特点, 能够提供浮式风力机所需的浮力和静水回复力.本文设计Spar型平台包括两段圆柱、连接塔架底端和1段圆柱的线性过渡段和连接两段圆柱的线性过渡段.表 2给出平台的总体参数, 图 3给出Spar平台二维关键尺寸示意图.
| 表 2 浮式平台几何参数 Table 2 Floating platform gross and geometry parameters |
|
图 3 Spar平台二维图 Figure 3 Spar platform 2D figure |
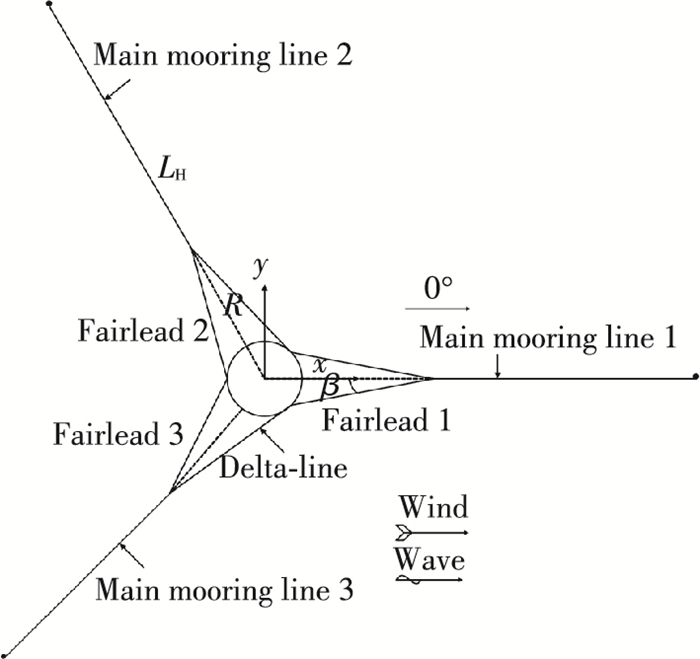
静水回复力、力矩能够控制平台的垂荡、横摇和纵摇运动, 且由于外力作用下发生的偏移在外力消失后平台能够回到原有的平衡位置; 对于纵荡、横荡和首摇需由锚链提供回复力、回复力矩.通过设计能够提供首摇回复力的delta-line[11]来控制平台的首摇运动, 系泊系统包括3根互相成120°的悬链线, 如图 4所示.锚链的直径和单位长度质量以及破断力根据API[12]的规范确定.系泊系统的具体参数见表 3.
|
图 4 系泊系统分布 Figure 4 Mooring system layout |
| 表 3 系泊系统参数 Table 3 Mooring system properties |
在利用气-液-固-弹性数值模拟软件FAST进行运动响应分析时, 需要对各个模块进行计算参数设置, 包括气动力模块、水动力模块、弹性模块和系泊系统模块等.锚链力计算采用考虑惯性力和阻力的FEAM(有限元)模型, 将锚链视为弹性杆模型[13].式(1)给出耦合风机、塔架、平台和锚链运动的完整的非线性时域运动方程为
| $ {M_{ij}}{{\ddot x}_i}\left( t \right) = {F_i}^{{\rm{Aero}}}\left( t \right) + {F_i}^{{\rm{Hyd}}}\left( t \right) + {F_i}^{{\rm{Moor}}}\left( t \right). $ | (1) |
式中:Mij为耦合系统的结构惯性质量矩阵的(i, j)部分, i, j=1, 2, 3, …, 6;FiAero为气动力载荷; FiHyd为水动力载荷; FiMoor为系泊张力;
Maruo[14]提出利用流域中的动量和能量守恒定理, 通过远场辐射面上的积分, 求解二阶平均波浪力.对单一频率规则波, 平均波浪力由式(2)给出并由此得到平均波浪力的二次传递函数即式(3).对于不规则波, 二阶平均波浪力即可由式(4)给出, 式(5)为代入式(3)得到的二阶平均波浪力:
| $ \overline {{F_t}^{(2)}} = {\zeta _{aj}}^2{T_{{F_i}}}\left( {{\omega _j}} \right), $ | (2) |
| $ {T_{{F_i}}}\left( {{\omega _j}} \right) = \frac{{\overline {{F_t}^{(2)}} }}{{{\zeta _{aj}}^2}}, $ | (3) |
| $ \begin{array}{l} \overline {{F_t}^{{\rm{irr}}}} = \sum\limits_{{\rm{ }}j = 1}^N {{\zeta _{aj}}^2} {T_{{F_i}}}\left( {{\omega _j}} \right) = \sum\limits_{{\rm{ }}j = 1}^N {2S\left( {{\omega _j}} \right)} \Delta \omega {T_{{F_i}}}\left( {{\omega _j}} \right) = \\ \;\;\;\;\;\;\;\;\;\;2\int_0^\infty {{T_{{F_i}}}} \left( {{\omega _j}} \right)S(\omega ){\rm{d}}\omega , \end{array} $ | (4) |
| $ \overline {{F_t}^{{\rm{irr}}}} = 2\int_0^\infty {\frac{{\overline {{F_t}^{(2)}} }}{{{\zeta _{aj}}^2}}} S\left( \omega \right){\rm{d}}\omega . $ | (5) |
式中:ζaj为第j个入射波波幅, S(ω)为波浪谱密度函数.
2.3 二阶低频慢漂波浪力系泊浮式结构物在波浪上的典型运动不仅包括一阶波频运动, 还包括长周期二阶慢漂运动.这是由于系泊系统水平恢复力小导致平台固有周期长, 在二阶低频波浪力[15]作用下, 产生低频共振运动, 诱发较大的系泊力和低频慢漂运动.根据二次传递函数、不规则波波谱计算二阶波浪慢漂力谱的公式:
| $ {S_{{F_t}^{(2)}}}\left( \mu \right) = 2\int_0^\infty {{S_\mathit{\zeta }}} \left( \omega \right){S_\mathit{\zeta }}\left( {\omega + \mu } \right)\left| {{T_{jk}}\left( {\omega ,\omega + \mu } \right)} \right|{^2}{\rm{d}}\omega , $ | (6) |
式中, |Tjk(ω, ω+μ)|2为差频二阶力的二次传递函数.本文二阶波浪力的计算采用压力积分法求得.
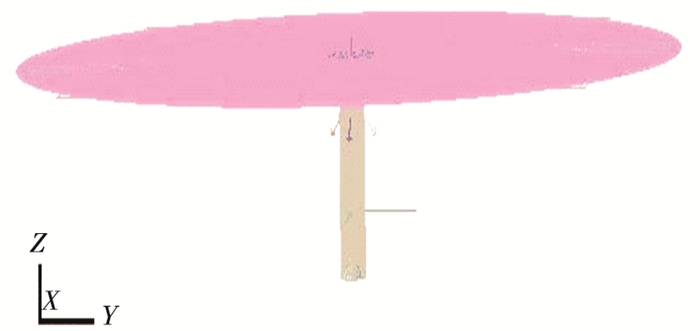
2.4 二阶波浪力模型建立和计算本文关于二阶差频波浪力的计算, 选择的波浪频率范围是0.05~3.00 rad/s, 步长0.05 rad/s共60组频率, 这意味着需要每组浪向需计算3 600个二次传递函数, 耗时远超一阶水动力的计算.模型如图 5、6所示.

|
图 5 Spar平台和自由面模型 Figure 5 Spar platform and free surface model |
|
图 6 二阶波浪力计算的水动力模型 Figure 6 HydroD model for 2nd wave force |
本文主要研究spar风力机在恶劣海况下的生存情况.定义4种类型工况(LC):LC1为衰减实验工况; LC2只有波浪载荷, 波浪周期从4.00~125.66 s变化, 求得浮式风力机在各浪向下的幅值响应算子(RAOs); LC3取北海50年一遇海况[16], 波浪谱采用JONSWAP谱, 风采用稳定风; LC4为只有极限波浪的工况, 各工况见表 4.
| 表 4 工况条件 Table 4 Summary of load cases |
利用自由衰减法确定平台固有周期, 计算时风机处于停机状态且桨距角设置为90°.表 5给出该风力机各自由度的固有周期.
| 表 5 6 MW spar浮式风力机的固有周期 Table 5 Natural periods of the 6 MW spar-type FOWT |
响应幅值算子(RAOs)可以表征浮式风力机系统的水动力性能.在本文中, 通过一系列规则波模拟得到风力机总体运动响应RAOs.图 7~10给出不同浪向下各自由度RAOs的仿真结果.
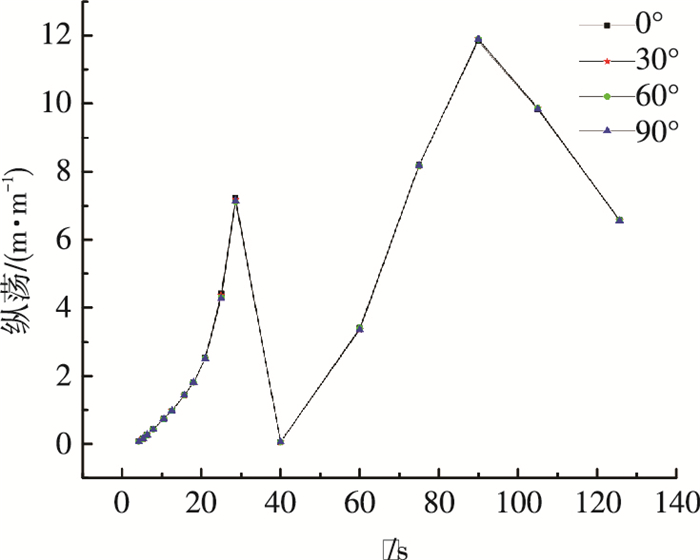
|
图 7 纵荡RAO Figure 7 RAO for surge motion |
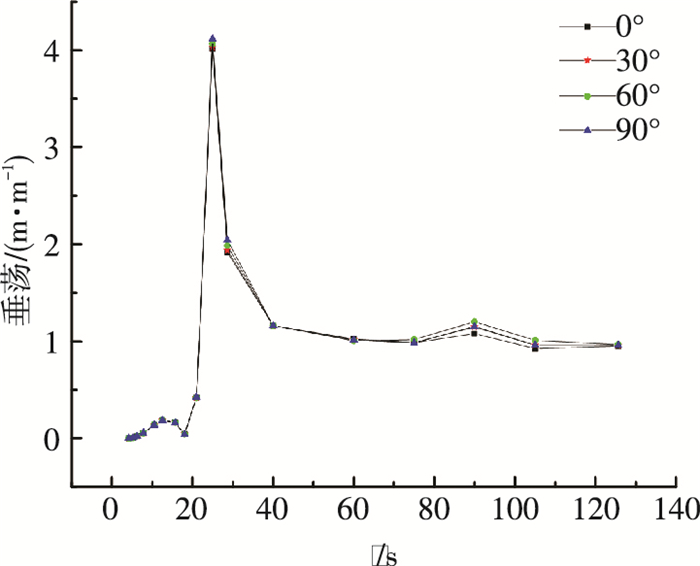
|
图 8 垂荡RAO Figure 8 RAO for heave motion |
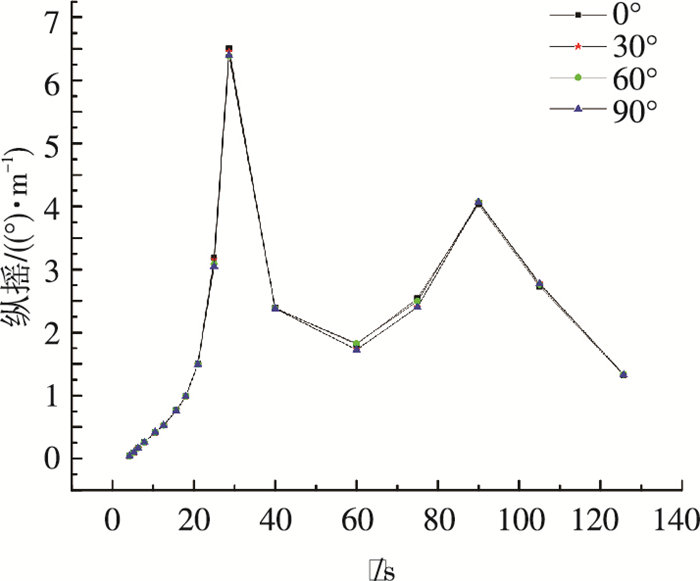
|
图 9 纵摇RAO Figure 9 RAO for pitch motion |
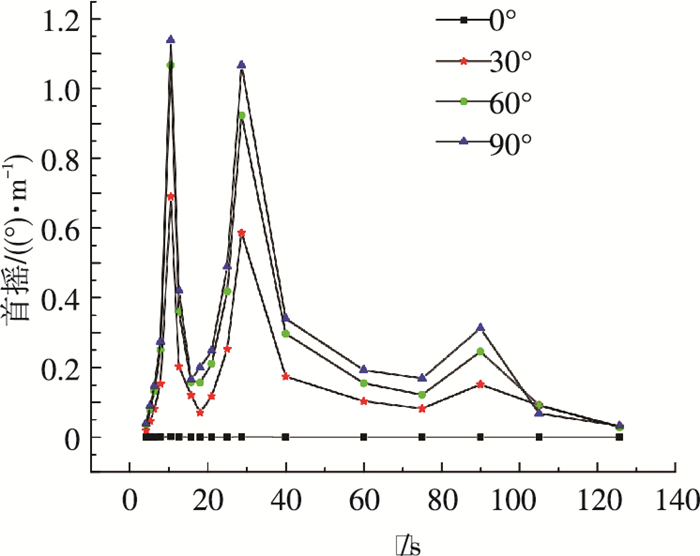
|
图 10 首摇RAO Figure 10 RAO for yaw motion |
值得注意的是, 这里给出的不同浪向下各自由度的RAOs的坐标系均只与各自浪向角有关, 对应的各自由度运动都是相当于各坐标系的运动.即0°浪向情况下, x轴正方向对应着0°方向, z轴竖直向上按右手定则建立坐标系, 纵荡(其他自由度类似)对应着x轴所在直线; 30°浪向时, x轴正方向对应着30°方向, z轴竖直向上按右手定则建立坐标系, 纵荡(其他自由度类似)对应着x轴所在直线(下同).
图 7~10表明对于同一自由度, 各自由度的固有周期处均对应着各自RAOs的最大值.对于纵荡、纵摇运动, 各浪向均存在对应于纵摇固有周期和纵荡固有周期的两个峰值, 说明纵摇和纵荡运动的耦合效应较为明显; 对于垂荡运动, 可以发现在垂荡固有周期处有着显著的峰值; 同时不同的波浪入射角对各自由度RAOs(除了首摇)的影响不大, 表明三对称的系泊系统稳定性较好; 对于首摇运动, 各浪向均存在分别对应于首摇、纵荡和纵摇固有周期的3个峰值, 同时随着波浪入射角的增大, 在同一波浪周期处其RAOs呈现上升趋势.
3.3 不同浪向一阶波浪力下平台运动响应通过对50年一遇海况即LC3和LC4条件下处于停机状态的风力机运动响应比较发现, 两种工况的运动响应相差较小.表 6给出0°浪向角下, 两种工况的运动响应极值对比.
| 表 6 不同海况下各自由度运动响应极值 Table 6 Extreme motion response values of each DOF under different sea conditions |
事实上由于停机状态下叶片的桨距角均设置为与风向夹角90°, 此时的风力与波浪力相比非常小, 且只考虑波浪会大大提高计算速度, 因此涉及极限海况的计算可仅考虑极限波浪.
极限海况下风力机的生存状态, 最重要的就是各自由度尤其是纵摇(横摇)角的最大值不能过大, 以避免发生风力机倾覆的危险.本文中, 利用随机数生成5对不同的波种子, 对于一阶运动, 每种浪向分别计算5组极限波浪工况, 每组计算3 h, 各运动响应极值的确定取该5个工况极值的平均值.表 7给出各浪向下风力机各自由度运动响应极值, 这里的坐标系同不同浪向下平台RAOs.根据表 7可以看出, 浪向角的变化对各自由度(首摇除外)运动响应影响较小, 因此在分析二阶波浪力对平台运动的影响时, 考虑一个波浪入射角即可; 首摇运动极值随着波浪入射角的增大而增大, 但其最大值仍在7°以内.
| 表 7 不同浪向角下各自由度运动响应极值 Table 7 Extreme motion response values of each DOF in different wave direction |
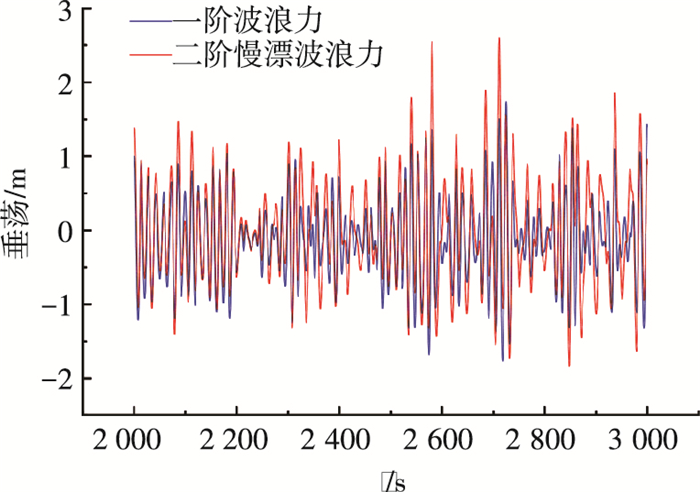
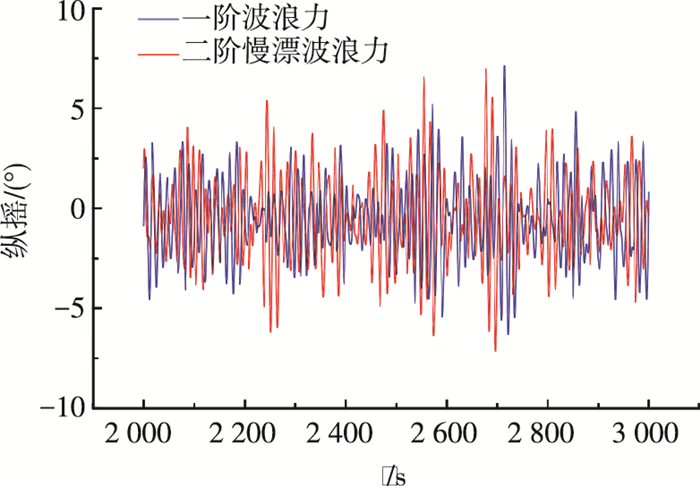
考虑二阶波浪力的运动响应计算, 这里给出90°浪向下的运动极值结果, 此时需比较平均波浪力和慢漂波浪力对平台运动的影响, 故各自计算5组即共10组工况.表 8给出风力机各自由度运动响应极值.图 11、12给出平台垂荡运动、纵摇运动2 000~3 000 s的时域响应对比, 图 13、14给出经傅里叶变换后, 平台垂荡运动、纵摇运动的频域响应对比.
| 表 8 二阶波浪力作用下各自由度运动响应极值 Table 8 Extreme motion response of each DOF under second order wave force |
|
图 11 垂荡时域响应 Figure 11 Time domain response of heave |
|
图 12 纵摇时域响应 Figure 12 Time domain response of pitch |
|
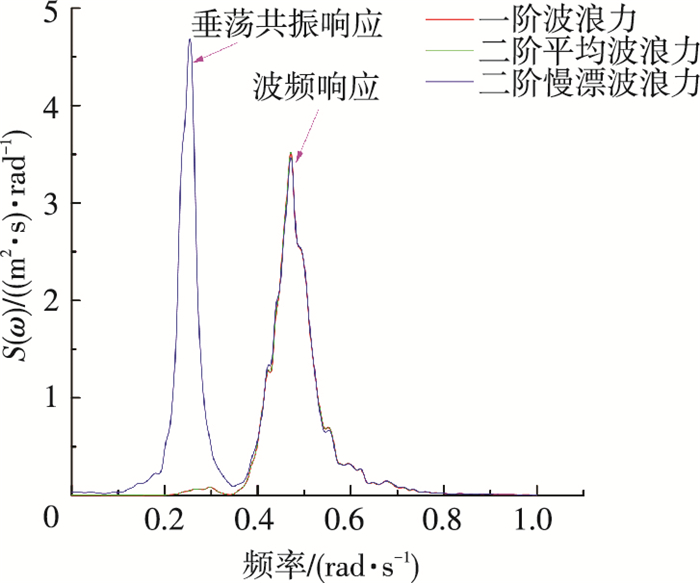
图 13 垂荡频域响应 Figure 13 Frequency response of heave |
|
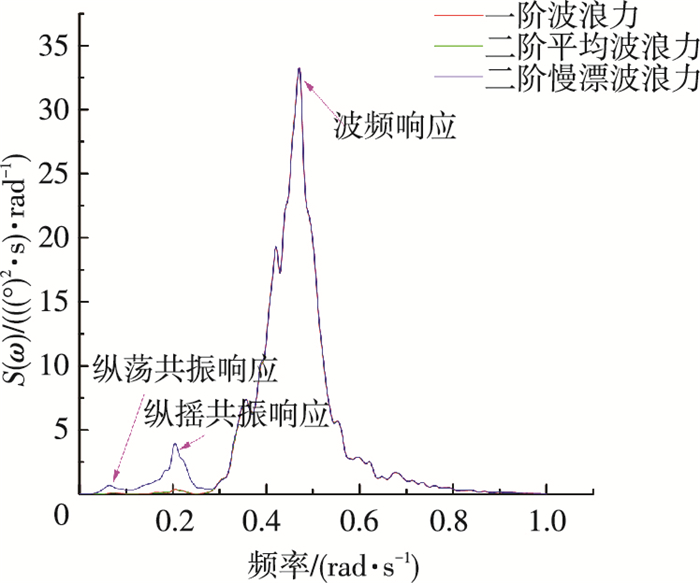
图 14 纵摇频域响应 Figure 14 Frequency response of pitch |
由表 8可明显看出二阶平均波浪力对平台各自由度运动响应影响均较小; 而纵荡、横荡、首摇运动在二阶慢漂波浪力作用下, 有一定增大但不明显; 而对于垂荡运动, 二阶慢漂波浪力影响显著, 运动极值增幅达63%;同样的, 二阶慢漂波浪力对纵摇的影响也比较明显, 极值增幅达19%左右.
图 13可以看出考虑二阶慢漂波浪力后, 垂荡运动较只考虑一阶波浪力明显增大, 说明二阶慢漂力会激发较大的垂荡运动响应; 图 14可以看出二阶慢漂波浪力在垂荡自然频率处的功率谱幅值远远大于一阶运动, 表明能量在低频处尤其是垂荡自然频率处较为集中, 二阶慢漂波浪力激发了垂荡自由度的低频共振效应, 这与时域计算结果一致; 对于纵摇运动, 考虑二阶慢漂波浪力下的时域运动响应也较一阶波浪力为大, 同时在纵摇自然频率处, 二阶慢漂波浪力下的纵摇功率谱幅值同样大于一阶运动, 但不如垂荡运动明显; 对于各自由度, 均可看出波浪能量在谱峰频率处均较为集中且受二阶慢漂波浪力影响较小, 再次表明慢漂波浪力主要激发低频共振效应, 对波频运动影响较小.
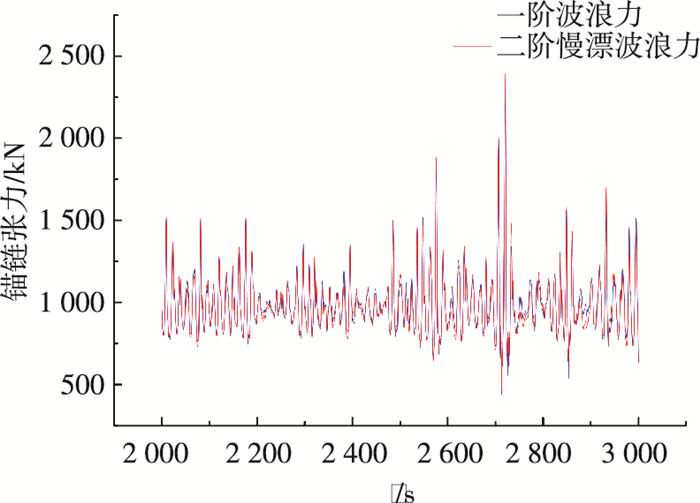
3.5 不同浪向下锚链张力响应考虑到锚链张力最大的情况, 本文只给出0°浪向系缆1导缆孔处的张力响应.张力极值的确定依然如不同浪向一阶波浪力下平台运动响应所述, 表 9给出系缆1导缆孔处的张力极值.图 15给出系缆1张力的2 000~3 000 s的时域响应对比, 图 16给出系缆1张力的频域响应对比.
| 表 9 系缆1导缆孔处张力极值 Table 9 Extreme fairlead tension force of mooring line1 |
|
图 15 张力时域响应 Figure 15 Frequency response of heave |
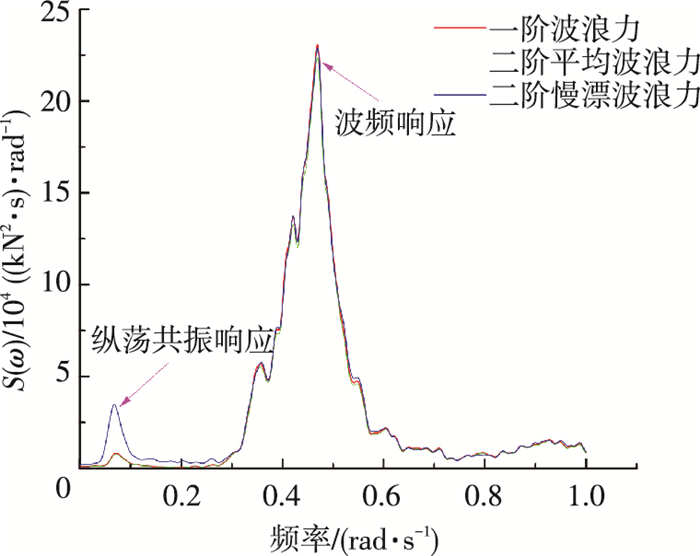
|
图 16 张力频域响应 Figure 16 Frequency response of tension force |
根据表 9可以看出, 二阶慢漂波浪力对锚链张力的影响比较明显, 极值增大了200 kN; 图 15可以看出考虑二阶慢漂波浪力下的张力时域响应也较一阶波浪力为大; 图 16表明二阶慢漂波浪力在纵荡固有周期即低频处激发了共振运动, 诱发更大的锚链张力, 在波频处二阶慢漂波浪力影响甚微.
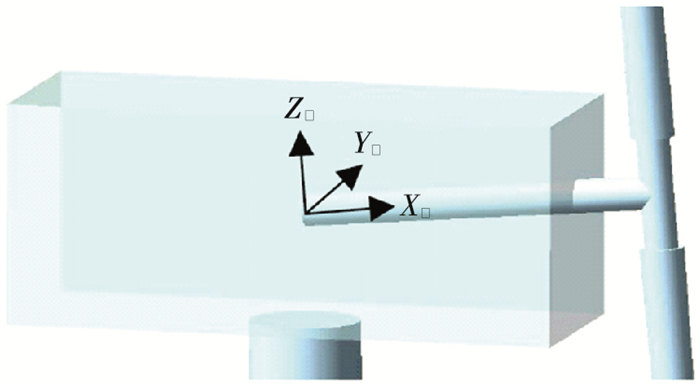
3.6 不同浪向下机舱加速度响应机舱加速度极值的确定依然如不同浪向一阶波浪力下平台运动响应所述, 表 10给出不同浪向下机舱3个方向加速度的极值.其中“NcAxs”为机舱沿Xs轴方向的单位平移加速度, “NcAys”、“NcAzs”类似, “Overall-Max”为机舱最大总加速度, 机舱坐标系如图 17所示.
| 表 10 极限波浪下各浪向机舱加速度 Table 10 Nacelle acceleration of each wave direction in extreme wave conditions |
|
图 17 机舱坐标系 Figure 17 Shaft coordinate system |
1) 采用3根互相成120°的锚链构成的系泊系统稳定性较好, 波浪入射角越大, spar型浮式风力机首摇运动越大, 而入射角对其他自由度运动响应影响较小, 实际分析可只考虑一个波浪入射角.
2) 二阶慢漂波浪力对垂荡运动的影响非常显著, 对纵荡和首摇的影响较小; 二阶慢漂波浪力会激发较大的纵摇运动响应, 在spar浮式风力机的设计中应注意慢漂波浪力的影响.本文中设计出的spar平台, 最大纵摇角不超过10°, 符合设计标准; 机舱设计的加速度应能承受一个重力加速度的载荷.
3) 设计出的6 MW spar浮式风力机在极限海况下具有良好的运动响应, delta-line能够避免首摇角过大, 从而不会发生锚链互相缠绕的现象, 且即使考虑二阶慢漂波浪力后, 系泊系统的最大张力远在破断力之下, 完全能够保证浮式风力机在恶劣海况下依然能够生存.
| [1] |
SKAARE B, NIELSEN F G, HANSON T D, et al. Analysis of measurements and simulations from the Hywind Demo floating wind turbine[J].
Wind Energy, 2015, 18(6): 1105-1122.
DOI: 10.1002/we.1750 |
| [2] |
JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development: NREL/TP-500-38060[R]. Golden, Colorado: National Renewable Energy Laboratory (NREL), Golden, CO., 2009. DOI: 10.2172/947422.
|
| [3] |
JONKMAN J M. Dynamics modeling and loads analysis of an offshore floating wind turbine: NREL/TP-500-41958[R]. Golden, Colorado: National Renewable Energy Laboratory (NREL), Golden, CO., 2009. DOI: 10.2172/921803.
|
| [4] |
JONKMAN J, MUSIAL W. Offshore code comparison collaboration (OC3) for IEA wind task 23 offshore wind technology and deployment: NREL/TP-5000-48191[R]. Golden, Colorado: National Renewable Energy Laboratory (NREL), Golden, CO., 2009. DOI: 10.2172/1004009.
|
| [5] |
KARIMIRAD M, MOAN T. Extreme dynamic structural response analysis of catenary moored spar wind turbine in harsh environmental conditions[J].
Journal of Offshore Mechanics & Arctic Engineering, 2011, 133(4): 41103.
DOI: 10.1115/1.4003393 |
| [6] |
COULING A J, GOUPEE A J, ROBERTSON A N, et al. Importance of second-order difference-frequency wave-diffraction forces in the validation of a fast semi-submersible floating wind turbine model: preprint[C]//Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering (OMAE2013), Nantes, France: NREL, 2013, DOI: 10.1115/OMAE2013-10308.
|
| [7] |
ROALD L, JONKMAN J, ROBERTSON A, et al. The effect of second-order hydrodynamics on floating offshore wind turbines☆[J].
Energy Procedia, 2013, 35(1): 253-264.
DOI: 10.1016/j.egypro.2013.07.178 |
| [8] |
KARIMIRAD M. Modeling aspects of a floating wind turbine for coupled wave-wind-induced dynamic analyses[J].
Renewable Energy, 2013, 53: 299-305.
DOI: 10.1016/j.renene.2012.12.006 |
| [9] |
BAYATI I, JONKMAN J, ROBERTSON A, et al. The effects of second-order hydrodynamics on a semisubmersible floating offshore wind turbine[J].
Journal of Physics Conference Series, 2014, 524(1): 12094-12103.
DOI: 10.1088/1742-6596/524/1/012094 |
| [10] |
BORG M, MANUEL L, COLLU M, et al. Long-term global performance analysis of a vertical-axis wind turbine supported on a semi-submersible floating platform[C]//Proceedings of the 34th International Conference on Ocean, Offshore and Arctic Engineering. St. John's, Newfoundland, Canada: ASME, DOI: 2015.10.1115/OMAE2015-41734.
|
| [11] |
HORDVIK T. Design analysis and optimisation of mooring system for floating wind turbines[D]. Trondheim, Norway: Norwegian University of Science and Technology. 2011.
|
| [12] |
API. API 2F Specification for mooring chain: API 2F-1997[S]. Washington: American Petroleum Institute, 1997.
|
| [13] |
BAE Y H. Development of a dynamic mooring module feam for fast v8[D]. College Station, TX: Texas A & M University (TAMU), 2014.
|
| [14] |
MAURO H. The drift of a body floating on waves[J].
Journal of Ship Research, 1960, 4: 1-5.
|
| [15] |
PINKSTER J A. Low frequency second order wave exciting forces on floating structures[D]. Delft, Nederland: Delft University of Technology, 1980.
|
| [16] |
KARIMIRAD M, MOAN T. Wave and wind-induced dynamic response of a spar-type offshore wind turbine[J].
Journal of Waterway Port Coastal & Ocean Engineering, 2012, 138(1): 9-20.
DOI: 10.1061/(ASCE)WW.1943-5460.0000087 |
 2018, Vol. 50
2018, Vol. 50


