2. 西安电子科技大学 机电工程学院,西安 710071
2. School of Mechatronic Engineering, Xidian University, Xi'an 710071, China
航空工业中,大多数机械和工程结构都是在复杂的多轴应力状态下工作,如航空发动机中的叶片常发生高周疲劳失效,而轮盘、轴等结构多发生低周疲劳(LCF)失效,因此,多轴疲劳破坏在工程结构中十分常见.相对于单轴低周疲劳而言,无论在微观机制、试验研究、还是在力学分析方面,多轴低周疲劳都更为复杂[1-3],目前对于多轴低周疲劳的研究远没有像单轴低周疲劳那样全面、深入.因此,从理论上全面系统深入地研究多轴低周疲劳寿命预测方法,解决复杂载荷下材料的多轴低周疲劳问题,对于更为准确地预测机械结构的多轴低周疲劳寿命具有重要的理论意义和工程实用价值.
概括来讲,目前常用的多轴LCF寿命预测方法主要有等效应变法、能量法和临界平面法.上述3类方法中,等效应变法最为简单,应用也较为广泛,如美国机械工程师协会(ASME)制定的锅炉与压力容器规范[4]就是基于von-Mises准则.但是,等效应变法没有合理区分比例加载和非比例加载的不同,非比例加载下,由于应力应变主轴旋转,一般会给出偏于危险的预测结果.
为弥补非比例加载下等效应变法预测结果偏于危险的缺陷,一些研究者引入附加强化系数和非比例度因子来修正不同的等效应变范围.Itoh等[5-7]利用14种加载路径,系统地研究了加载路径对304不锈钢低周疲劳寿命的影响.引入附加强化系数和非比例度因子,对最大主应变范围进行了修正,修正后的模型可以较好地预测非比例加载下304不锈钢的疲劳寿命[6-7].Li等[8]、陈家权等[9]、钟波等[10]、王雷等[11]分别从不同角度描述了加载路径的非比例程度,并利用附加强化系数和各自定义的非比例度因子修正了不同的等效应变范围.与修正前的等效应变法相比,修正后的等效应变法可以更好地预测某些材料的非比例疲劳寿命.但是,已有研究[12-17]表明,诸如Ti-6Al-4V钛合金[12], 30CrNiMo8HH合金钢等[13-14]材料,非比例加载下虽然不存在明显的附加强化现象,但是疲劳寿命却明显降低.对于这一类材料,由于附加强化系数为零,因此利用附加强化系数和非比例度因子修正后的等效应变法[5-11]预测材料的非比例疲劳寿命会偏于危险.姜潮等[18]利用非比例度因子和附加强化系数定义了一个新的非比例损伤系数,并利用该系数提出一个基于临界平面法的疲劳寿命预测模型.但是,该模型至少存在两方面的问题:1)对于不存在明显非比例附加强化现象的材料,仅仅通过非比例度因子来反映非比例加载下疲劳寿命缩短的现象,没有考虑材料本身对此现象的影响,导致不同材料在给定非比例加载路径下具有相同的非比例损伤系数;2)预测模型基于MC(Manson-Coffin)方程进行寿命估算,但是在单轴加载下该模型无法退化为MC方程.赵而年等[19]也利用非比例度因子和附加强化系数定义了一个新的非比例损伤系数,并利用该系数修正了FS(Fatemi-Socie)模型[20].与文献[18]提出的模型类似,对于不存在明显非比例附加强化现象的材料,修正后的FS模型也是仅仅通过非比例度因子来反映非比例加载下疲劳寿命减少的现象,也没有考虑材料本身对此现象的影响.
为克服上述模型的不足,本文首先引入寿命缩减因子的概念,并明确了其确定方法.然后,利用最小法向应变范围,提出一种计算非比例度因子的新方法,并针对一般的多轴加载情形,明确了最小法向应变范围的计算步骤.在此基础上,通过修正ASME等效应变范围提出一种新的多轴低周疲劳寿命预测方法,并利用10种材料(包括7种不存在明显非比例附加强化现象的材料)的试验数据对所建模型进行了验证,预测寿命与试验寿命吻合较好.
1 多轴低周疲劳寿命预测模型 1.1 模型的建立文献[5-11]中,利用非比例度因子fnp和附加强化系数αnp修正后的等效应变法可统一表述为
| $ (1 + {\alpha _{{\rm{np}}}}{f_{{\rm{np}}}})\frac{{\Delta {\varepsilon _{{\rm{eq}}}}}}{2} = f(2{N_{\rm{f}}}), $ | (1) |
其中
| $ {\alpha _{{\rm{np}}}} = \frac{{{\sigma _{{\rm{OP}}}}^a}}{{{\sigma _{{\rm{IP}}}}^a}}-1. $ |
式中:σOPa为非比例圆路径加载(fnp=1)下的等效应力幅值;σIPa为相同等效应变时,比例加载路径(fnp=0)下的等效应力幅值;Nf为疲劳寿命.需要注意的是,不同文献中对式(1)中非比例度因子fnp和等效应变范围Δεeq的定义各不相同.
由式(1)可见,对于非比例加载下不存在明显附加强化现象的材料(αnp=0),式(1)可变为
| $ \frac{{\Delta {\varepsilon _{{\rm{eq}}}}}}{2} = f(2{N_{\rm{f}}}), $ | (2) |
由式(2)可见,式(1)左端退化为修正前的等效应变范围,无法反映非比例加载路径引起的寿命减少现象.
最近,钟波等[10]在文献[7, 21]定义的载荷路径非比例度的基础上,提出一种新的非比例度因子计算方法,并结合附加强化系数和ASME规范中的等效应变范围,发展了一种新的多轴疲劳寿命预测模型.所建模型形式如式(1)所示,其中:
| $ \begin{array}{l} \Delta {\varepsilon _{{\rm{eq}}}} = \Delta {\varepsilon _{{\rm{ASME}}}} = \max [{({\varepsilon _{\rm{A}}}-{\varepsilon _{\rm{B}}})^2} + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{3}{({\gamma _{\rm{A}}}-{\gamma _{\rm{B}}})^2}{]^{\frac{1}{2}}}, \end{array} $ | (3) |
| $ f(2{N_{\rm{f}}}) = \frac{{\sigma {'_{\rm{f}}}}}{E}{(2{N_{\rm{f}}})^b} + \varepsilon {'_{\rm{f}}}{(2{N_{\rm{f}}})^c}, $ | (4) |
| $ {f_{{\rm{np}}}} = {\left( {\frac{{\int_S ' {y^2}{\rm{d}}S'}}{{\int_{{S_0}} {'{y^2}{\rm{d}}{S_0}} }}} \right)^{\left( {1-\frac{S}{{{S_0}}}} \right)\frac{{{L_{{\rm{cyc}}}}}}{{4\mathit{\Delta }{r_{\max }}}}}}. $ | (5) |
式中:σ′f为疲劳强度系数;b为疲劳强度指数;ε′f为疲劳延性系数;c为疲劳延性指数;E为弹性模量;εA、εB和γA、γB分别为非比例加载历程中任意A、B时刻的轴向应变和剪切应变.公式中各参数的具体意义详见文献[10].由于文献[10]中建立的模型采用式(1)的表达形式,因此对于非比例加载下不存在明显附加强化现象的材料,该模型也无法反映非比例加载路径引起的寿命减少现象.为了更好地预测材料的多轴疲劳寿命,需要对该类模型进行进一步修正.
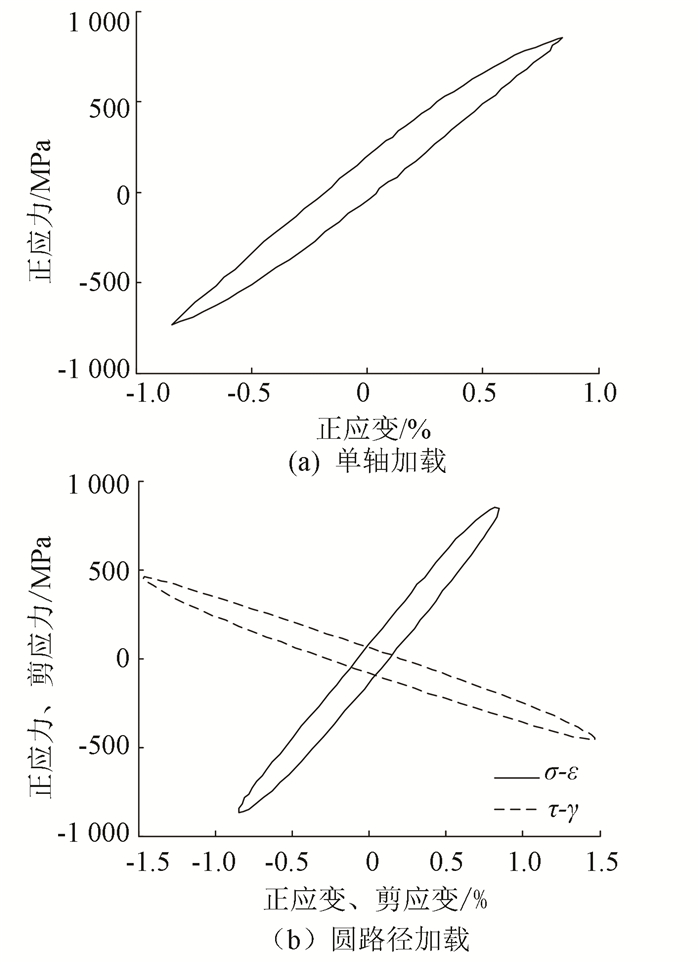
通常认为,控制应变加载时,相同等效应变下,材料非比例圆路径下的疲劳寿命最短.也就是说,圆路径的非比例程度最大(fnp=1).图 1(a)、(b)所示为Ti-6Al-4V钛合金[12]分别在单轴和非比例圆路径加载下的稳态应力应变滞回环曲线(von-Mises等效应变范围Δεeq均为1.7%).图 2所示为Ti-6Al-4V钛合金[12]分别在单轴和非比例圆路径加载下,ASME等效应变幅与等效应力幅之间的关系.图 3所示为Ti-6Al-4V钛合金[12]分别在单轴和非比例圆路径加载下,ASME等效应变幅与疲劳寿命之间的关系.
|
图 1 Ti-6Al-4V钛合金稳态循环应力应变滞环曲线(Δεeq=1.7%)[12] Figure 1 Stabilized cyclic stress-strain hysteresis loops for Ti-6Al-4V (Δεeq=1.7%)[12] |
|
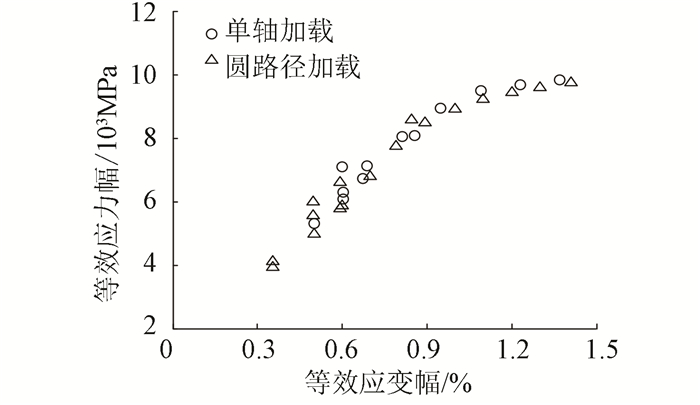
图 2 Ti-6Al-4V钛合金等效应变幅与等效应力幅之间的关系[12] Figure 2 Correlation between equivalent strain amplitude and equivalent stress amplitude for Ti-6Al-4V[12] |
|
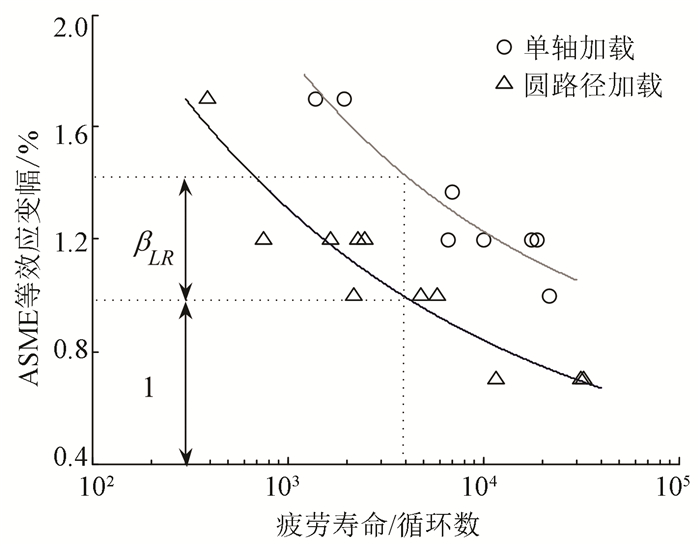
图 3 Ti-6Al-4V钛合金ASME等效应变幅与疲劳寿命之间的关系 Figure 3 Correlation between ASME equivalent strain amplitude and fatigue lives for Ti-6Al-4V |
由图 2、3可知,非比例加载下Ti-6Al-4V钛合金不存在明显的附加强化现象,但相同等效应变幅,非比例加载下的疲劳寿命却明显降低.多轴加载下,为了利用基于单轴疲劳试验数据建立的寿命预测模型,需要将ASME等效应变幅进行多轴修正.由图 3可见,如果修正后的ASME等效应变幅在圆路径加载时乘以一个大于1的系数,那么不管是圆路径加载还是单轴加载,修正后的ASME等效应变幅与疲劳寿命之间将遵循相同的变化规律.为此,本文引入寿命缩减因子,提出如下疲劳寿命预测模型:
| $ (1 + {\beta _{{\rm{LR}}}}{f_{{\rm{np}}}})\frac{{\Delta {\varepsilon _{{\rm{ASME}}}}}}{2} = \frac{{{\sigma ^\prime }_{\rm{f}}}}{E}{(2{N_{\rm{f}}})^b} + {\varepsilon ^\prime }_{\rm{f}}{(2{N_{\rm{f}}})^c}. $ | (6) |
式中:βLR为寿命缩减因子;(1+βLRfnp) ΔεASME为修正后的ASME等效应变范围;βLRfnp反映了相同等效应变,非比例加载下疲劳寿命的缩减程度.
1.2 寿命缩减因子前已述及,非比例圆路径加载下,加载路径非比例程度最大,fnp=1.此时,式(6)变为
| $ (1 + {\beta _{{\rm{LR}}}})\frac{{\Delta {\varepsilon _{{\rm{ASME}}}}}}{2} = \frac{{{\sigma ^\prime }_{\rm{f}}}}{E}{(2{N_{\rm{f}}})^b} + {\varepsilon ^\prime }_{\rm{f}}{(2{N_{\rm{f}}})^c}, $ | (7) |
由式(7)可得
| $ {\beta _{{\rm{LR}}}} = \frac{{\frac{{{\sigma ^\prime }_{\rm{f}}}}{E}{{(2{N_{\rm{f}}})}^b} + {\varepsilon ^\prime }_{\rm{f}}{{(2{N_{\rm{f}}})}^c}}}{{\frac{{\Delta {\varepsilon _{{\rm{ASME}}}}}}{2}}}-1. $ | (8) |
结合MC方程,式(8)变为
| $ {\beta _{{\rm{LR}}}} = \frac{{\Delta \varepsilon /2-\Delta {\varepsilon _{{\rm{ASME}}}}/2}}{{\Delta {\varepsilon _{{\rm{ASME}}}}/2}}. $ | (9) |
由于单轴加载下ΔεASME/2退化为Δε/2,式(9)表明寿命缩减因子βLR即为具有相同疲劳寿命时,单轴和圆路径加载下的ASME等效应变幅之差与圆路径加载下ASME等效应变幅的比值,如图 3所示.
从严格意义上来讲,由式(8)可见,寿命缩减因子βLR并不是一个常数,而是一个与疲劳寿命相关的参数.一般来说,βLR随疲劳寿命的增大而逐渐减小.原因在于,当材料的疲劳寿命较低时,产生较大的塑性变形,此时载荷路径的非比例度对材料的疲劳寿命影响较大,而当材料的疲劳寿命较高时,塑性变形较小,此时载荷路径的非比例度对材料的疲劳寿命影响也较小,相同等效应变非比例加载下的疲劳寿命趋近于比例(或单轴)加载下的疲劳寿命.
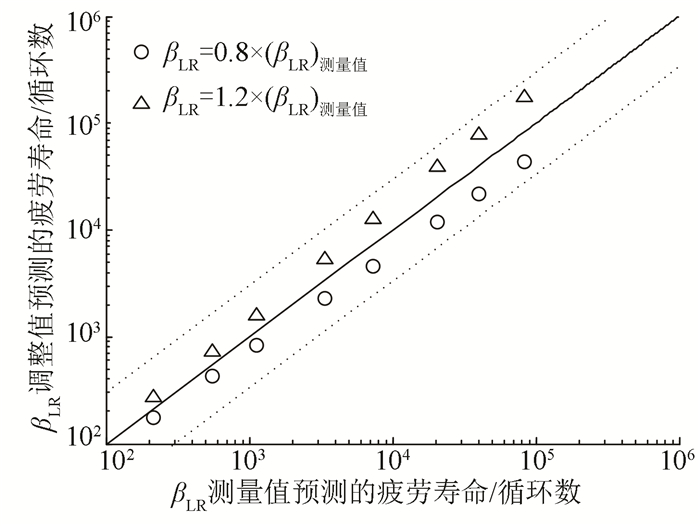
图 4所示为圆路径加载下Ti-6Al-4V钛合金[12]在不同ASME等效应变范围(ΔεASME分别为0.70%、0.75%、0.80%、0.90%、1.00%、1.20%、1.40%、1.80%)下的疲劳寿命.图中,横坐标为寿命缩减因子βLR取测量值时利用式(7)预测的疲劳寿命,纵坐标为寿命缩减因子βLR分别增大或减小20%时预测的疲劳寿命.由图 4可见,当疲劳寿命较小时,βLR取值对寿命预测结果的影响较小.因此,对于低周疲劳,为了计算的方便,本文将寿命缩减因子βLR看作是材料常数.
|
图 4 βLR对Ti-6Al-4V钛合金寿命预测结果的影响 Figure 4 The effect of βLR on fatigue life predictions of Ti-6Al-4V |
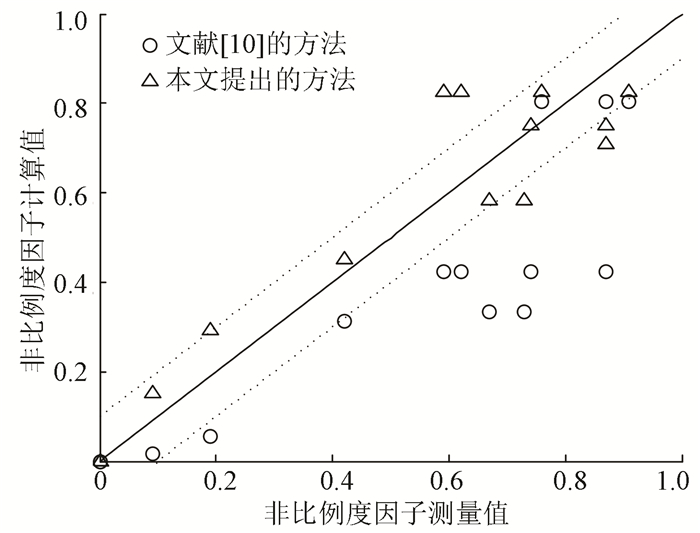
文献[7]中对304不锈钢进行了14种不同比例和非比例加载路径下的多轴疲劳试验.Meggiolaro等[22]利用文献[7]的试验数据,给出了上述14种载荷路径的非比例度的试验测量值.钟波等[10]利用其所提出计算方法,也分别预测了上述14种载荷路径的非比例度.文献[10]的预测结果与试验结果的对比如图 5所示.由图 5可知,在所研究的12种非比例加载路径中,文献[10]计算方法低估了其中11种非比例加载路径的非比例度.而且,由文献[10]可知,提出的非比例度因子计算方法比较繁琐,不便于应用.
|
图 5 非比例度因子计算值与测量值的对比 Figure 5 Comparison of the fnp observed from measured with the predicted values |
薄壁圆管试件在拉扭加载下,与其轴向成α角的平面上的剪切应变γα和法向应变εn, α分别为[23]:
| $ {\gamma _\alpha } =-(1 + {\nu _{{\rm{eff}}}}){\varepsilon _x}\sin 2\alpha + {\gamma _{xy}}\cos 2\alpha, $ | (10) |
| $ {\varepsilon _{n, \alpha }} = \frac{{1-{\nu _{{\rm{eff}}}}}}{2}{\varepsilon _x} + \frac{{1 + {\nu _{{\rm{eff}}}}}}{2}{\varepsilon _x}\cos 2\alpha + \frac{1}{2}{\gamma _{xy}}\sin 2\alpha . $ | (11) |
式中: εx、γxy分别为加载正应变和加载剪应变;为了简单起见,可将等效泊松比νeff取为0.5[1].
如果加载波形为正弦波,即:
| $ {\varepsilon _x} = \frac{{\Delta {\varepsilon _{{\rm{app}}}}}}{2}\sin \omega t, $ | (12) |
| $ {\gamma _{xy}} = \frac{{\Delta {\gamma _{{\rm{app}}}}}}{2}\sin (\omega t-\varphi ), $ | (13) |
则,由式(10)~(13)可得,与薄壁圆管试件轴向夹角为α的平面上的法向应变范围Δεn, α为[23]
| $ \begin{array}{l} \mathit{\Delta }{\varepsilon _{n, \alpha }} = \frac{1}{2}\mathit{\Delta }{\varepsilon _{{\rm{app}}}}\{ {[\lambda \sin 2\alpha \sin \varphi]^2} + \\ \;\;\;\;\;\;\;\;\;\;\;{[2(1 + {\nu _{{\rm{eff}}}}){\rm{co}}{{\rm{s}}^2}\alpha - 2{\nu _{{\rm{eff}}}} + \lambda \sin 2\alpha \cos \varphi ]^2}{\} ^{0.5}}. \end{array} $ | (14) |
式中:Δεapp为轴向加载应变范围;Δγapp为剪切加载应变范围;φ为相位差;λ(=Δγapp/Δεapp)为应变比.
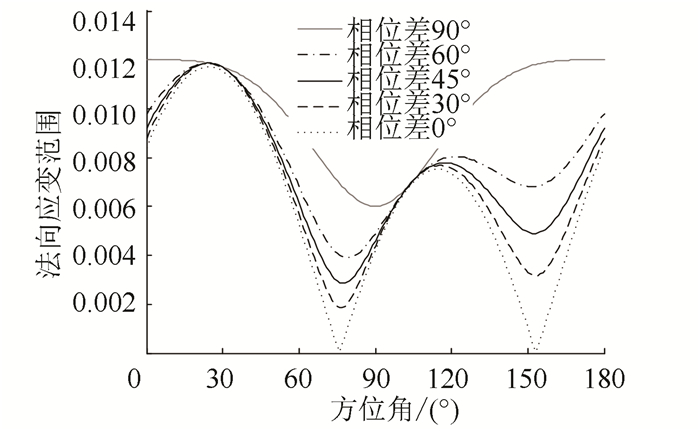
图 6为薄壁圆管试件在不同相位差的正弦波加载下(
|
图 6 正弦波加载下各平面上的法向应变范围 Figure 6 The normal strain range of each plane under different loading paths with sinusoidal wave |
| $ {f_{{\rm{np}}}} = \frac{{{{(\mathit{\Delta }{\varepsilon _{n, \alpha }})}_{\min }}}}{{\max ({{(\mathit{\Delta }{\varepsilon _{n, \alpha }})}_{\min }})}}. $ | (15) |
对于多轴加载下的一般情形而言,利用式(15),可由下述步骤计算加载路径的非比例度因子:
1) 根据输入的剪切应变γxy和轴向应变εx,明确加载路径的形状.
2) 以微小的时间步长Δt,将一个加载周期内的γxy和εx进行离散.
3) 不同时刻下,分别计算第i个平面(αi)上的法向应变:
| $ \begin{array}{l} {\varepsilon _{n, {\alpha _i}}}(j) = \left( {\frac{{1-{\nu _{{\rm{eff}}}}}}{2} + \frac{{1 + {\nu _{{\rm{eff}}}}}}{2}\cos \;2{\alpha _i}} \right){\varepsilon _x}({\rm{j}}\mathit{\Delta }t) + \\ \frac{1}{2}{\gamma _{xy}}({\rm{j}}\mathit{\Delta }t)\sin 2{\alpha _i}, j = 1, 2, \cdots, q \end{array} $ |
式中q为离散后一个循环中的子步数.
4) 计算第i个平面(αi)上的法向应变范围为
| $ \mathit{\Delta }{\varepsilon _{n, {\alpha _i}}} = \max ({\varepsilon _{n, {\alpha _i}}}(j))-\min({\varepsilon _{n, {\alpha _i}}}(j)). $ |
5) 在[0°, 180°)内,i以步长1°变化,分别计算不同平面上的法向应变范围,并比较其大小,从而确定(Δεn, α)min的值.
6) 对应相同加载等效应变,利用式(14)计算圆加载路径下的最小法向应变范围,即max((Δεn, α)min).
7) 利用式(15)来计算所研究加载路径的fnp.
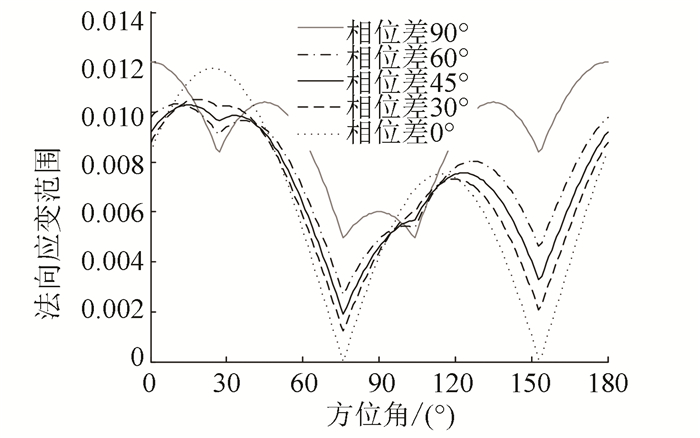
对于三角波加载(
|
图 7 三角波加载下各平面的法向应变范围 Figure 7 The normal strain range of each plane under different loading paths with triangle wave |
莫德峰等[24]在0.22%等效应变幅下,研究了Al-7Si-0.3Mg铸铝合金在不同加载路径下的循环变形行为,发现疲劳寿命(平均值)与加载路径相关,其从大到小的顺序为:比例路径>正方形路径>菱形路径>圆形路径.利用式(12)计算上述4种加载路径下的非比例度因子分别为0、0.71、0.82、1.00,与Al-7Si-0.3Mg铸铝合金疲劳寿命变化趋势相符.而利用文献[10]中所提方法(式(5))计算上述4种加载路径下的非比例度因子分别为0、0.8、0.8、1.0,与Al-7Si-0.3Mg铸铝合金疲劳寿命变化趋势并不相符.
利用本文所提方法计算文献[7]中14种载荷路径的非比例度因子,并将计算值与测量值的对比也列于图 5.通过对比可见,本文所提方法可以更好的计算加载路径的非比例度因子.因此,与文献[10]中计算非比例度因子的方法相比,本文所提方法不仅计算过程简单,而且计算结果更为合理.
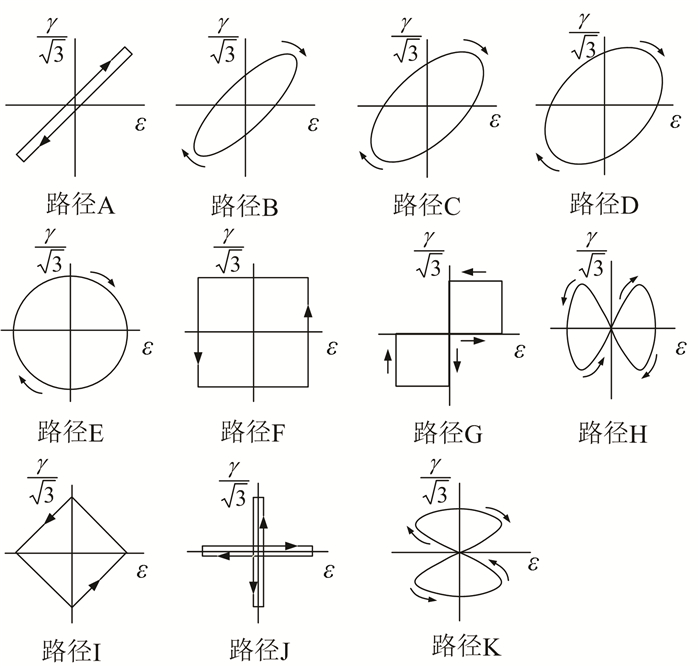
2 试验验证本文选用文献[12-17, 25-28]中,10种材料的试验数据对所建模型进行验证.这10种材料分别是,Ti-6Al-4V钛合金[12]、30CrNiMo8HH合金钢[13-14]、1050N钢[15]、1050QT钢[15]、1050IH钢[15]、纯钛[16]、16MnR钢[17]、S460N钢[25-26]、304不锈钢[27]和TC4钛合金[28].其中,前7种材料非比例加载下不存在明显附加强化现象[12-17],后3种材料非比例加载下存在明显附加强化现象[25-28].试样均为薄壁圆管试件,所有试验均为拉扭比例或非比例加载(如图 8所示),各材料的机械性能和疲劳性能参数见表 1.利用试验数据,由式(9)计算得到的寿命缩减因子也列于表 1中.利用式(15)计算得到图 8所示加载路径下的非比例度因子见表 2.
|
图 8 多轴拉扭加载路径 Figure 8 The multiaxial axial-torsional loading paths |
| 表 1 机械性能和疲劳性能参数及寿命缩减因子 Table 1 Summary of the static and fatigue properties of the considered materials and their life reduction factor |
| 表 2 各加载路径下的非比例度因子 Table 2 Value of nonproportionality factors for each loading path |
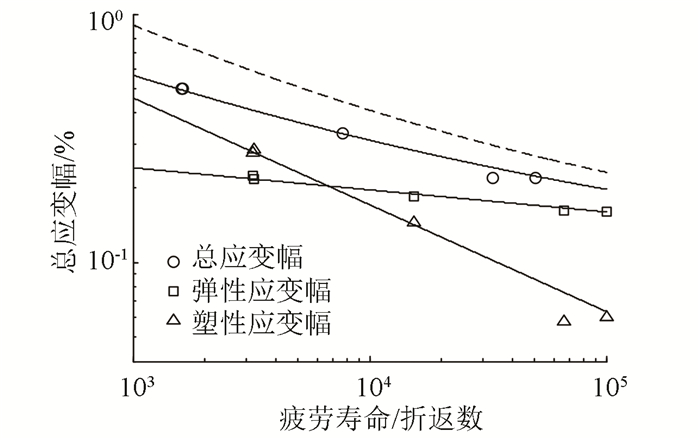
需要说明的是,由于文献[12, 17]中未给出Ti-6Al-4V钛合金和16MnR钢的疲劳性能参数,因此本文利用文献[12, 17]中的试验数据,由最小二乘法拟合得到这两种材料的疲劳性能参数.对于S460N钢,利用文献[26]中给出的相关疲劳性能参数,结合MC方程,计算得到的单轴应变-寿命曲线如图 9中双划线所示.由图 9可见,利用该疲劳性能参数预测S460N钢的单轴疲劳寿命偏于危险.因此,本文中S460N钢的疲劳性能参数也是利用试验数据由最小二乘法拟合得到(见图 9中的实线),进而进行进一步的多轴疲劳寿命预测.
|
图 9 S460N钢的单轴应变疲劳寿命曲线 Figure 9 The uniaxial strain-life curve for S460N steel |
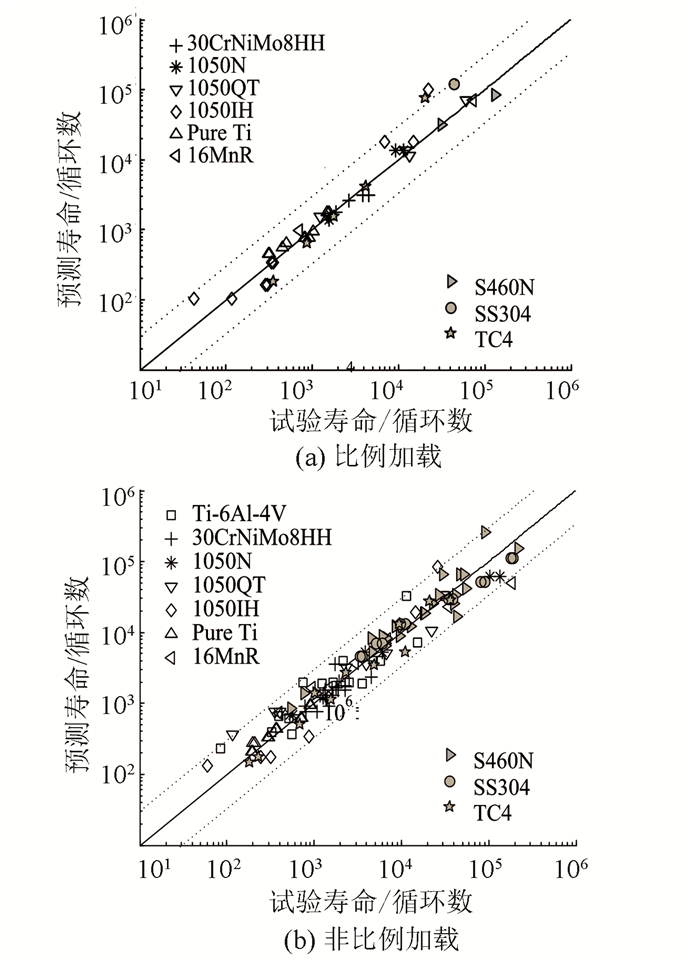
图 10所示为本文所建模型对上述10种材料在比例和不同非比例加载路径下的寿命预测结果.由图 10可见,无论材料的非比例附加强化现象是否明显,也无论是比例加载还是非比例加载,绝大多数数据点都位于3倍因子范围内.
|
图 10 预测寿命和疲劳寿命试验值的比较 Figure 10 Comparison of the fatigue life observed from predicted and experimental values |
1) 对于不存在明显非比例附加强化现象的材料,利用附加强化系数和非比例度因子修正后的等效应变法无法反映这类材料在非比例加载下的疲劳寿命缩短现象,预测寿命偏于危险,而利用寿命缩减因子取代修正模型中的附加强化系数可以取得较好的寿命预测结果.
2) 加载等效应变相同时,加载路径非比例程度的增大,最小法向应变范围也随之增大.基于最小法向应变范围,提出一种计算加载路径非比例度的新方法.与文献[10]中的计算方法相比,本文所提方法不仅计算过程简单,而且计算结果更为合理.
3) 利用寿命缩减因子和非比例度因子对ASME等效应变范围进行修正,提出一种新的低周疲劳寿命预测方法.模型验证结果表明, 所提模型不但适用于不存在明显非比例附加强化现象的材料,也适用于非比例加载下存在明显附加强化现象的材料.
| [1] |
SOCIE D F, MARQUIS G B. Multiaxial fatigue[M]. Warrendale, PA: Society of Automotive Engineers Inc., 2000.
|
| [2] |
李静, 孙强, 李春旺, 等. 一种新的多轴疲劳寿命预测方法[J].
机械工程学报, 2009, 45(9): 285-290.
LI Jing, SUN Qiang, LI Chunwang, et al. New prediction method for multiaxial fatigue life[J]. Journal of Mechanical Engineering, 2009, 45(9): 285-290. DOI: 10.3901/JME.2009.09.285 |
| [3] |
姜潮, 李博川, 韩旭. 一种考虑路径影响的剪切式多轴疲劳寿命模型[J].
机械工程学报, 2014, 50(16): 21-26.
JIANG Chao, LI Bochuan, HAN Xu. New multiaxial fatigue life prediction model with shear form based on the strain path[J]. Journal of Mechanical Engineering, 2014, 50(16): 21-26. DOI: 10.3901/JME.2014.16.021 |
| [4] |
ASME. Cases of ASME Boiler and Pressure Vessel Code:Sec. Ⅲ, Div. 1, Code Case N47-23[S]. New York, NY:[s.n.], 1988.
|
| [5] |
ITOH T, KAMEOKA M, OBATAYA Y. A new model for describing a stable cyclic stress-strain relationship under non-proportional loading based on activation state of slip systems[J].
Fatigue & Fracture of Engineering Materials & Structures, 2004, 27(10): 957-967.
DOI: 10.1111/j.1460-2695.2004.00818.x |
| [6] |
ITOH T, SAKANE M, HATA T, et al. A design procedure for assessing low cycle fatigue life under proportional and non-proportional loading[J].
International Journal of Fatigue, 2006, 28(5/6): 459-466.
DOI: 10.1016/j.ijfatigue.2005.08.007 |
| [7] |
ITOH T, SAKANE M, OHNAMI M, et al. Non-proportional low cycle fatigue criterion for type 304 stainless steel[J].
Journal of Engineering Materials and Technology, 1995, 117(3): 285-292.
DOI: 10.1115/1.2804541 |
| [8] |
LI B, REIS L, De FREITAS M. Simulation of cyclic stress/strain evolutions for multiaxial fatigue life prediction[J].
International Journal of Fatigue, 2006, 28(5/6): 451-458.
DOI: 10.1016/j.ijfatigue.2005.07.038 |
| [9] |
陈家权, 陈国军, 温洁明. 考虑应变路径的多轴低周疲劳寿命预测模型[J].
工程力学, 2012, 29(4): 84-89.
CHEN Jiaquan, CHEN Guojun, WEN Jieming. Multiaxial low cycle fatigue life prediction model based on strain path[J]. Engineering Mechanics, 2012, 29(4): 84-89. |
| [10] |
钟波, 王延荣, 魏大盛, 等. 基于应变路径非比例度的多轴疲劳寿命预测[J].
航空动力学报, 2016, 31(2): 317-322.
ZHONG Bo, WANG Yanrong, WEI Dasheng, et al. Multiaxial fatigue life prediction based on nonproportionality of strain path[J]. Journal of Aerospace Power, 2016, 31(2): 317-322. DOI: 10.13224/j.cnki.jasp.2016.02.008 |
| [11] |
王雷, 王德俊. 多轴疲劳寿命预测及验证[J].
东北大学学报(自然科学版), 2002, 23(2): 174-177.
WANG Lei, WANG Dejun. Fatigue life prediction under multiaxial loading[J]. Journal of Northeastern University (Natural Science), 2002, 23(2): 174-177. DOI: 10.3321/j.issn:1005-3026.2002.02.020 |
| [12] |
WU Min, ITOH T, SHIMIZU Y, et al. Low cycle fatigue life of Ti-6Al-4V alloy under nonproportional loading[J].
International Journal of Fatigue, 2012, 44: 14-20.
DOI: 10.1016/j.ijfatigue.2012.06.006 |
| [13] |
NOBAN M, JAHED H, IBRAHIM E, et al. Load path sensitivity and fatigue life estimation of 30CrNiMo8HH[J].
International Journal of Fatigue, 2012, 37: 123-133.
DOI: 10.1016/j.ijfatigue.2011.10.009 |
| [14] |
NOBAN M, JAHED H, WINKLER S, et al. Fatigue characterization and modeling of 30CrNiMo8HH under multiaxial loading[J].
Materials Science and Engineering A, 2011, 528(6): 2484-2494.
DOI: 10.1016/j.msea.2010.11.075 |
| [15] |
SHAMSAEI N, FATEMI A. Effect of hardness on multiaxial fatigue behaviour and some simple approximations for steels[J].
Fatigue & Fracture of Engineering Materials & Structures, 2009, 32(8): 631-646.
DOI: 10.1111/j.1460-2695.2009.01369.x |
| [16] |
SHAMSAEI N, GLADSKYI M, PANASOVSKYI K, et al. Multiaxial fatigue of titanium including step loading and load path alteration and sequence effects[J].
International Journal of Fatigue, 2010, 32(11): 1862-1874.
DOI: 10.1016/j.ijfatigue.2010.05.006 |
| [17] |
GAO Zengliang, ZHAO Tianwen, WANG Xiaogui, et al. Multiaxial fatigue of 16MnR steel[J].
Journal of Pressure Vessel Technology, 2009, 131(2): 021403(1-9).
DOI: 10.1115/1.3008041 |
| [18] |
姜潮, 邓群, 李博川. 考虑非比例附加损伤的多轴低周疲劳寿命预测模型[J].
力学学报, 2015, 47(4): 634-641.
JIANG Chao, DENG Qun, LI Bochuan. A new multiaxial fatigue life prediction model based on the nonproportional additional damage[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(4): 634-641. DOI: 10.6052/0459-1879-15-050 |
| [19] |
赵而年, 瞿伟廉. 一种新的多轴非比例多轴低周疲劳寿命预测临界面模型[J].
力学学报, 2016, 48(4): 944-952.
ZHAO Ernian, QU Weilian. A new proposal for multiaxial low cycle fatigue life prediction under nonproportional loading[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(4): 944-952. DOI: 10.6052/0459-1879-15-377 |
| [20] |
FATEMI A, SOCIE DF. A critical plane to multiaxial fatigue damage including out-of-phase loading[J].
Fatigue & Fracture of Engineering Materials & Structures, 1988, 11(3): 149-165.
|
| [21] |
BORODII M V, STRIZHALO V A. Analysis of the experimental data on a low cycle fatigue under nonproportional straining[J].
International Journal of Fatigue, 2000, 22(4): 275-282.
DOI: 10.1016/S0142-1123(00)00005-0 |
| [22] |
MEGGIOLARO M A, De CASTO J T P. Prediction of nonproportionality factors of multiaxial histories using the Moment of Inertia method[J].
International Journal of Fatigue, 2014, 61: 151-159.
DOI: 10.1016/j.ijfatigue.2013.11.016 |
| [23] |
LI Jing, LI Chunwan, QIAO Yanjiang, et al. Fatigue life prediction for some metallic materials under constant amplitude multiaxial loading[J].
International Journal of Fatigue, 2014, 68: 10-23.
DOI: 10.1016/j.ijfatigue.2014.06.009 |
| [24] |
莫德峰, 何国球, 朱正宇, 等. 非比例载荷下Al-7Si-0.3Mg合金的循环特性及微观机理[J].
金属学报, 2009, 45(7): 861-865.
MO Defeng, HE Guoqiu, ZHU Zhengyu, et al. Fatigue fractures and mechanism of Al-7Si-0.3Mg cast alloy under nonproportional loadings[J]. Acta Metallurgica Sinica, 2009, 45(7): 861-865. DOI: 10.3321/j.issn:0412-1961.2009.07.015 |
| [25] |
JIANG Yanyao, HERTEL O, VORMWALD M. An experimental evaluation of three critical plane multiaxial fatigue criteria[J].
International Journal of Fatigue, 2007, 29(8): 1490-1502.
DOI: 10.1016/j.ijfatigue.2006.10.028 |
| [26] |
HOFFMEYER J, DORING R, SEEGER T, et al. Deformation behaviour, short crack growth and fatigue lives under multiaxial nonproportional loading[J].
International Journal of Fatigue, 2006, 28(5/6): 508-520.
DOI: 10.1016/j.ijfatigue.2005.05.014 |
| [27] |
SOCIE D F. Multiaxial fatigue damage models[J].
Journal of Engineering Materials and Technology, 1987, 109(4): 293-298.
DOI: 10.1115/1.3225980 |
| [28] |
WU Zhirong, HU Xuteng, SONG Yingding. Multiaxial fatigue life prediction for titanium alloy TC4 under proportional and nonproportional loading[J].
International Journal of Fatigue, 2014, 59: 170-175.
DOI: 10.1016/j.ijfatigue.2013.08.028 |
 2018, Vol. 50
2018, Vol. 50


