2. 农业部都市农业重点实验室,上海 200240;
3. 华中农业大学 园艺林学学院,武汉 430070;
4. 天津科技大学 机械工程学院,天津300222
2. Key Laboratory of Urban Agriculture, Ministry of Agriculture, Shanghai 200240, China;
3. College of Horticulture and Forestry Sciences, Huazhong Agricultural University, Wuhan 430070, China;
4. College of Mechanical Engineering, Tianjin University of Science and Technology, Tianjin 300222, China
伴随城市快速发展,高密度的建筑群日益增多,导致城市热岛和建筑能耗显著提高.由于城市环境的复杂性,建筑能耗不仅要考虑单体建筑与气候间关系,还需考虑布局影响下的建筑之间以及建筑与城市微气候之间的交互作用[1].不同布局造成建筑的采光与遮挡、得热与失热,供暖与制冷等明显变化.那么,建筑布局如何影响城市建筑能耗,以及如何确定合理的布局参数等则成为重要问题.
目前,国内外针对城市建筑布局对能耗的影响研究,主要集中在布局方式、建筑高差、间距、朝向和密度等方面[2].张宁波等[3]通过对北京地区的围合式建筑仿真模拟,发现相对于行列式布局,围合式更有利于降低供暖能耗,且间距越小节能效率越高.沈燕[4]对杨凌地区的农村住宅布局进行CFD仿真,从建筑高度和间距上提出相应的节能策略.Str∅mann-Andersen等[5]发现城市街谷形态(主要是建筑高度与间距之比)对办公和居住建筑总能耗的影响分别达30%、19%.de la Flor等[6]利用城市微气候模型分析了城市肌理对建筑能耗的影响.上述研究都是布局方式固定或少数几种变化,针对布局参数也是考虑单一参数影响.但是,实际的城市环境非常复杂,建筑形态和间距变化也无固定模式.因此,考虑多种布局参数共同变化下,参数对能耗的影响更接近真实的城市环境.从遮挡太阳辐射的角度,分析不同布局下建筑之间交互作用对能耗的影响规律,将是本文重点探讨的内容.全局敏感性分析(global sensitivity analysis)可以在多参数变化的情况下判断参数的相对重要性及影响机制,广泛应用于各种模型的参数筛选与优化.在建筑能耗领域,主要应用于建筑能耗模型关键参数的分析[7-8]、建筑节能优化设计[9-10]、原有建筑的节能改造等[11].但针对中国气候和标准下城市建筑布局参数的全局敏感性分析还比较欠缺.
本文选取夏热冬冷地区的武汉作为研究的气候和地理位置条件.庭院建筑相对于普通矩形建筑,遮阳情况更加复杂,并且在高密度城市中,庭院建筑有助于减轻城市热岛,因此,选取庭院建筑作为目标建筑.以办公建筑为例,采用标准回归系数(standard regression coefficient,SRC)和树状高斯过程模型(treed Gaussian process,TGP)两种全局敏感性分析方法,分析9个与布局相关的设计参数对目标建筑年均制冷、供暖和总能耗不确定性的贡献,明晰各个参数自身及交互作用下对能耗的影响机制,为低碳城市规划和建筑布局提供理论依据.
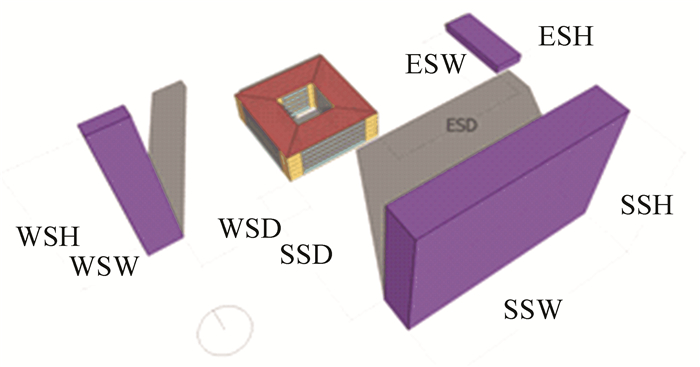
1 模型构建 1.1 几何模型与参数设置以行列式布局为例,目标建筑为中心对称方形5层办公庭院建筑,建筑高度20 m,面积15 000 m2(3 000*5),庭院面积600 m2.建筑面宽和进深同为60 m,庭院面宽和进深各约24.5 m.建筑和庭院的长宽比同为1:1,并且所有外墙的窗墙比都为0.5,避免了不同方向上窗墙面积因素对能耗的影响.朝向设定为正南北向,从周边遮阳的角度考虑,选择目标建筑东、西和南3个方向上的布局参数为研究变量,即间距、面宽和高度.目标建筑东南和西南转角外侧拐点分别为东侧建筑和西侧、南侧建筑面宽变化的起始点.为了便于统一比较,本文假设周边建筑进深同为20 m.依据目前武汉地区建筑高度以100 m以下为主的情况,设周边建筑高度最小取3 m,最大取100 m;由于国家规范相对地方标准更具稳定性,周边建筑间距根据国家标准中建筑防火规范,最小值取9 m,考虑到城市用地日益紧张的现状,间距最大值取与最大高度相同的尺寸,即100 m;从目标建筑能否有效遮挡的角度考虑,周边建筑面宽设置最小为5 m,最大面宽为目标建筑的2倍,即120 m.具体参数名称和变化范围见表 1.
| 表 1 能耗模型输入参数 Table 1 Input parameters for energy model |
建筑布局几何模型利用SketchUp软件中的Openstudio插件建立,具体的建筑形体及参数如图 1所示.
|
图 1 建筑布局模型 Figure 1 Model of courtyard building layout |
一种布局相应有一组建筑能耗数据,在计算能耗时,需要对每一种布局进行设备系统等参数设置并转化成能耗模型.图 1是随机的一种典型布局,设置为基本能耗模型.能耗模型采用动态能耗模拟软件EnergyPlus8.1创建并计算.气象参数选用EnergyPlus自带的武汉典型气象年数据,暂不考虑建筑周边微气候下风环境变化的影响.室内照明与设备功率、室内舒适性要求、人员活动与时间控制等参数依据GB50189-2015《公共建筑节能设计标准》规定[12]设置.主要参数设置有:照明功率密度设为10 W·m-2,电器设备功率设为15 W·m-2,人员密度设定为10 m2·p-1.暖通空调系统采用风机盘管加新风系统,在工作时间的制冷温度,7:00-8:00设为28 ℃,8:00-18:00设为26 ℃;供暖温度,7:00-8:00设为18 ℃,8:00-18:00设为20 ℃.能耗模型输出主要结果是单位建筑面积的制冷、供暖、照明和总能耗,kWh·m-2.
2 方法 2.1 敏感性分析敏感性分析是研究各种模型输入的不确定性如何影响模型输出的方法[13],即不确定的参数输入对模型输出不确定性的影响研究.全局敏感性分析可以探索多参数共同变化下,各参数自身及参数间交互作用对模型输出的影响[14].主要方法有筛选法、基于回归分析、基于方差分解和元模型法[15].本文选用计算高效的多元线性回归和可以分析非线性关系的元模型敏感性分析法.
2.1.1 标准回归系数法(SRC)周边建筑越高,对目标建筑的遮挡效应越明显,制冷能耗就会越低,而对供暖能耗的影响刚好相反,其他参数也有类似规律.因此,先假设布局参数与建筑能耗关系符合线性模型,利用修正决定系数(adjusted coefficient of determination,R2)判断拟合效果.根据文献[13],当R2≥0.7时,认为线性模型可行.由于不同参数的取值范围不同,回归系数不便于比较相对的重要性,需要将其转化为标准化回归系数(SRC).通过SRC绝对值大小可以判断参数对能耗影响的相对敏感性,绝对值越大,参数越重要.参数正值表示参数与模型输出呈正相关,负值则相反[16].多元线性回归模型和标准回归系数计算公式为:
| $ \begin{array}{l} y({x_1}, {x_2}, \cdots, {x_n}) = {\beta _0} + \sum\limits_{i = 1}^n {{\beta _i}{x_i} + \varepsilon }, \\ {\rm{SR}}{{\rm{C}}_i}({x_i}, y) = \frac{{{\beta _i}{\sigma _i}}}{{{\sigma _y}}}. \end{array} $ |
式中:y为模型输出(能耗);β0为截距;βi为第i个参数的回归系数;xi为第i个参数;n为参数个数(9个);SRCi为第i个参数的标准回归系数;σy为模型输出总标准差;σi为第i个参数的标准差.
2.1.2 树状高斯过程模型(TGP)敏感性分析法高斯过程(Gaussian process,GP)在处理高维数、小样本、非线性等复杂的问题上具有很好的适应性[17].决策树基于分而治之(divide and conquer)的思想,对待非静态回归问题,是一个简单而有效的方法[18].TGP是高斯过程和决策树的结合,具有两者的优点,适用于非线性和非静态回归模型[18].相对于SRC来说,TGP敏感性分析可以处理非线性动态模型,能对影响力做区间估计,还可以反映参数的影响趋势.相对于一般的基于方差分析方法,TGP需要的能耗模型少、计算量小、效率高[19].本文采用的TGP敏感性分析方法为:1)根据抽样的布局参数与能耗数据,利用TGP建立预测模型;2)利用Sobol'法对这些模型结果进行敏感性分析,计算各个参数的变动对能耗变化的贡献.
TGP敏感性分析法有两个敏感性指数,即主效应(main effect)和全效应(total effect)指数,指数越大,说明该参数对模型输出的影响越大[14].主效应指各参数独自作用引起模型输出的方差与输出总方差的比值;全效应指各参数及与其他参数交互作用下引起的模型输出的方差与输出总方差的比值,两种效应的值都在[0, 1]内.两者之差就是参数交互作用的影响.具体的计算公式[18]为:
| $ \begin{array}{l} {S_i} = \frac{{V(E(Y|{X_i}))}}{{V(Y)}}, \\ {T_i} = 1-\frac{{V(E(Y|{X_{ \sim i}}))}}{{V(Y)}}. \end{array} $ |
式中:Si为主效应;Ti为全效应;Xi为输入参数;X~i为不包括Xi的其余参数;Y为模型输出.
另外,为了便于比较不同参数的敏感性,需要对模型输出进行标准化处理.在下面参数影响的趋势图中,模型输出(效应)从小到大统一于区间[-0.5,0.5].
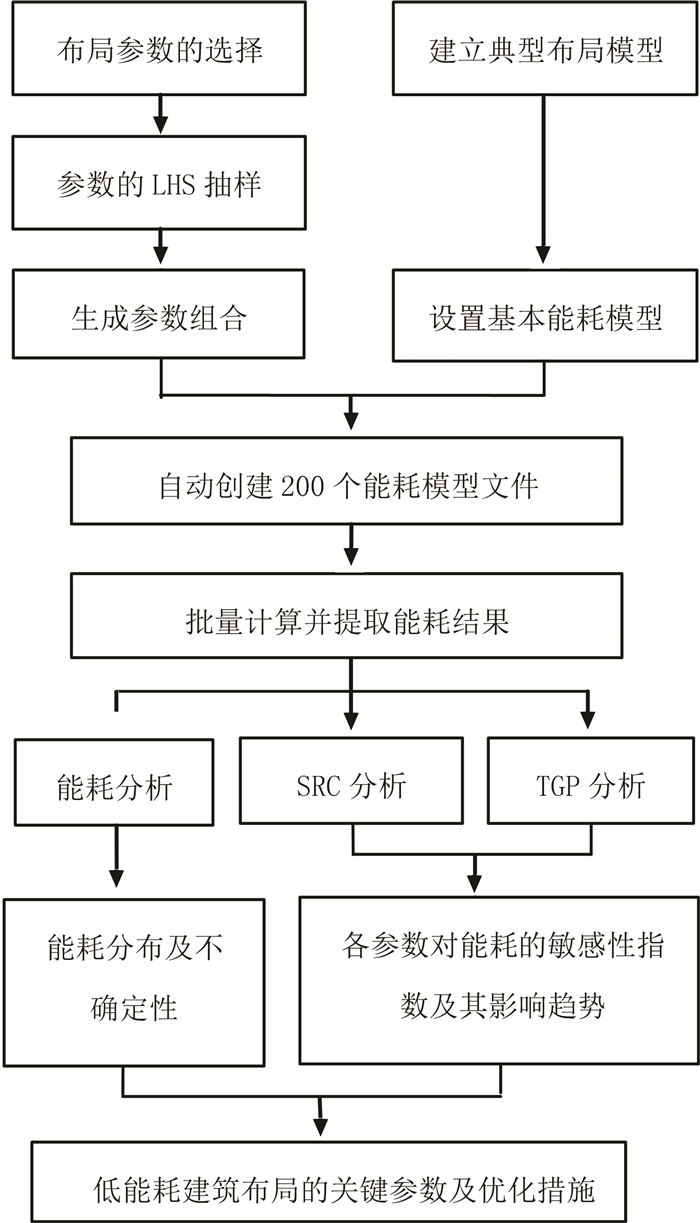
2.2 研究步骤本文研究利用计算机仿真试验[20]完成,具体的研究流程如图 2所示,概括来说,主要有以下3个步骤.
|
图 2 研究流程 Figure 2 Schematic flow diagram for sensitivity analysis |
布局参数的抽样与组合利用R语言编程生成.仿真试验常用的拉丁超立方抽样方法(latin hypercube sampling,LHS),在空间分布上可以实现更好的均匀性,避免了重复抽样[15],本文利用LHS对设计参数进行均匀抽样.抽样的数量因分析方法而定,在元模型分析中,一般依据一个参数至少变化10次的原则抽样[21].本文有9个参数,至少要抽样90次,为了让模型更好的收敛,抽样200次,共建200种布局.
2.2.2 能耗模型的建立与计算首先,利用SketchUp软件建立典型布局的几何模型,并导入EnergyPlus设置参数与计算,将该模型作为基本能耗模型.再利用R语言改写基本能耗模型,将200种布局的数据分别放入模型里,自动生成200个能耗模型.最后,利用EnergyPlus软件对模型进行批量计算,得到制冷、供暖和总能耗等数据.
2.2.3 敏感性分析利用R语言收集能耗结果数据后运用Sensitivity和TGP软件包分析各参数敏感性,绘制建筑能耗分布图和敏感性分析图.
3 结果与讨论通过对200个能耗模型进行批量计算,得到200组能耗数据.做9个布局参数与各项能耗数据的回归分析,分别得到制冷、供暖和总能耗回归模型的修正决定系数R2为0.79、0.73、0.72,R2均大于0.70,并且p值同为2.2×10-16(p < 0.001).计算说明,布局参数与各项能耗线性关系显著,标准回归系数可以反映各参数对能耗的影响程度.
在能耗结果中,通过直方图与概率密度曲线叠加的方式展示目标建筑的能耗分布.在SRC敏感性分析中采用回归系数均值来反映各参数的敏感性,在TGP敏感性分析结果中,通过各参数主效应、全效应和最主要参数的主效应趋势图(中间实线代表均值,两边虚线代表 90%影响区间)并列的方式展示各个参数对能耗的影响规律.本文将从3项能耗和两种敏感性分析结果的对比上探索各参数对各项能耗的影响.
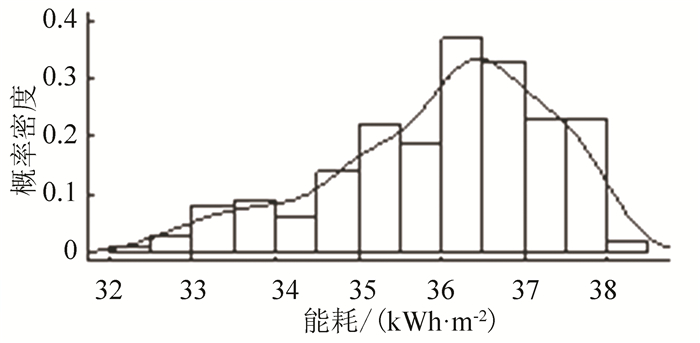
3.1 制冷能耗制冷能耗分布左低右高,呈左偏态分布,能耗值主要分布在32~38 kWh·m-2之间,36~37 kWh·m-2为最大概率范围,如图 3所示.经数据整理,制冷能耗均值约36 kWh·m-2,标准差为1.3,最大与最小值之差为5.7 kWh·m-2.可见,9个布局参数对制冷能耗变动的影响达15.8%(5.7/36),且高能耗的可能性较大,反映出建筑布局对城市建筑制冷能耗影响明显.
|
图 3 制冷能耗分布 Figure 3 Cooling energy distribution of buildings |
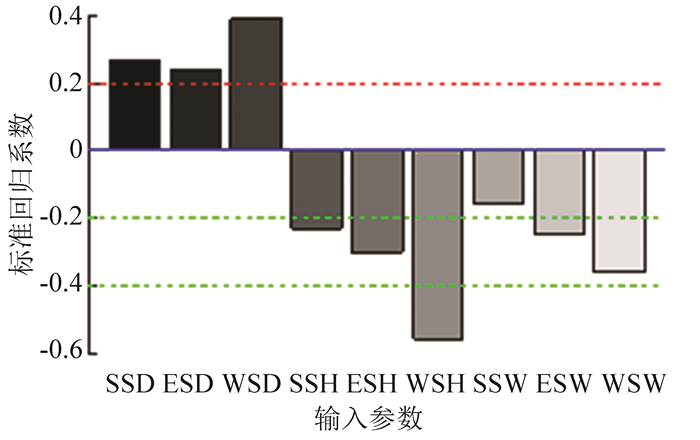
从布局参数对制冷能耗影响的SRC大小和排序来看,西侧建筑高度(WSH)对制冷能耗的影响最大,西侧建筑间距(WSD)和面宽(WSW)紧随其后,影响最小的是南侧建筑面宽(SSW).3个方向的间距与制冷能耗呈正相关,其他参数都与之呈负相关.另外,无论是水平参数还是垂直参数,西侧建筑的影响力最大,如图 4所示.说明,从节约制冷能耗的角度考虑,控制西侧布局参数最为关键.
|
图 4 制冷能耗SRC敏感性分析 Figure 4 SRC sensitivity analysis of cooling energy for buildings |
从TGP敏感性分析结果的两种效应来看,参数排序与SRC敏感性分析结果一致.不过,从参数的影响强度来看,同一参数的影响力取值在SRC中最大,全效应次之,主效应最小,且参数间的交互作用明显.例如,WSH对制冷能耗的影响取值分别是0.6、0.4、0.3左右.南侧和东侧建筑的布局参数对制冷能耗影响较弱,如图 5(a)所示.图中说明,参数的排序结果可靠,在低能耗城市建筑布局中,需要重点考虑WSH等影响力大的参数,适当舍弃SSW等次要参数,有助于重点节能.
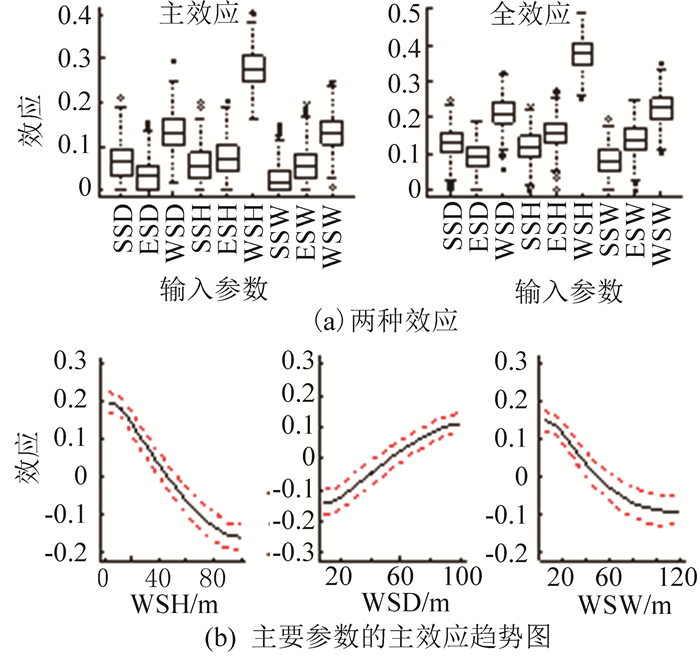
|
图 5 制冷能耗TGP敏感性分析 Figure 5 TGP sensitivity analysis of cooling energy for buildings |
从排名前3位参数对制冷能耗影响的趋势来看,制冷能耗随各参数的变化都呈单调性上升或下降,变化方向与SRC分析结果相同.不过,线性关系并未一直保持,当参数值超过一定范围时,出现非线性特征.比如,当WSW超过目标建筑1倍(60 m)后,影响趋势变缓,出现曲线变化,如图 5(b)所示.由于城市建筑周边遮阳效果是由布局尺寸和目标建筑尺寸共同决定的,当布局尺寸过大时(超出目标建筑寸尺1倍),布局参数的影响力减弱,能耗随参数值的增大却未有明显变化.这刚好与线性回归的R2不是太高相吻合,说明利用TGP来分析布局参数对制冷能耗的敏感性更合理.同时,从节约制冷能耗的角度看,在武汉地区的建筑布局中,增大西侧建筑的高度和面宽,同时减少西侧建筑间距,有利于城市节能.
3.2 供暖能耗供暖能耗分布呈右偏态,能耗值主要分布在15~19 kWh·m-2之间,15~17 kWh·m-2为最大概率范围, 如图 6所示.能耗均值约16.4 kWh·m-2,标准差为0.99,最大与最小值之差为4.4 kWh·m-2.这些参数共同作用下,引起供暖能耗近26.8%(4.4/16.4)的波动.说明,布局参数对供暖能耗影响十分显著.虽然较低能耗的可能性较大,但高能耗也有一定比例,在建筑群布局中应避免较高能耗.
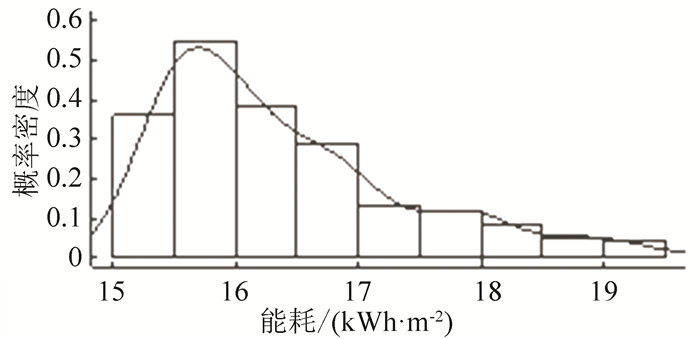
|
图 6 供暖能耗分布 Figure 6 Heating energy distribution of buildings |
在回归分析中,布局参数对供暖能耗的影响刚好与制冷情况相反,间距与供暖能耗呈负相关,建筑面宽和高度与供暖呈正相关.影响最大的参数是南侧建筑间距(SSD),紧随其后的是南侧建筑高度(SSH),影响最小的是东侧建筑面宽(ESW).从3个方向的布局上看,南侧建筑参数影响最大,西侧排名第2,东侧参数影响最小, 如图 7所示.说明,为了争取冬季的太阳辐射和减少供暖能耗,建筑群布局中主要控制南侧建筑参数,特别是南侧建筑间距,而东侧建筑参数的影响较弱,可不做重点考虑.
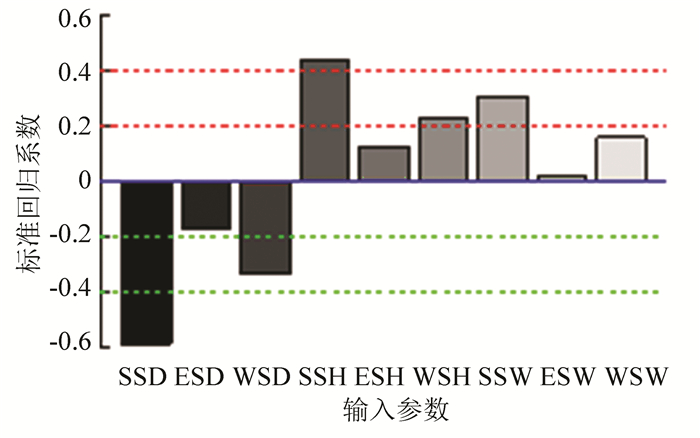
|
图 7 供暖能耗SRC敏感性分析 Figure 7 SRC sensitivity analysis of heating energy for buildings |
从TGP与SRC敏感性分析的对比来看,布局参数对供暖能耗的影响排名和关键参数的影响方向基本一致,SSD占有绝对的优势地位,在主效应中引起供暖能耗30%~40%左右的变化,在全效应中这个比例达50%左右.排名在第2的参数是SSH.全效应相对主效应明显上升,如图 8(a)所示.反映出,参数间的交互作用明显,特别是SSW主效应不及10%,而在全效应达20%左右.从主要参数的影响趋势上看,与制冷能耗情况类似,当取值较小时,参数对能耗是线性影响,到达一定取值时,继续增加参数的值,影响关系呈曲线变化,且波动变缓,如图 8(b)所示.同理,当取值较小时,可以假设为线性模型,当取值较大时,考虑非线性模型更加合理.
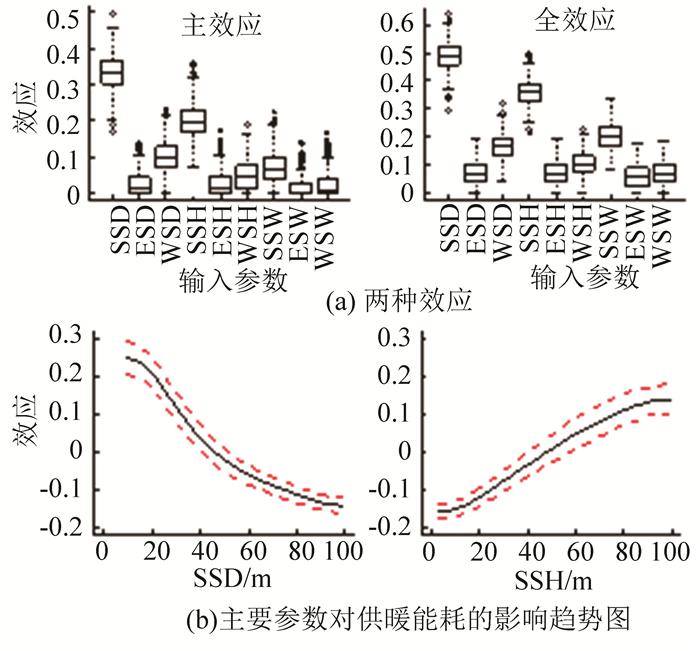
|
图 8 供暖能耗TGP敏感性分析 Figure 8 TGP sensitivity analysis of heating energy for buildings |
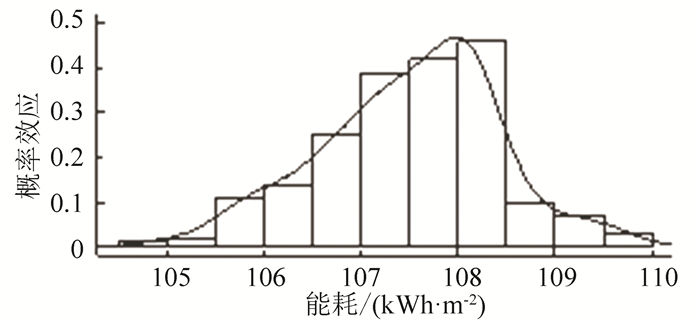
目标建筑的总能耗分布呈左偏态,概率密度逐渐升高,达到峰值后,断崖式下降.能耗值主要分布在105~110 kWh·m-2之间,107.5~108.5 kWh·m-2为最大概率范围, 如图 9所示.且能耗均值约107.5 kWh·m-2,标准差为0.92,最大与最小值之差为4.76 kWh·m-2.从能耗均值上看,制冷与供暖能耗之和占总能耗的48.7%,是节能的重点.这也说明,影响制冷和供暖能耗的重要参数对总能耗也会有较大影响.9个参数共同作用下,引起能耗近4.4%(4.76/107.5)的波动.值得注意的是,总能耗的相对波动明显小于制冷和供暖能耗的波动,由于布局参数对制冷和供暖的影响方向相反,在总能耗中叠加后,参数对总能耗的影响不再显著.
|
图 9 总能耗分布 Figure 9 Total energy distribution of buildings |
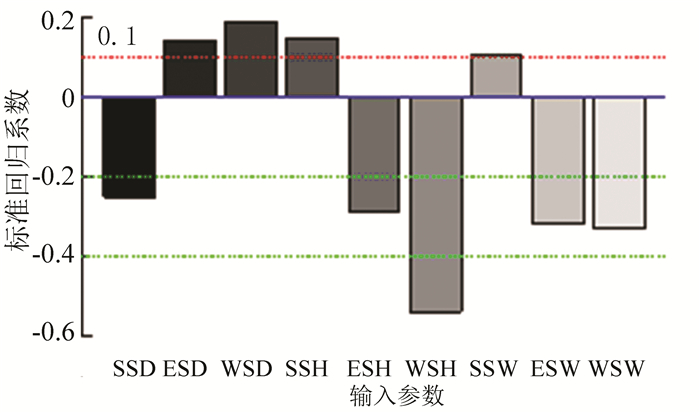
从影响方向上看,ESD、WSD、SSH和SSW与总能耗呈正相关,其他参数与之呈负相关.影响最大的参数是WSH,排名第2的是WSW,紧随其后是ESW、ESH、SSD,其他参数回归系数在0.2以下,影响不明显.从建筑布局看,西侧建筑影响最大,南侧次之,东侧影响最小.从间距上看,南侧间距的影响强于西侧,从面宽和高度上看,西侧建筑尺寸最为关键, 如图 10所示.
|
图 10 总能耗SRC敏感性分析 Figure 10 SRC sensitivity analysis of total energy for buildings |
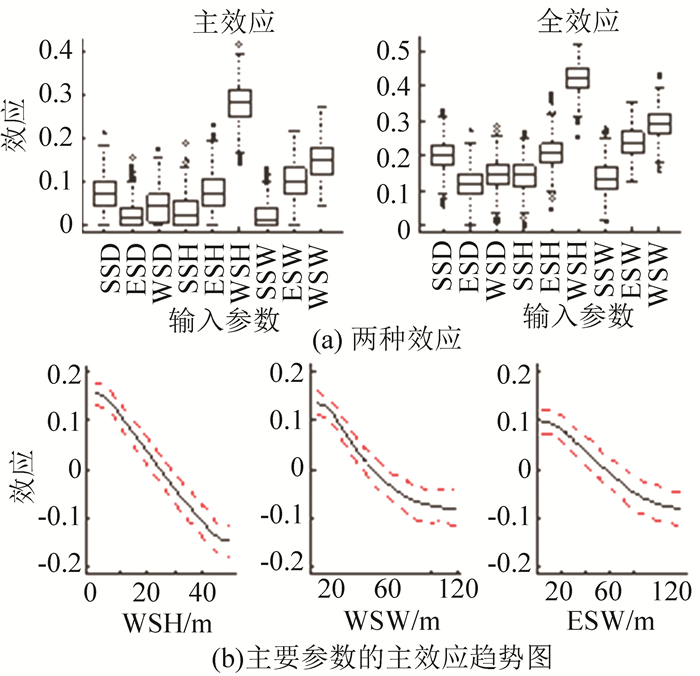
TGP敏感性分析的结果与SRC相似,WSH对总能耗影响最大,紧随其后的是WSW和ESW,最小的是SSW.对比主效应和全效应,参数间交互作用明显, 如图 11(a)所示.因此,从节能的角度,控制西侧建筑高度和面宽最为关键.南侧建筑对总能耗影响较小,除高度有一定影响外,间距和面宽影响都较弱.说明,在武汉地区,南向建筑的遮挡效应对节约建筑能耗并无显著效用,在用地不紧张的情况下,增大间距、减少面宽,可以使建筑具有良好的采光和视线,能耗却不会显著增加.
|
图 11 总能耗TGP敏感性分析 Figure 11 TGP sensitivity analysis of total energy for buildings |
从最主要参数影响趋势来看, 如图 11(b)所示,排名前3位的参数都与总能耗呈负相关.参数超过一定值时,总能耗下降变缓,这一点与参数对制冷和供暖的影响趋势类似.说明,控制过大的布局尺寸有利于高效节能.
从制冷和总能耗的主效应和总效应可以看出,最主要的影响参数是相同的,但是,参数影响顺序略有变化.可见,由于武汉为夏热冬冷地区,减少制冷能耗是关键,增加东西两侧建筑的高度有利于节约制冷和总能耗.
4 结论1) 从SRC和TGP两种敏感性分析来看,参数分析结果在影响趋势和强度上类似,其影响呈单调性变化,参数影响力排序基本相同.当参数取值较小时,线性关系明显,采用SRC敏感性分析快捷且准确.当参数取值较大时,能耗变化非线性特征显现,运用TGP敏感性分析更合理.
2) 从布局参数对城市建筑能耗的影响机制上看,首先,发现布局参数对能耗有显著影响.9个参数的总变化,分别引起制冷、供暖和总能耗15.8%、26.8%、4.4%的变化.其次,对比9个参数的相对敏感性,对取暖、制冷和总能耗影响最大因素各不相同.南侧建筑布局参数对能耗影响不明显,这有利于南北向灵活设计.最后,从低能耗城市的建筑布局出发,在垂直和水平布局上侧重点应不同;适当减少东西两侧建筑间距,而加大南向间距,这样既有利于节能,也有利于良好的视线和采光.
3) 上述结论成立的条件是满足模型构建中的各种设置和假设.但本文所提的研究方法和思路可以应用到不同城市环境中,不受地域、气候、建筑形态等限制.从节能减排的角度,建议在高密度旧城区建设时,先分析周边建筑对场地的遮挡效用,然后从低能耗布局的角度提出目标建筑的合理尺寸.需要指出,影响布局的因素很多,最后的方案应该是节能、采光、视线、通风等相协调的结果.
| [1] |
田玮, 魏来, 朱丽, 等. 城市规模的建筑能耗研究综述[J].
建筑节能, 2016, 44(2): 59-64.
TIAN Wei, WEI Lai, ZHU Li, et al. Building energy analysis at urban scale[J]. Building Energy Efficiency, 2016, 44(2): 59-64. DOI: 10.3969/j.issn.1673-7237.2016.02.015 |
| [2] |
XI Chen, YANG Hongxing, LU Lin. A comprehensive review on passive design approaches in green building rating tools[J].
Renewable and Sustainable Energy Reviews, 2015(50): 1425-1436.
DOI: 10.1016/j.rser.2015.06.003 |
| [3] |
张宁波, 付海明, 钟珂, 等. 围合式建筑布局形式冬季的附加节能效应[J].
东华大学学报(自然科学版), 2013, 39(3): 368-374.
ZHANG Ningbo, FU Haiming, ZHONG Ke, et al. Additional energy-saving effect of an enclosed building in winter[J]. Journal or Donghua University (Natural Science), 2013, 39(3): 368-374. DOI: 10.3969/j.issn.1671-0444.2013.03.020 |
| [4] |
沈燕. 杨凌地区农村住宅建筑能耗与节能布局研究[D]. 西安: 西北农林科技大学, 2012: 48-49.
SHEN Yan. The rural residential energy consumption and energy saving layout research in Yangling[D].Xi'an: Northwest A&F University, 2012: 48-49. |
| [5] |
STR∅MANN-ANDERSEN A J, SATTRUP P A. The urban canyon and building energy use: Urban density versus daylight and passive solar gains[J].
Energy and Buildings, 2011, 43(8): 2011-2020.
DOI: 10.1016/j.enbuild.2011.04.007 |
| [6] |
DE LA FLOR F S, DOMINGUEZ S A. Modelling microclimate in urban environments and assessing its influence on the performance of surrounding buildings[J].
Energy and Buildings, 2004, 36(5): 403-413.
DOI: 10.1016/j.enbuild.2004.01.050 |
| [7] |
SINGH R, LAZARUS I J, KISHORE V V N. Uncertainty and sensitivity analyses of energy and visual performances of office building with external venetian blind shading in hot-dry climate[J].
Applied Energy, 2016, 184: 155-170.
DOI: 10.1016/j.apenergy.2016.10.007 |
| [8] |
IOANNOU A, ITARD L C M. Energy performance and comfort in residential buildings: Sensitivity for building parameters and occupancy[J].
Energy and Buildings, 2015, 92: 216-233.
DOI: 10.1016/j.enbuild.2015.01.055 |
| [9] |
HEMSATH T L, BANDHOSSEINI K A. Sensitivity analysis evaluating basic building geometry's effect on energy use[J].
Renewable Energy, 2015, 76: 526-538.
DOI: 10.1016/j.renene.2014.11.044 |
| [10] |
HEISELBERG P, BROHUS H, HESSELHOLT A, et al. Application of sensitivity analysis in design of sustainable buildings[J].
Renewable Energy, 2009, 34(9): 2030-2036.
DOI: 10.1016/j.renene.2009.02.016 |
| [11] |
LAM J C, WAN K K W, LIU yang. Sensitivity analysis and energy conservation measures implications[J].
Energy Conversion and Management, 2008, 49(11): 3170-3177.
DOI: 10.1016/j.enconman.2008.05.022 |
| [12] |
中华人民共和国住房和城乡建设部. 公共建筑节能设计标准: GB50189--2015 [S]. 北京: 中国建筑工业出版社, 2015: 5-30.
National Standard of the People's Republic of China. Design standard for energy efficiency of public buildings: GB50189-2015[S]. Beijing:China Construction Industry Press, 2015: 5-30. |
| [13] |
SALTELLI A, RATTO M, ANDRES T, et al. Global sensitivity analysis:the primer[M]. England: John Wiley & Sons, 2008. DOI: 10.1002/9780470725184.
|
| [14] |
蔡毅, 邢岩, 胡丹. 敏感性分析综述[J].
北京师范大学学报(自然科学版), 2008, 44(2): 9-16.
CAI Yi, XING Yan, HU Dan. On sensitivity analysis[J]. Journal of Beijing Normal University (Natural Science), 2008, 44(2): 9-16. DOI: 10.3321/j.issn:0476-0301.2008.01.003 |
| [15] |
TIAN Wei. A review of sensitivity analysis methods in building energy analysis[J].
Renewable and Sustainable Energy Reviews, 2013, 20(4): 411-419.
DOI: 10.1016/j.rser.2012.12.014 |
| [16] |
PUDLEINER D, COLTON J. Using sensitivity analysis to improve the efficiency of a Net-Zero Energy vaccine warehouse design[J].
Building and Environment, 2015, 87: 302-314.
DOI: 10.1016/j.buildenv.2014.12.026 |
| [17] |
何志昆, 刘光斌, 赵曦晶, 等. 高斯过程回归方法综述[J].
控制与决策, 2013, 28(8): 1121-1129.
HE Zhikun, LIU Guangbin, ZHAO Xijing, et al. Overview of Gaussian process regression[J]. Control and Decision, 2013, 28(8): 1121-1129. DOI: 10.13195/j.kzyjc.2013.08.018 |
| [18] |
GRAMACY R B, TADDY M A. Categorical inputs, sensitivity analysis, optimization and importance tempering with tgp version 2, an R package for treed gaussian process models[J].
Journal of Statistical Software, 2010, 33(6): 1-48.
DOI: 10.18637/jss.v033.i06 |
| [19] |
SONG Jitian, LAI Wei, YU Sun, et al. Implementation of meta-modeling for sensitivity analysis in building energy analysis[C]//eSim 2014. Ottawa, Canada: [s.n.], 2014: 1-12.
|
| [20] |
何成, 朱丽, 田玮, 等. 基于低能耗目标的建筑功能布局研究[J].
建筑学报, 2016, 14(S1): 155-158.
HE Cheng, ZHU Li, TIAN Wei, et al. Study on the layout of architectural function for low energy consumption[J]. Architectural journal, 2016, 14(S1): 155-158. |
| [21] |
LOEPPKY J L, SACKS J, WELCH W J. Choosing the sample size of a computer experiment: a practical guide[J].
Technometrics, 2009, 51(4): 366-376.
DOI: 10.1198/TECH.2009.08040 |
 2018, Vol. 50
2018, Vol. 50


