Massive multiple-input multiple-output (MIMO)无线技术[1-3]被视为是未来无线通信的关键技术之一. Massive MIMO系统通过在基站部署大规模的天线阵列能够极大提高频谱利用率[4-5]. Massive MIMO技术带来的系统性能提升固然可观[6],但寻求低复杂度的检测算法需要亟待解决[7].最大似然检测算法(MLD)[8],可以使误比特率达到最小,但其复杂度随着发送端数据流的数目呈指数增长,尤其在Massive MIMO系统中复杂度将极其庞大.传统MIMO线性检测算法[9],诸如迫零检测算法、最小均方误差检测算法(Minimum Mean Square Error,MMSE)、最小均方误差串行相消算法[10],虽然能一定程度上降低复杂度,但由于算法检测过程存在矩阵求逆,使得检测算法复杂度仍是制约检测性能的瓶颈,尤其在Massive MIMO系统中,检测算法复杂度极大地增加了系统实现难度[11].
超松弛迭代方法[12-14]是解决大型稀疏矩阵问题的优良方法.本文将此迭代方法引入信号检测中,利用迭代求解而规避矩阵求逆带来的高复杂度,并通过适当选取优化松弛因子,保证在一定检测性能下,减少迭代次数,降低计算复杂度.同时考虑信道存在相关性,数学构建三维空间相关信道模型,推导出相关性解析解,通过计算机仿真,定量分析三维空间信道相关性影响和算法检测性能.
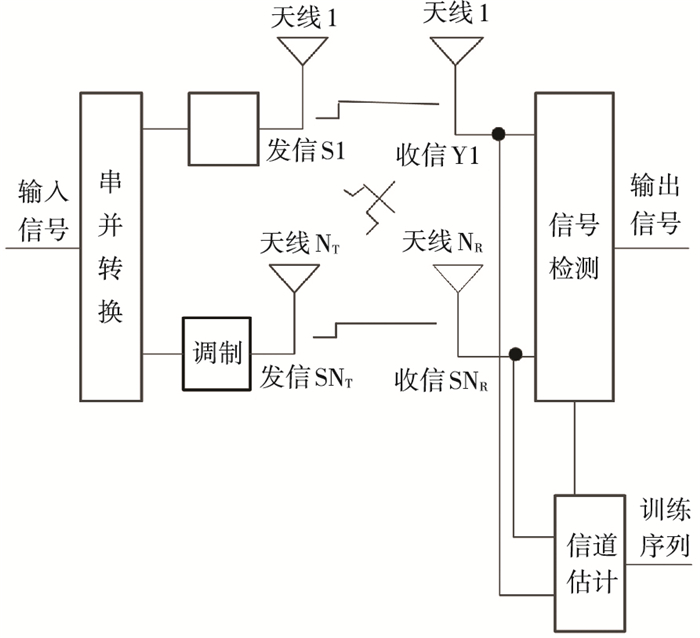
1 Massive MIMO系统模型 1.1 系统模型如图 1所示Massive MIMO系统模型,发射天线数目为NT,接收天线数目为NR.假定信道在一帧内为准静态时不变平坦衰落信道.因此,第l根接收天线的接收信号yl可以表示为
| $ {y_l} = \sum\limits_{k = 1}^{{N_{\rm{T}}}} {{h_{lk}}{s_k}} + {n_l}. $ | (1) |
|
图 1 Massive MIMO系统模型 Figure 1 Massive MIMO system model |
式中:hlk表示第l根接收天线与第k根发射天线间的信道系数,nl表示第l根接收天线收到的加性高斯噪声.将式(1)简化为矢量形式
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Hs}} + \mathit{\boldsymbol{n}}. $ | (2) |
式中:y为接收信号,H为信道矩阵,s为发射信号,n为噪声.
1.2 三维空间相关信道模型使用相关信道模型[15]分析信道相关性:
| $ \mathit{\boldsymbol{H}} = {\mathit{\boldsymbol{H}}_{\rm{w}}}{\mathit{\boldsymbol{R}}^{1/2}}. $ | (3) |
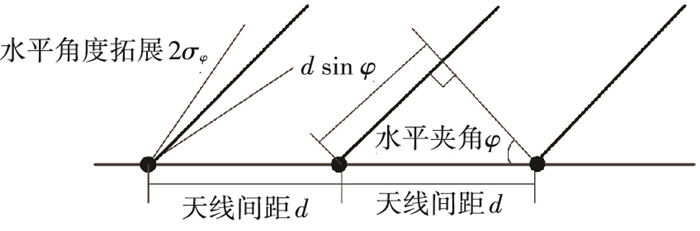
Massive MIMO信道的相关性主要表现为不同天线间出入射波的相位差,如图 2均匀线性阵列天线所示.
|
图 2 Massive MIMO空间相关信道 Figure 2 Massive MIMO spatially correlated channel |
MIMO发射天线间相关性由式(4)计算数学期望得到:
| $ R = E\left( {\exp \left( { - {\rm{j2 \mathit{ π} }}d\sin \varphi /\lambda } \right)} \right). $ | (4) |
式中:d为MIMO天线阵列阵元间距,λ为信号波长,φ为平面波与天线单元对之间夹角,且为高斯分布分布的随机变量,均值为φ,方差为σφ2,推导出相关性近似解析形式的解[16].
| $ R \approx \exp \left( { - \frac{{\sigma _\varphi ^2{{\hat \theta }^2}{{\cos }^2}\bar \varphi }}{2}} \right) \times \exp \left[ { - j\left( {1 - \frac{{\sigma _\varphi ^2}}{2}} \right)\hat \theta \sin \bar \varphi } \right]. $ | (5) |
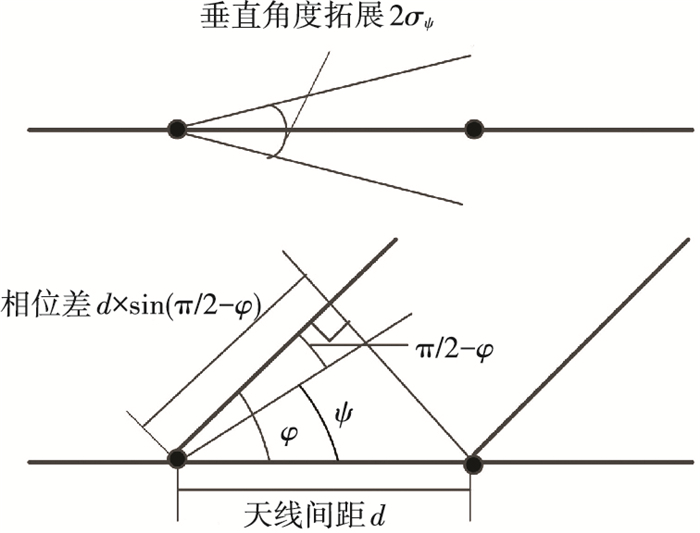
但其信道模型只在水平方向上具有角度拓展,将同时考虑在水平和垂直两个方向上角度扩展进行三维空间相关信道建模.信道模型见图 3.
|
图 3 Massive MIMO 3D空间相关信道 Figure 3 Massive MIMO 3D spatially correlated channel |
图 3中上部分为天线出射波在垂直方向的角度拓展,下部分为水平和垂直方向都有角度拓展的三维空间相关信道建模. 图 3中角度关系为
| $ \cos \varphi = \cos \left( {{\rm{ \mathit{ π} }}/2 - \varphi } \right) \times \cos \psi , $ | (6) |
代入式(4)得
| $ R = E\left( {\exp \left( {{\rm{j2 \mathit{ π} }}d\sin \left( {{\rm{ \mathit{ π} }}/2 - \varphi } \right)/\lambda } \right)} \right). $ | (7) |
再由式(5)得出Massive MIMO三维空间相关信道近似解析形式解为
| $ \begin{array}{l} R \approx \exp \left( { - \frac{{\sigma _\varphi ^2{{\hat \theta }^2}{{\cos }^2}\left( {{\rm{ \mathit{ π} }}/2 - \bar \varphi } \right)}}{2}} \right) \times \\ \;\;\;\;\;\exp \left[ { - {\rm{j}}\left( {1 - \frac{{\sigma _\varphi ^2}}{2}} \right)\hat \theta \sin \left( {{\rm{ \mathit{ π} }}/2 - \bar \varphi } \right)} \right]. \end{array} $ | (8) |
线性检测算法利用一个加权矩阵实现逆转信道的作用,基本的线性检测算法包括迫零检测算法和最小均方误差(MMSE)检测算法.
| $ \mathit{\boldsymbol{x}} = {\mathit{\boldsymbol{H}}^ + }\mathit{\boldsymbol{y}}. $ | (9) |
式中H+为信道矩阵的伪逆矩阵.
当接收天线数目大于发射天线数目时.信道矩阵的秩为发射天线数目,伪逆矩阵可以表示为
| $ {\mathit{\boldsymbol{H}}^ + } = {\left( {{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{H}}}, $ | (10) |
代入式(9)得:
| $ \mathit{\boldsymbol{x}} = {\left( {{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{H}}}y. $ | (11) |
上式即为迫零检测算法表达式.
当HHH为奇异矩阵时,伪逆矩阵可由下式得出:
| $ {\mathit{\boldsymbol{H}}^ + } = \mathop {\lim }\limits_{\delta \to \infty } {\left( {{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}} + \delta \mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{H}}}. $ | (12) |
式中I为单位矩阵,将δ用信号噪声σn2定义,则得下式为
| $ {H^ + } = \mathop {\lim }\limits_{\delta \to \infty } {\left( {{H^{\rm{H}}}H + \sigma _n^2I} \right)^{ - 1}}{H^{\rm{H}}}, $ | (13) |
代入式(9)即得
| $ x = \left( {{H^{\rm{H}}}H + \sigma _n^2I} \right){H^{\rm{H}}}y. $ | (14) |
上式即为最小均方误差(MMSE)检测算法表达式.
3 迭代检测算法 3.1 权重矩阵对称正定性证明由MMSE检测算法表达式(14)得
| $ \mathit{\boldsymbol{\hat x}} = {\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{\hat y}}, $ | (15) |
| $ \mathit{\boldsymbol{P}} = {\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}} + \sigma _n^2\mathit{\boldsymbol{I}}. $ | (16) |
式中:P为权矩阵,HH为信道矩阵的复共轭转置,由矩阵乘积性质,则矩阵HHH为对称矩阵.
| $ \mathit{\boldsymbol{\hat y}} = {\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{y}}. $ | (17) |
设存在任意复数域非零列向量X有
| $ \mathit{\boldsymbol{X}} \ne 0 \Rightarrow \mathit{\boldsymbol{HX}} \ne 0. $ | (18) |
根据矩阵二次型理论则有
| $ {\left( {\mathit{\boldsymbol{HX}}} \right)^{\rm{H}}}\mathit{\boldsymbol{HX}} = {\mathit{\boldsymbol{X}}^{\rm{H}}}{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{HX}} > 0. $ | (19) |
且由于噪声能量大于零,则权矩阵:
| $ \mathit{\boldsymbol{P}} = \left( {{\mathit{\boldsymbol{H}}^{\rm{H}}}\mathit{\boldsymbol{H}} + \sigma _n^2\mathit{\boldsymbol{I}}} \right) > 0. $ | (20) |
权矩阵P为对称正定矩阵,矩阵的对称正定性为利用迭代算法检测信号奠定了数学基础.
3.2 矩阵分解及迭代推导将式(15)变形为
| $ \mathit{\boldsymbol{P\hat x}} = \mathit{\boldsymbol{\hat y}}. $ | (21) |
将权矩阵P分解为
| $ \mathit{\boldsymbol{P}} = \mathit{\boldsymbol{D}} + \mathit{\boldsymbol{L}} + \mathit{\boldsymbol{U}}. $ | (22) |
式中:D为对角矩阵,L为下三角矩阵,U为上三角矩阵.代入式(21)得
| $ \left( {\mathit{\boldsymbol{D}} + \mathit{\boldsymbol{L}} + \mathit{\boldsymbol{U}}} \right)\mathit{\boldsymbol{\hat x}} = \mathit{\boldsymbol{\hat y}}. $ | (23) |
将公式逐步变形得
| $ \mathit{\boldsymbol{D\hat x}} = - \left( {\mathit{\boldsymbol{L}} + \mathit{\boldsymbol{U}}} \right)\mathit{\boldsymbol{\hat x}} + \mathit{\boldsymbol{\hat y}}. $ | (24) |
| $ \mathit{\boldsymbol{\hat x}} = - {\mathit{\boldsymbol{D}}^{ - 1}}\left( {\mathit{\boldsymbol{L}} + \mathit{\boldsymbol{U}}} \right){{\mathit{\boldsymbol{\hat x}}}^{\left( i \right)}} + {\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{\hat y}}. $ | (25) |
由此可得迭代公式为
| $ {{\mathit{\boldsymbol{\hat x}}}^{\left( {i + 1} \right)}} = - {\mathit{\boldsymbol{D}}^{ - 1}}\left( {\mathit{\boldsymbol{L}} + \mathit{\boldsymbol{U}}} \right){{\mathit{\boldsymbol{\hat x}}}^{\left( i \right)}} + {\mathit{\boldsymbol{D}}^{ - 1}}\mathit{\boldsymbol{\hat y}}. $ | (26) |
式中i为迭代次数,将矩阵写成分量形式为
| $ \hat x_j^{\left( {i + 1} \right)} = \frac{1}{{{P_{jj}}}}\left( {{{\hat y}_j} - \sum\limits_{m = 1}^{j - 1} {{p_{jm}}\hat x_m^{\left( i \right)}} - \sum\limits_{m = j + 1}^n {{p_{jm}}\hat x_m^{\left( i \right)}} } \right). $ | (27) |
分析式(27),在迭代过程中,每次迭代都是使用前一次迭代的全部分量
| $ \hat x_j^{\left( {i + 1} \right)} = \frac{1}{{{P_{jj}}}}\left( {{{\hat y}_j} - \sum\limits_{m = 1}^{j - 1} {{p_{jm}}\hat x_m^{\left( {i + 1} \right)}} - \sum\limits_{m = j + 1}^n {{p_{jm}}\hat x_m^{\left( i \right)}} } \right). $ | (28) |
加快迭代收敛速度,引入松弛因子ω,首先将上式改写为
| $ \hat x_j^{\left( {i + 1} \right)} = \hat x_j^{\left( i \right)} = \frac{1}{{{P_{jj}}}}\left( {{{\hat y}_j} - \sum\limits_{m = 1}^{j - 1} {{p_{jm}}\hat x_m^{\left( {i + 1} \right)}} - \sum\limits_{m = j}^n {{p_{jm}}\hat x_m^{\left( i \right)}} } \right), $ | (29) |
并记误差项为
| $ r_j^{\left( {i + 1} \right)} = \frac{1}{{{P_{jj}}}}\left( {{{\hat y}_j} - \sum\limits_{m = 1}^{j - 1} {{p_{jm}}\hat x_m^{\left( {i + 1} \right)}} - \sum\limits_{m = j + 1}^n {{p_{jm}}\hat x_m^{\left( i \right)}} } \right). $ | (30) |
当迭代收敛时,所有的误差趋于零.
使用松弛因子对误差项加以修正,得公式
| $ \hat x_j^{\left( {i + 1} \right)} = \hat x_j^{\left( i \right)} + \omega \times r_j^{\left( {i + 1} \right)}. $ | (31) |
将式(30)代入式(31)即得
| $ \hat x_j^{\left( {i + 1} \right)} = \hat x_j^{\left( i \right)} + \frac{\omega }{{{P_{jj}}}}\left( {{{\hat y}_j} - \sum\limits_{m = 1}^{j - 1} {{p_{jm}}\hat x_m^{\left( {i + 1} \right)}} - \sum\limits_{m = j + 1}^n {{p_{jm}}\hat x_m^{\left( i \right)}} } \right). $ | (32) |
将式(32)写成矩阵向量形式有
| $ \begin{array}{l} {{\hat x}^{\left( {i + 1} \right)}} = {\left( {\mathit{\boldsymbol{D}} + \omega \mathit{\boldsymbol{L}}} \right)^{ - 1}}\left[ {\left( {1 - \omega } \right)\mathit{\boldsymbol{D}} - \omega \mathit{\boldsymbol{U}}} \right]{{\mathit{\boldsymbol{\hat x}}}^{\left( i \right)}} + \\ \;\;\;\;\;\;\;\;\;\omega {\left( {\mathit{\boldsymbol{D}} + \omega \mathit{\boldsymbol{L}}} \right)^{ - 1}}\mathit{\boldsymbol{\hat y}}. \end{array} $ | (33) |
通过适当选取松弛因子,可以使式(33)迭代收敛更快.
3.3 松弛因子选取范围确定令式(33)的迭代矩阵为
| $ \mathit{\boldsymbol{B}} = {\left( {\mathit{\boldsymbol{D}} + \omega \mathit{\boldsymbol{L}}} \right)^{ - 1}}\left[ {\left( {1 - \omega } \right)\mathit{\boldsymbol{D}} - \omega \mathit{\boldsymbol{U}}} \right]. $ | (34) |
设迭代矩阵的特征值为依此为λ1, λ1, …, λn则迭代矩阵行列式为
| $ \left| \mathit{\boldsymbol{B}} \right| = \left| {{\lambda _1}{\lambda _1} \cdots {\lambda _{\rm{n}}}} \right| \le {\left[ {\rho \left( \mathit{\boldsymbol{B}} \right)} \right]^n}. $ | (35) |
式中ρ (B)为迭代矩阵的谱半径,同时由迭代方法收敛的充要条件为谱半径小于1[8]固有:
| $ {\left| \mathit{\boldsymbol{B}} \right|^{\frac{1}{n}}} = \rho \left( \mathit{\boldsymbol{B}} \right) < 1. $ | (36) |
迭代矩阵的行列式为
| $ \begin{array}{*{20}{c}} {\left| \mathit{\boldsymbol{B}} \right| = \left| {{{\left( {\mathit{\boldsymbol{D}} + \omega \mathit{\boldsymbol{L}}} \right)}^{ - 1}}} \right|\left| {\left[ {\left( {1 - \omega } \right)\mathit{\boldsymbol{D}} - \omega \mathit{\boldsymbol{U}}} \right]} \right| = }\\ {\left| {{{\left( {\mathit{\boldsymbol{D}} + \omega \mathit{\boldsymbol{L}}} \right)}^{ - 1}}} \right|\left| {\left( {1 - \omega } \right)\mathit{\boldsymbol{D}} - \omega \mathit{\boldsymbol{U}}} \right| = }\\ {{{\left| {\mathit{\boldsymbol{D}} + \omega \mathit{\boldsymbol{L}}} \right|}^{ - 1}}\left| {\left( {1 - \omega } \right)\mathit{\boldsymbol{D}} - \omega \mathit{\boldsymbol{U}}} \right| = }\\ {{{\left( {\prod\nolimits_{j = 1}^{j = n} {{p_{jj}}} } \right)}^{ - 1}} \times {{\left( {1 - \omega } \right)}^n} \times \left( {\prod\nolimits_{j = 1}^{j = n} {{p_{jj}}} } \right) = }\\ {{{\left( {1 - \omega } \right)}^n}.} \end{array} $ | (37) |
所以成立关系式有
| $ {\left| \mathit{\boldsymbol{B}} \right|^{\frac{1}{n}}} = {\left| {{{\left( {1 - \omega } \right)}^n}} \right|^{\frac{1}{n}}} < 1. $ | (38) |
即得松弛因子的范围为
| $ 0 < \omega < 2. $ | (39) |
当松弛因子等于1.0时,即为式(28).通常希望选择一个优化的松弛因子加快收敛速度,但是,目前尚无确定优化松弛因子的一般理论.必须结合具体实际工程确定一个优化超松弛因子.因此,通过仿真分析给出优化松弛因子便有了工程意义.
4 性能仿真 4.1 仿真条件计算机仿真验证算法性能,仿真参数见表 1.
| 表 1 仿真参数 Table 1 Simulation parameters |
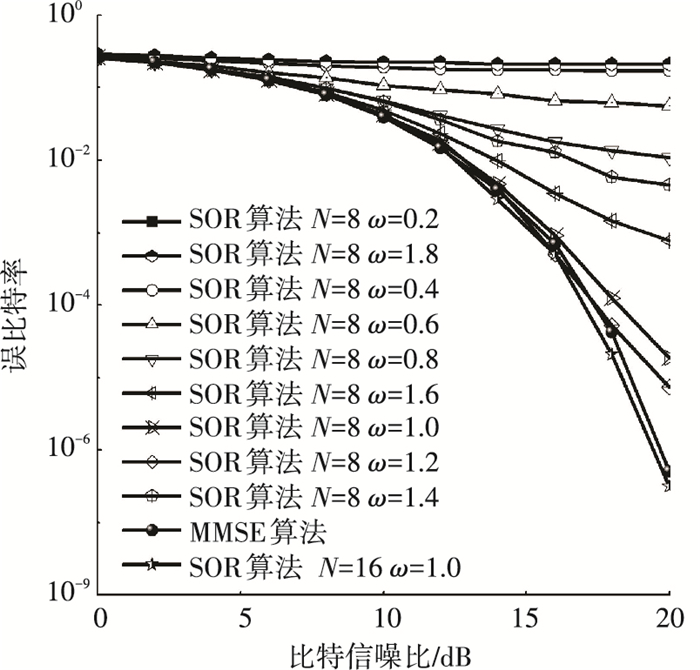
图 4所示为不同松弛因子迭代算法及MMSE检测算法的误比特率性能,迭代次数分别设定为8和16,按间距设定不同松弛因子,由图可见,在松弛因子为1.4时,误比特率性能接近迭代次数16时的误比特率检测性能和MMSE检测算法性能.迭代次数减少50%,信噪比10 dB到20 dB分集增益为3.96,分集增益较松弛因子为1.0提升1.71,在信噪比为20 dB时,误比特率下降近两个数量级.由此可见,优化松弛因子1.4能实现较少迭代次数下较低误比特率,同时说明的是此仿真帧数为十万次,所得结论不失一般性.分析原因是,在数学处理上引入优化松弛因子能减少迭代次数的同时尽可能逼近真值解,故而能实现少迭代次数低误比特率性能.
|
图 4 不同松弛因子下算法检测性能 Figure 4 The performance of detection algorithm for different relaxation factor |
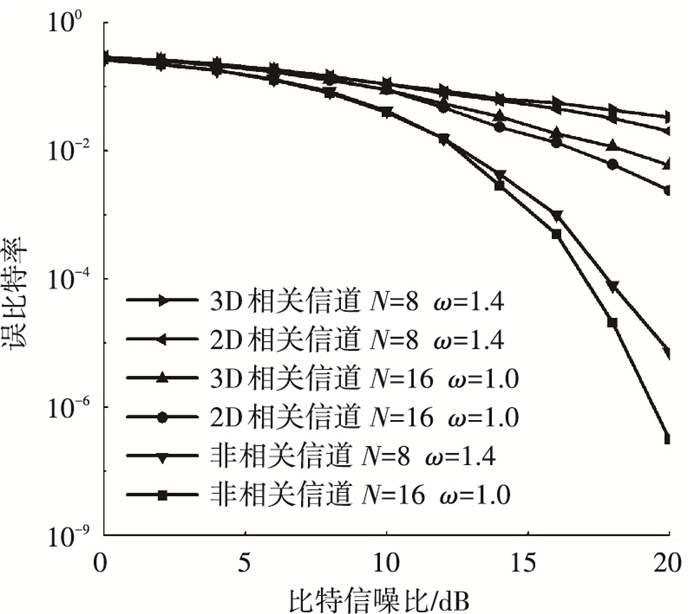
图 5所示Massive MIMO三维空间相关信道下超松弛检测算法的检测性能.由图可见,相关信道与非相关信道误比特率下降曲线相距较大,说明信道相关性对误比特率影响较大,且相关信道下误比特率曲线下降缓慢,则相关信道下分集增益较差,同时,在水平方向和垂直方向上都有角度扩展的三维空间相关信道,相比只有在水平方向上有角度扩展的二维空间相关信道,误比特率曲线更高,则其误比特率性能更差,这是因为在三维建模空间相关信道下其天线阵元间入射波相位差减小,等效阵元天线间距变小,信道相关性增大.因此,在实际性能分析时,要加以考虑信道相关性,更应注意由三维角度拓展造成的信道相关性加剧影响.
|
图 5 Massive MIMO空间相关信道下检测性能 Figure 5 The performance of detection for Massive MIMO in spatially correlated channel |
计算复杂度主要分析算法检测过程中复数乘法的运算次数.假定信道在一帧内时不变,同时将计算复杂度分为起始部分和过程部分.其中,起始部分是指权矩阵的计算部分,过程部分是指后续检测部分. MMSE检测算法起始部分包括信道矩阵伪逆过程和权矩阵求逆过程,后续检测部分是指信号检测矩阵运算部分.迭代算法起始部分是权矩阵的得出过程,后续部分是迭代检测部分,其中,未引入松弛因子迭代算法按式(28)分析,引入松弛因子按式(32)分析.
计算复杂度分析见表 2,其中M为调制阶数,NT为发射天线数目,NR为接收天线数目,N为迭代次数.
| 表 2 计算复杂度 Table 2 Computational complexity |
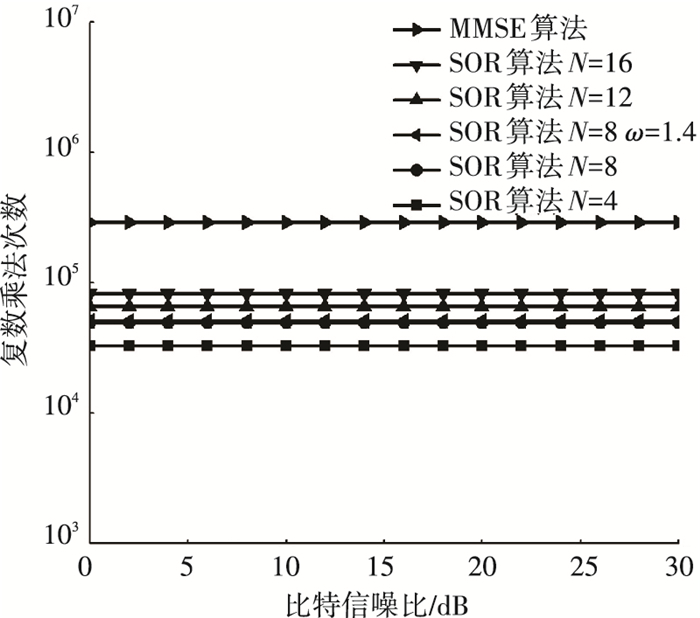
图 6所示为检测算法的计算复杂度.由图可见MMSE检测算法的复杂度高出迭代次检测算法近一个数量级.迭代检测算法中,迭代次数为8时,其计算复杂度处于较低位置.迭代算法的计算复杂度主要是由迭代次数引起,显然,随着迭代次数的增加,计算复杂度逐渐增加,第8次迭代产生的计算复杂度约占总复杂度的8.32%,而第16次迭代产生的计算复杂度,只占总复杂度的5.00%,可见,由迭代产生的计算复杂度占比逐渐下降,这是因为每次迭代产生的复杂度保持不变,而总复杂度在逐渐增加,但总复杂度增加比率在下降.同时注意到无论是MMSE检测算法,还是迭代检测算法其计算复杂度不随信噪比变化而变化,能一定程度保证检测算法的稳定性.
|
图 6 检测算法计算复杂度 Figure 6 The computational complexity of detection algorithm |
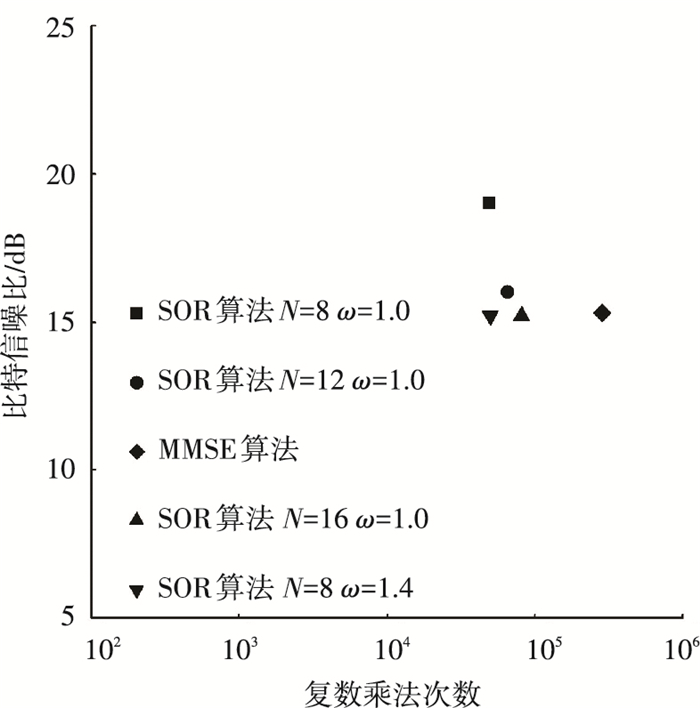
图 7所示在误比特率为10-3下,信噪比与计算复杂度权衡分析图.由图可见,优化松弛因子为1.4相比较正常松弛因子1.0,当迭代次数为8时,所需信噪比下降近4 dB,误比特率性能与迭代次数16相近,且计算复杂度低近20%,优化松弛因子1.4超松弛迭代算法能在计算复杂度和信噪比综合下实现较优检测.
|
图 7 信噪比与复杂度权衡分析 Figure 7 The trade-off between the signal-to-noise ratio and the computational complexity |
本文首先以只在水平方向上具有角度拓展空间相关信道为基础,构建在水平和垂直两个方向上都具有角度扩展的三维空间相关信道模型,推导出信道相关性解析形式表达式.同时采用低复杂度的优化松弛因子超松弛迭代方法进行信号检测.仿真结果表明:三维空间相关信道模型相比较二维空间相关信道模型加剧信道相关性,在优化松弛因子为1.4下,相比较同等迭代次数为8、松弛因子为1.0、误比特率10-3时,所需信噪比降低约4 dB,分集增益提升1.71,接近迭代次数为16的误比特率检测性能,计算复杂度降低近20%,在权衡分析信噪比和计算复杂度情况下,能获得较优检测性能.
| [1] |
MARETTAT L. Noncooperative cellular wireless with unlimited numbers of base station antennas[J].
IEEE Transactions on Wireless Communication, 2010, 9(11): 3590-3600.
DOI: 10.1109/TWC.2010.092810.091092 |
| [2] |
RUSEKF, PERSSON D, LAU B K, et al. Scaling up MIMO opportunities and challenges with very large arrays[J].
Signal Processing Magazine, 2013, 30(1): 40-60.
DOI: 10.1109/TWC.2010.092810.091092 |
| [3] |
LU L, LI Y G, ASHIKGMIN A, et al. An overview of massive MIMO benefits and challenges[J].
IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 742-758.
DOI: 10.1109/JSTSP.2014.2317671 |
| [4] |
NGO H, LARSSON E, MARZETTA T. Energy and spectral efficiency of very large multiuser MIMO systems[J].
IEEE Transactions on Communication, 2012, 61(4): 1436-1449.
DOI: 10.1109/TCOMM.2013.020413.110848 |
| [5] |
HOYDIS J, BRINK T S, DEBBAH M. Massive MIMO in the UL/DL of cellular networks how many antennas do we need[J].
IEEE Journal on Selected Areas in Communications, 2013, 31(2): 160-171.
DOI: 10.1109/JSAC.2013.130205 |
| [6] |
ISHIHARA K, TAKATORI Y, KUBOTA S, et al. Multiuser detection for asynchronous broadband single-carrier transmission systems[J].
IEEE Transactions on Vehicular Technology, 2009, 58(6): 3066-3071.
DOI: 10.1109/TVT.2009.2012716 |
| [7] |
WU M, YIN B, WANG Guohui, et al. Large-scale MIMO section for 3GPP LTE algorithms and FPGA implementations[J].
IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 916-929.
DOI: 10.1109/JSTSP.2014.2313021 |
| [8] |
ZHU X, MURCH R D. Performance analysis of maximum likelihood detection in a MIMO antenna system[J].
IEEE Transactions on Communication, 2002, 50(2): 187-191.
DOI: 10.1109/26.983313 |
| [9] |
YIN B, WU M, STUDER C, et al. Implementation trade-offs for linear detection in large-scale MIMO systems[C]// International Conference on Acoustics Speech and Signal Processing Vancouver: IEEE Press, 2013: 2679-2683. DOI: 10.1109/ICASSP.2013.6638142.
|
| [10] |
TSUNG L. Some results for fast MMSE-SIC detection in spatially multiplexed MIMO systems[J].
IEEE Transaction on Wireless Communication, 2009, 8(11): 5443-5448.
DOI: 10.1109/TWC.2009.090196 |
| [11] |
BAI D, PARK C, LEE J, et al. LTE-advanced modem design: challenges and perspectives[J].
IEEE Communications Magazine, 2012, 50(2): 178-186.
DOI: 10.1109/MCOM.2012.6146497 |
| [12] |
HACKBUSCHW. Iterative solution of large linear systems[M]. Leipzig: Springer Nature, 1994: 78-83.
|
| [13] |
吴勃英.
数值分析原理[M]. 北京: 科学出版社, 2003: 76-79.
WU Boying. Numerical analysis principle[M]. Beijing: Science Press, 2003: 76-79. |
| [14] |
GOLUB G H, WANLOAN C F.
Matrix computations[M]. Baltimore: Johns Hopkins University Press, 2012: 441-443.
|
| [15] |
KERMOAL J P, SCHUMACHER L, PEDERSENK I, et al. A stochastic MIMO radio channel model with experimental validation[J].
IEEE Areas Communication, 2002, 20(6): 1211-1226.
DOI: 10.1109/JSAC.2002.801223 |
| [16] |
ZHENG Liming, FUKAWA K, SUZUKI H, et al. Low-complexity signal detection by multi-dimensional search for correlated MIMO channels[C]// International Conference on Communications. Kyoto: IEEE Press, 2011: 1-5. DOI: 10.1109/icc.2011.5962771.
|
 2018, Vol. 50
2018, Vol. 50


