柔性薄膜天线具有重量轻、可卷曲展开、易与结构一体化等特点,在航空航天、雷达、手机通信、物联网等领域具有广阔的应用前景[1-3].丝网印刷技术因其制备工艺简单、成本低、印刷精度高等优点,在柔性电子和天线领域得到了广泛地应用.目前,基于丝网印刷技术制备的柔性薄膜天线性能研究主要包括:丝网印刷工艺研究[4]、辐射层微观形貌和电阻特性研究[5-6]、辐射层与基体界面粘接强度研究[7]及电磁性能研究[8-10].采用丝网印刷工艺制备的天线辐射层依附薄膜基体存在,难以获得独立样件,因此对辐射层的基本力学性能研究甚少.从已有的文献来看,针对导电银浆辐射层和薄膜基体之间的界面性能只进行了定性分析,然而在薄膜天线实际破坏中,辐射层与基体界面脱粘是常见的失效模式,而有关基于丝网印刷技术的导电辐射层/薄膜基体之间的界面性能没有深入定量地研究.
为解决上述问题,本文将导电银浆辐射层看作颗粒增强复合材料,利用Mori-Tanaka复合材料细观力学方法和拉伸叠加法得到辐射层的有效弹性模量,二者吻合良好.建立了基于内聚力单元的辐射层/薄膜基体界面剥离性能有限元分析模型,揭示薄膜印刷天线界面破坏机理,得到了界面剥离强度,并与实验结果进行了比较.并研究了薄膜印刷天线的电磁性能.
1 薄膜天线设计及其实验方法 1.1 天线设计设计的微带准八木天线结构见图 1.天线由导电辐射层和薄膜基体组成,设计的谐振频率为3.0 GHz,聚酰亚胺薄膜基体的介电常数为3.4,介电损耗为0.002,厚度为0.05 mm.

|
图 1 微带准八木天线示意 Figure 1 Microstrip quasi-yagi antenna geometry |
八木天线辐射层尺寸参数对天线的阻抗匹配(反射系数特性)和方向图性能有很大的影响.有源振子的长度约为半波长,其它尺寸参数基于微带天线基本理论确定初始值,然后通过商用电磁场分析软件CST Microwave Studio(CST微波工作室)优化仿真获得.最终得到的部分参数值见表 1.
| 表 1 天线辐射层结构尺寸值 Table 1 Dimension values of the antenna radiation layer |
丝网印刷工艺印刷工作原理见图 2.利用刮刀将导电银浆油墨印刷到聚酰亚胺薄膜基体上,形成天线辐射层,然后在高温干燥箱140℃温度下烧结45min,待温度降至常温时取出试件便可得到薄膜天线试件,见图 3(a).本文采用聚酯网版,目数为300目,网框材料为铝合金,利用半自动丝网印刷机实现薄膜天线的印刷制备,在印刷前将聚酰亚胺薄膜表面用酒精清洗并干燥以保证印刷效果.采用丝网印刷工艺制备的薄膜天线具有柔性、可与结构共形、易卷曲等特点,见图 3(b).

|
图 2 丝网印刷工艺原理示意 Figure 2 Schematic diagram of screen printing technology |

|
图 3 薄膜天线实物样件 Figure 3 Prototypes of the membrane antenna |
利用光学显微镜(Keyence VHX900,日本)测量天线辐射层不同区域20个位置的厚度,计算其平均值,得到的导电银浆辐射层厚度为0.010 2 mm.薄膜天线拉伸试验在Instron5569电子万能试验机上进行,加载速度为5 mm/min,试验标准参考GB13022-91《塑料薄膜拉伸性能试验方法》.
剥离强度是表征膜/基体系界面粘接强度的重要参数之一.利用90°剥离试验可获得出辐射层与基体之间的界面强度.剥离试验依据IEC 60326-2标准,采用HY0580—50N量程的传感器(有效测力范围0.1%~100%,测力精度为示指的±0.5%以内)进行测试.本文剥离试验样件尺寸为110 mm×10 mm,每次试验最少5个试件.本文将导电银浆辐射层利用强力胶粘接到有机玻璃板上,利用夹具夹住聚酰亚胺薄膜一端进行剥离试验,使得聚酰亚胺薄膜能够与辐射层完全剥离.剥离强度的计算方法为辐射层从基体材料上分离单位宽度上所需的力,以N/m表示.天线反射系数利用微波网络矢量分析仪测试,增益方向图测试在微波暗室中进行.
2 薄膜天线力学性能表征 2.1 Mori-Tanaka方法预测辐射层弹性模量导电银浆高温烧结后的主要成分为银颗粒和环氧树脂.固化后银颗粒以不同的形状分散在树脂基体中,可以将辐射层看作银颗粒增强环氧树脂复合材料,根据复合材料细观力学理论来预测其有效弹性模量. Mori-Tanaka方法由于计算简单,在一定程度上考虑了复合材料中夹杂之间的相互作用,成为预测复合材料有效模量的常用方法.对于两相复合材料,利用Mori-Tanaka方法计算复合材料弹性模量和泊松比的公式为[11]
| $ E = \frac{{9GK}}{{3K + G}}, $ | (1) |
| $ \mu = \frac{{3K - 2G}}{{6K + 2G}}, $ | (2) |
| $ \frac{K}{{{K_0}}} = 1 + \frac{{{c_1}}}{{\frac{{3{c_0}}}{{3{K_0} + 4{G_0}}} + \frac{{{K_0}}}{{{K_1} - {K_0}}}}}, $ | (3) |
| $ \frac{G}{{{G_0}}} = 1 + \frac{{{c_1}}}{{\frac{6}{5}\frac{{{c_0}\left( {{K_0} + 2{G_0}} \right)}}{{3{K_0} + 4{G_0}}} + \frac{{{G_0}}}{{{G_1} - {G_0}}}}}. $ | (4) |
式中:K为体积模量,G为剪切模量,c为体积分数,E为有效弹性模量,μ为泊松比,下标1表示银颗粒,0表示基体.
环氧树脂和银颗粒的材料性能参数见表 2.利用式(1)~(4)可得到辐射层弹性模量和泊松比随着银颗粒体积含量的变化关系见图 4.由图 4可知,随着银颗粒体积含量的增加,辐射层的弹性模量逐渐增大.导电银浆中银颗粒含量的质量分数为71%,转化成体积分数为20.12%.由Mori-Tanaka理论可以得到导电银浆涂层的有效弹性模量为3 292 MPa、有效泊松比为0.364.
| 表 2 导电银浆辐射层各组分性能参数 Table 2 Material properties of components of silver paste radiation layer |

|
图 4 辐射层弹性模量和泊松比随着银颗粒体积含量的变化 Figure 4 Elastic modulus and poisson ratio of the radiation layer with variable volume fraction of silver particle |
单轴拉伸试验可直观地得到材料的弹性模量和屈服强度等力学性能参数.通过分别对聚酰亚胺薄膜基体和辐射层/基体进行宏观单向拉伸试验,根据叠加原理可得到辐射层的弹性模量和屈服强度[12]
| $ {E_{\rm{f}}} = \frac{1}{{{A_{\rm{f}}}}}\left[ {{A_{{\rm{total}}}}{E_{{\rm{total}}}} - {A_{\rm{s}}}{E_{\rm{s}}}} \right] = \left( {1 + \frac{{{h_{\rm{s}}}}}{{{h_{\rm{f}}}}}} \right){E_{{\rm{total}}}} - \left( {\frac{{{h_{\rm{s}}}}}{{{h_{\rm{f}}}}}} \right){E_{\rm{s}}}, $ | (5) |
| $ {\sigma _{\rm{f}}} = \frac{1}{{{A_{\rm{f}}}}}\left[ {P - {P_{\rm{s}}}} \right] = \left( {1 + \frac{{{h_{\rm{s}}}}}{{{h_{\rm{c}}}}}} \right){\sigma _{{\rm{total}}}} - \left( {\frac{{{h_{\rm{s}}}}}{{{h_{\rm{c}}}}}} \right){\sigma _{\rm{s}}}. $ | (6) |
式中:P为载荷,E为弹性模量,σ为应力,h为厚度,下标total为辐射层/薄膜体系,s为薄膜基体,f为辐射层.
聚酰亚胺薄膜和辐射层/基体的实测应力—应变曲线见图 5.由图可知,辐射层/基体的弹性模量Etotal和屈服强度σtotal分别为2 464 MPa、52.17 MPa,聚酰亚胺薄膜基体的弹性模量Es和屈服强度σs分别为2 358 MPa、50.92 MPa.由式(5)、(6)可计算得到辐射层的弹性模量为2 983 MPa、屈服强度为58.30 MPa.

|
图 5 薄膜基体及辐射层/基体的应力—应变测试曲 Figure 5 Measured stress-strain curves of the PI film and radiation layer/PI film |
由以上分析可知,利用Mori-Tanaka细观力学方法预测的辐射层弹性模量比拉伸叠加法高出312 MPa,误差为10.46%.在拉伸法实验过程中,辐射层与聚酰亚胺薄膜基体界面之间可能出现相对滑移现象,另外,拉伸会导致辐射层表面产生微裂纹,降低整个辐射层/基体的力学性能.因此,利用拉伸法预测银浆涂层的弹性模量要比其实际值偏小.
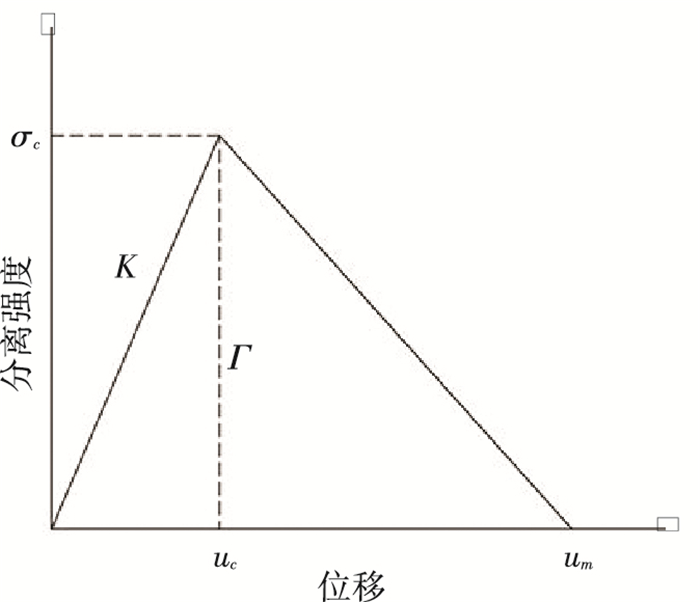
2.3 薄膜天线辐射层与基体界面结合强度分析内聚力模型可以反映出界面层物质的模量、强度和韧度等力学性能,在材料或结构界面性能表征的有限元分析中得到了广泛运用.内聚力模型采用一层内聚力单元来模拟界面的作用,单元的变形遵守内聚本构关系Traction-Separation响应曲线[13],本文选择双线性内聚力模型来模拟薄膜天线界面性能.双线性内聚力模型的应力-位移曲线见图 6.控制内聚力模型的两个关键参数分别是单元分离极限强度和单元的断裂能:单元分离极限强度为单元应力-位移曲线峰值点对应的最大应力值σm,它决定了单元破坏的起始条件;单元断裂能是应力—位移曲线与横轴所包围的面积大小,决定单元的破坏演变过程.
|
图 6 双线性内聚力模型应力-位移曲线 Figure 6 Bilineartraction-separation laws of the cohesive-zone model |
双线性内聚力单元材料刚度的失效分为破坏起始阶段和破坏演变阶段.破坏起始是指界面刚度开始弱化的时刻,当单元的应力满足破坏判定准则的时单元的刚度开始下降.采用平方应力准则来表征单元破坏.
| $ {\left( {\frac{{\left\langle {{\sigma _{\rm{n}}}} \right\rangle }}{{{\sigma _{{\rm{nc}}}}}}} \right)^2} + {\left( {\frac{{\left\langle {{\sigma _{\rm{t}}}} \right\rangle }}{{{\sigma _{{\rm{tc}}}}}}} \right)^2}{\left( {\frac{{\left\langle {{\sigma _{\rm{s}}}} \right\rangle }}{{{\sigma _{{\rm{sc}}}}}}} \right)^2} = 1. $ |
式中:σn是单元法向应力,σt和σs是单元的2个切向应力,σnc是单元法向应力失效控制值,σtc和σsc是单元切向应力失效控制值.
内聚力模型破坏演化是指单元破坏起始后,单元力学性能退变的过程,在这个阶段单元的刚度不断弱化.弱化过程引入刚度弱化参数D,当D为1时表示材料完全破坏.破坏起始后D的值从0开始不断增加至到达到1时为止,双线性内聚力模型刚度弱化参数D的计算方法如下
| $ D = \frac{{\delta _{\rm{m}}^{\rm{f}}\left( {\delta _{\rm{m}}^{{\rm{max}}} - \delta _{\rm{m}}^{\rm{0}}} \right)}}{{\delta _{\rm{m}}^{{\rm{max}}}\left( {\delta _{\rm{m}}^{\rm{f}} - \delta _{\rm{m}}^{\rm{0}}} \right)}}. $ |
式中:δm0是破坏起始时单元节点的张开量,δmf是D=1时节点的张开量,δmmax是在载荷历程中节点的最大张开量.破坏起始时单元节点对应的张开量δm0的计算如下:
| $ {\sigma _{\rm{n}}} = {K_{\rm{n}}}{\delta _{\rm{n}}}, $ |
| $ {\sigma _{\rm{t}}} = {K_{\rm{t}}}{\delta _{\rm{t}}}, $ |
| $ \delta _{\rm{m}}^0 = \sqrt {1 + {\beta ^2}} \frac{{{\delta _{{\rm{nc}}}}{\delta _{{\rm{tc}}}}}}{{\sqrt {K_{\rm{n}}^2\delta _{{\rm{tc}}}^2 + {\beta ^2}K_{\rm{t}}^2\delta _{{\rm{nc}}}^2} }}. $ |
式中:σn为单元法向应力,σt为单元切向应力,Kn为单元法向刚度,Kt分单元切向刚度,δn为单元节点的法向张开量,δt为切向张量,β为位移复合比.
利用ABAQUS有限元分析软件模拟辐射层/薄膜基体之间的界面粘接强度,有限元模型见图 7.在聚酰亚胺薄膜和辐射层之间为内聚力单元,内聚力单元层与薄膜基体和辐射层单元共节点.聚酰亚胺薄膜右侧自由端为剥离臂,剥离臂长度为5 mm,在辐射下表面施加固定约束.

|
图 7 剥离分析有限元模型(部分显示) Figure 7 FEA model of the peel analysis |
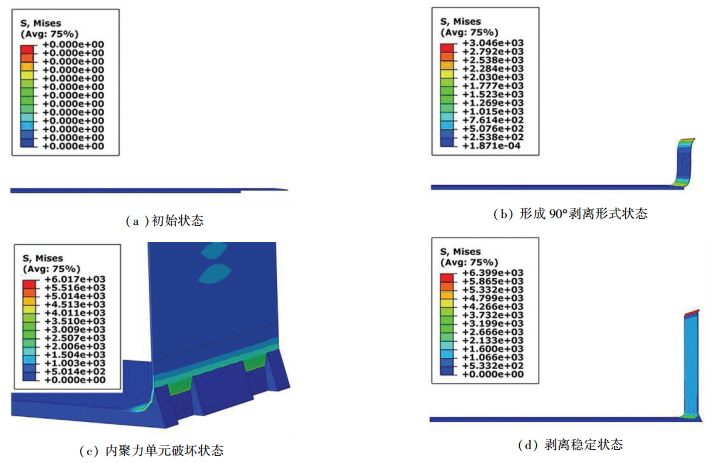
采用有限元方法可揭示薄膜天线界面破坏过程,见图 8,具体过程如下:
|
图 8 剥离过程有限元仿真 Figure 8 The finite element simulation of the peel process |
1) 初始有限元模型见图 8(a),在初始时刻剥离臂位于水平状态,在剥离臂末端施加竖直向上的位移载荷,形成90°剥离的形式.此时,由于界面剥离还未开始,薄膜基体和内聚力单元层的应力均为零,见图 8(b);
2) 继续施加载荷,当辐射层和基体界面单元的应力满足平方应力破坏准则时,单元刚度逐渐变小进入破坏演化阶段,当单元的刚度减低到零时则完全失效,失效的单元从有限元模型中自动消失,见图 8(c);
3) 上述失效单元消失后与其相邻的单元相继失效,且重复这个失效过程.最后,随着失效的内聚力单元越来越多,剥离区域变的越来越长,直至模型收敛,见图 8(d).
通过有限元和实验得到的剥离力—位移曲线见图 9.计算剥离曲线处于稳定阶段力的平均值(位移为5 mm~17 mm范围内力的平均值).用剥离强度来表征界面粘接性能,其计算方法为单位宽度上的剥离力,单位为N/m.则得到有限元和实测的剥离强度分别为64 N/m和59.2 N/m,误差为8.11%,结果吻合良好.

|
图 9 剥离力—位移有限元和实验曲线 Figure 9 Peel force-displacement curve by FEA and experiment |
图 10为薄膜天线仿真与实测反射系数曲线图.由图可知,天线仿真和实测谐振频率分别为3.02 GHz和2.95 GHz,吻合良好,且均在设计谐振频率3 GHz附近.阻抗匹配效率是天线的主要指标,当阻抗匹配效率为100%时,表示天线处于理想阻抗匹配状态,当阻抗匹配效率为0%时,表示天线阻抗完全失配.实际中,一般要求天线阻抗匹配效率大于95%,天线阻抗匹配效率与反射系数的关系为[14]
| $ {e_z} = 1 - {\left( {{{10}^{\frac{{{L_{\rm{R}}}}}{{20}}}}} \right)^2}, $ |

|
图 10 柔性薄膜天线反射系数仿真与测试曲线 Figure 10 Simulated and measured reflection coefficient of the flexible membrane antenna |
式中ez和LR表示阻抗匹配效率和反射系数.
天线在谐振频率处仿真与实测的反射系数值分别为-19.75 dB和-21.1 dB,对应的阻抗匹配效率分别为98.9%和99.2%,阻抗匹配良好,仿真与测试反射系数误差为6.4%.
天线带宽是衡量天线性能的另一重要指标,是指反射系数值小于-10 dB的频率范围.薄膜天线仿真与实测带宽分别为392 MHz(2.758~3.15 GHz)和364 MHz(2.7~3.064 GHz),仿真与实测值误差为7.69%.
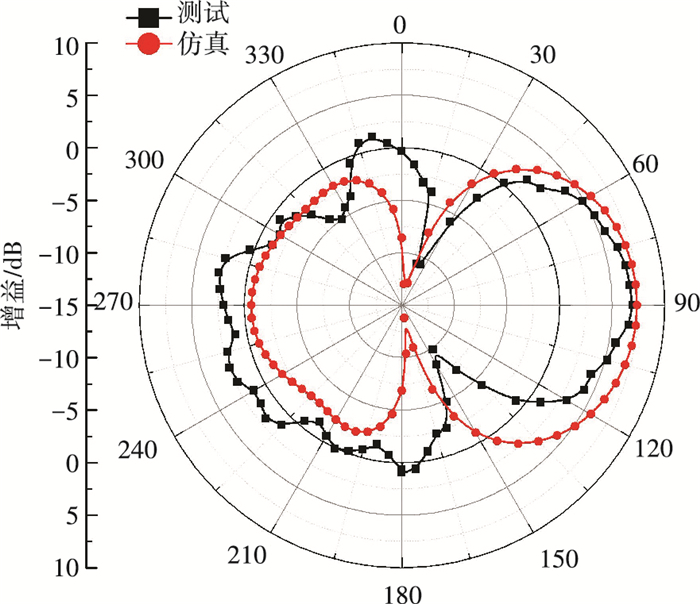
薄膜天线H面辐射方向图曲线见图 11,天线主辐射方向沿着结构表面,为端射辐射.仿真与实测方向图在主瓣范围内吻合良好,仿真和实测增益分别为7.38和6.96 dB.天线方向图在后瓣区域仿真与实测误差较大,这是由于在天线测试过程中,薄膜天线会产生一定程度的倾角,从而与标准测试天线不在同一水平位置,导致薄膜天线后瓣误差较大.但是薄膜天线在主瓣区域吻合良好,满足实际工程应用.
|
图 11 柔性薄膜天线仿真与测试H面辐射方向 Figure 11 Simulated and measured H plane radiation patterns of the flexible membrane antenna |
1) 基于天线设计理论和丝网印刷工艺技术设计并制备了柔性薄膜天线,具有轻质、柔性、易弯曲并易与结构一体化等特点,有广泛的应用前景.
2) 为快速、方便且较准确的计算导电银浆辐射层力学参数,利用Mori-Tanaka复合材料细观力学方法预测其弹性模量,并与拉伸叠加法结果比较,误差为10.46%.为其它丝网印刷油墨材料的力学参数预测提供了一定的理论依据.
3) 基于双线性内聚力有限元模型分析了导电银浆辐射层和薄膜基体的界面剥离性能,揭示了薄膜天线界面破坏过程.有限元模型得到的剥离强度与实验吻合良好.
4) 薄膜天线具有良好的电磁性能,其测试谐振频率为2.95GHz,带宽364MHz,增益为6.96dB,与仿真结果吻合良好,均满足设计要求.
| [1] |
CHEN M Y, LU X, SUBBARAMAN H, et al. Fully printed phased-array antenna for space communications[C]// Proceedings of SPIE-The International Society for Optical Engineering. Baltimore, Maryland: SPIE press, 2009: 731814-6. DOI: 10.1117/12.819036.
|
| [2] |
RIDA A, YANG L, REYNOLDS T, et al. Inkjet-printing UHF antenna for RFID and sensing applications on liquid crystal polymer[C]// Antennas and Propagation Society International Symposium, IEEE. Charleston, South Carolina: IEEE press, 2009: 1-4. DOI: 10.1109/APS.2009.5171791.
|
| [3] |
RIDA A, YANG L, VYAS R, et al. Conductive inkjet-printed antennas on flexible low-cost paper-based substrates for RFID and WSN applications[J].
IEEE Antennas and Propagation Magazine, 2009, 51(3): 13-23.
DOI: 10.1109/MAP.2009.5251188 |
| [4] |
何雪梅, 何为, 陈苑明, 等. 卷到卷丝网印刷RFID天线的工艺优化研究[J].
印制电路信息, 2011(4): 117-120.
HE Xuemei, HE Wei, CHEN Yuanming, et al. Study on process parameters of RFID antenna printed with roll to roll technology[J]. Printed Circuit Information, 2011(4): 117-120. DOI: 10.3969/j.issn.1009-0096.2011.04.025 |
| [5] |
MERILAMPI S, LAINE T, RUUSKANEN P. The characterization of electrically conductive silver ink patterns on flexible substrates[J].
Microelectronics Reliability, 2009, 49(7): 782-790.
DOI: 10.1016/j.microrel.2009.04.004 |
| [6] |
KIM Y, LEE B, YANG S, et al. Use of copper ink for fabricating conductive electrodes and RFID antenna tags by screen printing[J].
Current Applied Physics, 2012, 12(2): 473-478.
DOI: 10.1016/j.cap.2011.08.003 |
| [7] |
JOO S, BALDWIN D F. Interfacial adhesion of nano-particle silver interconnects for electronics packaging application[C]// Electronic Components and Technology Conference. IEEE. Orlando, Florida: IEEE press, 2008: 1417-1423. DOI: 10.1109/ECTC.2008.4550163.
|
| [8] |
SHIN D Y, LEE Y, KIM C H. Performance characterization of screen printed radio frequency identification antennas with silver nanopaste[J].
Thin Solid Films, 2009, 517(21): 6112-6118.
DOI: 10.1016/j.tsf.2009.05.019 |
| [9] |
SALMERON J F, MOLINA-LOPEZ F, BRIAND D, et al. Properties and printability of inkjet and screen-printed silver patterns for RFID antennas[J].
Journal of Electronic Materials, 2014, 43(2): 604-617.
DOI: 10.1007/s11664-013-2893-4 |
| [10] |
NELO M, SOWPATI A K, PALUKURU V K, et al. Utilization of screen printed low curing temperature cobalt nanoparticle ink for miniaturization of patch antennas[J].
Progress in Electromagnetics Research, 2012, 127(3): 427-444.
DOI: 10.2528/PIER12031408 |
| [11] |
WENG G J. Some elastic properties of reinforced solids, with special reference to isotropic ones containing spherical inclusions[J].
International Journal of Engineering Science, 1984, 22(7): 845-856.
DOI: 10.1016/0020-7225(84)90033-8 |
| [12] |
AVILES F, LANES L, OLIVA A I. Elasto-plastic properties of gold thin films deposited onto polymeric substrates[J].
Journal of Materials Science, 2009, 44(10): 2590-2598.
DOI: 10.1007/s10853-009-3339-5 |
| [13] |
CHANDRA N, LI H, SHET C, et al. Some issues in the application of cohesive zone models for metal-ceramic interfaces[J].
International Journal of Solids and Structures, 2002, 39(10): 2827-2855.
DOI: 10.1016/S0020-7683(02)00149-X |
| [14] |
钟顺时.
天线理论与技术[M]. 北京: 电子工业出版社, 2011: 52-53.
ZHONG Shunshi. Antenna theory and techniques[M]. Beijing: Publishing House of Electronics Industry, 2011: 52-53. |
 2018, Vol. 50
2018, Vol. 50


