战场中机动目标状态往往呈现随机性、多样性等特点,使得传统雷达难以对其有效追踪,这成为当前研究热点和难点.多数研究从接收端数据处理出发,侧重目标状态建模及滤波算法改进[1-3];忽视目标跟踪精度不仅与数据处理方式有关,且受发射波形影响,导致跟踪误差大、鲁棒性差等问题.对此,新体制认知雷达可视为解决此类问题的有效途径,其能够感知目标状态机动并自适应地调整波形及接收端信号处理方式,以获取更为准确的目标信息[4-6].
文献[7]针对目标跟踪问题构造多站场景,集中处理多站接收数据来选择波形及发射-接收位置配对,提升目标跟踪性能;文献[8]考虑多传感器数据融合思路,分析两部雷达接收数据并结合粒子滤波算法来设计波形以提高跟踪性能.上述研究均侧重于接收数据处理而忽视目标机动随机性、多样性问题,若模型失配或先验知识缺失则多站跟踪性能也难以保证.为了解决目标模型失配问题,文献[9]构造多项式预测模型并以目标状态预测误差椭圆为基准,通过FrFT旋转量测误差椭圆使其与状态预测误差椭圆正交来选择最优波形;但其对于机动检测窗口设置缺乏先验指导,而难以应用于具体场景.文献[10]引入交互多模型(Interacting Multiple Model,IMM)跟踪算法框架,并利用FrFT旋转波形模糊函数得到新的量测误差椭圆,实现波形捷变;文献[11]针对多站跟踪场景,引入IMM-扩展卡尔曼滤波算法来对各站接收数据进行集中处理,并用跟踪误差协方差矩阵构建目标函数进行波形参数调整;文献[12]在IMM框架下考虑波形模糊函数与Fisher信息矩阵中波形参数的对应关系, 以目标距离、速度估计性能克拉美罗下界作为评价标准来得到最优波形;上述IMM算法中往往采用概率加权来联接不同子模型状态输出,忽视目标状态向量及其误差协方差矩阵中不同维度元素间相关性,影响目标状态匹配性能,使得跟踪误差随时间积累而逐步增大[13].另外,文献[14-15]指出常规IMM中固定马尔科夫转移矩阵亦使模型转换速度变慢、精度降低.
针对上述机动目标跟踪问题,本文基于多模型融合思想,引入矩阵加权多模型融合的自适应波形设计算法.首先,利用多模型思路对机动目标状态进行建模,并考虑各模型目标状态估计及其误差协方差矩阵中元素间相关性,以矩阵加权融合方式代替传统概率加权方式,构造多模型跟踪算法框架;然后,以状态融合估计误差协方差矩阵为基准,利用特征值分解求取矩阵椭圆参数;最后,通过FrFT来旋转量测误差椭圆使其与融合状态误差椭圆正交,实现波形自适应调整.仿真实验表明,所提算法相比当前流行算法能够获得更低跟踪误差和更强稳健性.
1 基于交互多模型的目标跟踪方法简介IMM算法对于机动目标跟踪表现出良好性能优势;其核心在于考虑目标可能多个机动模型,并分配线性或非线性滤波器,各滤波器并行工作得到模型概率,进而综合输出目标估计状态及误差协方差矩阵.由文献[16-17]知,多模型思路建模往往假定模型间转移服从已知转移概率的一阶马尔科夫链,从而可利用模型先验概率及转移概率来计算各滤波器交互估计.
1.1 目标运动模型目标状态方程和量测方程如下:
| $ \mathit{\boldsymbol{x}}\left( {k + 1} \right) = {\mathit{\boldsymbol{F}}_j}\left( {\mathit{\boldsymbol{x}}\left( k \right)} \right) + {\mathit{\boldsymbol{w}}_j}\left( k \right), $ | (1) |
| $ \mathit{\boldsymbol{z}}\left( k \right) = {\mathit{\boldsymbol{H}}_j}\left( {\mathit{\boldsymbol{x}}\left( k \right)} \right) + \mathit{\boldsymbol{v}}\left( k \right). $ | (2) |
式中:x(k)表示目标状态向量,包含x, y方向位置和速度状态,z(k)为量测向量;j∈{1, …, s}为模型库中第j个模型,s为模型数目;当上式表示线性运动模型时,Fj(·)或Hj(·)为转移矩阵,非线性运动模型时Fj(·)或Hj(·)为非线性函数;wj(k)和v(k)表示均值为零、协方差矩阵分别为Qj和R的高斯过程噪声和量测噪声.令Mjk表示k时刻目标机动模型j,则模型从k-1时刻跳变到k时刻转移过程可用具有转移概率矩阵
| $ {{\mathit{\boldsymbol{\hat \pi }}}_{ij}} = \mathit{Prob}\left( {M_j^k\left| {M_i^{k - 1}} \right.} \right), $ | (3) |
| $ 0 \le {{\mathit{\boldsymbol{\hat \pi }}}_{ij}} \le 1,\sum\limits_{j = 1}^s {{{\hat \pi }_{ij}}} = 1;i,j \in \left\{ {1, \cdots ,s} \right\}. $ | (4) |
式中Prob(·)为转移概率密度函数.
1.2 交互多模型跟踪算法IMM算法步骤可概括为以下4步:
1) 各模型对应滤波器初始化;
2) 模型修正:模型Mjk混合权重更新、混合状态估计及混合误差协方差矩阵计算;
3) 各子模型滤波过程计算、模型概率更新;
4) 模型输出:融合状态估计及融合误差协方差矩阵更新.
其中,步骤4)的融合状态
| $ {{\mathit{\boldsymbol{\hat x}}}_{\rm{I}}}\left( k \right) = \sum\limits_{j = 1}^s {u_j^k{{\mathit{\boldsymbol{\hat x}}}_j}\left( k \right)} , $ | (5) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{\rm{I}}}\left( k \right) = \sum\limits_{j = 1}^s {u_j^k\left\{ {{\mathit{\boldsymbol{P}}_j}\left( k \right) + \left[ {{{\mathit{\boldsymbol{\hat x}}}_j}\left( k \right) - {{\mathit{\boldsymbol{\hat x}}}_{\rm{I}}}\left( k \right)} \right] \times } \right.} }\\ {\left. {{{\left[ {{{\mathit{\boldsymbol{\hat x}}}_j}\left( k \right) - {{\mathit{\boldsymbol{\hat x}}}_{\rm{I}}}\left( k \right)} \right]}^{\rm{T}}}} \right\}.} \end{array} $ | (6) |
式中:
| $ u_j^k = P\left\{ {M_j^k\left| {{\mathit{\boldsymbol{Z}}^k}} \right.} \right\} = \frac{{P\left( {z\left( k \right)\left| {M_j^k} \right.,{\mathit{\boldsymbol{Z}}^{k - 1}}} \right) \cdot P\left( {M_j^k\left| {{\mathit{\boldsymbol{Z}}^{k - 1}}} \right.} \right)}}{c}. $ | (7) |
式中:c为正则化常数,P(·)为高斯概率密度函数;Zk-1=[z (1), …, z (k-1)]为历史观测值向量.
对于机动跟踪而言,位置、速度误差往往存在耦合关系,体现在各子模型获得目标状态估计及误差协方差矩阵中;传统IMM采用近似概率密度函数作为融合权值,难以应对大机动时可能出现概率函数失效问题;且忽视了目标状态向量及误差协方差矩阵中元素间关系,跟踪稳健性较差.文献[13]引入对角阵加权融合方式在一定程度上增强了跟踪稳健性,但同样忽视各模型位置误差与速度误差间关系,易造成大机动时跟踪误差过大.
2 基于矩阵加权多模型融合的自适应波形设计算法从接收端数据处理与发射端波形联合优化角度出发,引入基于矩阵加权多模型融合的波形捷变算法,以实现认知跟踪雷达的闭环反馈调整.
2.1 矩阵加权多模型融合跟踪算法对于n×1维状态向量x而言,设s个子模型相应局部无偏滤波器估值为
| $ {{\mathit{\boldsymbol{\hat x}}}_i} = \mathit{\boldsymbol{x}} + \left( { - {{\mathit{\boldsymbol{\tilde x}}}_i}} \right),i = 1, \cdots ,s. $ | (8) |
同样,可定义“集中式观测方程”为
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{ex}} + \mathit{\boldsymbol{v}}, $ | (9) |
其中:
| $ \mathit{\boldsymbol{y}} = {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat x}}}_i}}& \cdots &{{{\mathit{\boldsymbol{\hat x}}}_s}} \end{array}} \right]^{\rm{T}}}, $ | (10) |
| $ \mathit{\boldsymbol{e}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_n}}& \cdots &{{\mathit{\boldsymbol{I}}_n}} \end{array}} \right]^{\rm{T}}}, $ | (11) |
| $ \mathit{\boldsymbol{v}} = {\left[ {\begin{array}{*{20}{c}} { - {{\mathit{\boldsymbol{\hat x}}}_i}}& \cdots &{ - {{\mathit{\boldsymbol{\hat x}}}_s}} \end{array}} \right]^{\rm{T}}}. $ | (12) |
由无偏性知
| $ \mathit{\boldsymbol{P}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{11}}}& \cdots &{{\mathit{\boldsymbol{P}}_{1s}}}\\ \cdots &{}& \cdots \\ {{\mathit{\boldsymbol{P}}_{s1}}}& \cdots &{{\mathit{\boldsymbol{P}}_{ss}}} \end{array}} \right]_{ns \times ns}}. $ | (13) |
式中Pij为n×n维分块矩阵;若P正定,由线性无偏最小方差估计(Linear Unbiased Minimum Variance estimation, LUMV)定理知,关于x的集中式融合LUMV估值
| $ {{\mathit{\boldsymbol{\hat x}}}_{{\rm{LUMV}}}} = {\left( {{\mathit{\boldsymbol{e}}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{e}}} \right)^{ - 1}}{\mathit{\boldsymbol{e}}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{ - 1}}y. $ | (14) |
且有最小误差方差阵PLUMV
| $ {\mathit{\boldsymbol{P}}_{{\rm{LUMV}}}} = {\left( {{\mathit{\boldsymbol{e}}^{\rm{T}}}{\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{e}}} \right)^{ - 1}}. $ | (15) |
同理,线性无偏融合估值
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_1}}& \cdots &{{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_s}} \end{array}} \right]. $ | (16) |
因此,线性无偏融合估计误差为:
| $ {{\mathit{\boldsymbol{\hat x}}}_{{\rm{LU}}}} = \sum\limits_{i = 1}^s {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}{{\mathit{\boldsymbol{\hat x}}}_i}} , $ | (17) |
| $ \sum\limits_{i = 1}^s {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}} = {\mathit{\boldsymbol{I}}_n}. $ | (18) |
假定各子模型滤波误差互不相关,即Pij=0(i≠j),则在线性无偏最小方差意义下按矩阵加权最优融合状态估值
| $ {{\mathit{\boldsymbol{\hat x}}}_{\rm{M}}} = \sum\limits_{i = 1}^s {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}{{\mathit{\boldsymbol{\hat x}}}_i}} , $ | (19) |
其中最优加权矩阵为
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i} = {\left( {\sum\limits_{j = 1}^s {\mathit{\boldsymbol{P}}_j^{ - 1}} } \right)^{ - 1}}\mathit{\boldsymbol{P}}_i^{ - 1}, $ | (20) |
且融合误差协方差阵为
| $ {\mathit{\boldsymbol{P}}_{\rm{M}}} = {\left( {\sum\limits_{i = 1}^s {\mathit{\boldsymbol{P}}_i^{ - 1}} } \right)^{ - 1}}. $ | (21) |
另由文献[1, 18]知,带矩阵加权最优状态融合估计
| $ {\rm{tr}}\left( {{\mathit{\boldsymbol{P}}_{\rm{M}}}} \right) < {\rm{tr}}\left( {{\mathit{\boldsymbol{P}}_i}} \right). $ | (22) |
式中tr(·)为求取矩阵迹.
为解决传统IMM中马尔科夫转移概率矩阵固化问题,考虑相邻时刻模型概率之差反映模型与实际运动模式间匹配程度,构造指数形式模型概率变化率为
| $ {\kappa _j}\left( k \right) = \exp \left( {\rho \cdot \left( {u_j^k - u_j^{k - 1}} \right)} \right). $ | (23) |
式中ρ∈[1, 2]为转换因子,常取ρ=1.5;利用式(23)实时修正模型转移概率,即:
| $ {{\hat \pi }_{ij}} = {\kappa _j}\left( k \right){{\hat \pi }_{ij}},\;\;\;i,j = 1,2, \cdots ,s. $ | (24) |
当模型j概率随时间增大时,有κj(k)>1, 矩阵
由文献[11, 19]知,量测噪声协方差矩阵视为波形参数的函数,而目标状态估计误差与量测噪声协方差矩阵相关,因此跟踪性能提升可通过调整波形来实现.文献[11]分别讨论:1)子模型似然概率最大者所对应的估计误差协方差矩阵,2)子模型所对应估计误差协方差矩阵迹最大者,3)IMM输出融合估计误差协方差矩阵,来构造目标函数;其设计方法在于选取波形参数使得误差协方差矩阵迹最小.上述方法可视为寻优过程,需各时刻对波形库中参数进行遍历;也就是说,每次参数遍历都需利用滤波算法进行评估,计算量较大.文献[20]从信息论角度讨论线性调频参数在其优选准则下只需保留最大或最小调频率,这亦增加波形参数选择难度.因此,以矩阵迹最小或互信息最大作为目标函数,该方式需考虑具体场景,计算量取决于波形类型及参数范围.文献[21]证明最优跟踪波形为使得量测误差椭圆与先验估计误差椭圆正交的波形;这为波形设计提供新思路.
假设下一时刻估计误差协方差矩阵为
| $ \mathit{\boldsymbol{\hat P = }}\left[ {\begin{array}{*{20}{c}} {{{\hat p}_{11}}}&{{{\hat p}_{12}}}\\ {{{\hat p}_{21}}}&{{{\hat p}_{22}}} \end{array}} \right]. $ | (25) |
式中
| $ \beta = \arctan \left( {{v_{\max }}\left( 2 \right)/{v_{\max }}\left( 1 \right)} \right). $ | (26) |
式中β∈[-π/4, π/4].令R0表示特定波形估计位置与速度CRLB,由文献[11]知其可被视为量测噪声协方差矩阵;同理可得R0的误差椭圆角度参数ψ.假定θk+1为发射波形旋转参数,则量测误差椭圆旋转关系为
| $ \begin{array}{l} \mathit{\boldsymbol{R}}\left( {{\theta _{k + 1}}} \right) = {\left[ {\begin{array}{*{20}{c}} {\cos {\theta _{k + 1}}}&{ - \sin {\theta _{k + 1}}}\\ {\sin {\theta _{k + 1}}}&{\cos {\theta _{k + 1}}} \end{array}} \right]^{ - 1}}{\mathit{\boldsymbol{R}}_0} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} {\cos {\theta _{k + 1}}}&{ - \sin {\theta _{k + 1}}}\\ {\sin {\theta _{k + 1}}}&{\cos {\theta _{k + 1}}} \end{array}} \right]^{ - {\rm{T}}}}. \end{array} $ | (27) |
通过旋转特定波形模糊函数以使其量测误差椭圆R(θk+1)与估计误差椭圆
| $ {\theta _{k + 1}} = \mp {\rm{ \mathit{ π} }}/2 - \psi + \beta . $ | (28) |
进而利用FrFT获得相应波形.
将矩阵加权融合估计误差协方差矩阵作为误差椭圆基准,旋转特定波形模糊函数以使其量测误差椭圆与融合估计误差椭圆正交,来获得最优波形.
基于矩阵加权多模型融合的自适应波形设计算法(Adaptive waveform design based on Matrix-weighted Interacting Multiple Model fusion, AMIMM)步骤如下所示:
步骤1 计算与模型Mjk相对应滤波器混合矩阵权值:
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{i\left| j \right.}}\left( {k\left| k \right.} \right) = P\left( {M_i^{k - 1}\left| {M_i^k,{\mathit{\boldsymbol{Z}}^k}} \right.} \right) = \frac{{{{\hat \pi }_{ij}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}\left( {k - 1} \right)}}{{\sum\limits_{i = 1}^s {{{\hat \pi }_{ij}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}\left( {k - 1} \right)} }} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {\sum\limits_{i = 1}^s {{{\hat \pi }_{ij}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}\left( {k - 1} \right)} } \right)^{ - 1}}{{{\rm{ \mathit{\hat π} }}}_{ij}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}\left( {k - 1} \right), \end{array} $ | (29) |
式中:Ωi(k-1)=P(Mik-1|Zk-1),可由式(20)求得;
步骤2 计算模型Mjk混合输入状态及对应估计误差协方差矩阵:
| $ {{\mathit{\boldsymbol{\hat x}}}_{0j}}\left( {k\left| k \right.} \right) = \sum\limits_{i = 1}^s {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{i\left| j \right.}}\left( {k\left| k \right.} \right){{\mathit{\boldsymbol{\hat x}}}_i}\left( {k - 1} \right)} , $ | (30) |
| $ \begin{array}{l} {\mathit{\boldsymbol{P}}_{0j}}\left( {k\left| k \right.} \right) = \sum\limits_{i = 1}^s {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{i\left| j \right.}}\left( {k\left| k \right.} \right)\left\{ {{\mathit{\boldsymbol{P}}_i}\left( {k - 1} \right) + \left[ {{{\mathit{\boldsymbol{\hat x}}}_i}\left( {k - 1} \right) - } \right.} \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {{{\mathit{\boldsymbol{\hat x}}}_{0j}}\left( {k\left| k \right.} \right)} \right] \times {{\left[ {{{\mathit{\boldsymbol{\hat x}}}_i}\left( {k - 1} \right) - {{\mathit{\boldsymbol{\hat x}}}_{0j}}\left( {k\left| k \right.} \right)} \right]}^{\rm{T}}}} \right\}. \end{array} $ | (31) |
步骤3 利用线性或非线性滤波算法获得各子模型的
步骤4 按式(19)~(21)进行矩阵权值更新以获得融合状态估计
步骤5 基于PM(k)按式(26)~(28)获得旋转参数θk+1, 利用FrFT旋转特定波形得到新的量测误差椭圆及发射波形;
步骤6 按式(23)、(24)进行马尔科夫转移概率矩阵更新.
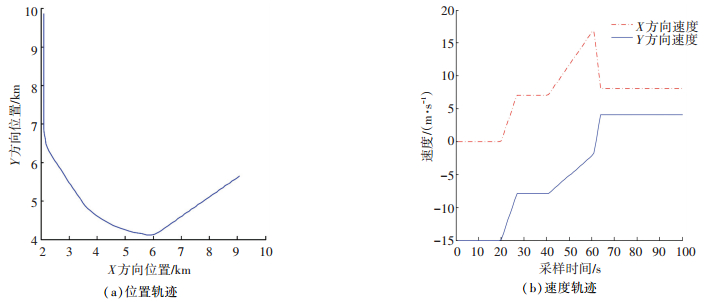
3 仿真结果和分析仿真设置参照文献[1],将所提AMIMM与文献[1]中采用固定波形MIMM、IMM,文献[10]中采用自适应波形AIMM做比较.目标初始状态为:x(0)=[2 100 0 10 000 -15];先匀速运动200 s,然后在x方向进行机动转弯,加速度为ax=ay=0.1 m/s2,并在t=270 s时完成转弯,加速度为0;第二个状态机动在t=410 s处以ax=0.05 m/s2,ay=0.03 m/s2至t=610 s;再以ax=-0.3 m/s2,ay=0.2 m/s2持续至t=640 s.其x-y平面位置、速度轨迹如图 1(a)、(b)所示.本文采用两个具有不同过程噪声强度的恒速度模型来构造多模型框架,如下
| $ {\mathit{\boldsymbol{F}}_i} = \left[ {\begin{array}{*{20}{c}} 1&T&0&0\\ 0&1&0&0\\ 0&0&1&T\\ 0&0&0&1 \end{array}} \right],{\mathit{\boldsymbol{H}}_i} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&0&1&0 \end{array}} \right]; $ | (32) |
| $ {\mathit{\boldsymbol{Q}}_i} = \left[ {\begin{array}{*{20}{c}} {{q_i}}&0\\ 0&{{q_i}} \end{array}} \right],\mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} r&{r/20}\\ {r/20}&r \end{array}} \right]. $ | (33) |
|
图 1 目标真实轨迹示意 Figure 1 True trajectory target |
式中:Fi为第i个模型状态转移矩阵,Hi为量测矩阵;Qi为过程噪声协方差矩阵,取q1=0.5,q2=50;R为量测误差协方差矩阵,r为量测误差强度;采样间隔T=10 s;另定义目标初始状态误差协方差矩阵为
| $ {\mathit{\boldsymbol{P}}_{ii}}\left( 0 \right) = \left[ {\begin{array}{*{20}{c}} r&{r/T}&0&0\\ {r/T}&{2r/{T^2}}&0&0\\ 0&0&r&{r/T}\\ 0&0&{r/T}&{2r/{T^2}} \end{array}} \right]. $ | (34) |
模型转移概率矩阵为
| $ \mathit{\boldsymbol{\hat \pi }} = \left[ {\begin{array}{*{20}{c}} {0.9}&{0.1}\\ {0.1}&{0.9} \end{array}} \right]. $ | (35) |
模型初始概率为φ1=φ2=0.5;本文以1 000次独立蒙特卡洛实验来评估各算法统计性能,并以目标状态估计均方根误差RMSE作为评价指标.
| $ {\rm{RMS}}{{\rm{E}}_k} = \sqrt {\frac{1}{N}\sum\limits_{n = 1}^N {{{\left( {{{\mathit{\boldsymbol{\hat x}}}^n}\left( k \right) - {\mathit{\boldsymbol{x}}^n}\left( k \right)} \right)}^2}} } . $ | (36) |
式中:xn(k)和
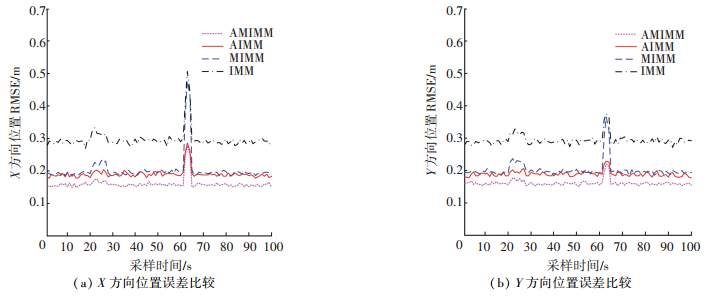
位置、速度跟踪误差比较(r=50)如图 2、3所示;各算法平均跟踪误差及耗时比较(r=50)见表 1.
|
图 2 位置跟踪误差比较(r=50) Figure 2 Comparison of position tracking RMSE (r=50) |

|
图 3 速度跟踪误差比较(r=50) Figure 3 Comparison of velocity tracking RMSE (r=50) |
| 表 1 各算法平均跟踪误差及耗时比较(r=50) Table 1 RMSE and time-consumption comparison of different algorithms (r=50) |
由表 1中1 000次蒙特卡洛实验分析可知,AMIMM在位置跟踪、速度跟踪方面都取得最好跟踪效果;AIMM采用自适应波形调整策略获得的跟踪误差小于固定波形IMM;同时,MIMM利用矩阵加权方式来弥补传统概率加权的弊端,使得其跟踪误差亦优于IMM. 表 1中各算法差异与图 2、3中各算法RMSE变化一致.从图 2、3可知,发生机动时位置、速度跟踪误差均出现较大波动,但AMIMM、AIMM相比固定波形MIMM、IMM反应迅速,速度、位置跟踪误差均小于固定波形MIMM及IMM.另外,固定波形MIMM性能好于IMM,这是因为位置、速度估计误差往往存在一定耦合关系,而这种关系体现在各子模型获得的目标状态估计及其误差协方差矩阵中,矩阵加权多模型融合方式能够充分考虑位置跟踪与速度跟踪间联系,并以各模型估计误差协方差矩阵来构造各加权矩阵,使得跟踪精度提高.
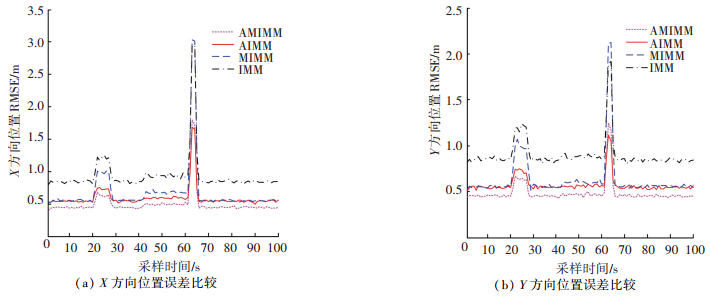
由平均耗时比较可知,AMIMM耗时最多,IMM耗时最少;对比MIMM与IMM耗时差异可知,矩阵加权操作计算量明显大于概率加权方式;由AMIMM与MIMM耗时比较知,自适应波形调整步骤也在一定程度上增加了计算量.由表 1知,AMIMM相比IMM平均耗时较长(相差0.036 5s),这是由于AMIMM矩阵加权操作、自适应波形调整步骤造成的;另由MIMM与IMM、AMIMM与MIMM平均耗时差异知,AMIMM与IMM耗时差异正好等于MIMM与IMM、AMIMM与MIMM耗时差异之和,从而验证造成AMIMM计算量较大的原因.位置、速度跟踪误差比较(r=500)如图 4、5所示;各算法平均跟踪误差及耗时比较(r=500)见表 2.
|
图 4 位置跟踪误差比较(r=500) Figure 4 Comparison of position tracking RMSE (r=500) |
|
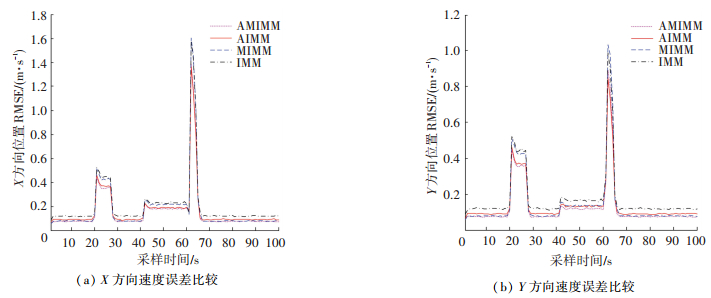
图 5 速度跟踪误差比较(r=500) Figure 5 Comparison of velocity tracking RMSE (r=500) |
| 表 2 各算法平均跟踪误差及耗时比较(r=500) Table 2 RMSE and time-consumption comparison of different algorithms (r=500) |
由表 2知,AMIMM同样在位置、速度跟踪方面均取得最佳跟踪效果;而固定波形IMM获得较差跟踪效果,这与表 1结论一致;固定波形IMM中传统概率加权方式忽视各模型状态向量及估计误差协方差矩阵中元素间关系,难以应对大机动时可能出现的概率函数失效问题,跟踪稳健性降低,跟踪效果差于MIMM、AMIMM.同样,表 2中各算法差异与图 4、5中各算法RMSE变化一致.另由图 4、5知,发生机动时AMIMM、AIMM相比固定波形MIMM和IMM反应迅速,速度、位置跟踪误差迅速降低. 表 2与表 1耗时差异相似,AMIMM耗时最多,IMM耗时最少;由MIMM与IMM、AMIMM与MIMM(或AIMM与IMM)耗时差异可知,矩阵加权操作、自适应波形调整步骤均增加了计算量.
对比表 1、2可知,随着量测噪声强度增大,位置、速度跟踪误差也相应增大,但AMIMM依然表现出较明显性能优势,这与AMIMM内部机制相关;本文所提AMIMM利用矩阵加权来联接目标状态估计向量及误差协方差矩阵,而该矩阵权值由各模型估计误差协方差矩阵计算得到,使得位置跟踪误差与速度跟踪误差间的关系能够充分考虑,另外自适应马尔科夫转移概率矩阵利用量测数据自适应地修正模型转移概率,放大匹配模型作用,抑制非匹配模型作用,提高了误差收敛速度.
4 结论针对机动目标状态跟踪问题,本文从认知跟踪雷达发射-接收联合处理角度出发,利用多模型思路构造矩阵加权多模型融合跟踪算法框架,以融合状态估计误差协方差矩阵为基准,通过FrFT来旋转量测误差椭圆使其与融合状态估计误差椭圆正交,实现波形自适应调整.仿真实验表明,不同量测噪声强度下,所提AMIMM相比自适应波形AIMM、固定波形MIMM、IMM均取得较好性能优势,提高了机动目标跟踪精度和稳健性.
| [1] |
FU Xiaoyan, JIA Yingmin, DU Junping, et al. New interacting multiple model algorithms for the tracking of the maneuvering target[J].
IET Control Theory & Applications, 2010, 4(10): 2184-2194.
DOI: 10.1049/iet-cta.2009.0583 |
| [2] |
WANG Jiantao, QIN Yuliang, WANG Hongqiang, et al. Dynamic waveform selection for maneuvering target tracking in clutter[J].
IET Radar, Sonar & Navigation, 2013, 7(7): 815-825.
DOI: 10.1049/iet-rsn.2012.0310 |
| [3] |
DU Y K, MOONGU J. Data fusion of radar and image measurements for multi-object tracking via Kalman filtering[J].
Information Sciences, 2014, 278: 641-652.
DOI: 10.1016/j.ins.2014.03.080 |
| [4] |
HAYKIN S, ZIA A, XUE Yanbo, et al. Control theoretic approach to tracking radar: first step towards cognition[J].
Digital Signal Processing, 2011, 21(5): 576-585.
DOI: 10.1016/j.dsp.2011.01.004 |
| [5] |
BELL K L, BAKER C J, SMITH G E, et al. Cognitive radar framework for target detection and tracking[J].
IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1427-1439.
DOI: 10.1109/JSTSP.2015.2465304 |
| [6] |
黎湘, 范梅梅. 认知雷达及其关键技术研究进展[J].
电子学报, 2012(09): 1863-1870.
LI Xiang, FAN Meimei. Research advance on cognitive radar and its key technology[J]. ACTA Electronica Sinica, 2012(09): 1863-1870. DOI: 10.3969/j.issn.0372-2112.2012.09.025 |
| [7] |
KILANI M B, NIJSURE Y, GAGNON G, et al. Cognitive waveform and receiver selection mechanism for multistatic radar[J].
IET Radar, Sonar & Navigation, 2016, 10(2): 417-425.
DOI: 10.1049/iet-rsn.2015.0319 |
| [8] |
盛丹, 王国宏, 张翔宇. 基于波形捷变的多传感器机动目标跟踪[J].
系统工程与电子技术, 2015(03): 485-491.
SHENG Dan, WANG Guohong, ZHANG Xiangyu. Maneuvering target tracking based on waveform agility with multi-sensor[J]. Systems Engineering and Electronics, 2015(03): 485-491. DOI: 10.3969/j.issn.1001-506X.2015.03.02 |
| [9] |
檀甲甲, 张建秋. 跟踪机动目标的雷达波形选择新方法[J].
系统工程与电子技术, 2011(03): 515-522.
TAN Jiajia, ZHANG Jianqiu. New waveform selection approach to tracking maneuver targets[J]. Systems Engineering and Electronics, 2011(03): 515-522. DOI: 10.3969/j.issn.1001-506X.2011.03.10 |
| [10] |
SAVAGE C O, MORAN B. Waveform selection for maneuvering targets within an IMM framework[J].
IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3).
DOI: 10.1109/TAES.2007.4383612 |
| [11] |
NGUYEN N H, DOGANCAY K, DAVIS L M. Adaptive waveform selection for multistatic target tracking[J].
IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(1): 688-701.
DOI: 10.1109/TAES.2014.130723 |
| [12] |
靳标, 纠博, 苏涛, 等. 针对机动目标跟踪的雷达发射波形选择[J].
电子与信息学报, 2014(08): 1912-1918.
JIN Biao, JIU Bo, SU Tao, et al. Radar transmitted waveform selection for maneuvering target tracking[J]. Journal of Electronics & Information Technology, 2014(08): 1912-1918. DOI: 10.3724/SP.J.1146.2013.01744 |
| [13] |
FU Xiaoyan, SHANG Yuanyuan, YUAN Huimei. Improved diagonal interacting multiple model algorithm for maneuvering target tracking based on H∞ filter[J].
IET Control Theory & Applications, 2015, 9(12): 1887-1892.
DOI: 10.1049/iet-cta.2014.0685 |
| [14] |
封普文, 黄长强, 曹林平, 等. 马尔可夫矩阵修正IMM跟踪算法[J].
系统工程与电子技术, 2013, 11: 2269-2274.
FENG Puwen, HUANG Changqiang, CAO Linping, et al. Research on adaptive markov matrix IMM tracking algorithm[J]. Systems Engineering and Electronics, 2013, 11: 2269-2274. DOI: 10.3969/j.issn.1001-506X.2013.11.07 |
| [15] |
郭志, 董春云, 蔡远利, 等. 时变转移概率IMM-SRCKF机动目标跟踪算法[J].
系统工程与电子技术, 2015, 01: 24-30.
GUO Zhi, DONG Chunyun, CAI Yuanli, et al. Time-varying transition probability based IMM-SRCKF algorithm for maneuvering target tracking[J]. Systems Engineering and Electronics, 2015, 01: 24-30. DOI: 10.3969/j.issn.1001-506X.2015.01.05 |
| [16] |
杨永建, 樊晓光, 王晟达, 等. 基于自适应CS模型的IMM算法[J].
系统工程与电子技术, 2016(05): 977-983.
YANG Yongjian, FAN Xiaoguang, WANG Shengda, et al. Interacting multiple model algorithm based on adaptive current statistical model[J]. Systems Engineering and Electronics, 2016(05): 977-983. DOI: 10.3969/j.issn.1001-506X.2016.05.01 |
| [17] |
杨峰, 张婉莹. 一种多模型贝努利粒子滤波机动目标跟踪算法[J].
电子与信息学报, 2017, 39(3): 634-639.
YANG Feng, ZHANG Wanying. Multiple model bernoulli particle filter for maneuvering target tracking[J]. Journal of Electronics & Information Technology, 2017, 39(3): 634-639. DOI: 10.11999/JEIT160467 |
| [18] |
YAAKOV B S, LI X R, THIAGALINGAM K. Estimation with applications to tracking and navigation[M]. New York: John Wiley and Sons, 2001.
|
| [19] |
KERSHAW D J, EVANS R J. Optimal waveform selection for tracking systems[J].
IEEE Transactions on Information Theory, 1994, 40(5): 1536-1550.
DOI: 10.1109/18.333866 |
| [20] |
SUVOROVA S, HOWARD S D, MORAN W, et al. Waveform libraries for radar tracking applications: maneuvering targets[C]// Proceedings of 2006 40th Annual Conference on Information Sciences and Systems. Princeton, NJ: IEEE, 2006: 1424-1428. DOI: 10.1109/CISS.2006.286688.
|
| [21] |
NIU R, WILLETT P. Tracking considerations in selection of radar waveform for range and range-rate measurements[J].
IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(2): 467-487.
DOI: 10.1109/TAES.2002.1008980 |
 2018, Vol. 50
2018, Vol. 50


