在社交网络中, 社区(community)被用来表示具有相似性、共同爱好、或联系的共同体, 它具有“内部节点之间连接紧密, 与外部连接稀疏”的特点.社区成员之间因社交关系不均匀, 使社区表现出社区结构特性[1].通过社区发现(community detection)算法分析复杂网络的拓扑结构和层次结构, 理解其形成过程, 有助于揭示复杂系统的内部规律, 为信息传播控制[2]、维护社会安全[3]、推荐系统建设等领域提供有力支撑, 已成为social network analysis领域的一个研究热点.
社区发现算法源于Girvan和Newman提出的GN算法[1], 但该算法需要预知社区的个数来确定算法终止条件, 并且时间复杂度较高.标签传播法(label propagation algorithm, LPA)[4]是Raghavan提出的一种基于图的半监督学习的社区发现算法, 虽复杂度低, 但其每次迭代结果不稳定, 准确度不高, 后来张鑫等[5]提出稳定标签法作为改进.而后很多社区发现算法也相继被提出, 如:基于随机游走的算法[6]、基于信息编码的算法[7]以及基于网络拓扑结构的算法[8]等.这些算法都在一定程度上提高社区发现的精度, 然而绝大部分社区发现算法都对参数敏感, 一旦参数选择不当就会对结果产生很大影响.除此之外, 划分结果的真实性逐渐被更多的学者所关注, 基于模块度指标优化的社区发现算法, 对于较大规模社区具有倾向性, 不善于识别小规模社区, 具有分辨率限制[9].因此, 社区发现算法在复杂度、准确度、自适应等方面都有着提升的空间.
在一定意义上, 社区发现就是某种类型的聚类, 一般被认为是广义的图聚类.二者区别就在于:常见的聚类一般是假设任意对象都是互连的, 只是距离(或者相似度)不同, 数据集可表示为一张完全连通图, 如:划分、层次、密度聚类等, 而社区发现过程中可能存在孤立节点;此外, 聚类一般是将数据集划分为k个不相交的子集, 而社区发现包含非重叠社区与重叠社区, 允许子集重叠.但这两者的过程极为相似, 因此出现很多将聚类算法改成社区发现的例子, 如DBSCAN改进为SCAN, 层次聚类等.
Rodriguez等在14年提出一种基于密度峰值的聚类算法[10].该方法只依赖于节点之间的距离, 根据节点分布的局部密度选择聚类中心, 降低参数选择对算法影响的影响, 使得该方法能够获得稳定的聚类结果.黄岚[11]等通过相似度定义网络中各节点之间的距离, 将密度峰值聚类算法应用于社区发现中;Yan[12]等引入箱线图选取核心节点, 将密度峰值聚类算法应用于重叠社区发现;Wang[13]等采用启发式算法划分社区的自然结构.但是上述几种算法虽然成功将密度峰值聚类算法的原理应用到社区发现当中, 但却又引入一些新的额外参数.并且参数的选取并没有非常合适的方法, 需要大量实验数据来获得, 通常只对某一种或几种数据集的结果较好, 无法自适应地对社区进行划分, 算法在性能存在缺陷.
因此, 本文提出一种基于核密度估计的密度峰值聚类的社区发现算法(Community detection algorithm of density peak clustering based on kernel density estimation, KDED), 首先引入一种基于信任度的距离度量, 将社交网络中的用户关系量化为距离矩阵;然后通过基于热扩散理论的核密度估计方法对距离度量进一步处理, 利用密度峰值聚类确定聚类中心, 并将节点分配到相应的社区当中.选取Fastgreed算法、Informap算法、Walktrap算法、LPA算法在真实数据集进行比较, 与Fastgreed算法、Informap算法、Walktrap算法、LPA算法、VDDPC算法[12]、LCCD算法[13]在LFR人工基准网络上进行比较, 结果充分验证KDED算法的可行性和有效性.
1 密度峰值聚类算法Rodriguez等所提出的基于密度峰值的聚类算法[10]通过“距离”来寻找聚类中心.聚类中心基于两个假设:1)聚类中心的密度大于环绕它的邻居节点;2)聚类中心到比其局部密度高的节点的距离较远.
设数据集中的数据点总数为N, 对于数据集中的任意点i, 使用局部密度ρi和到更高密度节点的距离δi进行描述.其中局部密度ρi的定义为
| $ {\rho _i} = \sum\limits_j {\chi \left( {{d_{ij}} - {d_{\rm{c}}}} \right)} . $ | (1) |
式中:设x=dij-dc, 若x < 0, 则χ(x)=1, 否则χ(x)=0, dij为数据点i到j的距离, dc为截断距离. i点的局部密度ρi等于到其距离小于截断距离dc点的个数.因此dc的选取将直接影响ρi的取值, 进而决定聚类结果的准确性.
节点i到比其局部密度更高节点的距离δi的定义为
| $ {\delta _i} = \mathop {\min }\limits_{j:{\rho _j} > {\rho _i}} \left( {{d_{ij}}} \right). $ | (2) |
式中:若i点为数据集中局部密度最大的点, 则δi=maxj(dij), 选取i点到相邻节点距离的最大值作为其δi;否则, 选取局部密度大于i点的数据点到i点的距离中的最小值, 作为i点的δi.
由上述定义可知, 作为聚类中心的数据点一定会比一般节点具有更高的ρi和δi, 可根据此原理选取社区中心, 再将一般节点分配到其最近的聚类中心, 完成整个社区的划分.
2 峰值密度聚类的自适应社区发现算法 2.1 基于用户信任度的距离度量由于社交网络图中的点没有坐标值, 仅通过边来表征两点是否存在一定联系,所以不能用传统的Euclidean距离和Manhattan距离来计算相异度;Jaccard距离可以突出节点间的局部关系, 但无法度量节点之间的全局距离;而最短距离作为一种常用距离度量, 在社区划分当中不考虑社区内部样本的方差, 只考虑均值, 因此分类精度不高.因此本文首先提出一种将节点关系转化为距离度量的方法.根据Ziegler C N[14]提出的“在社交网络中, 人们之间的信任和偏好相似度存在着一种正相关的联系”的观点, 提出假设:1)具有相同爱好、兴趣的群体内部成员, 彼此会获得更多信任;2)成员偏向和受信任的成员进行联系, 因此会具有更短的相对距离;3)最受信任的几个成员普遍也存在联系, 满足“富人俱乐部”效应.基于3点假设, 结合Jaccard相似度, 提出基于“信任度”的距离度量, 如式(3)~(6)所示:
| $ D\left( {i,j} \right) = \frac{1}{{\alpha \left( {i,j} \right) \times \beta \left( {i,j} \right)}}, $ | (3) |
| $ \alpha \left( {i,j} \right) = \frac{{\left| {C\left( {i,j} \right)} \right| + 1}}{{\left| {{N_i} \cup {N_j}} \right|}}, $ | (4) |
| $ \beta \left( {i,j} \right) = \left\{ \begin{array}{l} \frac{{\left| {E\left( {C\left( {i,j} \right)} \right)} \right|}}{{\left( {\left| {C\left( {i,j} \right)} \right|} \right)\left( {\left| {C\left( {i,j} \right)} \right| - 1} \right)/2}} + 1\left| {C\left( {i,j} \right)} \right| > 2,\\ \left| {C\left( {i,j} \right)} \right| \le 2 \end{array} \right. $ | (5) |
| $ C\left( {i,j} \right) = {N_i} \cap {N_j}. $ | (6) |
式中:D(i, j)代表基于信任度的距离度量, 使用描述点关系的因子α(i, j)和描述边关系的因子β(i, j)刻画点i和点j之间的紧密程度, 距离越近代表着节点间的关系越紧密.因子α(i, j)基于Jaccard相似系数, 代表节点i与节点j的共同邻居节点在其邻居节点并集中的比例, |C(i, j)|为节点i与节点j的公共邻居个数, Ni和Nj分别为与节点i与j邻居节点的数量.因子β(i, j)描述点i和点j公共邻居节点相连边之间的紧密程度, |E(C(i, j))|为节点i与节点j公共邻居中的连边的数量, 当节点i与节点j的公共邻居点数大于2时, 认为边的连接强度较大, 计算两点相连的边数与公共节点间可能连接的最大边数之比;否则, 直接置1, 这样会使得联系疏远的节点, 在距离度量中得到体现, 符合“信任”假设.此外, 为避免因子等于0时对距离度量产生影响, 均在因子的定义中做加1处理.
这种定义方法将成员社交关系的邻接矩阵转化为距离度量, 充分考虑节点之间的局部拓扑联系, 可以使潜在社区内部的距离变得紧密, 而不同社区的节点距离较远, 为划分社区的层次结构奠定基础.
2.2 局部密度ρi的等效峰值密度聚类算法中的ρi、δi与截断距离dc有着很大关系, 但只能通过大量实验选取出一个比较合理的值, 这样对社区发现的结果产生较大影响, 易出现误差.
非参数密度估计是数据统计分析的重要工具, 它用于评估偏度, 多模态, 总结贝叶斯后验, 判别分析和约束[15-16], 它对于数据集的建模更加灵活, 并且不受规范偏差的影响.核密度估计(kernel density estimation, KDE)是较为常用的非密度估计方法之一, 引入核方法, 可将低维特征空间的样本通过核函数映射到高维特征空间, 增加对特征的优化, 使其特征在高维特征空间线性可分, 可突出样本点之间根据距离远近体现出的关系紧密程度, 更易聚类.
借鉴Rashid等提出的将热扩散模型(heat diffusion)应用到聚类算法的思想[17], 在得到距离矩阵的基础上, 选取Gaussian核函数进行核密度估计, 统计每个点对于其他节点影响的大小, 代替局部密度ρ, 可以合理规避dc选取的不合理对实验结果的影响. Gaussian核密度为
| $ k\left( {d,{d_j};h} \right) = \frac{1}{{\sqrt {2{\rm{ \mathit{ π} }}h} }}{{\rm{e}}^{ - \frac{{d_j^2}}{{2h}}}}. $ | (7) |
式中:k代表核函数, h为带宽, dj为距离矩阵中的分量, 代表当前节点到点j的距离.在根据上式对距离矩阵进行处理后, 会得到一个关于k的矩阵, 纵列意义为节点自身的影响在其他节中得到的反馈, 与峰值密度函数中局部密度的意义一致.
但Gaussian核密度估计具有一些局限性, 例如, 敏感参数带宽h难以选择, 积分时的边界偏差以及计算过程中欠平滑或过平滑的问题[16].因此, 使用热扩散方法解决此问题.
热扩散模型中, 将核密度估计视为求解扩散过程中偏微分方程的唯一解, 使用时间参数t代替带宽h.通过热扩散对KDE求解的思想源自维纳过程(weiner process), 它是一种连续时间随机过程, 其下一时间状态可直接由之前的时间状态算出, 与Gaussian核密度估计结合的形式如下所示:
1) 准备概率通过d纬数据点{d1, d2, d3, …, dn}平均分配.
2) 使用Gaussian核估计估计点i到点j的转移概率,
| $ {P_{{\rm{transition}}\left( {d,{d_j};t} \right)}} = \frac{1}{n}\sum\limits_{j = 1}^n {\frac{1}{{\sqrt {2{\rm{ \mathit{ π} }}t} }}\exp \left[ { - \frac{{{{\left( {d - {d_j}} \right)}^2}}}{{2t}}} \right]} , $ |
此种情况下, KDE被转化为时长为t过程中的概率分布函数, 但函数形式类似于Gaussian核函数.
| $ {{\hat f}_t}\left( {d;t} \right) = \frac{1}{2}\sum\limits_{j = 1}^n {\frac{1}{{\sqrt {2{\rm{ \mathit{ π} }}t} }}\exp \left[ { - \frac{{{{\left( {d - {d_j}} \right)}^2}}}{{2t}}} \right]} . $ | (8) |
式(8)代表迭代过程, 因此要满足扩散过程的偏微分方程(partial differential equation, PDE)条件, 即
| $ \frac{\partial }{{\partial t}}\hat f\left( {d;t} \right) = \frac{1}{2}\frac{{{\partial ^2}}}{{\partial {d^2}}}\hat f\left( {d;t} \right),\;\;\;\;d \in D,t > 0 $ |
式中,
| $ \Delta d = \frac{1}{n}\sum\nolimits_{j = 1}^n {\delta \left( {d - {d_j}} \right)} , $ |
为D的经验密度, δ(d-dj)是狄拉克函数.为消除Gaussian函数在有限节点时带来的边界误差需进行边界修正, 同时满足Neumann边界条件,
综上, 考虑到Neumann边界条件和域[0, 1]的概率密度, 该PDE的解析解可以通过θ核的形式求解, 以此实现Gaussian核的转化.
| $ \hat f\left( {d;t} \right) = \frac{1}{n}\sum\limits_{j = 1}^n {\theta \left( {d,{d_j};t} \right)} ,d \in \left[ {0,1} \right], $ |
其中θ核函数为
| $ \theta \left( {d,{d_j};t} \right) = \sum\limits_{i = - \propto }^ \propto {\mathit{Ø }\left( {d,2k + {d_i};t} \right) + \mathit{Ø }\left( {d,2k - {d_i};t} \right)} , $ |
进一步变换得到
| $ \hat f\left( {d;t} \right) = \frac{1}{n}\sum\limits_{j = 1}^n {\sum\limits_{k = - \propto }^ \propto {{e^{ - {k^2}{{\rm{ \mathit{ π} }}^2}t/2}}\cos \left( {k{\rm{ \mathit{ π} }}d} \right)\cos \left( {k{\rm{ \mathit{ π} }}{d_j}} \right)} } , $ |
最终, 上式可近似为
| $ \hat f\left( {d;t} \right) \approx \sum\limits_{k = 0}^{n - 1} {{a_k}{e^{ - {k^2}{{\rm{ \mathit{ π} }}^2}t/2}}\cos \left( {k{\rm{ \mathit{ π} }}d} \right)} . $ | (9) |
其中n为足够大的正整数, ak为
| $ {a_k} = \left\{ \begin{array}{l} 1,\;\;\;\;\;k = 0;\\ \frac{1}{n}\sum\nolimits_{i = 1}^n {\cos \left( {k{\rm{ \mathit{ π} }}{d_i}} \right)} ,\;\;\;\;\;k = 1,2, \cdots ,n - 1. \end{array} \right. $ |
式(9)是KDE的完全自适应和替代形式, 并考虑最佳带宽选择和边界校正.此外, 式(9)可以使用快速傅立叶变换求解, 复杂度为O(nlog2n)[18].对于小带宽, 式(9)的表现与Gaussian核相似;对于大的带宽其表现接近Uniform核, 这样可以为KDED算法提供更好的性能并且更加接近与真实的密度, 改善Gaussian核函数在边界处存在的误差, Krishanaswamy S等说明通过热扩散理论快速评估KDE的优越性[19].
2.3 到高密度点的距离δi的计算依照第一章介绍的密度峰值聚类的原理, δ在社区发现过程中保证社区之间相对稀疏的特性, 其计算基于局部密度ρ以及距离矩阵D.首先将节点的ρ值进行排列;对于节点i, 统计局部密度ρ值大于ρi的点到i的距离{d};δi是到该点的距离的最小值, 即δi=min{d}, 若节点i为局部密度最大的点, 则取δi=maxj(dij).值得注意的是, 依照定义, 对于局部密度或全局密度最大的点, 显然会是一个社区中心, 其δ值会普遍大于到它最近邻居的距离, 若以ρ和δ为坐标系画出决策图, 则此点会出现在决策图的右上角;而对于其它的社区中心, 其δ值也会大于一般节点, 结合筛选条件, 即可发现所有的社区中心.
2.4 最优带宽以及核心节点选取本文使用改进的Sheather-Jones(ISJ)算法计算最优带宽.它的优势是可以使用快速余弦变换来估计带宽, 而无需考虑分布上的正态性假设. Botev等[15]提出非线性方程的独特解, 可自适应地找出KDE的最优带宽t,
| $ t = \xi {\gamma ^{\left[ l \right]}}\left( t \right). $ | (10) |
ISJ算法的详细原理本文不再叙述, 最佳带宽t可以缩放内核函数来估计更精确的密度.本文使用Tboundary=sqrt(t)/3.3修复集群的边界点.
在依次计算每个节点对应的ρi、δi的后, 选取δ≥E(δi)+σ(δi)作为社区划分中的核心节点, 每一个核心节点代表一个社区.然后将一般节点分配到距其最近的核心节点所在的社区. E(δi)和σ(δi)分别代表均值和方差.到此, 完成社区发现的所有过程.
算法1.峰值密度聚类的自适应社区发现算法
输入:数据集G
输出:社区划分
1) 初始化邻接关系
2) 根据式(3)~(6)计算距离矩阵
3) 根据式(10)计算t
4) 根据式(9)的KDE替代式计算ρ
5) 利用密度峰值聚类原理计算δ
6) 选择核心节点
7) 将一般节点划分到距其距离最近的核心节点处构成社区
8) 整理社区划分结果
3 实验与分析 3.1 实验数据集为验证KDED算法的可行性和有效性, 本文选取4个真实数据集和2种规模的人工合成数据集进行实验仿真.
3.1.1 真实数据集表 1列出4个真实数据集, 且这些数据集具有已知的社区结构, 分别为Karate数据集、Dolphins数据集、Football数据集和Polbooks数据集.
| 表 1 真实数据集 Table 1 Real data set |
Karate网络反应某大学空手道俱乐部之间的成员关系, 节点连接的边代表成员的关系紧密.由于校长与俱乐部主管间存在矛盾, 该网络分裂为两个社区.
Dolphins网络反应Doubtful Sound海峡中海豚的群居情况.一个节点代表一只海豚, 节点相连的边代表海豚之间接触频繁.经过长期观察, 该网络被分为两个社区.
Football网络数据集中每一个节点代表一只球队, 节点之间的连边代表球队之间曾经进行过比赛.由于球队属于不同的州, 每个州内的比赛场次多, 因此该网络被分为12个社区.
Polbooks网络反映亚马逊政治书籍的分类.网络数据集中每一个节点代表一本在亚马逊销售的政治类书籍, 节点之间的连边代表两本书被同时购买的频率高.由于政治类书籍代表的政治立场不同, 所以该网络被划分为3个社区, 分别代表“自由”、“保守”和“中立”.
3.1.2 人工网络数据集Lancichinetti A提出著名的LFR人工基准网络构造模型[20], 已成为测试社区发现算法性能的一种主要方法. LFR基准网络有两大优势:(1)它模拟节点度数和社区大小的无标度特征;(2)已知社区划分结构.
本文中一共采用两组LFR基准网络, 具体参数如表 2所示.其中表中N为网络的节点数, K为平均度数, Kmax为最大度数, t1和t2分别为度分布和社区大小分布的幂指数, 本文统一使用t1=2和t2=1, u为模糊参数, Cmin和Cmax为社区规模的最大值和最小值.通过u调节网络结构的模糊程度来验证算法性能.具体参数如表 2所示.
| 表 2 LFR基准网络参数 Table 2 Parameters of LFR benchmark networks |
模块度Q是由Girvan和Newman提出的一种被广泛应用于社区划分结果的评价指标, 它反应社区结构的稳定性, 其定义为
| $ Q = \sum\limits_{ij} {\left[ {\frac{{{A_{ij}}}}{{2m}} - \frac{{{k_i} * {k_j}}}{{\left( {2m} \right)\left( {2m} \right)}}} \right]\delta \left( {{c_i},{c_j}} \right).} $ | (10) |
Q表示网络中社区内部节点之间的连边所占的比例和另一个随机网络中社区内部节点连边所占比例的期望相减得到的差值.
式中:A是网络G对应的邻接矩阵, ki和kj对应点i和j的度数, m是总连接边数.实际连边数越是高于随机期望, 说明节点越有集中在某些社区内的趋势, 即网络的模块化结构越明显.其取值范围为-1到1.数值越接近1表示社区划分的结果越好.
3.2.2 标准化互信息标准化互信息(normalized mutual information, NMI)是由Danon等提出的一种衡量已知社区结构网络的评价标准, 它反应社区划分结果与实际划分结果的相似性, 其定义为
| $ {N_{{\rm{NMI}}}}\left( {R\left| P \right.} \right) = 1 - \left[ {H\left( {R\left| P \right.} \right) + H\left( {P\left| R \right.} \right)} \right]/2. $ | (11) |
式中:R为真实划分结果, P为预测划分结果, H(R|P)为R关于P的归一化条件熵. NNMI的取值范围为0到1, 其值越高表明所划分的社区结构与已知的社区结构越接近.当其取值为1时, 所划分的社区结构与已知社区结构相同.
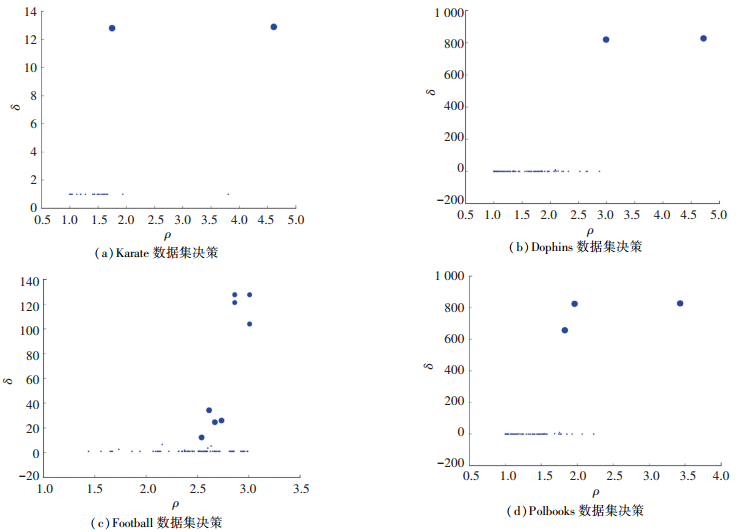
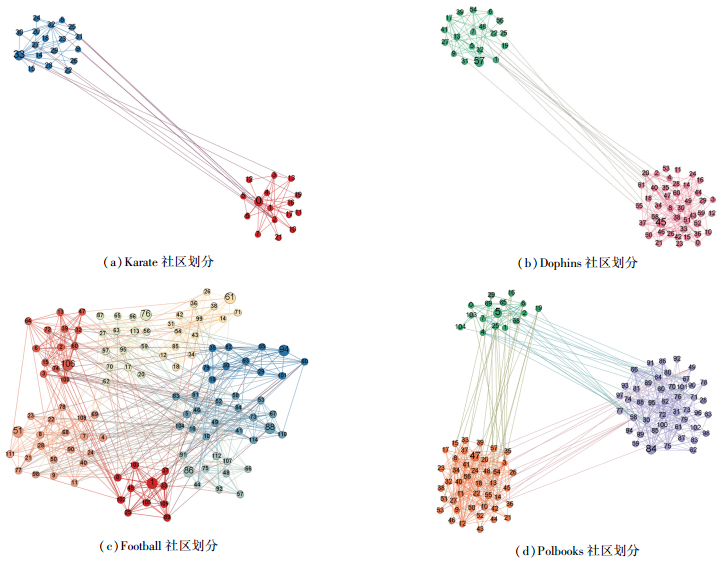
3.3 实验结果与分析本文将所提出的KDED算法与Fastgreed算法、Informap算法、Walktrap算法、LPA算法在真实数据集上进行对比, 与Fastgreed算法、Informap算法、Walktrap算法、LPA算法、VDDPC算法、LCCD算法在人工基准网络上进行比较. 图 1和图 2为KDED算法在真实数据集上的到的决策图和社区划分结果, 表 3列出5种算法在真实数据集上得到的仿真结果, 图 3描绘7种算法在人工数据集上的仿真结果. 图 1(a)~(d)为在Karate数据集、Dolphins数据集、Football数据集和Polbooks数据集上得到的决策图.可以看出, 核心节点的局部密度ρ以及到更高密度节点的距离δ明显大于一般节点, 这会使后续核心节点的筛选过程更为直观、准确;此外, 在选取核心节点与以及划分社区结构之后, 结合距离矩阵可以得到十分清晰的社区内部的层次结构. 图 2(a)~(d)为KDED算法在4个真实数据集上得到的社区划分结果.这样首先从划分结果的角度上粗略地说明本文提出的基于信任度的距离度量以及使用核密度估计规避截断距离dc的方法是合理有效的.
|
图 1 KDED算法下的决策 Figure 1 Decision diagramof KDED algorithm |
|
图 2 KDED算法下的社区划分 Figure 2 Community division under KDED algorithm |
| 表 3 真实网络仿真结果 Table 3 Real network simulation results |
|
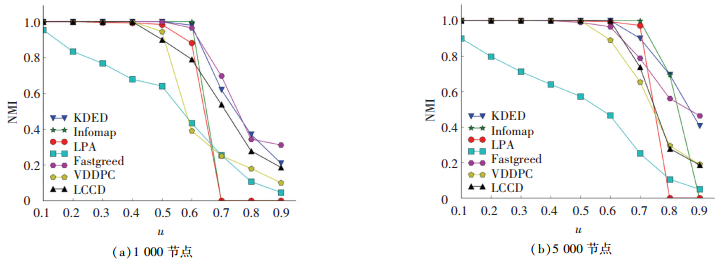
图 3 LFR人工基准网络下的仿真结果 Figure 3 Simulation results of LFR benchmark networks |
接下来评估划分结果的性能. 表 3为本文所提出的KDED算法与其他4个算法在Karate、Dophins、Polbooks、Football4个真实网络数据所得到的结果.可以观察到, KDED算法在Q值上与几种算法相近, 没有十分优秀的表现, 在karate网络中取得最好的Q值, 在其他的网络中与各种经典算法效果相近;但正如前文所讲, 在模块度Q长期作为衡量社区发现算法性能好坏的地位受到部分学者质疑之后, NMI逐渐成为社区发现领域比较被看重的指标, 在已知社区划分的真实网络数据集中, 通过NMI可以更为直观的观察出算法的准确性, 更具有参考价值. LPA具有令人满意的时间效率, 但由于标签传播的不确定性, 其性能远远不能令人满意.通过数据可以观察到, 相比较于其它算法, KDED算法具有很高的NMI值, 虽然在Football数据集上的NMI略低于LPA算法, 但二者相差不大.这意味着本文提出的KDED算法在不同规模的真实网络下可以得到较为符合实际社区划分的结果, 初步验证其可行性与准确性.
图 3为KDED算法与其他几种算法在LFR基准网络中的实验结果, 节点的规模为1000节点(a)和5000节点(b), 刻画NMI随着模糊度u的增加的变化趋势.从曲线趋势走向来看, 随着模糊参数u的增加, 社区之间的界限逐渐模糊, 划分难度增加, 曲线的下降代表着NMI值逐渐降低, 也意味着算法性能的下降.在1000节点规模的网络中, u < 0.6时, KDED算法的NNMI=1, 这意味着可以得到符合真实社区划分的结果, 与其他算法相比, 当u>0.5后, LPA算法和Informap算法的NMI值迅速下降至0, 通过后台观察社区划分结果发现其划分的社区个数为1, 这说明算法因社区间模糊度过高, 已无法继续划分有效社区.从总体上看, Informap算法在u≤0.6时取得最好的整体效果, 但在u>0.6后算法性能急剧下降;Fastgreed算法在整个实验过程中表现较差, VDDPC与LCCD算法在u>0.4后算法性能下降较快;KDED算法与Walktrap算法整体性能最好, 当u < 0.6时, 两种算法均能划分出真实的社区结构, 即NNMI=1, 随后其性能下降.值得注意的是, 在节点规模与社区规模增加时, 如图 3(b), 曲线变化的趋势是不同的, KDED与Walktrap在u≥0.7时性能上有明显的下降, Walkstrap性能下降的速度快于KDE;但是Informap与LPA算法在大规模社区的检测上具有更好的性能, 0.6≤u≤0.7时二者的性能优于KDED, 但是KDED的曲线没有发生急剧下降至0的情况, 总体性能较为平稳.
相比于一般社区发现算法只能发现社区外部的自然结构的情况, KDED可以通过各个节点在社区中到中心节点距离来发现社区内部的层次机构.在算法原理的叙述中可以充分地体现, 可以为需要解社区内部结构的学科带来便利, 如:舆论检测、推荐系统.基于以上分析, KDED算法具有比较突出的性能和最好的稳定性, 还可发现社区的层次结构, 可以认为它的表现是非常具有竞争力的.
4 总结1) 本文提出的KDED算法, 具有2个特点:1.提出一种基于信任度的新的距离度量, 该距离度量促进同社区内节点的相互靠拢, 使得其更易被聚类算法所应用;2.通过核密度估计规避仅能通过主观决策或的参数选择, 使算法自适应地根据网络特性进行有效的社区划分, 划分结果更加准确、有效.
2) 通过在真实数据集以及LFR人工网络下的实验仿真, 对于已有社区划分的数据集, KDED算法的NMI值普遍高于现有算法, 证明KDED算法所划分的社区结构, 更加接近真实划分结果, 验证算法的可行性与有效性.
3) KDED不仅有效发现自然社区结构, 而且可以展示社区内部的层次结构, 将来可以对KDED进行一些有意义的延伸, 如:结合一些改进, 还可以用于发现重叠的社区.
| [1] |
GIRVAN M, NEWMAN M E J. Community structure in social and biological networks[J].
Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(12): 7821-7826.
DOI: 10.1073/pnas.122653799 |
| [2] |
VINCENT D B. Fast unfolding of communities in large networks[J].
Journal of Statistical Mechanics Theory & Experiment, 2008, 2008(10): 155-168.
DOI: 10.1088/1742-5468/2008/10/P10008 |
| [3] |
JOHNSON N F, ZHENG M, VOROBYEVA Y, et al. New online ecology of adversarial aggregates: ISIS and beyond[J].
Science, 2016, 352(6292): 1459.
DOI: 10.1126/science.aaf0675 |
| [4] |
RAGHAVAN U N, ALBERT R, KUMARA S. Near linear time algorithm to detect community structures in large-scale networks[J].
Physical Review E Statistical Nonlinear & Soft Matter Physics, 2007, 76(2): 036106.
DOI: 10.1103/PhysRevE.76.036106 |
| [5] |
张鑫, 刘秉权, 王晓龙. 稳定标签传播的社区发现方法[J].
哈尔滨工业大学学报, 2016, 48(11): 47-52.
ZHANG Xin, LIU Bingquan, WANG Xiaolong. Community detection method based on stable label propagation[J]. Journal of Harbin Institute of Technology, 2016, 48(11): 47-52. DOI: 10.11918/j.issn.0367-6234.2016.11.008 |
| [6] |
ROSVALL M, BERGSTROM C T. Maps of random walks on complex networks reveal community structure[J].
Proceedings of the National Academy of Sciences, 2007, 105(4): 1118-1123.
DOI: 10.1073/pnas.0706851105 |
| [7] |
ZHOU Haijun. Network landscape from a Brownian particle's perspective.[J].
Physical Review E Statistical Nonlinear & Soft Matter Physics, 2003, 67(4Pt1): 041908.
DOI: 10.1103/PhysRevE.67.041908 |
| [8] |
LIU Wei. Detecting Communities Based on Network Topology[J].
Scientific Reports, 2014, 4(4): 5739.
DOI: 10.1038/srep05739 |
| [9] |
AGARWAL G, KEMPE D. Modularity-maximizing graph communities via mathematical programming[J].
The European Physical Journal B, 2008, 66(3): 409-418.
DOI: 10.1140/epjb/e2008-00425-1 |
| [10] |
RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J].
Science, 2014, 344(6191): 1492-1496.
DOI: 10.1126/science.1242072 |
| [11] |
黄岚, 李玉, 王贵参, 等. 基于点距离和密度峰值聚类的社区发现方法[J].
吉林大学学报(工), 2016, 46(6): 2042-2051.
HUANG Lan, LI Yu, WANG Guisheng, et al. Community Detection Method Based on Point Distance and Density Peak Clustering[J]. Journal of Jilin University Engineering Edition, 2016, 46(6): 2042-2051. DOI: 10.13229/j.cnki.jdxbgxb201606038 |
| [12] |
HUANG Lan, WANG Guisheng, WANG Yan, et al[J]. International Journal of Modern Physics B, 2016, 30(24): 1650167. DOI: 10.1142/S0217979216501678.
|
| [13] |
HENNIG C, HAUSDORF B. Design Of Dissimilarity Measures: A New Dissimilarity Between Species Distribution Areas[J].
Data Science & Classification, 2006: 29-37.
DOI: 10.1007/3-540-34416-0_4 |
| [14] |
ZIEGLER C N, LAUSEN G. Analyzing Correlation between Trust and User Similarity in Online Communities[C]// International Conference on Trust Management. Springer Berlin Heidelberg, 2004: 251-265. DOI: 10.1007/978-3-540-24747-0_19.
|
| [15] |
BOTEV Z I, GROTOWSKI J F, KROESE D P. Kernel density estimation via diffusion[J].
Annals of Statistics, 2010, 38(5): 2916-2957.
DOI: 10.1214/10-AOS799 |
| [16] |
LEHMANN E L. Model Specification: The Views of Fisher and Neyman, and Later Developments[M]// Selected Works of E. L. Lehmann. 2012: 955-963. DOI: 10.1007/978-1-4614-1412-4_78.
|
| [17] |
RASHID M. Clustering by fast search and find of density peaks via heat diffusion[J].
Neurocomputing, 2016, 208(6191): 210-217.
DOI: 10.1016/j.neucom.2016.01.102 |
| [18] |
XU Xiaoyuan, YAN Zheng, XU Shaolun. Estimating wind speed probability distribution by diffusion-based kernel density method[J].
Electric Power Systems Research, 2015, 121: 28-37.
DOI: 10.1016/j.epsr.2014.11.0 |
| [19] |
KRISHNASWAMY S, SPITZER M H, MINGUENEAU M, et al. Systems biology. Conditional density-based analysis of T cell signaling in single-cell data[J].
Science, 2014, 346(6213): 1250689.
DOI: 10.1126/science.1250689 |
| [20] |
LANCICHINETTI A, FORTUNATO S. Benchmarks for testing community detection algorithms on directed and weighted graphs with overlapping communities[J].
Physical Review E Statistical Nonlinear & Soft Matter Physics, 2009, 80(1Pt2): 016118.
DOI: 10.1103/PhysRevE.80.016118 |
 2018, Vol. 50
2018, Vol. 50


