2. 哈尔滨工业大学 电气工程及其自动化学院, 哈尔滨 150001
2. School of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin 150001, China
图像分割在视觉信息分析过程中起到很大的作用,例如目标识别和场景理解.虽然目前已经有很多方法被成功应用到相应领域,但图像分割仍然是一个很具有挑战性的研究. Kass提出的主动轮廓模型(Active Contour Model,ACM)[1]作为一个非常成功的图像分割模型,主要可以分为两大类:基于边界的模型[1-3]和基于区域的模型[4-10].虽然它们共同的特点都是把图像分割成多个封闭且边界光滑的子区域,但是基于边界的方法存在一些缺点,如它对图像噪声很敏感、弱边界,需要确定曲线的初始化位置、很难改变图像的拓扑结构、对参数过于依赖等.与基于边界模型相比,Osher和Sethian提出的基于区域的模型[10],则具有两个基于边界模型所不具有的优点:1)对噪声具有很好的鲁棒性且对弱边界图像具有很好的分割准确度; 2)对初始曲线的位置不敏感.所以该方法的轮廓可以根据拓扑结构的改变而进行合并或拆分.从而成功的避免了基于边界方法应对拓扑变化困难且过分依赖参数的缺点,提高了对图像噪声和水平集初始位置的鲁棒性,以及对弱边界图像的分割精度.
在基于区域的模型中,Mumford和Shah提出的Mumford-Shah模型[5],把图像分解成一些子区域,每个区域都可以用一个平滑函数来代替, 所以可通过最小化Mumford-Shah函数来获得图像的最佳分割结果. Chan等在Mumford-Shah模型的基础上提出了Chan-Vese(CV)模型[6].该模型最显著的特点是计算量少、速度快.但是CV模型只能在分割区域的亮度分布满足均匀统计时才会取得较好的分割结果; 当目标细节或亮度分布不均匀时,CV模型就不能很好地进行分割,所以该模型只在比较小的区域内才能获得较好的分割结果.针对这类问题,一些学者提出了基于区域相似的主动轮廓模型,即分段光滑(Piecewise Smooth, PS)模型[9],来进行处理,但分段光滑模型也存在计算代价高的问题.
如上所述,基于区域的图像分割模型通常依赖待分割区域中的亮度描述(如亮度平均值或高斯分布)来进行分割,然而当亮度不均匀时,每个图像子区域的亮度分布会出现重叠现象,所以获得不均匀亮度区域的特征描述是十分困难的.为了解决亮度不均匀这个问题,一些文献[7, 11-16]使用局部亮度统计信息(亮度的局部均值、局部亮度分布或亮度的直方图)来进行目标逼近,进而提高图像的分割精度.例如Li提出的区域可伸缩拟合能量模型(RSF)方法[7]和Wang提出的局部高斯分布拟合(LGD)方法[11].但是它们也存在对初始曲线位置敏感、计算复杂度高等问题.为克服局部信息对曲线初始位置敏感的问题,Wang[8]提出了局部Chan-Vese (LCV)模型.它利用全局和局部信息来对图像进行分割. LCV模型在一定程度上改进了对不均匀图像区域的分割能力,提高了对初始曲线位置的鲁棒性.但是文献[17]指出在某种程度上LCV模型仍然是CV模型,虽然全局和局部信息的整合可以解决亮度不均匀和初始位置敏感等问题[18].但这些模型只利用了全局信息和局部信息,没有充分利用特征点的分布信息,所以本文提出了基于布雷格曼(Bregman)散度分布和RSF模型的水平集图像分割方法.它利用包含Bregman散度(特征点分布情况)的全局信息来克服局部信息对曲线初始位置敏感的问题,通过泰勒展开式把Bregman散度看作是对数据加权L2范数的逼近,并把相关数据的加权项视为先验信息,进而保证系统的稳定性、加快曲线的演化; 同时利用局部信息来提高对不均匀亮度图像的处理能力.因此本文模型与其它基于区域的模型(如RSF模型、LCV模型)相比,在分割效果上变得更有效和更强大; 在不损失处理能力的前提下,运行速度也比RSF模型更快.
1 基于布雷格曼散度的RSF模型首先引入一个先验假设,即待分割图像的前景(Foreground)和背景(Background)的像素值相对具有大小顺序关系.这个先验假设是很弱的,因为在很多实际应用中,这种情况(如MIR图像和X-RAY图像分割)是经常出现的,所以该先验假设是成立的.
1.1 基于布雷格曼散度的RSF模型为实现不均匀图像的分割,并解决对初始位置敏感的问题,本文在RSF模型中通过Bregman散度引入了像素点的全局信息来加速算法的收敛速度和对初始位置的鲁棒性, 参数见表 1.这是因为Bregman方法不需要正则化,连续性和不等式约束的强制等,所以可以快速并且更好地解决L1正则优化问题[19].改进后的布雷格曼散度的局部二元拟合模型的定义可以看作是如式(1)所示的最小化问题
| 表 1 本文模型和其它模型的关系 Table 1 The parameter's relationship between the Bregman-MLBF model and the other model |
| $ E\left( {\mathit{\boldsymbol{C}}, {c_1}, {c_2}, {f_1}\left( \mathit{\boldsymbol{x}} \right), {f_2}\left( \mathit{\boldsymbol{x}} \right)} \right) = w{E^B} + \left( {1-w} \right){E^L} + {E^R}. $ | (1) |
其中:
| $ \begin{array}{l} {E^B} = \lambda_1 \int\limits_{{\rm{in}}\left( C \right)} {{B_{\varphi \left( \cdot \right) = {{\left( \cdot \right)}^{2\alpha }}}}\left( {{c_1}||I\left(x\right)} \right){\rm{d}}\mathit{\boldsymbol{x}}} + \\ \;\;\;\;\;\;\;\;\lambda_2 \int\limits_{{\rm{out}}\left( C \right)} {{B_{\varphi \left( \cdot \right) = {{\left( \cdot \right)}^{2\beta }}}}\left( {{c_2}||I\left(x\right)} \right){\rm{d}}\mathit{\boldsymbol{x}}}, \\ {E^L} = \int\limits_\mathit{\Omega } {{E_x}\left( {\mathit{\boldsymbol{C}}, {f_1}\left( \mathit{\boldsymbol{x}} \right), {f_2}\left( \mathit{\boldsymbol{x}} \right)} \right){\rm{d}}\mathit{\boldsymbol{x}}, } \\ {E^R} = \mu {\rm{length}}\left( \mathit{\boldsymbol{C}} \right), \end{array} $ |
α, β, λ1, λ2, w是正的常数, α≥1≥β>0, C是曲线, c1和c2分别表示曲线C内部或外部的平均亮度. EB(C, c1, c2)是全局信息能量泛函,表达式中的Bφ(·)=(·)2α(c1‖I(x))和Bφ(·)=(·)2β(c2‖I(x))是对应点对(c1, I(x))和(c2, I(x))的Bregman散度[20]. I(x)是像素点x处的亮度. w≥0,是平衡全局信息能量泛函项EB和局部信息能量项EL的权重值.
为便于对能量函数EB进行求解,本文根据泰勒展开式,把EB展开得到下面的表达式
| $ \left\{ \begin{array}{l} {B_{\varphi \left( x \right) = {{\left( x \right)}^{2\alpha }}}}\left( {{c_1}||I\left( \mathit{\boldsymbol{x}} \right)} \right) = \alpha \left( {2\alpha-1} \right){I^{2\alpha-2}}\left( \mathit{\boldsymbol{x}} \right)\left( {I\left( \mathit{\boldsymbol{x}} \right)-} \right.\\ \;\;\;\;\left. {{c_1}} \right)2 + o\left( {|I\left( \mathit{\boldsymbol{x}} \right) - {c_1}{|^2}} \right), \\ {B_{\varphi \left( x \right) = {{\left( x \right)}^{2\beta }}}}\left( {{c_2}||I\left( \mathit{\boldsymbol{x}} \right)} \right) = \beta \left( {2\beta - 1} \right){I^{2\beta - 2}}\left( \mathit{\boldsymbol{x}} \right)\left( {I\left( \mathit{\boldsymbol{x}} \right) - } \right.\\ \;\;\;\;\left. {{c_2}} \right)2 + o\left( {|I\left( \mathit{\boldsymbol{x}} \right) - {c_2}{|^2}} \right). \end{array} \right. $ |
为降低计算复杂度,本文模型去掉了二阶项o(|I(x)-c1|2)和o(|I(x)-c2|2),把能量函数EB改写成式(2)所示的表达式
| $ \begin{array}{l} {E^B} = {\lambda _1}\int\limits_{{\rm{in}}\left( C \right)} {\alpha \left( {2\alpha-1} \right){I^{2\alpha-2}}\left( \mathit{\boldsymbol{x}} \right){{\left( {I\left( \mathit{\boldsymbol{x}} \right)-{c_1}} \right)}^2}{\rm{d}}\mathit{\boldsymbol{x + }}} \\ \;\;\;\;\;\;\;\;{\lambda _2}\int\limits_{{\rm{out}}\left( C \right)} {\beta \left( {2\beta - 1} \right){I^{2\beta - 2}}\left( \mathit{\boldsymbol{x}} \right){{\left( {I\left( \mathit{\boldsymbol{x}} \right) - {c_2}} \right)}^2}{\rm{d}}\mathit{\boldsymbol{x}}} . \end{array} $ | (2) |
此外还添加一个惩罚项[21]来避免耗时的重新初始化,并保持水平集函数的正则性.
| $ {E^P}\left( \varphi \right) = v\int\limits_\Omega {\frac{1}{2}{{\left( {|\nabla \varphi \left( x \right)|-1} \right)}^2}{\rm{d}}x} . $ |
式中v是正常数,通常ν=1.
根据等式(1)、(2)可重写水平集的能量函数,新的表达形式如式(3)所示
| $ \begin{array}{l} {E^{{\rm{Bregman- LBF}}}}\left( {\varphi, {c_1},{c_2}, {f_1}\left( \mathit{\boldsymbol{x}} \right), {f_2}\left( \mathit{\boldsymbol{x}} \right)} \right) = \\ \;\;\;{\lambda _1}\int\limits_\mathit{\Omega } {[\left( {1-w} \right)\int\limits_\mathit{\Omega } {{g_k}\left( {\mathit{\boldsymbol{x}}-\mathit{\boldsymbol{y}}} \right){{\left( {I\left( \mathit{\boldsymbol{y}} \right)-{f_1}\left( \mathit{\boldsymbol{x}} \right)} \right)}^2}{H_\varepsilon }\left( {\varphi \left( \mathit{\boldsymbol{x}} \right)} \right){\rm{d}}\mathit{\boldsymbol{y + }}} } \\ \;\;\;\;w\alpha \left( {2\alpha - 1} \right){I^{2\alpha - 2}}\left( \mathit{\boldsymbol{x}} \right){\left( {I\left( \mathit{\boldsymbol{x}} \right) - {c_1}} \right)^2}{H_\varepsilon }\left( {\varphi \left( \mathit{\boldsymbol{x}} \right)} \right)]{\rm{d}}\mathit{\boldsymbol{x + }}\\ \;\;\;{\lambda _2}\int\limits_\mathit{\Omega } {[\left( {1-w} \right)\int\limits_\mathit{\Omega } {{g_k}} } \left( {\mathit{\boldsymbol{x}}-\mathit{\boldsymbol{y}}} \right){\left( {I\left( \mathit{\boldsymbol{y}} \right)-{f_2}\left( \mathit{\boldsymbol{x}} \right)} \right)^2}(1 - \\ \;\;\;{H_\varepsilon }\left( {\varphi \left( \mathit{\boldsymbol{x}} \right)} \right)){\rm{d}}\mathit{\boldsymbol{y + }}w\beta \left( {2\beta - 1} \right){I^{2\beta - 2}}\left( \mathit{\boldsymbol{x}} \right)(I\left( \mathit{\boldsymbol{x}} \right) - \\ \;\;\;\;\;{c_2}{)^2}\left( {1 - {H_\varepsilon }\left( {\varphi (\mathit{\boldsymbol{x}}} \right)} \right)]{\rm{d}}\mathit{\boldsymbol{x + }}\mu \int\limits_\mathit{\Omega } {{\delta _\varepsilon }\left( \varphi \right){\rm{d}}\mathit{\boldsymbol{x}}} + \\ \;\;\;\;\;v\int\limits_\mathit{\Omega } {\frac{1}{2}} {\left( {|\nabla \varphi \left( \mathit{\boldsymbol{x}} \right)| -1} \right)^2}{\rm{d}}\mathit{\boldsymbol{x}}\mathit{\boldsymbol{.}} \end{array} $ | (3) |
利用变分法和梯度下降法,得到梯度流方程,如表达式(4)所示
| $ \begin{array}{l} \frac{{\partial \varphi \left( {x, t} \right)}}{{\partial t}} = {\delta _\varepsilon }\left( \varphi \right)w\left( {- {\lambda _1}{e_1} + {\lambda _2}{e_2}} \right) + \mu {\delta _\varepsilon }\left( \varphi \right){\rm{div}}\left( {\frac{{\nabla \varphi }}{{|\nabla \varphi |}}} \right)- \\ \;\;\;\;\;\;v\left( {{\nabla ^2}- {\rm{div}}\left( {\frac{{\nabla \varphi }}{{|\nabla \varphi |}}} \right)} \right) + {\delta _\varepsilon }\left( \varphi \right)(1 - \\ \;\;\;\;\;\;w)[-{\lambda _1}\alpha \left( {2\alpha-1} \right){I^{2\alpha-2}}\left( x \right)\left( {I\left( x \right) - {c_1}} \right)2 + \\ \;\;\;\;\;\;{\lambda _2}\beta \left( {2\beta - 1} \right){I^{2\beta - 2}}\left( x \right)\left( {I\left( x \right) - {c_2}} \right)2], \end{array} $ | (4) |
其中:
| $ \begin{array}{l} {e_1} = \int\limits_\mathit{\Omega } {{g_k}\left( {\mathit{\boldsymbol{y}}-\mathit{\boldsymbol{x}}} \right)|I\left( \mathit{\boldsymbol{x}} \right)-{f_1}\left( \mathit{\boldsymbol{y}} \right){|^2}{\rm{d}}\mathit{\boldsymbol{y}}}, \\ {e_2} = \int\limits_\mathit{\Omega } {{g_k}\left( {\mathit{\boldsymbol{y}}-\mathit{\boldsymbol{x}}} \right)|I\left( \mathit{\boldsymbol{x}} \right) - {f_2}\left( \mathit{\boldsymbol{y}} \right){|^2}{\rm{d}}\mathit{\boldsymbol{y}}} . \end{array} $ |
在求解式(4)所示的梯度流时,使用两步迭代方法来进行处理.
第一步,首先固定水平集函数φ(x),然后利用式(5)分别对曲线内部和外部的平均亮度c1、c2,以及局部拟合亮度f1(x)、f2(x)进行更新.
第二步, 根据等式(5)更新本文模型的水平集函数φ(x).
| $ \begin{array}{*{20}{c}} {{{\hat c}_1} = \frac{{\int\limits_\mathit{\Omega } {I\left( \mathit{\boldsymbol{x}} \right){H_\varepsilon }\left( {\varphi \left( \mathit{\boldsymbol{x}} \right)} \right){\rm{d}}\mathit{\boldsymbol{x}}} }}{{\int\limits_\mathit{\Omega } {{H_\varepsilon }\left( {\varphi \left( \mathit{\boldsymbol{x}} \right)} \right){\rm{d}}\mathit{\boldsymbol{x}}} }}, }\\ {{{\hat c}_2} = \frac{{\int\limits_\mathit{\Omega } {I\left( \mathit{\boldsymbol{x}} \right)\left( {1- {H_\varepsilon }\left( {\varphi \left( \mathit{\boldsymbol{x}} \right)} \right)} \right){\rm{d}}\mathit{\boldsymbol{x}}} }}{{\int\limits_\mathit{\Omega } {\left( {1- {H_\varepsilon }\left( {\varphi \left( \mathit{\boldsymbol{x}} \right)} \right)} \right){\rm{d}}\mathit{\boldsymbol{x}}} }}, }\\ {{f_1}\left( {\mathit{\boldsymbol{\hat x}}} \right) = \frac{{\int\limits_\mathit{\Omega } {{g_k}\left( {\mathit{\boldsymbol{x}}- \mathit{\boldsymbol{y}}} \right)*\left[{{H_\varepsilon }\left( {\varphi \left( \mathit{\boldsymbol{x}} \right)} \right)I\left( \mathit{\boldsymbol{y}} \right)} \right]{\rm{d}}\mathit{\boldsymbol{y}}} }}{{\int\limits_\mathit{\Omega } {{g_k}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right)*{H_\varepsilon }\left( {\varphi \left( \mathit{\boldsymbol{x}} \right)} \right){\rm{d}}\mathit{\boldsymbol{y}}} }}, }\\ {{f_2}\left( {\mathit{\boldsymbol{\hat x}}} \right) = \frac{{\int\limits_\mathit{\Omega } {{g_k}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right)*\left[{\left( {1-{H_\varepsilon }\left( {\varphi \left( \mathit{\boldsymbol{x}} \right)} \right)} \right)I\left( \mathit{\boldsymbol{y}} \right)} \right]{\rm{d}}\mathit{\boldsymbol{y}}} }}{{\int\limits_\mathit{\Omega } {{g_k}\left( {\mathit{\boldsymbol{x}} -\mathit{\boldsymbol{y}}} \right)*\left( {1 -{H_\varepsilon }\left( {\varphi \left( \mathit{\boldsymbol{x}} \right)} \right)} \right){\rm{d}}\mathit{\boldsymbol{y}}} }}.} \end{array} $ | (5) |
考虑文献[21]中局部序能量泛函引入RSF模型以保持前景与背景中的局部拟合亮度f1(x)、f2(x)的序关系,所以在本文中,利用同样的思想,并且将其推广至全局和局部序保持,为此在式(5)中引入max和min运算操作,曲线内部和外部的平均亮度c1、c2,以及局部拟合亮度f1(x)、f2(x)更新步骤如式(6)所示
| $ \begin{array}{*{20}{c}} {{c_1} = \min \left( {{{\hat c}_1}, {{\hat c}_2}} \right), }\\ {{c_2} = \max \left( {{{\hat c}_1}, {{\hat c}_2}} \right), }\\ {{f_1}\left( \mathit{\boldsymbol{x}} \right) = \min \left( {{f_1}\left( {\mathit{\boldsymbol{\hat x}}} \right), {f_2}\left( {\mathit{\boldsymbol{\hat x}}} \right)} \right), }\\ {{f_2}\left( \mathit{\boldsymbol{x}} \right) = \max \left( {{f_1}\left( {\mathit{\boldsymbol{\hat x}}} \right), {f_2}\left( {\mathit{\boldsymbol{\hat x}}} \right)} \right).} \end{array} $ | (6) |
从式(1)可知, 本模型的特色在全局能量泛函EB处,所以主要讨论表达式(2)中的全局能量泛函EB.为避免讨论的复杂性,假设图像I(x)为二值图像,d1和d2分别表示曲线内和曲线外的亮度值.并满足d1>d2条件,同时α≥1≥β>0,曲线C和目标点位置关系的可能情况见图 1; 假如x∈in(C)则水平集函数φ(x)>0;否则φ(x) < 0;这样得到下面的等式:

|
图 1 曲线和目标点位置关系的可能情况 Figure 1 The possibility of the relationship between the curve and the target point |
| $ \begin{array}{*{20}{c}} {{F^B}\left( {{\mathit{\boldsymbol{p}}_1}, {d_2}} \right) = {\delta _\varepsilon }\left( {{\mathit{\boldsymbol{p}}_1}} \right)[-{\lambda _1}\alpha \left( {2\alpha-1} \right)d_2^{2\alpha-2}{{\left( {{d_2} - {c_1}} \right)}^2} + }\\ {{\lambda _2}\beta \left( {2\beta - 1} \right){d_2}^{2\beta - 2}{{\left( {{d_2} - {c_2}} \right)}^2}], }\\ {{F^B}\left( {{\mathit{\boldsymbol{p}}_2}, {d_1}} \right) = {\delta _\varepsilon }\left( {{\mathit{\boldsymbol{p}}_2}} \right)[-{\lambda _1}\alpha \left( {2\alpha-1} \right){d_1}^{2\alpha-2}{{\left( {{d_1} - {c_1}} \right)}^2} + }\\ {{\lambda _2}\beta \left( {2\beta - 1} \right){d_1}^{2\beta - 2}{{\left( {{d_1} - {c_2}} \right)}^2}], }\\ {{F^B}\left( {{\mathit{\boldsymbol{p}}_3}, {d_1}} \right) = {\delta _\varepsilon }\left( {{\mathit{\boldsymbol{p}}_3}} \right)[-{\lambda _1}\alpha \left( {2\alpha-1} \right){d_1}^{2\alpha-2}{{\left( {{d_1} - {c_1}} \right)}^2} + }\\ {{\lambda _2}\beta \left( {2\beta - 1} \right){d_1}^{2\beta - 2}{{\left( {{d_1} - {c_2}} \right)}^2}], }\\ {{F^B}\left( {{\mathit{\boldsymbol{p}}_4}, {d_2}} \right) = {\delta _\varepsilon }\left( {{\mathit{\boldsymbol{p}}_4}} \right)[-{\lambda _1}\alpha \left( {2\alpha-1} \right){d_2}^{2\alpha-2}{{\left( {{d_2} - {c_1}} \right)}^2} + }\\ {{\lambda _2}\beta \left( {2\beta - 1} \right){d_2}^{2\beta - 2}{{\left( {{d_2} - {c_2}} \right)}^2}].} \end{array} $ |
其中, FB(p1, d1), FB(p2, d1), FB(p3, d2), FB(p4, d2)分别是水平集函数φ(x)在点p1, p2, p3, p4的梯度. c1, c2分别是表示曲线C内部和外部的平均亮度.由于在本文中c1, c2的更新运算中引入了max和min运算,所以,曲线C的内部平均亮度、外部平均亮度、前景亮度和背景亮度值间的关系满足d2≤c1≤c2≤d1; 得到式(7)所示的不等式
| $ \begin{array}{l} {F^B}\left( {{\mathit{\boldsymbol{p}}_1}, {d_2}} \right) \le 0, {F^B}\left( {{\mathit{\boldsymbol{p}}_2}, {d_1}} \right) \ge 0, \\ {F^B}\left( {{\mathit{\boldsymbol{p}}_3}, {d_1}} \right) \ge 0, {F^B}\left( {{\mathit{\boldsymbol{p}}_4}, {d_2}} \right) \le 0. \end{array} $ | (7) |
分析水平集的梯度,计算点p1处的水平集为正值.这意味着,在点p1处不会形成新的零水平集,它仍然在水平集内部.同样,依次分析剩余的点,这样可以将所有的点进行正确的分类.获得的全局能量泛函
| $ \begin{array}{l} {E^B}\left( {\mathit{\boldsymbol{C}}, {c_1}, {c_2}} \right) = {\lambda _1}\int\limits_{{\rm{in}}\left( C \right)} {\alpha \left( {2\alpha-1} \right){c_1}^{2\alpha-2}{{\left( {I\left( \mathit{\boldsymbol{x}} \right)-{c_1}} \right)}^2}{\rm{d}}x + } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\lambda _2}\int\limits_{{\rm{out}}\left( C \right)} {\beta \left( {2\beta - 1} \right){c_2}^{2\beta - 2}{{\left( {I\left( \mathit{\boldsymbol{x}} \right) - {c_2}} \right)}^2}{\rm{d}}\mathit{\boldsymbol{x}}.} \end{array} $ | (8) |
如文献[7]所述,RSF模型的力(梯度)是和边界有关的,而加权CV模型的能量是和区域相关的.所以为了更容易的分析两个模型,本文对二值图像Ⅰ进行讨论,在等式(2)和RSF模型对应的梯度流方程(并没有讨论Delta函数)中,直接讨论像素的水平集函数梯度.那么P点对应的水平集函数梯度可表示成如下的形式:
| $ \begin{array}{l} {F^{{\rm{Bregman}}}} =-{\lambda _1}\alpha \left( {2\alpha-1} \right){I^{2\alpha-2}}\left( p \right){\left( {I\left( p \right) - {c_1}} \right)^2} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\lambda _2}\beta \left( {2\beta - 1} \right){I^{2\beta - 2}}\left( p \right){\left( {I\left( p \right) - {c_2}} \right)^2}, \\ {F^{{\rm{LBF}}}} = - {\lambda _1}{e_1} + {\lambda _2}{e_2}. \end{array} $ |
其中c1和c2分别表示曲线C内部或外部的平均亮度. λ1和λ2是常量. I(p)是点P的亮度,e1和e2的定义见等式(8).因为图像I是二值化图像,FBregman是平方差之和,所以该项不可能为0;而FRSF只有当点P离边缘的距离超过高斯核的尺寸时,FRSF才为0,否则FRSF非零.
总体来说,与RSF模型对比,本文方法具有以下3个优点:1)水平集函数的更新更加有效; 2)获得全局最优解的改进意味着本文模型具有获得较好分割结果的能力; 3)本文提出的模型对初始位置的鲁棒性更高.与LCV模型相比,由于本文模型还利用了局部信息,所以对图像亮度不均匀所带来的问题也能进行很好的处理.
2 实验在本部分针对不同类型的图像, 使用本文模型与RSF模型、LCV模型、LGIF模型进行对比分析.在提出的模型中使用了参数λ1, λ2, μ, ν, α, β和时间步长Δt,其中本文模型对于λ1, λ2, μ, ν的选择不是很敏感,一般都会取固定值:λ1=1, λ2=1, α = 1.05, β =0.95, v=1.约束项中的长度参数μ会随着被分割图像的不同而改变.权重函数w则是由图像质量直接决定.因为本文模型的全局能量项可以很好对分段图像进行分割; 而局部能量项可以很好的处理不均匀图像分割.其他方法的参数在本文参数的附近进行适当的修改.
2.1 对高斯噪声和不均匀亮度的鲁棒性图 2中对一个目标生成8个不同的图像,并把该目标已知的边界作为真实数据.这8个图像是通过填加不同等级的噪声和不同强度的亮度不均匀性生成的.在图 2的头二行中,每一行都具有相同的亮度不均匀性,但噪声强度是不同的.对于每一列,它们的噪声强度相同,但亮度的不均匀性不同.每个处理图像的初始轮廓用红色的圆圈表示,处理后的分割结果用绿色轮廓线表示.从图 2中可知处理结果都小于3%,说明本文模型对高斯噪声和不均匀亮度具有很强的鲁棒性.但同时也可以看出当亮度不均匀性或/和噪声强度比较严重时,就需要更多次的迭代.

|
图 2 在不同的图像条件的布雷格曼-RSF模型分割的结果 Figure 2 Segmentation results of the Bregman-MRSF model in different image conditions |
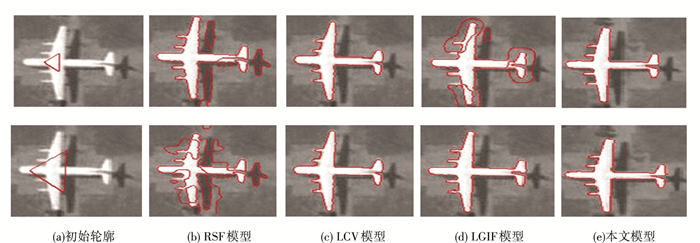
为演示本文模型对初始轮廓的鲁棒性.分别对合成图像、医学图像(典型的亮度不均匀图像)和真实图像(分段图像)进行实验,处理结果分别在图 3~5中显示.其中在每组图像的(a)列显示了不同的初始轮廓; 在图 3~5第(b)~(e)列分别显示RSF模型、LCV模型、LGIF模型和本文模型的处理结果.

|
图 3 对合成图像的分割比较结果 Figure 3 Segmentation results of synthetic image with different initial locations |

|
图 4 对医学图像的分割比较结果 Figure 4 Segmentation results of medical image with different initial locations. |
|
图 5 飞机图像的分割比较结果 Figure 5 Segmentation results with different initial locations |
图 3显示了对合成图像的处理结果,从图 3中可以看出RSF模型、LCV模型在三个不同的初始轮廓上都不能很好地进行图像分割.与RSF模型和LCV模型相比,显示在图 3第(d)列的LGIF模型,在某些情况下能得到很好的分割结果.但是在大多数情况下(见图 2中的第二行),RSF模型、LCV模型和LGIF模型都不能很好的完成对边界的分割.而本文模型则可从3个不同初始轮廓开始,对目标的边界进行很好的提取,所以可看出本文方法在对合成图像进行分割时具有很好的鲁棒性.
医学图像的处理结果见图 4,这两个图像都属于典型的亮度不均匀图像,在图 4的血管X-RAY图像中,部分血管的特征很弱,因此对它进行分割是一个非常艰巨的任务.从图 4第(b)、(d)列的显示结果可知:RSF模型和LGIF模型虽然具有一定处理亮度不均匀图像的能力,但处理结果也显示这两个模型对水平集的初始位置比较敏感,尤其是在图 4第2行(b)列,显示了不断缩小的轮廓产生了很坏的处理结果,没有获取到任何图像边缘.换句话说,对于这两种模型,如果选择好的初始轮廓,则可以得到一个满意的分割结果,否则这两个模型只能得到一个无法满足应用需求的局部解.对于图 4(c)列的LCV模型,因其具有全局属性,所以使它对于不同的初始轮廓都可以得到相同的分割结果.但该结果并不是最优的分割结果.从图 4(f)列的处理结果可知,本文模型对初始轮廓具有很强的鲁棒性,能够很好地处理亮度不均匀问题,并得到满意的分割结果.
图 5显示了上述4个模型对分段图像的处理结果.通过处理结果的对比可知[7],RSF模型对于多层次分段图像不具有很好的分割能力; 而LCV模型在一定程度上可看作是改进的CV模型,它与RSF模型和LGIF模型相比取得了较好的分割结果; LGIF模型在一定程度上可以简单的看作是CV模型和RSF模型的结合,它在某些情况下能够得到较好的结果.而本文模型与RSF模型、LCV模型、LGIF模型相比,具有更好的分割处理能力.从图 3~5,显示了RSF模型、LCV模型、LGIF模型和本文模型针对不同初始位置、不同的不均匀图像或分段图像的分割结果.对某些情况下,前三个模型能够得到和本文模型相同的分割结果,但是相应结果也显示了前3个模型在不同的初始位置,所得到的处理结果是不同的,当选择一个较好的初始位置时,会得到一个较好的分割结果,否则只能得到一个不满意的分割结果; 而本文模型则能够得到相同的结果,这表明本文模型与其它模型相比,在处理不均匀亮度图像和初始位置选择方面都具有更加稳定的能力.这是因为本文模型利用局部信息来提高对亮度不均匀图像的处理能力,同时针对计算局部信息的卷积操作比较费时这个问题,引进了全局信息项,即把Bregman散度加入到能量表达式中,从而加快水平集函数的收敛速度和有效性.
2.3 实验结果的比较和评价本模型的分割结果是目标的边界轮廓,因此我们使用基于轮廓的测度[21]来对分割结果进行精确评价,但是基于轮廓的测度e′mean是不对称的,所以它不是数学量度.它在真实数据由一个部分组成时,会是一个比较好的测量方法,但是当真实数据由多于二个部分组成时,它就不能很好地拟合数据,还可能会造成错误的评价结果.因此提出一个改进的基于轮廓的测量方法来避免上面存在的问题.通过定义从轮廓S到真实数据G的偏差来进行测量,表达式如式(14)所示
| $ {e_{{\rm{mean}}}}\left( {S, G} \right) = \max \left( {\frac{1}{{{N_S}}}\sum\limits_{i = 1}^{{N_s}} {d\left( {{P_i}, G} \right), \frac{1}{{{N_G}}}\sum\limits_{j = 1}^{{N_G}} {d\left( {{Q_j}, S} \right)} } } \right). $ | (14) |
其中, NG=Card(G),Qi, i=1, 2, …, NG是真实数据上的点,本文提出的基于轮廓的度量可用来评价一种亚像素精度的分割结果,输出的取值范围为[0, +∞). 图 6显示了本文模型与RSF模型、LCV模型、LGIF模型的比较结果.其中图 6(a)列是初始图像; 图 6(b)列是手工标定的分割结果; 图 6(c)列是RSF模型的分割结果; 图 6(d)列是LCV模型的分割结果; 图 6(e)列是LGIF模型的分割结果; 图 6(f)列是本文方法的分割结果.第一行处理的图像是合成图像; 第二行处理的图像是医学MRI图像(来自Brain Web[23]); 第3、4行处理的图像来自于BSD300数据库[24]; 其中图 6(b)列手工标定的分割结果被当作真实数据进行对比. 表 2给出了使用emean得到的评价结果,从表中可以看出本文模型的评价结果具有最小的emean值,因此它的分割结果好于其它三种模型的分割结果.

|
图 6 本文方法和其它方法的比较结果 Figure 6 Comparison of the segmentation results |
| 表 2 emean得到的评价结果(单位:像素点) Table 2 Results of the quantitative evaluation with emean(pixel) |
本文提出了一个基于Bregman散度和RSF模型相结合的水平集图像分割方法,通过把Bregman散度信息引入到RSF模型中,有效地利用了全局和局部信息来构建能量函数,进而对曲线的演变进行有效控制,其中全局信息可以提高对初始轮廓的鲁棒性,加速曲线收敛,提高分割效果,减少计算复杂度; 局部信息可以提高模型对亮度不均匀图像的处理能力.通过与传统基于区域信息的模型(如LCV,RSF等)进行实验对比,可以证明本文提出的模型对亮度不均匀图像具有更好的处理能力,且对初始位置具有很好的鲁棒性.
| [1] |
KASS M, WITKIN A, TERZOPOULOS D. Snakes: active contour models[J].
International Journal of Computer Vision, 1987, 1(4): 321-331.
DOI: 10.1007/BF00133570 |
| [2] |
TU S, LI Y, Su Y. Ratio and distribution-metric-based active contours for SAR image segmentation[C]// Proc 5th International Conference on Intelligent Control and Information Processing, Piscataway, NJ: IEEE Press, 2014 : 227-232.
http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7010344
|
| [3] |
AWADALLAH M, ABBOTT, L., GHANNAM, S. Segmentation of sparse noisy point clouds usingactive contour models[C]// Proc of International Conference on Image Processing, Piscataway, NJ: IEEE Press, 2014 : 6061-6065.
http://ieeexplore.ieee.org/document/7026223/
|
| [4] |
Liu S, Peng Y. A local region-based chan and vese model for image segmentation[J].
Pattern Recognition, 2012, 45(7): 2769-2779.
DOI: 10.1016/j.patcog.2011.11.019 |
| [5] |
MUMFORD D, SHAH J. Optimal approximations of piecewise smooth functions and associated variational problems[J].
Communications of Pure and Applied Mathematics, 1989, 42(5): 577-685.
DOI: 10.1007/BF01235533 |
| [6] |
CHAN T, VESE L. Active contours without edges[J].
IEEE Transactions on Image Processing, 2001, 10(2): 266-277.
DOI: 10.1109/83.902291 |
| [7] |
LI C, KAO C, GORE J, et al. Minimization of region-scalable fitting energy for image segmentation[J].
IEEE Transactions on Image Processing, 2008, 17(10): 1940-1949.
DOI: 10.1109/TIP.2008.2002304 |
| [8] |
WANG X, HUANG D, XU H. An efficient local chan-vese model for image segmentation[J].
Pattern Recognition, 2010, 43(3): 603-618.
DOI: 10.1016/j.patcog.2009.08.002 |
| [9] |
VESE L, CHAN T. A multiphase level set framework for image segmentation using the mumford and shah model[J].
International Journal of Computer Vision, 2002, 50(3): 271-293.
DOI: 10.1023/A:102087430 |
| [10] |
OSHER S, SETHIAN J. Fronts propagating with curvature-dependent speed: algorithms based on hamilton-jacobi formulations[J].
Journal of Computational Physics, 1988, 79(1): 12-49.
DOI: 10.1016/0021-9991(88)90002-2 |
| [11] |
WANG L, LI C, SUN Q, et al. Active contours driven by local gaussian distribution fitting energy[J].
Signal Processing, 2009, 89(12): 2435-2447.
DOI: 10.1016/j.sigpro.2009.03.014 |
| [12] |
DONG F F, CHEN Z S, WANG J W. A new level set method for inhomogeneous image segmentation[J].
Image and Vision Computing, 2013(31): 809-822.
DOI: 10.1016/j.imavis.2013.08.003 |
| [13] |
WANG Y, XIANG S, PAN C, et al. Level set evolution with locally linear classification for image segmentation[J].
Pattern Recognition, 2013, 46(6): 1734-1746.
DOI: 10.1109/ICIP.2011.6116263 |
| [14] |
WU Y F, HEN C J. A convex variational level set model for image segmentation[J].
Signal Processing, 2015, 106(C): 123-133.
DOI: 10.1016/j.sigpro.2014.07.013.DOI:10.4310/CMS.2015.v13.n6.a5 |
| [15] |
WANG L, SHI F, LI G. Segmentation of neonatal brain MR images using patch-driven level sets[J].
NeuroImage, 2014, 84(1): 141-158.
DOI: 10.1016/j.neuroimage.2013.08.008 |
| [16] |
WANG Y, XIANG S, PAN C. Level set evolution with locally linear classification for image segmentation[J].
Pattern Recognition, 2013, 46(6): 1734-1746.
DOI: 10.1016/j.patcog.2012.12.006 |
| [17] |
LIU S, PENG Y. A local region-based chan-vese model for image segmentation[J].
Pattern Recognition, 2012, 45(7): 2769-2779.
DOI: 10.1016/j.patcog.2011.11.019 |
| [18] |
LIU L, ZHANG Q, WU M, et al. Adaptive segmentation of magnetic resonance images with intensity inhomogeneity using level set method[J].
Magnetic Resonance Imaging, 2013, 31(4): 567-574.
DOI: 10.1016/j.mri.2012.10.010 |
| [19] |
GOLDSTEIN T, OSHER S. The split bregman method for L1 regularized problems[J].
SIAM J. Imaging SCI, 2009, 2(2): 323-343.
DOI: 10.1137/080725891 |
| [20] |
PAUL G, CARDINALE J, SBALZARINI I F. Coupling image restoration and segmentation: a generalized linear model/bregman perspective[J].
International Journal of Computer Vision, 2013, 104(1): 69-93.
DOI: 10.1007/s11263-013-0615-2 |
| [21] |
LI C M, XU C Y, GUI C F. Distance regularized level set evolution and its application to image segmentation[J].
IEEE Transactions on Image Processing, 2010, 19(12): 3243-3254.
DOI: 10.1109/TIP.2010.2069690 |
| [22] |
WANG L, YU Z, PAN C. Medical image segmentation based on novel local order energy[C]// Proc 10th Asian Conference on Computer Vision, Berlin, Germany: Springer, 2010: 148-159.
|
| [23] |
KWAN R, EVANS A, PIKE G. Mri simulation based evaluation of image-processing and classification methods[J].
IEEE Transactions on Medical Imaging, 1999, 18(11): 1085-1097.
DOI: 10.1109/42.816072 |
| [24] |
MARTIN D, FOWLKERS C, TAL D, et al. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics[C]// Proc of International Conference on Image Processing, Piscataway, NJ: IEEE Press, 2001, (2): 416-423.
|
 2018, Vol. 50
2018, Vol. 50


