微博因其用户数量巨大和消息传播快速及时的特点,已成为很多政府机构、企业单位和公众平台发布信息的重要媒介[1],所以对微博的研究分析有助于社会舆论的预警和监控[2].而作为消息传播的源头,发布消息的用户的重要性不言而喻,它在一定程度上决定了该消息的传播路径和传播范围[3].可用微博用户影响力来衡量不同微博用户在消息传播过程中所发挥的不同作用.通常来讲,影响力越大的用户表明其追随者数量越多、质量越高[4],那么他所发布的消息比影响力小的用户传播范围更大,对社会造成的影响也更大.鉴于微博在社会信息传播和商业营销方面巨大的影响力,国内外许多学者都对微博用户影响力进行了研究,也提出了一些关于微博用户影响力的评价算法,如侧重用户追随者数量的F-F算法,侧重用户微博被转发数量的平均转发数算法,侧重用户之间级联关系的K-覆盖度算法,侧重网络拓扑结构的PageRank算法以及一些改进算法.上述这些算法虽然都有各自的研究重点,但整体来看,都存在着考虑问题不够全面,单纯地以某一个或某两个指标来衡量用户的影响力问题,使得最终的评估结果不够真实和准确.因此,本文提出了一种基于PageRank的用户影响力评价改进算法(Self and Followers User Influence Rank)SF-UIR.相比于其他算法而言,该算法考虑因素更多,计算公式更复杂,评价更真实客观.
1 微博用户影响力 1.1 定义影响力通常指的是用一种潜移默化的方式,使周围人的思维和行为发生转变的能力[5].
微博用户影响力主要反映不同账号的微博用户对微博群成员的影响程度,主要基于微博用户的基本数据[6],结合行业市场规模、用户活跃程度、业内平均发展水平等因素,综合加权计算得出.微博用户影响力是一个综合的衡量指标,相较于传统的追随者数量来说,能够更加客观的反映每日微博用户在微博社区中的动态.
1.2 影响因素到达率和接收率.到达率是指微博用户所发布的消息能够出现在多少追随者的页面中,通常用追随者的数量来衡量[9];接收率是指用户所发消息可被多少追随者看到.但要使微博用户发的每条消息都能被所有追随者看到是不可能的.因为必定会有部分消息由于追随者没有及时查看而被其他用户所发的信息淹没,所以,接收率通常小于到达率.
一般认为,用户的追随者越多表明其影响力越大,但完全用追随者数量代替影响力既不全面也不客观的.现实中,微博影响力的构成是很繁杂的,受多种因素的影响,比较重要的因素包括追随者数量、追随者的追随者数量、追随者的关注数量、追随者的活跃度、微博平台自身影响力、微博用户自身知名度等[8-10].
2 PageRank算法PageRank算法是由Google创始人Sergey Brin和Lawrence Page于1998年提出的一种网页排名算法,其核心思想是通过研究网络的拓扑结构和计算页面的入度(即页面被链接的次数),进而确定该页面的排名顺序.页面的入度越大,那么它的重要性就越大,排名也越靠前.一个页面之所以有指向另一个页面的链接,是因为它认为该页面比较权威,内容真实可信,在相关领域有一定知名度. PageRank算法中最重要也是最关键的一点是,它不光计算页面的入度数量,还将指向目标页面的其它页面自身的PageRank值考虑在内[11].例如有两个页面A和B,A被一个非常重要的页面所认同,而B被很多普通的页面所认同,则页面A的PageRank值可能比页面B的PageRank值更大.一个页面的PageRank值为
| $ P\left( {{V_i}} \right) = \left( {1-d} \right) + d\sum\limits_{{V_{\rm{j}}} \in F\left( {{V_{\rm{i}}}} \right)} {\frac{{P\left( {{V_{\rm{j}}}} \right)}}{{L\left( {{V_{\rm{j}}}} \right)}}.} $ | (1) |
式中:P(Vi)为页面Vi的PageRank值,F(Vi)为指向页面Vi的页面集,P(Vj)为页面集F(Vi)中的任意一个页面Vj的PageRank值,L(Vj)为页面Vj中链接到其它页面的链接集,d为阻尼系数,用来解决某些特殊情况导致的个别页面PageRank值因无法收敛而难以计算情况的发生,通常d=0.85.
为更加方便的理解和研究PageRank算法,将整个网络抽象成一个巨大的有方向的图,图中的节点代表现实网络中的web页面,图中的有向边代表web页面之间的链入链出关系.现在假设有一个非常简单的网络,其中只有4个页面:A、B、C、D,其结构见图 1.

|
图 1 web拓扑结构 Figure 1 Topology of websites |
从图 1中可看出,A中有指向B、C、D的链接,假设用户从A跳转到其它页面的概率是相等的,即A到B的概率是1/3,B到C的概率是1/2,而D没有指向C的链接,所以D到C的概率是0.假设网络中一共有N个页面,那么可以定义一个N维的转移矩阵(Transition Matrix):其中第x行第y列的值为用户从页面y跳转到页面x的概率.下面的M矩阵是图 1所对应的转移矩阵.
| $ \mathit{\boldsymbol{M}} = \left[{\begin{array}{*{20}{c}} 0&1&0&{1/2}\\ {1/3}&0&0&{1/2}\\ {1/3}&{1/2}&0&0\\ {1/3}&0&1&0 \end{array}} \right]. $ |
然后,假设每个页面的初始rank值为1/N,N是网络中web页面的总数量,这里为4.将页面A、B、C、D的rank值组成的向量设为
| $ \mathit{\boldsymbol{\vec v = }}{\left[{1/4\;\;1/4\;\;1/4\;\;1/4} \right]^{\rm{T}}}. $ |
注意,矩阵M第一行的数值对应的是A、B、C和D跳转到A的概率,而向量
| $ \mathit{\boldsymbol{M}} \cdot \mathit{\boldsymbol{\vec v = }}{\left[{1/4\;\;5/24\;\;5/24\;\;1/3} \right]^{\rm{T}}}. $ |
将
| $ \mathit{\boldsymbol{\vec v}} = {\left[{3/9\;\;2/9\;\;2/9\;\;2/9} \right]^{\rm{T}}}. $ |
此时,
由于微博的拓扑结构与网络的拓扑结构有着天然的相似性,微博平台上的海量用户相当于网络世界里成千上万的页面,而微博用户关注其他用户的行为相当于页面添加了一个指向其它页面的链接,微博用户被其他用户关注的行为相当于页面增加了一个入度[12].所以可借鉴PageRank的经典算法来计算微博用户的影响力.但由于微博用户是活跃的、动态的,他们会产生各种各样的用户行为,例如发布或转发微博、关注好友等,而页面却是静止的.所以若直接利用PageRank算法来计算微博用户影响力,仅仅是对其追随者的PageRank值进行叠加,则会忽视用户本身行为所产生的影响因素,使得最终得到的微博用户影响力不够准确和客观.为此,本文提出了一种基于PageRank经典算法的微博用户影响力评价改进算法——SF-UIR(Self and Followers User Influence Rank)算法.
SF-UIR算法的核心优势在于综合考虑了以下两方面因素:
1) 基于用户行为的自身影响因素
a) 用户的追随者数量.这是最能直观体现一个微博用户影响力的指标,通常来讲,追随者数量越大,意味着该节点有更多的链接边数,那么该用户就有更大的接触面,其影响力也会增大.
b) 用户是否认证.一般普通的微博账号在搜索引擎中是搜不到的,因为微博信息并不对搜索引擎开放.但是,当用户做了认证之后,该账号就有很大可能性被搜索引擎收录,可见搜索引擎认为认证用户更值得信赖.账号被搜索引擎收录,这样无形中就扩大了用户微博的影响力,因为认证用户发的微博也很有可能会被搜索引擎认可收录,只要用户在搜索引擎上面搜索相似或者相关的字,那么微博账号名就可能会被搜到,这意味着认证用户比普通用户有更多“曝光”的手段,从而有更多的机会让人们关注他的微博.
一旦你认证之后,你所发布的微博信息也会让人觉得更可靠,大家也更愿意去相信你要表达的信息.通过认证的用户,也会被大家认为是具有一定影响力的名人,发表的言论更加权威,当然也会有更多的追随者.因此用户通过认证对其影响力有很大提升.
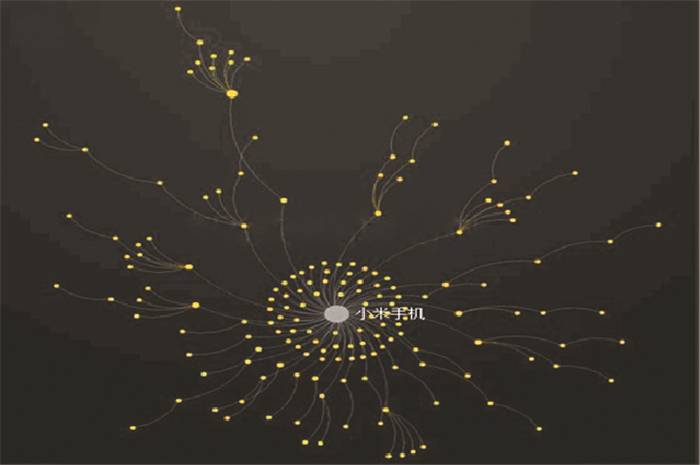
c) 用户微博的传播能力.一篇微博的传播能力主要是依靠其被其他用户评论或转发的次数来衡量.通过知微工具来分析微博消息的传播过程,以小米手机于2015年1月7日发布的一条微博为例[13],图 2显示了这条微博的传播路径和传播范围.
|
图 2 微博传播路径 Figure 2 Propagation path of microblog |
图中灰色节点代表根节点小米手机,黄色的节点代表转发了这条微博的用户.由图可见,微博是以根节点为中心,呈放射状并以级联的形式向外传播,经大量研究表明,绝大部分微博的传播深度值不会超过6,平均传播深度值约为3.5.
图 3中,在微博的传播过程中,第1层转发占比为43.7%,第2层为38.7%,第3层为15.3%,第4层及第4层以后的为2.3%.由此可见,一条微博的传播范围和能力大部分是由第1层和第2层用户的转发数决定的,则微博用户的影响力范围主要覆盖它的第一级追随者(直接的追随者)和第二级追随者(追随者的追随者).

|
图 3 微博传播的层级分析 Figure 3 Hierarchy analysis of microblog propagation |
2) 基于拓扑结构的追随者影响因素
借鉴PageRank的思想,将微博用户视为网页节点,用户之间的关注关系视为网页的链入链出,着重分析微博用户的追随者群、每个追随者的自身的影响力以及他们如何将自身的影响力合理地分配给他们所关注的用户.由PageRank的计算公式可知,网页将自身PageRank值均匀地分给它所链出的网页,例如,假设网页A的PageRank值是1,它一共包含5个指向其它网页的链接,那么它对每一个网页贡献的PageRank值为1/5.对比于微博用户,则表现为每个用户将自身的影响力值均分给他关注的所有用户,这样的分配显然是不合理的,因为尽管关注了很多用户,但是不可能做到对所有的用户都一视同仁,总是对其中的一部分更加感兴趣,更愿意去转发和评论他们所发的微博.因此,如果直接套用PageRank公式来计算追随者的影响力贡献值是不准确的.
鉴于PageRank算法中追随者影响力等值传递的这种弊端[14],在式(1)的基础上增加一个权重因子来反映追随者与其所关注用户的密切程度,追随者根据权重因子的大小来分配他的贡献值.权重因子越大,表明二者的关系越密切,互动性越强,相应的追随者会将更大比例的贡献值分配给该用户.这样既很好地解决了PageRank算法的弊端,又保留了其原有的优势,使得最终结果更加符合实际情况,使得评估模型更客观、更合理.
4 SF-UIR算法的具体实现 4.1 算法推导考虑基于用户行为的自身影响因素和基于拓扑结构的追随者影响因素,将SF-UIR算法定义为
| $ {P_{{\rm{SF-UIR}}}}\left( {{U_{\rm{i}}}} \right) = {P_{{\rm{SF-UIR\_self}}}}\left( {{U_{\rm{i}}}} \right) + {P_{{\rm{SF-UIR\_fans}}}}\left( {{U_{\rm{i}}}} \right). $ | (2) |
式中:PSF-UIR(Ui)为用户i的影响力,PSF-UIR_self(Ui)为用户i的自身影响因素,PSF-UIR_fans(Ui)为用户i的追随者影响因素.
SF-UIR算法的物理意义在于对用户追随者数量、用户是否认证、用户微博的传播能力等三方面的用户自身影响因素进行了量化,同时还根据权重因子量化计算了追随者对其所关注用户的影响力贡献值,从而克服了单纯以某一个或某两个指标来衡量用户影响力的问题,考虑因素更多,计算公式更复杂,评价更真实,更能反映微博用户的影响力.
| $ {P_{{\rm{SF-UIR\_self}}}}\left( {{U_{\rm{i}}}} \right) = \frac{{{F_{{U_{\rm{i}}}}}}}{N} + {B_{{\rm{verified}}}}\left( {{U_{\rm{i}}}} \right) + {A_{{U_{\rm{i}}}}}*{T_{{U_{\rm{i}}}}} $ |
式中:FUi为用户i的追随者数,N为所有用户中追随者数最多的用户所拥有的追随者数,Bverified(Ui)=(e, 0)为用户i是否经过认证,是一个布尔类型,若用户i经过认证则Bverified(Ui)=e,反之,Bverified(Ui)=0. AUi为用户i在统计周期内发布微博的频率,即其在统计周期内的微博传播能力.
| $ {A_{{U_{\rm{i}}}}} = \frac{{{M_{{U_{\rm{i}}}}}}}{T}. $ |
式中:MUi为用户i在T内所发微博的集合,T为统计周期,将统计周期设定为15天,即T=15.
| $ {T_{{U_{\rm{i}}}}} = \sum\limits_{{m_{\rm{j}}} \in {M_{{U_{\rm{i}}}}}} {\left( {a{R_{{m_{\rm{j}}}}} + b{C_{{m_{\rm{j}}}}} + c{L_{{m_{\rm{j}}}}}} \right)} . $ | (3) |
式中:mj为用户i在统计周期内所发微博集合中的任意一条微博,Rmj为mj这条微博的转发率,它等于mj被转发的总数与用户i的追随者数的比值,Cmj为评论率,Lmj为点赞率. a、b、c分别为各自的权重.
| $ {P_{{\rm{SF-UIR\_fans}}}}\left( {{U_{\rm{i}}}} \right) = \left( {1-d} \right) + d\sum\limits_{{U_{\rm{j}}} \in {F_{{U_{\rm{i}}}}}} {S\left( {i, j} \right)} {P_{{\rm{SF-UIR}}}}\left( {{U_{\rm{j}}}} \right). $ | (4) |
式中:FUi为用户i的追随者集合,用户j为用户i追随者集合中的任意一个用户,S(i, j)为用户j分配给用户i的SF-UIR值的比例,由用户i的微博传播能力占用户j所有好友的微博传播能力之和的大小所决定.
| $ S\left( {i, j} \right) = \frac{{R\left( {i, j} \right)}}{{\sum\limits_{{U_{\rm{p}}} \in {I_{{U_{\rm{j}}}}}} {R\left( {p, j} \right)} }}. $ |
式中:IUj为用户j所关注好友的集合,R(i, j)为用户i在统计时间内传递给用户j的信息量,
| $ R\left( {i, j} \right) = \frac{{Rt\left( {i, j} \right)}}{{S\left( i \right) + 1}}. $ |
式中:Rt(i, j)为用户j在统计周期内转发、评论和点赞用户i的微博次数,S(i)为用户i在统计周期内发布和转发的微博数量,S(i)+1是为避免分母为零的情况出现,因为有些用户可能在统计周期内没有发布或转发过微博.
将式(4)进一步分解
| $ \begin{array}{l} {P_{{\rm{SF- UIR\_fans}}}}\left( {{U_{\rm{i}}}} \right) = \left( {1- d} \right) + d\sum\limits_{{U_{\rm{j}}} \in {F_{{U_{\rm{i}}}}}} {S\left( {i, j} \right)} \cdot \\ \;\;\;\;\;\;\;\;\left[{{P_{{\rm{SF-UIR\_self}}}}\left( {{U_{\rm{j}}}} \right) + {P_{{\rm{SF-UIR\_fans}}}}\left( {{U_{\rm{j}}}} \right)} \right] \end{array} $ |
代入到公式(2)中得
| $ \begin{array}{l} {P_{{\rm{SF-UIR}}}}\left( {{U_{\rm{i}}}} \right) = {P_{{\rm{SF-UIR\_self}}}}\left( {{U_{\rm{i}}}} \right) + \\ d\sum\limits_{{U_{\rm{j}}} \in {F_{{U_{\rm{i}}}}}} {S\left( {i, j} \right)} {P_{{\rm{SF-UIR\_self}}}}\left( {{U_{\rm{j}}}} \right) + \\ d\sum\limits_{{U_{\rm{j}}} \in {F_{{U_{\rm{i}}}}}} {S\left( {i, j} \right)} {P_{{\rm{SF - UIR\_fans}}}}\left( {{U_{\rm{j}}}} \right) + 1 - d. \end{array} $ |
式中:
式(2)中N为所有用户中追随者数最多的用户所拥有的追随者数,在mysql数据库中可使用以下命令进行查询:
select*from user_info order by fn desc limit 10
式(3)中a、b、c为不同变量的权重值.通过这些权重值能直观地反映出评价人对不同变量的不同重视程度,实现了重要程度的量化,使人们可很轻松地分辨出各变量之间的差异程度.但每个变量的权重其实是很难直接确定的,尤其是评价指标较多时,评价人通常只能粗略的估计每个变量的重要程度,但要给出具体的、精确的数值是不现实的,所以需要运用合理有效的方法去解决这个问题.
首先将各个变量的重要程度做成对比较,然后将比较的结果按一定的方式聚合起来,经过计算,最终得到各个变量的权重值.
1) 设有m个变量,对这m个变量按照重要程度两两作比较,一共要比较的次数为
| $ C_{\rm{m}}^2 = \frac{1}{2}m\left( {m-1} \right). $ |
把第i个变量对第j个变量的相对重要性记为bij,并认为这就是变量i的权重wi和变量j的权重wj的比值,即
2) 由转发率、评论率、点赞率3个变量成对比较的结果构成矩阵B
| $ \mathit{\boldsymbol{B}} = \left[{\begin{array}{*{20}{c}} {{b_{11}}}&{{b_{12}}}&{{b_{13}}}\\ {{b_{21}}}&{{b_{22}}}&{{b_{23}}}\\ {{b_{31}}}&{{b_{32}}}&{{b_{33}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {a/a}&{a/b}&{a/c}\\ {b/a}&{b/b}&{b/c}\\ {c/a}&{c/b}&{c/c} \end{array}} \right]. $ | (5) |
显然有:
| $ {b_{{\rm{ij}}}} = \frac{1}{{{b_{{\rm{ji}}}}}}, {b_{{\rm{ij}}}} = {b_{{\rm{ik}}}} \cdot {b_{{\rm{kj}}}}, {b_{{\rm{ii}}}} = 1. $ |
3) 表 1为Saaty参考普通人对事物重要程度的认知方式和判断习惯总结出的变量间相对重要性等级表.参照该表来确定第i个变量对第j个变量的相对重要性,即求取bij的值.转发率与评论率相比,介于略微重要和相当重要之间,取b12=4;转发率与点赞率相比,介于明显重要和绝对重要之间,取b13=8;评论率和点赞率相比,介于同等重要和略显重要之间,取b23=2.代入式(5)中,可得
| 表 1 变量间相对重要性等级 Table 1 Relative importance level between variables |
| $ B = \left[{\begin{array}{*{20}{c}} 1&4&8\\ {1/4}&1&1\\ {1/8}&{1/2}&1 \end{array}} \right]. $ |
最终,求得a=0.727,b=0.182,c=0.091.
5 算法结果对比分析 5.1 数据采集、预处理及相关说明为更加客观地反映本文所提SF-UIR算法的优越性,搭建了基于Spark平台的实验环境.以目前最流行、最受广大网民欢迎的新浪微博作为数据源,运用中国爬萌网站提供的“新浪微博微博信息采集器”采集所需微博用户的基本信息,采集到的用户基本信息字段见表 2.运用八爪鱼数据采集系统从新浪微博上获取所需微博用户在一定周期内的行为信息,主要采集5个字段,分别为:用户名、发布时间、转发数量、评论数量、点赞数量.
| 表 2 用户信息字段 Table 2 Fields of user information |
采集到的实验数据通常存在格式不规范、内容冗余、部分信息缺失等问题,为保证实验的顺利进行以及实验结果的真实可靠,需经过格式转换、冗余字段删除、实验数据入库、僵尸粉和沉默用户的删除、关系提取等一系列数据预处理过程后再将其上传到分布式文件系统HDFS中,最终综合Spark GraphX、Spark SQL、MLlib等技术实现了追随者数量排名算法、平均转发数算法、K-覆盖度算法、PageRank算法和SF-UIR算法.
由于本文的实验数据是通过爬虫工具从新浪微博上爬取的,因此会造成部分微博用户信息的缺失,如某些用户的关注列表不完整、固定周期内用户所发的微博没有全部采集到等,这会导致实验结果与真实的结果之间存在一定的偏差.但是本文的所有实验都是基于相同的实验数据进行的,因此通过分析实验结果所得出的实验结论仍具有一定的说服力和可信力.
为更加形象地反映微博用户在网络中的影响力程度,将借助“用户排名”的概念,依据不同的算法规则对其进行量化排名,同时进行比较分析.需要指出的是文中追随者数量排名算法、平均转发数算法、K-覆盖度算法和PageRank算法均是依据各算法的原始方法实现的. SF-UIR算法亦是与它们的原始方法进行对比,但这并不影响比较因素的全面性和结果的正确性.这是因为,一方面当前主流算法的原始方法能充分反映该算法的本质特征;另一方面一些基于主流算法的改进算法本身依然具有一些不够全面的问题,如文献[8]考虑了微博用户的粉丝数、微博发布频率、用户的活跃度等因素只解决了僵尸粉对用户影响力的干扰问题,文献[14]构建了用户活跃度和历史关注度两个指标,只从微博传播能力方面改进了PageRank算法,等等,而本文算法已经将这些不全面的方面进行了考虑和完善.
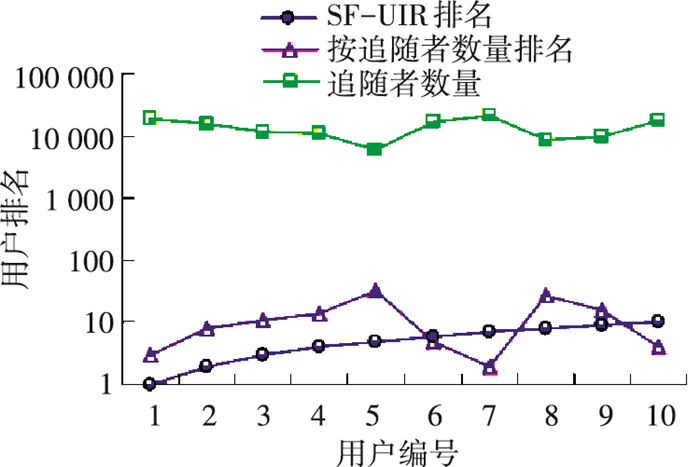
5.2 SF-UIR算法同追随者数量排名算法对比表 3给出本文SF-UIR算法排名前十的用户,以及这10名用户按照追随者数量排名的次序. 图 4用对数刻度(纵坐标呈对数分布,当纵坐标数值差较大时更便于观察)直观展示了两种排名算法与追随者数量间的对应变化情况.
| 表 3 SF-UIR算法同追随者数量排名算法对比 Table 3 SF-UIR compared with the number of followers ranking |
|
图 4 SF-UIR算法同追随者数量排名算法对比折线 Figure 4 The line chart of comparing SF-UIR with the number of followers ranking algorithm |
实验结果表明,追随者数量虽然是支撑影响力排名的重要因素,但并非绝对因素.因此,按照追随者数量来判断一个用户的影响力的方法太过于片面,极其容易受到“僵尸粉”的误导.而考虑了追随者质量的SF-UIR算法对用户影响力评价则更全面,且可以用来杜绝微博上的某些陋习,例如,由于虚荣心或商业目的,有些用户会花钱去购买追随者,甚至通过发布一些哗众取宠的内容来吸引人们的注意,以此来增加自己的追随者数量.
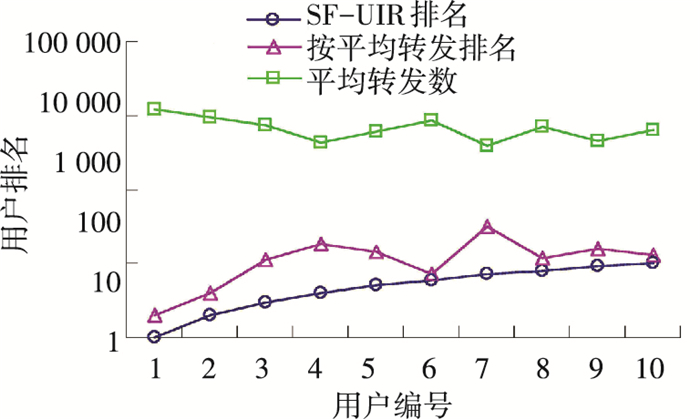
5.3 SF-UIR算法同平均转发数算法对比表 4给出本文SF-UIR算法排名前十的用户,以及这10名用户按照平均转发数排名的次序. 图 5用对数刻度直观展示了两种排名算法与平均转发数间的对应变化情况.
| 表 4 SF-UIR算法同平均转发数排名算法对比 Table 4 SF-UIR compared with average forward |
|
图 5 SF-UIR算法同平均转发数算法对比折线 Figure 5 The line chart of comparing SF-UIR with average forward |
从实验结果来看,在SF-UIR算法中排名前10的用户,除了“心*小谈”、“路-*不遥远”和“木*藤藤”之外,在按平均转发数算法的排名中都没能排进前10,排名第7的“De*rperi”用户甚至排到了第32名.这说明用户的影响力与用户微博的平均转发数量并非呈现一定的正相关性,影响力高的用户,其微博的平均转发数并不一定高.
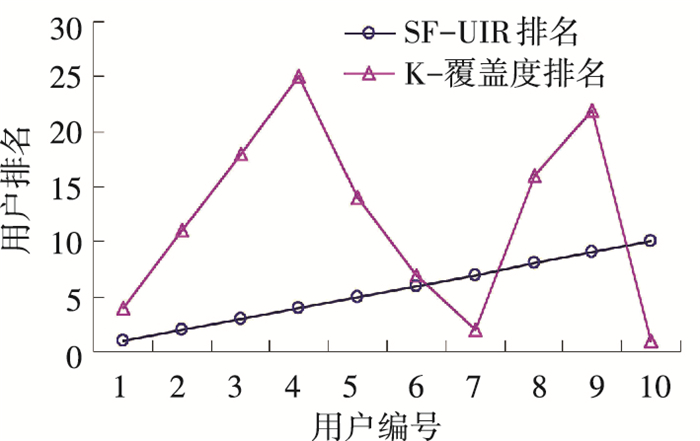
5.4 SF-UIR算法同K-覆盖度算法对比表 5给出了SF-UIR算法与K-覆盖度算法的排名结果对比情况. 图 6从SF-UIR算法排名前10位用户的角度直观展示了两种排名算法对应变化情况.
| 表 5 SF-UIR算法同K-覆盖度算法对比 Table 5 SF-UIR compared with K-coverage algorithm |
|
图 6 SF-UIR算法同K-覆盖度算法对比折线 Figure 6 The line chart of comparing SF-UIR with K-coverage |
无论从表 5的连续排名比较,还是从图 6的统一用户排名比较来看,两种算法得到的排名结果很接近,但仍有不小的差别.经过分析可知,虽然K-覆盖度算法将多级用户的影响力都考虑了进去,但也存在两点不足:1)没有将微博用户自身行为特征所产生的影响力考虑在内;2)将微博消息被转发的概率统一设为m,这种一视同仁的做法忽略了不同用户消息的差异性.从而导致了与SF-UIR算法相比,不具有很强的说服力.
5.5 SF-UIR算法同PageRank算法对比表 6给出了SF-UIR算法与PageRank算法的排名结果对比情况. 图 7从SF-UIR算法排名前10位用户的角度直观展示了两种排名算法对应变化情况.
| 表 6 SF-UIR算法同PageRank算法对比 Table 6 SF-UIR compared with PageRank |

|
图 7 SF-UIR算法同PageRank算法对比折线 Figure 7 The line chart of comparing SF-UIR with PageRank |
从表 6的连续排名结果和图 7的统一用户排名结果可以看出,SF-UIR的排名与PageRank的排名差别不是特别大,尤其是第1名和第4名的排名结果是一致的,这就证明SF-UIR是基于PageRank算法改进而来的,因此两种排名在总体上接近,在某些情况下甚至是一致的.但是,由于PageRank算法只考虑了用户之间的链入链出关系,是基于静态的网络拓扑结构生成的排名,影响力的大小主要由追随者的数量和追随者的质量决定的.例如,用户“De*rperi”在PageRank排第二名,但在SF-UIR中排名掉落到第7名,通过分析发现,在研究的周期内,用户“De*rperi”相比于榜单上的其他用户而言,活跃度较低,微博平均转发量、评论量、点赞量都相对较低,因此SF-UIR_Self的值比较低,那么在SF-UIR算法中排名降低也是合情合理的.由于SF-UIR算法在考虑用户追随者贡献值的同时,还兼顾用户自身的行为特征和活跃程度,因此,它比PageRank更加合理,更加全面,更加贴近实际情况.
综上所述,通过比较分析不难发现SF-UIR算法在考虑用户追随者贡献值的同时,还兼顾用户自身的行为特征和活跃程度,因此,它比其他算法更加合理、全面、贴近实际情况.
6 结论本文基于微博用户影响力评价与网页排名PageRank算法天然相似的客观实际,在PageRank算法的基础上结合微博用户自身的行为特征提出了SF-UIR算法,综合考虑了基于用户行为的自身影响因素和基于拓扑结构的追随者影响因素.通过与代表性算法相比较,表明该算法考虑的信息更全面、给出的评价更真实、更能客观地反映出用户的实际影响力.
| [1] |
张俊豪, 顾益军, 张士豪. 基于PageRank和用户行为的微博用户影响力评估[J].
信息网络安全, 2015(6): 73-78.
ZHANG Junhao, GU Yijun, ZHANG Shihao. Microblog user influence evaluation based on pagerank and user behavior[J]. Netinfo Security, 2015(6): 73-78. DOI: 10.3969/j.issn.1671-1122.2015.06.012 |
| [2] |
简小军. 浅析微博的舆论功能及其发展[J].
新闻世界, 2014(8): 110-111.
JIAN Xiaojun. Brief analysis of microblog public opinion function and development[J]. News World, 2014(8): 110-111. |
| [3] |
易续平. 微博影响力的量化研究[D]. 昆明: 云南财经大学, 2014.
YI Xuping. Quantitative research of microblog influence[D]. Kunming: Yunnan University of Finance and Economics, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D515767 |
| [4] |
程志强. 基于新浪微博主题的用户影响力研究[D]. 沈阳: 东北大学, 2013.
CHENG Zhiqiang. User influence research based on the theme of sina microblog[D]. Shenyang: Northeastern University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10145-1014180623.htm |
| [5] |
李军, 陈震, 黄霁崴. 微博影响力评价研究[J].
信息网络安全, 2012(3): 10-13.
LI Jun, CHEN Zhen, HUANG Jiwai. Microblog influence evaluation research[J]. Netinfo Security, 2012(3): 10-13. DOI: 10.3969/j.issn.1671-1122.2012.03.003 |
| [6] |
尹杰. 基于用户分析的微博信息过滤研究[D]. 大连: 大连理工大学, 2013.
YIN Jie. The microblog information filtering based on user analysis[D]. Dalian: Dalian University of Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10141-1013201595.htm |
| [7] |
梁宏. 微博复杂网络适应度模型的研究[D]. 北京: 北京化工大学, 2013.
LIANG Hong. The research of fitness network model on weibo complex network[D]. Beijing: Beijing University of Chemical Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10010-1013273938.htm |
| [8] |
杨科. 基于改进PageRank算法的微博用户影响力研究[D]. 西安: 西安建筑科技大学, 2014.
YANG Ke. Microblog user influence research based on the improved pagerank[D]. Xi'an: Xi'an University of Architecture & Technology, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D560680 |
| [9] |
张昊, 刘功申, 苏波. 一种微博用户影响力的计算方法[J].
计算机应用与软件, 2015(3): 41-44.
ZHANG Hao, LIU Gongshen, SU Bo. A method of calculating the influence of weibo users[J]. Computer Applications and Software, 2015(3): 41-44. DOI: 10.3969/j.issn.1000-386x.2015.03.012 |
| [10] |
姚茜, 卜彦芳. 基于影响力研究的微博营销模式探析[J].
经济问题探索, 2011(12): 117-121.
YAO Xi, BO Yanfang. The analysis of microblog marketing model based on influence research[J]. Inquiry into Economic Issues, 2011(12): 117-121. DOI: 10.3969/j.issn.1006-2912.2011.12.023 |
| [11] |
张亚楠. 基于用户行为的信任感知推荐方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.
ZHANG Ya'nan. Research on recommendation methods based on trust perception of user behavior[D]. Harbin: Harbin Engineering University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10217-1017243109.htm |
| [12] |
陆毅. 微博社会网络构造与分析技术研究[D]. 上海: 复旦大学, 2011.
LU Yi. The study of microblog social network structure and analysis techniques[D]. Shanghai: Fudan University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10246-1012330361.htm |
| [13] |
马晓娟, 李玉贞, 胡勇. 微博用户影响力的评估[J].
信息安全与通信保密, 2013(6): 53-55.
MA Xiaojuan, LI Yuzhen, HU Yong. The evaluation on microblog user influence[J]. Information Security and Communications Privacy, 2013(6): 53-55. |
| [14] |
王琛, 陈庶樵. 一种改进的微博用户影响力评价算法[J].
信息工程大学学报, 2013, 14(3): 380-384.
WANG Chen, CHEN Shuqiao. Improved user influence evaluation algorithm of microblog[J]. Journal of Information Engineering University, 2013, 14(3): 380-384. DOI: 10.3969/j.issn.1671-0673.2013.03.021 |
 2018, Vol. 50
2018, Vol. 50


