2. 天津财经大学 理工学院, 天津 300222;
3. 中央财经大学 保险学院, 北京100081
2. School of Science and Engineering, Tianjin University of Finance and Economics, Tianjin 300222, China;
3. School of Insurance, Central University of Finance and Economics, Beijing 100081, China
目前,针对优化问题的研究在科学、工程和金融领域占有重要的地位,引起国内外学者的广泛关注.群体智能算法凭借其自适应、自组织、协同性、强鲁棒性和良好的分布性并行性等优点,已经成为求解优化问题的主要方法[1].人工蜂群(Artificial Bee Colony, ABC)算法模拟蜂群的智能采蜜行为,根据蜜蜂的分工不同实现蜜源信息的共享和交流,继而找到问题的最优解.由于该算法具有结构简单、易于实现、参数较少等特点,因此相对于蚁群算法、遗传算法及粒子群优化算法而言具有一定优势[2].然而,标准ABC算法仍面临易陷入局部最优、进化后期收敛速度慢等问题,继而限制了该算法在实际中的应用[2].果蝇优化算法(Fruit Fly Optimization Algorithm, FOA)是一种通过模拟果蝇觅食行为获得全局最优解的新型群体智能优化算法[3-4].与传统群体智能算法相比,FOA算法实现简单、执行速度较快、所需参数较少.但是,该算法极易陷入局部最优,导致后期收敛速度变慢,收敛精度降低,尤其是对于高维多极值的复杂优化问题.文献[5]提出动态双子群协同进化的果蝇优化算法(DDSCFOA).该算法动态地将整个种群划分为先进子群和后进子群,较好地平衡了局部搜索能力和全局搜索能力.文献[6]提出一种基于随机扰动的改进果蝇优化算法(IFOA).该算法通过计算果蝇适应值大小决定是向最优位置靠近还是进行全局搜索.算法全局寻优能力较强,但不足之处在于全局搜索随机性大,影响了算法的收敛速度及稳定性.文献[7]提出一种迭代步进值自适应调整的果蝇优化算法(FOAMR).该算法引入果蝇群体速度进化因子和聚集度因子,同时定义自适应调整因子实现搜索距离大小的动态调整,但无法对负值参数进行寻优.文献[8]对FOA算法进行改进,使用果蝇位置向量直接计算适应度函数实现针对负值参数的寻优,但不足之处在于寻优结果对于搜索半径依赖较强.文献[9]考虑过去对现在的影响的启发,增加“历史认知”部分的改进策略,通过线性递增的动态变化系数调整在迭代寻优过程中历史位置对本次学习的价值,避免了因单纯聚集行为使得寻优过程迂回曲折导致错过全局最优解的问题.
现有的基于FOA的优化算法仍面临以下问题:
1) 在果蝇位置更新过程中只强调当前全局最优位置的驱动作用,忽略了实际最优解出现在其他表现较好的位置附近的可能性,因此丢失了必要的全局化驱动信息,易导致算法陷入局部最优;
2) 文献[5-7]等算法通过混沌搜索、调整搜索半径等方法跳出局部最优,未能有效利用果蝇个体的历史认知经验,导致新位置产生随机性较大、算法收敛速度较慢、结果不稳定等问题.为此,本文对传统果蝇算法做出改进,引入先进群组、记忆空间等相关概念,实现了一种基于全局-局部双向驱动的果蝇优化新算法.
1 传统果蝇优化算法与粒子群算法、遗传算法类似,传统果蝇算法以随机值作为初始位置,在迭代寻优过程中所有个体都飞向到上一代最优个体,通过在最优个体附近搜索寻找全局最优解.算法主要执行步骤如下[3-4]:
输入:果蝇种群X={xi}(1 < i≤N, N为种群中果蝇数量)、搜索范围[xmin, xmax]、最大迭代次数Tmax.
输出:果蝇最优位置(xb1, xb2)、果蝇最优气味浓度Smellgb.
初始化参数.具体包括:果蝇数量N、最大迭代次数Tmax、果蝇最优气味浓度φgb(φgb=-∞)等;
更新每只果蝇xi的位置(xi1, xi2):
| $ {x_{i1}} = {x_{{\rm{b1}}}} + {\rm{Rand}}\left( {} \right), {x_{i2}} = {x_{{\rm{b2}}}} + {\rm{Rand}}\left( {} \right) $ | (1) |
式(1)中Rand()产生一个(0, 1)区间内的随机数.
求得xi对应的气味浓度判定值si,如下式:
| $ {d_i} = \sqrt {{x_{i1}}^2 + {x_{i2}}^2}, {s_i} = \frac{1}{{{d_i}}}. $ | (2) |
根据适应度函数f求得果蝇xi的气味浓度φi:
| $ {\varphi _i} = f\left( {{s_i}} \right). $ | (3) |
将气味浓度最大的果蝇对应的位置及气味浓度值分别记为(xm1, xm2)、φm;
若φm>φgb,则按照公式(4)更新果蝇最优位置(xb1, xb2):
| $ {x_{{\rm{b1}}}} = {x_{{\rm{m1}}}}, \;\;\;\;{x_{{\rm{b2}}}} = {x_{{\rm{m2}}}}. $ | (4) |
循环执行上述步骤直到达到最大迭代次数.
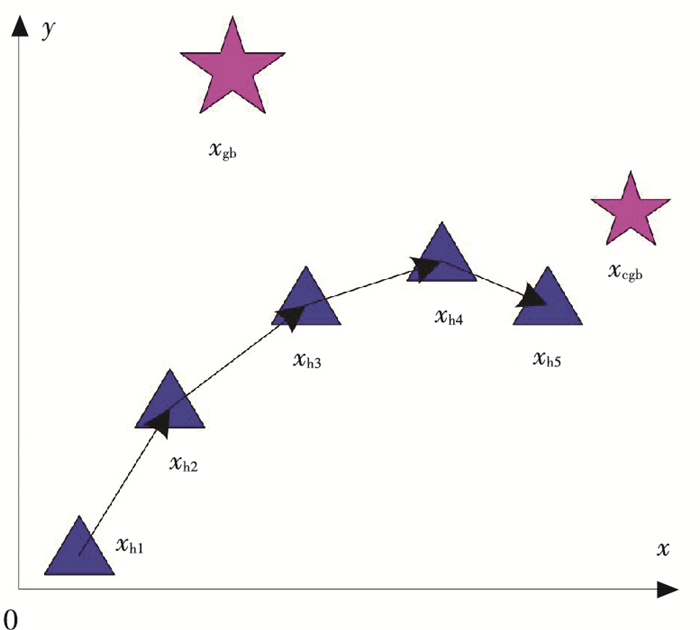
2 基于全局-局部双向驱动的果蝇优化算法 2.1 算法描述为提高搜索性能,FOABHC算法[9]融合了当前最优位置及果蝇历史位置对位置更新的驱动作用.但是,该算法只关注全局最优位置,忽略了表现较好的那些优秀果蝇的引导作用.并且,该算法只将果蝇当前位置作为历史位置,忽略了那些可能导致全局最优解的历史位置信息见图 1,假定xcgb1为当前最优位置,xgb为实际最优位置,xcgb2、xcgb3、xcgb4为3个表现与xcgb1相近但稍逊于xcgb1的果蝇位置.由于现有算法仅考虑当前最优值的导向作用,因此果蝇x将直接向xcgb1靠近.但实际上,xcgb2(xcgb3)离实际最优位置xgb更近,因此,在位置xcgb2(xcgb3)附近搜索将更有可能找到全局最优值xgb.如图 2所示,假定果蝇x的移动轨迹为:xh1→xh2→xh3→xh4→xh5,xh5为x的当前位置,xcgb为当前最优位置,xgb为实际最优位置.由于FOABHC在果蝇位置更新过程中仅考虑当前最优位置及果蝇当前位置,因此若x在位置xh3处错过实际最优位置xgb而转向xh4的话,其后续位置xh5便由xh4及当前最优位置xcgb共同决定.由图 2知,x将由xh4转向一个靠近xcgb而远离xgb的位置xh5,因此x将极有可能陷入局部最优状态.

|
图 1 现有优化算法面临的问题 Figure 1 Problems of existing optimization algorithms |
|
图 2 FOABHC算法面临的问题 Figure 2 Problems of FOABHC algorithm |
由此可见,FOABHC算法虽然融合了优秀果蝇个体及果蝇自身认知经验在果蝇位置更新的驱动作用,但缺乏对基于多个最优位置的全局化信息及基于个体自身认知经验的局部化信息的综合运用.为此,本文引入两个概念:先进群组和记忆空间,并以最小化问题为例给出相关定义如下:
定义1 先进群组
给定果蝇种群X={xi}(1≤i≤N),将第t(t≤Tmax)次迭代情况下适应值最小的前n值果蝇集合称为该迭代次数下的先进群组,记为
| $ {G_t} = \left\{ {{x_g}^1, {x_g}^2, \cdots, {x_g}^u, {x_g}^v, \cdots, {x_g}^n} \right\}. $ | (5) |
式中1≤u≤v≤n,f(xgu)≤f(xgv).
定义2 记忆空间
给定果蝇个体xi,假定xi在第t迭代前所经历的历史位置为hpi ={hpi1, hpi2, …, hpit},则将hpi中适应值最小的前m(m≤t)个位置称为xi在第t迭代时对应的记忆空间,记为
| $ {M_{it}} = \left\{ {{h_i}^1, {h_i}^2, \cdots, {h_i}^{u'}, {h_i}^{v'}, \cdots {h_i}^m} \right\}. $ | (6) |
式中1≤u′ < v′≤m,f(hiu′)≤f(hiv′).
在此基础上,将给出基于全局-局部双向驱动的果蝇位置更新过程,具体包括:
1) 基于全局化信息驱动的果蝇位置更新:
如图 3所示,为充分利用先进群组中的全局性驱动信息,针对果蝇xi,本文将结合轮盘赌策略[10]从先进群组Gt中选择某只果蝇xs并向其靠近.此外,IFFO算法[8]通过随机修改位置向量的某个维度实现果蝇位置的更新,虽然有效降低了算法时间复杂度,但所选维度随机性较大,易造成不稳定的收敛结果.为此,本文将在迭代过程中顺序选择位置向量的各个维度进行更新,以保证每个维度都能被公平选择.具体而言,选择xs的过程如下:

|
图 3 基于全局-局部双向驱动的果蝇位置更新过程 Figure 3 Global-local bidirectional driving based position updating process of fruit flies |
步骤1 按照式(7)计算xi选择先进群组Gt中每只果蝇xgj的概率pj:
| $ {p_j} = 1-{f_{\rm{g}}}^j/\sum\limits_{k = 1}^n {f_{\rm{g}}^k} . $ | (7) |
其中fgj为xgj对应的适应值.
步骤2 根据文献[11]知,随机数产生函数Chebyshev表现优于Sine、Logistic、Circle等函数,因此将使用该函数(简记为cbs())产生随机数r.根据轮盘赌策略,按照式(8)选择一只果蝇个体xs:
| $ {x_{\rm{s}}} = \left\{ {\begin{array}{*{20}{l}} {{x_{\rm{g}}}^1, }&{{\rm{if}}\;\;r \in (0, \;{p_1}];}\\ {{x_{\rm{g}}}^{j + 1}}&{{\rm{if}}\;\;r \in (\sum\limits_{k = 1}^j {{p_k}, \sum\limits_{k = 1}^{j + 1} {{p_k}} }]\left( {1 \le j \le n -1} \right).} \end{array}} \right. $ | (8) |
2) 基于局部化信息驱动的果蝇位置更新:
为避免陷入局部最优,本文将在果蝇种群接近收敛时执行全局化搜索.与文献[5-7]等算法不同的是,本文将在全局化搜索过程中结合果蝇个体的历史认知经验降低盲目搜索的可能性,在保证全局优化效果的同时加快算法的收敛速度见图 3,当全局最优位置xb在连续L次迭代后仍未改变时,果蝇个体xi将从其记忆空间Mit中选择一个特定位置his并在该位置附近搜索以跳出局部最优状态.具体而言,选择his的过程如下:
步骤1 式(9)计算xi选择记忆空间Mit中位置hij的概率pij:
| $ {p_i}^j = 1-{f_i}^j/\sum\limits_{k = 1}^m {f_i^k} . $ | (9) |
式中fij为果蝇xi历史位置hij对应的适应值.
步骤2 令r=cbs(),根据轮盘赌策略,按照公式(10)选择一个最优位置his:
| $ {h_i}^{\rm{s}} = \left\{ {\begin{array}{*{20}{l}} {{h_i}^1, }&{{\rm{if}}\;\;r \in (0, \;{p_i}^1];}\\ {{h_i}^{j + 1}}&{{\rm{if}}\;\;r \in (\sum\limits_{k = 1}^j {{p_i}^k, \sum\limits_{k = 1}^{j + 1} {{p_i}^k} }]\left( {1 \le j \le m -1} \right).} \end{array}} \right. $ | (10) |
在此基础上,以最小化问题为例,给出本文算法的执行过程如下:
输入 果蝇种群X(数量为N), 最大迭代次数Tmax, 当前迭代次数t, 位置向量维数D, 搜索半径r最大值rmax, 搜索半径r最小值rmin, 搜索范围[xmin, xmax], 迭代次数阈值L.
输出 全局最优果蝇xb.
1) for (i←1;xi∈X; i++)
2) 按照下面公式随机生成果蝇xi的位置:
| $ {x_{ij}} \leftarrow {x_{\min }} + \left( {{x_{\max }}-{x_{\min }}} \right) \times {\rm{cbs}}\left( {} \right), 1 \le j \le D. $ | (11) |
式(11)中xij为果蝇xi的第j维数值.
3) 令果蝇xi的记忆空间Mi←null.
4) end for
5) for (i←1;xi∈X; i++)
| $ {M_i} \leftarrow {M_i} \cup \left\{ {{x_i}} \right\}. $ |
6) end for
| $ 7)\;\;\;\;\;\;\;\;{x_{\rm{b}}} \leftarrow \arg \left( {\mathop {\max }\limits_{{x_i} \in X} f\left( {{x_i}} \right)} \right). $ | (12) |
8) 构造先进群组Gt={xgj}(1≤j≤n):
| $ X' \leftarrow {\rm{rank}}\left( X \right), {G_t} \leftarrow {\rm{sel}}\left( {X', n} \right). $ | (13) |
式(13)中rank函数实现对果蝇种群X按照适应值从小到大排序,sel(X′, m)表示排序后种群X′中的前n只果蝇.
9) t←1, d←0.
10) while(t < Tmax)
11) for(i←1; xi∈X; i++)
| $ 12)\;\;\;\;\;\;\;\;j = d\% D + 1. $ | (14) |
13) if xb在L次迭代后仍未改变then
式(10)从xi对应的记忆空间Mit中选择位置his, 令xs←his.
按照式(15)更新xi在第j维上的值xij:
| $ {x_{ij}} = {x_{ij}} + \left( {{x_{{\rm{b}}j}}-{x_{ij}}} \right) \times \left( {{\rm{cbs}}\left( {} \right)-0.5} \right) \times 2. $ | (15) |
14) else
式(8)从Gt中选择个体xs.
式(16)更新xij:
| $ {x_{ij}} = {x_{sj}} + r \times {\rm{cbs}}\left( {} \right). $ | (16) |
15) end if
16) if xij>xmax then xij=xmax endif
17) if xij < xmin then xij=xmin endif
18) d++.
19) end for
20)更新全局最优值xb、先进群体Gt及半径r.
21) end while
本文算法输出步骤13中,迭代次数阈值L根据经验取L=500.式(16)中,参数r为动态搜索半径,随着迭代次数增加,r将逐渐减小,具体更新过程如下:
| $ r = {r_{\max }}-\left( {{r_{\max }}-{r_{\min }}} \right) \times \frac{t}{{{T_{\max }}}}. $ | (17) |
参照文献[8],设置rmin=0.001、rmax=(xmax-xmin)/2.可见,改进后的果蝇优化算法相对于传统算法(FOA[3-4],IFOA[6],IFFO[8]等)而言具有以下优势:1)引入先进群组的概念,利用种群中表现较好的个体构建先进群组(本文算法输出步骤8);综合考虑先进群组中的优秀个体在果蝇位置更新过程中的驱动作用(本文算法输出步骤14),避免传统算法单纯依赖全局最优位置而可能造成的局部收敛问题;2)引入记忆空间的概念,将果蝇个体的历史最优位置定义为该果蝇的记忆空间(本文算法输出步骤5);每只果蝇在种群接近收敛时利用自身历史认知经验的局部化驱动作用从记忆空间中选择特定位置并向其靠近(本文算法输出步骤13),以此在避免局部最优的同时提高算法的收敛速度.
2.2 算法时间复杂度分析1) 初始化过程对应本文算法描述中步骤1~9.其中,构造先进群组过程(本文算法输出步骤8)使用quicksort算法[11]对果蝇种群进行排序,因此其时间复杂度为
| $ {T_1} = O\left( {D \times N + N \times {{\log }_2}N} \right). $ | (18) |
2) 果蝇位置更新过程对应本文算法中步骤10~19,对应的时间复杂度为
| $ {T_2} = O\left( {{T_{\max }} \times N \times \left( {p \times m + q \times n} \right)} \right). $ | (19) |
式中:m、n分别为果蝇记忆空间大小与先进群组中果蝇数量,p、q分别为本文算法执行步骤13、14的权重系数,满足0 < p, q < 1且p+q=1.
3) 参数更新过程对应本文算法中步骤20.该过程时间复杂度为
| $ {T_3} = O\left( {{T_{\max }} \times N \times {{\log }_2}N} \right). $ | (20) |
本文算法的时间复杂度为
| $ \begin{array}{l} T = {T_1} + {T_2} + {T_3} = O(N \times (D + {\log _2}N + {T_{\max }} \times \\ \;\;\;\;\;\;(p \times m + q \times n + {\log _2}N))). \end{array} $ | (21) |
由于m、n均为固定值,因此去掉式(21)中的常数项,可得
| $ T = O\left( {N \times \left( {D + {T_{\max }} \times {{\log }_2}N} \right)} \right). $ | (22) |
表 1分析了几种典型算法的时间复杂度.其中,Nc为FOAMR算法在计算果蝇聚集度因子时所采用的迭代次数阈值.由表知,IFFO及ABC算法对应的时间复杂度最小.由公式(22)知,当存在:
| 表 1 不同算法的时间复杂度对比 Table 1 Comparison of time complexities of different algorithms |
实验所采用的平台为:Win7 64位操作系统,Matlab 2013.见表 2,分别选取3个单峰标准函数(F1~F3)[6, 9, 12]、3个多峰标准函数(F4~F6)[9]进行测试.实验选用的对比算法包括:FOA[3-4]、IFOA[6]、FOAMR[7]、IFFO [8]、FOABHC [9]及ABC[1-2].公平起见,设置果蝇数量N=50,先进群组中个体数量n=5,记忆空间大小m=5,最大迭代次数Tmax=5 000.
| 表 2 函数公式、最优值及最优位置分量 Table 2 Function formulas, optimal values and optimal position components |
为衡量优化算法的性能,将从不同角度测试算法在不同测试函数上的表现.分别用指标A、S、C表示算法在某测试函数上的收敛精度、收敛稳定性及达到收敛状态时的迭代次数. A、S、C定义为
| $ \begin{array}{l} A = \frac{1}{{{n_{\rm{e}}}}}\sum\limits_{j = 1}^{{n_{\rm{e}}}} {\left( {{f_j}-f} \right)}, S = \sqrt {\frac{1}{{{n_{\rm{e}}}}}\sum\limits_{j = 1}^{{n_{\rm{e}}}} {{{\left( {{f_j}-f-A} \right)}^2}} }, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;C = \frac{1}{{{n_{\rm{e}}}}}\sum\limits_{j = 1}^{{n_{\rm{e}}}} {{n_j}} . \end{array} $ | (23) |
式中:ne为算法针对测试函数进行的实验次数,f为测试函数对应的理论最优值,fj(1≤j≤ne)为算法针对测试函数进行第j次实验所得的实际最优值,nj为算法在测试函数上的第j次实验达到收敛状态时对应的迭代次数.为便于比较,使用指标A′衡量算法的收敛精度,对应公式如下:
| $ A' =-\lg A. $ | (24) |
可见,指标A(A′)反映函数最优值理论最优值与实际最优值之间的平均差异,该值越小(大),说明算法收敛精度越高;指标S反映算法收敛结果的稳定性,该值越小,说明算法表现越稳定;指标C反映算法的收敛速度,该值越小,说明算法达到收敛状态所需迭代次数越少,算法收敛得越快.
3.1.3 收敛精度及稳定性比较设置每个测试函数的维数D分别取2、4、6、8、10,针对每种算法在每个函数上实验100次,统计每种算法对应的A值及S值,结果见表 3、4.由表知,当处理单峰函数F1时,FOA、FOABHC、IFOA及FOAMR算法对应A值均普遍大于6,原因在于它们直接使用味道浓度作为选择全局最优果蝇的判定标准,因此无法实现针对负值参数的寻优.当处理F2时,本文表现最好;当处理F3时,本文表现虽稍逊于ABC算法,但对应的A值仍低于其他算法.进一步发现,本文虽在多峰函数F4上所得结果较ABC算法偏高,但在F5、F6上均获得最小A值、S值,这说明:1)鉴于多峰函数的复杂性,传统算法存在易陷入局部最优、全局搜索随机性较大等问题,因此难以有效协调算法的收敛精度及稳定性;2)本文基于全局-局部双向驱动的果蝇位置更新策略能有效利用果蝇群体的最优位置信息及果蝇个体的认知经验,在避免算法局部收敛、提高全局搜索稳定性方面起到一定作用.
| 表 3 不同算法对应的A值比较 Table 3 Comparison of A values of different algorithms |
| 表 4 不同算法对应的S值比较 Table 4 Comparison of S values of different algorithms |
令每个测试函数的维数D分别取2、4、6、8、10,针对每种参数优化算法在每个测试函数上实验100次,统计每种算法达到收敛状态时对应的C均值(Ca)及Ca均值(Caa),结果见表 5.由表知,FOA收敛最快,对应的Caa值为805,ABC收敛最慢,对应的Caa值为1518;IFFO及FOABHC表现相近,对应Caa值分别为1 045、1 048,明显小于IFOA、FOAMR及ABC算法.但是,FOA、IFFO及FOABHC没有在局部收敛后进行全局搜索,因此由表 3结果知,这些算法将面临过早陷入局部极值的风险.与IFOA、FOAMR及ABC算法相比,本文对应的Ca值及Caa值均明显偏小,这主要是因为IFOA、FOAMR及ABC算法在局部收敛后随机产生果蝇新位置,而本文利用个体历史认知信息能有效降低全局搜索的盲目性、提高算法收敛速度.
| 表 5 不同算法对应的Ca值及Caa值比较 Table 5 Comparison of Ca and Caa values of different algorithms |
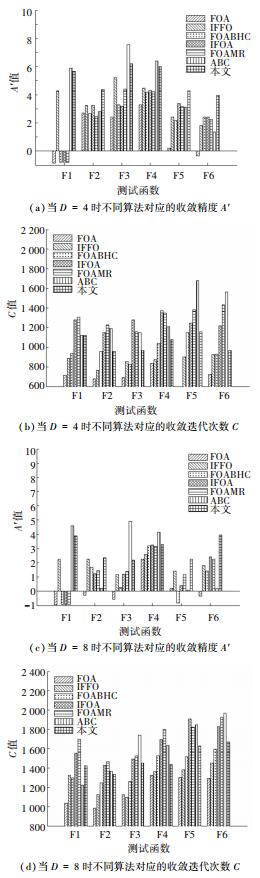
当维数D分别取4、8时,针对每种参数优化算法在每个测试函数上实验100次,统计不同算法对应的A′值及C值,结果见图 4.可见,随着维数的增加,所有算法在收敛精度及收敛速度等方面的表现均变差.当处理单峰函数时,本文在F2上精度明显高于其他算法,虽然在F1、F3上精度不及ABC,但对应A′值仍明显高于IFFO、IFOA等算法.当处理多峰函数F4时,ABC算法表现最好;当处理多峰函数F5、F6时,本文所得A′值均明显高于其他方法,并且在收敛速度上表现优于IFOA、FOAMR及ABC算法.可见,随着维数增加,本文性能虽有所下降,但在收敛精度及收敛速度方面相对于其他算法仍具有一定优势.
|
图 4 维数变化对算法性能的影响 Figure 4 Effect of dimension change on algorithm performances |
基于支持向量机(Support Vector Machine, SVM)的网络异常检测技术具有精度高、泛化能力强等优势,因此在网络异常检测中得到广泛的应用[13].将从该领域中涉及的参数优化、特征选择及运行时间比较等方面对不同优化算法进行比较.
3.2.1 异常检测中的参数优化实验在基于径向基函数(Radial Basis Function, RBF)的SVM异常检测中,惩罚系数c及RBF核函数中的δ系数是影响分类性能的重要参数[14].由文献[14]知,针对样本向量x的类别决策函数为
| $ f\left( \mathit{\boldsymbol{x}} \right) = {\mathop{\rm sgn}} \left( {\sum\limits_{i = 1}^{{n_a}} {\alpha _i^*{y_i}{\rm{RBF}}\left( {x, {x_i}} \right) + {b^*}} } \right). $ | (25) |
式中:
| $ {F_{{\rm{ma}}}} = \frac{{2 \times \rho \times \tau }}{{\rho + \tau }}. $ | (26) |
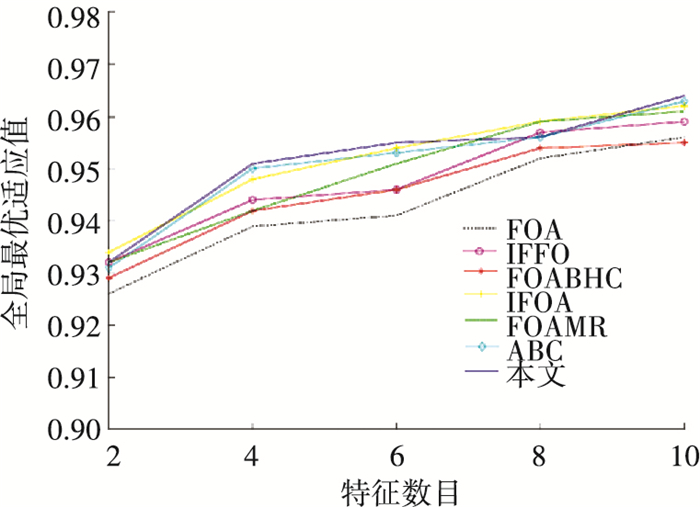
式中ρ、τ分别为异常检测准确率及召回率[15].可见,Fma值越大,c、δ值越准确,算法优化能力越强.公平起见,设置相关参数如下:c、δ最小值xmin=0.000 1,c、δ最大值xmax=5、果蝇数量N=10、最大迭代次数Tmax=200.在此基础上,统计各算法在特征数目(ns)不同情况下达到收敛状态时对应的全局最优适应值(Fa),结果见图 5.
|
图 5 网络异常检测中不同算法对应的最优适应值比较 Figure 5 Comparison of best fitness values of different algorithms in web anomaly detection |
由图 5可知,随着所选特征数目ns的增加,使用不同算法优化后的c、δ值对应的Fa值均呈现递增趋势. FOA算法表现最差,且当ns=2时获得最小Fa值0.926;FOABCH对应结果明显低于除FOA以外的其他算法,原因在于该算法仅结合全局最优位置及当前位置确定果蝇新位置,因此所得结果受果蝇初始位置影响较大,导致算法极易陷入局部最优.与其他算法相比,本文在ns分别取4、6、10时获得最大值0.951、0.955、0.964,可见本文在大多数情况下能获得更合适的c、δ值,说明该算法在获取异常检测分类器重要参数的最佳取值方面起到一定作用.
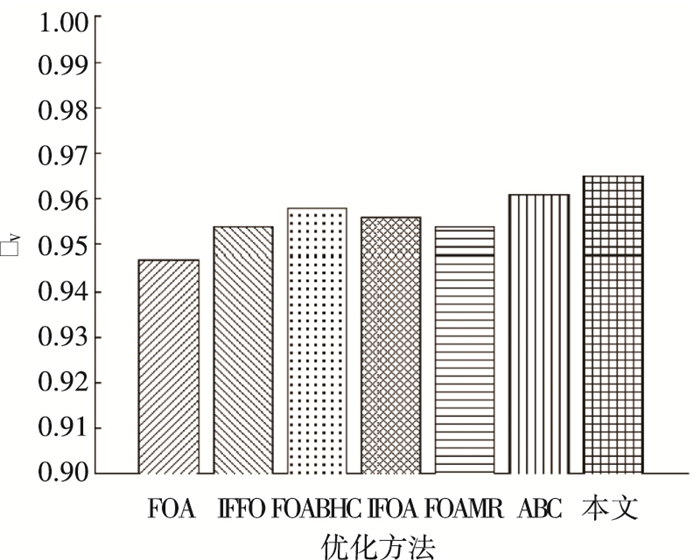
3.2.2 异常检测中的特征选择实验如何优化特征质量、提高检测速度和精度,是网络异常检测要解决的关键问题[16].将使用不同算法从KDDcup99数据集中选择最优特征子集,以测试算法在高维环境中的优化性能.不同于连续型参数优化算法,在果蝇位置更新过程中,需要对更新后位置xij进行离散化处理,即:如果
|
图 6 网络异常检测中不同算法对应的Fv值比较 Figure 6 Comparison of Fv values of different algorithms in web anomaly detection |
为测试算法在不同维数D下的执行效率,分别统计网络异常检测中参数优化(D=2)及特征选择(D=41)过程不同算法对应的运行时间tR,结果见表 6.由表知,在参数优化实验中,本文在效率上优势并不明显;但当处理维数较高的特征选择问题时,本文及IFFO对应的运行时间明显低于FOA、IFOA及ABC等算法.可见,本文通过在迭代中顺序更新特定维度能有效降低维数变化的影响,使算法能较好地处理高维环境中的复杂优化问题.
| 表 6 参数优化及特征选择中不同算法的运行时间比较 Table 6 Comparison of running time of different algorithms in parameter optimization and feature selection |
提出一种基于全局-局部双向驱动的果蝇优化新算法,主要贡献如下:1)为防止算法早熟收敛,引入先进群组的概念,在果蝇位置更新过程中结合先进群组的全局化驱动作用,使用轮盘赌策略进行果蝇位置更新;2)为避免算法在陷入局部最优后盲目地进行全局搜索,引入记忆空间的概念,在全局化搜索过程中结合果蝇个体历史认知经验的局部化驱动作用提高种群的收敛速度;3)将改进后的果蝇算法应用于基于SVM的网络异常检测,并从参数优化、特征选择及运行时间等方面对几种典型的优化算法进行比较.针对6种典型函数的实验结果表明,本文在收敛精度、收敛速度、稳定性等方面表现较好,适合处理高维、多极值的优化问题;针对网络异常检测的仿真结果表明,本文能较准确地获得SVM重要参数,并且在特征选择、运行速度等方面相对于传统算法具有一定优势.
| [1] |
徐晓飞, 刘志中, 王忠杰, 等. S-ABC--面向服务领域的人工蜂群算法范型[J].
计算机学报, 2015(11): 2301-2317.
XU Xiaofei, LIU Zhizhong, WANG Zhongjie, et al. S-ABC-service domain-oriented artificial bee colony algorithm paradigm[J]. Chinese Journal of Computers, 2015(11): 2301-2317. DOI: 10.11897/SP.J.1016.2015.02301 |
| [2] |
高卫峰, 刘三阳, 黄玲玲. 受启发的人工蜂群算法在全局优化问题中的应用[J].
电子学报, 2012, 40(12): 2396-2403.
GAO Weifeng, LIU Sanyang, HUANG Lingling. Inspired artificial bee colony algorithm for global optimization problems[J]. Acta Electronica Sinica, 2012, 40(12): 2396-2403. DOI: 10.3969/j.issn.0372-2112.2012.12.007 |
| [3] |
潘文超. 应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J].
太原理工大学学报(社会科学版), 2011, 29(4): 1-5.
PAN Wenchao. Using fruit fly optimization algorithm optimized general regression neural network to construct the operating performance of enterprises model[J]. Journal of Taiyuan University of Technology (Social Sciences Edition), 2011, 29(4): 1-5. DOI: 10.3969/j.issn.1009-5837.2011.04.002 |
| [4] |
PAN W T. A new fruit fly optimization algorithm: taking the financial distress model as an example[J].
Knowledge-Based Systems, 2012, 26: 69-74.
DOI: 10.1016/j.knosys.2011.07.001 |
| [5] |
韩俊英, 刘成忠, 王联国. 动态双子群协同进化果蝇优化算法[J].
模式识别与人工智能, 2013, 26(11): 1057-1067.
HAN Junying, LIU Chengzhong, WANG Lianguo. Dynamic double subgroups cooperative fruit fly optimization algorithm[J]. Pattern Recognition & Artificial Intelligence, 2013, 26(11): 1057-1067. DOI: 10.3969/j.issn.1003-6059.2013.11.009 |
| [6] |
WANG Lin, SHI Yuanlong, LIU Shan. An improved fruit fly optimization algorithm and its application to joint replenishment problems[J].
Expert Systems with Applications, 2015, 42(9): 4310-4323.
DOI: 10.1016/j.eswa.2015.01.048 |
| [7] |
常鹏, 李树荣, 葛玉磊, 等. 迭代步进值自适应调整的果蝇优化算法[J].
计算机工程与应用, 2016, 52(3): 32-36.
CHANG Peng, LI Shurong, GE Yulei, et al. Fruit fly optimization algorithm with self-adapting adjustment of iteration step value[J]. Computer Engineering & Applications, 2016, 52(3): 32-36. DOI: 10.3778/j.issn.1002-8331.1405-0147 |
| [8] |
PAN Q K, SANG H Y, DUAN J H, et al. An improved fruit fly optimization algorithm for continuous function optimization problems[J].
Knowledge-Based Systems, 2014, 62: 69-83.
DOI: 10.1016/j.knosys.2014.02.021 |
| [9] |
韩俊英, 刘成忠. 基于历史认知的果蝇优化算法[J].
计算机科学与探索, 2014, 8(3): 368-375.
HAN Junying, LIU Chengzhong. Fruit fly optimization algorithm based on history cognition[J]. Journal of Frontiers of Computer Science & Technology, 2014, 8(3): 368-375. DOI: 10.3778/j.issn.1673-9418.1311028 |
| [10] |
KUMAR R, JYOTISHREE. Blending roulette wheel selection & rank selection in genetic algorithms[J].
International Journal of Machine Learning and Computing, 2012, 2(4): 365-370.
DOI: 10.7763/IJMLC.2012.V2.146 |
| [11] |
MITIC M, VUKOVIC N, PETROVIC M, et al. Chaotic fruit fly optimization algorithm[J].
Knowledge-Based Systems, 2015, 89(C): 446-458.
DOI: 10.1016/j.knosys.2015.08.010 |
| [12] |
SEDGEWICK R. Implementing quicksort programs[J].
Communications of the ACM, 1978, 21(10): 847-857.
DOI: 10.1145/359619.359631 |
| [13] |
刘敬, 谷利泽, 钮心忻, 等. 基于单分类支持向量机和主动学习的网络异常检测研究[J].
通信学报, 2015, 36(11): 136-146.
LIU Jing, GU Lize, NIU Xinxi, et al. Research on network anomaly detection based on one-class SVM and active learning[J]. Journal on Communications, 2015, 36(11): 136-146. DOI: 10.11959/j.issn.1000-436x.2015252 |
| [14] |
CHANG C C, LIN C J. LIBSVM: a library for support vector machines[J].
ACM Transactions on Intelligent Systems & Technology, 2007, 2(3): 1-27.
|
| [15] |
YANGJ M, LIU Y N, ZHU X D, et al. A new feature selection based on comprehensive measurement both in inter-category and intra-category for text classification[J].
Inform. Process. Manage, 2012, 48(4): 741-754.
DOI: 10.1016/j.ipm.2011.12.005 |
| [16] |
武小年, 彭小金, 杨宇洋, 等. 入侵检测中基于SVM的两级特征选择方法[J].
通信学报, 2015, 36(4): 19-26.
WU Xiaonian, PENG Xiaojin, YANG Yuyang, et al. Two-level feature selection method based on SVM for intrusion detection[J]. Journal on Communications, 2015, 36(4): 19-26. DOI: 10.11959/j.issn.1000-436x.2015127 |
 2018, Vol. 50
2018, Vol. 50


