透波性Si3N4陶瓷材料是一种广泛应用于航空航天领域的特种陶瓷材料,具有良好的综合力学性能和较低的介电损耗,主要制造成天线窗,应用于导弹、高超声速飞行器等,是一种集防热、透波、承载、抗冲击等高性能要求为一体的多功能部件[1-2].相比于其它工程陶瓷材料,透波性Si3N4陶瓷硬度低,其零件加工无需采用磨削或者超声磨削,普通铣削即可实现,且大大提高了加工效率.为保证透波性Si3N4陶瓷零部件苛刻工作环境下使用寿命和可靠性,其铣削加工表面形貌和表面质量要求较高.表面形貌与加工过程中刀具-工件摩擦特性紧密相关,因此加工过程中接触区摩擦特性研究受到越来越多关注[3-7].
针对接触区摩擦特性研究,王宁昌等[8]通过切削实验研究了TC4铣削过程刀-屑摩擦特性,并证明冷却介质的存在降低了刀具-切屑间摩擦系数.王大镇等[9]针对颗粒增强铝基复合材料切削过程中刀具与切屑之间的摩擦特点提出了以紧密接触为主要特征的摩擦特性方程式,并通过仿真验证了方程的合理性. HAGLIND等[10]提出了常系数摩擦模型、黏结区常极限剪切应力与滑动区常库伦摩擦力模型等6种不同的摩擦模型来模拟高速切削过程中前刀面的摩擦. ARRAZOLA[11]考虑到切削刃效应的变摩擦系数,提出了一种新的力学方法,并建立了前刀面的摩擦效应模型.
以上接触区摩擦特性研究主要针对典型难加工金属材料,但是透波性Si3N4陶瓷材料与金属材料性能差异很大.透波性Si3N4陶瓷材料弹塑性性能差,铣削过程中难以形成连续性切屑,切屑形式主要为陶瓷粉末,因此切削刃前角与切屑无显著摩擦效应,刀具-工件摩擦区域集中于加工表面与切削刃后刀面.低断裂韧性仍是透波性Si3N4陶瓷的固有特征,其断裂韧性值约为2.6MPa·m1/2,在不同切削深度下,材料去除机理也不相同,因此其摩擦特性也将发生变化[12-13].根据功能要求,其加工只能采用干切削,切屑粉末容易在加工表面堆积,对摩擦系数的影响也应考虑.本文通过建立透波性Si3N4陶瓷材料铣削加工中刀具-工件接触分析模型,研究接触表面摩擦机理和摩擦系数,为提高透波性Si3N4陶瓷铣削加工表面质量提供理论支撑.
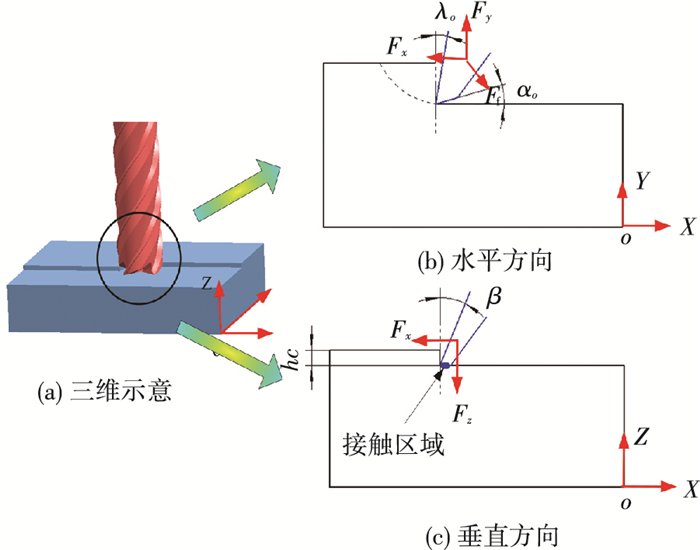
1 透波性Si3N4陶瓷加工过程透波性Si3N4陶瓷平面铣削加工过程,见图 1,刀具切削刃与材料去除侧面断续接触.分别平行于XOY面和XOZ面,分割刀具与材料面接触区域,得到刀具切削刃与材料接触关系,见图 1(b)、(c),且λo为刀具前角,β为刀具螺旋角,α0为刀具侧刃后角,hc为铣削深度.
|
图 1 铣削过程接触关系 Figure 1 Contact relationship inthe milling |
透波性Si3N4陶瓷平面铣削可分为塑性域加工和脆性域加工.塑性域加工切屑类型主要为陶瓷粉末,脆性域加工切屑类型为陶瓷粉末和陶瓷断裂颗粒.由于切屑为离散、微小颗粒,图 1(b)中刀具主切削刃与切削接触长度和接触时间都非常短,因此刀具-切屑摩擦效应可忽略.刀具-工件摩擦接触区域为切削刃后刀面与工件表面,见图 1(c).
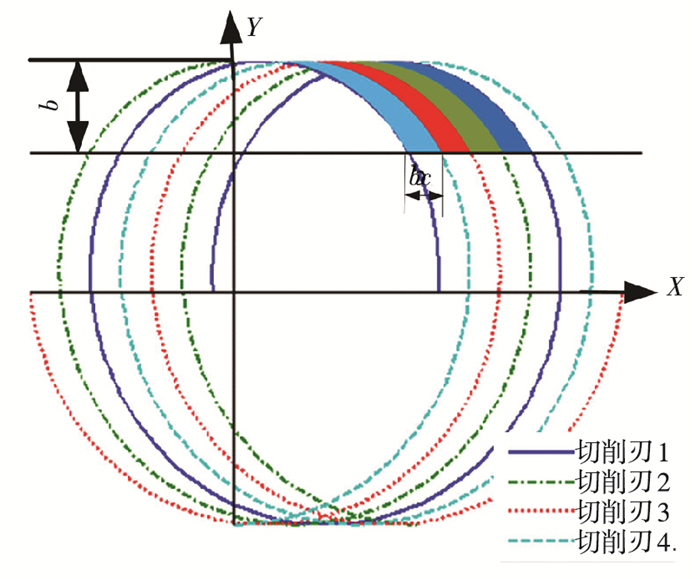
设铣刀切削刃数目为4,考虑刀具转动和进给,可以得到铣刀切削刃在加工表面运动轨迹,见图 2.图中b为加工宽度,阴影区域则对应切削刃加工面积投影,bc为接触线长度.加工过程中切削刃可以分为空转和去除材料两个过程.去除材料过程中,不同时间节点去除材料体积也是不同的,因此造成加工过程中切削力周期变化.为了便于数据处理,后文将以切削力最大时,即bc最大时分析加工过程中刀具-工件摩擦特性.
|
图 2 切削刃运动轨迹 Figure 2 Cutting edge motion trajectory |
透波性Si3N4陶瓷铣削中刀具-工件摩擦接触区域为切削刃后刀面与工件表面,因此摩擦力平行于XOY平面,且与X、Y方向切削力矢量和相反.塑性域和脆性域加工条件下,摩擦力可为
| $ {F_f} = \sqrt {F_x^2 + F_y^2} - {b_c}{h_c}{\tau _b}, $ | (1) |
| $ {F_f} = \sqrt {F_x^2 + F_y^2} - {b_c}{h_c}{\sigma _f}. $ | (2) |
式中:τb(MPa)为透波性Si3N4陶瓷剪切应力值,σf(MPa)为断裂应力值.
2 摩擦系数计算公式模型通过分析已经得出透波性Si3N4陶瓷铣削中刀具-工件接触区域为切削刃后刀面与工件表面,因此加工过程中摩擦特性研究集中于切削刃后刀面与工件表面.
当两个固体表面接触时,由于表面粗糙,在载荷作用下,硬度较低的透波性Si3N4陶瓷加工表面在硬度较高的硬质合金刀具表面挤压下将发生微观弹塑性变形,并且在相互运动作用下,形成粘着摩擦.
透波性Si3N4陶瓷加工表面粗糙度较大,约为2~4 μm,而硬质合金刀具表面粗糙度很低,约为0.2 μm,因此后刀面与工件表面接触情况可简化为一个光滑刚性表面和一个具有均方根值为σ的粗糙弹塑性表面相接触,见图 3.其中刀具表面基准与零件表面基准距离h等于透波性Si3N4陶瓷加工表面轮廓算术平均偏差.

|
图 3 刀具与工件表面接触关系 Figure 3 Contact relationship between tool and work-piece surface |
设透波性Si3N4陶瓷加工表面轮廓曲线为z.只有当z>h时,后刀面才与陶瓷表面发生接触.这种接触是一种混合的弹塑性系统,较高的波峰发生塑性变形,较低的波峰发生弹性变形.根据弹塑性力学,单个波峰在变形量为δ′(δ′=z-h)时所承受的法向载荷和接触面积为[14]
| $ W = \frac{4}{3}E'{R^{1/2}}{{\delta '}^{3/2}}, $ | (3) |
| $ A = {\rm{ \mathsf{ π} }}R\delta '. $ | (4) |
式中:
则接触波峰所受平均压力为[15]
| $ {P_c} = \frac{W}{A}. $ | (5) |
通常选取Pc=H/3作为塑性变形的条件,其中H是陶瓷材料布氏硬度值,HB.同时引入适当裕度,得到出现塑性变形时粗糙度轮廓曲线变形量为[15]
| $ {\delta ^{1/2}} = \frac{H}{{\rm{E}}}{R^{1/2}} $ | (6) |
因此得出当0<z-h<δ时,接触峰点发生弹性变形;当z-h>δ时,接触峰点发生塑性变形.根据接触波峰概率密度曲线,可得出出现弹性变形波峰和塑性表面波峰的概率分别为
| $ P\left( {h + \delta > z > h} \right) = \int_h^{h + \delta } {\varphi \left( z \right){\rm{d}}z} , $ | (7) |
| $ P\left( {z > h + \delta } \right) = \int_{h + \delta }^\infty {\varphi \left( z \right){\rm{d}}z} . $ | (8) |
设接触曲线单位长度内波峰数目为n,则弹性变形波峰和塑性表面波峰数目为[14]
| $ {m_1} = n\int_h^{h + \delta } {\varphi \left( z \right){\rm{d}}z} , $ | (9) |
| $ {m_2} = n\int_{h + \delta }^\infty {\varphi \left( z \right){\rm{d}}z} . $ | (10) |
波峰实际接触面积为[14]
| $ {A_1} = {\rm{ \mathsf{ π} }}{m_1}{R_1}\left( {z - h} \right) = {\rm{ \mathsf{ π} }}n{R_2}\int_h^{h + \delta } {\left( {z - h} \right)\varphi \left( z \right){\rm{d}}z} , $ | (11) |
| $ {A_2} = {\rm{ \mathsf{ π} }}{m_2}{R_2}\left( {z - h} \right) = {\rm{ \mathsf{ π} }}n{R_2}\int_{h + \delta }^\infty {\left( {z - h} \right)\varphi \left( z \right){\rm{d}}z} . $ | (12) |
式中R1、R2为弹性变形波峰和塑性变形波峰处曲率半径单位为mm.
假设表面轮廓高度按照Gauss分布,则靠近z值较大部分简化为指数分布,则得到[14]:
| $ \varphi \left( z \right) = \exp \left( { - z/\sigma } \right), $ | (13) |
铣削加工过程中粘着摩擦系数为:
| $ {\mu _n} = {S_j}\frac{{{A_1}{\tau _b}P\left( {h + \delta > z > h} \right) + {A_2}{\tau _b}P\left( {z > h + \delta } \right)}}{{{F_z}}}. $ | (14) |
式中:Sj为刀具后刀面与陶瓷表面接触面积,Sj=bt·bc单位为mm2;bt为后刀面宽度单位为mm;bc为前文接触线长度单位为mm.
刀具与陶瓷材料表面相互运动时,由于刀具粗糙峰硬度较高,容易嵌入陶瓷表面,滑动过程中发生塑性流动,并犁出沟槽,形成犁沟摩擦,见图 4.

|
图 4 犁沟效应示意 Figure 4 Furrow effect |
将刀具表面轮廓波峰简化成圆锥体,则嵌入到陶瓷表面的深度与刀具表面粗糙度相关,并设嵌入到陶瓷表面深度c的值等于硬质合金刀具表面算术平均值.接触区域在水平面方向投影面积A=πe2/8,在垂直面上投影面积S=e·c/2.犁沟摩擦过程中也存在粘着摩擦,考虑到粘着效应,犁沟滑动时摩擦力为[14]
| $ {F_t} = A{\tau _b} + S{\sigma _s}. $ | (15) |
式中σs为陶瓷塑性变形屈服应力单位为MPa.
设刀具表面单位长度内发生犁沟摩擦波峰数目为ρ1,则加工过程中犁沟摩擦系数可为[14]
| $ {\mu _l} = {S_j}\frac{{{\rho _1}{F_t}}}{{{F_z}}} = {S_j}\frac{{{\rho _1}\left( {A{\tau _b}/2 + S{\sigma _s}} \right)}}{{{F_z}}}. $ | (16) |
铣削过程为干切削,根据图 4可看出在两固体表面存在大量切屑.当加工过程为脆性域加工时,切屑中含有大量碎裂型陶瓷颗粒,且体积大于陶瓷粉末.两固体表面发生滑动时,这些碎裂型陶瓷颗粒也会嵌入到陶瓷表面,通过挤压导致表面塑性流动并形成沟槽,其摩擦机理与犁沟摩擦相同.将破碎型陶瓷颗粒简化为球形,可以得到碎裂型陶瓷颗粒与加工表面接触区域在水平面和垂直面上投影面积为
| $ {A_d} = \frac{1}{4}{\rm{ \mathsf{ π} }}{D^2}, $ | (17) |
| $ {S_d} = \frac{1}{4}{\rm{ \mathsf{ π} }}{D^2}. $ | (18) |
式中D为碎裂型陶瓷颗粒直径单位为mm.
设接触区域单位面积内碎裂型陶瓷颗粒数目为ρ2,则引起的犁沟摩擦系数为[14]
| $ {\mu _d} = {S_j}{\rho _2}\frac{{{A_d}{\tau _b} + {S_d}{\sigma _s}}}{{{F_z}}}. $ | (19) |
干切削过程中,材料去除形成的陶瓷粉末不可避免的残留于刀具表面与工件表面接触处.透波性Si3N4陶瓷材料制备时所选用的陶瓷粉末近似为球形,由于烧结温度只有1 400 ℃左右,且烧结后材料气孔率高,致密度低,粉体结构变化较小,故将铣削加工中陶瓷粉末仍简化为球形.当两固体表面发生滑动时,陶瓷粉末在切向力作用下将发生滚动,形成滚动摩擦.根据Dupuit定律,在陶瓷粉末作用下,加工过程中滚动摩擦系数为
| $ {\mu _{\rm{r}}} = {S_j}{\rho _3}\frac{k}{{\sqrt d }}. $ | (20) |
式中:ρ3为接触区域单位面积内陶瓷粉末数目;k为材料和表面状况确定的常量;d为陶瓷粉末直径单位为mm.
通过分析,可推导出透波性Si3N4陶瓷铣削加工过程中摩擦系数计算公式为
| $ \mu = {\mu _r} + {\mu _l} + \beta {\mu _d} + {\mu _r} $ | (21) |
式中:塑性域加工时,β=0,脆性域加工时,β=1.
3 实验与结果分析 3.1 实验设计为研究铣削加工过程摩擦特性和验证摩擦系数计算公式,设计不同铣削深度条件下透波性Si3N4陶瓷铣削加工实验.实验所用的透波性Si3N4陶瓷由哈尔滨工业大学特种陶瓷研究所制备(80% Si3N4,15%BN,5%Al2O3+Y2O3),样件尺寸大小为40 mm×40 mm×10 mm,陶瓷粉末直径约为0.1 μm,样件主要材料参数见表 1.
| 表 1 材料参数 Table 1 Material parameters |
实验方法为单因素实验,只改变铣削深度,每组实验总次数为8,实验参数安排见表 2.为保证实验结果的可靠性,每组实验将将重复做三次,分析时将离散较大的实验结果摒弃.
| 表 2 实验方案 Table 2 xperimental program |
实验所用机床为JDGR200_A10HCNC铣床,所用刀具材料为硬质合金YL10.2(晶粒度0.7 μm,WC 90%,Co10%),弹性模量为600 GPa,泊松比为0.3,表面粗糙度Ra为0.2 μm,刀具直径为10 mm,切削刃数目为4,后刀面宽度为1.5 mm,前角为8°, 后角为10°,螺旋角为30°.透波性Si3N4陶瓷固定在测力仪上,铣削宽度为1 mm,铣削加工过程见图 5所示.加工过程中采用KISTLER 9257A测力仪和KISTLER 5070电荷放大器进行切削力采集;采用OLS3000激光共聚焦显微镜和VHX-1000超景深显微镜对铣削后陶瓷表面形貌进行测量和观察;收集不同切削深度下切屑,并采用FEI HELIOS NanoLab 600I FIB/SEM进行观察.

|
图 5 实验过程 Figure 5 Experimental process |
透波性Si3N4陶瓷断裂韧性值较低,是典型脆性材料.不同切削深度下切削力并不相同,在切削力作用下,当刀具-工件接触区应力小于材料断裂应力时,加工机理为塑性域加工,切屑为陶瓷粉末;而当刀具-工件接触区应力大于材料断裂应力时,加工过程中出现微观裂纹扩展,相邻微观裂纹耦合相遇,实现材料去除,加工机理为脆性域加工,切屑除陶瓷粉末,还含有大量陶瓷断裂颗粒,因此通过切屑分析可以研究不同切削深度下透波性Si3N4陶瓷加工机理,从而便于后续分析摩擦机理和摩擦系数.
不同切削深度下切屑形态见图 6.当切削深度分别为0.1 mm、0.2 mm和0.3 mm时,透波性Si3N4陶瓷切屑主要为材料粉末. 图 6(c)中虽然存在部分颗粒,通过放大观察,发现颗粒实际为粉末集簇体,呈雪花状且形态粗糙,此时材料去除方式为塑性去除.当切削深度为0.4 mm时,切屑除材料粉末外,还出现大量碎裂型颗粒,且不同于集簇性粉末,其表面形态较为光滑,这是由于加工过程中出现材料剥落去除,即脆性去除.且当切削深度>0.4 mm时,切屑中碎裂型颗粒越来越明显.因此当切削深度≤0.3 mm时,材料去除机理为塑性去除;当切削深度≥0.4 mm时,材料去除方式为塑性和脆性并存去除.

|
图 6 不同切削深度切屑 Figure 6 Chips under different cutting depth |
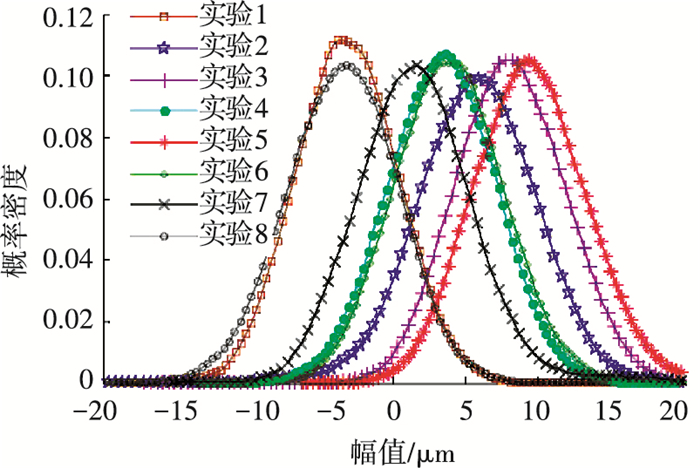
采用激光共聚焦显微镜对不同切深得到的加工表面进行幅值测量,然后对加工表面形貌高度值进行概率密度统计分布,得到不同切削深度加工表面形貌幅度分布统计图见图 7.可看出不论切削深度如何变化,加工后表面幅度值概率密度曲线都与高斯曲线一致,即加工表面为高斯表面,这也证明前文中将表面轮廓高度按照Gauss分布的假设是成立的.
|
图 7 表面幅度概率分布 Figure 7 Surface amplitude probability distribution |
当切削深度为0.3 mm和0.4 mm时,加工表面观察图见图 8.看出当切削深度为0.4 mm时,透波性Si3N4陶瓷加工表面明显有沟槽,而当切削深度为0.3 mm时,加工表面无显著沟槽.由于硬质合金刀具表面粗糙度值较低,其犁沟效应不显著;而脆性域加工过程中,所形成的碎裂型陶瓷颗粒体积远大于硬质合金粗糙度波峰,在刀具与工件相对滑动中,产生了显著沟槽,这也与前文犁沟摩擦分析一致.

|
图 8 不同切深加工表面 Figure 8 Surface under different cutting depth |
通过高频切削力采集,可以得到刀具每转一周时间段内X、Y和Z方向切削力,由于切削力周期变化,本文以周期内切削力最大时进行分析,此时bc也最大.根据式(1)、(2)可计算出加工过程中不同切削深度下摩擦力,分别除以对应的Z轴方向切削力,可得到摩擦系数实验值.将实验设计中参数和实验结果统计值,带入式(21)可得到不同切削深度下摩擦系数计算值见图 9.

|
图 9 不同切削深度下摩擦系数 Figure 9 Friction coefficient under different cutting depth |
从图中可看出,理论计算值与实验值保持相对一致性,其最大误差率约为20.46%,在一定程度上采用摩擦系数计算模型研究透波性Si3N4陶瓷铣削加工过程摩擦特性是合理的.塑性域和脆性域加工过程中,随着切削深度的增加,摩擦系数都增大.但是当塑性域加工转为脆性域加工初始阶段,摩擦系数反而降低.脆性域加工临界范围内,材料去除方式为断裂去除,加工表面波峰密度和粗糙度都降低,虽然切屑犁沟摩擦增加,但是粘着摩擦和和刀具粗糙度波峰犁沟摩擦都减少,从而造成摩擦系数降低.
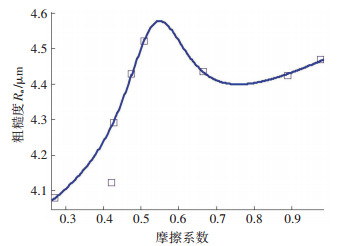
从摩擦系数模型中可看出,加工过程中摩擦系数与透波性Si3N4陶瓷表面粗糙度具有紧密关系.通过实验结果分析,得出摩擦系数对表面粗糙度影响规律,见图 10.从图中可看出,摩擦系数对表面粗糙度影响呈三阶多项式分布.随着摩擦系数的增大,表面粗糙度先递增;当摩擦系数大于0.55时,表面粗糙度下降,然后又呈现递增趋势.
|
图 10 摩擦系数对表面粗糙度影响 Figure 10 Effect of friction coefficient on surface roughness |
本文通过分析透波性Si3N4陶瓷铣削过程中刀具-工件接触关系,研究加工过程摩擦机理,给出摩擦系数计算公式,并通过实验证明了理论假设和计算公式.
1) 当切削深度≤0.3 mm时,透波性Si3N4陶瓷铣削为塑性域加工;当切削深度≥0.4 mm时,透波性Si3N4陶瓷铣削为脆性域加工.
2) 塑性域加工过程中,摩擦机理主要为粘着摩擦、刀具表面粗糙度波峰犁沟摩擦和陶瓷粉末滚动摩擦;脆性域加工过程中,摩擦机理除上述三种类型外,还应包括碎裂型陶瓷颗粒犁沟摩擦.
3) 根据透波性Si3N4陶瓷铣削过程中刀具-工件接触关系和摩擦机理,应用已有的微观表面形态与表面接触的摩擦力及摩擦系数理论给出了Si3N4陶瓷与铣刀材料的摩擦系数计算公式.结果表明,所给出公式计算结果与实验结果最大误差率为20.46%,能在一定程度上反映加工过程中摩擦特性演化规律.
4) 塑性域和脆性域加工过程中,随着切削深度的增加,摩擦系数都增大.但是当塑性域加工转为脆性域加工初始阶段,由于加工机理的改变,摩擦系数反而降低.且摩擦系数对表面粗糙度影响规律呈现三阶多项式分布.
| [1] |
方震宇, 曹峰, 张长瑞, 等. 氮化物陶瓷系高温透波材料的研究进展[J].
材料导报, 2011, 25(7): 54-57.
FANG Zhenyu, CAO Feng, ZHANG Changrui, et al. Progress on high temperature nitride based ceramic wave-transparent materials[J]. Materials Review, 2011, 25(7): 54-57. |
| [2] |
CHEN M, YIN X, LI M, et al. Electromagnetic interference shielding properties of silicon nitride ceramics reinforced by in situ grown carbon nanotubes[J].
Ceramics International, 2015, 41(2): 2467-2475.
DOI: 10.1016/j.ceramint.2014.10.062 |
| [3] |
程耀楠, 刘献礼, 李振加, 等. 极端重载切削条件下的刀—屑黏结失效[J].
机械工程学报, 2012, 48(19): 169-176.
CHENG Yaonan, LIU Xianli, LI Zhenjia, et al. Adhering failure of the tool-chip in the process of extremely heavy cutting[J]. Journal of Mechanical Engineering, 2012, 48(19): 169-176. DOI: 10.3901/JME.2012.19.169 |
| [4] |
CLAUDIN C, MONDELINA. Effects of a straight oil on friction at the tool-work material interface in machining[J].
International Journal of Machine tools & Manufacture, 2010, 50(1): 681-688.
DOI: 10.1016/j.ijmachtools.2010.04.013 |
| [5] |
AN Q L, FU Y C, XU J H. Experimental study on turning of TC9 titanium alloy with cold water mist jet cooling[J].
International Journal of Machine Tools and Manufacture, 2011, 51(6): 549-555.
DOI: 10.1016/j.ijmachtools.2011.03.005 |
| [6] |
李友生, 邓建新, 张辉, 等. 高速车削钛合金的硬质合金刀具磨损机理研究[J].
摩擦学学报, 2008, 28(5): 443-447.
LI Yousheng, DENG Jianxin, ZHANG Hui, et al. Wear mechanism of cemented carbide tool in high speed machining titanium alloy (Ti-6Al-4V)[J]. Tribology, 2008, 28(5): 443-447. |
| [7] |
郑敏利, 范依航. 高速切削典型难加工材料刀具摩擦与磨损机理研究现状[J].
哈尔滨理工大学学报, 2011, 16(6): 22-30.
ZHENG Minli, FAN Yihang. An overview of tool friction and wear behavior in high-speed machining-typical difficult-to-cut material[J]. Journal of Harbin University of Science and Technology, 2011, 16(6): 22-30. |
| [8] |
王宁昌, 程鑫, 姜峰, 等. 冷风油雾润滑对TC4铣削过程刀—屑摩擦的影响[J].
华侨大学学报(自然科学版), 2015, 36(3): 258-262.
WANG Ningchang, CHENG Xin, JIANG Feng, et al. Friction behavior between tool and chip during TC4 milling with cold air oil mist lubricant[J]. Journal of Huaqiao University (Natural Science), 2015, 36(3): 258-262. DOI: 10.11830/ISSN.1000-5013.2015.03.0258 |
| [9] |
王大镇, 韩荣第, 刘华明, 等. 铝基复合材料超精密加工中的刀—屑摩擦磨损性能及模型研究[J].
摩擦学学报, 2005, 25(6): 569-573.
WANG Dazhen, Han Rongdi, LIU Huaming, et al. Wear model and characteristics between cutting tool and chips in ultraprecision machining of SiC reinforced aluminum composites[J]. Tribology, 2005, 25(6): 569-573. |
| [10] |
HAGLID A J, KISHAWYH A, ROGERS R J. An exploration of friction models for the chip-tool interface using an arbitrary lagrangian-eulerian finite element model[J].
Wear, 2008, 265(3-4): 452-460.
DOI: 10.1016/j.wear.2007.11.025 |
| [11] |
ARRAZLA P J, UGARTE D, DOMINGUEZ X. A new approach for the friction identification during machining through the use of finite element modeling[J].
International Journal of Machine Tools and Manufacture, 2008, 48(2): 173-183.
DOI: 10.1016/j.ijmachtools.2007.08.022 |
| [12] |
RUSNALDY, KO T J, KIM H S. Micro-end-milling of single-crystal silicon[J].
International Journal of Machine Tools &Manufacture, 2007, 47(14): 2111-2119.
DOI: 10.1016/j.ijmachtools.2007.05.003 |
| [13] |
WANG Chengyong, ZHOU Li, FU Hao, et al. High speed milling of graphite electrode with end mill of small diameter[J].
Chinese Journal of Mechanical Engineering, 2007, 20(4): 27-31.
DOI: 10.3901/CJME.2007.04.027 |
| [14] |
温诗铸, 黄平.
摩擦学原理(第二版)[M]. 北京: 清华大学出版社, 2003: 256-274.
WEN Shizhu, HUANG Ping. Tribology principles (Second edition)[M]. Beijing: Tsinghua University Press, 2003: 256-274. |
| [15] |
GREENWOOD J A, WILLIAMSON J B. Contact of nominally flat surfaces[J].
Proceedings of the Royal Society of London A, 1966(295): 300-319.
DOI: 10.1098/rspa.1966.0242 |
 2018, Vol. 50
2018, Vol. 50


