2. 信息安全国家重点实验室(中国科学院信息工程研究所),北京 100093
2. State Key Laboratory of Information Security (Institute of Information Engineering, Chinese Academy of Sciences), Beijing 100093, China
图像质量评价(Image Quality Assessment, IQA)在很多实际应用中起着至关重要的作用,例如图像增强[1]、编码[2]、采集[3]、水印[4]和压缩[5]等. IQA不仅用于比较和评价图像处理系统和算法,而且它还可嵌入到图像处理算法中以优化其性能.因此,IQA已经成为一个非常重要的研究课题,受到广泛关注.
目前,一类具有代表性的方法是文献[6]提出的基于结构相似性(Structural Similarity, SSIM)的IQA度量指标.根据人眼能从图像中提取结构信息的理论,SSIM指标利用均值、方差和协方差衡量图像局部亮度、对比度和结构相似性,进而度量图像整体的相似性,其评价结果与人主观感知较为一致.然而,SSIM仍然有一定的局限性.为增强客观图像质量评价的准确性,研究者在SSIM指标基础上进行改进,涌现出大量改进SSIM的指标.
由于人眼对于图像边缘信息比较敏感,且图像边缘对于理解图像信息至关重要.研究者提出了很多基于梯度的SSIM改进指标[7-12].文献[7]提出基于梯度幅值相似性偏差的图像质量评价指标,对梯度幅值相似性使用标准差的方式进行池化.文献[10]利用图像的相位一致特征和梯度幅值特征,提出基于特征相似指数(FSIM)的图像质量评价指标.文献[11]提出基于梯度相似性(GSM)指标,将亮度和梯度相似性相结合.文献[12]将加权的梯度信息与SSIM相结合,可有效提高预测的准确性.文献[13]提出基于内在生成机制的方法,将图像分成有序区域和无序区域进行质量预测,采用多尺度和自适应权值结合两区域质量得到最终的质量预测值.文献[14]利用结构张量、对比度掩蔽和邻域掩蔽,对SSIM指标的结构比较函数和对比度比较函数进行改进.为有效地对几何变换图像的质量进行评价,文献[15]利用均值分段的标准差相关函数对SSIM的结构比较函数进行改进,并且考虑图像锐度的影响,引入锐度比较函数.文献[16]证明了权重应与局部信息内容成比例,提出基于信息内容加权的结构相似性度量指标(IWSSIM).
在现有的SSIM改进方案中,没有充分考虑人眼掩蔽效应、视觉选择注意机制对图像质量评价的影响.为此,本文结合最小可辨失真(just noticeable distortion,JND)和视觉显著性评价设计了改进的SSIM.首先,利用JND模型进行原始图像的视觉阈值分析,并结合绝对误差图和Sigmoid函数进行失真图像的修正;然后,利用视觉显著性模型提取子区域的权重;最后,结合SSIM指标对各子区域加权得到最终的图像质量.在LIVE2和CSIQ数据库上对本文指标进行测试,并与当前多种具有代表性的指标进行广泛比较.
1 基本的SSIMSSIM指标使用图像块结构信息的变化量衡量图像质量,其基本思想是结合参考图像和失真图像之间的局部亮度、对比度和结构相似性得到图像质量.给定x和y是参考图像和失真图像相同位置处对应的图像块,其大小为M×N(高×宽).
局部亮度相似性的度量使用图像局部平均值信息,对图像块x平均值定义如下:
| $ {\mu _x} = \frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {x\left( {i,j} \right)} } . $ | (1) |
式中x(i, j)为图像x在点(i, j)处的像素值.
局部对比度相似性的估计使用图像局部标准差信息,对图像块x标准差定义如下:
| $ {\sigma _x} = {\left[ {\frac{1}{{MN - 1}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{\left( {x\left( {i,j} \right) - {\mu _x}} \right)}^2}} } } \right]^{1/2}}. $ | (2) |
结构相似性使用图像块x和y的相关性进行度量,其定义为
| $ {\sigma _{xy}} = \frac{1}{{MN - 1}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {\left( {x\left( {i,j} \right) - {\mu _x}} \right)\left( {y\left( {i,j} \right) - {\mu _y}} \right)} } . $ | (3) |
利用上述定义,局部亮度相似性l(x, y)、对比度相似性c(x, y)和结构相似性s(x, y)为
| $ l\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = \frac{{2{\mu _x}{\mu _y} + {C_1}}}{{\mu _x^2 + \mu _y^2 + {C_1}}}, $ | (4) |
| $ c\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = \frac{{2{\sigma _x}{\sigma _y} + {C_2}}}{{\sigma _x^2 + \sigma _y^2 + {C_2}}}, $ | (5) |
| $ s\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = \frac{{{\sigma _{xy}} + {C_3}}}{{{\sigma _x}{\sigma _y} + {C_3}}}. $ | (6) |
式中:μy、σy分别为图像块y的平均值和标准差,其定义与μx、σx类同;常数Ci≥0(i=1, 2, 3),其数值一般较小,用以保持上述各式的稳定性.
参考图像和失真图像之间的SSIM是图像局部质量的平均值,表达为
| $ {\rm{SSIM}} = \frac{1}{K}\sum\limits_{i = 1}^K {{{\left[ {l\left( {{\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{y}}_i}} \right)} \right]}^\alpha }{{\left[ {c\left( {{\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{y}}_i}} \right)} \right]}^\beta }{{\left[ {s\left( {{\mathit{\boldsymbol{x}}_i},{\mathit{\boldsymbol{y}}_i}} \right)} \right]}^\gamma }} . $ | (7) |
式中:xi和yi分别是参考图像和失真图像的第i个图像块;K是图像块的个数;α>0、β>0和γ>0是各个分量的权重,用以调整相对重要性.
虽然SSIM在度量图像失真时考虑了像素点与其邻域像素之间的相关性,描述了图像结构信息,但SSIM指标仍然存在缺陷.首先,SSIM没有考虑HVS掩蔽效应对视觉感知的影响.其次,SSIM指标平等对待图像中视觉感兴趣程度不同的区域,忽略了视觉选择注意机制对图像质量评价的影响.因而,SSIM的性能受到极大的限制.
2 基于JND模型和视觉显著性评价的图像相似性度量为改进基本的SSIM,本文引进JND和视觉显著性评价,设计方案见图 1.
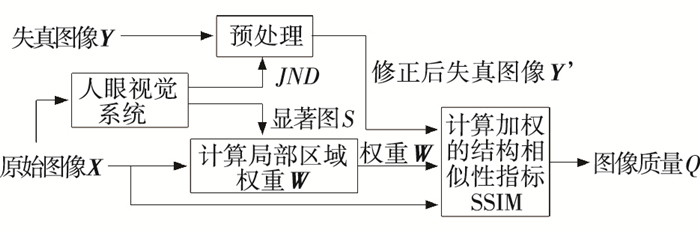
|
图 1 改进的IQA系统流程图 Figure 1 The improved IQA system |
从图 1可看出,本文的设计方案与原始SSIM的区别在于:失真图像需先经过一个预处理得到修正后的失真图像,且对图像的局部质量进行加权得到最终的图像质量评价指标.
本文利用JND模型和Sigmoid函数对失真图像进行预处理,以保留人眼可见失真,使图像的失真更符合人的主观感受.利用视觉显著性模型提取原始图像的显著图,以模拟图像不同区域的受关注程度.相同的失真发生在图像显著区域与非显著区域的影响不同,因此在进行图像局部质量融合时应对不同区域施加不同的权重.
3 基于JND模型的失真图像修正JND模型在图像视觉质量评价的研究中具有举足轻重的作用.使用JND模型可得出每个像素点的视觉阈值,并从而修正图像,使得失真图像更能反映图像的可见失真量.
3.1 JND模型文献[17]中给出一种空间域的JND模型.该模型采用亮度掩蔽和对比度掩蔽的非线性加权来计算JND值.
亮度掩蔽阈值取决于图像x各像素邻域的加权亮度值,像素邻域加权亮度值为
| $ \mathit{\boldsymbol{\bar x = }}\frac{1}{{{{\left\| \mathit{\boldsymbol{B}} \right\|}_1}}}\left( {\mathit{\boldsymbol{x}} * \mathit{\boldsymbol{B}}} \right). $ | (8) |
式中:‖·‖1为1范数;B是一个5×5的低通滤波器;符号*为卷积.
对比度掩蔽阈值的度量利用图像的梯度信息,文献[17]中采用像素邻域4个方向中最大的平均加权梯度
| $ \mathit{\boldsymbol{G}} = \mathop {\max }\limits_{k = 1,2,3,4} \left\{ {\frac{1}{{2 \cdot {{\left\| {{\mathit{\boldsymbol{g}}_k}} \right\|}_1}}}\left( {\mathit{\boldsymbol{x}} * {\mathit{\boldsymbol{g}}_k}} \right)} \right\}. $ | (9) |
式中gk (k=1, 2, 3, 4)是5×5的高通滤波器.
不同区域的视觉阈值应取不同值.因此,在对比度掩蔽阈值的度量中加入图像的边缘权重系数We,以调整图像边缘区域与非边缘区域的对比度阈值.即
| $ {\mathit{\boldsymbol{W}}_{\rm{e}}} = \mathit{\boldsymbol{L}} * \mathit{\boldsymbol{h}}. $ | (10) |
式中:L是图像边缘图;h是高斯低通滤波器.
利用上述定义,图像亮度掩蔽阈值Tl和对比度掩蔽阈值Tc定义如下:
| $ {T^l}\left( {i,j} \right) = \left\{ \begin{array}{l} 17\left( {1 - \sqrt {\frac{{\bar x\left( {i,j} \right)}}{{127}}} } \right) + 3,\;\;\;\;\;\;\bar x\left( {i,j} \right) \le 127;\\ \frac{3}{{128}}\left( {\bar x\left( {i,j} \right) - 127} \right) + 3,\;\;\;\;\;\bar x\left( {i,j} \right) > 127. \end{array} \right. $ | (11) |
| $ {T^c}\left( {i,j} \right) = \beta \cdot G\left( {i,j} \right) \cdot {W_e}\left( {i,j} \right); $ | (12) |
式中:β是控制参数;x(i, j)、G(i, j)和We(i, j)分别为x、G和We在坐标(i, j)处的值.
结合亮度掩蔽阈值和对比度掩蔽阈值得到图像像素JND阈值
| $ T\left( {i,j} \right) = {T^l}\left( {i,j} \right) + {T^c}\left( {i,j} \right) - C \cdot \min \left( {{T^l}\left( {i,j} \right),{T^c}\left( {i,j} \right)} \right). $ | (13) |
式中C为亮度通道所占的重叠效应.
式(8)~(10)中的B、gk、L和h的设计详见文献[17].
3.2 失真图像的修正由于亮度掩蔽和对比度掩蔽效应,并不是图像中所有的变化都能引起人眼的感知.图像失真程度在JND阈值以内,人眼无法感知,并且对图像相似性评价的影响很小甚至没有.相反,图像失真量超过JND阈值,对图像相似性的评价产生较大的影响.
利用JND模型建立预处理滤波器,对失真图像进行滤波预处理,移除人眼无法感知的失真,只保留可见失真更符合主观感知.该过程如下:
Step 1: 计算原始图像X中每个像素的视觉阈值T.利用式(13)进行视觉阈值的计算.
Step 2: 失真图像修正.为使图像质量评价更符合人眼的主观感知,对失真图像Y的每个像素进行修正
| $ \begin{array}{l} Y'\left( {i,j} \right) = X\left( {i,j} \right) \cdot {\bf{1}}\left\{ {\left| {D\left( {i,j} \right)} \right| \le T\left( {i,j} \right)} \right\} + \\ \;\;\;\left[ {Y\left( {i,j} \right) - {\rm{sign}}\left( {D\left( {i,j} \right)} \right) \cdot \lambda \left( {i,j} \right) \cdot T\left( {i,j} \right)} \right] \cdot \\ \;\;\;{\bf{1}}\left\{ {\left| {D\left( {i,j} \right)} \right| > T\left( {i,j} \right)} \right\}. \end{array} $ | (14) |
式中:1(·)是示性函数;|·|为绝对值;Y′是修正之后的失真图像;误差D(i, j)=X(i, j)-Y(i, j);sign(·)是符号函数;λ(i, j)≥0是惩罚因子.
从式(14)中可看出,当绝对误差小于JND值时,修正后的失真图像与原始图像的像素值相同.由于失真区域易受到人眼关注,相应的图像主观评价质量会降低.所以,绝对误差大于JND值时,失真图像取决于误差和JND值,增大误差,减小图像质量评价值.
惩罚因子λ(i, j)对于图像质量评价具有重要作用,λ(i, j)与图像每个像素的感知误差R(i, j) =|D(i, j)|/T(i, j)有关.本文设计λ(i, j)为Sigmoid函数,表达为
| $ \lambda \left( {i,j} \right) = \frac{1}{{1 + \exp \left( { - R\left( {i,j} \right)} \right)}}. $ | (15) |
λ(i, j)与R(i, j)之间的关系如图 2所示,可看出,惩罚因子随感知误差的增大而逐渐趋近于1,这表示可见性误差的影响增加了.
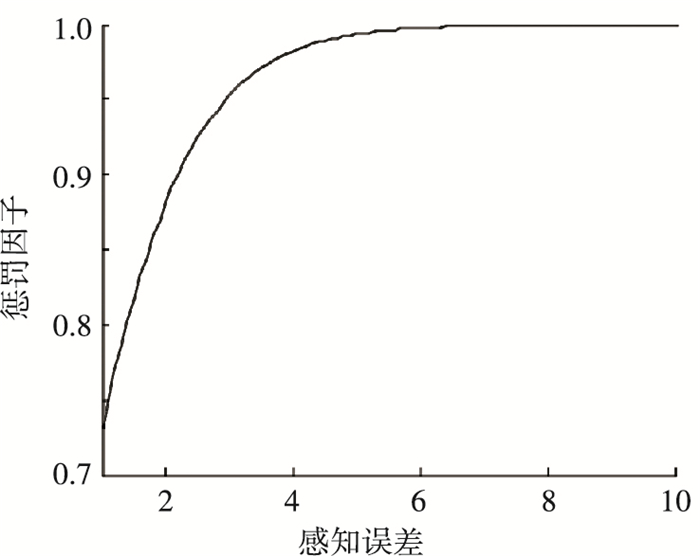
|
图 2 惩罚因子λ(i, j)与感知误差R(i, j)的关系 Figure 2 The relationship between penalty factor λ(i, j) and perceptual error R(i, j) |
使用修正的失真图像计算SSIM,可改善IQA的性能.具体实例如图 3和图 4所示.
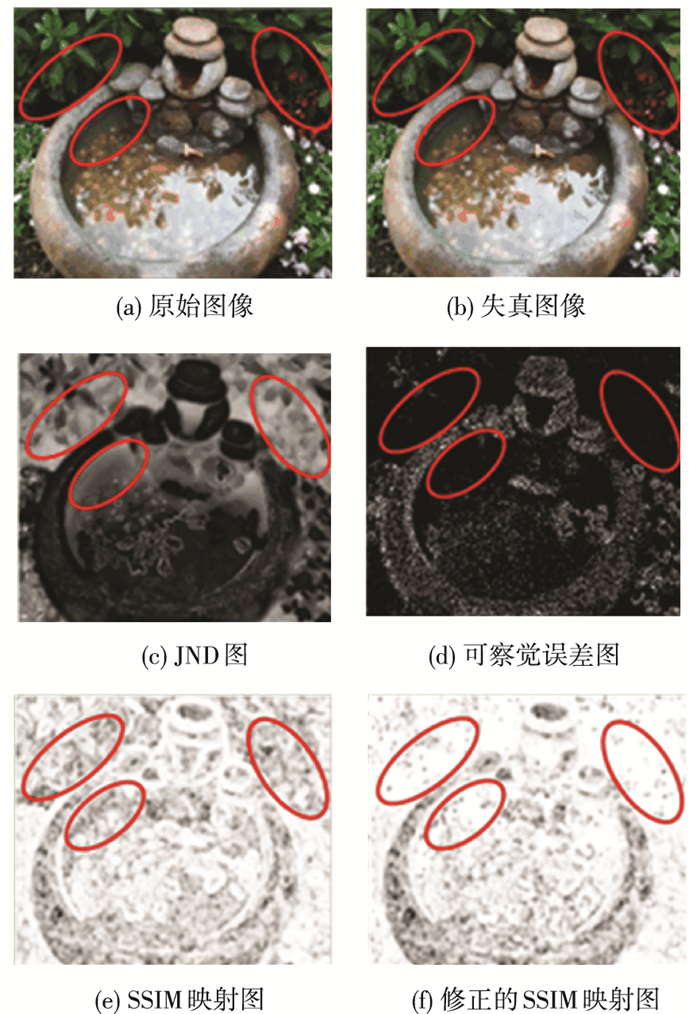
|
图 3 基于JND的失真图像修正“coinsinfountain”在图像上的有效性 Figure 3 The effectiveness of JND-based distortion image modification on "coinsinfountain" image |

|
图 4 基于JND的失真图像修正在“ocean”图像上的有效性 Figure 4 The effectiveness of JND-based distortion image modification on "ocean" image |
图 3(a)为原始图像;图 3(b)为失真图像;图 3(c)为基于JND模型计算的原始图像的JND图;图 3(d)为图 3(a)和图 3(b)之间的可察觉误差,图像中的黑色部分不会影响视觉;图 3(e)是图 3(a)和图 3(b)之间的SSIM映射图;图 3(f)是图 3(a)与修正失真图之间的SSIM映射图.映射图中亮度越高则表明原始图像与失真图像在此处的相似性越高,失真图像的质量损失越少,图像质量越好.
图 3标记区域(椭圆)为纹理区域,由于对比度掩蔽效应,人眼对于纹理区域的敏感度较低.从图中标记区域可以看出,其可察觉误差很低(图 3(d)),图像质量映射图的相应区域应比较明亮.然而图 3(e)对应区域亮度暗淡,与人的视觉判断相反. 图 3(f)可看出对应区域很明亮,与人眼判断一致.
图 4给出在另外一幅图像上显示的例子,其各子图与图 3中相应子图的表示含义相同. 图 4标记区域背景亮度较低,人眼对此处的失真敏感度较低,且从图 4(b)可看出此区域的失真不可见.同理,从图 4可做出与图 3类似的结论.
以上实例说明,利用JND和Sigmoid函数对失真图像进行修正可消除不可察觉误差,使可见失真更符合人眼主观感知,提高度量性能.
4 基于视觉显著性评价的局部质量融合人类视觉注意机制通常会关注图像中重要的刺激而抑制不重要的信息,所以还需考虑局部显著性对于图像质量的影响,根据受关注的程度而区别对待图像局部区域. 图 5展示了不同图像的显著性效果,图 5(a)和5(b)为原图,其相应的显著性图如图 5(c)和5(d)所示.可看出,显著性图像越亮的部分,其显著性越高,即关注度越高,对图像质量的影响更大.本文利用图像的局部显著性来改善图像质量评价指标.

|
图 5 图像显著性检测结果 Figure 5 Image saliency detection results |
本文采用基于相位谱的四元数傅里叶变换(PQFT)模型[18]对图像的显著性进行度量. PQFT模型将图像每个像素用颜色、亮度和运动向量进行表示,通过计算其傅里叶变换的相位谱提取图像的显著性区域.提取图像显著性时,运动向量为零.
利用PQFT模型处理原始图像X得到显著图S.按照图像质量评价指标中图像块的划分方法,设计尺寸相同的均值滤波器,对显著图S进行均值滤波,得到滤波后的显著图W.将W中每个坐标点的数值wi作为区域权重,即利用显著图S中各子区域的平均显著值表征图像区域权重.
4.2 融合将图像各子区域的权重进一步进行归一化处理,得到子区域的相对权重为
| $ {{w'}_i} = \frac{{{w_i}}}{{\sum\limits_{i = 1}^K {{w_i}} }}. $ | (16) |
式中K是显著图的分块数.
选取SSIM指标度量原始图像X与修正失真图像Y ′之间相对应子块的质量qi
| $ {q_i} = l\left( {{\mathit{\boldsymbol{x}}_i},{{\mathit{\boldsymbol{y'}}}_i}} \right) \cdot c\left( {{\mathit{\boldsymbol{x}}_i},{{\mathit{\boldsymbol{y'}}}_i}} \right) \cdot s\left( {{\mathit{\boldsymbol{x}}_i},{{\mathit{\boldsymbol{y'}}}_i}} \right). $ | (17) |
利用图像的显著性信息对图像各局部质量进行线性加权,得到整幅图像的客观评价值Q
| $ Q = \sum\limits_{i = 1}^K {{{w'}_i} \cdot {q_i}} . $ | (18) |
式中xi和y′i分别是原始图像和修正失真图像的第i个图像块.
从式(18)中可看出,权重wi越大的区域对图像质量的影响越显著,这比基本的SSIM把所有区域视为对图像质量具有相同的影响更合理.另外,通过实行式(16)的权重归一化处理,可确保客观评价值Q取值在0和1之间.
5 实验结果与分析 5.1 测试数据库与评价性能指标为验证图像质量评价指标的性能,本文采用LIVE2[19]和CSIQ[20]图像数据库进行仿真实验,并和已有的指标进行比较. LIVE2图像库包含29幅原始图像和779幅对应的失真图像,共有5种失真类型,其中JPEG2000失真(jpeg2k)175幅,JPEG失真(jpeg)169幅,白噪声失真(wn)145幅,高斯模糊失真(gblur)145幅以及快速瑞利衰减失真(fastfading)145幅. CSIQ图像库包含30幅原始图像和866幅对应的失真图像,共有6种失真类型,分别是加性高斯白噪声、加性高斯彩色噪声、JPEG失真、JPEG2000失真、高斯模糊和全局对比度退化.同时,LIVE2和CSIQ图像库都给出每幅失真图像相应的差分主观分值(DMOS),DMOS值越小表示失真图像的主观质量越好.
本文指标与7种具有代表性的全参考IQA指标进行性能比较,包括PSNR、SSIM[6]、IFC[21]、VIF[22]、FSIM[10]、IWSSIM[16]和GSM[11].其中,PSNR是峰值信噪比;IFC和VIF是基于信息保真度原则的评价指标;IWSSIM是采用信息内容加权的SSIM算法;FSIM和GSM是基于SSIM结构化方法构建的算法,其思想分别为结合相位一致相似性和梯度相似性,利用图像的梯度相似性和亮度相似性.
本文采用以下4种参数对IQA指标性能进行评价:均方根误差(RMSE)、Pearson相关系数(PLCC)、Spearman秩相关系数(SROCC)和Kendall秩相关系数(KROCC). RMSE和PLCC用于评估IQA指标的预测准确性,SROCC和KROCC用于评估IQA指标的预测单调性. RMSE值越小,SROCC、KROCC和PLCC值越接近于1,则表明客观评价结果越与主观感知一致.
为客观反映图像质量评价指标的性能,需对客观评价值Q和DMOS值进行非线性回归处理.本文采用5参数Logistic函数
| $ \begin{array}{l} f\left( Q \right) = {\beta _1} \cdot \left( {\frac{1}{2} - \frac{1}{{1 + \exp \left( {{\beta _2} \cdot \left( {Q - {\beta _3}} \right)} \right)}}} \right) + {\beta _4} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;Q + {\beta _5}, \end{array} $ | (19) |
式中βi(i=1, 2, …, 5)是拟合参数.
5.2 感知性能评价为验证本文指标的感知性能,图 6给出原始图像及其对应的不同类型的失真图像. 图 6(b)~(f)的DMOS值分别为25.743 2、28.869 1、48.072 7、52.573 9、58.507 7;SSIM值分别为0.958 5、0.963 7、0.815 1、0.541 4、0.679 2;FSIM值分别为0.976 9、0.981 5、0.926 7、0.867 4、0.836 4;本文指标评价值分别为0.961 5、0.945 0、0.792 3、0.680 3、0.655 6.不同指标的客观评价值应随DMOS的增大而减小.但只有本文指标的评价值的变化趋势与主观评价值一致.这说明本文指标可有效度量图像的失真量,且与视觉效果更一致.

|
图 6 测试图像及其失真图像 Figure 6 The test image and its distorted images |
为全面地评估IQA指标预测失真引起的图像质量变化的能力,计算本文指标在不同失真类型下的性能评价指标,并与其他7个最具代表性的IQA指标进行比较. 表 1列出了不同IQA指标在LIVE2数据库上不同失真类型的性能比较结果.对于每一个不同失真类型的性能评价指标,用粗体标出三个表现最好的指标.从表 1可看出,本文指标与VIF、FSIM指标性能相当,性能指标位于前三的次数分别为13次、10次和13次,优于其他IQA指标.与FSIM、VIF相比,本文指标更适合处理wn和fastfading失真,jpeg和gblur失真次之,而其他类型失真的性能指标只是略微低于表现最好的指标.此外,在不同类型失真情况下,本文指标具有更严格的预测单调性,其SROCC和KROCC值共有8次位于前三,多于其他IQA指标.
| 表 1 不同IQA指标对LIVE2数据库中不同失真类型的评价结果比较 Table 1 Comparison of IQA indices for each distortion type on LIVE2 database |
本文指标与不同IQA指标在LIVE2数据库上交叉失真实验的散点图如图 7所示,横轴是IQA指标预测的客观评价分,纵轴是DMOS值,图中曲线由式(19)非线性拟合得到.从图 7中可看出,与其他IQA指标相比,本文指标散点图中的点相对均匀地分布在拟合曲线两侧,且拟合结果更接近于线性.因此,本文指标预测的客观评价值与主观评价值更一致.
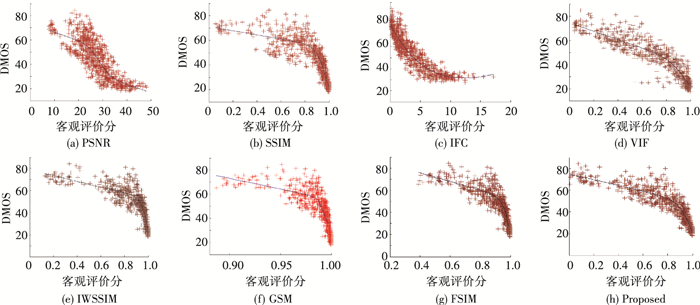
|
图 7 不同IQA指标在LIVE2数据库中的散点图 Figure 7 Scatter plot for different IQA indices on LIVE2 database |
不同IQA指标在LIVE2数据库上交叉失真的性能比较结果见表 2.对于每一个性能评价指标,用粗体标出三个表现最好的指标.本文指标RMSE为6.030 6,PLCC为0.9272, SROCC为0.924 5,KROCC为0.757 6.与相比较的IQA指标相比,其RMSE值最小,PLCC、SROCC和KROCC值最大.所以,本文指标在整体上性能优于其他IQA指标,具有更高的预测准确性和更严格的预测一致性,与人的主观感知更为一致.
| 表 2 不同IQA指标在LIVE2数据库中整体性能比较 Table 2 Performance comparison of different IQA indices on LIVE2 database |
不同指标在CSIQ数据库上的性能测试结果如表 3所示.对于每一个性能评价指标,仍然用粗体标出三个表现最好的指标.从表中可看出,本文指标在CSIQ数据库中依然具有很好的评价性能,其RMSE值最小,PLCC、SROCC和KROCC值最大.这些测试足以说明本文指标是有效的.
| 表 3 不同IQA指标在CSIQ数据库中整体性能比较 Table 3 Performance comparison of different IQA indices on CSIQ database |
为评价IQA指标的运行效率,在LIVE2数据库上运行每个被测试的IQA指标,通过多次运行,获得每幅图像客观评价指标计算所需时间的平均值.实验硬件平台是i3-3240CPU@3.40GHz和8G内存的台式机,所用软件为MATLAB R2014a,每幅图像的大小为632×505像素.从表 4可看出,本文指标的运行时间是0.126秒,处于所比较指标的中游.虽然运行时间长于SSIM,但远低于FSIM、IWSSIM等性能较好指标的运行时间.因此,本文提出的IQA指标获得了令人满意的运行效率.
| 表 4 不同IQA指标执行时间比较 Table 4 Comparisons of computation time |
本文提出了一种基于最小可辨失真和视觉显著性评价的图像质量评价指标.在该方案中,利用空间域JND模型与Sigmoid函数对失真图像进行修正.通过JND修正失真图像使其保留人眼可见失真,通过Sigmoid函数设计感知误差的惩罚系数,用于改进局部图像质量的度量.最后,利用视觉显著性模型提取图像中各子区域的权重,根据权重融合局部图像质量得到最终的图像质量评价结果.在LIVE2和CSIQ图像数据库上与其他最具代表性的IQA指标进行了比较.结果表明,本文所提指标与人的主观感知质量具有更好的一致性,运行效率较高.
| [1] |
GU Ke, ZHAI Guangtao, YANG Xiaokang, et al. Automatic contrast enhancement technology with saliency preservation[J].
IEEE Transactions on Circuits and Systems for Video Technology, 2015, 25(9): 1480-1494.
DOI: 10.1109/TCSVT.2014.2372392 |
| [2] |
TIAN Xin, LI Tao, TIAN Jinwen, et al. Prediction method for image coding quality based on differential information entropy[J].
Entropy, 2014, 16(2): 990-1001.
DOI: 10.3390/e16020990 |
| [3] |
KEDZIERSKI M, WIERZBICHI D. Radiometric quality assessment of images acquired by UAV's in various lighting and weather conditions[J].
Measurement, 2015, 76: 156-169.
DOI: 10.1016/j.measurement.2015.08.003 |
| [4] |
PAPAKOSTAS G A, TSOUGENIS E D, KOULOURIOTIS D E. Moment-based local image watermarking via genetic optimization[J].
Applied Mathematics and Computation, 2014, 227: 222-236.
DOI: 10.1016/j.amc.2013.11.036 |
| [5] |
ZIMBICO A, SCHNEIDER F, MAIA J. Comparative study of the performance of the JPEG algorithm using optimized quantization matrices for ultrasound image compression [C]// ISSNIP Biosignals and Biorobotics Conference. Piscataway NJ: IEEE, 2014: 89-94. DOI: 10.1109/BRC.2014.6880973.
|
| [6] |
WANG Zhou, BOVIK A C, SHEIKH H R, et al. Image quality assessment: from error visibility to structural similarity[J].
IEEE Transactions on Image Processing, 2004, 13(4): 600-612.
DOI: 10.1109/TIP.2003.819861 |
| [7] |
XUE Wufeng, ZHANG Lei, MOU Xuanqin, et al. Gradient magnitude similarity deviation: a highly efficient perceptual image quality index[J].
IEEE Transactions on Image Processing, 2014, 23(2): 684-695.
DOI: 10.1109/TIP.2013.2293423 |
| [8] |
CHEBBI E, BENZARTI F, AMIRI H. An improvement of structural similarity index for image quality assessment[J].
Journal of Computer Science, 2014, 10(2): 353-360.
DOI: 10.3844/jcssp.2014.353.360 |
| [9] |
WANG Zhengyou, LI Liying, WU Shuang, et al. A new image quality assessment algorithm based on ssim and multiple regressions[J].
International Journal of Signal Processing, Image Processing and Pattern Recognition, 2015, 8(11): 221-230.
DOI: 10.14257/ijsip.2015.8.11.20 |
| [10] |
ZHANG Lin, ZHANG Lei, MOU Xuanqin, et al. FSIM: A feature similarity index for image quality assessment[J].
IEEE Transactions on Image Processing, 201l, 20(8): 2378-2386.
DOI: 10.1109/TIP.2011.2109730 |
| [11] |
LIU Anmin, LIN Weisi, NARWARIA M. Image quality assessment based on gradient similarity[J].
IEEE Transactions on Image Processing, 2012, 21(4): 1500-1512.
DOI: 10.1109/TIP.2011.2175935 |
| [12] |
LI Qiaohong, FANG Yuming, LIN Weisi, et al. Gradient-weighted structural similarity for image quality assessments [C]// IEEE International Symposium on Circuits and Systems. Piscataway NJ: IEEE, 2015: 2165-2168. DOI: 10.1109/ISCAS.2015.7169109.
|
| [13] |
WU Jinjian, LIN Weisi, SHI Guangming, et al. Perceptual quality metric with internal generative mechanism[J].
IEEE Transactions on Image Processing, 2013, 22(1): 43-54.
DOI: 10.1109/TIP.2012.2214048 |
| [14] |
FEI Xuan, XIAO Liang, SUN Yubao, et al. Perceptual image quality assessment based on structural similarity and visual masking[J].
Signal Processing-Image Communication, 2012, 27(7): 772-783.
DOI: 10.1016/j.image.2012.04.005 |
| [15] |
LEE D, LIM S. Improved structural similarity metric for the visible quality measurement of images[J].
Journal of Electronic Imaging, 2016, 25(6): 063015.
DOI: 10.1117/1.JEI.25.6.063015 |
| [16] |
WANG Zhou, LI Qiang. Information content weighting for perceptual image quality assessment[J].
IEEE Transactions on Image Processing, 2011, 20(5): 1185-1198.
DOI: 10.1109/TIP.2010.2092435 |
| [17] |
YANG Xiaokang, LIN Weisi, LU Z, et al. Motion-compensated residue preprocessing in video coding based on just-noticeable-distortion profile[J].
IEEE Transactions on Circuits and Systems for Video Technology, 2005, 15(6): 742-752.
DOI: 10.1109/TCSVT.2005.848315 |
| [18] |
GUO Chenlei, MA Qi, ZHANG Liming. Spatio-temporal saliency detection using phase spectrum of quaternion fourier transform [C]// Proceedings-IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Piscataway NJ: IEEE, 2008: 2908-2915. DOI: 10.1109/CVPR.2008.4587715.
|
| [19] |
SHEIKH H R, WANG Zhou, CORMACK L, et al. LIVE image quality assessment database release 2 [EB/OL]. [2006-11] http://live.ece.utexas.edu/research/quality/subjective.htm.
|
| [20] |
LARSON E C, CHANDLER D M. Categorical Image Quality (CSIQ) database 2009 [EB/OL]. [2009-12-14]http://vision.eng.shizuoka.ac.jp/course/view.php?id=6.
|
| [21] |
SHEIKH H R, BOVIK A C, VECIANA G D. An information fidelity criterion for image quality assessment using natural scene statistics[J].
IEEE Transactions on Image Processing, 2005, 14(12): 2117-2128.
DOI: 10.1109/TIP.2005.859389 |
| [22] |
SHEIKH H R, BOVIK A C. Image information and visual quality[J].
IEEE Transactions on Image Processing, 2006, 15(2): 430-444.
DOI: 10.1109/TIP.2005.859378 |
 2018, Vol. 50
2018, Vol. 50


