2. 同济大学 土木工程学院,上海 200092
2. College of Civil Engineering, Tongji University, Shanghai 200092, China
材料(或介质)的导热系数是其最为关键的热物理特性参数之一,高效地测量各种材料的导热系数具有较重要的实际工程意义.
很多情况下,较多工程材料,比如木材和层积岩土材料具有横观各向同性特性.明确横观各向同性材料在横观同性平面内导热系数与平面外的差异,可为进一步探究这些材料的热物理特性奠定重要基础.对于横观各向同性材料平面内及平面外导热系数的量测,较为常用的方法是稳态热板法(GHP法)[1-3].该方法通过对试样施加热流,在材料内部产生稳态的温度分布,并在假定热流满足傅里叶定律的基础上,通过热流与温度梯度的关系反算导热系数.作为稳态法,该方法完成一次单一测试所需的时间较长,对于待测试样较多的情形还是具有一定的局限性.
热线法,也称瞬态线热源法,是一种利用瞬态温度场反演材料导热系数的方法.该方法无需等待材料中的温度分布达到稳态即可测得导热系数,因此,该法十分快速高效.利用热线法测量材料导热系数主要借助热探针型热特性分析仪(以下简称为“热探针仪”)来实现.热探针仪的基本原理是:首先将一根笔直细长的钢制热探针插入试样中,随即对试样释放一稳定的线分布热功率,这样热探针及试样内的平均温度都会升高,而且热探针内部平均温度升高的速率是和介质的导热系数存在一定的反相关关系;基于这种关系,通过分析热探针内部平均温度随时间的变化规律,可反算所测介质的导热系数.利用热探针仪可以迅速测得各种材料的导热系数,包括流体、固体以及粉末颗粒状材料[4-8],非常简便快捷.然而,目前热线法仅限于量测各向同性材料的导热系数,对于各向异性材料,也是将该材料等效成各向同性来看待.因此,对热线法进行拓展,使之能够量测横观各向同性材料导热系数的工作具有很大的实用价值.
本文拟基于横观各向同性介质中的热传导理论,借助现有商业热探针仪,将热线法的使用范围拓展到了横观各向同性材料,提出了一种测量横观各向同性材料导热系数的快捷方法,将该方法用于测量自制横观各向同性材料的导热系数,并与稳态热板法试验结果比对,验证本文方法的可靠性.
1 方法的建立以横观各向同性介质中的热传导理论作为基础,对热线法进行功能拓展,建立一种能够利用热线法量测横观各向同性材料导热系数的新方法.为了方便表述,文中将把拟建新方法称为“拓展热线法”.拓展热线法需要对一个立方体试样进行2次独立的测量,一次直接测量横观平面内的导热系数,另一次测量的是一个名义导热系数,再利用后文推导得到的转换公式将此名义导热系数转换成真正的平面外导热系数.转换公式的推导构成了本文的核心工作.
1.1 热线法原理建立拓展热线法的工作与热线法的原理具有较为密切的联系.
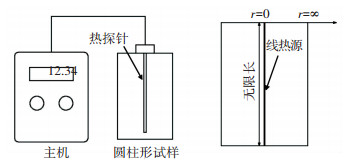
图 1所示的是热线法测量导热系数的原理示意图,如图 1(a)所示,热探针仪主机、热探针及圆柱形试样组成量测的实际系统;图 1(b)所示线热源与圆柱形计算域为对应于实际系统的理想模型.理想模型需符合以下假定:该圆柱形计算域在径向与轴向均为无限大,线热源与圆柱域的轴线重合且为无限长;该圆柱域由连续、匀质、各向同性的固体介质所组成;介质的导热系数、密度、比热容都与温度无关;介质中的热流密度服从傅里叶定律;介质拥有均匀分布的初始温度.
|
图 1 热线法原理示意 Figure 1 Schematic diagrams of transient line heat source method |
显然,实际系统应与理想模型保持足够的接近度,因此对于实际系统须满足以下限制条件:圆柱形试样,其轴向尺寸应能包含整根热探针,探针与试样间要保证充分接触,使用绝热试样筒以防止试样侧面的热量损失; 当探针半径、试样半径及加热时间给定时,试样热扩散系数的数量级应能分别满足式(3)、(16)的要求;所测材料具有较好的连续性、匀质性和各向同性,且导热系数、密度和比热容在热探针工作温度范围内变化较小.
假设理想模型介质的导热系数、密度、比热容分别为k、ρ、c,热线源释放出稳定的线分布热功率q,介质中的初始温度为T0,则任意时刻t,距离热线源r处的温度T(r, t)可表示为[9]
| $ T\left( {r,t} \right) = {T_0} + \frac{q}{{4{\rm{ \mathsf{ π} }}k}}\left[ { - {\rm{Ei}}\left( { - \frac{{{r^2}}}{{4Dt}}} \right)} \right]. $ | (1) |
其中,D=k/(ρc)为介质的热扩散系数,Ei(·)为指数积分函数.如果热探针半径应为半径为r0将r=r0代入式(1),即可得到热探针表面平均温度TTCP(t)
| $ {T_{{\rm{TCP}}}}\left( t \right) = {T_0} + \frac{q}{{4{\rm{ \mathsf{ π} }}k}}\left[ { - {\rm{Ei}}\left( { - \frac{{r_0^2}}{{4Dt}}} \right)} \right]. $ | (2) |
假设热探针在试样中的加热持时为th,考虑一个界限时间tB,一般可取th/3 ~ th/2.如有:
| $ \frac{{r_0^2}}{{4D{t_{\rm{B}}}}} \ll 1. $ | (3) |
则对于t≥tB,式(2)中Ei[-r02/(4Dt)]可近似展开为
| $ {\rm{Ei}}\left( { - \frac{{r_0^2}}{{4Dt}}} \right) = \gamma + \ln \left( {\frac{{r_0^2}}{{4D}}} \right) - \ln t. $ | (4) |
其中,γ为欧拉常数.将式(4)代入式(2)中,可得TTCP(t)的近似表达式:
| $ {T_{{\rm{TCP}}}}\left( t \right) = \left[ {{T_0} - \frac{{\gamma q}}{{4{\rm{ \mathsf{ π} }}k}} - \frac{q}{{4{\rm{ \mathsf{ π} }}k}}\ln \left( {\frac{{r_0^2}}{{4D}}} \right)} \right] + \frac{q}{{4{\rm{ \mathsf{ π} }}k}}\ln t, $ | (5) |
式(5)简洁形式可写为
| $ {T_{{\rm{TCP}}}}\left( t \right) = \varphi + \lambda \ln t. $ | (6) |
其中:
| $ \left\{ \begin{array}{l} \varphi = {T_0} - \frac{{\gamma q}}{{4{\rm{ \mathsf{ π} }}k}} - \frac{q}{{4{\rm{ \mathsf{ π} }}k}}\ln \left( {\frac{{r_0^2}}{{4D}}} \right),\\ \lambda = \frac{q}{{4{\rm{ \mathsf{ π} }}k}}. \end{array} \right. $ | (7) |
如图 2所示,在T-ln t(温度-对数时间)坐标平面内,两条关系曲线分别描述了热探针加热过程中实际与理论的升温规律.式(6)是描述理论升温曲线的近似表达式. 图 2中的理论升温曲线上方是实际升温曲线.实际升温曲线在一个时间段内(tⅠ<t<tⅡ)会呈现较好的线性关系,线性段斜率可通过拟合这段时间内的T-ln t数据点求得.假设有n个这样的有效数据点:(ln t1, T1), (ln t2, T2), …, (ln tn, Tn),则线性段斜率m可通过最小二乘法求取:
| $ m = \frac{{\left( {\sum\limits_{i = 1}^n {{T_i}\ln {t_i}} } \right) - n\left( {\frac{1}{n}\sum\limits_{i = 1}^n {{T_i}} } \right)\left( {\frac{1}{n}\sum\limits_{i = 1}^n {\ln {t_i}} } \right)}}{{\left[ {\sum\limits_{i = 1}^n {{{\left( {\ln {t_i}} \right)}^2}} } \right] - n{{\left( {\frac{1}{n}\sum\limits_{i = 1}^n {\ln {t_i}} } \right)}^2}}}. $ | (8) |

|
图 2 加热过程中实际与理论T-lnt关系示意 Figure 2 Actual and theoretical T-lnt relationship diagrams during heating process |
理论曲线的线性段斜率λ与实际曲线的线性段斜率m.从物理本质上讲,这两个斜率反映的都是热探针中热量集散的快慢程度.在其他条件不变的情况下,这种热量集散的快慢取决于介质导热系数的大小,介质导热系数越大,热量越容易散发,探针中温度升高得越慢,对应T-ln t图像上的直观反映就是斜率越小.对于同一介质,λ与m描述的是同一个热量集散的快慢程度,所以这两者应该相等.故有
| $ \lambda = m, $ | (9) |
即
| $ \frac{q}{{4{\rm{ \mathsf{ π} }}k}} = \frac{{\left( {\sum\limits_{i = 1}^n {{T_i}\ln {t_i}} } \right) - n\left( {\frac{1}{n}\sum\limits_{i = 1}^n {{T_i}} } \right)\left( {\frac{1}{n}\sum\limits_{i = 1}^n {\ln {t_i}} } \right)}}{{\left[ {\sum\limits_{i = 1}^n {{{\left( {\ln {t_i}} \right)}^2}} } \right] - n{{\left( {\frac{1}{n}\sum\limits_{i = 1}^n {\ln {t_i}} } \right)}^2}}}. $ | (10) |
由式(10)可求得导热系数k为
| $ k = \frac{q}{{4{\rm{ \mathsf{ π} }}}}\frac{{\left[ {\sum\limits_{i = 1}^n {{{\left( {\ln {t_i}} \right)}^2}} } \right] - n{{\left( {\frac{1}{n}\sum\limits_{i = 1}^n {\ln {t_i}} } \right)}^2}}}{{\left( {\sum\limits_{i = 1}^n {{T_i}\ln {t_i}} } \right) - n\left( {\frac{1}{n}\sum\limits_{i = 1}^n {{T_i}} } \right)\left( {\frac{1}{n}\sum\limits_{i = 1}^n {\ln {t_i}} } \right)}}. $ | (11) |
式(11)等号右边的计算结果正是一般商用热探针仪在主机屏幕上所输出的导热系数读数.
为了使实际系统能较好满足前述假定中“无限域”的条件,从试样侧面释放出的线分布热功率qB与q相比要足够小[10].假设试样的半径为rs,考虑使用了绝热试样筒,通过对式(1)应用傅里叶定律,可得到试样侧面与试样筒内壁交界面处的径向热流密度:
| $ \begin{array}{l} {I_r}\left( {r,t} \right)\left| {_{r = {r_{\rm{s}}}}} \right. = - k\frac{\partial }{{\partial r}}\left[ {{T_0} + \frac{q}{{4{\rm{ \mathsf{ π} }}k}}\left( { - {\rm{Ei}}\left( { - \frac{{{r^2}}}{{4Dt}}} \right)} \right)} \right]\left| {_{r = {r_{\rm{s}}}}} \right. = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{q}{{2{\rm{ \mathsf{ π} }}r}}\exp \left( { - \frac{{{r^2}}}{{4Dt}}} \right)\left| {_{r = {r_{\rm{s}}}}} \right. = \frac{q}{{2{\rm{ \mathsf{ π} }}{r_{\rm{s}}}}}\exp \left( { - \frac{{r_{\rm{s}}^2}}{{4Dt}}} \right). \end{array} $ | (12) |
式中Ir(r, t)代表任意径向距离r和任意时间t所对应的径向热流密度.将式(12)乘以试样侧面的圆周周长2πrs,即可得到qB:
| $ {q_{\rm{B}}} = q\exp \left( { - \frac{{r_{\rm{s}}^2}}{{4Dt}}} \right). $ | (13) |
将t=th代入式(13),便得到加热过程中qB的最大值(qB)max:
| $ {\left( {{q_{\rm{B}}}} \right)_{\max }} = q\exp \left( { - \frac{{r_{\rm{s}}^2}}{{4D{t_{\rm{h}}}}}} \right). $ | (14) |
显然,(qB)max与q的比值应足够小,即
| $ {\left( {{q_{\rm{B}}}} \right)_{\max }}/q \ll 1. $ | (15) |
将式(14)代入式(15),可得
| $ \exp \left( { - \frac{{r_{\rm{s}}^2}}{{4D{t_{\rm{h}}}}}} \right) \ll 1. $ | (16) |
式(3)、(16)即为当r0、rs及th都给定时,试样热扩散系数D的数量级须满足的限制要求.
1.2 拓展热线法利用热线法测各向同性材料导热系数,其实质是通过1次独立的测量从而反演出1个待测参数(即导热系数k).而横观各向同性材料有平面内导热系数和平面外导热系数2个待测参数,因此对于横观各向同性材料,1次独立的测量是不够的.
将横观各向同性材料平面内导热系数称作横向导热系数,记作KT;把平面外导热系数称作纵向导热系数,记作KL.为了能使热探针在KL方向以及任意一个KT方向上各实施一次独立的测量,可采用立方体试样,且试样的三组平行对面分别与KL方向以及两个KT方向垂直.热探针可分别沿着KL方向以及任意一个KT方向从试样表面的中央处垂直插入试样中,由此实现2次独立的测量.
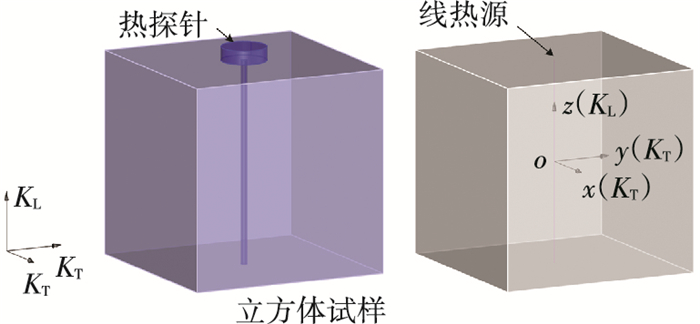
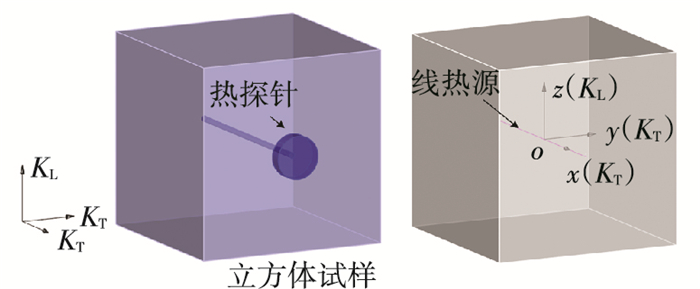
图 3及图 4为热探针分别沿KL方向以及任意一个KT方向插入立方体试样中完成测量的示意图. 图 3(a)和图 4(a)分别为两种测量工况下实际量测系统,图 3(b)和图 4(b)则为对应的理想模型.在图 3(b)和图 4(b)中,试样被抽象成一个立方体形状的计算域,由一种连续、匀质且横观各向同性的介质组成,该介质有两个相同的横向导热系数KT以及一个纵向导热系数KL;立方体区域的三组平行对面分别与两个KT方向和KL方向垂直;在立方体区域的中心处建立空间直角坐标系,坐标系的原点与中心重合,x轴及y轴分别与两个KT方向平行,z轴与KL方向平行;热探针被抽象成一个线热源,沿z轴或x轴贯穿计算域.
|
图 3 KL方向测量原理示意 Figure 3 Schematic diagrams for KL direction measurement |
|
图 4 KT方向测量原理示意 Figure 4 Schematic diagrams for KT direction measurement |
为确保理想模型对实际量测系统的模拟效果,图 3(a)和图 4(a)的实际系统,应满足以下限制条件:试样须制成棱长恰好等于所用热探针长度的立方体,探针与试样间要保证充分接触,当热探针半径、试样棱长、探针加热持时给定时,试样横向及纵向热扩散系数中的较小值和较大值的数量级,应满足后文中式(29)和(43)所给出的限制要求;所测材料具有较好的连续性、匀质性和横观各向同性,横向和纵向导热系数、密度、比热容在热探针的工作温度范围内变化较小;横向和纵向导热系数的比值不宜过小或过大,如KT:KL =1:20或100:3等.
假设介质的密度、比热容分别为ρ、c,热线源释放出稳定的线分布热功率q,介质初始温度为T0,介质中温度场的数学描述可分为两种情形,即KL方向测量情形如式(17),KT方向测量情形如式(18)[11]
| $ \left\{ \begin{array}{l} \left( {{K_{\rm{T}}}\frac{{{\partial ^2}}}{{\partial {x^2}}} + {K_{\rm{T}}}\frac{{{\partial ^2}}}{{\partial {y^2}}} + {K_{\rm{L}}}\frac{{{\partial ^2}}}{{\partial {z^2}}}} \right)T\left( {x,y,z,t} \right) + \\ \;\;\;q{\rm{ \mathsf{ δ} }}\left( x \right){\rm{ \mathsf{ δ} }}\left( y \right) = \rho c\frac{\partial }{{\partial t}}T\left( {x,y,z,t} \right);\\ t > 0,\left\{ \begin{array}{l} x = \mathop {\lim }\limits_{a \to + \infty } \left( { \pm a} \right),\frac{{\partial T}}{{\partial x}} = 0;\\ y = \mathop {\lim }\limits_{a \to + \infty } \left( { \pm a} \right),\frac{{\partial T}}{{\partial y}} = 0;\\ z = \mathop {\lim }\limits_{a \to + \infty } \left( { \pm a} \right),\frac{{\partial T}}{{\partial z}} = 0; \end{array} \right.\\ t = 0,T\left( {x,y,z,t} \right) = {T_0}. \end{array} \right. $ | (17) |
| $ \left\{ \begin{array}{l} \left( {{K_{\rm{T}}}\frac{{{\partial ^2}}}{{\partial {x^2}}} + {K_{\rm{T}}}\frac{{{\partial ^2}}}{{\partial {y^2}}} + {K_{\rm{L}}}\frac{{{\partial ^2}}}{{\partial {z^2}}}} \right)T\left( {x,y,z,t} \right) + \\ q{\rm{ \mathsf{ δ} }}\left( y \right){\rm{ \mathsf{ δ} }}\left( z \right) = \rho c\frac{\partial }{{\partial t}}T\left( {x,y,z,t} \right);\\ t > 0,\left\{ \begin{array}{l} x = \mathop {\lim }\limits_{a \to + \infty } \left( { \pm a} \right),\frac{{\partial T}}{{\partial x}} = 0;\\ y = \mathop {\lim }\limits_{a \to + \infty } \left( { \pm a} \right),\frac{{\partial T}}{{\partial y}} = 0;\\ z = \mathop {\lim }\limits_{a \to + \infty } \left( { \pm a} \right),\frac{{\partial T}}{{\partial z}} = 0; \end{array} \right.\\ t = 0,T\left( {x,y,z,t} \right) = {T_0}. \end{array} \right. $ | (18) |
式中:(x, y, z)为空间坐标;t为时间坐标;T(x, y, z, t)表示温度场;δ(·)为Dirac函数;a为所设的一个正变量.利用Green函数法可求得上述两式所描述的热传导边值问题的解析解[11].
边值问题式(17)的解
| $ T\left( {x,y,t} \right) = {T_0} + \frac{q}{{4{\rm{ \mathsf{ π} }}{K_{\rm{T}}}}}\left\{ { - {\rm{Ei}}\left[ { - \frac{1}{{4{D_{\rm{T}}}t}}\left( {{x^2} + {y^2}} \right)} \right]} \right\}. $ | (19) |
边值问题式(18)的解
| $ T\left( {y,z,t} \right) = {T_0} + \frac{q}{{4{\rm{ \mathsf{ π} }}\sqrt {{K_{\rm{T}}}{K_{\rm{L}}}} }}\left\{ { - {\rm{Ei}}\left[ { - \frac{1}{{4t}}\left( {\frac{{{y^2}}}{{{D_{\rm{T}}}}} + \frac{{{z^2}}}{{{D_{\rm{T}}}}}} \right)} \right]} \right\}. $ | (20) |
式中DT=KT/ρc与DL=KL/ρc分别为试样横向及纵向热扩散系数.由式(19)可看出,当热探针沿着z轴即KL方向插入试样进行测量时,试样中的热扩散近似是二维各向同性的,任意瞬时的等温线为一簇同心圆.若进一步将式(19)中“x2+y2”换成“r2”,不难发现,其形式与式(1)完全相同.所以当热探针沿着KL方向插入试样所得到的读数即是KT值.而当热探针沿着x轴即KT方向插入试样中进行测量时,由式(20)可见,试样中的热扩散则近似二维各向异性的,任意瞬时的等温线为一簇比例椭圆;热探针仪屏幕上显示的仅是一个名义读数,依据该读数并不能直接获取KL或KT的值.将在KT方向测量获取的名义读数记作KN.
以下基于式(20),探究KL、KT及KN三者之间的关系.由前文可知,热探针仪要获取最终读数,首先要明确加热过程中探针表面平均温度随时间的变化规律,即TTCP(t).为了区别于前文情形,这里将KT方向测量过程中热探针表面平均温度的时程函数记作TA(t).显然,TA(t)可通过将式(20)代入以下曲线积分计算求得:
| $ {T_{\rm{A}}}\left( t \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}{r_0}}}\oint\limits_{{y^2} + {z^2} = r_0^2} {T\left( {y,z,t} \right){\rm{d}}s} . $ | (21) |
此积分在直角坐标下很难计算,可考虑转换为极坐标.在图 4(b)中的yoz平面内建立r-θ极坐标系,其中r为极径,θ为极角,并且使“θ=0”轴与y轴正半轴重合,规定由y轴转向z轴的方向为θ正方向.由此,圆周y2+z2 =r02上的点可表示为
| $ \left\{ \begin{array}{l} y = {r_0}\cos \theta ;\\ z = {r_0}\sin \theta . \end{array} \right. $ | (22) |
将式(22)代入式(20)可得到KT方向测量情形下热探针表面温度分布的极坐标形式:
| $ \begin{array}{l} T\left( {r,\theta ,t} \right)\left| {_{r = {r_{\rm{0}}}}} \right. = {T_0} + \\ \frac{q}{{4{\rm{ \mathsf{ π} }}\sqrt {{K_{\rm{T}}}{K_{\rm{L}}}} }}\left\{ { - {\rm{Ei}}\left[ { - \frac{{r_0^2}}{{4t}}\left( {\frac{{{{\cos }^2}\theta }}{{{D_{\rm{T}}}}} + \frac{{{{\sin }^2}\theta }}{{{D_{\rm{L}}}}}} \right)} \right]} \right\}. \end{array} $ | (23) |
由式(23),式(21)可表示为
| $ {T_{\rm{A}}}\left( t \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_0^{2{\rm{ \mathsf{ π} }}} {T\left( {r,\theta ,t} \right)\left| {_{r = {r_{\rm{0}}}}} \right.{\rm{d}}\theta } . $ | (24) |
考虑到热探针表面温度分布的对称性,式(24)可进一步简化为
| $ {T_{\rm{A}}}\left( t \right) = \frac{2}{{\rm{ \mathsf{ π} }}}\int_0^{\frac{{\rm{ \mathsf{ π} }}}{2}} {T\left( {r,\theta ,t} \right)\left| {_{r = {r_{\rm{0}}}}} \right.{\rm{d}}\theta } . $ | (25) |
将式(23)代入式(25)得:
| $ \begin{array}{l} {T_{\rm{A}}}\left( t \right) = {T_0} - \frac{q}{{4{\rm{ \mathsf{ π} }}\left( {{K_{\rm{T}}}{K_{\rm{L}}}} \right)}} \cdot \\ \;\;\;\;\;\;\;\frac{2}{{\rm{ \mathsf{ π} }}}\int_0^{\frac{{\rm{ \mathsf{ π} }}}{2}} {{\rm{Ei}}\left[ { - \frac{{r_0^2}}{{4t}}\left( {\frac{{{{\cos }^2}\theta }}{{{D_{\rm{T}}}}} + \frac{{{{\sin }^2}\theta }}{{{D_{\rm{L}}}}}} \right)} \right]{\rm{d}}\theta } . \end{array} $ | (26) |
式(26)中与θ相关的积分项并不容易计算,故考虑对其中的指数积分函数进行近似展开,根据文献[9],展开的前提条件为
| $ \frac{{r_0^2}}{{4t}}\left( {\frac{{{{\cos }^2}\theta }}{{{D_{\rm{T}}}}} + \frac{{{{\sin }^2}\theta }}{{{D_{\rm{L}}}}}} \right) \ll 1. $ | (27) |
对于任意t>0,式(27)所示的是一个与θ相关的关于求解DT和DL取值范围的二元不等式,不便求解.式(27)左边与θ相关的表达式最大值为r02/(4min(DT, DL)t),在两次独立测量过程中,t都考虑取为界限时间tB,即th/3 ~ th/2.若存在
| $ \frac{{r_0^2}}{{4\min \left( {{D_{\rm{T}}},{D_{\rm{L}}}} \right){t_{\rm{B}}}}} \ll 1. $ | (28) |
则对于t≥tB,式(27)总能成立.可将式(28)写成
| $ \frac{{r_0^2}}{{4{D_{\min }}{t_{\rm{B}}}}} \le {\xi _1} \ll 1. $ | (29) |
式中:Dmin= min(DT, DL),ξ1为一精度参数,一般取值范围为(0, 10-2],考虑到本文提出的测量方法是一种快捷方法,且式(29)本身偏保守,建议可将ξ1的取值范围适当放松到(0, 10-1].式(29)可作为前述的限制要求,即当热探针半径且两次独立测量共同的加热持时给定时,试样横向及纵向热扩散系数中的较小值的数量级应满足的限制要求.当满足式(29)条件时,式(26)中的指数积分函数可近似展开为
| $ \begin{array}{l} {\rm{Ei}}\left[ { - \frac{{r_0^2}}{{4t}}\left( {\frac{{{{\cos }^2}\theta }}{{{D_{\rm{T}}}}} + \frac{{{{\sin }^2}\theta }}{{{D_{\rm{L}}}}}} \right)} \right] = \gamma + \\ \;\;\;\;\;\;\;\;\;\;\;\ln \left[ {\frac{{r_0^2}}{{4t}}\left( {\frac{{{{\cos }^2}\theta }}{{{D_{\rm{T}}}}} + \frac{{{{\sin }^2}\theta }}{{{D_{\rm{L}}}}}} \right)} \right] - \ln t. \end{array} $ | (30) |
将式(30)代入式(26)可得:
| $ \begin{array}{l} {T_{\rm{A}}}\left( t \right) = \left\{ {{T_0} - \frac{{\gamma q}}{{4{\rm{ \mathsf{ π} }}\sqrt {{K_{\rm{T}}}{K_{\rm{L}}}} }} - \frac{q}{{4{\rm{ \mathsf{ π} }}\sqrt {{K_{\rm{T}}}{K_{\rm{L}}}} }} \cdot } \right.\\ \;\;\;\;\;\;\left. {\frac{2}{{\rm{ \mathsf{ π} }}}\int_0^{\frac{{\rm{ \mathsf{ π} }}}{2}} {{\rm{ln}}\left[ {\frac{{r_0^2}}{4}\left( {\frac{{{{\cos }^2}\theta }}{{{D_{\rm{T}}}}} + \frac{{{{\sin }^2}\theta }}{{{D_{\rm{L}}}}}} \right)} \right]{\rm{d}}\theta } } \right\} + \\ \;\;\;\;\;\;\frac{q}{{4{\rm{ \mathsf{ π} }}\sqrt {{K_{\rm{T}}}{K_{\rm{L}}}} }}\ln t. \end{array} $ | (31) |
式(31)中与θ相关的积分项虽仍难以计算,但此积分项的结果必然为一个实常数.由此,可将式(31)写成
| $ {T_{\rm{A}}}\left( t \right) = \mathit{\Phi } + \mathit{\Lambda }\ln t. $ | (32) |
实常数Φ、Λ分别为
| $ \left\{ \begin{array}{l} \mathit{\Phi } = {T_0} - \frac{{\gamma q}}{{4{\rm{ \mathsf{ π} }}\sqrt {{K_{\rm{T}}}{K_{\rm{L}}}} }} - \frac{q}{{4{\rm{ \mathsf{ π} }}\sqrt {{K_{\rm{T}}}{K_{\rm{L}}}} }} \cdot \\ \;\;\;\;\;\;\frac{2}{{\rm{ \mathsf{ π} }}}\int_0^{\frac{{\rm{ \mathsf{ π} }}}{2}} {{\rm{ln}}\left[ {\frac{{r_0^2}}{4}\left( {\frac{{{{\cos }^2}\theta }}{{{D_{\rm{T}}}}} + \frac{{{{\sin }^2}\theta }}{{{D_{\rm{L}}}}}} \right)} \right]{\rm{d}}\theta } ,\\ \mathit{\Lambda = }\frac{q}{{4{\rm{ \mathsf{ π} }}\sqrt {{K_{\rm{T}}}{K_{\rm{L}}}} }}. \end{array} \right. $ | (33) |
显然,式(32)可作为描述KT方向测量情形下,图 2中所示的热探针理论升温曲线的近似表达式.如果在热探针加热过程中,有n个有效的T-ln t数据点:(ln t1, T1), (ln t2, T2), …, (ln tn, Tn),则图 2中所示的热探针实际升温曲线线性段的斜率M可通过最小二乘法求取
| $ M = \frac{{\left( {\sum\limits_{i = 1}^n {{T_i}\ln {t_i}} } \right) - n\left( {\frac{1}{n}\sum\limits_{i = 1}^n {{T_i}} } \right)\left( {\frac{1}{n}\sum\limits_{i = 1}^n {\ln {t_i}} } \right)}}{{\left[ {\sum\limits_{i = 1}^n {{{\left( {\ln {t_i}} \right)}^2}} } \right] - n{{\left( {\frac{1}{n}\sum\limits_{i = 1}^n {\ln {t_i}} } \right)}^2}}}. $ | (34) |
如前述,Λ与M这两个斜率应该相同
| $ \mathit{\Lambda } = M, $ | (35) |
| $ \frac{q}{{4{\rm{ \mathsf{ π} }}\sqrt {{K_{\rm{T}}}{K_{\rm{L}}}} }} = \frac{{\left( {\sum\limits_{i = 1}^n {{T_i}\ln {t_i}} } \right) - n\left( {\frac{1}{n}\sum\limits_{i = 1}^n {{T_i}} } \right)\left( {\frac{1}{n}\sum\limits_{i = 1}^n {\ln {t_i}} } \right)}}{{\left[ {\sum\limits_{i = 1}^n {{{\left( {\ln {t_i}} \right)}^2}} } \right] - n{{\left( {\frac{1}{n}\sum\limits_{i = 1}^n {\ln {t_i}} } \right)}^2}}}. $ | (36) |
式(36)可改写成
| $ \sqrt {{K_{\rm{T}}}{K_{\rm{L}}}} = \frac{q}{{4{\rm{ \mathsf{ π} }}}}\frac{{\left[ {\sum\limits_{i = 1}^n {{{\left( {\ln {t_i}} \right)}^2}} } \right] - n{{\left( {\frac{1}{n}\sum\limits_{i = 1}^n {\ln {t_i}} } \right)}^2}}}{{\left( {\sum\limits_{i = 1}^n {{T_i}\ln {t_i}} } \right) - n\left( {\frac{1}{n}\sum\limits_{i = 1}^n {{T_i}} } \right)\left( {\frac{1}{n}\sum\limits_{i = 1}^n {\ln {t_i}} } \right)}}. $ | (37) |
显然,名义读数KN为
| $ {K_{\rm{N}}} = \frac{q}{{4{\rm{ \mathsf{ π} }}}}\frac{{\left[ {\sum\limits_{i = 1}^n {{{\left( {\ln {t_i}} \right)}^2}} } \right] - n{{\left( {\frac{1}{n}\sum\limits_{i = 1}^n {\ln {t_i}} } \right)}^2}}}{{\left( {\sum\limits_{i = 1}^n {{T_i}\ln {t_i}} } \right) - n\left( {\frac{1}{n}\sum\limits_{i = 1}^n {{T_i}} } \right)\left( {\frac{1}{n}\sum\limits_{i = 1}^n {\ln {t_i}} } \right)}}. $ | (38) |
由式(37)及式(38)可得
| $ \sqrt {{K_{\rm{T}}}{K_{\rm{L}}}} = {K_{\rm{N}}}, $ | (39) |
| $ {K_{\rm{L}}} = \frac{{K_{\rm{N}}^2}}{{{K_{\rm{T}}}}}. $ | (40) |
式(40)即为在已知KT及KN的基础上,计算KL的公式.至此,通过在立方体试样上进行两次独立的测量,一次直接读取KT,另一次获取KN,再利用式(40),最终可以确定横观各向同性材料横向与纵向导热系数.
下面有必要考察KT方向测量情形下,在如图 4(a)所示的实际探针-试样系统中,对于“无限域”假定条件的接近程度.该情形要比前文各向同性材料所制成的圆柱形试样中更为复杂,主要因为:首先,试样中温度场的等势线不再是同心圆而是比例椭圆;再者,侧边为方形边界且直接裸露在环境中.要想在这样复杂条件下,用解析方法计算试样方形侧边所释放出的线分布热功率是较为困难的.所以还是需要对问题进行一定的简化,即假设:试样中的热扩散行为是以Dmax= max(DT, DL)的各向同性热扩散;设立方体试样棱长和热探针长度为l,以热探针为轴线,取一个半径为βl的圆柱面,其中β为一个小于却接近0.5的正参数,β值可取0.45.圆柱面上的线分布热功率qB,可通过与前文各向同性情形中相同的过程计算求得:
| $ {q_{\rm{B}}} = q\exp \left[ { - \frac{{{{\left( {\beta l} \right)}^2}}}{{4{D_{\max }}t}}} \right]. $ | (41) |
将两次独立测量中相同的加热持时th代入式(41)中,即可得到KT方向测量的加热过程中qB的最大值,(qB)max:
| $ {\left( {{q_{\rm{B}}}} \right)_{\max }} = q\exp \left[ { - \frac{{{{\left( {\beta l} \right)}^2}}}{{4{D_{\max }}{t_{\rm{h}}}}}} \right]. $ | (42) |
(qB)max与q值之间的比值应足够小,故有
| $ \exp \left[ { - \frac{{{{\left( {\beta l} \right)}^2}}}{{4{D_{\max }}{t_{\rm{h}}}}}} \right] \le {\xi _2} \ll 1. $ | (43) |
式中ξ2为一精度参数,一般取值范围为(0, 10-2].式(43)可作为前文的限制条件,即当试样的棱长(热探针长度)及两次独立测量的加热持时给定时,试样横向和纵向热扩散系数中的较大值的数量级应满足的限制要求.显然,式(29)和(43)对于Dmin和Dmax的限制要求是偏于保守的,但如果所测材料的横向、纵向导热系数之间的比值不是过大或过小,这种保守限制要求是可以接受的.
1.3 拓展热线法的总结建立的拓展热线法主要包括三个阶段:测前准备、测量阶段和测后数据处理.
测前准备主要包括:选取热探针,合适的探针长度与半径;试样制备;试样钻孔等步骤.在选取热探针时,首先要粗略估计待测材料横向和纵向热扩散系数的数量级,然后利用式(29)及式(43)分别估算合适的热探针半径和长度的取值范围,最后参考取值范围选取适宜的热探针.在试样制备时,预先要明确待测材料2个横向导热及1个纵向导热的方向,然后将待测材料制作成一个棱长恰好等于之前所选热探针长度的立方体,立方体的三组平行对面必须与之前所确定的2个横向导热及1个纵向导热方向垂直.在对试样钻孔时,要注意从试样表面的中央处垂直钻穿试样,孔道必须确保笔直,孔径要比实际测得的热探针直径略微大一些,沿着KL方向及任意的一个KT方向各钻一个孔.
在测量阶段,要保证所有的测量都在稳定的环境温度下进行.先将热探针插入之前钻好的KL方向的孔中,测得KT的值,然后拔出探针,待探针和试样都恢复至环境温度后再插入KT方向的孔中测得KN的值.在每次插入试样前,都要在探针表面涂抹一层导热硅脂以降低探针与孔壁之间的接触热阻.
完成测量后,将所得到的KT、KN值代入式(40),计算出KL的值.由此,待测材料的横向及纵向导热系数都能确定.
2 试验验证前文建立了量测横观各向同性材料导热系数的拓展热线法,这里将此方法应用于一种自制的人工横观各向同性材料,并将所得结果与相应的稳态平板法量测结果进行比较,从而验证本文方法的可靠性及可重复性.
2.1 试验仪器试验所用的主要仪器为美国Decagon公司出产的KD2 Pro热探针仪及配套TR-1热探针(图 5).

|
图 5 KD2 Pro热探针仪及TR-1热探针 Figure 5 KD2 Pro TCP analyzer with TR-1 single needle |
该热探针仪的主机由4节AA电池驱动,可在0~50 ℃的温度下工作,其闪存可以记录最多4 095个读数. TR-1热探针拥有10 cm的标准长度以及2.4 mm的标准直径,其工作温度范围为-50~150 ℃,导热系数的量程为0.1~4.0 W·m-1·K-1,长度范围内绝大部分为温感区段,温感区段的探针表面平均温度变化能被迅速感测到.
2.2 试验材料与试样如图 6,试验选用的制样原材料为一叠厚10 cm整齐叠放的A4打印纸.利用裁纸机将此原材料切出3个10 cm×10 cm×10 cm的立方体纸块,每个纸块在整齐叠放的状态下用透明玻璃胶带以图示方式裹紧.显然,每个纸块在平行于纸面的两个相互垂直的方向上有两个相同的横向导热系数KT,在垂直于纸面的方向上有一个纵向导热系数KL.在每个纸块的KL方向以及任意一个KT方向各钻一个直径2.5 mm的预留孔,孔径略大于TR-1热探针在室温(27 ℃)时的直径2.443 mm.由此制备得到3个试样,并将它们分别编号为:“Ⅰ”,“Ⅱ”,“Ⅲ”.

|
图 6 试验材料及试样 Figure 6 Experimental material and specimens |
在室温条件下,分别对试样Ⅰ、Ⅱ、Ⅲ使用前述“测量阶段”与“测后数据处理”的流程,得到了对应于每个试样的KN、KT、KL值,并在表 1中给出了这些结果. 表 1还给出了相应的稳态平板法测得的结果.
| 表 1 本文方法与稳态平板法各自的结果 Table 1 Results respectively obtained by the proposed method and the GHP method |
由表 1可看出,每个试样的KT、KL值与相应的稳态平板法的结果的相对误差都在6%以内,考虑本文方法为一种快速测量方法,其结果与对应的稳态平板法的结果还是吻合较好的.
试验采用的试样材料在宏观上具有较好的连续性和匀质性,并且在平行于纸面的各个方向上具有较好的同质性,垂直纸面的方向是分层结构,性状和纸面内不同,所以能作为较为理想的横观各向同性材料.此外,试验过程中,热探针的工作温度大约在27 ℃~35 ℃的狭小低温范围内,一般纸张在这样的温度范围内性状几乎不会发生什么变化,导热系数、密度、比热容可看作常数.在热扩散系数的数量级方面,考虑r0=1.2 mm;l=10 cm;β=0.45;th= 60 s;tB=25 s;ξ1=10-1;ξ2=10-2,利用式(29)和式(43)可估算出Dmin及Dmax的数量级应落在10-7 m2·s-1~10-6 m2·s-1.参考表 1中稳态平板法的结果,并取ρ=1 400 kg·m-3;c=1 900 J·kg-1·K-1,可估算出实际的热扩散系数:Dmin=0.24×10-7 m2·s-1;Dmax=1.16×10-7 m2·s-1.虽然Dmin的数量级与限制要求有一定的差距,但考虑到这里Dmin与Dmax之间的比值接近1:5,两者差异较大,因此式(29)和式(43)所给出的限制要求都偏于保守,有鉴于此,Dmin的数量级基本可以接受.
综上,在使用拓展热线法测量横观各向同性材料导热系数时,在测量过程中, 只要探针-试样实际量测系统与其对应的理想模型之间具有较高的接近度,此方法是具有一定可靠性及可重复性的.
3 结论本文基于横观各向同性介质中的热传导理论,对传统热线法进行了功能拓展,建立一种利用热线法测量横观各向同性材料导热系数的快捷新方法.通过将该方法用于测量自制横观各向同性材料的导热系数,并与稳态热板法试验结果比对,验证了该新方法的可靠性及可重复性.
1) 对于已经明确了平面内及平面外方向的横观各向同性材料的导热系数可以通过联立热探针对该材料所制成的立方体试样的两次独立测量来加以确定.
2) 本文所建立的方法可作为一种测量横观各向同性材料导热系数的快捷方法.
3) 在使用本文方法测量横观各向同性材料导热系数时,只要测量过程中探针-试样实际量测系统与其对应的理想模型之间具有较高的接近度,即能保证测量结果的可靠性及可重复性.
| [1] |
黄君丽. 热管式平板导热仪及木材导热特性的研究[D]. 杭州: 浙江大学, 2005.
HUANG Junli. Study on the hot-plate thermal conductivity analyzer with heat pipes and heat conduction properties of wood[D]. Hangzhou: Zhejiang University, 2005. http://cdmd.cnki.com.cn/article/cdmd-10335-2005126683.htm |
| [2] |
NARAYANAMURTI D, RANGANATHAN V. The thermal conductivity of indian timbers[J].
Proceedings of the Indian Academy of Sciences-mathematical Sciences, 1941, 13(4): 300-315.
DOI: 10.1007/BF03049008 |
| [3] |
ROLFES R, HAMMERSCHMIDT U. Transverse thermal conductivity of CFRP laminates: a numerical and experimental validation of approximation formulae[J].
Composites Science and Technology, 1995, 54(1): 45-54.
DOI: 10.1016/0266-3538(95)00036-4 |
| [4] |
SOPA C, CUMNUENG W, THAVACHAI T, et al. Effects of temperature and concentration on thermal properties of cassava starch solutions[J].
Songklanakarin Journal of Science and Technology, 2008, 30(3): 405-411.
|
| [5] |
YOSHIKI M, EⅡCHIRO S, TAKAHIRO O, et al. Simultaneous estimation of the thermophysical properties of three kinds of fruit juices based on the measured result by a transient heat flow probe method[J].
Journal of Food Engineering, 2010, 96: 607-613.
DOI: 10.1016/j.jfoodeng.2009.09.008 |
| [6] |
SHIVA K, DURGA P, BASAVARAJ M. The influence of moisture content and density on thermal conductivity of ficus carica linnaus (fig fruit) by transient line heat source method[J].
International Journal of Engineering and Innovative Technology, 2013, 3(6): 177-180.
|
| [7] |
叶为民, 王琼, 潘虹, 等. 高压实高庙子膨润土的热传导性能[J].
岩土工程学报, 2010, 32(6): 821-826.
YE Weimin, WANG Qiong, PAN Hong, et al. Thermal conductivity of compacted GMZ01 bentonite[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(6): 821-826. |
| [8] |
HOSAIN D, MOHAMMAD Z. Thermal conductivity of sunflower seed as a function of moisture content and bulk density[J].
World Applied Sciences Journal, 2012, 18(9): 1321-1325.
DOI: 10.5829/idosi.wasj.2012.18.09.56 |
| [9] |
CARSLAW H S, JAEGER J C.
Conduction of heat in solids[M]. Oxford: Claremore Press, 1959.
|
| [10] |
DE VRIES D A, PECK AJ. On the cylindrical probe method of measuring thermal conductivity with special reference to soils. Ⅰ. extension of theory and discussion of probe characteristics[J].
Australian Journal of Physics, 1958, 11(2): 255-271.
DOI: 10.1071/PH580255 |
| [11] |
贾力, 方肇洪, 钱兴华.
高等传热学[M]. 北京: 高等教育出版社, 2003: 3.
JIA Li, FANG Zhaohong, QIAN Xinghua. Advanced heat transfer[M]. Beijing: Higher Education Press, 2003: 3. |
 2018, Vol. 50
2018, Vol. 50


