近年来,中国铁路在六次大提速的背景下,客货运均呈现出高速化、重载化的趋势.由此导致的轨道质量日益恶化也影响着行车安全和乘车体验[1-2].传统的轨道养护方法主要分为“故障修”和“周期修”[3],已经无法满足铁路高速运行的需要.所以,利用轨道动态检测数据拟合轨道质量历史发展趋势[4-5],并对其未来的发展趋势进行有效预测[6],对于合理安排养护周期、提高养护效率具有重大意义.
轨道质量的发展具有趋势性和随机性.国内外的学者对轨道质量的预测进行了大量研究.日本学者三和雅史[7-8]等根据实际养护作业的经验提出基于Logistic分布的特征值推移法来指导大型养路机械(Multiple Tie Tamper,MTT)的作业;日本铁道技术研究所(RTRI)研究人员KAWAGUCHI A[9]等以轨向不平顺的标准偏差来建立非线性退化模型,并以此为依据确定工务部门的养护计划;曼彻斯特大学(University of Manchester)的HYSLIP J[10]提出以轨检车得到的轨道几何数据为基础,使用分形法对检测数据进行分析并做出预测.国内学者则主要围绕TQI开展研究.曲建军[11]将灰色系统不确定性理论引入轨道质量的预测领域,建立了轨道不平顺TITCGM(1,1)-PC灰色非线性预测模型;许玉德[12]提出了利用动态轨检数据建立线性预测模型,然后利用TQI预测值来编制养护计划;韩晋[13]提出了基于非等间距灰色理论和BP神经网络残差校正的预测方法.
但是,现有的预测方法均存在缺陷.例如,线性预测模型对异常点无法进行较好拟合,鲁棒性差;而以灰色理论为基础的BP神经网络残差校正模型,因BP网络初始权值和阈值均为随机赋值,导致预测结果缺乏稳定性,预测效果欠佳.
基于此,本文提出一种将非等间距灰色模型[14-16]和遗传算法[17-18]优化的Elman神经网络[19-20]相结合的预测方法(GM-GA-Elman).首先通过非等间距灰色模型GM(1,1)得到TQI序列的大致发展趋势和残差序列,然后利用遗传算法优化Elman神经网络的权值和阈值,最后使用优化后的Elman神经网络进行残差校正,最终得到一个更加准确的TQI预测序列.
1 非等间距灰色模型 1.1 非等间距序列的生成设原始TQI序列值为
| $ {X^{\left( 0 \right)}} = \left\{ {{x^{\left( 0 \right)}}\left( {{t_1}} \right),{x^{\left( 0 \right)}}\left( {{t_2}} \right), \cdots ,{x^{\left( 0 \right)}}\left( {{t_n}} \right)} \right\}. $ | (1) |
序列x(0)(ti)所对应的检测时间为ti,故原始TQI序列值的时间差为
| $ \Delta {t_i} = {t_i} - {t_{i - 1}},i = 2,3, \cdots ,n. $ | (2) |
由于TQI序列的检测时间并非等差分布,即
| $ \Delta {t_i} \ne {\rm{const,}}i = 2,3, \cdots ,n. $ | (3) |
式中const表示常量,X(0)为非等间距序列.
对原始TQI序列做一阶累加生成,并考虑到检测时间差Δti,则有
| $ {x^{\left( 1 \right)}}\left( {{t_i}} \right) = \sum\limits_{k = 1}^i {{x^{\left( 0 \right)}}\left( {{t_k}} \right)\Delta {t_k}} ,i = 2,3, \cdots ,n. $ | (4) |
x(1)的初值一般取x(1)(t1)=x(0)(t1),但是预测曲线不一定经过原始序列初值点,且由于原始序列中所有的点均与预测模型相关,所以本文将初值选取为原始序列均值,即
| $ {x^{\left( 1 \right)}}\left( {{t_1}} \right) = \frac{1}{n}\sum\limits_{k = 1}^n {{x^{\left( 0 \right)}}\left( {{t_k}} \right)} . $ | (5) |
非等间距序列模型得到的一阶累加生成序列X(1)为
| $ {X^{\left( 1 \right)}} = \left\{ {{x^{\left( 1 \right)}}\left( {{t_1}} \right),{x^{\left( 1 \right)}}\left( {{t_2}} \right), \cdots ,{x^{\left( 1 \right)}}\left( {{t_n}} \right)} \right\}. $ | (6) |
由一阶累加生成模块建立GM(1, 1)模型,白化形式微分方程为
| $ \frac{{{\rm{d}}{x^{\left( 1 \right)}}\left( t \right)}}{{{\rm{d}}t}} + a{x^{\left( 1 \right)}}\left( t \right) = u,t \in \left[ {0,\infty } \right). $ | (7) |
将上式离散化,即对上式左右两边在[ti-1, ti]上进行积分:
| $ {x^{\left( 0 \right)}}\left( {{t_i}} \right)\Delta {t_i} + a\int\limits_{{t_{i- 1}} }^{{t_i}} {{x^{\left( 1 \right)}}\left( t \right){\rm{d}}t} = u\Delta {t_i},i = 2,3, \cdots ,n. $ | (8) |
称
| $ {z^{\left( 1 \right)}}\left( {{t_i}} \right) = \int\limits_{{t_{i- 1}} }^{{t_i}} {{x^{\left( 1 \right)}}\left( t \right){\rm{d}}t} ,i = 2,3, \cdots ,n. $ | (9) |
为x(1)(ti)在区间[ti-1, ti]上的白化背景值,一般将其简化[15]为
| $ {z^{\left( 1 \right)}}\left( {{t_i}} \right) = \frac{{\left( {{x^{\left( 1 \right)}}\left( {{t_i}} \right) + {x^{\left( 1 \right)}}\left( {{t_{i - 1}}} \right)} \right)}}{2}\Delta {t_i}. $ | (10) |
离散化差分方程为
| $ {x^{\left( 0 \right)}}\left( {{t_i}} \right)\Delta {t_i} + a{z^{\left( 1 \right)}}\left( {{t_i}} \right) = u\Delta {t_i}. $ | (11) |
式中:a为发展系数,用来控制系统发展态势的大小,u为灰色作用量,用来反映数据变化的不确切关系.
利用最小二乘法求得待辨识参数a,u为
| $ {\left( {a,u} \right)^{\rm{T}}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Y}}. $ | (12) |
其中:
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} { - {z^{\left( 1 \right)}}\left( {{t_2}} \right)}&1\\ { - {z^{\left( 1 \right)}}\left( {{t_3}} \right)}&1\\ \vdots&\vdots \\ { - {z^{\left( 1 \right)}}\left( {{t_n}} \right)}&1 \end{array}} \right], $ | (13) |
| $ \mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} {{x^{\left( 0 \right)}}\left( {{t_2}} \right)}\\ {{x^{\left( 0 \right)}}\left( {{t_3}} \right)}\\ \vdots \\ {{x^{\left( 0 \right)}}\left( {{t_n}} \right)} \end{array}} \right]. $ | (14) |
将参数a,u代入微分方程解得时间响应函数为
| $ \begin{array}{l} {{\hat x}^{\left( 1 \right)}}\left( {{t_i}} \right) = \left( {{x^{\left( 0 \right)}}\left( {{t_1}} \right) - \frac{u}{a}} \right){{\rm{e}}^{ - a\left( {{t_i} - {t_1}} \right)}} + \frac{u}{a},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 2,3, \cdots ,n. \end{array} $ | (15) |
从而得到GM(1, 1)初步预测值为
| $ {{\hat x}^{\left( 0 \right)}}\left( {{t_i}} \right) = {{\hat x}^{\left( 1 \right)}}\left( {{t_i}} \right) - {{\hat x}^{\left( 1 \right)}}\left( {{t_{i - 1}}} \right),i = 2,3, \cdots ,n. $ | (16) |
由式(12)~(15)可知背景值z(1)(ti)的构造形式决定灰色模型的预测精度.由式(10)可知,在区间[ti-1, ti]上使用梯形公式来代替曲线x(1)(ti)与时间横轴围成的面积造成精度误差.为了减少此误差,利用文献[21]中的方法,即把背景值表达式优化为
| $ {z^{\left( 1 \right)}}\left( {{t_i}} \right) = \frac{{{x^{\left( 1 \right)}}\left( {{t_i}} \right) - {x^{\left( 1 \right)}}\left( {{t_{i - 1}}} \right)}}{{\ln {x^{\left( 1 \right)}}\left( {{t_i}} \right) - \ln {x^{\left( 1 \right)}}\left( {{t_{i - 1}}} \right)}} \cdot \Delta {t_i}. $ | (17) |
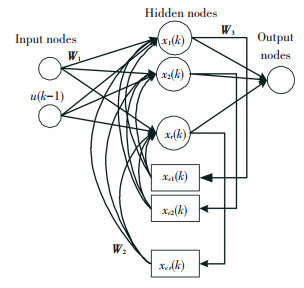
Elman神经网络是J.E.Elman于1990年首先提出来的一种典型的局部回归神经网络. Elman网络具有与多层前向网络(如BP神经网络)相似的多层结构.但是不同于传统的BP神经网络,Elman网络中多出的承接层,增加了网络处理动态信息的能力和适应时变特性的能力[19-20].其结构主要包括输入层、隐含层、输出层、承接层,网络模型见图 1.
|
图 1 Elman神经网络结构 Figure 1 The structure of Elman neural network |
遗传算法(Genetic Algorithm, GA)是一种经典的启发式搜索算法,通用性强,能对多个领域的问题进行全局最优解搜索[17-18].
轨道质量状态具有很强的趋势性和随机性,本文将遗传算法和Elman神经网络结合起来形成GA-Elman模型,即利用遗传算法对Elman神经网络的初始权值和阈值进行优化,优化后的网络在训练过程中能对突变数据进行充分学习并消除预测过程中随机因素的干扰,从而提高了预测精度. GA-Elman残差校正模型的原理如下:
1) 通过改进的非等间距灰色模型得到初步预测值并求得残差序列
| $ \delta \left( {{t_i}} \right) = {x^{\left( 0 \right)}}\left( {{t_i}} \right) - {{\hat x}^{\left( 0 \right)}}\left( {{t_i}} \right),i = 1,2, \cdots ,n. $ | (18) |
2) 为了避免不同量级的数据相互影响,对残差序列δ(ti)进行归一化处理如下:
| $ y = \frac{{\left( {{y_{\max }} - {y_{\min }}} \right) * \left( {\delta - {\delta _{\min }}} \right)}}{{{\delta _{\max }} - {\delta _{\min }}}} + {y_{\min }}. $ | (19) |
式中:ymin=-1,ymax=1.
3) Elman神经网络参数的确定:
神经网络的训练效果对参数极为敏感,具体参数的选取对实际情况的依赖度较高,采用经验值的场合较多[22-23].其中,隐含层节点数一般遵循公式
4) 遗传算法参数初始化:
待处理数据量较小,经多次实验发现,当Elman网络的隐含层节点数为3时,种群在30代以内基本接近收敛,故设置进化代数为30代,种群规模为10;同时,经多次测试发现在GA-Elman模型运算过程中,染色体的平均适应度容易快速下降接近至最佳适应度导致模型快速收敛,故选用较低的交叉概率pcross=0.2以降低收敛速度,选用较高的变异概率pmutation=0.1来提高种群产生更优个体的能力,保证了最终结果平稳地收敛至最优解;
5) 染色体编码:
实数编码方式可以扩大寻优范围,同时无需进行频繁地编解码,相较于二进制编码,运算效率显著提高[24],故本文选用实数编码方式.
神经网络在初始化权值和阈值系数时一般是在(-1, 1)的范围内随机产生.适当扩大编码范围可适当提高染色体多样性,产生新的优秀个体的概率也随之变大.此范围过大则会使得权值和阈值过于分散,不利于种群进化.故本文设置权值和阈值系数的范围为(-3, 3),在此范围内随机产生10组权值和阈值系数构成一条染色体,该染色体包含了构成一个完整神经网络的全部权值和阈值系数;
6) 确定适应度函数:
适应度函数的选取直接决定了遗传进化的效果.将每个个体携带的权值和阈值赋入神经网络进行训练并预测输出,把预测输出
| $ \begin{array}{*{20}{c}} {E = {k_1}\sum\limits_{i = 1}^N {\left( {\left| {{y_{\rm{f}}}\left( i \right) - {{\hat y}_{\rm{f}}}\left( i \right)} \right|} \right),} }\\ {{F_{{\rm{fitness}}}} = E.} \end{array} $ |
式中:k1为系数,N为网络输出节点数.
7) 遗传算法选择操作:
选择操作一般都有轮盘赌法、随机遍历抽样法、锦标赛法等[25].选用轮盘赌法.对于个体i,其被选择的概率是pi,则:
| $ {f_i} = {k_2}/{F_i} $ |
| $ {p_i} = \frac{{{f_i}}}{{\sum\limits_{j = 1}^N {{f_i}} }} $ |
式中:Fi为个体i的适应度值,k2为取倒系数,N为种群规模.
8) 交叉操作:
采用实数交叉,第k个染色体ak和第l个染色体al在第j位的交叉[26]操作如下
| $ \left\{ \begin{array}{l} {a_{kj}} = {a_{kj}}\left( {1 - b} \right) + {a_{lj}}b,\\ {a_{lj}} = {a_{lj}}\left( {1 - b} \right) + {a_{kj}}b. \end{array} \right. $ |
9) 变异操作:
选取第i个个体的第j个基因aij进行变异[26],方法如下:
| $ {a_{ij}} = \left\{ \begin{array}{l} {a_{ij}} + \left( {{a_{ij}} - {\rm{HB}}} \right) * f\left( g \right),r > 0.5;\\ {a_{ij}} + \left( {{\rm{LB}} - {a_{ij}}} \right) * f\left( g \right),r \le 0.5; \end{array} \right. $ |
| $ f\left( g \right) = {r_2}{\left( {1 - \frac{{{G_{{\rm{cur}}}}}}{{{G_{\max }}}}} \right)^2}. $ |
式中:HB和LB分别为基因编码值的上下限,Gcur为当前迭代次数,Gmax为总迭代次数,r和r2为[0, 1]间的随机数.
根据以上参数设置建立GA-Elman残差校正模型.当种群进化到每一代染色体满足以下条件之一时,视为满足终止条件:
a) 每一代平均适应度值都收敛于最佳适应度值时;
b) 当连续多代染色体的平均适应度与最佳适应度差值较小,但又不收敛于最佳适应度时,为了提高算法运算效率,终止进化.
最后,将满足终止条件得到的最优种群解码为网络权值和阈值系数,并赋值给Elman网络进行训练得到GA-Elman残差校正模型.
10)残差校正:
利用训练好的Elman网络对残差序列δ(ti)进行预测得到最终残差输出
| $ x\left( {{t_i}} \right) = {{\hat x}^{\left( 0 \right)}}\left( {{t_i}} \right) + \hat \delta \left( {{t_i}} \right),i = 1,2, \cdots ,n $ |
根据以上理论分析,GM-GA-Elman预测模型原理如下利用非等间距灰色模型对TQI序列进行预测,把得到的初步预测值与真实值进行比较得到残差序列.最后将残差序列输入到GA-Elman残差校正模型中,得到本文的最终预测值.
具体预测步骤如下:
1) 在进行灰色建模之前,要对输入数据进行级比检验以判断其是否适用于灰色模型建模.方法如下
| $ \lambda \left( {{t_i}} \right) = \frac{{{x^{\left( 0 \right)}}\left( {{t_{i - 1}}} \right)}}{{{x^{\left( 0 \right)}}\left( {{t_i}} \right)}},i = 2,3, \cdots ,n $ |
若对∀λ(ti), i=2, 3, …, n都有
| $ \lambda \left( {{t_i}} \right) \in \left( {{{\rm{e}}^{ - \frac{2}{{n + 2}}}},{{\rm{e}}^{\frac{2}{{n + 2}}}}} \right),i = 2,3, \cdots ,n $ |
则输入数据可以直接使用灰色模型建模.否则需要选取适当常数c对原始数据序列X(0)进行适当平移
| $ {X^{\left( 0 \right)}} = {X^{\left( 0 \right)}} + c. $ |
2) 将步骤1)中处理完以后的数据做累加处理,得到一阶累加序列X(1);
3) 将一阶累加序列X(1)输入至非等间距GM(1,1)模型,同时利用优化后背景值表达式(17)代替传统背景值表达式(10)进行灰色建模,求得辨识参数a,u;
4) 由a,u得到最终的时间响应函数并求得初步预测值
5) 将δ(ti)输入至GA-Elman残差校正模型中得到残差校正值
6) 由残差校正值
| $ x\left( {{t_i}} \right) = {{\hat x}^{\left( 0 \right)}}\left( {{t_i}} \right) + \hat \delta \left( {{t_i}} \right),i = 1,2, \cdots ,n $ |
7) 若在步骤1)中进行了平移,则反平移得到最终的TQI预测序列.流程图见图 2.

|
图 2 GM-GA-Elman预测模型流程图 Figure 2 Flow chart of GM-GA-Elman model |
选取提速干线沪昆线上行K226.0~K226.2以及K226.4~K226.6的轨检车TQI数据对GM-GA-Elman预测模型进行验证.为了验证本文模型的可靠性,选取参考文献[11~13]的方法进行对比.
决定系数(R-square)、相关系数以及均方根误差(Root Mean Square Error, RMSE)是统计学中常用的拟合优劣判定标准[26].
4.1 K226.0~K226.2区间段预测结果分析选取K226.0~K226.2线路段2007年9月~2008年8月期间共19组TQI序列作为原始训练序列,预测2008年9月~2008年12月共7组TQI值.
图 3为经过非等间距灰色模型预测后的结果.

|
图 3 K226.0~K226.2区间段初步预测值和原始TQI值对比 Figure 3 The comparison between preliminary data and measured data at K226.0~K226.2 |
由图 3可知,单一的非等间距灰色模型只能反映TQI序列的大致变化趋势,难以体现局部变化.然后,利用GA-Elman残差校正模型进行残差校正,得到的结果见图 4.

|
图 4 K226.0~K226.2区间段最终预测值和原始TQI值对比 Figure 4 The comparison between final data and measured data at K226.0~K226.2 |
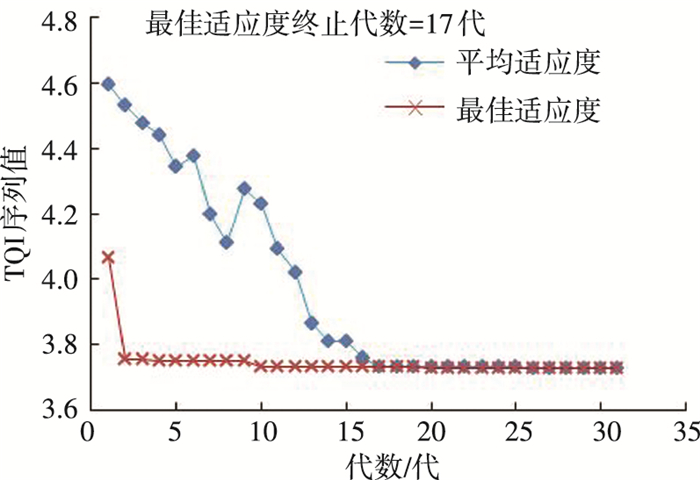
种群进化曲线见图 5,当进化至第17代时,种群趋于收敛,说明此时模型已接近最优解.
|
图 5 遗传算法适应度变化曲线(K226.0~K226.2区间段) Figure 5 Curves for fitness function of genetic algorithm at K226.0~K226.2 |
本文预测结果与参考文献[11~13]的方法预测结果的对比见表 1和表 2.
| 表 1 K226.0~K226.2区间段4种预测方法结果对比 Table 1 The comparison of conclusion of four forecasting methods at K226.0~K226.2 |
| 表 2 K226.0~K226.2区间段4种预测方法评价指标 Table 2 The comparison of evaluation index of four forecasting methods at K226.0~K226.2 |
结果表明,文献[11]中建立的TITCGM(1,1)-PC模型使用周期性函数对原始数据列中隐含周期成分和一定的随机成分进行拟合,平均相对误差为5.46%,RMSE较高,达到了0.430,模型预测效果一般;由于线性模型结构过于单一,所以文献[12]建立的线性预测模型预测效果较差,均方根误差过高;文献[13]中利用BP神经网络进行残差校正,虽然可以较好地拟合训练区间,但由于模型未对初始权值和阈值进行优化,导致预测结果不够理想,RMSE达到0.224;本文预测方法充分发挥了神经网络的优势,对原始TQI序列拟合效果较好,相对平均误差低至1.86%,同时,R-square、相关系数、均方根误差等三项统计指标均优于文献[11]、[13]的方法.虽然从相关系数来看,文献[12-13]的方法与本文方法差别不大,但是从R-square来看,本文方法的优势十分明显.
4.2 K226.4~K226.6区间段预测结果分析另选取K226.4~K226.6线路段2007年9月~2008年8月期间共19组TQI序列作为训练数据,预测2008年9月~2008年12月共7组TQI值.
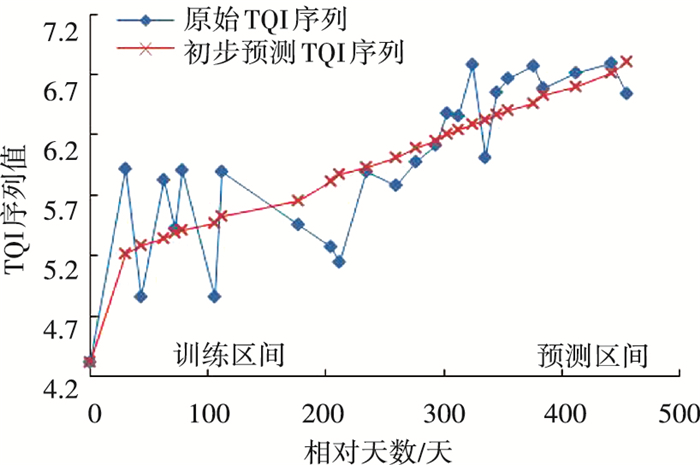
经过非等间距灰色模型预测后的结果见图 6.
|
图 6 K226.4~K226.6区间段初步预测值和原始TQI值对比 Figure 6 The comparison between preliminary data and measured data at K226.4~K226.6 |
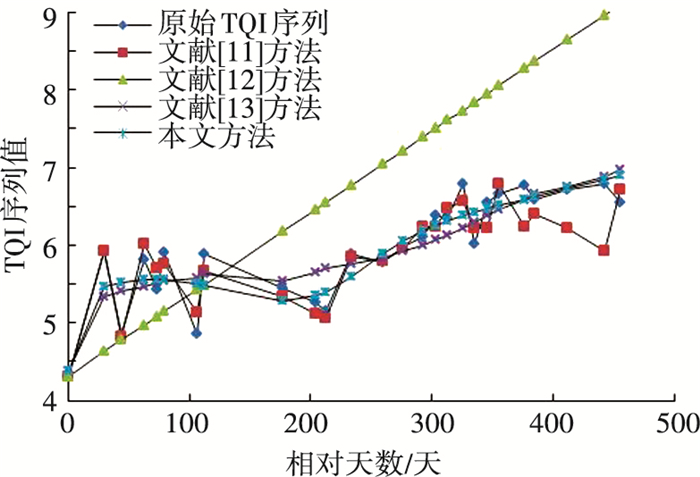
通过GA-Elman残差校正模型进行残差校正后得到的结果见图 7.
|
图 7 K226.4~K226.6区间段最终预测值和原始TQI值对比 Figure 7 The comparison between final data and measured data at K226.4~K226.6 |
遗传算法种群进化曲线见图 8,由图可知当种群进化至30代时,种群趋于收敛,说明此时模型已接近最优解.

|
图 8 遗传算法适应度变化曲线(K226.4~K226.6区间段) Figure 8 Curves for fitness function of genetic algorithm at K226.4~K226.6 |
结果表明,文献[12]中的方法由于未考虑突变数据点的影响,使得线性模型中的斜率过大,导致预测结果几乎不具备研究价值;预测序列平均相对误差低至1.89%,低于文献[11]的5.74%和文献[13]的2.59%;均方根误差显著下降,低至0.165;确定系数也明显优于文献[11]、[13].虽然在个别点的精度不如文献[11]、[13],但是整体来说,本文方法的多项统计性能均优于文献[11]、[13],且在不同区段上均保持稳定,鲁棒性更好.
| 表 3 K226.4~K226.6区间段4种预测方法结果对比 Table 3 The comparison of conclusion of four forecasting methods at K226.4~K226.6 |
| 表 4 K226.4~K226.6区间段4种预测方法评价指标 Table 4 The comparison of evaluation index of four forecasting methods at K226.4~K226.6 |
1) 对非等间距灰色模型进行背景值优化,利用积分的几何意义,将累加生成序列视为非齐次指数函数形式,重构非等间距灰色模型的背景值,有效提高了模型的预测精度值;
2) 利用遗传算法进行全局寻优得到权值和阈值的最优解,相对于其他方法中对初始权值和阈值随机赋值,本文方法稳定性更高;
3) 由于Elman神经网络具有动态反馈特性,对于发展趋势具有典型随机性的TQI序列来说,Elman神经网络能更好地拟合原始数据,预测效果更佳;
4) 使用多种统计指标评价本文方法,提高了评价的准确性和可靠性;
5) 本文验证了Elman神经网络在小样本、贫信息的预测问题中,可以对短期内的数据进行较好地预测,但是如何将其引入中长期预测问题中,还有待进一步研究.
| [1] |
李萌. 基于组合预测模型的轨道不平顺预测研究[D]. 成都: 西南交通大学, 2013. DOI: 10.7666/d.Y2334494.
LI Meng. Research on track irregularity prediction based on combination prediction model[D]. Chengdu: Southwest Jiaotong University, 2013. DOI: 10.7666/d.Y2334494. |
| [2] |
周宇, 许玉德. 基于遗传算法的轨道状态最优综合维修计划模型改进[J].
华东交通大学学报, 2005, 22(1): 15-20.
ZHOU Yu, XU Yude. Designing of optimization track synthetical maintenance plan model based on genetic algorithms[J]. Journal of East China Jiaotong University, 2005, 22(1): 15-20. DOI: 10.3969/j.issn.1005-0523.2005.01.005 |
| [3] |
汤国防. 铁路轨道几何不平顺变化特征及其预测模型研究[D]. 北京: 北京交通大学, 2010.
Tang Guofang. Study on variation characteristics and prediction models of railway track geometric irregularity[D]. Beijing: Beijing Jiaotong University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10004-2010119838.htm |
| [4] |
曲建军, 高亮, 田新宇, 等. 基于灰色理论的轨道几何状态中长期时变参数预测模型的研究[J].
铁道学报, 2010, 32(2): 55-59.
QU Jianjun, GAO Liang, TIAN Xinyu, et al. Study on the mid & long term prediction model of track geometry state based on the grey time-varying parameters theory[J]. Journal of the China Railway Society, 2010, 32(2): 55-59. DOI: 10.3969/j.issn.1001-8360.2010.02.010 |
| [5] |
PERRIN G, SOIZE C, DUHAMEL D, et al. Track irregularities stochastic modeling[J].
Probabilistic Engineering Mechanics, 2013, 34(34): 123-130.
|
| [6] |
许雯, 韩峰. 利用轨道质量指数TQI合理安排线路养护维修周期的方法研究[J].
兰州工业学院学报, 2015, 22(1): 45-47.
XU Wen, HAN Feng. Research on using track quality index (TQI) to reasonable arrangement of line maintenance and repair cycle[J]. Journal of Lanzhou Institute of Technology, 2015, 22(1): 45-47. DOI: 10.3969/j.issn.1009-2269.2015.01.011 |
| [7] |
三和雅史, 石川達也, 大山達雄. 軌道状態推移予測モデルの構築と最適軌道保守計画作成のための全整数型数理計画モデル分析[A]. 日本: 土木学会論文集, 2001, 681 : 51-65.
MIWA M, ISHIKAWA T, OYAMA T. Modeling the transition process of railway track irregularity and all integer mathematical programming model analyses for making optimal track maintenance schedule[J]. Japan: Proceedings of JSCE, 2001, 681 : 51-65. |
| [8] |
许玉德, 曾学贵. 建立整数型轨道状态最优综合维修计划模型[J].
铁道学报, 2003, 25(6): 85-88.
XU Yude, ZENG Xuegui. Foundation of the optimized comprehensive integral track maintenance plan model[J]. Journal of the China Railway Society, 2003, 25(6): 85-88. DOI: 10.3321/j.issn:1001-8360.2003.06.018 |
| [9] |
KAWAGUCHI A, MIWA M, TERADA K. Actual data analysis of alignment irregularity growth and its prediction model[J].
Quarterly Report of RTRI, 2005, 46(4): 262-268.
DOI: 10.2219/rtriqr.46.262 |
| [10] |
HYSLIP J. Fractal analysis of geometry data for railway track condition assessment[D]. Manchester: University of Manchester, 2002.
http://www.mendeley.com/research/fractal-analysis-geometry-data-railway-track-condition-assessment-1/
|
| [11] |
曲建军. 基于提速线路TQI的轨道不平顺预测与辅助决策技术的研究[D]. 北京: 北京交通大学, 2010. DOI: 10.7666/d.y1963423.
QU Jianjun. Study on the track irregularity prediction and decision-aided technology based on TQI of raising speed lines[D]. Beijing: Beijing Jiaotong University, 2010. DOI: 10.7666/d.y1963423. |
| [12] |
许玉德, 吴纪才. 利用线性预测模型分析轨道不平顺发展[J].
石家庄铁道大学学报自然科学版, 2005, 18(1): 6-9.
XU Yude, WU Jicai. Analysis on development of track irregularities with linear forecast model[J]. Journal of Shijiazhuang Railway Institute, 2005, 18(1): 6-9. DOI: 10.3969/j.issn.2095-0373.2005.01.002 |
| [13] |
韩晋, 杨岳, 陈峰, 等. 基于非等时距加权灰色模型与神经网络的轨道不平顺预测[J].
铁道学报, 2014, 36(1): 81-87.
HAN Jin, YANG Yue, CHEN Feng, et al. Prediction of track irregularity based on non-equal interval weighted grey model and neural network[J]. Journal of the China Railway Society, 2014, 36(1): 81-87. DOI: 10.3969/j.issn.1001-8360.2014.01.013 |
| [14] |
李嵩松, 惠晓峰. 股票指数模糊随机预测与灰色预测实证比较研究[J].
哈尔滨工业大学学报(社会科学版), 2010, 12(5): 48-53.
LI Songsong, HUI Xiaofeng. A Comparative study on stock index grey prediction and fuzzy stochastic prediction[J]. Journal of Harbin Institute of Technology (Social Sciences Edition), 2010, 12(5): 48-53. DOI: 10.3969/j.issn.1009-1971.2010.05.009 |
| [15] |
舒诗湖, 向高, 何文杰, 等. 灰色模型在城市中长期用水量预测中的应用[J].
哈尔滨工业大学学报, 2009, 41(2): 85-87.
SHU Shihu, XIANG Gao, HE Wenjie, et al. Application of GM(1, 1) in long-term urban water dem and forecast[J]. Journal of Harbin Institute of Technology, 2009, 41(2): 85-87. |
| [16] |
魏海龙, 李迅波, 沈艳, 等. 基于灰色模型的无线传感器网络动态功耗管理研究[J].
传感技术学报, 2011, 24(1): 140-144.
WEI Hailong, LI Xunbo, SHEN Yan, et al. The research on dynamic power management of wireless sensor networks based on grey model[J]. Chinese Journal of Sensors and Actuators, 2011, 24(1): 140-144. DOI: 10.3969/j.issn.1004-1699.2011.01.028 |
| [17] |
朱伟, 徐克林, 朱易. 敏捷制造中面向盟友选择问题的遗传算法[J].
哈尔滨工业大学学报, 2010, 42(9): 1500-1503.
ZHU Wei, XU Kelin, ZHU Yi. A genetic algorithm focusing on the problem of partner selection in agile manufacturing[J]. Journal of Harbin Institute of Technology, 2010, 42(9): 1500-1503. DOI: 10.11918/j.issn.0367-6234.2010.09.031 |
| [18] |
崔光照, 李小广, 张勋才, 等. 基于改进的粒子群遗传算法的DNA编码序列优化[J].
计算机学报, 2010, 33(2): 311-316.
CUI Guangzhao, LI Xiaoguang, ZHANG Xuncai, et al. The optimization of DNA encodings based on modified PSO/GA algorithm[J]. Chinese Journal of Computers, 2010, 33(2): 311-316. DOI: 10.3724/SP.J.1016.2009.00311 |
| [19] |
Song Q. On the weight convergence of elman networks[J].
IEEE Transactions on Neural Networks, 2010, 21(3): 463-80.
DOI: 10.1109/TNN.2009.2039226 |
| [20] |
Lin W M, Hong C M. A new elman neural network-based control algorithm for adjustable-pitch variable-speed wind-energy conversion systems[J].
IEEE Transactions on Power Electronics, 2011, 26(2): 473-481.
DOI: 10.1109/TPEL.2010.2085454 |
| [21] |
马洪霞, 丛林虎. 基于改进非等间隔灰色预测模型的导弹退化状态预测[J].
计算机与现代化, 2016(3): 5-10.
MA Hongxia, CONG Linhu. Prediction of missile degradation condition based on improved unequal interval grey model[J]. Computer and Modernization, 2016(3): 5-10. DOI: 10.3969/j.issn.1006-2475.2016.03.002 |
| [22] |
赵望达, 李卫高, 熊涵予, 等. 一种新型BP神经网络模型在火灾探测信息处理中的应用[J].
铁道科学与工程学报, 2015(5): 1212-1218.
ZHAO Wangda, LI Weigao, XIONG Hanyu, et al. Improved neural network model application in fire detection[J]. Journal of Railway Science and Engineering, 2015(5): 1212-1218. DOI: 10.3969/j.issn.1672-7029.2015.05.034 |
| [23] |
崔东文. 改进Elman神经网络在径流预测中的应用[J].
水利水运工程学报, 2013(2): 71-77.
CUI Dongwen. An improved Elman neural network and its application to runoff forecast[J]. Hydro-Science and Engineering, 2013(2): 71-77. DOI: 10.3969/j.issn.1009-640X.2013.02.012 |
| [24] |
张超群, 郑建国, 钱洁. 遗传算法编码方案比较[J].
计算机应用研究, 2011, 28(3): 819-822.
ZHANG Chaoqun, ZHENG Jianguo, QIAN Jie. Comparison of coding schemes for genetic algorithms[J]. Application Research of Computers, 2011, 28(3): 819-822. DOI: 10.3969/j.issn.1001-3695.2011.03.005 |
| [25] |
于莹莹, 陈燕, 李桃迎. 改进的遗传算法求解旅行商问题[J].
控制与决策, 2014, 29(8): 1483-1488.
YU Yingying, CHEN Yan, LI Taoying. Improved genetic algorithm for solving TSP[J]. Control and Decision, 2014, 29(8): 1483-1488. DOI: 10.13195/j.kzyjc.2013.0598 |
| [26] |
ABUDU S, KING J, ABUDUKADEER K. Comparison of performance of statistical models in forecasting monthly stream flow of Kizil river, China[J].
Water Science and Engineering, 2010, 3(3): 269-281.
DOI: 10.3882/j.issn.1674-2370.2010.03.003 |
 2018, Vol. 50
2018, Vol. 50


