目前，香农在有噪信道编码理论中指出，存在可以达到香农限的码字^[1].极化码(Polar Code)是2008年由E. Arikan提出的一种基于信道极化定理进行设计的新型信道编码，是第一种能够通过严格的数学方法证明达到信道容量的构造性编码方案^[2-5].因此极化编码激起了各国学者的广泛研究并开始应用于各个领域，拥有良好的发展前景.

串行抵消(SC)译码算法是极化码的基本译码算法, 当码长趋近于无穷时，可获得很好的渐进性能^[2].但是在中短码长时，SC译码的性能并不理想，相同条件下的编码增益不如Turbo码及LDPC码^[6].为提高SC译码性能，文献提出了串行抵消列表(SCL)算法，增加了每层译码搜索宽度, 降低了误码率.在此基础上，文献[9-10]提出基于对数似然比(LLR)的SCL译码算法，对译码码树中每一个节点的判决计算次数缩减了一半，降低了计算及硬件存储复杂度.但上述两种方法都是逐比特串行译码，运算量及运算复杂度随着码长的增加呈指数增长.针对此类问题，文献[11-13]中多比特译码算法，将传统SCL的单比特译码增强为多比特同时译码.此算法尽管减少了译码器判决次数降低了译码延时，但由于其译码算法结构，随着每次译码的比特数增加，运算次数及硬件存储复杂度都会随之增加.基于上述问题，本文提出了基于构造虚拟多比特信道的SCL译码算法.将传统的多个单比特信道构造成多比特虚拟信道，降低了译码运算及存储复杂度，并结合文献[14]中提出的基于信道可靠度的阈值判决的译码方案，进一步增强了此算法，提高译码效率.

1 背景算法描述 1.1 极化码SCL译码算法

(N, K)极化编码输入的N比特信息u₁^N=(u₁, u₂, …, u_n)由K比特的信息比特和(N-K)位冻结比特(一般为全0)两部分组成.根据信道极化理论，分别对N=2ⁿ个独立的二进制离散无记忆信道(B-DMC)W进行信道合成及信道分解的操作后，可得到N个独立等价子信道W_N⁽ⁱ⁾，i =1, 2, …, N.其中一部分子信道的对称容量I(W_N⁽ⁱ⁾)接近于1，视作无噪信道，用于传输信息比特; 而另一部分子信道的对称容量I(W_N⁽ⁱ⁾)接近于0，视作全噪信道，用于传输冻结比特.

根据文献[2]中提到的有关信道可靠性的计算方法，u₁^N中的K比特消息通过可靠性高的子信道进行传输，而(N-K)位冻结比特通过可靠度低的子信道进行传输.其次，依据编码式(1)，完成极化编码，其中G_N为生成矩阵.

$ x_1^N = u_1^N{\mathit{\boldsymbol{G}}_N} = {\mathit{\boldsymbol{u}}_A}{\mathit{\boldsymbol{G}}_N}\left( \mathit{\boldsymbol{A}} \right) \oplus {\mathit{\boldsymbol{u}}_{{A^c}}}{\mathit{\boldsymbol{G}}_N}\left( {{\mathit{\boldsymbol{A}}^c}} \right). $

(1)

式中：A为信息信道下标的集合; A^c为其补集即冻结信道的下标集合; 符号$ \oplus $为模二加运算.生成矩阵G_N为

$ {\mathit{\boldsymbol{G}}_N} = {\mathit{\boldsymbol{B}}_N}{\mathit{\boldsymbol{F}}^{ \otimes n}}. $

(2)

式中：符号$ \otimes $为张量积运算; ${\mathit{\boldsymbol{B}}_N} = {\mathit{\boldsymbol{R}}_N}({\mathit{\boldsymbol{I}}_2} \otimes {\mathit{\boldsymbol{B}}_{N/2}}) $，实现索引位逆转操作; R_N是比特翻转矩阵即实现元素的奇偶分离重排.

由此可见，极化码也是线性分组码的一种，(N, K)极化码的码率R=N/K.极化编码可视作根据信道可靠度的计算选取合适的信道，确定编码参数(N, K, A, u_A^c)的G_N陪集编码过程.

在仿真实验中，极化码的码字序列经二进制相移键控(BPSK)调制为符号x₁^N∈{-1, 1}^N的序列，经过AWGN信道后得到的接收序列y₁^N=(y₁, y₂, …, y_N).采用串行抵消(SC)译码可看作逐个依次地根据接收端计算出的对数似然比(LLR)进行硬判决. u_i的似然函数为$W_n^{(i)}(y_1^N, \hat u_1^{i - 1}|{u_i}) $，LLR为

$ L\left( {{u_i}} \right) = \ln \left( {\frac{{W_n^{\left( i \right)}\left( {y_1^N,\hat u_1^{i - 1}\left| 0 \right.} \right)}}{{W_n^{\left( i \right)}\left( {y_1^N,\hat u_1^{i - 1}\left| 1 \right.} \right)}}} \right). $

(3)

式中$ \hat u_1^{i - 1}$是接收端对前i-1个比特的估计序列.根据上述得到的LLR值结合硬判决即可完成对u_i的估计，具体判决依据如下：

$ {{\hat u}_1} = \left\{ \begin{array}{l} 0,i \in \mathit{\boldsymbol{A}},L\left( {{u_i}} \right) > 0;\\ 1,i \in \mathit{\boldsymbol{A}},L\left( {{u_i}} \right) < 0;\\ {u_i},i \in {\mathit{\boldsymbol{A}}^c}. \end{array} \right. $

(4)

在上述基于LLR的SC译码算法的基础上，根据译码码树，若在每次按位搜索时将搜索宽度扩大为L，即保留L条候选路径.然后基于L条路径依次扩展，直到叶子节点即最后一层.从最后一层保留的L条路径中选择一个路径度量值最大的路径作为译码输出，此种方法即为基于LLR的SCL译码算法.因此，SCL算法可看作是多路径同时进行的SC译码算法.

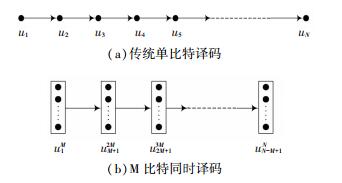
1.2 多比特判决译码算法

在极化码的译码算法中，路径度量的判决筛选过程是整个系统延迟的主要来源.无论是SC译码还是SCL译码算法都依据硬判决式(4)逐次逐位进行判决.当码长增加时，该算法的系统延迟增加，降低了译码效率.针对此问题，文献[13]提出了多比特判决的译码算法(2^Kb-rSCL算法)，译码时可每次同时计算出M比特消息的路径度量值进行判决筛选.如图 1所示，当M=1时等价于传统SCL译码，当M时，该算法即为最大似然(ML)译码.

假设W: X → Y为一个B-DMC信道，则N个并列单比特信道为W_N⁽ⁱ⁾: X → Y^N× X^i-1, 1≤i≤N.在多比特同步译码算法中，M(M=2^K)比特码字的路径可靠性度量过程视作由M个独立的单比特信道进行信道合成得到，即$W_{N, M}^{(j)}:{\rm{ }}\mathit{\boldsymbol{X}}{^M} \to {\rm{ }}\mathit{\boldsymbol{Y}}{^N} \times {\rm{ }}\mathit{\boldsymbol{X}}{^{jM - M}}, 1 \le j \le {\rm{ }}\frac{N}{M} $，其转移概率为$W_{N, M}^{(j)}(y_1^N, x_1^{jM - M}|x_{jM - M + 1}^{jM}) $.基于信道与信道的输出码字u₁^N的独立性，上述算法可描述为：当M比特码字同时译码判决时，信道转移概率$W_{N, M}^{(i)}(y_1^N, \hat u_1^{iM - M}|u_{iM - M + 1}^{iM}) $转化成M个独立的单比特信道之积，即

$ \begin{array}{l} W_{N,M}^{\left( i \right)}\left( {y_1^N,\hat u_1^{iM - M}\left| {u_{iM - M + 1}^{iM}} \right.} \right) = \prod\limits_{j = 0}^{M - 1} {W_{\frac{N}{M}}^{\left( i \right)}\left( {y_{j\frac{N}{M} + 1}^{\left( {j + 1} \right)\frac{N}{M}},} \right.} \\ \;\;\;\;\left. {\hat \alpha _{1 + j\frac{N}{M}}^{\left( {i + 1} \right) + j\frac{N}{M}}\left| {{\alpha _{i + j\frac{N}{M}}}} \right.} \right). \end{array} $

(5)

式中$ u_{iM - M + 1}^{iM} = \left( {{\alpha _i}, {\alpha _{i + \frac{N}{M}}}, \ldots, {\alpha _{i + N - \frac{N}{M}{\rm{ }}}}} \right){\mathit{\boldsymbol{G}}_M}$; 生成矩阵${\mathit{\boldsymbol{G}}_M} = {\rm{ }}{\mathit{\boldsymbol{B}}_M}\mathit{\boldsymbol{F}}{^{ \otimes K}} $.根据得到的似然值$W_{N, M}^{(j)}(y_1^N, \hat u_1^{iM - M}|u_{iM - M + 1}^{iM}) $，结合SCL译码算法，通过路径度量模块(MCU)进行筛选保留L条候选路径以及通迫零算法模块(ZFU)将冻结位至“0”.通过增加了每次译码比特数从而提高译码效率.

2 基于虚拟多比特信道的SCL译码

多比特译码算法的核心是对似然值$W_{N, M}^{(i)}(y_1^N, \hat u_1^{iM - M}|u_{iM - M + 1}^{iM}) $的计算.在对图 1(b)中每组M比特码字进行译码时，上述算法将其转化为传统单比特信道似然值之积.然而该算法只是通过路径度量上的多位判决降低了译码延迟，随着码长以及M的增加，计算复杂度以及进行路径度量判决(MCU)的查表复杂度也随之增加.并没有从信道转移概率这个根本问题上解决多比特运算的运算及存储复杂度.

将每组M比特码字即M个独立信道视作一个整体.在进行译码判决时，可将M个独立单比特信道通过信道合成构造为一个独立的M比特虚拟信道.此虚拟信道可以同时对M比特码字进行传输并根据信道递归公式进行同步判决，而不是M个单比特信道之积.这个虚拟信道为$W_N^{(i)}:\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} \to {\mathit{\boldsymbol{Y}}^N} \times {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{i - 1}}, 1 \le i \le \frac{N}{M} $，信道转移概率为$W_n^{(i)}(y_1^N, \lambda _1^{i - 1}|{\lambda _i}), {\lambda _i} = ({u_{jM - M + 1}}, \ldots, {u_{jM}}) $.根据虚拟信道的性质，对上述转移概率$W_{N, M}^{(i)}(y_1^N, \hat u_1^{iM - M}|u_{iM - M + 1}^{iM}) $的计算可通过信道递归计算有进一步地简化，并有下述定理1.

定理1  假设u₁^N中每一个比特u_i分别独立的等概率的判决为0或1，那么给定0 < m≤n，N=2ⁿ，M=2^m，对任意的1 < k≤m，0≤ω < n，令K=2^k，Ω=2^ω，并且$0 \le i < \frac{{2\mathit{\Omega} }}{K} $，则K比特虚拟信道W_{2Ω, K}⁽ⁱ⁺¹⁾可以由两个独立的虚拟$ \frac{K}{2}$比特信道W_{Ω, K/2}⁽ⁱ⁺¹⁾通过单步信道变换得到，即

$ \left( {W_{\mathit{\Omega },K/2}^{\left( {i + 1} \right)},W_{\mathit{\Omega },K/2}^{\left( {i + 1} \right)}} \right) \mapsto W_{2\mathit{\Omega },K}^{\left( {i + 1} \right)} $

且信道转移概率满足

$ \begin{array}{*{20}{c}} {W_{2\mathit{\Omega },K}^{\left( {i + 1} \right)}\left( {y_1^{2\mathit{\Omega }},u_1^{iK}\left| {u_{iK + 1}^{iK + K}} \right.} \right) = }\\ {W_{\mathit{\Omega },K/2}^{\left( {i + 1} \right)}\left( {y_1^\mathit{\Omega },u_{1,o}^{iK} \oplus u_{1,e}^{iK}\left| {u_{iK + 1,o}^{iK + K} \oplus u_{iK + 1,e}^{iK + K}} \right.} \right) \cdot }\\ {W_{\mathit{\Omega },K/2}^{\left( {i + 1} \right)}\left( {y_{\mathit{\Omega } + 1}^{2\mathit{\Omega }},u_{1,e}^{iK}\left| {u_{iK + 1,e}^{iK + K}} \right.} \right).} \end{array} $

(6)

证明  由条件概率公式Pr(B |A)=Pr(A, B)/Pr(A)可得

$W_{2\mathit{\Omega}, K}^{(i + 1)}\left( {y_1^{2\mathit{\Omega} }, u_1^{iK}|u_{iK + 1}^{iK + K}} \right) = \frac{{W_{2\mathit{\Omega}, 1}^{(iK + K)}\left( {y_1^{2\mathit{\Omega} }, u_1^{iK + K - 1}|{u_{iK + K}}} \right)}}{{{\rm{Pr}}\left( {u_{iK + 1}^{iK + K - 1}|{u_{iK + K}}} \right)}} $由于每一个比特u_i分别独立的等概率的判决为0或1，则

$ \Pr \left( {u_1^{iK + K - 1}\left| {{u_{iK + K}}} \right.} \right) = \Pr \left( {u_1^{iK + K - 1}} \right) = {2^{ - \left( {K - 1} \right)}} $

因此

$ \begin{array}{*{20}{c}} {W_{2\mathit{\Omega },K}^{\left( {i + 1} \right)}\left( {y_1^{2\mathit{\Omega }},u_1^{iK}\left| {u_{iK + 1}^{iK + K}} \right.} \right) = }\\ {{2^{\left( {K - 1} \right)}}W_{2\mathit{\Omega },K}^{\left( {i + 1} \right)}\left( {y_1^{2\mathit{\Omega }},u_1^{iK + K - 1}\left| {{u_{iK + K}}} \right.} \right).} \end{array} $

(7)

根据文献[2]中的式(23)可得

$ \begin{array}{l} W_{2\mathit{\Omega },1}^{\left( {iK + K} \right)}\left( {y_1^{2\mathit{\Omega }},u_1^{iK + K - 1}\left| {{u_{iK + K}}} \right.} \right) = \frac{1}{2}W_{\mathit{\Omega },1}^{\left( {\frac{{iK + K}}{2}} \right)}\left( {y_1^\mathit{\Omega },u_{1,o}^{iK + K - 2} \oplus } \right.\\ \;\;\;\left. {u_{1,e}^{iK + K - 2}\left| {{u_{iK + K - 1}} \oplus {u_{iK + K}}} \right.} \right) \cdot \\ \;\;\;W_{\mathit{\Omega },1}^{\left( {\frac{{iK + K}}{2}} \right)}\left( {y_{\mathit{\Omega } + 1}^{2\mathit{\Omega }},u_{1,e}^{iK + K - 2}\left| {{u_{iK + K}}} \right.} \right) \end{array} $

(8)

可以推出

$ \begin{array}{l} W_{\mathit{\Omega },1}^{\left( {\frac{{iK + K}}{2}} \right)}\left( {y_1^\mathit{\Omega },u_{1,o}^{iK + K - 2} \oplus u_{1,e}^{iK + K - 2}\left| {{u_{iK + K - 1}}} \right. \oplus {u_{iK + K}}} \right) = \\ {2^{ - \left( {\frac{K}{2} - 1} \right)}}W_{\mathit{\Omega },K/2}^{\left( {i + 1} \right)}\left( {y_1^\mathit{\Omega },u_{1,o}^{iK} \oplus u_{1,e}^{iK}\left| {u_{iK + 1,o}^{iK + K}} \right. \oplus u_{iK + 1,e}^{iK + K}} \right) \end{array} $

(9)

同理

$ \begin{array}{*{20}{c}} {W_{\mathit{\Omega },1}^{\left( {\frac{{iK + K}}{2}} \right)}\left( {y_{\mathit{\Omega } + 1}^{\mathit{2\Omega }},u_{1,e}^{iK + K - 2}\left| {{u_{iK + K}}} \right.} \right) = }\\ {{2^{ - \left( {\frac{K}{2} - 1} \right)}}W_{\mathit{\Omega },K/2}^{\left( {i + 1} \right)}\left( {y_{\mathit{\Omega } + 1}^{\mathit{2\Omega }},u_{1,e}^{iK}\left| {u_{1K + 1,e}^{iK + K}} \right.} \right)} \end{array} $

(10)

综上，由式(7)~(10)，即可推出(6)，证毕.

当利用上述多比特虚拟信道算法进行译码时，译码码树每层对K位信息u_iK+1^iK+K的判决有2^K条候选路径，因此基于LLR的二元判决模式不再实用.针对此问题，结合上述基于阈值度量的算法采取了对数似然(LL)结构，由上述定理1可得到每条候选路径的LL值即$ {\rm{log}}W_{2\mathit{\Omega}, K}^{(i + 1)}\left( {y_1^{2\mathit{\Omega}}, u_1^{iK}|u_{iK + 1}^{iK + K}} \right)$.

随着虚拟信道数K的增加，译码判决候选路径数2^K也呈指数增长.为解决此问题，引入AWGN信道下基于高斯近似的低分裂次数优化算法，进一步增强上述译码算法，降低路径度量运算以及存储复杂度.文献[14]提出的ESR-SCL译码算法中，引入P_e(u_i)为在译码过程中节点u_i的平均错误概率，即在子信道$W_n^{(i)}(y_1^N, \hat u_1^{i - 1}|{u_i}) $中，当u₁^i-1判决全部正确时u_i被错误译码判决的概率.则1-P_e(u_i)为u_i节点的译码可靠性度量值即置信度，并作为译码节点的阈值. ${P_e}\left( {{u_i}} \right) = Q(\sqrt {E\left[{L\left( {{u_i}} \right)} \right]/2} {\rm{ }}) $其中$ Q\left( x \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} }}\int_x^{ + \infty } {{e^{ - \frac{{{t^2}}}{2}}}{\rm{d}}t} $.根据阈值的预先计算提出了上述算法的核心，即只有当$W_N^{(i)}(y_1^N, \hat u_1^{i - 1}|{u_i} = 0) > 1 - {P_e}({u_i}) $或$W_N^{(i)}(y_1^N, \hat u_1^{i - 1}|{u_i} = 1) > 1 - {P_e}({u_i}) $时，译码码树在此层不分裂直接判为0或1，从而减少了历经节点数，降低了复杂度.

由高斯近似可知，当任意i∈[1, N]时，u_i取1或0的L(u_i)值具有相同的概率密度函数^[15].因此K比特信息u_iK+1^iK+K的置信度为(1-P_e(u_j))^K，其中iK+1≤j≤iK+K.然而由上述公式，P_e(u_i)中变量L(u_i)的计算需要得到已经译码判决出的u₁^i-1.根据多比特虚拟信道的译码码树构造可知，在对${u_{iK + 1}^{iK + K}} $进行判决时，$\hat u_1^{iK} $的判决结果是已知的，故只有u_iK+1的LLR值L(u_iK+1)可以通过计算得到.因此上述计算中取j=iK+1，则${u_{iK + 1}^{iK + K}} $置信度可定义为(1-P_e(u_iK+1))^K.其中：

$ \begin{array}{l} {P_e}\left( {{u_{iK + 1}}} \right) = {\rm{Q}}\left( {\sqrt {E\left[ {L\left( {{u_{iK + 1}}} \right)} \right]/2} } \right),\\ \;\;\;L\left( {{u_{iK + 1}}} \right) = \log \frac{{W_N^{\left( i \right)}\left( {y_1^N,\hat u_1^{iK}\left| 0 \right.} \right)}}{{W_N^{\left( i \right)}\left( {y_1^N,\hat u_1^{iK}\left| 1 \right.} \right)}}. \end{array} $

(11)

结合虚拟信道的信道转移概率LL值以及上述给出的可靠性度量的阈值算法，定义通过上述虚拟信道传输算法译码时只有当${\rm{log}}\left( {W_{2\mathit{\Omega}, K}^{(i + 1)}\left( {y_1^{2\mathit{\Omega} }, u_1^{iK}|u_{iK + 1}^{iK + K} = \psi _{iK + 1}^{iK + K}} \right)} \right) > K{\rm{log}}(1 - {P_e}({u_{iK + 1}})) $时，译码码树在此层不分裂直接判为$\psi _{iK + 1}^{iK + K} $，其中$\psi _{iK + 1}^{iK + K} $为$u_{iK + 1}^{iK + K} $的2^K种可能码字中任意一个码字.其余情况下结合多比特虚拟信道SCL译码算法正常分裂.即

$ \hat u_{iK + 1}^{iK + K} = \left\{ \begin{array}{l} \psi _{iK + 1}^{iK + K},\log \left( {W_{2\mathit{\Omega },K}^{\left( {i + 1} \right)}\left( {y_1^{2\mathit{\Omega }},u_1^{iK}\left| {u_{iK + 1}^{iK + K} = \psi _{iK + 1}^{iK + K}} \right.} \right)} \right) \ge \\ \;\;\;\;\;\;\;\;K\log \left( {1 - {P_e}\left( {{u_{iK + 1}}} \right)} \right)\\ {\rm{split}},{\rm{else}}. \end{array} \right. $

(12)

基于可靠性度量的计算可以推断，在路径正常分裂后，若出现${\rm{log}}\left( {W_{2\mathit{\Omega}, K}^{(i + 1)}\left( {y_1^{2\mathit{\Omega} }, u_1^{iK}|u_{iK + 1}^{iK + K} = \psi _{iK + 1}^{iK + K}} \right)} \right) \le K{\rm{log}}(1 - {P_e}({u_{iK + 1}})) $则该路径默认为错误路径不再保留或扩展，直接删除.

基于上述算法的译码路径可分为两类，第一类是基本上不分裂，此类路径以很高的概率包含正确的码字; 第二类是进行频繁地分裂，此类路径译码正确的概率相对较低.因此，定义变量S_l(i)为第l条路径在到达译码树第i层时中间经历的分裂次数.即假如第l条路径在第i层扩展到第i+1层时没有分裂，那么S_l(i+1)=S_l(i)+1.正确的译码路径很少分裂，而错误的译码路径会频繁地分裂，定义阈值S.当S_l(i)≥S，则此路径很大可能为正确译码，予以保留，其余S_l(i) < S的路径予以抛弃，从而减少保留的路径数量，以较慢的速度达到SCL译码中定义的L值.

综上所述，提出基于阈值判决的多比特虚拟信道SCL译码算法，描述步骤如下:

第1步：根据式(6)的计算，得到译码输出每组K比特信息的LL值，共计2^k个值.

第2步：将上一步得到的2^k个LL值依据式(12)和(13)对其进行判决，筛选出不分裂的、被删除的以及正常分裂的子节点，S_l(i)值也随时保持更新.

第3步：在第2步筛选基础上，若此时保留路径数量P>L，则删除S_l(i) < S的路径; 若所有路径S_l(i) < S，或删除S_l(i) < S的路径后P仍大于L，则保留剩余路径中路径度量值最大的L条.

第4步：若$i < \frac{N}{K} $，则令i=i+1并重复第一步至第3步; 若$i = \frac{N}{K} $，则在最后一层保留路径中取出路径度量值最大的一条路径作为译码输出.

3 仿真结果及性能分析

在AWGN信道下选取码长为1024，码率为1/2的(1024, 512)极化码，经过二进制频移键控(BPSK)调制，分别对上述多比特虚拟信道的SCL译码及基于不同阈值判决的虚拟信道SCL译码算法进行1 000次蒙特卡洛仿真.

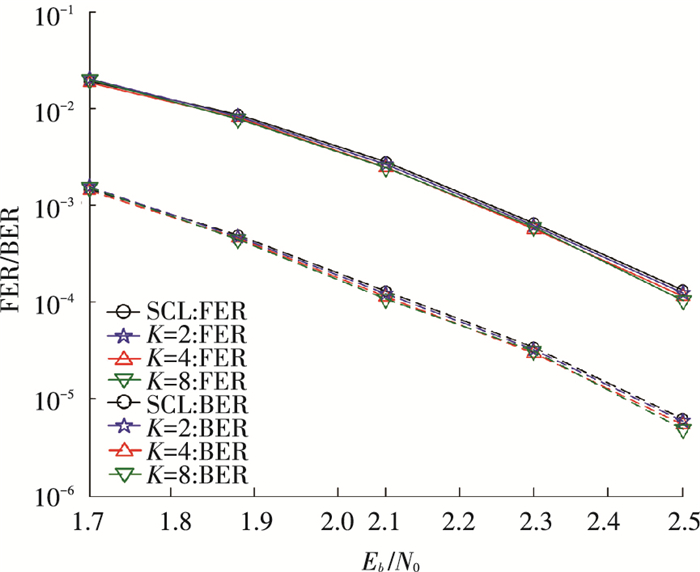
图 2为(1024, 512)极化码的传统的SCL译码算法与K分别取2、4、8的多比特虚拟信道SCL译码算法的误码率及误帧率的对比.从FER/BER曲线可以看出，当虚拟信道的比特数增大时，该算法的译码性能由略微的增加但是并不明显，性能与传统的SCL译码算法基本保持一致.

以4比特同时译码为例，由式(6)对$ {\rm{log}}(W_{N, 4}^{(j)}(y_1^N, \hat u_1^{4i - 4}|u_{4i - 4 + 1}^{4i}))$的计算共需要经历(2⁴+2×2²)共计24次加法运算，而由式(5)对${\rm{log}}(W_{N, 4}^{(j)}(y_1^N, \hat u_1^{4i - 4}|u_{4i - 4 + 1}^{4i})) $的计算需进行(2⁴×(4-1))共计48次加法运算，以此类推，得到如下复杂度对比表.

由图 2和表 1的分析可得出，上述多比特虚拟信道的译码算法与文献[13]中多比特判决译码相比，在K=4与K=8时可分别减少50%及83%的加法运算次数.在降低了译码计算复杂度的同时，译码性能与传统SCL算法基本保持一致.

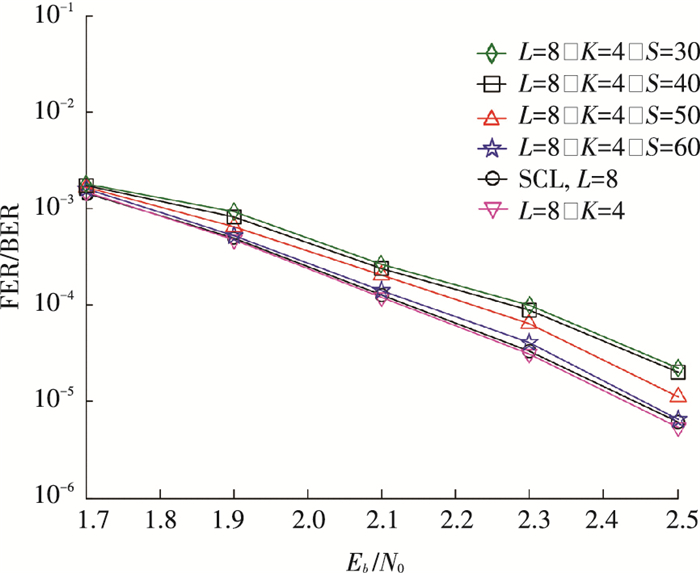
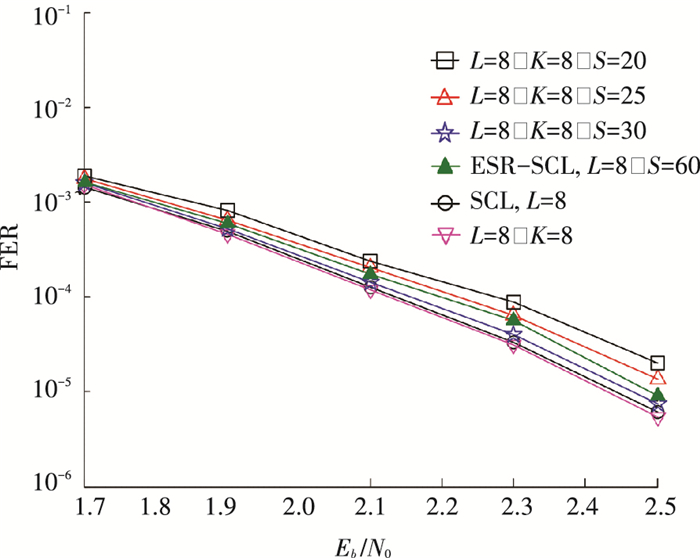
图 3、4为当(1 024, 512)极化码多比特虚拟信道译码时的K值分别取4、8时，在不同译码码树节点阈值S下的译码性能曲线.由不同阈值下的对比可知，根据阈值判决的虚拟比特信道译码由于减少了码树分裂次数即历经节点数导致译码性能略差.当所选取的阈值越大越接近传统SCL译码或虚拟比特信道SCL译码，随着阈值S的减小，译码性能也随之下降.在阈值S达到30时，性能略优于文献[14]中的ESR-SCL译码算法，S=20和25时译码性能较ESR-SCL算法略差.

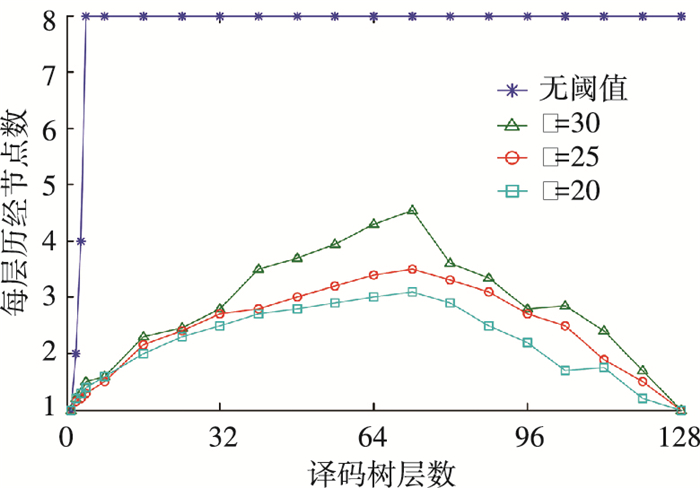
由上述实验得到，在K=8、信噪比为2.5 dB时误码率可达到10^-5.图 5为当信噪比E_b/N₀=2.5 dB时，无预设阈值与不同阈值下虚拟8比特信道SCL译码码树每层历经的节点总数.从图 3、4观察对比可以发现，设定阈值后，虽然译码性能略有下降，但每层历经的节点数量明显减少，在图 5中可观察不同阈值下历经节点数减少的具体情况.表 3记录了信噪比E_b/N₀=2.5 dB时不同参数下1 000次实验译码树平均历经的节点总数.

仿真实验表明，当阈值S=30时，虚拟8比特信道SCL译码性能接近于传统SCL译码，但是总历经节点数降低了63.7%，所需加法计算次数与8比特同时判决译码算法相比减少了83%.降低了译码算法的复杂度及历经节点次数，降低了硬件存储复杂度.

4 结论

本文回顾了极化码编码及SCL译码的原理，分析论证了现有多比特判决译码的优缺点.在此基础上提出了基于构造多比特虚拟信道的SCL译码算法并给出了多比特虚拟信道的递归公式，并结合上述算法的译码码树的构造结合了基于节点阈值判决的减少译码树分裂次数的算法，最后对上述算法进行了仿真实验与复杂度分析.结果表明，采用虚拟8比特信道SCL译码，取预设阈值S=30时译码性能接近传统SCL算法，在信噪比E_b/N₀=2.5 dB时误码率可达到10^-5.总历经节点数降低了63.7%，总加法计算次数与8比特同时判决译码算法相比减少了83%，降低了译码算法的计算复杂度及硬件存储复杂度，因此，该算法更适合于硬件实现, 更有应用价值.