2. 中南大学 机电工程学院,长沙 410083
2. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China
高强铝合金厚板制备的整体薄壁结构件由于具有质量轻和强度高等特点[1-2],常被应用于大飞机的生产制备中.但制备此类薄壁件的毛坯件存在初始应力,以及加工引入的表面应力[3-4],往往使零件成形后发生变形,达不到设计的精度要求,这已成为飞机零件制造急需解决的难题[5-6].
在导致航空铝合金薄壁构件加工变形的诸多影响因素里面,装夹力、毛坯材料内初始应力以及铣削过程中引入的加工应力影响显著[7-9].而在一些形状和特定工艺下制备的航空结构件中,原始毛坯材料里初始内应力又是引起构件变形的主要原因[10-12],如HUANG[10]通过有限元模拟仿真和实验研究了铝合金框架件整体应力分布对构件变形的影响,发现坯料初始残余应力引起的变形占部件总变形的90%;杨吟飞等[11]在对某型飞机7085铝合金主起支撑接头加工变形研究中,同样发现铝合金毛坯残余应力是导致零件加工后变形的主要因素.而在其它一些航空类结构件制备研究中,加工应力会严重影响构件的形状[13-15],通过控制和优化粗加工和精加工中的铣削参数,可以有效降低残余应力大小及改善变形[16],研究发现构件的加工变形与构件类型、材料类型和加工工艺有关.在变形预测方面,国内外进行过大量研究,如S. Nervi[17]考虑在材料毛坯初始状态和构件形状处于初始板材的位置情况下,预测零件的最终变形; 黄晓明等[18-19]基于刚度与应力演变机制,借助实验和有限元模拟方法建立了航空整体结构件的加工变形预测理论模型.目前构件变形预测多是基于非线性有限元仿真研究,仿真建模与实验存在一定差距,因此开展基于加工变形的薄壁件力学模型研究,建立应力分布与变形的数学关系,对指导初始加工材料的选择,加工工艺的确定以及表面处理工艺的制定有重要意义.
本文对薄壁构件加工应力分布下的变形机制进行力学分析与模型构建,推导出薄壁构件应力-变形数学模型,并完成对变形不确定性的分析计算.
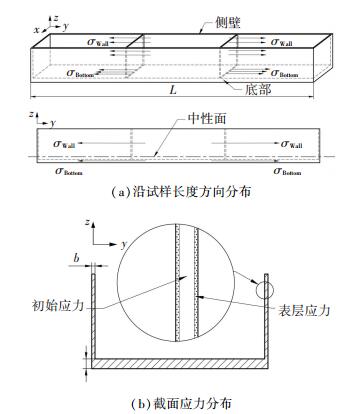
1 模型构建 1.1 薄壁件应力分布以等壁厚型薄壁框架件为研究对象,分析其在长度方向上的纯弯曲变形.若制备后构件上应力均以压力应力形式存在,其在薄壁和底部沿长度方向(Y方向)上的应力σWall和σBottom分布作用方式如图 1(a).薄壁构件的薄壁与底部表面会出现一层深度较浅而强度较大加工表面应力,其与厚板初始应力共同形成了此类框架件在长度方向上的应力分布格局,如图 1(b).需要注意的是,表面应力与初始应力的分布差异很大,表面应力强度大但分布浅,而初始应力强度很小,属于结构性应力分布.
|
图 1 应力分布模型 Figure 1 Stress distribution model |
由弯曲变形理论可知,若处于构件中性面两侧应力产生的合力矩不为零时,构件会发生弯曲变形,直到内部应力场达到新的平衡状态.
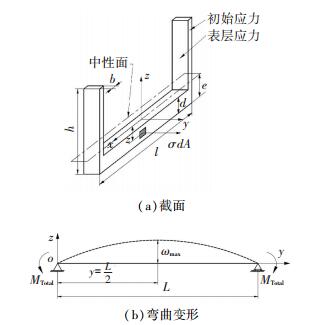
1.2 力学模型数学解析由对称加工的特点,可将薄壁框架件在Y轴线沿Z方向上弯曲变形挠度值为计算目标.一般情况下,在X正交方向上分布肋板,其厚度相对构件长度尺寸很小时,其对长度方向的影响可忽略不计.图 1(a)中沿Y方向分布的内应力作用机制近似如图 2(a),将图 1中的薄壁件模型简化为梁件,则沿Y方向内应力产生的弯曲变形如图 2(b).
|
图 2 试样力学示意 Figure 2 Mechanical schematic diagram of samples |
为计算构件在Y方向的弯曲挠度,需要已知构件在该方向变形时中性面的位置,图 2(a)中性面距离底面的距离e由截面形心公式计算得
| $ e = \frac{{2b{h^2} + {d^2}l - 2b{d^2}}}{{2ld + 4bh - 4bd}}. $ | (1) |
式中:l为构件宽度; b为薄壁厚度; h为高度; d为底部的厚度.则该截面上的惯性矩为
| $ {I_{\rm{x}}} = \frac{1}{3}\left[ {l{e^3} - \left( {l - 2b} \right){{\left( {e - d} \right)}^3} + 2b{{\left( {h - e} \right)}^3}} \right]. $ | (2) |
如上所述,变形是由初始应力和表面应力共同作用,并导致结构上应力不平衡所致.为便于分析,定义构件总应力σTotal,由表面应力和初始应力构成,分布形式可由实验直接获得.由材料力学可得到构件在Y方向上分布的整体应力σTotal作用下的总弯矩为
| $ {M_{{\rm{Total}}}} = \iiint {{\sigma _{{\rm{Total}}}}{\rm{d}}A{\rm{d}}z}. $ | (3) |
式中dA=dxdz,A为截面面积.挠曲线的近似微分方程(4)和构件在两端挠度为零的边界条件,通过积分法求得构件弯曲变形挠度为
| $ \frac{{{{\rm{d}}^2}{\omega _z}\left( y \right)}}{{{\rm{d}}{y^2}}} = \frac{{{M_{{\rm{Total}}}}}}{{E{I_{\rm{x}}}}}, $ | (4) |
| $ {\omega _z}\left( y \right) = \iint {\left( {\frac{{{M_{{\rm{Total}}}}}}{{E{I_{\rm{x}}}}}{\rm{d}}y} \right){\rm{d}}y} - \frac{{{M_{{\rm{Total}}}} \cdot L}}{{2E{I_{\rm{x}}}}}y. $ | (5) |
式中:E为材料弹性模量,L为构件在Y方向上的长度.由上式可以计算出构件最大挠度值出现在中部y=L/2处
| $ {\omega _{\max }} = \frac{{{M_{{\rm{Total}}}} \cdot {L^2}}}{{8E{I_{\rm{x}}}}}. $ | (6) |
设引起构件拱曲变形的弯矩为正,则当Y方向上总弯矩MTotal为正时,构件会发生图 2(a)所示拱曲变形,反之构件会发生凹曲变形.
2 实验设计加工变形主要受应力分布影响,通过铣削和喷砂实验来改变构件应力场分布,从而获得变形,以此来验证上述数学模型的有效性.
实验材料为7075-T651铝合金厚板,经过固溶处理和预拉伸处理, 板坯尺寸为500 mm×108 mm×60 mm,弹性模量E为71 GPa,厚板铣削时采用真空吸附夹具夹紧,以减小装夹力对构件造成的变形影响[7].加工后构件尺寸如图 3,试样薄壁厚为2 mm,底部厚度6 mm.

|
图 3 试样结构尺寸 Figure 3 Structure and size of samples |
随后,对试样薄壁和底部先后进行表面全覆盖的喷砂处理,参照航空零件喷丸强化标准[21], 喷砂时选用石英砂为喷料,喷料规格为0.5 mm(32目),喷射压力为0.3 MPa,喷射距离为80 mm,垂直构件表面喷射.喷砂会改变构件表面的应力大小[22],促使构件变形,这样可以获得铣削加工和喷砂处理的变形试样,实验步骤如图 4(a).铣削加工前后以及喷砂前后的构件在长度方向(Y方向)的挠曲线使用三标测量仪扫描获得.扫描时精度为1 μm/m,步长10 mm,图 4(b)为被喷砂全覆盖后的构件形状测试.毛坯板内初始应力可以采用逐层铣削方法,通过应力释放后的变形反求结构残余应力分布[23],这种方法针对规则厚板类毛坯件非常有效.而表面应力则利用化学逐层腐蚀后,采用PROTO-X射线衍射表面应力测试仪测量获得[24],具体方法为:在铣削加工和喷砂后的试样表面先利用5%的NaOH溶液逐层腐蚀到不同深度,再利用XRD测量表面应力,以获得表面逐层深度上的应力分布,如图 4(c).

|
图 4 实验与测试 Figure 4 Experiment and measurement |
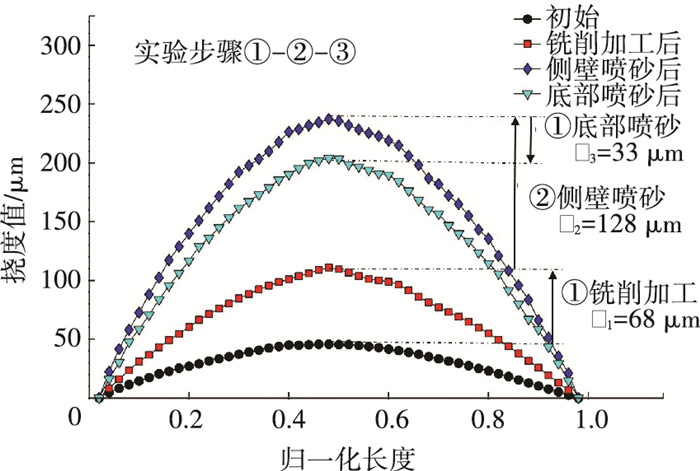
图 5为构件的初始态、铣削加工、薄壁喷砂和底部喷砂4种状态下长度方向(Y方向)挠曲线分布,横坐标长度做了归一化处理,构件实际长度为500 mm.
|
图 5 样变形 Figure 5 Deformation of samples |
图中,构件变形最大位置与式(5)计算结果一致,处于构件中间位置.相比初始状态,铣削加工后的构件出现了拱曲变形,中间位置的最大挠度增大了68 μm.随后,在薄壁上采用喷砂处理,构件出现了进一步拱曲变形,中间位置最大挠度增大128 μm.当在构件的底部采用同样喷砂工艺后,构件中间位置最大挠度值开始减小约33 μm.从实验变形数值可以发现,当仅对构件的薄壁部位喷砂处理时,虽然喷砂应力影响深度只有120 μm,但其造成的构件变形却接近铣削加工变形的2倍.
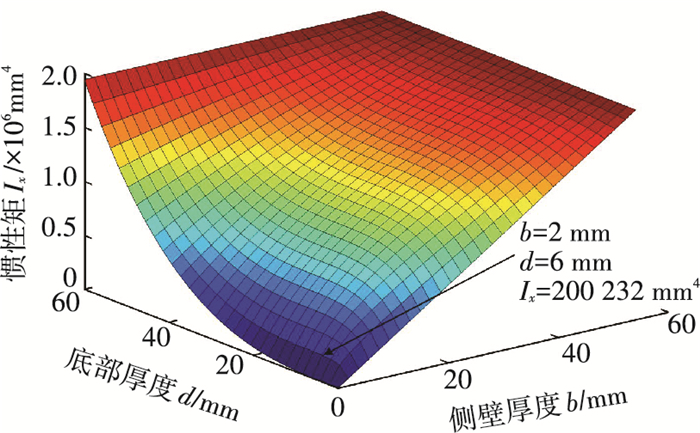
3.2 结果分析针对上述实验结果,运用解析函数进行验证.由式(1)、(2)可得,当构件整体尺寸一定时,以薄壁b和底部厚度d为自变量,构件在Y方向上的中性面位置与截面惯性矩变化如图 6、7.图 3中试样长度方向的弯曲中性面离构件底面距离e为10.5 mm,截面惯性矩Ix为200 232 mm4.

|
图 6 中性面位置e的三维描述 Figure 6 3D plot of Neutral surface's position e |
|
图 7 惯性矩Ix的三维描述 Figure 7 3D plot of inertia moment Ix |
沿Y方向上初始应力分布随厚度(Z方向)变化而变化,如图 8(a).框架件在铣削加工和喷砂后沿此方向表面逐层分布的应力大小如图 8(b).

|
图 8 试样应力分布 Figure 8 Stress distribution of samples |
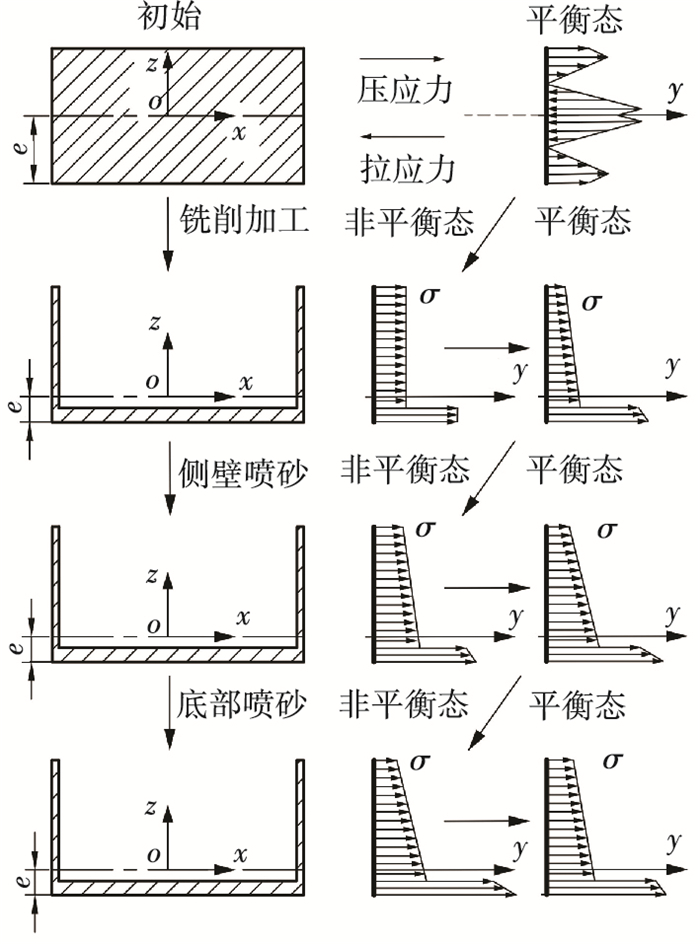
图 8(a)中厚板初始应力分布呈现出“外压内拉”的分布规律,边缘处6 mm区域应力为-4~-2 MPa,构件底部会继承该区域初始应力; 边缘处2 mm区域应力为-4~-3 MPa,构件薄壁则会继承该区域初始应力.图 8(b)中,被铣削加工和喷砂处理后的框架件表面会出现一层深度较浅但强度较大的压应力,作用深度约为120 μm.综合图 8中应力分布测试结果,可得到构件在初始态、加工后、薄壁喷砂后和底部喷砂后4个状态下总应力σTotal大小分布.在实验过程中,薄壁件在铣削加工、喷砂过程中的整体应力σTotal分布变化如图 9.铣削加工和喷砂处理均会造成构件整体应力大小及其分布的改变,导致构件原有结构下应力平衡的破坏,使总弯矩不为零,从而造成构件变形,同时,应力分布向平衡态转变.
|
图 9 构件应力平衡态演变过程 Figure 9 Evolution of equilibrium state in the component |
在铣削后、薄壁和底部喷砂后3种非平衡状态下的总弯矩MTotal由式(3)计算获得.假设使构件发生拱曲变形的力矩为正力矩,则3个非平衡状态下长度方向截面弯矩沿高度方向(Z方向)变化如图 10.

|
图 10 非平衡态下截面总弯矩变化 Figure 10 Evolution of bending moment under non-equilibrium state in profile |
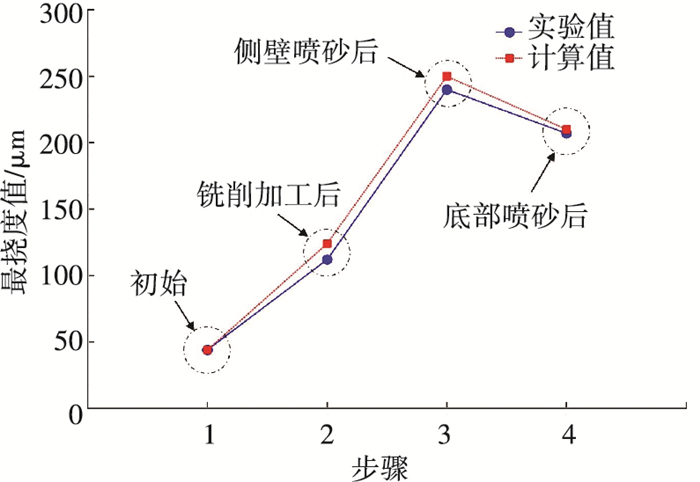
图 10中,构件非平衡态下的总弯矩MTotal在3种状态下均不为零,将促使构件发生变形达到新的平衡态,在结构应力平衡后的变形量大小可由式(4)、(5)计算得到.为便于对构件变形的实验和计算值进行比较,图 11中以构件中间部位最大挠度为对比量,对实验中3个应力状态下实验和计算变形量进行对比. 3个状态下计算值与实验结果偏差值分别为12 μm、10 μm和3 μm,偏差率(计算值实验值之差与实验值之比)分别为10.7%、4.1%和1.4%,发现计算值与实测值吻合度较好.
|
图 11 挠度实验与计算值对比 Figure 11 Deflection contrast between experiment and calculation |
变形函数计算准确性受到很多因素的影响,需要对相关主要因素进行变形不确定度计算和分析.分析认为,应力测试误差产生的总弯矩(MTotal)偏差、构件加工形状误差产生的截面惯性(Ix)值偏差以及形状测量偏差为主要误差源.故此,确定构件铣削加工尺寸误差、应力测试误差以及形状测量误差,作为加工变形总不确定度的计算依据.
采用A类不确定度的评定方法较为合适[25],用数理统计方法实验标准差s(x)表示,并以单个影响因素n次测量的平均值作为估计值,其不确定度u(x)为
| $ u\left( x \right) = \frac{{s\left( x \right)}}{{\sqrt n }}. $ | (7) |
对于多因素影响,可采用分量合成方法,将单个因素影响的不确定度进行一定规则下的分量合成,称为合成标准不确定度uc(ω),在直接测量情况下一般表示为
| $ {u_{\rm{c}}}\left( \omega \right) = \sqrt {\sum\limits_{i = 1}^m {{u^2}\left( {{\omega _i}} \right)} + 2\sum\limits_{i = 1}^m {{\rho _{ij}}u\left( {{\omega _i}} \right)u\left( {{\omega _j}} \right)} } . $ | (8) |
式中:u(ωi)为直接引起变形计算偏差的不确定度; ρij为误差因素的相关系数; m为误差因素个数.由于实验中各个影响因素对误差的作用效果具有独立性,因此,ρij=0.实验中引起实验不确定度的主要因素有应力测试误差,加工形状误差和形状测量误差,则实验合成标准不确定度uc(ω)为
| $ {u_{\rm{c}}}\left( \omega \right) = \sqrt {{u_{\rm{M}}}{{\left( \omega \right)}^2} + {u_{{{\rm{I}}_{\rm{x}}}}}{{\left( \omega \right)}^2} + {u_{\rm{m}}}{{\left( \omega \right)}^2}} . $ | (9) |
式中:uM(ω)为应变测试中总和力矩引起的不确定度; uIx(ω)为构件截面惯性矩引起的不确定度; um(ω)为实测形状引起的不确定度.
X射线衍射法和层削法测得的应力值误差会引起合力弯矩误差,表面应力测试误差带如图 8(b),层削法应力测试误差则通过重复测量求标准差获得.通过式(3)、(5)和(7),应力测试误差引起合力矩导致的形状预测不确定度uM(ω)为
| $ {u_{\rm{M}}}{\left( \omega \right)^2} = {\left( {\frac{{\partial \omega }}{{\partial M}}\frac{{\partial M}}{{\partial \sigma }}} \right)^2} \cdot u_\sigma ^2. $ | (10) |
构件尺寸误差导致的变形不确定度主要由构件薄壁引起.由于构件壁厚较薄,薄壁在铣削加工出现让刀现象,导致构件薄壁的加工误差[20].通过对壁厚b进行10次测量,薄壁尺寸最大值bmax=2.23 mm,最小值bmin=2 mm,采用极差法求壁厚标准差,则为
| $ s\left( b \right) = \frac{{\Delta b}}{{{d_{\rm{n}}}}} = 0.075\;{\rm{mm}}{\rm{.}} $ | (11) |
极差值Δb=bmax-bmin=0.23 mm,样本数量为10时,查阅工具手册得dn=3.08.通过式(1)、(2)、(5)和(7)获得有加工尺寸误差导致的不确定度uIx(ω),则为
| $ {u_{{{\rm{I}}_{\rm{x}}}}}{\left( \omega \right)^2} = {\left( {\frac{{\partial \omega }}{{\partial {I_{\rm{x}}}}}\frac{{\partial {I_{\rm{x}}}}}{{\partial b}}} \right)^2} \cdot u_{\rm{b}}^2. $ | (12) |
构件变形测量误差通过极差法求取标准差,对同一状态下构件最大变形挠度值进行10次测量,获得变形最大挠度值的极差值Δω=7 μm,则形状测量直接误差的标准差sm(ω)=0.7 μm,由式(7)获得形状测量导致计算模型的不确定度um(ω)为
| $ {u_{\rm{m}}}{\left( \omega \right)^2} = u_{\rm{m}}^2. $ | (13) |
最后计算得到构件在铣削加工、侧壁喷砂和底面喷砂3个状态下变形不确定度如表 1所示.
| 表 1 变形不确定度(μm) Table 1 Deformation uncertainty (unit, μm) |
表 1可见变形函数计算的不确定度主要来源于应力测试误差. 3个不同状态下实验值均处于模型计算值的不确定度范围内如图 12所示,表明变形函数解析计算准确性得到保证.

|
图 12 变形的不确定度分布 Figure 12 Uncertainty distribution of deformation calculation |
为检验变形函数的可重复性,对3块表面全覆盖喷砂处理的薄壁构件进行了测算,主要测试了表面应力及分布深度,相关文献见文献[26],实验和计算结果如表 2所示.
| 表 2 试样变形实验和计算值 Table 2 Deformation of experiment and calculation of samples |
3个试样的变形值与计算值吻合度较好,均处在理论模型不确定度范围内,说明变形函数在计算方法和准确性上具有重复性.
4 结论1) 力学模型客观反映出薄壁构件上存在的应力场,不论是表面加工应力,还是毛坯初始应力,都是构件变形的原因和动力.改变构件上弯曲扭矩的平衡能使构件变形.
2) 以材料力学为基础,推导出薄壁构件应力-变形函数表达方法,并在实验中得到验证.其误差在不确定度计算值范围内,说明对应力场分布适当简化并没有影响函数的有效性,而同时又提高了函数实用性.
3) 在加工尺寸、毛坯制备和表面应力分布已知条件下,可以提前预知加工后构件的变形,这对薄壁构件加工变形可以起到工程指导作用,说明函数具有了一定预测功能.
| [1] |
MASOUDI S, AMINI S, SAEIDI E, et al. Effect of machining-induced residual stress on the distortion of thin-walled parts[J].
International Journal of Advanced Manufacturing Technology, 2015, 76(1-4): 597-608.
DOI: 10.1007/s00170-014-6281-x |
| [2] |
LIU Changqing, LI Yingguang, Hao Xiaozhong. An adaptive machining approach based on in-process inspection of interim machining states for large-scaled and thin-walled complex parts[J].
International Journal of Advanced Manufacturing Technology, 2017, 90(9-12): 3119-3128.
DOI: 10.1007/s00170-016-9647-4 |
| [3] |
常艳艳, 孙涛, 李增强. 硬铝合金超精密车削残余应力的仿真及试验[J].
哈尔滨工业大学学报, 2015, 47(7): 41-46.
CHANG Yanyan, SUN Tao, LI Zengqiang. Simulation and experiments of residual on ultra-precision turning of hard aluminum alloy[J]. Journal of Harbin Institute of Technology, 2015, 47(7): 41-46. DOI: 10.11918/j.issn.0367-6234.2015.07.006 |
| [4] |
张壮南, 张耀春. 残余应力对单轴对称工字梁稳定承载力的影响[J].
哈尔滨工业大学学报, 2007, 39(12): 1864-1868.
ZHANG Zhuangnan, ZHANG Yaochun. Effects of welding residual stresses on the stability capacity of the monosymmetric I-beam[J]. Journal of Harbin Institute of Technology, 2007, 39(12): 1864-1868. DOI: 10.3321/j.issn:0367-6234.2007.12.004 |
| [5] |
张峥. 飞机弱刚性铝合金结构件的残余应力和加工变形控制技术研究[D]. 南京: 南京航空航天大学, 2016.
ZHANG Zheng. Research on residual stress and machining distortion of aeronautic weak rigidity in aluminum structure[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016. |
| [6] |
GAO Yuanyuan, MA Jianwei, JIA Zhenyuan, et al. Tool path planning and machining deformation compensation in high-speed milling for difficult-to-machine material thin-walled parts with curved surface[J].
International Journal of Advanced Manufacturing Technology, 2016, 84(9-12): 1757-1767.
DOI: 10.1007/s00170-015-7825-4 |
| [7] |
ZHANG FP, YAN Y, BUTT SI. Integrated model based thin-walled part machining precision control for the workpiece-fixture system[J].
International Journal of Advanced Manufacturing Technology, 2016, 85(5-8): 1745-1758.
DOI: 10.1007/s00170-015-8036-8 |
| [8] |
SINGH A, AGRAWAL A. Investigation of surface residual stress distribution in deformation machining process for aluminum alloy[J].
Journal of Materials Processing Technology, 2015, 225: 195-202.
DOI: 10.1016/j.jmatprotec.2015.05.025 |
| [9] |
JIANG Xiaohui, WANG Yifei, DING Zishan, et al. An approach to predict the distortion of thin-walled parts affected by residual stress during the milling process[J].
International Journal of Advanced Manufacturing Technology, 2017(1): 1-14.
DOI: 10.1007/s00170-017-0811-2 |
| [10] |
HUANG Xiaoming, SUN Jie, Li Jianfeng. Finite ele-ment simulation and experimental investigation on the residual stress-related monolithic component deformation[J].
The International Journal of Advanced Manu-facturing Technology, 2015, 77(5): 1035-1041.
DOI: 10.1007/s00170-014-6533-9 |
| [11] |
杨吟飞, 张峥, 李亮, 等. 7085铝合金残余应力及加工变形的数值仿真与试验[J].
航空学报, 2014, 35(02): 574-581.
YANG Yinfei, ZHANG Zheng, LI Liang, et al. Numerical simulation and test of bulk residual stress and machining distortion in aluminum alloy 7085[J]. Acta Aeronautica ET Astronautica Sinica, 2014, 35(02): 574-581. DOI: 10.7527/S1000-6893.2013.0469 |
| [12] |
YANG Y, Li M, Li K R. Comparison and analysis of main effect elements of machining distortion for aluminum alloy and titanium alloy aircraft monolithic component[J].
International Journal of Advanced Manufacturing Technology, 2014, 70(9-12): 1803-1811.
DOI: 10.1007/s00170-013-5431-x |
| [13] |
DENKENA B, BOEHNKE D, LEN L D. Machining induced residual stress in structural aluminum parts[J].
Production Engineering, 2008, 2(3): 247-253.
DOI: 10.1007/s11740-008-0097-1 |
| [14] |
王民, 刘宇男, 孙国智, 等. 初始残余应力和切削残余应力对薄壁件加工变形的影响[J].
北京工业大学学报, 2017, 43(07): 55-61.
WANG Min, LIU Yu'nan, SUN Guozhi, et al. Influence of initial residual stress and cutting stress on machining deformation of thin-walled parts[J]. Journal of Beijing university of technology, 2017, 43(07): 55-61. DOI: 10.11936/bjutxb2016040066 |
| [15] |
SALEEM W, IJAZ H, ZAIN-UL-ABDEIN M, et al. Studying control strategies for dimensional precision in aerospace parts machining[J].
International Journal of Precision Engineering and Manufacturing, 2017, 18(1): 39-47.
DOI: 10.1007/s12541-017-0005-8 |
| [16] |
LI Beizhi, JIANG Xiaohua, YANG Jianguo, et al. Effects of depth of cut on the redistribution of residual stress and distortion during the milling of thin-walled part[J].
Journal of Materials Processing Technology, 2015, 216: 223-233.
DOI: 10.1016/j.jmatprotec.2014.09.016 |
| [17] |
NERVI S. A mathematical model for the estimation of effects of residual stresses in aluminum parts[D]. Washington: Washington University, 2005.
|
| [18] |
唐志涛. 航空铝合金残余应力及切削加工变形研究[D]. 济南: 山东大学, 2008.
TANG Zhitao. Residual stresses and deformations of aerospace aluminum alloy in machining[D]. Jinan: Shandong University, 2008. |
| [19] |
黄晓明, 孙杰, 李剑峰. 基于刚度与应力演变机制的航空整体结构件加工变形预测理论建模[J].
机械工程学报, 2017, 53(09): 201-208.
HUANG Xiaoming, SUN Jie, LI Jianfeng. Mathematical modeling of aeronautical monolithic component machining distortion based on stiffness and residual stress evolvement[J]. Journal of Mechanical Engineering, 2017, 53(09): 201-208. DOI: 10.3901/JME.2017.09.201 |
| [20] |
LIU Simeng, SHAO Xiaodong, GE Xiaobo, et al. Simulation of the deformation caused by the machining cutting force on thin-walled deep cavity parts[J].
International Journal of Advanced Manufacturing Technology, 2017, 92(9-12): 3503-3517.
DOI: 10.1007/s00170-017-0383-1 |
| [21] |
HB/Z 26-2011, 航空零件喷丸强化工艺[S].
HB/Z 26-2011, Shot blasting strengthening technology for aviation parts[S]. Beijing: SATIND, 2001. |
| [22] |
LV You, LEI Liqun, SUN Lina. Effect of shot peening on the fatigue resistance of laser surface melted 20CrMnTi steel gear[J].
Materials Science & Engineering A, 2015, 629: 8-15.
DOI: 10.1016/j.msea.2015.01.074 |
| [23] |
廖凯. 铝合金厚板淬火—预拉伸内应力形成机理及其测试方法研究[D]. 长沙: 中南大学, 2010.
LIAO Kai. Research mechanism and measurement method of quenching-prestretching stress in aluminum alloy thick plate[D]. Changsha: Central South University, 2010. |
| [24] |
MARCISZKO M, BACZMAN. SKI A, BRAHAM C, et al. Stress measurements by multi-reflection grazing-incidence X-ray diffraction method (MGIXD) using different radiation wavelengths and different incident angles[J].
Acta Materialia, 2017, 123: 157-166.
DOI: 10.1016/j.actamat.2016.10.029 |
| [25] |
田芳宁. 实验室认可中的测量不确定度评定[D]. 合肥: 合肥工业大学, 2012.
TIAN Fangning. Measurement uncertainty evaluation in calibration laboratory accreditation[D]. Hefei: Hefei university of technology, 2012. |
| [26] |
ZHANG Xiaodi, LIAO Kai, JI V, et al. Effect of the shot peening on the deformation of Al alloy component[J].
Surface Engineering, .
DOI: 10.1080/02670844.2017.1380359 |
 2018, Vol. 50
2018, Vol. 50


