2. 哈尔滨工业大学 计算机科学与技术学院, 哈尔滨 150001
2. School of Computer Science and Technology, Harbin Institute of Technology, Harbin 150001, China
在基于图的众多研究中,互模划分在许多应用领域中都起着至关重要的作用[1].直观上,图的互模划分是指将图中的点按照预先定义的“特征”进行划分的操作,“特征”相同的点被划分到同一集合中. “特征”可以根据需要而灵活定义,例如它可以包含点的内容以及点在图中的位置信息.
互模划分有着广泛的应用.在数据压缩领域[2-3],同一集合中的点使用相同的编号; 通过适当的定义,互模划分可以被用来为XML以及RDF数据库建立结构化索引[4-5];此外,在数据的查询优化以及分析[6]中互模划分也有明确的应用.
随着图数据规模(点数目、边数目)的增长,许多图数据,如社交网络图等,已经包含数以亿计的点和边.传统的运行在单机上的互模划分算法面临着越来越大的挑战,分布式算法以及并行算法则成为提高图计算可扩展性的重要途径.
针对图的互模划分(k-互模划分)问题,Luo[7]以及Alexander Schätzle[8]分别提出基于MapReduce计算模型的局部互模划分算法.这两种算法均使用Hadoop作为分布式数据处理平台,解决了传统算法难以胜任的在大图数据上进行互模划分的问题. Stefan Blom等[9]提出的the naive method算法是一种迭代算法,该算法的分布式版本分为多次迭代,每次迭代执行下面的三步操作:计算点的特征、为点的特征计算一个全局唯一的编号(也就是标识)、邻居点之间交换信息—为下一轮迭代做准备. Luo以及Schätzle提出的算法也是采用这种思想,其中Luo的方法每轮迭代需要三次完整的MapReduce操作来完成这三步操作; 而Schätzle的方法中则采用哈希方法获得点的特征编号,同时通过在MapReduce操作中直接“输出“完整的图. Hadoop平台中数据在Mapper和Reducer之间的传输全部通过网络.这种设计使得采用Hadoop平台实现的上述两种算法不可避免地会有沉重的网络数据传输任务.采用MapReduce计算框架意味着计算点的k-互模特征的时候,无差别地对待图中的每个点.但是为计算图中点的k-互模特征,只需要获取该点的邻居信息(与点距离为k以内)即可,所以图中不同的点应该被差别对待以减少不必要的通信代价.
本文算法中采用GPS[10]/Pregel[11]的计算模型来解决这一问题,在GPS/Pregel平台上图中的点通过边向相邻点传递信息,只有边的起点和终点由不同工作节点处理的情况下,数据传输需要通过网络.这个特点有效地减少了网络数据通信量.
1 局部互模相关概念 1.1 局部互模为便于表述,下文中采用k-互模来表示局部互模. k-互模是指预先定义点的特征只包含距离它k以内(包含k)的邻居信息以及点自身的信息(k≥0).
N表示有限的点集,
定义1.1 [7] k是一个非负整数,G= < N, E, λN, λE>是一个图,那么点u, v∈N被称为k-互模(表示为u≈kv),当且仅当下述条件成立
1) λN(u)= λN(v);
2) 当k>0时,则
| $ \forall u\prime \in N\left[{\left( {u, u\prime } \right) \in E} \right] = > {\rm{ }}\exists v\prime \in N\left[{\left( {v, v\prime } \right) \in E} \right], $ |
使得u′≈k-1v′,λE (u, u′) =λE (v, v′);
3) 当k>0时,则
| $ \forall v\prime \in N\left[{\left( {v, v\prime } \right) \in E} \right] = > {\rm{ }}\exists u\prime \in N\left[{\left( {u, u\prime } \right) \in E} \right], $ |
使得v′≈k-1u′,λE (v, v′) =λE (u, u′).
本文提出的的算法不是为了判断两个图是否是k-互模,而是将图中的点划分为不同的集合,同一集合内的点之间k-互模.
1.2 k-互模划分标识定义1.2 k是一个非负整数,G= < N, E, λN, λE>是一个图,k-互模划分标识是k+1个函数映射的集合P={pId0,K,pIdk}; 对于0≤i ≤k, pIdi是从点集N到点编号集合的一个映射,并且对于
将每个点划分到对应的集合中,基于每个点所在的位置为每个点建立“特征”,特征的严格定义如下
定义1.3 k是一个非负整数,G= < N, E, λN, λE>是一个图,P={pId0,K,pIdk}是图G的k-互模划分标识,那么u∈N的k-互模划分特征sigk(u)=(pId0(u), L). L为点的位置信息,
| $ L = \left\{ \begin{array}{l} \mathit{\emptyset} ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;\;\;k = 0;\\ \left\{ {\left( {{\lambda _E}\left( {u, {u^\prime }} \right), pI{d_{k1}}\left( {{u^\prime }} \right)} \right){\rm{| }}\left( {u, {u^\prime }} \right) \in E} \right\}{\rm{ }}, \;\;\;\;\;\;\;{\rm{if}}\;\;\;k > 0. \end{array} \right. $ |
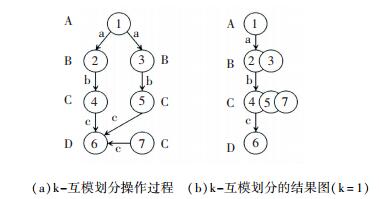
互模划分样例图见图 1,图 1(a)用来演示1-局部互模划分的操作过程,图 1(b)是操作的结果.
|
图 1 K-互模划分样例 Figure 1 Example graph for K-bisimulation |
首先计算点的1-互模划分特征,点1的初始特征编号为A.由定义1.3可知,点1的1-互模划分特征为(A, ((a, B)(a, B))),点2和点3的1-互模划分特征均为(B, ((b, C))),点4、5和7的1-互模划分特征均为(C, ((c, D))),点6点的1-互模划分特征为(D, ()).
1.5 GPS分布式图数据处理平台GPS分布式图数据处理平台专门用于处理大图上的计算任务,其系统架构包含一个Matser节点(称为主节点)以及多个Worker节点(称为工作节点),工作节点使用HDFS分布式文件系统进行数据的存储,各节点之间的通信使用Apache MINA[12]. GPS分布式图数据处理平台的系统架构图, 见图 2[10].

|
图 2 GPS系统架构 Figure 2 GPS architecture |
图数据的存储使用HDFS分布式文件系统,点被随机划分到各个工作节点中.
任务的计算分为多次迭代.图中每个点有休眠态和激活态两种状态.每个点的初始状态为激活态.每一轮迭代开始,处于激活态的点向其出边邻居传输数据.数据传输完成后,所有接收到数据的点都被系统设置为激活态,点根据从其入边邻居传来的数据进行计算,并根据计算结果更新自己的信息.在一轮迭代中,如果某个点并没有从其入边邻居中接受到数据,则自动在下轮迭代开始前进入休眠态.当图中所有的点都处于休眠态的时候,程序结束.
数据传输只在有边直接相连的点之间进行,从有向边的起点传输数据到有向边的终点.当点和某一出边相邻点处在同一个工作节点(Worker)中的时候,它们之间的数据传输是不需要经过网络; 当点和出边相邻点处在不同的工作节点上时,它们之间的数据传输通过网络完成.为降低网络数据传输量,可以考虑减少处于不同工作节点上的点之间的边数,使文中图预划分处理可以取得良好效果.
基于GPS平台编程,就本文的互模划分算法而言,图中每个点的计算任务在Vertex.compute()函数中完成.
2 基于GPS的局部互模划分算法为了高效并行进行图k-互模划分计算, 进行图的预划分操作,较大幅度地减少位于不同工作节点上的点之间的边数,这将较大幅度地减少通过网络传输的数据量;
“自动”实现点特征编号的更新,而不用为此增加额外操作; Luo为了实现节点特征编号的更新,增加一次MapReduce操作. Schätzle为实现节点特征编号的更新,不惜额外将图中每条边通过MapReduce处理,增加网络数据传输负担.本文算法采用分布式图数据处理平台及相应的算法框架,无需为此增加额外操作.
采用哈希函数来计算节点特征的编号,这相比较于Luo的算法节省了很多运算;
为计算图中每个点的k-互模划分特征,算法只需要利用到点的邻居(与点距离不超过k)信息,采用GPS分布式图数据处理平台,可以充分利用到这种空间局域性.
2.1 算法描述定义输入到GPS分布式图数据处理平台的图数据格式
< vertex-id> < opt-vertex-value> < outgoing-edge-id-1> < opt-outgoing-edge-id-1-value> < outgoing-edge-id-2> < opt-outgoing-edge-id-2-value>...
每一行数据代表了图中一个点的信息,其中vertex-id表示点编号,opt-vertex-value表示点的内容,outgoing-edge-id-1表示该点的第一条出边指向的点的编号,opt-outgoing-edge-id-1-value表示该点第一条出边的边值(在接下来的实验中,边值为该边的编号).
GPS是要求输入按照点的标号从0开始输入,如果某个点没有边,那么也应独自占一行输入.
互模划分算法的部分(伪)代码实现
Pre_Process(G)
1void compute(inMessages, superstepNum)
2if(superstepNum == 0)
3 HashId = Hash(this.getVertexValue())
4 this.setID(HashId)
5 for(outEdge : this.getOutEdges())
6 edgeValue = outEdge.getEdgeValue()
7 sendMessage(outEdge.getNeighborId()
, (edgeValue, this.getID())
8 return
9if(superstepNum < = k)
10 m_string = this.getVertexValue()
11 for(mValue : inMessages)
12 m_string += mValue.toString()
13 HashId = Hash(m_string)
14 this.setID(HashId)
15 for(outEdge : this.getOutEdges())
16 edgeValue = outEdge.getEdgeValue()
17 sendMessage(outEdge.getNeighborId()
, (edgeValue, this.getID()))
18 return
19voteToHalt()
互模划分算法中,Pre_Process(G)代表算法的第一部分,进行图的预处理.在整个算法的执行过程中,图的预处理只需要执行一次.图的预处理需要完成以下4部分的工作:
1) 将原始图数据转换成GPS要求的输入格式.
2) 实现图中有向边方向的倒转,因为计算点的特征需要从其外向相邻点中获取信息,而Pregel/GPS中信息的发送是沿着有向边指向的方向,由有向边的起点向终点传递.
3) 使用METIS(由Karypis Lab开发的图切分软件包)程序对图做预划分处理,为将划分后的多个子图输入到GPS中,需要对图数据进行转换.
4) 平衡各个工作节点的工作量; 为均衡负载,实验在做预划分的时候将图划分后获得的子图数目是实验中使用的工作节点数目的5倍,即每个工作节点处理5个子图.算法运行样例中预处理划分的子图数目等于工作节点数目.
函数compute()代表算法的第二部分代码.在第superstepNum轮迭代中,每个点均会执行一次compute函数,执行完毕后superstepNum自动加一具体算法说明:
1) 3~4行代码根据点的内容计算点的初始特征编号,即0-互模划分特征编号(k=0);
2) 5~8行代码向所有外出边相邻点发送点的初始特征编号以及边的编号,即发送(λE(u, u′), pId0(u′));
3) 10~12行代码从相邻点中获取自身的特征信息;
4) 13~14行代码计算点的特征编号,采用哈希函数来处理获取到的特征信息集合,进而获取特征编号; 需要注意的是哈希值应当与特征信息集中元素的顺序无关;
5) 15~18行代码向所有外出边相邻点发送点的特征编号以及边的编号,即发送(λE(u, u′), pId0(u′));
6) 当计算完k-互模划分后,在第19行代码中点将自己的运行状态设置为休眠态.程序中所有点在下一轮迭代开始前进入休眠态,程序结束.
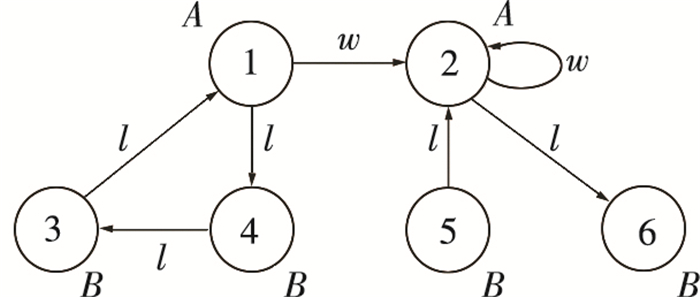
2.2 算法运行样例算法样例见图 3[7], 为原始样例图的翻转图,即将原始样例图中的每条有向边边的指向颠倒.
|
图 3 算法运行样例 Figure 3 The example graph for our algorithm |
点的初始内容(图中的A, B)可根据需要选择是否输入到GPS中; 出于完整性的考虑,互模划分算法的伪代码中以及本节的算法运行样例中均默认点的初始内容是存在的.点的初始内容经过哈希函数的计算即可获得点的初始特征编号,即0-互模划分特征编号.
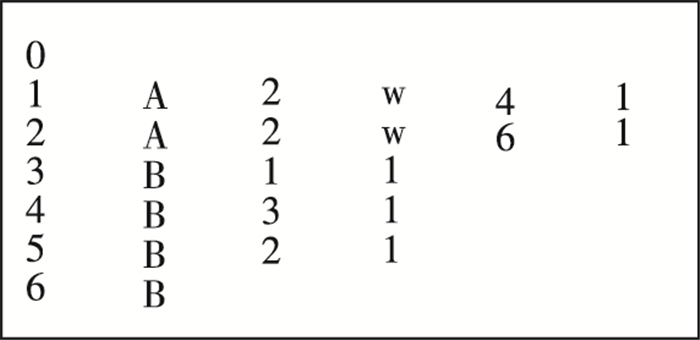
图 4是图 3输入到GPS平台的数据,每一行代表一个点的信息,第一列表示点标号,其中点0是GPS平台要求的输入,图 3中并没有标识出这个点.以“1A2w4l”为例,输入表示点的编号是1,点的内容是A,点的第一条出边指向点2,该出边的内容为w,点的第二条出边指向点4,该出边的内容为l.根据GPS平台的默认处理(假设有两个工作节点),点0、2、4、6会被放在第一个工作节点中,点1、3、5会放在第二个工作节点中.有4条边的起点和终点处于不同的工作节点中.
|
图 4 算法运行样例输入 Figure 4 The input to our algorithm |
经过图的预划分处理,图从边(1, w, 2)处分为两块子图.第一个工作节点处理点1、3、4,而第二个工作节点处理点2、5、6、0,此时只有1条边的起点和终点处于不同的工作节点中.为了将经过预划分的子图输入到GPS分布式图数据处理平台中,需要按照划分结果处理图 4的算法运行样例输入,以便在GPS中实际的将点1、3、4放置于同一个工作节点中,将点0、2、5、6放置于另一个工作节点中.处理的方法是将图 4中的编号0、1、2、3、4、5、6分别映射成0、1、2、3、5、4、6,再按照第一列排序.这样做的依据是GPS平台内部默认的分配算法是将编号为node_id的点分配到编号为vertex_id = node_id % vertex_num的工作节点上,其中vertex_num为工作节点的数目.
第0轮迭代,图中各点根据点的内容计算初始特征编号,并沿着有向边向相邻点发送信息{边值,初始特征编号};
从第1轮到第k轮迭代,首先从相邻点获取其特征以及对应边的边值,加上点的内容,即上文提到的sigi(u)=(pId0(u), L),然后利用哈希函数计算点的当前特征编号,并更新;
当k-互模划分计算完成后,所有的点进入休眠态,程序结束.
2.3 算法的网络通讯量分析对比前面提到的3种算法的本质是一样的,故而认为对于同一个计算任务三种算法所需要的迭代次数也是相同的,同时算法均需要有个终止条件判断部分,这部分需要的通讯量非常少,故而没有考虑这部分; 对于Hadoop平台而言,无论Mapper和Reducer是否运行于同一台机器,两者之间的数据传输均使用网络,即可认为Mapper和Reducer之间所有的数据均通过网络传输.
通过网络传输的数据主要有特殊标志、出发点编号、有向边的编号、终止点编号以及出发点所在的划分集合编号.假定这5个元素的长度都是a个字节、图中点的个数为N、边的个数为M.
对于Luo的算法,第一次MapReduce操作通过网络传输的数据有两部分点编号,特别标注,点的初始集合编号,点在上一轮迭代后所在的集合编号以及发出点编号,有向边的编号,终止点编号,终止点在上一轮迭代后所在的集合编号.合并起来,第一轮通过网络传输的数据规模为4×a×N+4×a×M; 第二次通过网络传输的数据为点编号,特殊标志,点的初始集合编号,点的特征,其中点的特征包括点上一轮迭代后所在的集合编号、从它出发的边编号以及指向的点的上一轮迭代后所在集合编号.合并起来,第二次MapReduce操作通过网络传输的数据规模为4×a×N+2×a×M;第三次MapReduce操作通过网络传输的数据为点编号,特殊标志,点所在的初始集合编号,点的本轮迭代后所在集合编号,故而为4×a×N.综合整个过程,每一轮迭代需要通过网络传输的数据总量为6×a×M+8×a×N.
对于Schätzle的算法,其需要通过网络传输的数据也有两部分:起始点编号,数字0,起始点编号,边编号,终止点编号,终止点所在的集合编号和终止点编号,数字1,起始点编号,边编号,终止点编号,终止点所在的集合编号,为方便起见可认为数字0和数字1的大小也是a个字节.可计算出来,通过网络传输的数据规模为6×a×M+6×a×M =12×a×M.
对于本文提出的算法,仅当边的起点和终点位于不同工作节点的时候,它们之间的数据传输才需要通过网络,假设这样的边的数目为M′.需要通过网络传输的数据为边编号,点在上一轮迭代后所在集合编号,终止点编号则总的网络数据传输规模为3×a×M′.
Luo的算法的网络通讯量为6×a×M+8×a×N,图中边的数目一般比点的数目要多许多,如Twitter[13]的数据中边的数目几乎为点的数目的30倍.故而可认为Luo算法的网络通讯量为6×a×M. Schätzle的算法的网络数据通讯量为12×a×M.
实验数据,M′在多数情况下相当于M的1/3,有些情况下甚至仅为M的1/50.这里取M′=M/3,所以本文提出的算法网络数据通讯量近似为a×M.算法的网络数据通讯量下降为Luo的算法的1/6,Schätzle的算法的1/12.最坏情况下M′=M,算法的网络数据通讯量下降为Luo的算法的1/2,Schätzle的算法的1/4.
通过分析,本文提出的算法的网络数据通讯量下降为Luo的算法的1/2~1/6,Schätzle的算法的1/4~1/12.
3 数据转换算法GPS图数据处理平台对于图的输入格式有着较为严格的要求.本文以SP2Bench图数据为例,介绍如何一般性的将格式迥异的大图数据转化为GPS要求的格式.对于小图而言,由原始图数据生成GPS需要的数据相对简单,而对于本文实验采用的大图图包含几亿边、点而言则必须设计专门的分布式程序来处理. SP2Bench的数据,每行对应一个三元组(点,边,点).三元组的每一项都是字符串.而GPS的输入要求边、点的编号均为整数且按照图的邻接表格式组织.
实验采用Hadoop平台来处理SP2Bench生成GPS的输入图.程序分为三次MapReduce操作.
3.1 第一次MapReduce操作第一次MapReduce操作的目的是获取SP2Bench生成的RDF三元组中每个元素的编号,算法伪代码见下面算法GenID:
Map操作:
GenIDMapper(key, value)
v[] = value.split (“ ”)
output(v[0], value+”, ”+”0”)
output(v[1], value+”, ”+”1”)
output(v[2], value+”, ”+”2”)
Reduce操作:
GenIDReducer(key, values)
for(value : values)
output(startNum+count++, value)
endfor
GenIDMapper的执行分为以下3步:
1) 读取输入:按照Hadoop中默认的TextInputFormat方式从输入文件(SP2Bench生成的图)中读取数据; 读取到的key是一个LongWritable型的数值,表示当前读取的value数据相对于文件头的偏移量,value是一行数据;
2) 中间处理:SP2Bench生成的数据每一行都是一个按照空格隔开的三元组,所以读取数据后按照空格划分value,获得v[i]数组,该数组长度为3;
3) 输出结果:一共有三组键值对输出,第i组键值对的键为v[i],值为value+", "+"i".
GenIDReducer中有两个变量需要设置,变量startNum和count均为Reducer的变量,只在每个Reducer启动时初始化,每次执行GenIDReducer函数的时候并不会对它们再次初始化.使用counti来表示第i个Reducer中的变量count,使用startNumi来表示第i个Reducer中的变量startNum. counti等于第i个Reducer中处理key的数目,初始化为0. startNumi等于前面i-1个reducer所处理的key数目countj之和,0 < =j < =i-1.由于程序运行前就需要设定startNumi的值,所以可以先执行一遍算法,然后利用实验结果去设定startNumi的值,之后再执行算法,得到最终的结果.计算startNumi的公式如下所示:
| $ startNu{m_i} = \sum\limits_{j = 1}^{j \le i - 1} {coun{t_j}} $ |
GenIDReducer的执行分为以下3步:
1) 读取输入:获得GenIDMapper输出的键值对中的键以及该键对应的所有值的集合values; Hadoop将所有GenIDMapper输出的键值对中同一个键对应的值合并为值集合,且同一个键只会被一个Reducer处理.
2) 中间处理:对于中的每个值value,计算它的编号.编号等于startNum+count++;
3) 输出结果:对于values中的每个值value输出一个键值对,键为它的编号,值为value本身.
3.2 第二次MapReduce操作第二次MapReduce操作的目的将RDF三元组的每个元素用编号替换,实现伪代码见算法GenTriple:
Map操作:
GenTripleMapper(key, value)
v[] = value.split (“, ”)
output(v[0], key+”, ”+value)
Reduce操作:
GenTripleReducer(key, values)
for(value : values)
v[] = value.split(“, ”)
t[v[1]] = v[0]
output(null, t[0]+” ”+t[1]+” ”+t[2])
endfor
GenTripleMapper的执行分为3步:
1) 读取输入:按照Hadoop中KeyValueTextInputFormat格式输入,读取到的key为GenIDReducer输出的键,读取到的value为GenIDReducer输出的值;
2) 中间计算:将value按照逗号分成两部分,第一部分代表SP2Bench生成的RDF三元组,第二部分是一个数字,代表key在这个三元组中的位置.
3) 输出结果:输出键值对的键为SP2Bench生成的RDF三元组,值为key(RDF三元组中元素的编号)以及该key代表的元素在三元组中的位置.
GenTripleReducer的执行分为3步:
1) 读取输入:由于同一个键的值会被同一个Reducer处理,所以获取的输入key为SP2Bench生成的RDF三元组,values集合包括该三元组三个元素的编号以及元素在三元组中的位置;
2) 中间计算:合并values中的三个value,获得RDF三元组3个元素的编号;
3) 输出结果:输出的键为空,值为结果编号后的RDF三元组.
3.3 第三次MapReduce操作第三次MapReduce操作的目的是将编号后的三元组(边)转变为GPS输入文件,实现伪代码
Map操作
MergeMapper(key, value)
v[] = value.split (“ ”)
output(v[2], v[0]+”, ”+v[1])
output(v[0], “”)
分区操作:
MergePartitioner(key, value, numPartition)
return key >> k
Reduce操作:
MergeReducer(key, values)
result = key
for(value : values)
result += “ ”+value
output(null, result)
endfor
MergeMapper的执行分为3步:
1) 读取输入:按照Hadoop中默认的TextInputFormat方式读取,获取的value为编号后的三元组(边);
2) 中间处理:从三元组中读取3个元素;
3) 输出结果:输出两个键值对,第一个键值对键为三元组中的第三个元素,第一个键值对的值为三元组的第一个、第二个元素; 第二个键值对的键为三元组的第一个元素,值为空,确保没有入边的点也存在于最终的输出中.这样处理使得每条边的指向发生改变.
MergeReducer的执行分为3步:
1) 读取输入:获取的key为点(三元组中的元素)编号,values集合中每个value代表为该点的一条出边;
2)中间处理:将同一个点的所有出边合并;
3) 输出结果:键值对的键为空,值为点以及其所有出边.
Hadoop通过Partitioner来将Mapper输出的数据分配到不同的Reducer上处理.
MergePartitioner的作用是便于输出结果的合并.由于Hadoop中Reducer处理的时候是按照键的先后顺序来一次处理的,所有Reducer输出的文件是有序的.修改Partitioner使得不同Reducer处理的key是有序的,这样使得不同Reducer输出结果之间也是有序的.
MergePartitioner执行的时候键值对(key, value)被分配到第(key>>k)个Reducer中去.计算变量k值的公式所示:
| $ k = {\rm{}}\left[ {{\rm{lo}}{{\rm{g}}_2}\left( {\frac{{maxKey}}{{reducerNum}}} \right)} \right]{\rm{ }}. $ | (1) |
式中的变量maxkey为图中最大的点编号,reducerNum为Reducer的数目.
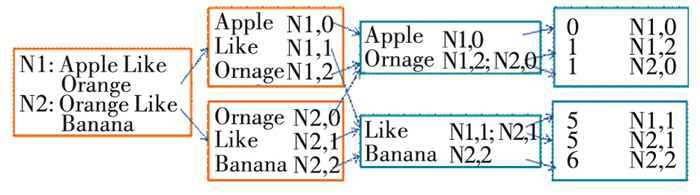
图 5~7分别表示了算法GenID、算法GenTriple以及算法Merge的运行过程.
|
图 5 算法GenID运行过程示例 Figure 5 Computation process for algorithm GenID |

|
图 6 算法GenTriple运行过程示例 Figure 6 Computation process for algorithm GenTriple |
|
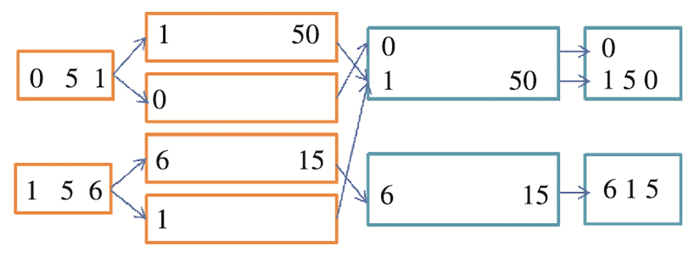
图 7 算法Merge运行过程示例 Figure 7 Computation process for algorithm Merge |
每个算法是一次MapReduce操作,分为4个阶段:从文件读取输入; 执行Mapper操作并输出Mapper结果; Reducer获取输入、执行并输出; 获取最终输出,存入文件.图 5~7中从左到右的四列图分别对应上述4个阶段.
图 5中的N1, N2分别指代输入的第1行RDF三元组和第2行三元组,仅仅处于方便表示的目的.实验中第一列并没有存储字符串N1、N2,而第二列(以及图 6)中的N1、N2分别为字符串“Apple like Orange”以及“Orange like Banana”.至此,完成了从RDF数据中生成GPS所需的输入图数据的过程.
对于Twitter图数据而言,数据本身已经是经过编号后的图数据,每行的两个整数分别代表着一条边的起点编号和终点编号.可将上述算法稍加修改即可获得需要的GPS输入图数据.
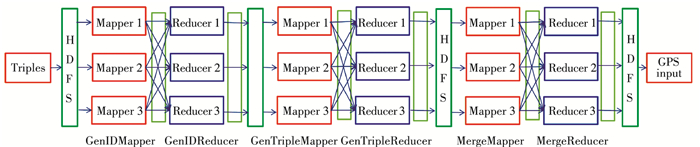
数据流过程概括见图 8.
|
图 8 转换三元组图数据输入到GPS Figure 8 Whole computation process for converting initial graph to input into GPS |
第一部分实验完整地执行了互模划分算法,而第二部分的实验并没有执行互模划分算法的Pre_Process(G)的图划分的操作.这是因为实验预处理部分需要使用METIS程序对图进行划分,但是实验缺乏大内存机器,难以在大图上使用METIS程序进行划分操作.
4.1 小图实验 4.1.1 实验环境实验使用了21台机器(一个主节点,20个工作节点)的机群.其中,每台机器具备8核Intel(R) Xeon(R) CPU,内存8G.实验存储使用HDFS,版本为Apache Hadoop 0.21.0;编程使用Java 1.6;GPS使用的版本为GPS 1.0;METIS的版本为METIS-5.1.0;
实验采用的数据有真实世界的数据(包含普通图数据[14]以及RDF数据[15]),也有生成的RDF数据SP2Bench[16]表 1~8中缩写为SP2-为系列数据集,此外为公共数据集.表 1是实验采用的图数据(非RDF),表 2是实验采用的RDF数据.
| 表 1 小图实验采用的图数据(非RDF) Table 1 Non-RDF dataset for the small-graph experiments |
| 表 2 小图实验采用的图数据(RDF) Table 2 RDF dataset for the small-graph experiments |
| 表 3 图划分实验结果 Table 3 Experimental results for graph partition |
| 表 4 k-互模划分实验结果 Table 4 Experimental results for k-bisimulation |
| 表 5 大图实验采用的图数据(非RDF) Table 5 Non-RDF dataset for the large-graph experiments |
| 表 6 大图实验采用的图数据(RDF) Table 6 RDF dataset for the large-graph experiments |
| 表 7 实验机群配置对比 Table 7 Comparison of cluster settings |
| 表 8 计算采用的机器数目和计算时间 Table 8 Machine number and running time for computation |
实验采用的数据规模相对较小,这是由于预划分处理使用的METIS是内存程序,而实验使用的机器内存空间不够,难以处理更大级别的数据.
4.1.2 局部互模划分实验实验中预划分处理使用METIS中的METIS_PartGraphKwang()函数来对图进行预划分,该函数可将图划分为大小均匀的n个子图.同时为获得更为均匀负载,将图预划分为100个子图,每个工作节点处理5个子图数据.
在GPS中,图中各个点是依据点编号node_id,将其放在编号为node_id % num_vertex的工作节点上面处理,其中num_vertex代表工作节点的数目.这是一种随机均匀划分,未经划分处理的图数据实验作为对照组实验.实验组采用划分后的图数据.
实验数据见表 3,其中Edge_M表示经过METIS划分之后分配到不同Vertex点之间的边数; Edge_R表示经过Random划分之后分配到不同Vertex点之间的边数; r = Edge_M/ Edge_R表示经过METIS划分后,起点和终点处于不同工作节点上的边数目的减少幅度.
实验之所以统计不同工作节点之间的边数,是因为在GPS中,信息是沿着有向边传输的,而同一工作节点内部点之间信息传递不用通过网络,不同工作节点之间信息传递通过网络,前者速度远高于后者(不考虑特殊情况,如建立超高速网络).减少不同工作节点之间边数可有效地减少通过网络传输的信息量,从而提升性能.
从表 3中可很明显地看出来,使用METIS划分后,不同工作节点之间的边数明显减少.大多数图能获得3倍左右的收益(边数为对照组的0.33倍),其中roadNet-PA,roadNet-CA, roadNet-TX三个图甚至能获得几百倍的收益.对于生成的SP2Bench图数据而言,收益稳定在3倍左右.
为衡量划分对于算法速度的提升,实验对比了划分前后算法运行时间,表 4是实验结果,由于预处理只需要处理一次,下述时间统计并没有包含预处理时间; 其次,k=20,也就是计算了图的20-互模划分.
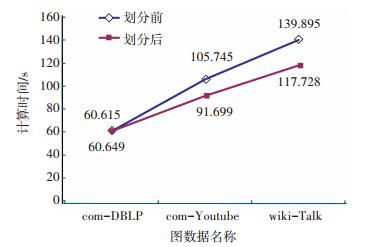
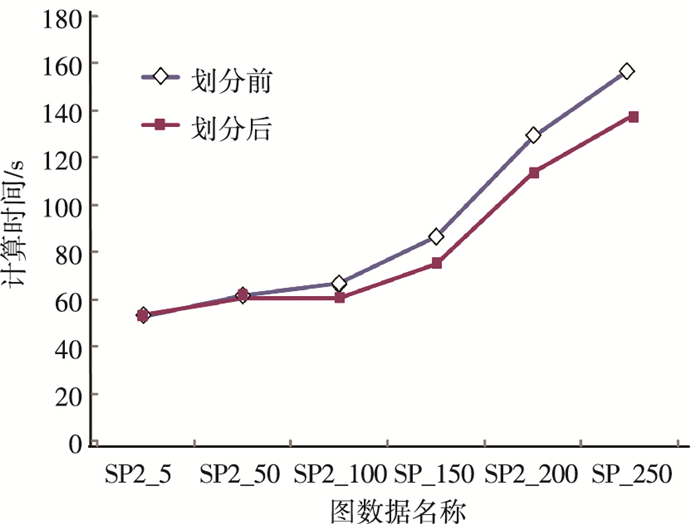
图 9为真实数据预处理前后算法运行时间对比图,图 10为RDF数据数据预处理前后算法运行时间对比图.
|
图 9 真实数据预处理前后运行时间对比 Figure 9 Run time comparisons for pre-partition on real dataset |
|
图 10 RDF数据预处理前后运行时间对比 Figure 10 Run time comparisons for pre-partition on RDF dataset |
当数据集合相对较小的时候,预划分处理对于算法性能影响不大,随着数据规模的增大,预划分的作用就逐渐显现出来.
4.1.3 实验结果分析由于实验使用的数据规模有限且实验使用的机器设备性能差距悬殊,故而无法与前两种方法[7-8]做详细的对比,但是可以就部分数据进行对比.
对于使用SP2Bench生成的1 000 000个三元组的数据,Schätzle的方法使用了170 s的时间.他们使用的机器配置是这样的:Xeon E5-2420 1.9 GHz、6-core CPU, 32 GB RAM, 4 TB磁盘空间.而且他们只计算了图的4-互模划分.
相比较而言,本文实验使用的机器设备性能要差许多,而且计算的是图的20-互模划分,即使如此,本文的方法仅需要66 s,而进一步优化可使得所需时间下降到60 s.
这个对比在一定程度上说明了本文的算法在时间效率上面的巨大优势.
4.2 大图实验 4.2.1 实验环境实验采用的机群有101台机器(1台机器作为主节点,100台机器作为工作节点),每台机器具备8 G内存和1 T硬盘. Hadoop(HDFS)版本为1.2.1,GPS版本为GPS1.0.表 5, 表 6为实验采用的数据.
4.2.2 图扩展性实验图可扩展性实验,选取从SP2Bench_100M(1亿条边)到SP2Bench_1000M(10亿条边)十组图数据.实验由于机器内存限制,对于SP2Bench_100M图数据使用10个计算节点(10台机器),而对于SP2Bench_200M数据则使用20台计算节点,以此类推,对于SP2Bench_1000M数据则使用100个计算节点.为了方便表示,将实验的计算时间t重新计算,计算公式为:
| $ {t^\prime } = \frac{{t*NumofNode}}{{10}}. $ | (2) |
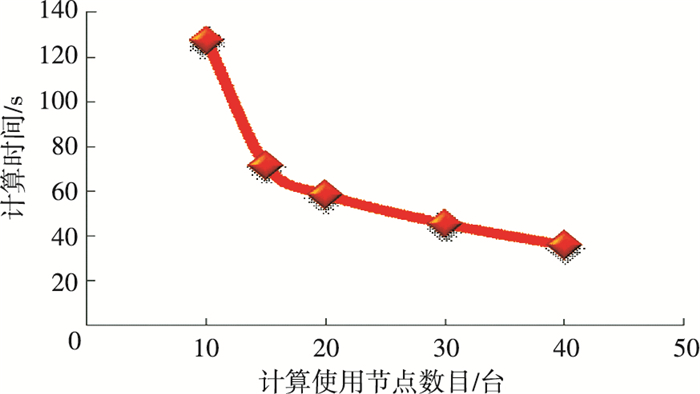
该计算公式默认计算节点增加的倍数同由此获得的计算时间加速的倍速相同.而根据图 11加速比的实验结果,实验节点增加4倍,实际获得的计算时间加速比为3.5,这说明重新计算出的时间t′可以被用来近似t.
|
图 11 SP2Bench_100M加速比实验 Figure 11 Experiment for speedup on SP2Bench_100M dataset |
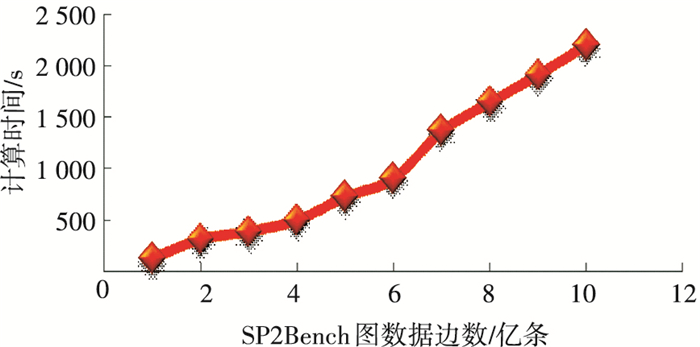
图 12中的计算时间采用t ′近似表示,实验结果显示算法计算大图上的4-局部划分任务所需的时间同图的规模呈线性关系.算法显示出了良好的可扩展性.
|
图 12 算法的可扩展性实验 Figure 12 Experimental results for scalability |
实验难以与Luo以及Schätzle的实验算法做出相对准确的对比,这是由于Luo以及Schätzle实验使用的机群与本实验使用的机群在配置上差距甚殊.表 7是三组实验使用的机群配置.
三组实验机群的配置差别很大,在机器内存上的差距更是明显.为便于比较三种算法的效率,实验分为两组,Twitter图数据实验以及SP2Bench图数据实验.两组实验分别用来同Luo以及Schätzle的实验算法进行效率比较.
Twitter图数据实验使用66台机器作为工作节点(Worker node)以及1台机器作为主节点(Master node),计算Twitter图数据的10-局部划分.
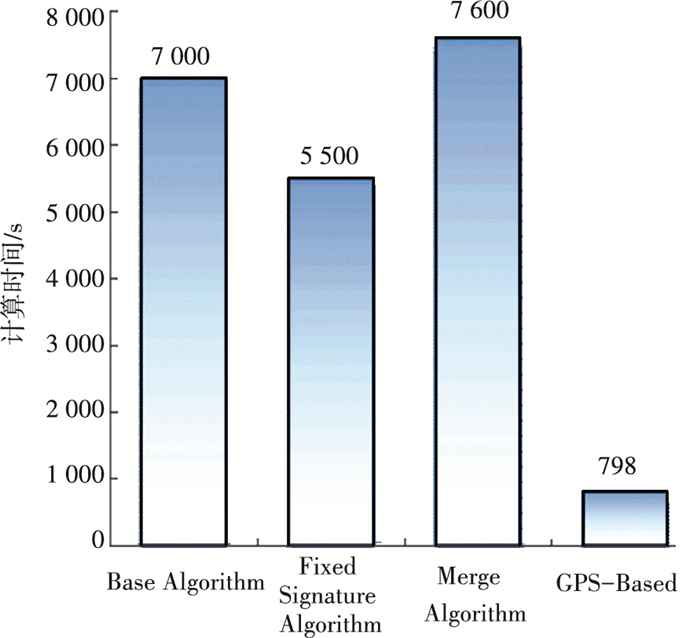
Luo的算法包括基本的算法Base Algorithm以及两种改进版本算法,分别称之为Fixed Signature Algorithm以及Merge Algorithm.这三种算法在执行10-局部划分实验的详细试验时间并没有给出,图 13中的计算时间是根据其实验结果图近似估算的.
|
图 13 计算Twitter图数据10-局部划分实验对比 Figure 13 Run time comparison for 10-bisimulation on Twitter dataset |
由图 13可以直观地观察到,本文提出的GPS-Based算法明显快于Luo的算法.与Luo三种算法中最快的Fixed Signature Algorithm相比,GPS-Based算法的计算时间仅为其1/7.考虑到Luo实验使用的机群配置明显地优于本实验使用的机群配置,本文提出的GPS-Based算法的计算时间应当比Luo的算法快7倍以上.
SP2Bench图数据实验分为11小组,由于机器内存的限制,对于部分数据采用多于10台机器来执行计算任务,表 8详细地列出了各组实验使用的机器数目.
为与Schätzle的实验结果作对比,需要将实际的计算时间转化为使用10台机器计算的时间.加速比实验结果表明机器数目增加4倍可以获取3.5倍的时间加速,故而采用式(2)来近似估计只采用10台机器的计算时间.
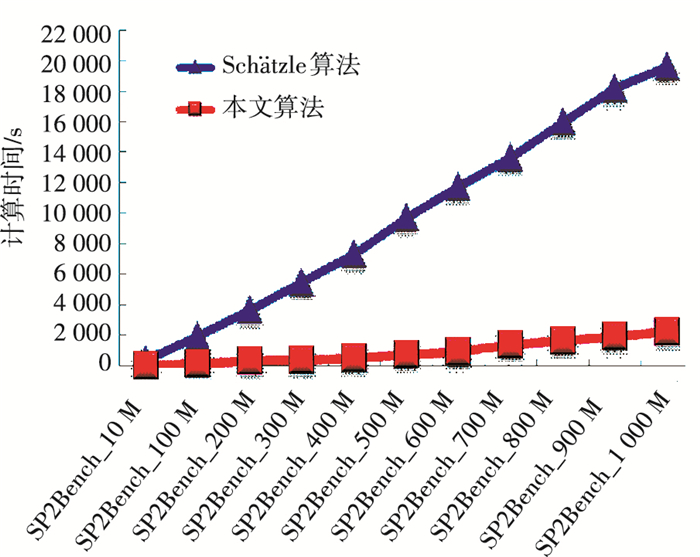
图 14表示在计算SP2Bench的11组图数据的4-局部划分实验中,本文提出的GPS-Based算法同Schätzle的时间效率对比.从图中可以很直观地看出,GPS-Based算法的时间效率明显地优于Schätzle算法的时间效率.
|
图 14 计算SP2Bench图数据4-局部划分实验对比 Figure 14 Run time for 4-bisimulation on SP2Bench dataset |
综合上述Twitter图数据10-局部划分实验以及SP2Bench图数据4-局部划分实验的实验结果,本文提出的GPS-Based算法明显地优于Luo以及Schätzle的实验算法.图 15表示三种算法的时间效率对比图,对于Luo的三种算法,本计算选用的是Luo结果优化后的Fixed Signature Algorithm.

|
图 15 综合时间效率对比 Figure 15 Comparison on efficiency |
从图 15可看出,本文提出的GPS-Based算法相较于Luo以及Schätzle的实验算法,在时间效率上有大幅度的提升,与Schätzle的算法相比有10倍的时间效率提升,与Luo的算法相比有7倍的时间效率提升.如果考虑到实验机群配置对实验计算时间的影响,那么本文提出的GPS-Based算法在计算图的k-局部划分任务上的时间效率优势还将进一步扩大.
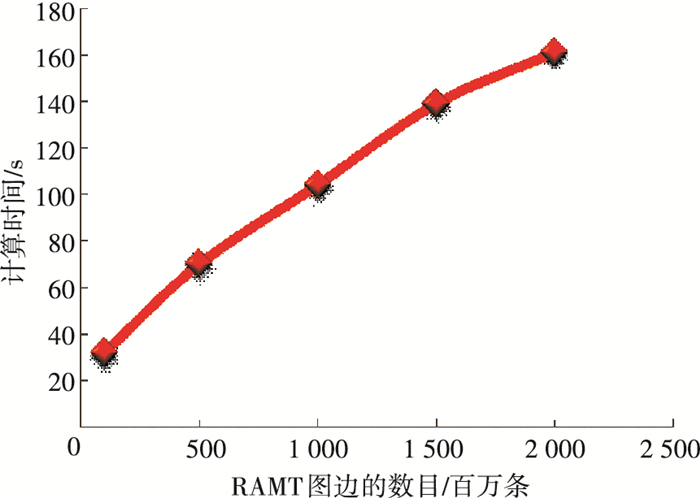
4.2.4 图密度对算法性能的影响实验本节实验衡量了图密度对于算法性能的影响,实验使用表 5中的RMAT[18]图数据集.实验使用100台工作节点,计算图的4-局部划分.图 16是实验结果.
|
图 16 图密度对算法性能的影响 Figure 16 Experimental results on the impact of graph density |
随着图密度的增加,算法执行所需的时间基本呈线性变化.
4.2.5 大图实验与小图实验的对比分析在小图实验中,在SP2_100(包含100万个RDF三元组)做20-互模划分需要的实验时间是66.8秒,经过预划分处理,实验的时间是60.6 s.而在本节的实验中,在SP2Bench_10(包含1 000万个RDF三元组)上的实验却只用了22.3 s.这是由于以下几个原因导致的:
1) 小图实验中实验计算的是图上的20-互模划分,而本节实验为便于同Schätzle的实验算法作比较,计算的是图上的4-互模划分;
2) SP2_100数据仅包含100万个RDF三元组,数据规模较小,未能完全使用20个工作节点的性能; 根据表 4的实验结果,SP2_50图数据的规模为SP2_5图数据规模的10倍,而实际的运行时间却分别为60.6 s以及53.6 s;
3) 实验采用的机群不同,本节实验采用的机群配置虽然难以与Schätzle的实验机群以及Luo的实验机群相比较,但是与小图实验使用的机群相比性能还是高出不少;
4) 本节实验针对之前的代码进行了较大幅度的优化,使用之前的代码计算SP2Bench_10数据上的4-互模划分的时间是33秒,而优化后的计算时间是22.3 s.
4.3 实验结果总结通过上述实验,我们得到如下结论:
1) 小图实验详细对比了各组数据在执行图的预划分处理(METIS程序)前后的运行时间对比,充分地说明了图的预划分处理对于算法效率的影响.
2) 图 11所示的加速比实验,使用10台、15台、20台、30台、40台机器计算图数据Sp2bench_100M上的4-互模划分.计算节点增加了4倍获得了3.5倍时间加速,算法显示出了良好的加速比.
3) 基于算法良好的加速比性能,实验将可扩展性各组实验的运行时间统一用式(2)进行计算,即该实验在用十台机器来执行的时候所需的运行时间.
4) 在图密度对于算法性能的影响实验中,使用表 5中的RMAT图数据集,实验结果显示,随着图密度的增加,算法执行所需的时间基本呈线性变化.
5) 表 7给出了Luo、Schätzle以及本文大图实验所使用的实验环境对比,本文实验使用的机器性能最差,尤其以单机器内存上的差距最为悬殊.
6) 图 13给出了本文算法同Luo的算法(一个基本算法以及两个改进版本)在Twitter图数据10-局部划分的实验对比.本文算法的运行时间,是其三种算法中最快的算法的运行时间的1/7,本文算法的高效性获得了很好的说明.
7) 图 14给出了本文算法同Schätzle的算法在10组大图数据上的执行4-互模划分任务所需的计算时间对比,基本上本文算法运行时间仅为其1/10左右.
8) 图 15总结了本文算法相比较于Luo和Schätzle算法的时间效率对比,本文算法的高效性获得了充分的证明.
5 结论1) 本文提出了目前第一个基于分布式图数据处理平台GPS/Pregel的k-互模划分算法;
2) 采用图的预处理操作,大幅减少子图之间的边数;
3) 本文算法的网络通讯量仅为之前采用MapReduce计算模型算法的网络通讯量的1/2~1/12;
4) 在没有进行图的预处理操作的情况下,计算包含数亿条边的大图上的k-互模划分任务,时间效率同之前的两种基于MapReduce计算模型的算法相比,提升了7~16倍;
第五,初步处理了不同工作节点之间的负载均衡问题.
| [1] |
SANGIORGI D, RUTTEN J.
Advanced topics in bisimulation and coinduction[M]. New York, NY, USA: Cambridge University Press, 2011: 19-63.
|
| [2] |
BUNEMAN P, GROHE M, KOCH C. Path queries on compressed XML[C]// Johann C, Lockemann P C, Abiteboul S, Carey. In Proc. VLDB 2003, Berlin, Germany: Morgan Kaufmann, 2003: 141-152.
|
| [3] |
FAN W, LI J, WANG X, et al. Query preserving graph compression[C]// Chen Y, Richard S, Gravano L. In Proc. SIGMOD, Scottsdale, AZ, USA: ACM, 2012: 157-168.
|
| [4] |
MILO T, DAN S. Index structures for path expressions[C]// Beeri C, Buneman P. In Proc. ICDT 1999. Germany : Springer, 1999: 277-295.
|
| [5] |
PICALAUSA F, LUO Y, FLETCHER G H L, et al. A structural approach to indexing triples[C]// Simperl E, Cimiano P, Polleres A, et al. In ESWC, Heraklion. Greece: Springer, 2012: 406-421.
|
| [6] |
FAN W. Graph pattern matching revised for social network analysis[C]// Deutsch A. In Proc. ICDT, Berlin, Germany, USA: ACM, 2012: 8-21.
|
| [7] |
LUO Y, LANGE Y D, FLETCHER G H L, et al.
Bisimulation reduction of big graphs on mapReduce[M]. Berlin Heidelberg: Springer, 2013: 189-203.
|
| [8] |
SCHÄTZLE A, NEU A, LAUSEN G, et al. Large-scale bisimulation of RDF graphs[C]// Virgilio R D, Giunchiglia F, Tanca L. In Proc. SWIM. USA: ACM, 2013: 1-11.
|
| [9] |
BLOM S, ORZAN S. A distributed algorithm for strong bisimulation reduction of state spaces[J].
STTT, 2005, 7(1): 74-86.
DOI: 10.1007/s10009-004-0159-4 |
| [10] |
SALIHOGLU S, WIDOM J. Gps: A graph processing system[C]//Balazinska M, Szalay A, Budavari T, et al. In Proc. SSDBM, Baltimore, Maryland. USA: ACM, 2013: 22-33.
|
| [11] |
MALEWICZ G, AUSTERN M H, BIK A J C, et al. Pregel: a system for large-scale graph processing[C]// Agrawal D, Elmagarmid A. In Proc. SIGMOD. USA: ACM, 2010: 135-146.
|
| [12] |
Apache. Apache MINA[EB/OL]. (2015). http://mina.apache.org/.
|
| [13] |
KWAK H, LEE C, PARK H, et al. What is twitter, a social network or a news media?[C]// Rappa M, Jones P, Freire J. Proceedings of the 19th International Conference on World Wide Web. USA: ACM, 2010: 591-600
|
| [14] |
LESKOVEC J, KREVL A. Stanford large network dataset collection[DB/OL]. http://snap.stanford.edu/data/index.html
|
| [15] |
RIXHAM N, SPORNY M, BIRBECK M. RDF[EB/OL]. (2012. 7). http://www.w3.org/standards/techs/rdf.
|
| [16] |
BONCZ P, ERLING O. Social Network Intelligence BenchMark[EB/OL]. (2013. 7). https://www.w3.org/wiki/Social_Network_Intelligence_BenchMark
|
| [17] |
Semantic Web Education, Outreach. jamendo. [DB/OL]. http://dbtune.org/jamendo/
|
| [18] |
CHAKRABARTI D, ZHAN Y, FALOUTSOS C. R-MAT: A recursive model for graph mining[C]// Berry M W, Dayal U, Kamath C, et al. SDM 2004. USA: SIAM, 2004: 442-446.
|
 2018, Vol. 50
2018, Vol. 50


