随着化石燃料的消耗以及减少二氧化碳排放协议的制定,可再生能源已成为世界各国关注的重点.作为可再生能源的一种,潮流能具有能量密度高、可预测性强、载荷稳定等特点,竖轴水轮机则是开发潮流能的一种主要换能装置[1-3].随着潮流能电站逐步走向大型化、多组化,合理优化水轮机阵列排放位置已成为一项引人关注的课题.对于前后串列排布的竖轴水轮机而言,下游水轮机由于受到上游水轮机尾流的干扰,相对来流将不是均匀来流,水动力性能也会随之改变,因此有必要对水轮机的尾流进行研究,并给出串列水轮机间合理的参考距离.
目前,很多学者对竖轴水轮机及其尾流场进行了研究,Bachant等[4-5]利用OpenFOAM软件对三维竖轴水轮机附近的尾流场进行了模拟研究,分析了不同流场雷诺数对水轮机附近尾流场的影响; Gebreslassie等[6]通过CFD方法分析多种不同安放位置的竖轴水轮机阵列得出,对于前后串列放置的水轮机而言,较小的纵向间距会引起下游水轮机功率的大幅度亏损.由于竖轴水轮机与竖轴风机结构的相似性,竖轴风机的研究成果对竖轴水轮机也有一定的借鉴价值,Lam等[7]通过研究二维与三维条件下竖轴风机的尾流场特性,分析了风机后方各剖面尾流场的速度及涡量特性.Zuo等[8]应用商业软件FlowVision模拟了两个串列放置的竖轴风机算例,得出了上游风机尾流场会在后方15倍风机直径距离处基本恢复为均匀流,但由于水轮机和风机的来流介质及适用流速范围不同,因此该结论不能直接应用于水轮机,本文将借鉴其研究方法对竖轴潮流能水轮机进行研究.首先以单个三叶片水轮机为研究对象,提出模拟参数选取策略并得出水轮机能量利用率随叶尖速比的变化曲线,然后重点分析两个串列放置的水轮机,取水轮机之间距离S为变量,研究S对下游水轮机水动力性能的影响并得出S的建议范围.此外本文还分析了水轮机尾流场的特性,分析结论将为水轮机实际布放提供理论和工程实践的参考.
1 OpenFOAM数值模拟目前,竖轴潮流能水轮机的理论研究方法主要有流管法、涡方法和CFD方法等[9].流管法及涡方法对竖轴叶轮的应用起源于竖轴风机的研究,两者计算时间短,但结果精度低,难以描述叶片附近的复杂流动; CFD法是近些年得益于计算机的蓬勃发展而兴起的方法,这种方法通常借助计算流体软件对研究对象进行数值模拟,模拟结果精确且能充分描述壁面处的复杂流动,通过后处理可将流场可视化有利于进行分析研究,因此本文选取CFD法进行数值研究.
1.1 坐标及参数定义考虑到竖轴水轮机在展长方向各横截面相同的特点,可将叶片绕转心旋转的三维问题简化成二维问题,并做出以下假设:1)忽略叶片的三维效应; 2)不考虑自由液面和海底的影响; 3)假设来流为均匀流.通过这些简化可大幅度减少模拟时间[10-11].
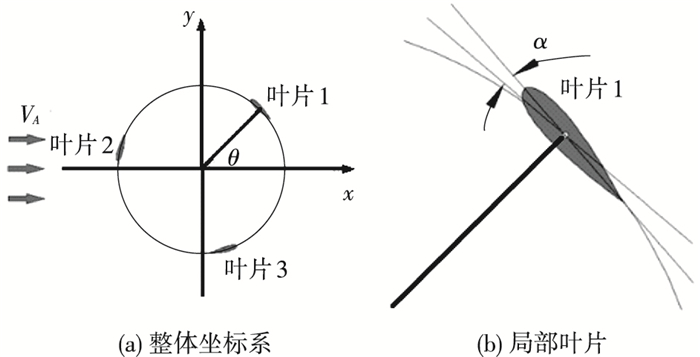
图 1给出竖轴水轮机坐标系,取水轮机的旋转中心为坐标原点,x轴方向与前方来流方向一致,y轴经过原点与来流方向垂直.θ为叶片的位置角,取x轴正向为起点逆时针旋转为正.叶片偏角α为叶片弦线与叶片轨迹圆切线的夹角,内偏为正,外偏为负.为了方便分析,定义部分量纲一的参数如下:
|
图 1 竖轴水轮机坐标系 Figure 1 Coordinate of vertical axis tidal turbine |
叶尖速比
单个叶片转矩系数
水轮机转矩系数
水轮机能量利用率系数
式中:R为水轮机半径; ω为水轮机旋转角速度; VA为来流速度; D为水轮机直径; H为叶片展长; ρ为流体密度; q为单个叶片所受力矩; Q为水轮机所受合力矩.
1.2 计算域与边界条件本文竖轴水轮机参数来源于浙江省岱山县“海能Ⅲ”号潮流能发电站设计的竖轴水轮机,此水轮机为NACA0022翼型的三叶片水轮机,叶片弦长C为0.7 m,叶片展长H为4.5 m,水轮机直径D为6 m,设均匀来流速度VA为3 m/s,叶片偏角α为-3 °.
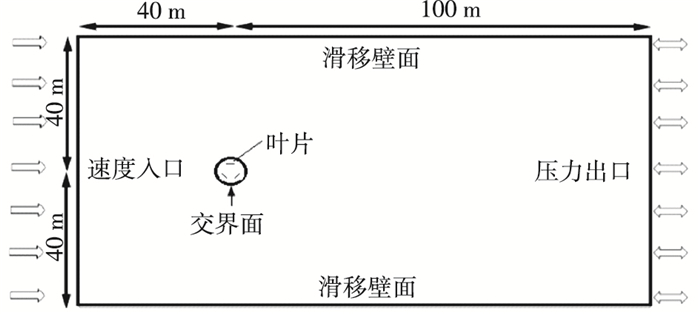
1.2.1 单个水轮机算例单个水轮机计算域如图 2所示,整个模型分为两个子域,分别为矩形外域和包含叶片的圆形旋转域.
|
图 2 单个水轮机计算域 Figure 2 Computational domain of a single vertical turbine |
模型算例中设置左侧边界为速度入口(velocity inlet),速度大小恒定,参照文献[12-13]中的计算域尺度选取策略,设置速度入口距离水轮机轴心6.67D; 右侧边界为压力出口(pressure outlet),相对压力为0,距离水轮机主轴轴心16.67D,上、下边界设置为滑移壁面(slip wall),距离水轮机轴心6.67D; 圆形旋转域的直径为1.07D,与矩形域通过交界面(CyclicAMI)相连.
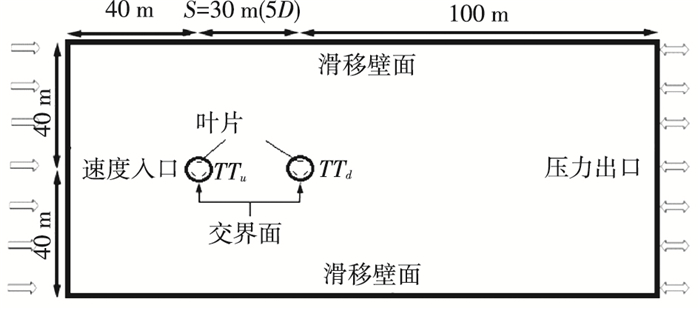
1.2.2 串列水轮机算例串列水轮机算例中,两个水轮机前后并排放置,如图 3所示(S=5D算例).
|
图 3 串列水轮机计算域(S=5D) Figure 3 Computational domain of tandem vertical turbines |
在串列水轮机算例中,水轮机间距S分别取5D、10D、20D、30D、40D与50D,上游水轮机TTu轴心到速度入口和上下滑移壁面距离均为6.67D,下游水轮机TTd轴心与压力出口距离为16.67D,其他参数设置均与单个水轮机算例一致.
1.3 网格与时间步图 4分别给出单个水轮机和串列水轮机算例的整体计算域、旋转域及叶片周围局部网格示意图.模型网格质量直接决定着计算精度和模拟时间,精细的网格能更好的描述模型物理特性,但模拟时间也会增加,因此选取网格时,应兼顾时间消耗性和模拟准确性.以单个水轮机算例为例,本文分别对比了3种不同级别的网格模型,具体信息见表 1.

|
图 4 模型网格 Figure 4 Grid of model |
| 表 1 3种对比网格信息 Table 1 Details of three different grids |
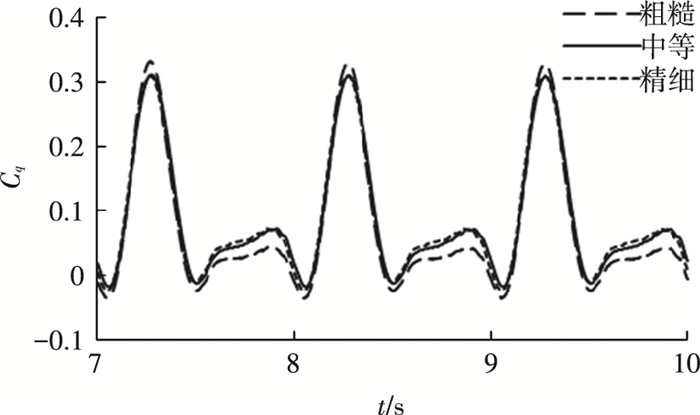
图 5为3种网格条件下水轮机稳定旋转时单个叶片的转矩系数曲线图.可以看出,中等与精细网格的Cq曲线差异较小,即中等级别网格基本达到无关性要求,为了减少计算时间,选取中等级别网格作为算例网格.
|
图 5 叶片转矩系数曲线(网格无关性验证) Figure 5 Torque coefficient curves of a single blade(grid in dependence test) |
在研究时间步长无关性时,时间步长分别选取0.010 0、0.001 0、0.000 5 s,其他参数设置均相同,图 6为3种时间步长下水轮机叶片转矩系数曲线图.可见时间步长为0.001 0、0.000 5 s时,转矩曲线几乎一致,因此选取0.001 0 s作为本算例的时间步长.
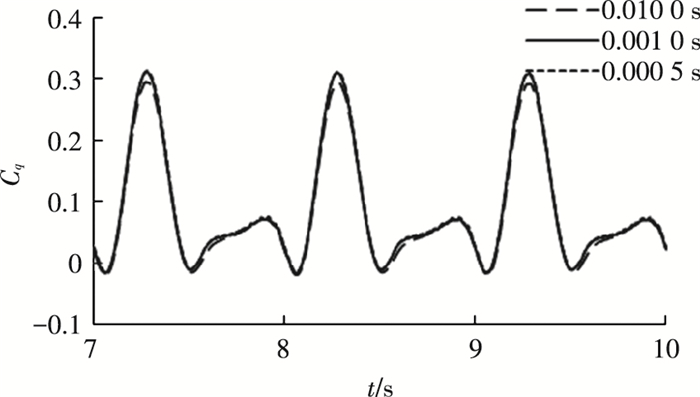
|
图 6 叶片转矩系数曲线(时间步长无关性验证) Figure 6 Torque coefficient curves of a single blade(timestep in dependence test) |
本文采用的软件为OpenFOAM,它是一个完全由C++语言编写面向对象的开源CFD软件,采用的离散方式为有限体积法.本文在它若干求解器中选取了PimpleDyMFoam求解器,该求解器是基于PISO-SIMPLE(PIMPLE)算法瞬态求解不可压缩流体的Navier-Stokes方程[14-15].可应用动网格及滑移网格技术,水轮机算例中旋转域与外域的动态连接属滑移网格范畴,故适用于本算例.
本数值模拟的湍流模型选取k-ω SST (shear stress transport)模型.此两方程模型结合了k-ε与k-ω模型的特点,可精准模拟出突然失速现象,计算时间相对较少,在水轮机研究中得到了较多的应用[16-17].
1.5 湍流度为探究速度入口湍流度对水轮机性能的影响,在此分别选取速度入口湍流度I为0.1%、0.5%、1.0%、5.0%和10.0%.表 2给出不同速度入口湍流度下稳定旋转后的平均能量利用率系数Cp,其中水轮机叶尖速比均取2.0.
| 表 2 平均能量利用率随湍流度的变化 Table 2 Average Cp under different turbulence intensity |
根据表 2数据可以得出,入口湍流度对水轮机的平均Cp影响十分小,基本可以把湍流度当做本数值模拟的次要参数.考虑到水轮机运行水道的湍流度范围,下文算例中速度入口湍流度均取5%.
2 有效性验证为验证本文所采用二维数值模型的有效性,选取Bachant等[18]研究的竖轴水轮机作为验证算例.该水轮机主要参数如下:直径D=1.0 m,叶片弦长C=0.14 m,叶片展长H=1.0 m,来流速度VA=1.0 m/s,叶片翼型为NACA0020.图 7为验证水轮机能量利用率系数计算值与实验值的对比曲线.其中,peter实验值是文献[18]中给出的实测曲线,2D计算值是本文二维数值模型计算所得的数据曲线.根据文献[19]中对水轮机三维效应及支撑结构影响效应的研究,当水轮机展长直径比为1.0时,三维效应会降低水轮机约8%的能量利用率,支撑结构会降低约9%的能量利用率[19].根据上述结论对本文2D模拟的结果进行修正,图 7中3D修正值代表修正后数值计算的结果.
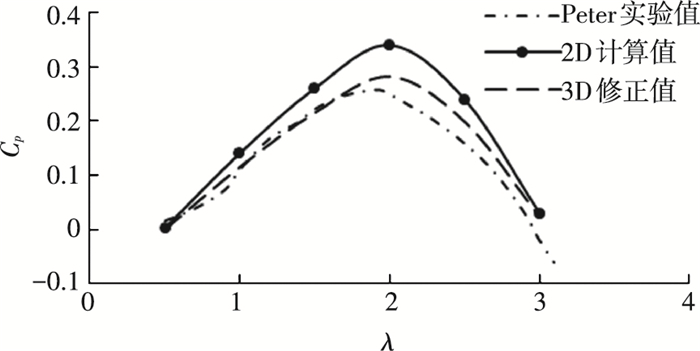
|
图 7 能量利用率系数对比 Figure 7 Comparison of power coefficient curves |
由3组对比曲线可以看出,数值计算值与实验值变化趋势相似,都在速比为2.0附近时达到最大Cp值.计算值整体高于实验值,这是因为计算模型无法完全模拟拖曳水池的实验状态,没有考虑叶片三维效应,叶片支撑结构和主轴的干扰,机械摩擦损失,测量误差和数据传输的延迟等因素的影响.考虑三维效应和支撑结构影响修正后的计算结果与实验值测得的能量利用率最大误差为4.15%,证明了本文采用的数值模型在竖轴水轮机研究中具有一定的适用性与准确性.
3 结果及分析 3.1 单个水轮机为了研究竖轴水轮机的水动力性能,首先对不同速比下单个水轮机进行模拟.
3.1.1 能量利用率系数竖轴水轮机能量利用率系数Cp是水轮机水动力性能的最重要参数,图 8为不同速比下的水轮机能量利用率曲线.
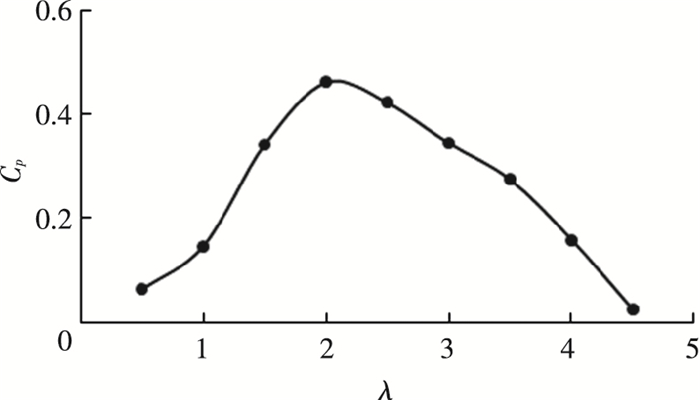
|
图 8 能量利用率系数曲线 Figure 8 Efficiency coefficient curve |
图 8显示,水轮机在速比2.0时达到最大能量利用率系数0.461,因此2.0为此水轮机的最佳速比; 当速比为4.5时,能量利用率系数接近0,此时来流几乎不对水轮机做功,称飞逸状态.当速比范围在1.5~3.0之间时,水轮机的能量利用率系数较高,在实际运行中若将转速控制在此范围内可有效的提高发电量.
3.1.2 叶片转矩系数除了水轮机能量利用率外,对单个叶片所受载荷的研究也具有一定价值.图 9为4种速比为下单叶片转矩系数随位置角变化曲线.
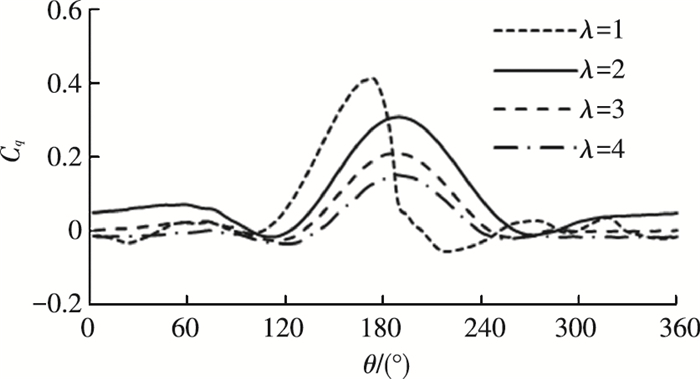
|
图 9 单叶片转矩系数曲线 Figure 9 Torque coefficient curves of single blade |
图 9显示叶片位置角处于145 °~225 °区间时,叶片受到的转矩较大,且峰值出现在180 °位置角附近,此外叶片在低速比下的转矩系数峰值要高于高速比时.而其他位置角处,转矩系数始终处于0附近.由此可以得出145 °~225 °这一范围为提供水轮机旋转转矩的主导区域.
3.2 串列水轮机两个串列水轮机算例中,分别设置水轮机间距S为5D、10D、20D、30D、40D、50D,水轮机叶尖速比均设置为最佳速比2.0.
3.2.1 能量利用率系数图 10为下游水轮机与上游水轮机能量利用率系数比Cpd/Cpu随水轮机间距S变化曲线,结果显示随着前后水轮机距离S增加,能量利用率系数比值也不断增加且逐渐接近1.0.当S为5D时系数比约为-0.02,这时下游水轮机能量利用率小于0,可判断上游水轮机尾流场对后方5D处的下游水轮机干扰严重; 当S为40D、50D时,系数比分别约为0.90、0.92,两者近似相等.可近似认为上游水轮机产生的不稳定尾流场在40D距离处基本恢复,因此可初步判断对于两个串列水轮机的放置间距应不小于40D.

|
图 10 能量利用率对比曲线 Figure 10 Comparison of efficiemcy coefficients curves |
为了进一步研究水轮机尾流场特性及水轮机水动力性能,以10D、40D两算例来进行分析.
3.2.2 叶片转矩系数当两个水轮机距离S为10D、40D时,能量利用率系数比Cpd/Cpu分别约为0.07、0.90,图 11为两算例中各叶片旋转1周所受到的转矩系数Cq曲线图.图中显示当S为10D,下游水轮机各叶片的转矩系数均小于0.1,且峰值没有上游水轮机叶片明显; 当S为40D,下游水轮机各叶片的转矩系数变化趋势与上游水轮机接近且峰值明显.

|
图 11 转矩系数曲线 Figure 11 Torque coefficient curves |
为探究水轮机尾流场特性,图 12、13给出了3种算例水轮机的尾流场的速度云图、涡量云图.

|
图 12 水轮机速度云图 Figure 12 Velocity contours of turbines |

|
图 13 水轮机涡量云图 Figure 13 Vorticity contours of turbines |
从图 12中可以看出,上游水轮机后方尾流场速度较前方均匀来流有大幅度的亏损,随着下游距离的增加,速度亏损程度不断变小.当S=10D时,下游水轮机处速度亏损严重,不稳定尾流场的影响较大,因此下游水轮机能量利用率系数大幅度降低; 当S=40D时,下游水轮机处尾流场速度亏损基本恢复,此时下游水轮机受到尾流场的干扰程度较低,可初步认为前后水轮机无干扰.从图 13的涡量图可以看出,当水轮机逆时针旋转时,后上方和后下方分别脱落符号相反的尾涡,一定距离后呈现正负交替状.当S=10D时,下游水轮机会暴露在高强度尾涡中,此时来流大小及方向将极不稳定; 而当S=40D时,上游水轮机产生的尾涡到达下游水轮机处基本消散.
3.2.4 速度分布为了直观的观察尾流场的发展特性,给出S为10D、40D算例中两个水轮机后方多组剖面处的速度分布,如图 14、15所示.其中Hd为流场宽度方向坐标,水轮机转心位置Hd为0.
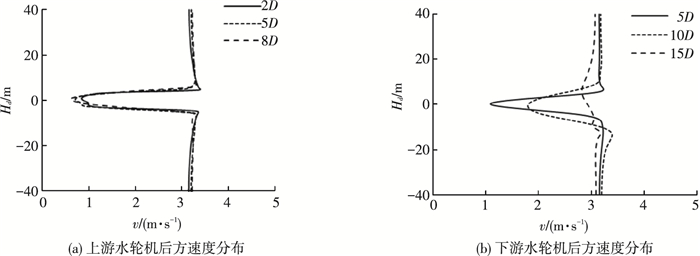
|
图 14 尾流场速度分布(S =10D) Figure 14 Velocity distribution of the wake field(S=10D) |
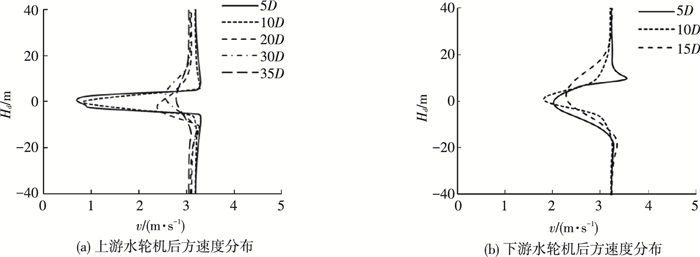
|
图 15 尾流场速度分布(S=40D) Figure 15 Velocity distribution of the wake field(S=40D) |
从图 14、15可以观察到,当S=10D时,两水轮机之间Hd范围为-0.75D~0.75D的矩形区域内速度亏损严重,减小幅度平均约为70%,而当Hd处于其他范围时,流场速度基本与前方来流速度相同.当S=40D时,上游水轮机后方尾流速度亏损程度随距离增加而减小,当距离为35D时,速度基本恢复.两个算例中下游水轮机后方流场由于受到两个串列水轮机共同的影响,速度分布会产生波动变化呈现不稳定规律,当Hd范围为-3.0D~3.0D时,速度变化幅度较大且Hd在0附近时亏损最严重.
4 结论1) 本文验证了OpenFOAM数值模型在合理的计算域、网格密度和时间步的设置下,采用k-ω SST湍流模型和PIMPLE算法,可以准确的模拟二维竖轴水轮机的流场,在估算水轮机能量利用率等平均性能时,可忽略速度入口湍流度对计算结果的影响.
2) 单个竖轴水轮机在运行过程中,叶片位置角处于145 °~225 °这一范围时,叶片受到的转矩系数较大且峰值出现在180 °位置角附近.这说明水轮机的功率贡献主要来源于叶片处于上游盘面的位置,即叶片在迎流时对主轴产生的驱动力最大.而水轮机串列布置时,上游水轮机的尾流场造成了下游水轮机迎流的速度亏损,尤其是上游盘面位置的速度亏损,因此造成了叶片受力的变化,导致水轮机功率的亏损.
3) 串列放置的两个竖轴水轮机,上游水轮机尾流场的速度亏损会随着下游距离的增加而逐渐恢复.在S < 40D的区域内,下游水轮机的功率恢复速度基本呈线性分布; 当S>40D的区域内,下游水轮机的功率恢复速度减缓; 在S=40D处,下游水轮机的功率可恢复到上游水轮机的90%.因此可以认为串列水轮机的间距大于40倍水轮机直径时,上游水轮机尾流场对下游水轮机性能的影响可以忽略.
| [1] |
张亮, 李新仲, 耿敬, 等. 潮流能研究现状2013[J].
新能源进展, 2013, 1(1): 53-68.
ZHANG Liang, LI Xinzhong, GENG Jing, et al. Tidal current energy update 2013[J]. Advances in New and Renewable Energy, 2013, 1(1): 53-68. DOI: 10.3969/j.jssn.2095-560X.2013.01.006 |
| [2] |
王传崑. 海洋能发电原理[J].
太阳能, 2008, 11: 19-20.
WANG Chuankun. Principle of ocean energy power generation[J]. Solar Energy, 2008, 11: 19-20. |
| [3] |
戴军, 单忠德, 王西峰, 等. 潮流水轮机的研究进展[J].
可再生能源, 2010, 28(4): 130-133.
DAI Jun, SHAN Zhongde, WANG Xifeng, et al. Current research progress of water turbine[J]. Renewable Energy Resources, 2010, 28(4): 130-133. DOI: 10.3969/j.issn.1671-5292.2010.04.031 |
| [4] |
BACHANT P, WOSNIK M. Characterising the near-wake of a cross-flow turbine[J].
Journal of Turbulence, 2015, 16(4): 392-410.
DOI: 10.1080/14685248.2014.1001852 |
| [5] |
BACHANT P, WOSNIK M. Effects of reynolds number on the energy conversion and near-wake dynamics of a high solidity vertical-axis cross-flow turbine[J].
Energies, 2016, 9(2): 73.
DOI: 10.3390/en9020073 |
| [6] |
GEBRESLASSIE G M, TABOR G R, BELMONT M R. CFD simulations for sensitivity analysis of different parameters to the wake characteristics of tidal turbine[J].
Open Journal of Fluid Dynamics, 2012, 2(3): 56-64.
DOI: 10.4236/ojfd.2012.23006 |
| [7] |
LAM H F, PENG H Y. Study of wake characteristics of a vertical axis wind turbine by two and three-dimensional computational fluid dynamics simulations[J].
Renewable Energy, 2016, 90: 386-398.
DOI: 10.1016/j.renene.2016.01.011 |
| [8] |
ZUO Wei, WANG Xiaodong, KANG Shun. Numerical simulations on the wake effect of H-type vertical axis wind turbines[J].
Energy, 2016, 106: 691-700.
DOI: 10.1016/j.energy.2016.02.127 |
| [9] |
LI Ye, CALISAL S M. Preliminary results of a vortex method for stand-alone vertical axis marine current turbine[C]//ASME 2007 26th International Conference on Offshore Mechanics and Arctic Engineering. San Diego, California: ASME, 2007: 589-598. DOI: 10.1115/OMAE2007-29708.
|
| [10] |
XIAO Qing, LIU Wendi, INCECIK A. Flow control for VATT by fixed and oscillating flap[J].
Renewable Energy, 2013, 51: 141-152.
DOI: 10.1016/j.renene.2012.09.021 |
| [11] |
MATHILFE B, SYLVAIN G, PHILIPPE G, et al. Wake numerical study of a vertical marine current turbine[J].
La Houille Blanche, 2014, 19(6): 74-78.
DOI: 10.1051/lhb/2014066 |
| [12] |
LAIN S, QUINTERO B, TRUJILLO D, et al. Simulation of vertical axis water turbines[C]//IEEE International Symposium on Alternative Energies and Energy Quality. Barranquilla, Colombia: IEEE, 2012: 1-6. DOI: 10.1109/SIFAE.2012.6478908.
|
| [13] |
KHALID S S, JIN Zhiguang, TANG Fuding, et al. CFD simulation of vertical axis tidal turbine using two-way fluid structure interaction method[C]//Proceedings of the 10th International Bhurban Conference on Applied Sciences and Technology. Islamabad, Pakistan: IEEE, 2013: 286-291. DOI: 10.1109/IBCAST.2013.6512167.
|
| [14] |
MARIC T, HOPKEN J, MOONEY K. The OpenFOAM technology primer[M]. 1st ed. [S. L. ]: Sourceflux, UG, 2014: 15-18.
|
| [15] |
SU Junwei. Pimple algorithm description[OL]. 2009, http://blog.sina.com.cn/s/blog_5fdfa7e60100fbb1.html.
|
| [16] |
MENTERF R. Two-equation eddy-viscosity turbulence models for engineering applications[J].
AIAA Journal, 1994, 32(8): 1598-1605.
DOI: 10.2514/3.12149 |
| [17] |
DAI Yongming, GARDINER N, LAM W H. CFD modelling strategy of a straight-bladed vertical axis marine current turbine[C]//Proceedings of the 20th International Offshore and Polar Engineering Conference. Beijing, China: [s. n. ], 2010, 767-773.
|
| [18] |
BACHANT P, WOSNIK M. Performance and near-wake measurements for a vertical axis turbine at moderate reynolds number[C]// ASME Fluids Engineering Division Summer Meeting. Incline Village, Nevada: ASME, 2013: V01BT12A005. DOI: 10.1115/FEDSM2013-16575.
|
| [19] |
LI Ye, CALISAL S M. Three-dimensional effects and arm effects on modeling a vertical axis tidal current turbine[J].
Renewable Energy, 2010, 35(10): 2325-2334.
DOI: 10.1016/j.renene.2010.03.002 |
 2018, Vol. 50
2018, Vol. 50


